Anti-discrimination learning: a causal modeling-based framework

Abstract

Anti-discrimination learning is an increasingly important task in data mining. Discrimination discovery is the problem of unveiling discriminatory practices by analyzing a dataset of historical decision records, and discrimination prevention aims to remove discrimination by modifying the biased data and/or the predictive algorithms. Discrimination is causal, which means that to prove discrimination one needs to derive a causal relationship rather than an association relationship. Although it is well known that association does not mean causation, the gap between association and causation is not paid enough attention by many researchers. In this paper, we introduce a causal modeling-based framework for anti-discrimination learning. Discrimination is categorized according to two dimensions: direct/indirect and system/group/individual level. Within the causal framework, we introduce a work for discovering and preventing both direct and indirect system-level discrimination in the training data, and a work for extending the non-discrimination result from the training data to prediction. We then introduce two works for group-level direct discrimination and individual-level direct discrimination respectively. The aim of this paper is to deepen the understanding of discrimination in data mining from the causal modeling perspective, and suggest several potential future research directions.

1 Introduction

Discrimination refers to unjustified distinctions in decisions against individuals based on their membership, or perceived membership, in a certain group. In the last fifty years, the problem of detecting the presence of discrimination and preventing discrimination in decision making has been studied from legal, social, economic perspectives [29]. Recently, discrimination discovery and prevention have been an active research area in the data science field, due to increasing worries of discrimination as data analytic technologies could be used to digitally unfairly treat unwanted groups, either as customers, employees, tenants, or recipients of credit. In 2014, US President Obama called for a 90-day review of data collecting and analyzing practices. An important conclusion from the resulting report [6] is that “Big data technologies can cause societal harms beyond damages to privacy, such as discrimination against individuals and groups”. In May 2016, the Executive Office of the President made the recommendation to “support research into mitigating algorithmic discrimination, building systems that support fairness and accountability, and developing strong data ethics frameworks” [22]. Big data can be used for great social good, it can also be used in ways that perpetrate social harms or render outcomes that have inequitable impacts, even when discrimination is not intended.

Laws and regulations have been established to prohibit discrimination in many countries. For example, In the European Union, Council Directive 76/207/EEC implements the principle of equal treatment for men and women as regards access to employment, vocational training and promotion, and working conditions. In the USA, the Civil Rights Act of 1964 prohibits employment discrimination based on race, color, religion, sex, or national origin. Although a remarkable amount of legal regulations have been established, however, current anti-discrimination laws are not yet well equipped to deal with various issues of discrimination in data analysis [3]. In addition, laws in different countries are different and there does not exist a legal consensus. Therefore, we do not restrict our attention to specific anti-discrimination laws, but focus on situations where discrimination can in principle take place. In the following, we first give a set of definitions used in anti-discrimination learning.

• Protected attribute is an attribute that can be used to discriminate people and whose usage is prohibited. Examples of protected attributes include: gender, age, marital status, sexual orientation, race, religion or belief, membership in a national minority, disability or illness.

• Protected group is a group of people who are subject to discrimination analysis. A protected group is specified by a protected attribute or a combination of multiple protected attributes, for example, all females, or all black females, in a dataset.

• Direct discrimination is one type of discrimination, which occurs when individuals receive less favorable treatment explicitly based on the protected attributes. An example of direct discrimination would be rejecting a qualified female in applying for a university just because her gender.

• Indirect discrimination refers to the situation where the treatment is based on apparently neutral non-protected attributes but still results in unjustified distinctions against individuals from the protected group. A well-known example of indirect discrimination is redlining, where the residential Zip Code of an individual is used for making decisions such as granting a loan. Although Zip Code is apparently a neutral attribute, it correlates with race due to the racial composition of residential areas. Thus, the use of Zip Code may indirectly lead to racial discrimination.

• Redlining attribute is a non-protected attribute that can cause indirect discrimination, e.g., the Zip Code in the above example.

• Discrimination-free dataset is a dataset that does not contain discrimination based on certain discrimination measurement.

• Discrimination-free classifier is a classifier that will not make discriminatory predictions. A common assumption is that a classifier learned from a discrimination-free dataset is a discrimination-free classifier. The validity of this assumption is examined in Sect. 5.

In anti-discrimination learning, discrimination discovery is the problem of unveiling discriminatory practices by analyzing a dataset of historical decision records; and discrimination prevention aims to remove discrimination by modifying the biased data and/or the predictive algorithms built on the data. Various business models have been built around the collection and use of individual data to make important decisions like employment, credit, and insurance. It is imperative to develop predictive algorithms such that the decisions made with their assistance are not subject to discrimination as those predictive algorithms have been increasingly used in real-world applications. For important decisions like employment, credit, and insurance, consumers have a right to learn why a decision was made against them and what information was used to make it, and whether they were fairly treated during the decision making process. On the other hand, the decision makers want to ensure that the business models they built are discrimination-free even if the historical data contains bias. Therefore, the historic data and the predictive algorithms must be carefully examined and monitored.

Our society has endeavored to discover and prevent discrimination; however, we face several challenges. First, discrimination claims often require plaintiffs to demonstrate a causal connection between the challenged decision and a protected characteristics. In order to prove discrimination, we need to derive a causal relationship between the protected attribute and the decision rather than an association relationship. However, randomized experiments, which are gold-standard for causal relationship inferring in statistics, are not possible or not cost-effective in the context of discrimination analysis. In most cases, the causal relationship needs to be derived from the observational data rather than controlled experiments. Second, algorithmic decisions, which may not be directly based on protected attribute values, could still incur discrimination against the protected group. In such situations, indirect discriminatory effects present even if we remove the protected attributes from the training data.

The state of the art of discrimination discovery has developed different approaches for discovering discrimination [20, 21, 26, 27, 29, 30, 43]. These approaches classify discrimination into different types such as group discrimination, individual discrimination, direct and indirect discrimination. Based on that, methods for discrimination prevention have been proposed [1, 7, 9, 12,13,14,15, 17,18,19, 21, 35, 37, 43] which either use data preprocessing or algorithm tweaking. However, these works are mainly based on correlation or association-based measures which cannot be used to estimate the causal effect of the protected attributes on the decision. In addition, each of them targets one or two types of discrimination only. In real situations, several types of discrimination may present at the same time in a dataset. Thus, a single framework that is able to deal with all types of discrimination is a necessity.

This paper introduces a causal modeling-based framework for anti-discrimination learning. A causal model [24] is a structural equation-based mathematical object that describes the causal mechanisms of a system. It is evolved from the nonparametric structural equation model, and enriched with ideas from logic and graph theory. With well-established conceptual and algorithmic tools, the causal model provides a general, formal, yet friendly calculus of causal and counterfactual effects. In the introduced framework, causal models are adopted for modeling the mechanisms in data generation and discrimination. Discrimination is categorized based on whether discrimination is across the whole system, occurs in one subgroup, or happens to one individual, and whether discrimination is a direct effect or an indirect effect. In the following we first briefly review the anti-discrimination learning literature and revisit the background of causal modeling. Then we organize the discussion based on the categorization of discrimination, and introduce several works based on the causal modeling framework to deal with various types of discrimination. In Sect. 7, we suggest several potential future research directions.

2 Reviewing association-based anti-discrimination methods

2.1 Discrimination discovery

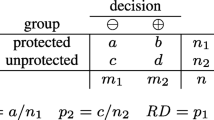
Statistical tools and methods have been widely adopted in measuring and discovering discrimination. A set of classic metrics for statistical analysis consider the proportions of receiving positive decisions for the protected group ($p_{1}$), the non-protected group ($p_{2}$), and the overall sample (p). These metrics include the risk difference ($p_{1}-p_{2}$), risk ratio ($\frac{p_{1}}{p_{2}}$), relative chance ($\frac{1-p_{1}}{1-p_{2}}$), odds ratio ($\frac{p_{1}(1-p_{2})}{p_{2}(1-p_{1})}$), extended difference ($p_{1}-p$), extended ratio ($\frac{p_{1}}{p}$), and extended chance ($\frac{1-p_{1}}{1-p}$) [29]. Another similar conception is called statistical parity, which means that the demographics of the set of individuals receiving positive (or negative) decisions are identical to the demographics of the population as a whole. Equivalent formulations of this conception have been used in many works (e.g., [9, 37]). In [28], the authors attempted to obtain an unbiased discrimination measurement by using the statistical tool—propensity score.

A number of data mining techniques have also been proposed. Pedreschi et al. proposed to extract from the dataset classification rules which represent certain discrimination patterns [26, 27, 30]. If the presence of the protective attribute increases the confidence of a classification rule, it indicates possible discrimination in the data set. Based on that, the authors in [21] further proposed to use the Bayesian network to compute the confidence of the classification rules for detecting discrimination. The authors in [20] exploited the idea of situation testing to discover individual discrimination. For each member of the protected group with a negative decision outcome, testers with similar characteristics are searched from a historical dataset. When there are significantly different decision outcomes between the testers of the protected group and the testers of the non-protected group, the negative decision can be considered as discrimination. Conditional discrimination, i.e., part of discrimination may be explained by other legally grounded attributes, was studied in [43]. The task was to evaluate to which extent the discrimination apparent for a group is explainable on a legal ground.

2.2 Discrimination prevention

Proposed methods for discrimination prevention are either based on data preprocessing or algorithm tweaking. Data preprocessing methods [1, 12, 13, 17, 21, 37, 43] modify the historic data to remove discriminatory effect according to some discrimination measure before learning a predictive model. For example, in [17] several methods for modifying data were proposed. These methods include Massaging, which changes the labels of some individuals in the dataset to remove discrimination, Reweighting, which assigns weights to individuals to balance the dataset, and Sampling, which changes the sample sizes of different subgroups to make the dataset discrimination-free. In [12], the distribution of the non-protected attributes in the dataset is modified such that the protected attribute cannot be estimated from the non-protected attributes. Proposed methods for discrimination prevention using algorithm tweaking require some tweak of predictive models [7, 9, 14, 15, 18, 19, 35]. For example, in [18], the authors developed a strategy for relabeling the leaf nodes of a decision tree to make it discrimination-free. In [35], the authors proposed the use of loglinear modeling to capture and measure discrimination and developed a method for discrimination prevention by modifying significant coefficients from the fitted loglinear model. In [9], the authors addressed the problem of constructing a predictive model that achieves both statistical parity and individual fairness, i.e., similar individuals should be treated similarly. In [15], the authors proposed a framework for optimally adjusting any predictive model so as to remove discrimination. Preventing discrimination when training a classifier consists of balancing two contrasting objective: maximizing accuracy of the extracted predictive model and minimizing the number of predictions that are discriminatory.

2.3 Gap between association and causation

Although it is well known that association does not mean causation, the gap between association and causation is not paid enough attention by many researchers. As a result, a large amount of existing works are based on statistical tools and association only, without knowing whether the obtained results truly capture the causal effect of discrimination. An empirical example that using the risk difference can lead to an opposite judgment of discrimination is the Berkeley’s gender bias in graduate admission [5]. The data showed a higher admission rate for male applicants than female applicants, and the difference was so large that it was unlikely to be due to chance. According to the risk difference, this is a clear evidence of discrimination. However, when examining the individual departments, the data in fact showed a slight bias toward female applications. The explanation was that female applications tended to apply to the more competitive departments with low rates of admission, whereas male applicants tended to apply to the less-competitive departments with high rates of admission. As a result, contrary to what indicates by the risk difference, Berkeley was exonerated from charges of discrimination.

As another example, propensity score is a statistical tool widely used for causal analysis in observational studies to obtain an unbiased measurement of the causal effect. For example, in [28], the authors proposed a discrimination discovery method based on propensity score analysis. However, as thoroughly discussed in the causal inference literature, the use of the propensity score method sometimes may actually increase, not decrease, the bias in the measurement. Assuming a binary treatment X, and an arbitrary set ${\mathbf {S}}$ of measured covariates, the propensity score $L({\mathbf {s}})$ is the conditional probability of $X=1$ given ${\mathbf {S}}={\mathbf {s}}$, i.e., $L({\mathbf {s}}) = P(X=1|{\mathbf {S}}={\mathbf {s}})$. The effectiveness of propensity score rests with whether the set ${\mathbf {S}}$ renders X “strongly ignorable”. However, the condition of “strongly ignorable” is not automatically satisfied, nor likely to be satisfied if one includes in the analysis as many covariates as possible. In addition, it is even impossible to judge whether the condition of “strongly ignorable” holds or not without further knowledge about the causal structure of data. Therefore, the propensity score merely offers an efficient way of estimating a statistical quantity, whose correctness needs to be further verified using causal-related knowledge. To better understand the role of propensity score in causal analysis, we encourage the intrigued reader to refer to discussions in Section 11.3.5 of [24].

The golden rule of causal analysis is: no causal claim can be established by a purely statistical method [24]. Therefore, in principle no statistical tool or association-based anti-discrimination methods can ensure correct result since discrimination is substantially causal, and it is imperative to adopt the causal-aware methods in discovering and preventing discrimination. Although the conceptual framework and algorithmic tools for causal analysis are well established, they are not known to or adopted by many researchers in anti-discrimination learning. Only most recently, several studies have been devoted to analyzing discrimination from the causal perspective. Studies in [38,39,40,41,42] are built on causal modeling and the associated causal inference techniques, and the study in [4] is based on the Suppes–Bayes causal network and random-walk-based methods. The construction of the Suppes–Bayes causal network is impractical with the large number of attribute-value pairs. In addition, it is unclear how the number of random walks is related to meaningful discrimination metrics, e.g., the difference in acceptance rates. This paper presents an overview of the causal modeling-based framework and the related studies. The aim of this paper is to introduce the background of causal modeling that is needed in conducting causal-aware anti-discrimination study, deepen the understanding of existing works’ advantages and challenges, and propose potential future research directions in this field.

3 Causal modeling-based anti-discrimination framework

From Sects. 3.1 to  3.4, we revisit background of causal modeling. In Sect. 3.5, we give a discrimination categorization and provide an overview of the causal modeling-based anti-discrimination learning framework.

Throughout the paper, we denote an attribute by an uppercase alphabet, e.g., X; denote a subset of attributes by a bold uppercase alphabet, e.g., ${\mathbf {X}}$. We denote a domain value of attribute X by a lowercase alphabet, e.g., x; denote a value assignment of attributes ${\mathbf {X}}$ by a bold lowercase alphabet, e.g., ${\mathbf {x}}$.

3.1 Structural equation model

Causal models are generalizations of the structural equations, which are widely used in social science, engineering, biology and economics. The laws of the world are represented as a collection of stable and autonomous mechanisms, each of which is represented as an equation. As a result, a causal model is a mathematical object that describes the causal mechanisms of a system as a set of structural equations. A causal model is formally defined as follows [24].

Definition 1

(Causal Model) A causal model is a triple ${\mathcal {M}} = \langle {\mathbf {U}},{\mathbf {V}},{\mathbf {F}} \rangle$ where

• 1. ${\mathbf {U}}$ is a set of arbitrarily distributed random variables (called exogenous) that are determined by factors outside the model.

• 2. A joint probability distribution $P({\mathbf {u}})$ is defined over the variables in ${\mathbf {U}}$.

• 3. ${\mathbf {V}}$ is a set of variables (called endogenous) $\{X_{1},\ldots , X_{i},\ldots \}$ that are determined by variables in the model, namely variables in ${\mathbf {U}}\cup {\mathbf {V}}$.

• 4. ${\mathbf {F}}$ is a set of deterministic functions $\{f_{1},\ldots ,f_{i},\ldots \}$ where each $f_{i}$ is a mapping from ${\mathbf {U}}\times ({\mathbf {V}}\backslash X_{i})$ to $X_{i}$. Symbolically, the set of equations ${\mathbf {F}}$ can be represented by writing

  $$\begin{aligned} x_{i} = f_{i}(pa_{i},u_{i}) \end{aligned}$$

  where $pa_{i}$ is any realization of the unique minimal set of variables $PA_{i}$ in ${\mathbf {V}}\backslash X_{i}$ that renders $f_{i}$ nontrivial. Here variables in $PA_{i}$ are referred to as the parents of $X_{i}$. Similarly, $U_{i}\subset {\mathbf {U}}$ stands for the unique minimal set of variables in ${\mathbf {U}}$ that renders $f_{i}$ nontrivial.

A causal model describes the physical mechanisms that govern a system. Thus, we can conduct causal analysis on the causal model by manipulating it, as if we are manipulating the physical mechanisms by some physical interventions or hypothetical eventualities. In causal modeling, the manipulation is represented by standard operations called interventions. Each intervention is treated as a local modification to the equations. Specifically, an intervention that forces a set of variables ${\mathbf {X}}\in {\mathbf {V}}$ to take certain constants ${\mathbf {x}}$ is achieved by replacing each variable $X_{i}\in {\mathbf {X}}$ appeared in all equations with a constant $x_{i}$, while keeping the rest of the model unchanged. This operation is mathematically formalized as $do({\mathbf {X}}={\mathbf {x}})$ or simply $do({\mathbf {x}})$. Then, for any two disjoint sets of nodes ${\mathbf {X}},{\mathbf {Y}}$, the effect of intervention $do({\mathbf {X}}={\mathbf {x}})$ on ${\mathbf {Y}}$, represented by the post-intervention distribution of ${\mathbf {Y}}$, is denoted by $P({\mathbf {Y}}=\mathbf {y}|do({\mathbf {X}}={\mathbf {x}}))$ or simply $P(\mathbf {y}|do({\mathbf {x}}))$. From this distribution, we can assess the causal effect of ${\mathbf {X}}$ on ${\mathbf {Y}}$ by comparing aspects of this distribution under different interventions of ${\mathbf {X}}$, e.g., $do({\mathbf {x}}_{1})$ and $do({\mathbf {x}}_{0})$. A common measure of the causal effect is the average difference

$$\begin{aligned} {\mathbb {E}}({\mathbf {Y}}|do({\mathbf {x}}_{1}))-{\mathbb {E}}({\mathbf {Y}}|do({\mathbf {x}}_{0})), \end{aligned}$$

(1)

where ${\mathbb {E}}(\cdot )$ denotes the expectation.

3.2 Estimating causal effect

Although the post-intervention distribution $P({\mathbf {y}}|do({\mathbf {x}}))$ is hypothetical, under certain assumptions it can be estimated from the observational data governed by the pre-intervention distribution. A common assumption is called Markovian. A causal model is said to be Markovian if: (1) each variable in ${\mathbf {V}}$ is not directly or indirectly determined by itself; and (2) all variables in ${\mathbf {U}}$ are mutually independent. Under the assumption of Markovian, the joint probability distribution over all variables in ${\mathbf {V}}$, i.e., $P({\mathbf {v}})$, can be formulated as an expression of the conditional probabilities of each variable $X_{i}\in {\mathbf {V}}$ given all its parents, i.e., $P(x_{i}|pa_{i})$, known as the factorization formula

$$\begin{aligned} P({\mathbf {v}}) = \prod _{X_{i}\in {\mathbf {V}}}P(x_{i}|pa_{i}). \end{aligned}$$

For example, given a causal model shown in Fig. 1a, the joint probability of x, y, z is given by

$$\begin{aligned} P(x,y,z) = P(x)P(y|x,z)P(z|x). \end{aligned}$$

More importantly, the joint post-intervention distribution, i.e., $P({\mathbf {y}}|do({\mathbf {x}}))$ for any set of variables ${\mathbf {X}}\subseteq {\mathbf {V}}$ and its complement ${\mathbf {Y}} = {\mathbf {V}}\backslash {\mathbf {X}}$, can also be formulated as an expression of the pre-intervention conditional probabilities $P(x_{i}|pa_{i})$, known as the truncated factorization

$$\begin{aligned} P({\mathbf {y}}|do({\mathbf {x}})) = \prod _{X_{i}\in {\mathbf {Y}}}P(x_{i}|pa_{i})\delta _{{\mathbf {X}}={\mathbf {x}}}, \end{aligned}$$

where $\delta _{{\mathbf {X}}={\mathbf {x}}}$ means assigning attributes in ${\mathbf {X}}$ involved in the term ahead with the corresponding values in ${\mathbf {x}}$. For example, the post-intervention distribution $P(x,y|do(z_{0}))$ associated with the model shown in Fig. 1a is given by

$$\begin{aligned} P(x,y|do(z_{0})) = P(x)P(y|x,z_{0}). \end{aligned}$$

Note that this distribution is different from the conditional distribution $P(x,y|z_{0})$, which is given by

$$\begin{aligned} P(x,y|z_{0}) = P(x|z_{0})P(y|x,z_{0}). \end{aligned}$$

Fig. 1

An example of a causal model; b causal graph

3.3 Causal graph

Each causal model ${\mathcal {M}}$ is associated with a direct graph ${\mathcal {G}}$, called the causal graph associated with ${\mathcal {M}}$. Each node in ${\mathcal {G}}$ corresponds to a variable $X_{i}$ in ${\mathbf {V}}$. Each direct edge, denoted by an arrow $\rightarrow$, points from each member of $PA_{i}$ toward $X_{i}$ representing the direct causal relationship. Each node is associated with a conditional probability table (CPT), i.e., $P(x_{i}|pa_{i})$. For example, Fig. 1b shows the causal graph of the causal model in Fig. 1a. Standard terminology is used in the causal graph. The parents of node $X_{i}$ are the nodes in ${\mathbf {V}}$ with directed edges oriented into $X_{i}$, i.e., the nodes from $PA_{i}$. Similarly, the children of $X_{i}$ are the nodes ${\mathbf {V}}$ with directed edges pointing from $X_{i}$ to them. A path between nodes X and Y is a sequence of edges connecting a sequence of nodes which are all distinct from one another and the first node starts with X and the last node ends with Y. A direct path from X to Y is a path where all edges are pointing in the same direction from X to Y. If there exists a direct path from X to Y, then X is said to be an ancestor of Y and Y is said to be a descendent of X.

It is important to note that, a causal graph partially specifies the causal model. The connection between a causal model and its associated causal graph is as follows: the parents of each variable in the causal model are specified by the parents in the graph, and the distribution of ${\mathbf {U}}$ is partially specified by the CPTs $P(x_{i}|pa_{i})$ due to the relationship

$$\begin{aligned} P(x_{i}|pa_{i}) = \sum _{\{u_{i}:f_{i}(pa_{i},u_{i})=x_{i}\}}P(u_{i}), \end{aligned}$$

but the exact forms of functions $f_{i}$ and the joint distribution $P({\mathbf {u}})$ are unknown.

When Markovian is assumed, the associated casual graph is a direct acyclic graph (DAG). As shown above, under the Markovian assumption, each post-intervention distribution can be calculated using the truncated factorization given the conditional probability $P(x_{i}|pa_{i})$ of each variable. Then, all post-intervention distributions are identifiable given the causal graph. Many algorithms have been proposed to learn the causal graph from data without completely specifying the causal model. For a detailed survey on the causal graph learning algorithms please refer to [10].

An equivalent graphical expression of the Markovian assumption is called the local Markov condition. A causal graph satisfies the local Markov condition if: (1) the graph is acyclic; and (2) each node in ${\mathbf {V}}$ is independent of all its non-descendants conditional on its parents. The Markov condition is further equivalent to a more useful graphical relation called the d-separation, using which we can read off from the graph all the conditional independence relationships encoded in the causal model. Specifically, d-separation is a relation between three disjoint sets of nodes ${\mathbf {X}},{\mathbf {Y}},{\mathbf {Z}}$. Nodes ${\mathbf {X}}$ and ${\mathbf {Y}}$ are said to be d-separated by ${\mathbf {Z}}$ in causal graph ${\mathcal {G}}$, denoted by , if the following requirement is met:

Definition 2

(d-Separation) Nodes ${\mathbf {X}}$ and ${\mathbf {Y}}$ are d-separated by ${\mathbf {Z}}$ if and only if ${\mathbf {Z}}$ blocks every path from a node in ${\mathbf {X}}$ to a node in ${\mathbf {Y}}$. A path p is said to be blocked by a set of nodes ${\mathbf {Z}}$ if and only if

• 1. p contains a chain $i\rightarrow m\rightarrow j$ or a fork $i\leftarrow m \rightarrow j$ such that the middle node m is in ${\mathbf {Z}}$, or

• 2. p contains an collider $i\rightarrow m\leftarrow j$ such that the middle node m is not in ${\mathbf {Z}}$ and no descendant of m is in ${\mathbf {Z}}$.

Variables ${\mathbf {X}}$ and ${\mathbf {Y}}$ are said to be conditionally independent given a set of variables ${\mathbf {Z}}$, denoted as , if $P({\mathbf {x}}|{\mathbf {y}},{\mathbf {z}})=P(x|{\mathbf {z}})$ holds for all values $x,y,{\mathbf {z}}$. Under the Markov condition, if we have , then we must have . Therefore, the graphical meaning of d-separation can be interpreted as to block the paths between ${\mathbf {X}}$ and ${\mathbf {Y}}$ such that no influence can be transmitted from any node in ${\mathbf {X}}$ to any node in ${\mathbf {Y}}$.

3.4 Path-specific effect

Let us come back to the causal effect estimation. When we perform an intervention on ${\mathbf {X}}$, all the descendents of ${\mathbf {X}}$ will be influenced by the intervention. For example, in the causal model in Fig. 1a, if we perform an intervention $do(x_{0})$, then the value of Z will become $z_{x_{0}} = f_{Z}(x_{0},u_{Z})$, and the value of Y will become $y_{x_{0}} = f_{Y}(x_{0},z_{x_{0}},u_{Y})$. From the graphical perspective, the influence of an intervention $do({\mathbf {x}})$ is transmitted along the direct paths starting from ${\mathbf {X}}$. Therefore the direct paths in a causal graph are also called the causal paths. For example in Fig. 1b, the influence of intervention $do(x_{0})$ on Y is transmitted along two causal paths, one is $X\rightarrow Y$, and the other is $X\rightarrow Z\rightarrow Y$.

In Eq. (1), we allow the intervention to be transmitted along all the causal paths. However, in some situations, we may be interested in the causal effect where the influence of the intervention is transmitted only along certain paths. Later we will see that this is important when studying the causal effect of direct and indirect discrimination. For example in Fig. 1b, if we allow the influence of $do(x_{0})$ to be transmitted only along path $X\rightarrow Y$, then the value of Z will remain the same had the intervention not taken place, i.e., $z_{x_{0}} = z = f_{Z}(x,u_{Z})$, and the value of Y will become $y_{x_{0}} = f_{Y}(x_{0},z,u_{Y})$. On the other hand, if we allow the influence of $do(x_{0})$ to be transmitted only along path $X\rightarrow Z\rightarrow Y$, then the value of Z will become $z_{x_{0}} = f_{Z}(x_{0},u_{Z})$, but the value of Y will become $y_{x_{0}} = f_{Y}(x,z_{x_{0}},u_{Y})$, as if Y does not know that the intervention happens. The causal effect that is transmitted along a set of paths is called the path-specific effect [2], which is specified to $\pi$ -specific effect if the set of paths is given by set $\pi$. Correspondingly, the causal effect measured in Eq. (1) is called the total effect.

Fig. 2

The kite pattern

Different from the total effect, even under the Markovian assumption or Markov condition, it is not guaranteed that the path-specific effect can be computed from the data. A graphical condition for judging whether the path-specific effect can be computed is called the recanting witness criterion [2]. In general, the recanting witness criterion describes a specific sub-network pattern, and is satisfied if the set of paths match this pattern. The pattern can be illustrated graphically as the ‘kite pattern’ in Fig. 2. Suppose that X, Y are two nodes and we want to analyze the $\pi$-specific effect of X on Y given a set of paths $\pi$. Let Z be a node such that: (1) there exists a path in $\pi$ from X to Z; (2) there exists a path in $\pi$ from Z to Y; and (3) there exists another path not in $\pi$ from Z to Y. Then, the recanting witness criterion for the $\pi$-specific effect is satisfied with Z as a witness.

The path-specific effect cannot be computed from data in theory if the recanting witness criterion is satisfied. This situation is referred to as the unidentifiable situation [2]. Otherwise, the path-specific effect can be computed from data following a set of steps. The explicit statement of these steps is omitted here. We recommend the reader to refer to the original papers [2, 31]. As an example, in Fig. 1b, both paths $X\rightarrow Y$ and $X\rightarrow Z\rightarrow Y$ do not satisfy the recanting witness criterion, and hence the path-specific effects can be calculated. The post-intervention distribution of Y under intervention $do(x_{1})$ (assuming the value of X prior to the intervention is $x_{0}$) when the influence is transmitted only along $X\rightarrow Y$ is given by

$$\begin{aligned} \sum _{z}P(z|x_{0})P(y|x_{1},z), \end{aligned}$$

and the distribution when the influence is transmitted only along $X\rightarrow Z\rightarrow Y$ is given by

$$\begin{aligned} \sum _{z}P(z|x_{1})P(y|x_{0},z). \end{aligned}$$

For comparison, the post-intervention distribution of Y when the influence is transmitted along both paths, i.e., $P(y|do(x_{1}))$, is given by

$$\begin{aligned} \sum _{z}P(z|x_{1})P(y|x_{1},z). \end{aligned}$$

3.5 Discrimination categorization and framework overview

Discrimination has been studied from different perspectives in the literature. Several types of discrimination have been proposed, which can be categorized based on two dimensions. Firstly, from the perspective of in what way discrimination occurs, discrimination is legally divided into direct discrimination and indirect discrimination. Secondly, from the perspective of different level of granularity in studying, discrimination can be divided into system level, group level, and individual level. System-level discrimination deals with the average discrimination across the whole system, e.g., all applicants to a university. Group-level discrimination deals with discrimination that occurs in one particular subgroup, e.g., the applicants applying for a particular major, or the applicants with a particular score. Individual-level discrimination deals with the discrimination that happens to one particular individual, e.g., one particular applicant. We can describe a type of discrimination by combining the two dimensions mentioned above. For example, there can be a direct discrimination at the system level, thus forming a system-level direct discrimination.

As reviewed in Sect. 2, existing anti-discrimination methods are mainly based on correlation or association. In discrimination discovery, it is critical to derive causal relationship, and not merely association relationship. We need to determine what factors truly cause discrimination and not just which factors might predict discrimination. Besides, we need a unifying framework and a systematic approach for determining all types of discrimination rather than using different types of techniques for some specific types of discrimination. This motivated the causal modeling-based anti-discrimination framework.

Consider a decision making system where discrimination may happen. Each individual in the system is specified by a set of attributes ${\mathbf {V}}$, which contains the protected attributes (e.g., gender), the label/decision (e.g., admission), and a set of non-protected attributes ${\mathbf {X}}=\{X_{1},\ldots ,X_{m}\}$ (e.g., major). For ease of presentation, we assume that there is only one protected attribute/label with binary values. We denote the protected attribute by C associated with two domain values $c^{-}$ (e.g., female) and $c^{+}$ (e.g., male); denote the label by L associated with two domain values $l^{-}$ (i.e., negative label) and $l^{+}$ (i.e., positive label). For computational convenience, we also define that $l^{-}=0$ and $l^{+}=1$. The proposed framework can be extended to handling multiple domain values of C/L and multiple $C\hbox {s}/L\hbox {s}$. We assume that there exists a fixed causal model ${\mathcal {M}}$ representing the mechanisms that determine the values of all the attributes in the system. Two reasonable assumptions can be further made under the context: (1) the protected attribute C has no parent in ${\mathbf {V}}$; and (2) the label L has no child in ${\mathbf {V}}$. Then, the causal model can be written as follows.

$$\begin{aligned} \text {Model }{\mathcal {M}} \quad \quad \begin{array}{l} c = f_{C}(u_{C}) \\ x_{i} = f_{i}(pa_{i},u_{i}) \quad i=1,\ldots ,m \\ l = f_{L}(pa_{L},u_{L}) \end{array} \end{aligned}$$

We partially specify the causal model by a causal graph that correctly represents the causal structure of the system. In practical, the causal graph can be learned from the data using the structure learning algorithms [8, 16, 23, 33]. Throughout this paper, we make the Markovian assumption to facilitate the causal inference in the model. In Sect. 7.2, we discuss how this assumption can be relaxed.

In general, discrimination is a causal effect of C on L. Using the causal model, we study different types of discrimination by considering the causal effect transmitted along different paths. In the following, we first show how to discover and remove the system-level discrimination, including both direct and indirect, from the training data. Then, we show how the non-discrimination result is extended from training data to prediction. After that, we show how the problem becomes different when discrimination is confined to a particular subgroup or an individual as well as the strategies to tackle them.

4 System-level discrimination discovery and removal

System-level discrimination refers to the average effect of discrimination in a whole system. This section introduces the work in [42] that studies the discovery and removal of both direct and indirect discrimination at the system level. We start from the formal modeling of direct and indirect discrimination using the causal model, then discuss the quantitative discrimination criterion, and finally present the algorithm for removing discrimination from a given dataset.

4.1 Modeling of direct and indirect discrimination

To define discrimination in a system, we always ask this question: if the protected attribute C changed (e.g., changing from protected group $c^{-}$ to non-protected group $c^{+}$), how would the label change on average? A straightforward strategy is to measure the average causal effect of C on L using Eq. (1), i.e., ${\mathbb {E}}(L|do(c^{+}))-{\mathbb {E}}(L|do(c^{-}))$, which represents the expected change of L when C changes from $c^{-}$ to $c^{+}$. Since we define $l^{+}=1$ and $l^{-}=0$, this equation equals to $P(l^{+}|do(c^{+}))-P(l^{+}|do(c^{-}))$, which can be proven to equal to $P(l^{+}|c^{+})-P(l^{+}|c^{-})$ by using the truncated factorization. As can be seen, we obtain a discrimination measurement that is the same as the risk difference which is widely used as the discrimination metric in existing association-based discrimination discovery literature.

Fig. 3

The toy model

The problem with the above measurement is that it measures all causal effect of C on L, i.e., the total effect. This means that the total effect takes the causal effect transmitted along all the causal paths from C to L as discriminatory. However, it is usually not the case when measuring discrimination. Consider a toy model of a loan application system shown in Fig. 3. We treat Race as the protected attribute, Loan as the label. Assume that the use of Income in determining the loan can be objectively justified as it is reasonable to deny a loan if the applicant has low income. In this case, the causal effect transmitted along path Race $\rightarrow$ Income $\rightarrow$ Loan is explainable, which means that part of the difference in loan issuance across different race groups can be explained by the fact that some race groups in the dataset tend to be under-paid. Thus, using the total effect for measuring discrimination may produce incorrect result because ignoring that part of the causal effect is in fact explainable. In addition, the total effect does not distinguish direct and indirect discrimination.

To exactly measure the causal effect of direct and indirect discrimination, different constraints need to be placed on the causal model when we derive the post-intervention distribution. For direct discrimination, we want to measure the causal effect that is only due to the change of C and not due to the change of other attributes. Thus, when the intervention is performed on C, we can make L respond to the intervention and every other attribute be fixed to what it was prior to the intervention. To be specific, to examine the direct discrimination caused by the advantage of the non-protected group over the protected group, we first perform an intervention $do(C=c^{-})$ with no constraint, i.e., for each child of C, the value of C in its function is fixed to $c^{-}$. Under this setting, we obtain the expected label of all individuals who are assumed to be from the protected group. Then, we perform another intervention $do(C=c^{+})$. In this process, only L responds to the intervention. That is to say, if C is a parent of L, then its value is changed to $c^{+}$ in function $f_{L}$. However, the values of C in the functions of all other children still remain to be $c^{-}$. Under this setting, we obtain the expected label of all individuals assuming that each of them is from the non-protected group but everything else remains the same. As a result, the difference in the two labels represents the average advantage that can be obtained directly from changing the protected group to the non-protected group. Hence, it represents the average effect of the direct discrimination.

Similarly, for indirect discrimination, we want to measure the causal effect that is not directly due to the change of C (e.g., assume that C is invisible to the decision maker) but due to the change of some non-protected but unjustified attributes, i.e., the redlining attributes. Thus, when the intervention is performed on C, we can make L not respond to the intervention, but respond to the change of the redlining attributes which instead directly or indirectly respond to the intervention. Specifically, we first similarly perform the intervention $do(C=c^{-})$ with no constraint and obtain the expected label. Then we perform the intervention $do(C=c^{+})$, during which the value of C in function $f_{L}$ remains to be $c^{-}$. However, for the children variables of C that can transmit the influence of the intervention to any redlining attribute, i.e., they are the ancestors of any redlining attribute, the values of C in their functions are changed to $c^{+}$. Under this setting we obtain the expected label of all individuals assuming that each of them is still from the protected group but the values of the redlining attributes are changed as if they were from the non-protected group. As a result, the difference in the two labels represents the average advantage that can be obtained indirectly from changing the protected group to the non-protected group and hence represents the average effect of the indirect discrimination.

If we look at the causal graph, we can see that for direct discrimination we are actually measuring the causal effect that is transmitted along the direct path from C to L, and for indirect discrimination we are in fact measuring the causal effect that is transmitted along the causal paths from C to L that contain the redlining attributes. For example, in the toy model shown in Fig. 3, direct discrimination means the causal effect transmitted along path Race $\rightarrow$ Loan, and indirect discrimination means the causal effect transmitted along path Race $\rightarrow$ ZipCode $\rightarrow$ Loan. Therefore, the average effect of direct/indirect discrimination can be quantitatively measured by employing the path-specific effect technique.

An important result we obtain is that, the risk difference may not correctly measure direct and indirect discrimination. As been shown, the risk difference is equivalent to the total effect. Thus, the risk difference correctly measures direct discrimination if there is only one causal path from C to L—the direct path, and correctly measures indirect discrimination if every causal path from C to L passes through redlining attributes. In other cases, it cannot correctly measure either direct discrimination or indirect discrimination.

4.2 Quantitative discrimination criterion

To apply the path-specific effect technique, we define two sets of paths. One is $\pi _{d}$ which contains the direct path $C\rightarrow L$. The direct discrimination can be measured by the $\pi _{d}$-specific effect. The other is $\pi _{i}$ which contains all causal paths from C to L that pass through at least one redlining attribute. The indirect discrimination can be measured by the $\pi _{i}$-specific effect.

As stated in Sect. 3.4, a path-specific effect cannot always be computed and the recanting witness criterion should be used to examine the path set. It is proved in [42] that the $\pi _{d}$-specific effect can always be computed from data as the recanting witness criterion for the $\pi _{d}$-specific effect is guaranteed to be not satisfied. However, the recanting witness criterion for the $\pi _{i}$-specific effect might be satisfied, in which case the $\pi _{i}$-specific effect is unidentifiable.

As an example, in Fig. 3 both the $\pi _{d}$ and $\pi _{i}$-specific effects are identifiable. Following the general formulation derived in [42], the average effect of direct discrimination is given by

$$\begin{aligned} \sum _{Z,I}\left( P(l^{+}|c^{+},z,i)-P(l^{+}|c^{-},z,i) \right) P(z|c^{-})P(i|c^{-}), \end{aligned}$$

and the average effect of indirect discrimination is given by

$$\begin{aligned} \sum _{Z,I}P(l^{+}|c^{-},z,i) \left( P(z|c^{+})-P(z|c^{-}) \right) P(i|c^{-}), \end{aligned}$$

where C, Z, I, L are four variables (please read their meanings off Fig. 3).

An observation got from the formulation of path-specific effect is that, if we divide all the causal paths from C to L into several non-intersect subsets of paths, then the sum of the path-specific effect measured on each subset of paths does not necessarily equal to the total causal effect. Therefore, the average effect of indirect discrimination cannot be obtained by subtracting the average effect of indirect discrimination from the total effect.

Based on the measurement of the discriminatory effect, the quantitative discrimination criterion is readily to be defined. As shown in [42], direct discrimination is claimed to be exist if the average effect of direct discrimination is larger than a user-defined threshold $\tau$. The value of $\tau$ should depend on the law. For instance, we can set $\tau =0.05$ for sex discrimination as the 1975 British legislation for sex discrimination requires no more than a $5\%$ difference. Similar criterion is defined for indirect discrimination.

4.3 Discrimination removal algorithm

After direct or indirect discrimination is discovered, the next step is to remove these discriminatory effects from the dataset. An intuitive method would be simply deleting the protected attribute from the dataset. It is not difficult to see that, although this method can eliminate direct discrimination, it cannot remove indirect discrimination. What is more, indirect discrimination may not be removed even if we delete all the redlining attributes.

In [42], the authors proposed a causal graph-based discrimination removal algorithm to remove both direct and indirect discrimination without deleting any attribute. The general idea is to modify causal graph ${\mathcal {G}}$ so that the model associated with the modified network does not contain discrimination, and then generate a new dataset using the modified causal graph. To be specific, the algorithm modifies the CPT of L, i.e., P(l|Pa(L)), to obtain a new CPT $P'(l|Pa(L))$, so that the average effect of direct/indirect discrimination measured is below the threshold $\tau$. To maximize the utility of the new dataset, the algorithm minimizes the Euclidean distance between the joint distributions of the original causal graph and the modified causal graph. The joint distributions are computed using the factorization formula. As a result, it forms a quadratic programming problem with $P'(l|Pa(L))$ as variables, and the optimal solution is obtained by solving the problem. Finally, the new dataset is generated based on the joint distribution of the modified network.

As stated, sometimes the average effect of indirect discrimination is unidentifiable due to that the recanting witness criterion is satisfied. However, the structure of the recanting witness criterion itself in these situations implies that there may exist potential indirect discrimination. This is because there exist causal paths from C to L passing through redlining attributes, meaning that the effect of indirect discrimination can be transmitted through these paths. From a practical perspective, it is meaningful to remove discrimination while preserving reasonable data utility even though the discriminatory effect cannot be accurately measured. To deal with this situation, the authors in [42] proposed a causal graph preprocessing method, which cuts off several paths in $\pi _{i}$ to remove the “kite pattern” so that the recanting witness criterion is no longer satisfied.

5 Ensuring non-discrimination in prediction

The work introduced in Sect. 4 targets detecting and removing discrimination from the training data. An implicit assumption is that, if the classifier is learned from a non-discriminatory training dataset, then it is likely that the classifier will also be discrimination-free, i.e., the future predictions will not incur discrimination. Although this assumption is plausible, there is no theoretical guarantee to show “how much likely” and “how” discrimination-free the predictions would be given a training data and a classifier. The lack of the theoretical guarantee places uncertainty on the performance of the developed discrimination removal algorithms.

To fill this gap, the work in [41] attempted to mathematically bound the probability that the discrimination in predictions is within a given interval in terms of the given training data and classifier. The challenge lies in modeling discrimination in predictions over a fixed but unknown population, while the classifier is learned from a sample dataset drawn from the population. Although this work is somewhat preliminary as the discriminatory effect is measured by the risk difference metric which we have shown can only measure the total effect, the conclusion obtained is important and enlightening: even when discrimination in the training data is completely removed, the prediction can still contain non-negligible amount of discrimination, caused by the bias in the classifier. This section briefly introduces the work in [41] and proposes some possible extensions on this issue.

Let us maintain the assumption that there exists a fixed causal model ${\mathcal {M}}$ representing the data generation mechanism of the system or population. The discrimination in ${\mathcal {M}}$ is measured by the risk difference $P(l^{+}|c^{+})-P(l^{+}|c^{-})$, which is denoted by ${\mathrm {DE}}_{{\mathcal {M}}}$. In practice, ${\mathcal {M}}$ is unknown and we can only observe a dataset ${\mathcal {D}}$ generated by ${\mathcal {M}}$. Straightforwardly, discrimination in ${\mathcal {D}}$ can be defined as the maximum likelihood estimation of ${\mathrm {DE}}_{{\mathcal {M}}}$, denoted by ${\mathrm {DE}}_{{\mathcal {D}}}$. Then, a bound for the difference between ${\mathrm {DE}}_{{\mathcal {M}}}$ and ${\mathrm {DE}}_{{\mathcal {D}}}$ is derived based on the Hoeffding’s inequality, which shows that with high probability this difference will be small if the sample size of ${\mathcal {D}}$ is large enough.

A classifier h is a function mapping from $C\times {\mathbf {X}}$ to L, i.e., $h:C\times {\mathbf {X}}\rightarrow L$. A classifier learning algorithm analyzes the training dataset ${\mathcal {D}}$ to find a function that minimizes the difference between the predicted labels and the true labels. Once training completes, the classifier is deployed to make predictions on the unlabeled new data, i.e., the classifier computes the predicted label for any unlabeled individual. It can be assumed that the unlabeled data (C and ${\mathbf {X}}$) is drawn from the same population as the training data, i.e., it is also generated by ${\mathcal {M}}$, except the labels unknown. Therefore, in the predictions, the values of all the attributes other than the label are still determined by the mechanisms in ${\mathcal {M}}$, while the classifier now acts as a new mechanism for determining the value of the label. Consider the mechanisms from ${\mathcal {M}}$ with function $f_{L}$ replaced with classifier h as a new causal model, denoted by ${\mathcal {M}}_{h}$. It is written as

$$\begin{aligned} \text {Model }{\mathcal {M}}_{h} \quad \quad \begin{array}{l} c = f_{C}(u_{C}) \\ x_{i} = f_{i}(pa_{i},u_{i}) \quad i=1,\ldots ,m \\ l = h(c,{\mathbf {x}}) \end{array} \end{aligned}$$

In this way, discrimination in prediction is given by discrimination in ${\mathcal {M}}_{h}$, denoted by ${\mathrm {DE}}_{{\mathcal {M}}_{h}}$. Similarly, ${\mathrm {DE}}_{{\mathcal {M}}_{h}}$ can be measured by the risk difference, where the labels are determined by the classifier. Note that ${\mathcal {M}}_{h}$ is also unknown. It can be estimated by applying the classifier on the training data ${\mathcal {D}}$. A new dataset ${\mathcal {D}}_{h}$ is obtained by replacing the original labels with the predicted labels. Thus, discrimination in ${\mathcal {D}}_{h}$ is similarly defined as the maximum likelihood estimation of ${\mathrm {DE}}_{{\mathcal {M}}_{h}}$, denoted by ${\mathrm {DE}}_{{\mathcal {D}}_{h}}$. A bound for the difference between ${\mathrm {DE}}_{{\mathcal {M}}_{h}}$ and ${\mathrm {DE}}_{{\mathcal {D}}_{h}}$ is similarly derived. In addition, the difference between ${\mathrm {DE}}_{{\mathcal {D}}}$ and ${\mathrm {DE}}_{{\mathcal {D}}_{h}}$ is given by a measurement depending on the classification error rates of h, which is referred to as the error bias denoted by $\varepsilon _{h,{\mathcal {D}}}$.

The goal is to derive a relationship between ${\mathrm {DE}}_{{\mathcal {D}}}$, the discrimination measured in the training data, and ${\mathrm {DE}}_{{\mathcal {M}}_{h}}$, the discrimination in prediction. The result from [41] is that, if $|{\mathrm {DE}}_{{\mathcal {D}}}+\varepsilon _{h,{\mathcal {D}}}|$ is bounded within a threshold, then with high probability $|{\mathrm {DE}}_{{\mathcal {M}}_{h}}|$ will also be bounded within a close threshold if the sample size of ${\mathcal {D}}$ is large enough. This result indicates that, to ensure non-discrimination in prediction, in addition to having a non-discriminatory training dataset, the disturbance from the classification error must also be considered. A following result is about achieving non-discrimination in prediction if $|{\mathrm {DE}}_{{\mathcal {D}}}+\varepsilon _{h,{\mathcal {D}}}|$ is not bounded. Let ${\mathcal {D}}^{*}$ be a new dataset derived from ${\mathcal {D}}$ when only $f_{L}$ is modified, and $h^{*}$ is a new classifier $h^{*}$ trained on ${\mathcal {D}}^{*}$. The result from [41] shows that, if we can make $|{\mathrm {DE}}_{{\mathcal {D}}^{*}}+\varepsilon _{h^{*},{\mathcal {D}}^{*}}|$ be bounded by the threshold, then with high probability $|{\mathrm {DE}}_{{\mathcal {M}}_{h^{*}}}|$, i.e., discrimination in prediction of the new classifier $h^{*}$, will also be bounded within a close threshold.

The above results provide a guideline of how to modify the training data to the researchers when designing anti-discrimination algorithms. The guideline can be summarized as a two-phase framework. Denote the threshold by $\tau$. In the first phase, if $|{\mathrm {DE}}_{{\mathcal {D}}}|>\tau$, then modify ${\mathcal {D}}$ to reduce the discrimination it contains. The modification process should only change $f_{L}$. For example, we can modify the CPT of L, or we can directly modify the labels in ${\mathcal {D}}$. However, we can neither modify other CPTs, nor directly modify the values of other attributes. The result of the first phase is a modified dataset ${\mathcal {D}}^{*}$ with $|{\mathrm {DE}}_{{\mathcal {D}}^{*}}|\le \tau$. In the second phase, a new classifier $h^{*}$ is learned from ${\mathcal {D}}^{*}$ with its error bias $\varepsilon _{h^{*},{\mathcal {D}}^{*}}$ calculated. If we still have $|{\mathrm {DE}}_{{\mathcal {D}}^{*}}+\varepsilon _{h^{*},{\mathcal {D}}^{*}}|>\tau$, then modify $h^{*}$ to reduce its error bias. Finally, we meet the requirement that $|{\mathrm {DE}}_{{\mathcal {D}}^{*}}+\varepsilon _{h^{*},{\mathcal {D}}^{*}}|\le \tau$.

As a preliminary work, [41] used the risk difference metric as the measurement of discrimination. As discussed in Sect. 4.2, the risk difference metric correctly measures direct discrimination only when there is a single causal path from C to L, and correctly measures indirect discrimination only when every causal path from C to L passes through redlining attributes. Therefore, future investigations are needed on whether the theoretical results in [41] can be extended to more elaborate discrimination measurements such as those introduced in Sect. 4. On the other hand, we can see that both phases in the framework reduce discrimination at the cost of utility loss. Thus, how to balance the trade-off between non-discrimination and utility loss is another challenge.

6 Group and individual-level discrimination

In Sect. 4, the developed discrimination discovery and removal methods rely on the system-level post-intervention distribution $P(l^{+}|do(c))$, which can be certainly computed from the data with the Markovian assumption. However, this assumption may not be true when we confine the scope of discrimination to a particular subgroup or even an individual, which makes these methods not applicable to the group or individual-level discrimination. This is because unlike the system-level post-intervention distribution, the post-intervention distribution on a particular subgroup becomes a counterfactual statement that may not be identifiable from the data without knowing the exact functional relationships in the causal model. In this section, we introduce two recent works for studying group and individual-level discrimination within the causal modeling framework but adopting different strategies than path-specific effect. Both works deal with direct discrimination only.

6.1 Group-level direct discrimination

The work [38] considers group-level direct discrimination as the discrimination measured on subgroups produced by partitioning the dataset. Here a partition is determined by a subset of non-protected attributes and a subgroup is specified by a value assignment to the subset. This work proposed to use the classic metric, risk difference, as the measurement of group-level direct discrimination. The idea is as follows. It is known that the risk difference may not correctly measure direct discrimination due to the spurious influences caused by the confounders and the part of differences that are explainable by justified attributes. However, it correctly measures direct discrimination if there is a single path from C to L. Therefore, the risk difference is meaningful for a subgroup if all effects other than the direct causal effect are shielded or blocked within the subgroup. Such subgroup is referred to as the meaningful subgroup. The partition that determines the meaningful subgroup is referred to as the meaningful partition.

Table 1 Summary statistics of the example

Consider a toy model for a university admission system that contains four attributes: gender, major, test_ score, and admission, where gender is the protected attribute, and admission is the label. The summary statistics of the admission rate is shown in Table 1, and the causal graph is shown in Fig. 4. Intuitively, test_score should not be used for partitioning the data as it is uncorrelated with the protected attribute. As can be seen, when conditioning on test_score, there exist significant differences (from either $35{-}25\%$ for L or from $65{-}55\%$ for H) between the admission rates of females and males within the two subgroups. However, this result is misleading since carefully examining the admission rates of females and males of each major and each score level shows no bias against any of the groups. Therefore, test_score is not a meaningful partition. On the other hand, the combination {major,test_score} is a meaningful partition based on which we can obtain the correct result. The goal of this work is to identify all meaningful partitions, measure discrimination for each meaningful partition, and develop algorithms to ensure non-discrimination for all meaningful partitions.

We start from introducing the criterion for identifying meaningful partitions. Given a partition ${\mathbf {B}}$ and a subgroup ${\mathbf {b}}$ produced by ${\mathbf {B}}$, let $\varDelta P|_{{\mathbf {b}}}$ denote the risk difference measured on subgroup ${\mathbf {b}}$. We already know that all influences from C to L are transmitted along paths connecting C and L. Assume that the only desired influence is the effect transmitted along path $C\rightarrow L$. Thus, the partition ${\mathbf {B}}$ is meaningful if all the influences from C to L transmitted through all paths except $C\rightarrow L$ are blocked conditional on ${\mathbf {b}}$. The condition of identifying whether these influences are blocked is derived based on the d-separation criterion. As introduced in Sect. 3.3, if C and L are d-separated, no influence can be transmitted from C to L. Therefore, we first delete edge $C\rightarrow L$ from the causal graph, and then find a set of nodes ${\mathbf {B}}$ that d-separates C and L in the modified causal graph. As a result, all influences transmitted through paths other than $C\rightarrow L$ are blocked within each subgroup produced by partition ${\mathbf {B}}$. Under this situation, if $\varDelta P|_{{\mathbf {b}}}$ does not equal to zero, the difference must be due to the effect transmitted along $C\rightarrow L$, which means that the risk difference can be used to measure the group-level discrimination for subgroup ${\mathbf {b}}$.

Based on the above analysis, the criterion for the meaningful partition is derived as follows. A partition ${\mathbf {B}}$ is a meaningful partition if the node set ${\mathbf {B}}$ d-separates C and L in the graph ${\mathcal {G}}$ with $C\rightarrow L$ deleted. By using the criterion of the block set, we can identify all the meaningful partitions. For each subgroup ${\mathbf {b}}$ produced by a block set ${\mathbf {B}}$, the group-level discrimination can be measured using $\varDelta P|_{{\mathbf {b}}}$. Then, similar to Sect. 4.2, the quantitative evidence of discrimination can be given by comparing $\varDelta P_{{\mathbf {b}}}$ with a user-defined threshold, i.e., whether inequality $|\varDelta P_{{\mathbf {b}}}|\le \tau$ holds or not.

Fig. 4

Causal graph of an example university admission system

Although the above result provides a clear criterion for group-level discrimination, one drawback is that it requires examining every subgroup of every meaningful partition, i.e., every block set. A brute force algorithm may have an exponential complexity. Thus, instead of examining all block sets, a further result shows that we only need to examine one set ${\mathbf {Q}}$, which is the set of all L’s parents except C, i.e., ${\mathbf {Q}} = pa_{L}\backslash \{C\}$. If $|\varDelta P_{{\mathbf {q}}}|\le \tau$ holds for every subgroup of ${\mathbf {Q}}$, then it is guaranteed that $|\varDelta P_{{\mathbf {b}}}|\le \tau$ holds for every subgroup of every block set. Therefore, if there is no discrimination for every subgroup of ${\mathbf {Q}}$, it guarantees there is no discrimination for every meaningful subgroups.

To modify the dataset to ensure that there exists no meaningful subgroup with discrimination, two algorithms were proposed. The first algorithm is similar to the one introduced in Sect. 4.3. It modifies the causal graph so that the modified graph does not contain discrimination, and then generates a new dataset using the modified graph. The difference is in the constraints in the quadratic programming problem, which ensures that $|\varDelta P_{{\mathbf {q}}}|\le \tau$ holds for every ${\mathbf {q}}$. The second algorithm directly modifies the labels of selected individuals from the dataset to meet the non-discrimination criterion. For each ${\mathbf {q}}$ with $\varDelta P_{{\mathbf {q}}}>\tau$, a number of tuples with $C=c^{-}$ and $L=l^{-}$ are randomly selected and their labels are changed from $l^{-}$ to $l^{+}$. For each ${\mathbf {q}}$ with $\varDelta P_{{\mathbf {q}}}<-\tau$, a number of tuples are similarly selected and their labels are changed from $l^{+}$ to $l^{-}$. As a result, it is ensured that $|\varDelta P_{{\mathbf {q}}}|\le \tau$ holds for each ${\mathbf {q}}$.

In real situations, a subgroup ${\mathbf {q}}$ may have a small sample size, which decreases the reliability of the discrimination measurement. In order to handle randomness and small sample size, a relaxed discrimination criterion was proposed. For the node set ${\mathbf {Q}}$, $\varDelta P|_{{\mathbf {Q}}}$ is treated as a random variable and $\varDelta P|_{{\mathbf {q}}}$s across all subgroups are treated as samples. A user-defined parameter $\alpha$ ($0<\alpha <1$) is introduced to indicate a threshold for the probability of $|\varDelta P|_{{\mathbf {Q}}}|<\tau$. If $P(|\varDelta P|_{{\mathbf {Q}}}|<\tau ) \ge \alpha$, then we say there is no group-level discrimination under partition ${\mathbf {Q}}$. It is proved that if we observe no discrimination for ${\mathbf {Q}}$, then it guarantees no discrimination for every meaningful partitions. One issue here is that the exact distribution of $\varDelta P|_{{\mathbf {Q}}}$ for accurately estimating $P(|\varDelta P|_{{\mathbf {Q}}}|<\tau )$ is not known. To deal with this issue, the Chebyshev’s inequality is employed to provide a lower bound of probability $P(|\varDelta P|_{{\mathbf {Q}}}|<\tau )$ using the mean and variance of $\varDelta P|_{{\mathbf {Q}}}$.

6.2 Individual-level direct discrimination

Situation testing is a legally grounded technique for analyzing the discriminatory treatment on an individual. It has been widely adopted both in the USA and the European Union. Situation testing is carried out in responding to a complaint about discrimination from an individual. Pairs of testers who are similar to the individual are sent out to participate in the same decision process (e.g., applying for the same job). For each pair, the two testers possess the same characteristics except the membership to the protected group. For example, in the case of employment, the resumes of a pair of testers with different gender can be made equivalent in the education background, work experience, expertise and skills, and only vary in details and formats to avoid being considered as duplicates. The objective is to measure the treatments or decisions given to the members from the same pair. If one of the pair receives a different decision, the distinction implies discriminatory behavior.

By simulating situation testing, individual-level direct discrimination can be detected by finding a representative group of individuals who are closest to the target individual. The representative group contains pairs of individuals, where each pair has the same characteristics apart from belonging to the protected group and non-protected group. Then, the target individual is considered as discriminated if significant difference is observed between the decisions from the two parts of tuples.

The key issue in the implementation of situation testing is how to determine the closest individuals for the target. To deal with this issue, we can extend the group-level direct discrimination to the individual-level direct discrimination when the subgroup is specified by all attributes except C and L. Consider an individual described by profile ${\mathbf {x}}$, where ${\mathbf {X}}$ is the set of all attributes except C and L. It can be proved that ${\mathbf {X}}$ must be a meaningful partition. Therefore, according to the notion of the block set, the individual-level direct discrimination can be measured using $\varDelta P|_{{\mathbf {x}}}$. In fact, it can be further proved that $\varDelta P|_{{\mathbf {x}}} = \varDelta P|_{{\mathbf {q}}}$, where ${\mathbf {q}}$ is the subset of ${\mathbf {x}}$ which are the parents of L. This result implies that for determining the closest individuals, we should first select the individuals from subgroup ${\mathbf {q}}$, and then select the individuals from the following appropriate subgroups when subgroup ${\mathbf {q}}$ has a small size. This enforces a requirement on the distance measuring such that we cannot directly adopt the classic distance functions (e.g., the Manhattan distance or overlap measurement), but also need to consider the causal structure of the dataset and the causal effects among attributes.

It turns out that the above requirement is a natural result when the causal graph is used as a guideline of measuring the similarity, as shown in [40]. The ideas are as follows. First, only the attributes that are the direct causes of the decision should be used in the distance computation. Other attributes are either not causally related to L or have the causal effects on L that are transmitted by the direct causes. Including these attributes in the distance computation may lead to incorrect results in the similarity measurement. For illustration, consider a toy model for a university admission system. The profile of an applicant includes gender, major, score, height, weight, and admission. The causal graph is shown in Fig. 5, and part of the dataset is presented in Table 2. Suppose that tuple 1 is the target for testing, and we want to find the closest tuple from the tuples listed in the table. If we use all non-protected attributes to compute the distance, tuples 3 and 7 are the closest ones as both of them have only one attribute mismatch. However, from the causal graph we can see that, height and weight are not causally related to admission and should not be involved in the computation. In fact, tuple 2 is closest to the target since their majors and scores are exactly the same.

Fig. 5

Causal graph of the illustrative example

Table 2 Part of the dataset of the illustrating example

Second, distance function is usually defined by first establishing a distance metric for measuring the per-attribute distance, and then computing the joint effect by summing up all the per-attribute distances. When measuring the per-attribute distance, the causal effect of each attribute on the decision can reveal important information relating to similarity. The response of the decision to change of the attribute reflects the difference in how the two domain values affect the decision. Thus, two values can be considered to be closer if changing the attribute from one value to the other produces smaller influence on the decision. Consider the same above example and we want to measure the distance between different values of attribute score. The distance between A and B and the distance between B and C are measured as equivalent if only the value difference is considered, e.g., using the Manhattan distance. However, from the tuples listed in the table we can see that, both the admission rates for A and B are $50\%$, and the admission rate for C is $0\%$. Thus, the causal effect of score on decision can facilitate to more accurately characterize the similarity in situations where A and B are closer than B and C with respect to the admission. Furthermore, the per-attribute distance should be instance dependent. For example, although both the score difference between tuples 3 and 2 and that between tuples 3 and 7 are the same A-to-B difference, they should not be equal since tuples 3 and 2 apply to the same major while tuple 7 applies to another, e.g., A and B stand for good and median and C stands for failure.

Following the above ideas, the distance function is defined as follows. Consider two individuals, each of whom has his/her own profile. First, the distance function is defined on the basis of ${\mathbf {Q}}$, where ${\mathbf {Q}}=pa_{L}\backslash \{C\}$. Denote one individual’s value assignment to ${\mathbf {Q}}$ is ${\mathbf {q}}$, and the other is ${\mathbf {q}}'$. Then, for each attribute $Q_{k}\in {\mathbf {Q}}$, its causal effect on the label is measured. The change of $Q_{k}$ from $q_{k}$ to $q_{k}'$ is modeled as two interventions that force $Q_{k}$ to take that two values, respectively, while keeping all other attributes unchanged. Thus, the causal effect is given by the difference of the two post-intervention distributions. Then, the causal effect is combined by a production with the value difference between $q_{k}$ and $q_{k}'$, which employs the classic distance metric such as the normalized Manhattan distance for ordinal/interval attributes and the overlap measurement for categorical attributes. The production can be interpreted in two aspects: (1) the causal effect can be considered as the weight of the value difference, indicating how significant this value difference is with regard to the decision; (2) the value difference can also be considered as the weight of the causal effect, indicating to what extend this causal effect is relating to the similarity between the two values. Finally, the distance function for the two individuals is obtained by summing up the production of the causal effect and value difference of all attributes in ${\mathbf {Q}}$.

7 Looking forward

This paper introduces a causal modeling-based framework for anti-discrimination learning, which adopts the causal models for modeling the mechanisms in data generation and discrimination. Discrimination is categorized based on two dimensions: direct/indirect and system/group/individual level. Within the framework, we introduce a work for discovering and preventing both direct and indirect system-level discrimination in the training data using the path-specific effect technique, and a work for extending the non-discrimination result from the training data to prediction. We then introduce two works for group-level direct discrimination and individual-level direct discrimination, by using the d-separation and simulating the situation testing methodology, respectively.

As can be seen, the framework is not complete yet, and one can directly identify several research problems that need to be addressed. Also, the framework makes the Markovian assumption to facilitate the causal inference. Whether this assumption can be relaxed is worthy of further exploration. In addition, the framework mainly focuses on classification, but there are other predictive models and data mining tasks beyond classification. How to extend the existing works to deal with anti-discrimination problems beyond classification is of great importance as well. In the following, we suggest several potential future research directions from the above three aspects.

7.1 Research problems within the framework

Several problems are remaining to be solved within the framework. Here we list four problems which we believe are especially worthy of devoting efforts.

In Sect. 4, we showed that indirect discrimination, i.e., the $\pi _{i}$-specific effect, is unidentifiable if the recanting witness criterion is satisfied. In the discrimination removal algorithm in [42], it simply cuts off several paths in $\pi _{i}$ to dissatisfy the recanting witness criterion. However, the $\pi _{i}$-specific effect in this situation is important since the structure of the recanting witness criterion itself implies potential indirect discrimination. Thus, how to approximate or bound the $\pi _{i}$-specific effect in the unidentifiable situation is an important problem. A potential solution may be to employ the bound for the probability of necessity and sufficiency [34], which was developed within the causal modeling framework for estimating the probability of causation.

The theoretical guarantee for non-discrimination in prediction introduced in Sect. 5 only considers the risk difference for measuring discrimination. As stated, risk difference is not an accurate discrimination measurement in several situations. It correctly measures direct discrimination only when a single causal path exists from C to L, and correctly measures indirect discrimination only when redlining attributes reside on every causal path from C to L. Thus, the theoretical guarantee is practically meaningful only if it can apply to causal-based discrimination measurements such as the direct/indirect discrimination criteria introduced in Sect. 4. The challenge lies in that, since the formulations of these discrimination measurements are significantly different from the risk difference, the results in Sect. 5 may not be directly applicable.

Section 6 deals with the direct discrimination on the group and individual level. However, it is unclear whether the proposed techniques can be applied to deal with indirect discrimination. It is also unclear whether the path-specific effect technique used in Sect. 4 is applicable to group and individual-level discrimination, due to the identifiable issue of the post-intervention distribution on a subgroup. Therefore, how to model, measure, and prevent group and individual-level indirect discrimination are still significant challenges in anti-discrimination learning.

From the practical view, it is important to study how to balance the trade-off between non-discrimination and utility loss. Recall the two-phase framework introduced in Sect. 5, which provides non-discrimination guarantee in prediction. Utility loss may occur during the first phase when modifying the training data to remove discrimination, as well as during the second phase when modifying the classifier to remove its error bias. The discrimination removal algorithm proposed in Sect. 4 tackles the problem of minimizing utility loss in the first phase, but minimizing utility loss in the second phase is unexplored.

7.2 Relaxing Markovian assumption

The Markovian assumption represents the situation where no part of the dependencies among endogenous variables ${\mathbf {V}}$ are due to exogenous (unobserved) variables ${\mathbf {U}}$, i.e., there is no unobserved confounders. In this situation, the presence of the unobserved variables does not hinder identifiability of the causal effect in the causal model. Thus, the Markovian assumption permits us to infer every post-intervention distribution from the pre-intervention distribution that can be derived from the observed data. However, when unobserved confounders are known to exist in the system, simply ignoring the presence of these variables in the causal model can lead to erroneous conclusions about the causal relationship among endogenous variables. In order to deal with unobserved confounders, the second requirement of the Markovian assumption needs to be relaxed, i.e., variables in ${\mathbf {U}}$ are no longer mutually independent. The corresponding causal model is called semi-Markovian [24]. The situation in the semi-Markovian model is much more complicated than that in the Markovian model, both in the causal graph learning and causal effect inference.

The causal graph of the semi-Markovian model is commonly represented by the acyclic directed mixed graph (ADMG) [32]. Different from the DAG, the ADMG contains two types of edges, directed $\rightarrow$ and bidirected $\leftrightarrow$. When there exists a bidirected edge between nodes X and Y, it implies presence of the unobserved confounder(s) for the two variables. The ADMG learning attempts to solve this problem: how to discover as much knowledge as possible from data regarding the causal structure among variables, including whether two endogenous variables are confounded, definitely not confounded, or is impossible to tell from data. Although difficult, many works have been done and several methods have been proposed such as the causal inference (CI) and fast causal inference (FCI) algorithms [33]. Some recent advances in ADMG learning include the ordinary Markov model [11] and the nested Markov Model [32].

When the ADMG is given, the presence of unobserved confounders can still cause troubles in anti-discrimination discovery and removal due to the difficulties in causal inference in semi-Markovian models. Unlike in the Markovian model, the post-intervention distribution in the semi-Markovian model is no longer always identifiable. Pearl has given two sufficient graphical criteria for determining whether a post-intervention distribution is identifiable, known as the back-door criterion and front-door criterion [24]. The complete criterion for the identifiability of the post-intervention distribution is given by the do-calculus [25]. Regarding the path-specific effect, Shpitser [31] has given the generalized version of the recanting witness criterion that holds in the semi-Markovian model, known as the recanting district criterion. Any anti-discrimination technique designed for models with unobserved confounders, i.e., semi-Markovian models, must be adapted to the differences in the causal inference techniques.

7.3 Discrimination in tasks beyond classification

Although the causal model is not limited for categorical attributes, the framework introduced in this paper mainly focuses on classification problems. There are predictive models other than classification. For example, for problems such as how to determine the salary of an employee, or how to determine the amount of loan granted to an applicant, where the decisions are continuous variables, regression models should apply. How to extend the current discrimination criterion to handling continuous decisions? In addition, there are a large number of data mining tasks other than classification and regression. For example, in the ranking problem, the outcome is not a single label but a ranking of candidates. In the recommendation problem, the outcome is a list of recommended items. How to judge whether a ranking or a recommendation list is discriminatory or not and how to ensure fairness in the systems? Some preliminary works (e.g., [36]) have proposed several association-based methods. However, no work has been done within the causal modeling framework.

With the causal framework and methodologies presented in the paper, we hope that we can deepen the understanding of discrimination from the causal perspective in the research society of anti-discrimination and fairness-aware data mining, and we look forward to continuous advancement in this field.