Analytical model for bond–slip behavior of the anchorage of deformed bars in reinforced concrete members subjected to bending

Abstract

The distribution of bond stresses along the anchorage of a reinforcing bar in concrete plays a key role in controlling the load transfer and inelastic deformation of a Reinforced Concrete (RC) member under load. The typical bond stress–slip relationships specified in the model codes are given as average ‘local bond stress’ versus ‘local slip’ relationships which may be taken as statistically acceptable to represent bond–slip behavior in RC specimens with short anchorage lengths. This paper demonstrates the use of a viable analytical procedure for calibration of bond–slip relationships of the anchorage of deformed bars in RC members subjected to bending. The analytical modelling of the bond–slip relationship is based on observations of load-deflection behavior in laboratory experiments of full-scale RC specimens designed with relatively long end development of anchored bars beyond a critical section. The calibrated bond–slip relationships for selected anchorage specimens have been used to develop a modified model of peak local bond stress for splitting type bond failure. The model proposed in this paper takes into account the effect of variations of anchorage length on the bond–slip behavior, in addition to the effects of bar diameters, concrete cover and concrete strength that are typically taken into account in the model codes.

1 Introduction

The distribution of bond stress along the anchorage of reinforcing bars in concrete is of crucial importance since it controls the load transfer and the inelastic deformation of a Reinforced Concrete (RC) member under load. The typical bond stress–slip relationships specified in the model codes (e.g., in FIB Model Code 2010 [1]) are formulated based on the assumption that under well-defined conditions, there exists an average ‘local bond stress’ versus ‘local slip’ relationship that is statistically acceptable for short anchorage lengths. The specifications in different codes of practices (e.g., in [2,3,4,5]) for determining the development length or lapped splice length of anchored bars are also based on data mostly obtained from small-scale RC “pull-out” test specimens with relatively short embedment lengths of bars. Local bond–slip models are mainly based on test data such as that obtained from the RILEM pull-out test [6, 7] with a short anchorage length typically five times the bar diameter and with a relatively thick concrete cover equal to 4.5 times the bar diameter [8, 9]. Although the FIB Model Code 2010 [1] has extended its local bond–slip model to cover splitting failure modes, bond–slip models for deformed bars have historically been derived first for well-confined conditions in which concrete cover of sufficient thickness ensures a pull-out failure mode in which the bar pulls out of the concrete leaving a smooth hole and without splitting the cover [9]. At the ultimate state of bond failure, the pull-out specimens with short anchorage length typically develop nearly uniform bond stress distributions at the bar concrete interface. Therefore, the scope of application of these bond–slip relationships for modelling typically longer anchorages of reinforcement in full-scale RC members is questionable [10].

Bond–slip phenomenon significantly affects the structural behavior and efficiency of different sub-elements in a RC frame, including column, foundation, interior and exterior beam–column joint [11]. It also affects the crack patterns and failure modes in RC beams and slabs [11]. The validation of the existing analytical models of bond–slip were mostly performed on small-size specimens, where only the elementary features of the models were tested [12, 13]. In many cases when RC structures are considered, one of the most used approaches of modelling is to consider a no slip relationship between steel and concrete, i.e., perfect bond [12, 14]. Although the assumption of perfect bond between the concrete and reinforcing bar is often a sufficient assumption when modelling the ultimate behavior of a large RC structure, it is not of course appropriate when modelling bond or anchorage failure in RC members [15].

The bar–concrete interface along the anchorage is treated as a continuum in the formulation of a typical analytical bond–slip model. However, the random development of cracks may affect the bond stresses [16, 17]. Existing models ignore such extreme variations or discontinuities in local bond stresses and the local slips that may occur at or in the vicinity of the flexural cracks. As the reinforcement–concrete bond directly influences the evolutions of cracks, implementation of the no slip relation may produce impractical model outputs in numerical simulations of practical situations of RC members under load (e.g., [12, 15, 18,19,20]). Notwithstanding, the bond–slip models proposed by different researchers vary widely depending on the particular anchorage type being modeled (e.g., [1, 21,22,23,24]) or depending on the particular type and geometry of a structure and its response under variable loading conditions (e.g., [25]).

Therefore, a reasonable representation of the highly nonlinear bond stress–slip relationships usually observed in laboratory experiments is required to obtain reliable outputs especially when modelling the behavior of full-scale RC specimens under overload. Based on observations of laboratory test results of the two types of anchorage length RC specimens reported elsewhere by Gilbert et al. [16, 26] and Mazumder et al. [27,28,29,30], it was evident that the average ultimate bond stresses along an anchored bar varied significantly depending on the variations of the anchorage lengths and the bar diameters in the specimens. In practical cases of longer anchorage lengths provided in RC members, average bond strength generally decreases with increasing anchorage length [8, 16, 31]. One of the possible reasons for the variations was ascribed to the presence of flexural cracks along the anchorage zone of full-scale RC specimens [10, 16, 17]. Therefore, it is reasonable to consider that the local bond–slip relationships to be used for analytical or numerical modelling in RC specimens should not only depend on the bar diameters but also on the anchorage lengths provided in the specimens.

This paper discusses the test results from a few selected anchorage length RC slab specimens that were tested by the authors under three-point bending action. The load-deflection behavior of the RC test specimens was observed during the experiment up to the point of anchorage failure. A simple but viable analytical model of bond–slip proposed by Yankelevsky [32] was used and a systematic procedure of calibration of bond–slip models was performed using the test results [31]. The efficacy and validation of the recalibrated analytical model of bond–slip relationships [31] for finite element (FE) modelling of full-scale RC anchorage length specimens has been reported by Mazumder and Gilbert [15]. This paper aims at presenting the detailed mathematical formulations and solutions of the analytical model of the local bond–slip relationships and also discusses the detailed procedure for verifying a local bond–slip relationship that is consistent with the experimental test data. The application of calibrated bond–slip relationships for the specimens is extended further to develop a modified model of peak local bond stress for splitting type bond failure.

2 Experimental program

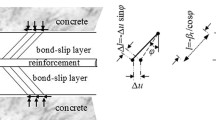
A series of tests on 18 full-scale anchorage length RC slab specimens had been fabricated and tested under static, cyclic and sustained loads and the test results have been reported elsewhere [16, 17, 26,27,28,29,30]. The discussion in this paper concerns the test results of seven selected anchorage length RC slab specimens that were tested under monotonic static loads. The RC slab specimens were of equal dimensions each being 2000 mm long, 600 mm wide and 200 mm deep. The two supports of the slab were at 1200 mm distance and the specimens overhung at one end by 700 mm. The location of the applied line load P was at a distance 600 mm past Support 1, as shown in Fig. 1a. Among the four reinforcement bars at the top of the specimen, the external two bars were discontinued with a 180° cog past Support 1. For the two middle bars resisting bending action in the cantilever, the bond between the bars and the concrete was discontinued at a distance l_d (anchorage length) past Support 1 by encasing each middle bar in a plastic sleeve through to the other end of the specimen. For testing with a convenient experimental set-up, the specimen was inverted to keep the anchored bars located at the bottom of the specimen (see Fig. 1c). A monotonically increasing static load was applied on the specimen by maintaining a suitably slow rate of deformation of the specimen until failure initiated in all specimens by bond failure within the region of anchorage length. The maximum load (P_max) reached at the state of bond failure in the specimen was recorded while deflection of the specimen was measured during the test utilizing LVDTs. The variables considered were the bar diameter d_b= 12 or 16 mm; the anchorage length l_d = 10d_b, 15d_b and 20d_b; and the bottom concrete cover c = 25 or 40 mm.

Fig. 1

Dimensions and loading arrangements of anchorage length slab specimens

3 Overview of the provisions of the FIB bond–slip model

The discussion of the analytical modelling for the bond–slip behavior is made using the FIB bond–slip models [1] as a reference model as it is one of the commonly used bond–slip models for analytical and finite element (FE) modelling of RC members. The FIB model code [1] specifies local bond stress versus local slip relationships as statistical mean curves for a broad range of cases of confined and unconfined concrete. The bond stress–slip relationships applicable for two different bond failure types are defined by Eqs. (1)–(5), with constituent parameters and parametric values shown in Fig. 2; Table 1 respectively. However, these relationships are valid for short anchorage lengths only under well-defined conditions and it is recommended [1] that a designer should proceed with caution while using the FIB bond–slip models to develop design bond–slip relationships for a particular bond and anchorage problem.

For monotonic loading, the local bond stress (τ) between the concrete and reinforcing bar for pull-out and splitting bond failure can be determined as a function of the relative displacement or slip (s) according to Eqs. (1)–(4) as specified by the FIB model code [1] (notations for the equations are illustrated in Fig. 2).

$$\tau=\tau_y{(s/s_1)}^\alpha\;\;\text{for}\;\;0\:\leq s\:\leq\:s_1.$$

(1)

$$\tau\;=\tau_y\;\;\text{for}\;\;s_1\:\leq\:s\:\leq\:s_2.$$

(2)

$$\tau=\tau_y-\left(\tau_y-\tau_f\right)\;\left(s-s_2\right)/ \left(s_3-s_2\right)\;\;\text{for}\;\;s_2\;\leq\;s\;\leq\;s_3.$$

(3)

$$\tau=\tau_f\;\;\text{for}\;s_3\:<\:s.$$

(4)

Fig. 2

Analytical bond stress–slip relationship for monotonic loading (adopted from [1])

Table 1 Parameters for defining mean local bond–slip relationship of deformed bars (according to [1])

The values in Table 1 (column 2 and 3) for the pull-out type bond failure are valid for bond in well confined concrete (i.e., with c_d ≥ 5d_b, clear spacing between bars  ≥  10d_b). A maximum of four bond zones (Zone I–IV, as shown in Fig. 2) exist in the bond–slip relationship for the pull-out type bond failure. Two types of bond–slip relationships can be defined for the splitting type bond failure in a specific bond condition, one is for unconfined anchorage conditions in concrete (K_tr = 0) and the other is for confined anchorage conditions with stirrups. With s₁ = s₂, and τ_f = 0 for the unconfined anchorage condition, there are two bond zones (Zone I and III, as shown in Fig. 2) in the bond–slip relationship; whereas three bond zones exist in the bond–slip relationship for the confined anchorage condition (with s₁ = s₂, and τ_f = 0.4τ_y). The expression for values of peak local bond stress, τ_y for the splitting type bond failures is given by Eq. (5).

$$\tau_{y(\mathrm{split}\;1,2)}=\eta_2 \cdot 6.54 \cdot \left(f^{\prime}_c/20\right)^{0.25}\left(20/d_b\right)^{0.20}\;\left[\left(c_d/d_b\right)^{0.33}\left(c_{\text{max}}/c_d\right)^{0.1}+8\;K_{tr}\right],$$

(5)

where η₂ = 1.0 for good bond conditions and 0.7 for all other cases; f′_c is the characteristic (cylinder) compressive strength of concrete, c_max and c_d are the maximum and minimum available concrete cover for a bar to its nearest concrete surface, and K_tr is a factor that accounts for the effects of passive confinement (stirrups or transverse reinforcement). The subscript 1 at τ_y(split) is to denote the expression of τ_y for the splitting type bond failure in unconfined concrete (K_tr = 0) and the bond–slip relationship for unconfined anchorage condition has two bond zones as shown in Fig. 2, while the subscript 2 at τ_y(split) is for the expression of τ_y for the splitting bond failure in confined concrete (with a value for K_tr) and the bond–slip relationship for confined anchorage condition has three bond zones as shown in Fig. 2. The values of τ_y for the splitting type bond failure, given in Table 1 (column 4–7), are valid for d_b ≤ 20 mm, c_max/ c_d = 2.0, c_d = d_b and Ktr = 2% in the case of stirrups. The factor K_tr is defined in the model code [1] according to Eq. (6).

$$K_{tr}=\eta_1\cdot A_{SV}/\left(n\cdot d_b\cdot s_v\right),$$

(6)

where η₁ is the number of legs of confining reinforcement at a section, A_sv is the cross-sectional area of one leg of confining bar (mm²), s_v is the longitudinal spacing of confining reinforcement (mm), n is the number of anchored bars or pairs of lapped bars, and d_b is the diameter of the anchored bar or of the smaller of the diameters of a pair of lapped bars.

4 Analytical modelling for bond–slip behavior

An example of the analytical modelling procedure that was used to calibrate bond–slip models for the anchorage of deformed bars in RC members subjected to bending is presented here. The nonlinear bond–slip relationships of the FIB model code [1] are idealized by piecewise linear curves, and are calibrated using the test results of the selected anchorage length slab specimens (denoted here as DL-1 to DL-7). The calibration [31] was done using a computationally viable analytical modelling and solution procedure that was originally proposed by Yankelevsky [32].

4.1 Mathematical formulations of analytical modelling

With minor changes in the mathematical formulations of local bond stress, τ (x) and slip, s(x) for the bond–slip relationship in bond zone III, the analytical model [32] used for modelling bond–slip behavior is outline below. The nonlinear bond stress–slip relationships are idealized by linear relationships in up to four possible bond zones (Fig. 3) and second-order linear differential equations for the different bond zones are defined. The boundary conditions are the strains in the reinforcing bar ε_s(x) at the two ends of the anchorage length (l_d):

$${\text{at}}\;\;x\:=\:0:\;\varepsilon_s\;(x)\:=\:0 {\text{at}}\;\;x\:=\:l_d:\;\varepsilon_s\;(x)\:=\:\varepsilon_0,$$

where ε_o is the strain calculated from the bar stress, σ_st (at P_max), based on the analysis of the cracked section at x = l_d.

Fig. 3

Linear approximation of a typical bond–slip relationship

Depending on the given boundary conditions and satisfying conditions of compatibility at the interface of the bond zones, the differential equations can be solved for any appropriate bond–slip relationship to find the unknown lengths of the bond zones within the anchorage length (e.g., Fig. 4) of an anchorage specimen. A detail description of mathematical formulations and solutions of the analytical model is outline below.

Fig. 4

Idealization of bond zones within the anchorage (for typical pull-out bond failure)

The formulation of typical analytical and numerical models for bond–slip in reinforced concrete is based upon the assumption that the influence of concrete deformation on slip is negligible especially when bond failure occurs with the strain in the reinforcing bar below the yield strain [32]. Hence, the strain in the bar is related to the slip by:

$${\varepsilon _{\text{s}}}(x)=\frac{{{\text{d}}s(x)}}{{{\text{d}}x}}$$

(7)

Equilibrium of an infinitesimal bar element at distance x, yields the relationship between the bond stress τ(x) and the axial force T_s(x) in the steel bar:

$$\tau (x)=\frac{1}{{\pi {d_{\text{b}}}}}\frac{{{\text{d}}{T_{\text{s}}}(x)}}{{{\text{d}}x}}$$

(8)

Assuming linear-elastic behavior of the steel bar:

$$\tau (x)=\frac{{{E_{\text{s}}}{A_{\text{s}}}}}{{\pi {d_{\text{b}}}}}\frac{{{\text{d}}{\varepsilon _{\text{s}}}(x)}}{{{\text{d}}x}}$$

(9)

in which E_s and A_s are the Young’s modulus of elasticity and the cross-sectional area of the reinforcing bar, respectively. Substituting Eqs. (7) into (9), when a circular cross-section of the bar is assumed, we get:

$$\tau (x)=\frac{{{E_{\text{s}}}{d_{\text{b}}}}}{4}\frac{{{{\text{d}}^{\text{2}}}s(x)}}{{{\text{d}}{x^2}}}$$

(10)

The solutions of the differential equation yields the expressions for slip, strain and bond stress variations within a particular bond zone and the mathematical expressions for the solutions are presented below.

(a) Zone I: 0 ≤ s(x) ≤ s₁

The variation of bond stress with slip is:

$$\tau (x)={K_{\text{y}}}s(x)$$

(11)

where ${K_{\text{y}}}={\tau _{\text{y}}}/{s_1}$. Substituting Eqs. (11) into (10) yields:

$$\frac{{{{\text{d}}^{\text{2}}}s(x)}}{{{\text{d}}{x^2}}} - \frac{{4{K_{\text{y}}}}}{{{E_{\text{s}}}{d_{\text{b}}}}}s(x)=0$$

(12)

and solving gives:

$$s(x)={C_1}{e^{{\alpha _1}x}}+{C_2}{e^{ - {\alpha _1}x}}$$

(13)

where ${\alpha _1}=\sqrt {{{4{K_{\text{y}}}} \mathord{\left/ {\vphantom {{4{K_{\text{y}}}} {{E_{\text{s}}}{d_{\text{b}}}}}} \right. \kern-0pt} {{E_{\text{s}}}{d_{\text{b}}}}}}$ and C₁ and C₂ are constants to be determined from the known boundary conditions.

The expression for strain variation becomes:

$${\varepsilon _{\text{s}}}(x)=\frac{{{\text{d}}s(x)}}{{{\text{d}}x}}={\alpha _1}\,[{C_1}{e^{{\alpha _1}x}} - {C_2}{e^{ - {\alpha _1}x}}]$$

(14)

(b) Zone II: s₁ ≤ s(x) ≤ s₂

The expression for bond stress in this zone is:

$$\tau (x)={\tau _{\text{y}}}$$

(15)

Substituting Eqs. (15) into (10) yields:

$$\frac{{{{\text{d}}^{\text{2}}}s(x)}}{{{\text{d}}{x^2}}}=\frac{{4{\tau _{\text{y}}}}}{{{E_{\text{s}}}{d_{\text{b}}}}}$$

(16)

and solving gives:

$$s(x)=\frac{{2{\tau _{\text{y}}}}}{{{E_{\text{s}}}{d_{\text{b}}}}}{x^2}+{C_3}x+{C_4}$$

(17)

where C₃ and C₄ are constants to be determined from the known boundary conditions.

The expression for strain variation is:

$${\varepsilon _{\text{s}}}(x)=\frac{{{\text{d}}s(x)}}{{{\text{d}}x}}=\frac{{4{\tau _{\text{y}}}}}{{{E_{\text{s}}}{d_{\text{b}}}}}x+{C_3}$$

(18)

(c) Zone III: s₂ ≤ s(x) ≤ s₃

The expression for bond stress in this zone is:

$$\tau (x)={\tau _{\text{y}}} - {K_2}[s(x) - {s_2}]$$

(19)

in which:

$${K_{\text{2}}}=\frac{{{\tau _{\text{y}}} - {\tau _{\text{f}}}}}{{{s_3} - {s_2}}}$$

(20)

Substituting Eqs. (19) into (10) yields:

$$\frac{{{{\text{d}}^{\text{2}}}s(x)}}{{{\text{d}}{x^2}}}+\frac{{4{K_2}}}{{{E_{\text{s}}}{d_{\text{b}}}}}s(x)=\frac{{4{\tau _{\text{y}}}}}{{{E_{\text{s}}}{d_{\text{b}}}}}+\frac{{4{K_2}{s_2}}}{{{E_{\text{s}}}{d_{\text{b}}}}}$$

(21)

and solving gives:

$$s(x)={C_5}\sin ({\alpha _2}x)+{C_6}\cos ({\alpha _2}x)+\frac{{{\tau _{\text{y}}}}}{{{K_2}}}+{s_2}$$

(22)

where ${\alpha _2}=\sqrt {{{4{K_{\text{2}}}} \mathord{\left/ {\vphantom {{4{K_{\text{2}}}} {{E_{\text{s}}}{d_{\text{b}}}}}} \right. \kern-0pt} {{E_{\text{s}}}{d_{\text{b}}}}}}$ and C₅ and C₆ are constants to be determined from the known boundary conditions. The expression for strain variation in the steel bar becomes:

$$\varepsilon_\text{s}(x)=\frac{\text{d}s(x)}{\text{d}x}=\alpha_2\,\left[C_5\cos(\alpha_2x)-C_6\sin(\alpha_2x)\right]$$

(23)

(d) Zone IV: s₃ ≤ s(x).

In this zone there exists a constant bond stress

$$\tau (x)={\tau _{\text{f}}}$$

(24)

Similarly to Zone II, where the bond stress is also uniform, the expressions for slip and strain are:

$$s(x)=\frac{{2{\tau _{\text{f}}}}}{{{E_{\text{s}}}{d_{\text{b}}}}}{x^2}+{C_7}x+{C_8}$$

(25)

$${\varepsilon _{\text{s}}}(x)=\frac{{4{\tau _{\text{f}}}}}{{{E_{\text{s}}}{d_{\text{b}}}}}x+{C_7}$$

(26)

With four distinct bond zones (Fig. 4) along the length of an anchored bar for the pull-out type bond failure, a maximum of 11 unknowns (eight constants C₁ to C₈ and three values for x (i.e. x₁, x₂, x₃) exist in the formulation and are required for the solution. These unknowns may be determined by an analytical solution procedure or using optimization algorithm for solution [31] with input values satisfying the boundary conditions and the conditions of compatibility as follows:

• At each of the three common boundaries between the four zones, the conditions of compatibility (equality) between bond stresses, slip and strain.

• At x = l_d, and at x = 0, the strain in the bar is known.

4.2 Calibration of bond–slip models for selected anchorage length specimens

An example of the procedure followed for calibrating bond–slip models using the test results of the selected anchorage length RC slab specimens (denoted as DL-1 to DL-7) is presented here. The anchored bars within each specimen were unconfined and splitting type bond failure was observed in all the specimens under overload. Therefore, according to the FIB model code [1], it is reasonable to assume that bond–slip relationship with two bond zones (bond zone I and III) controlled the bond–slip behavior in the selected specimens. Referring to Fig. 3, when bond failure occurs under the maximum applied load, at one location within the anchorage of the specimen the bond stress τ reaches τ_y with a local slip s₁. In this case, with no zone II (s₁ = s₂) existing in the bond–slip relationship, compatibility of strains, slips and bond stresses must exist at the point of transition between the two bond zones I and III. Bond zone III continues up to the point where τ_f = 0 and s = s₃. In this case, with no s₄, zone IV also does not exist. Figure 5 shows the idealization of the bond zones as assumed within the anchorage length of each selected specimen.

Fig. 5

Idealization of bond zones within the anchorage of the selected specimens

The boundary values of strains at the two ends of the anchorage length (l_d) are calculated by cracked section analysis from the experimental test results. Using the input boundary values and compatibility conditions in the analytical solution, a total of four unknowns exist (unknown bond zone I length x₁, as well as constants C₁, C₅ and C₆) and these can be solved in a trial and error method using a bond–slip relationship appropriate for a specimen. The mathematical formulations and solution procedure outlined in Sect. 4.1 is used to determine the value of the unknowns (length of bond zone I, x₁; value of constants C₁, C₅ and C₆). The known boundary and compatibility conditions used for the solutions are:

At x = l_d, ε(x) = ε₀, (ε₀ determined from P_max, by cracked section analysis),

At x = 0, ε(x) = 0,

Bond stress, strain and slip are equal at the transition between the two bond zones, τ_I(x₁) = τ_III(x₁)= τ_y, s_I(x₁) = s_III(x₁) = s₁ = s₂,

According to the solution procedure, Eqs. (27)–(30) provides solutions for each of the unknowns C₁, C₅, C₆ and x₁ for the two bond zone conditions (Zone I and III) existing in the bond–slip models for the selected specimens:

$${C_1}={C_2}=\frac{{s_{\text{1}}}}{{{\text{2cosh(}}{\alpha _{\text{1}}}{{\text{x}}_1}{\text{)}}}}$$

(27)

$${C_5}=\frac{{{\varepsilon _{{\text{so}}}}+{\alpha _2}{C_6}\sin ({\alpha _2}{l_{\text{d}}})}}{{{\alpha _2}\cos ({\alpha _2}{l_{\text{d}}})}}$$

(28)

$${C_6}=\frac{{{\alpha _2}{C_5}\cos ({\alpha _2}{x_1}) - 2{\alpha _2}{C_1}\sinh ({\alpha _1}{x_1})}}{{{\alpha _2}\sin ({\alpha _2}{x_1})}}$$

(29)

$${x_1}={\sin ^{ - 1}}\frac{{\left( {\frac{{ - \frac{{{\tau _y}}}{{{K_2}}} - {C_6}\cos ({\alpha _2}{x_1})}}{{{{\text{C}}_{\text{5}}}}}} \right)}}{{{\alpha _2}}}$$

(30)

The system of equations can be solved by manual calculations or using optimization algorithm for solution [31] with given input values of respective material parameters, boundary conditions of strains, constituent parameters of the bond–slip relationship, length of the anchorage (l_d) and assumed initial values of unknowns. The bond–slip relationships as specified according to the FIB model code [1] for splitting bond failure were first used to check the solutions of the unknown length of bond zones for the selected specimens. Table 2 shows the bond–slip relationships for the specimens, as specified according to the FIB model code. The structural and material parameters of the specimens are also shown in the table. With the bond–slip relationships of the FIB model code, i.e. with the values of s₁, s₃ and τ_y given in Table 2, no practical solutions of the unknown bond zone lengths (x₁ < l_d) could be found for the selected specimens except for the specimen DL-1. However, real solutions of the unknown bond zone lengths for the seven selected anchorage length specimens could be determined using a revised bond–slip relationship with constituent parameters reasonably estimated from measurements made in the experimental program. The experimentally measured end-slip of the debonded bars at P_max was used to decide reasonable initial values of the parameter s₁/s₂, and the post-peak end slip of the bars at 0.4P_max gave an indication of the spread of the tail end of the bond slip relationship (s₃).

Table 2 Parameters of bond–slip relationships for the selected specimens (specified according to the FIB Model Code 2010 [1])

Since more than one set of real solutions of unknowns for a specimen could be determined for different sets of parameters for the bond–slip relationships, further analyses were performed to calculate the local bond stresses at locations of the ribs of the reinforcement within the anchorage length of each specimen. The average of the calculated local bond stresses (τ_avg,cal) along the anchored bar of a specimen was compared for consistency with the experimentally determined average bond stress (τ_avg,exp at P_max) for that specimen. In a trial and error procedure, the bond–slip relationship was adjusted and the analytical solution procedure was repeated until the τ_avg,cal and τ_avg,exp agreed well. Trial and error calculations of the analytical solutions for local bond stresses and subsequently for checking consistency between τ_avg,cal and τ_avg,exp can be done using a simple and convenient programming routine (e.g., [31]).

In this way, the constituent parameters of the calibrated bond–slip relationships determined for two of the test specimens are shown in Figs. 6 and 7 respectively for DL-1 and DL-2, from which the real solutions of the unknown length of the bond zones (x₁) could be determined (as shown in the figures) while the τ_avg,cal also agreed reasonably well with measured τ_avg,exp for each specimen. The calibrated bond–slip relationships for the seven selected specimens as determined according to this procedure is shown in Table 3.

Fig. 6

Bond zone length and local bond stresses determined by calibrated bond–slip relationship for DL-1

Fig. 7

Bond zone length and local bond stresses determined by calibrated bond–slip relationship for DL-2

The limitation of the typical analytical modelling procedure is that the effect of concrete deformation on bond stresses is neglected, as is commonly assumed when ε_s < ε_s,y. If in fact there was no influence of concrete deformation on bond stress, the average bond stresses would be the same for identical specimens (where the same materials are used in the same structural geometry) regardless of the variation of anchorage lengths. The bond–slip relationships according to the FIB design model for the identical anchorage length specimens (e.g. DL-1, DL-2) are, in fact, the same regardless of the variations of the anchorage lengths. However, Table 3 shows that the constituent parameters of the recalibrated bond–slip relationships are, in fact, different for variations of anchorage lengths in otherwise identical specimens. Therefore, the changes of the constitutive parameters of the calibrated bond–slip relationships for each specimen indirectly accounts for the effect of concrete deformation on bond stresses. Table 3 also shows that the constituent parameters of some of the calibrated bond–slip relationships are significantly different when compared to the FIB bond–slip relationships for the respective specimens (e.g. for DL-2, DL-5, DL-6 and DL-7), both in terms of peak local bond stress, τ_y and constituent local slip values in different bond zones.

Table 3 Calibrated parameters of the bond–slip relationships for selected anchorage length specimens and results of analytical modelling

4.3 Modified model for peak local bond stress of the bond–slip model

The analyses presented in this section are aimed at developing a modified general model of the peak local bond stress (τ_y(split)) for splitting type bond failure, that is applicable for both the unconfined and confined anchorage conditions in RC members in bending. The modified model for τ_y(split) of the bond–slip relationship is developed for best consistency with the respective calibrated values of τ_y(split)/cal for all the seven selected specimens.

The bond–slip model of the FIB model code [1] for splitting type bond failure considers the effects of variations of the bar diameter, the concrete strength and the concrete cover on the mean local bond stresses of the bond–slip model. The FIB model Eq. (1) is specified according to Eq. (31) to determine peak local bond stress τ_y(split) (either τ_y(split)0.1 or τ_y(split)0.2) for the splitting type bond failure.

$${\tau _{{\text{y}}\left( {{\text{split~1,2}}} \right)}}={\eta _2}{k_1}{\left( {\frac{{{{f^{\prime}}_c}}}{{20}}} \right)^{0.25}}{\left( {\frac{{20}}{{{d_b}}}} \right)^{{k_2}}}\left[ {{{\left( {\frac{{{c_d}}}{{{d_b}}}} \right)}^{{k_4}}}{{\left( {\frac{{{c_{max}}}}{{{c_d}}}} \right)}^{0.1}}{\text{+}}8{K_{tr}}} \right]$$

(31)

where k₁ = 6.54, k₂ = 0.20, k₄ = 0.33 [as also shown in Eq. (5)].

The modified model will also include the effect of the anchorage length on the magnitude of τ_y(split). It additionally includes a factor (20d_b/l_d) with exponent k₃ which is newly introduced to account for the effect of the variation of anchorage lengths on peak local bond stress τ_y(split) (either τ_y(split)0.1 or τ_y(split)0.2) for the splitting type bond failure. The modified model for τ_{y(split 1,2)} now becomes

$${\tau _{{\text{y}}\left( {{\text{split~1,2}}} \right)}}={\eta _2}{k_1}{\left( {\frac{{{{f^{\prime}}_c}}}{{20}}} \right)^{0.25}}{\left( {\frac{{20}}{{{d_b}}}} \right)^{{k_2}}}{\left( {\frac{{20{d_b}}}{{{l_d}}}} \right)^{{k_3}}}\left[ {{{\left( {\frac{{{c_d}}}{{{d_b}}}} \right)}^{{k_4}}}{{\left( {\frac{{{c_{max}}}}{{{c_d}}}} \right)}^{0.1}}{\text{+}}8{K_{tr}}} \right]$$

(32)

An optimization function was solved to determine unknown values of coefficients of Eq. (32) [31]. The optimization routine gave outputs of best combination of the values of the coefficients k₁, k₂, k₃ and k₄ in Eq. (32) that optimally minimized differences between f(DL) and respective τ_y(split)/cal(DL), where f (DL) represents set of values of τ_y(split) for the selected specimens determined according to Eq. (32) and τ_y(split)/cal(DL) represents the calibrated values of τ_y(split) for the specimens as shown in Table 3. Hence, the optimized values of the factors are determined as k₁ = 3.3, k₂ = 0.9, k₃ = 0.5 and k₄ = 0.4. The modified model of τ_y(split) for splitting type bond failure is written in Eq. (33). The average difference between the calculated values of τ_y(split) (according to Eq. 33) and that of the calibrated bond–slip relationship for the selected specimens is 0.9%.

$${\tau _{{\text{y}}\left( {{\text{split~1,2}}} \right)}}=3.33{\eta _2}{\left( {\frac{{{{f^{\prime}}_c}}}{{20}}} \right)^{0.25}}{\left( {\frac{{20}}{{{d_b}}}} \right)^{0.9}}{\left( {\frac{{20{d_b}}}{{{l_d}}}} \right)^{0.5}}\left[ {{{\left( {\frac{{{c_d}}}{{{d_b}}}} \right)}^{0.4}}{{\left( {\frac{{{c_{max}}}}{{{c_d}}}} \right)}^{0.1}}{\text{+}}8{K_{tr}}} \right]$$

(33)

The modified model (Eq. 33) for estimating peak local bond stress τ_y(split) was successfully verified [31] in calibrating bonds–slip models for several full-scale RC beam specimens tested in bending where lapped splices of reinforcement were provided in the specimens under different confinement conditions (with specified K_tr).

5 Conclusions

The procedure for recalibration of bond–slip relationships for the anchorage of deformed bars as presented in this paper is based on observations of load–deflection behavior in laboratory experiments of a few selected full-scale RC anchorage specimens subjected to bending. The RC specimens were designed with relatively long end development of anchorage bars beyond a critical section. The specimens were tested under the application of monotonic static load which showed typical splitting type bond failure within the anchorage zone. The major finding of the experimental study was that the concrete deformation had a significant effect on bond stresses, especially when longer anchorages were provided in full-size RC specimens.

A simple but computationally viable analytical modelling procedure is used for calibrating bond–slip models for the anchorage of deformed bars in the RC members under bending. The constituent parameters of the bond–slip models recalibrated based on the test results of the RC anchorage length slab specimens show significant variations of mean local bond stresses and of local slip values when compared with the FIB model specifications of bond–slip relationships for the respective specimens. The variations of the calibrated bond–slip models depending on the variations of anchorage lengths in otherwise identical specimens indirectly account for the influences of concrete deformation on bond stresses.

A modified model for estimating peak local bond stress of the bond–slip model is also presented in this paper. The modified model proposed in the paper takes into account the effect of variations of anchorage length on the peak local bond stress, in addition to the effects of bar diameters, concrete cover and concrete strength that are typically accounted for in the model codes or specifications. However, the application of the bond–slip models presented in this paper should be limited for modelling short but practical anchorage lengths (l_d ≤ 20d_b with d_b≤ 20 mm) where splitting type bond failure is expected to occur within the anchorage length of RC members under bending.