Cracking behavior of reinforced concrete beams: experiment and simulations on the numerical influence of the steel-concrete bond

Abstract

Experimental and numerical results are provided in this contribution to study the global and cracking behaviors of two reinforced concrete beams subjected to four point bending. Experimentally, the use of image correlation technique enables to obtain precise information concerning the cracking properties (spacing, cumulated, maximum and mean values of the opening). Numerically, two simulations are compared taking into account a bond model between steel and concrete or supposing a perfect relation between the two materials. In both cases, a good agreement is achieved between numerical and experimental results even if the introduction of the bond effects has a direct influence during the development of the cracks (better agreement during the “active” cracking phase).

1 Introduction

Characterizing the cracking properties is of major concern when reinforced concrete structures are considered. Cracking (spacing and opening) may indeed directly impact different structural functions. One can cite aesthetic aspects for special engineering structures but also mechanical resistance (decrease of the mechanical resistance with the apparition of cracks) or durability (transfer properties directly function of the structural damage Picandet et al. 2001). That is why engineering codes (Eurocode 2007, for example) propose some limit values for the crack opening depending on the risk (corrosion, external chemical attacks...).

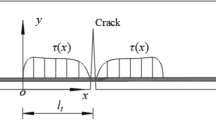
Cracking in reinforced concrete structures is generally influenced by the stress distribution along the interface between steel and concrete. The classical example to illustrate this effect is a reinforced tie (Eurocode 2007). Once the first crack appeared in the weakest point of the structure (minimum of the tensile strength), the concrete stress in the cracked zone drops to zero while the load is totally supported by the steel reinforcement. The stresses are then progressively transferred from steel to concrete (Fig. 1) defining a transition zone where no more crack can appear.

Fig. 1

Distribution of stresses in steel and concrete in a reinforced concrete tie after the first crack (${\sigma _c}$ and ${\sigma _s}$ are the stresses in concrete and steel respectively)

This stress transfer is directly influenced by the steel–concrete interface (Eurocode 2007). From this example, it seems essential to take into account the steel-concrete bond to correctly investigate the cracking properties. The steel—concrete bond has been widely studied in literature. Different numerical models have been proposed including spring elements (Ngo and Scordelis 1967, among others), zero thickness joint elements (Clément 1987; Daoud 2003; Lowes et al. 2004 for example) or embedded elements (Dominguez and Ibrahimbegovic 2012; Ibrahimbegovic et al. 2010) for example. Even if these models tend to correctly represent the interface effects, few authors investigated quantitatively (i.e. with an experimental comparison) the role of the steel—concrete bond on the cracking properties. This quantitative evaluation is important, especially when input data are required to feed the model. For example, for steel-concrete bond models, the bond stress – bond slip law that characterizes the evolution of the bond stress at the interface as a function of the bond slip (relative displacement between steel and concrete) is generally required (Fig. 2). Different ways exist in literature to describe this curve. For example, Ngo and Scordelis (1967) or Khalfallah and Ouchenane (2007) only focuses on the hardening part and propose simplified linear or bilinear laws. Their approaches are simple to calibrate but fail in representing the progressive degradation of the bond. Kwak and Kim (2001) propose to include a constant value of the bond stress at the end of the curve to represent the final degradation at the interface. Finally, Nilson (1968), Eligehausen et al. (1983) or Harajli (1994) consider more complex but also more representative evolutions, generally using an exponential law and including a softening branch. It is to be noted that in addition to the softening behavior, these propositions also differ in their initial slope: a secant slope in (Ngo and Scordelis 1967) to a highly stiffer evolution for (Eligehausen et al. 1983) (Fig. 3).

Fig. 2

Classical bond stress $\tau$—bond slip g curve

Fig. 3

Bond stress—bond slip laws. Propositions from literature (different values of parameter $k$ correspond to different values of the initial slope)

Generally, to evaluate the capacity of the numerical models, comparisons are performed on the global behavior (force—deflection curves) and some qualitative results are obtained on the cracks (spacing especially). For example, Ragueneau et al. (2006) or Dominguez and Ibrahimbegovic (2012) propose a steel—concrete bond model which is applied successfully on reinforced concrete ties from (Clément 1987) and (Daoud 2003). They especially show the good agreement between the experimental and numerical results on the force—displacement curve but produced only qualitative results on the cracking properties with a number of cracks depending on the steel-concrete model. Au and Bai (2007) or (Oliveira et al. 2008) get interested in the mechanical behavior of reinforced concrete beams tested in three or four point bending. The comparison on the force—midspan deflection curves show in both cases a good agreement. Concerning the crack properties, interesting information are provided on the crack spacing and opening (evolution of the crack width along the length of the beam in (Oliveira et al. 2008) especially) but no quantitative comparisons are proposed.

In fact, the few comparisons concerning the crack opening may be explained by the experimental difficulties to obtain this information. Up to recently, two main techniques were used to characterize the crack properties. Strain gages can be placed on the concrete (Clément 1987) to obtain local information. This technique presents two drawbacks: first it provides only local information (limited to the location of the strain gages) and it supposes to know the crack position (or to initiate the crack by pre-loading for example Castel and François 2011). Another technique uses displacement sensors applied at the crack position once the crack appeared on the concrete (Mivelaz 1996 for example). But, in this case, information about the crack initiation is not provided. To circumvent these drawbacks, more global techniques have been developed, based on image correlation. Compared to other techniques, image correlation enables to provide local information on the whole structure and does not need any hypothesis on the crack location. Moreover, it is a fully non-destructive and non-contact measurement.

In this paper, this technique is applied on an experimental campaign on four point bending beams. It aims especially at comparing a steel – concrete bond model developed in (Casanova et al. 2012) with new experimental results concerning the global (force—deflection curve) and local (crack spacing, crack maximum opening and distribution in the height of the beam) structural behaviors.

In a first part, the experimental campaign will be presented. In the second part, the hypothesis of the simulation will be explained before the comparison between experiment and simulation (third part).

2 Experimental campaign

2.1 Geometry and experimental device

Two simply supported beams are tested in this experimental campaign (3m length, 0.15 m width and 0.25 m height). The loading is applied by a hydraulic jack and distributed to the reinforced concrete structure using a stiff steel beam, in order to provide a constant moment zone (four point bending). The loading supports are located at 0.75 m from the center of the beam (Fig. 4). The beams are reinforced using conventional civil engineering ribbed bars with a diameter of 12 mm for tension zones and 8 mm for compressive zones and stirrups. There is no stirrup in the constant moment zone in order to avoid any perturbation in the crack apparition. Conventional curved anchorages are considered at each end of the tensile bars (Fig. 5).

Fig. 4

Principle of the experimental campaign

Fig. 5

Steel reinforcement and anchorages (dimensions in mm) a steel reinforcement in the half-length b anchorage, c section in the non-constant moment zone and d section in the constant moment zone

2.2 Material properties

Steel and concrete properties are measured using conventional uniaxial tests. Average values are given in Table 1 for 12 mm diameter steel reinforcement (direct tension tests). For concrete, uniaxial compressive and splitting tests are performed. Properties are given in Table 2 (mix design) and Table 3 (mechanical properties).

Table 1 Steel properties

Table 2 Mix design for concrete

Table 3 Mechanical properties for concrete

2.3 Experimental measures

The main objective of this experimental campaign on classical reinforced beams is to provide quantitative results concerning both global and local behaviors. The cracking properties are especially investigated. To this aim, different measures are performed during the test.

Displacements of the beams are measured through twenty three sensors located on the rear face (Fig. 6):

• Three sensors, located on the top of the beam enable to evaluate the displacement near the loading points and at the midspan (sensors $l, c$ and $r$ on Fig. 6).

• Twenty sensors located at 3.5 cm from the bottom of the beam are used to evaluate locally horizontal ($h$ sensors) and vertical ($v$) displacements.

  Fig. 6

  

  Position of the displacement sensors on the beam (rear face)

These measures are interesting because they give information about both global (vertical deformed shape, force—deflection curves for example) and local behaviors. For example, the measured relative horizontal displacements can be directly related to the value of the cumulated crack opening. Nevertheless, as already mentioned in the introduction, the information is limited to the position of the sensors and to the cumulated values.

To improve the measures, image correlation technique is used in order to follow the evolution of the crack properties (Fig. 7). The system is composed of three cameras ($2592 \times 1728$ pixel images) positioned to capture three different observation zones in the constant moment zone (Fig. 8) (one pixel is around $25\,\upmu \text{ m}$). The beam is prepared by using black and white paint on the front face and the quality of the obtained texture is checked to ensure a good performance of the correlation algorithm (Besnard et al. 2006).

Fig. 7

Image correlation device

Fig. 8

Observation zones in the constant moment zone for the picture correlation

From the obtained displacement fields ($\text{ using} \text{ Correli}^\mathrm{Q4}$ software Besnard et al. 2006), the crack properties are calculated: the crack position corresponds to the “jump” in the displacement while the opening is taken equal to its value (Fig. 9).

Fig. 9

Principle of the calculation of the crack properties (position and opening)

3 Simulation program

The aim of the paper is to evaluate the influence of a steel—concrete bond model on the crack properties by simulating the local and global behaviors of the tested four point bending beams. That is why a simulation program was launched after the test using the finite element code (Cast3m 2012). The principle of the simulation is briefly presented in the following parts.

3.1 Mesh, boundary conditions and loading

Due to the symmetry of the beams, only one fourth is modeled (half width and half length). Concrete is meshed using eight node elements (1.5 cm side) (Fig. 10). Steel is represented by 1D truss elements with the same horizontal density as concrete (Fig. 11). Steel elements are positioned at the exact experimental location. Due to the choice of the concrete mesh density in the cross section, steel and concrete elements are not coincident. The curved anchorages are not explicitly modeled. They are replaced by cinematic relations that impose the same displacement for steel and concrete at each end of the horizontal bars. It is to be noted that the simulation is performed using a three dimensional model in order to evaluate local effects like cover effects or the behavior around the steel bars.

Fig. 10

Concrete mesh (half-length and half-width) (dimensions in mm)

Fig. 11

Steel mesh (tensile bars, compressive bars and stirrups) on the left. Cross section in the constant moment zone on the right. Dimensions in mm

For the boundary conditions, a zero normal displacement is applied on each face of symmetry. A simple support (zero vertical displacement) is supposed at the location of the experimental support. Finally, the loading is considered by imposing a monotonic vertical displacement at the location of the loading support (Fig. 12).

Fig. 12

Boundary and loading conditions

3.2 Constitutive laws for steel and concrete

Steel reinforcements follow a usual Von Mises perfect plastic law. The model parameters are chosen to represent the experimental evolution (Young modulus equal to 190 GPa and elastic limit equal to 550 MPa)

For concrete, a damage model, including irreversible strains, is chosen (Costa et al. 2004). In this law, damage is represented by two independent variables $d^{+}$ and $d^{-}$ which have respectively an influence in tension and compression. The stress $\sigma$ is evaluated thanks to the following relation :

$$\begin{aligned} \sigma =\left[ {1-d^{+}\left( {\sigma ^{{\prime }+}} \right)} \right]\sigma ^{{\prime }+}+\left[ {1-d^{-}\left( {\sigma ^{{\prime }-}} \right)} \right]\sigma ^{{\prime }-} \end{aligned}$$

(1)

where $\sigma ^{{\prime }+}$ and $\sigma ^{{\prime }-}$ correspond respectively to the positive and the negative parts of the effective stress $\sigma ^{{\prime }}$:

$$\begin{aligned} \sigma ^{{\prime }}=C\left( {\varepsilon -\varepsilon ^{p}} \right) \end{aligned}$$

(2)

In this relation, $C$ is the tensor of elasticity and $\varepsilon$ represents the total strain. $\varepsilon ^{p}$ symbolizes the irreversible strains governed by the damage evolution in compression.

$$\begin{aligned} \dot{\varepsilon }^{p}=\beta EH(\dot{d}^{-})\frac{\left\langle {\sigma ^{{\prime }}:\dot{\varepsilon }} \right\rangle }{\sigma ^{{\prime }}:\sigma ^{{\prime }}}C^{-1}:\sigma ^{{\prime }} \end{aligned}$$

(3)

where $\beta$ is a model parameter, $E$ the Young modulus and $H$ the Heaviside function. $\langle .\rangle$ represents the positive part of the tensor.

The model parameters have been chosen to be as representative as possible to the experimental results. As already mentioned by different authors (Mivelaz 1996 for example), a special care was needed for the determination of the structural tensile strength. In our case, it was chosen equal to 2.5 MPa to correctly represent the threshold of cracking, experimentally observed on the beams. It is to be noted that this value is smaller than the splitting tensile strength (3.2 MPa). This difference can be attributed to the specificity of the splitting test (which generally leads to higher values of the strength) and also to the structural size effect which classically imposes smaller values. With these conditions, parameters given in Table 4 are chosen. The tensile part of the model is regularized using the Hillerborg concept of fracture energy that guarantees a constant energy release, independently from the mesh size (Hillerborg et al. 1976).

Table 4 Parameters for the concrete constitutive law

In the constant moment zone, a homogeneous loading is applied. To enable a localization of the damage, heterogeneity is introduced through a scattered distribution of the damage threshold strain defined as the ratio between the tensile strength and the Young modulus of concrete. The obtained distribution is illustrated in Fig. 13.

Fig. 13

Scattered distribution of the damage threshold strain

3.3 Bond conditions

One of the key points of the simulation is the modeling of the bond between steel and concrete. In this contribution, two simulations are compared.

First, a perfect relation is considered. It is the classical hypothesis used for structural applications. It means that the same displacement is imposed in each direction for both steel and surrounding concrete, using kinematic relations between the nodal displacements:

$$\begin{aligned} \left\{ {\begin{array}{l} u_{s1,x} =\sum \limits _{i=1}^8 {N_i (s_1 )u_{ci,x} } \\ u_{s1,y} =\sum \limits _{i=1}^8 {N_i (s_1 )u_{ci,y} } \\ u_{s1,z} =\sum \limits _{i=1}^8 {N_i (s_1 )u_{ci,z} } \\ \end{array}} \right. \end{aligned}$$

(4)

where $\vec {u}_{s1}$ (with components $u_{s1,x}, u_{s1,y}, u_{s1,z})$ and $\vec {u}_{ci}$ (with components $u_{ci,x}, u_{ci,y}, u_{ci,z})$ correspond to the displacement of the steel node ($\text{ s}_{1})$ and of the ith node ($\text{ c}_{i})$ of the concrete element in which $\text{ s}_{1}$ is included (configuration presented in Fig. 14 for the x direction). $N_{i}(\text{ s}_{1})$ is the ith shape function evaluated at the initial position of the steel node $s_{1}$. Even if this model is easy to implement, it fails, by definition, in taking into account the slip between steel and concrete (same displacement $=$ no slip).

Fig. 14

Nodal configuration between steel and surrounding concrete elements. Perfect relation (Casanova et al. 2012)

In the second simulation, the model proposed in (Casanova et al. 2012) is used. Instead of the perfect relation in the direction of the steel elements, internal nodal forces, function of the slip between steel and concrete at the position of the steel node, are introduced to represent the bond effects (Fig. 15). These forces are explicit functions of the slip, following the equation:

$$\begin{aligned} \vec {F}_{cs1/s1} =\delta \pi d_s lf_b \left( {\left| s \right|} \right)\cdot \vec {t} \end{aligned}$$

(5)

where $\vec {F}_{cs1/s1}$ is the internal bond force applied to the steel node, $\delta$ is a function of the slip sign, $d_s$ is the bar diameter, $l$ is a function of the size of the steel element, $\vec {t}$ is the direction of the steel element and $f_b \left({\left| s \right|} \right)$is a law that relates the bond stress to the bond slip.

Fig. 15

Principle of the bond model. Top: definition of the nodal bond slip at the steel node. Bottom: definition of the internal bond forces at the concrete and steel nodes. In this case, the direction of the steel element is taken equal to the x direction (Casanova et al. 2012)

In the simulation, the bond model is only applied to the tensile reinforced bar while a perfect relation is always assumed for the compressive reinforcement and the stirrups. The bond stress $\tau$ (in MPa)—bond slip $s$ (in mm) law $f_{b}$ is defined using the methodology proposed in (Torre-Casanova 2012) and follows the equation:

$$\begin{aligned} \begin{array}{ll} \uptau =10^{3}\text{ s}&for\,\tau <2\,MPa \\ \uptau =10^{2}\text{ s}+1.8&for\, 2\,MPa<\uptau <5\,MPa \\ \uptau =15s+4.5&for\, 5\,MPa<\tau <12\,MPa \\ \end{array} \end{aligned}$$

(6)

Figure 16 illustrates the obtained evolution and a comparison with the one proposed in (Harajli 1994). The curve is only defined in the hardening phase as the values of the simulated slips remain below 0.5 mm (checked after the simulation). The exponential law proposed by Harajli (1994) is taken as a reference as it reproduces the experiments performed in (Torre-Casanova 2012). It just has been simplified to become piecewise linear with a strong attention to the beginning of the curve (initial slope especially). The maximum values of the bond stress and the associated bond slip have been computed using the methodology proposed in (Torre-Casanova et al. 2013).

Fig. 16

Bond stress—bond slip law. Comparison between the proposed model and the evolution from (Harajli 1994)

3.4 Characterization of the crack properties

Using a damage model for concrete asks the question of how to characterize the crack discontinuity from a continuous description of the problem. To answer this question, the principle proposed by (Matallah et al. 2010) is used. It consists in defining a cracking strain $\varepsilon _f$ from the distribution of the total strain $\varepsilon$ and of the total stress $\sigma$ following the equation:

$$\begin{aligned} \varepsilon _f =\varepsilon -\varepsilon _{el} \end{aligned}$$

(7)

where

$$\begin{aligned} \varepsilon _{el} =\frac{1+\nu }{E}\sigma -\frac{\nu }{E}tr\left( \sigma \right)I \end{aligned}$$

(8)

with $E$ and $\nu$ respectively the concrete Young modulus and Poisson ratio. “tr” stands for the trace operator and $I$ is the identity matrix. With this technique, the cracking strain corresponds to the inelastic part of the total strain.

From the distribution of the cracking strain, the crack opening is calculated by multiplying it by the length $h_{n}$ of each concrete element in the direction $n$ normal to the crack (computed from the direction of the strain localization bands)

$$\begin{aligned} w_n =\left( {n^{t}\cdot \varepsilon _f \cdot n} \right). h_n \end{aligned}$$

(9)

In our case, as the cracks have a vertical direction in the constant moment zone, $h_{n}$ will be taken equal to the length of each concrete element in the horizontal direction. It is to be noted that this technique is especially applicable for softening laws associated to Hillerborg concept of fracture energy for which the strain is still localized in one element (for reasonably fine element size).

4 Results

In this part, numerical and experimental results are compared in order to evaluate the influence, and the interest, of the bond model on the global and local structural behaviors of the tested reinforced concrete beams.

4.1 Global behavior

Figure 17 illustrates the global force—deflection curves (vertical displacement at midspan for the top of the beam–c sensor in Fig. 6) with a comparison between experiment and numerical results. In both cases, the simulation is able to reproduce the experimental behavior in three stages: a linear elastic evolution where steel and concrete behave elastically, the cracking stage where damage develops in concrete while steel remains elastic and the plastic stage with inelastic behaviors for both steel and concrete. No real difference is observed between perfect relation and bond model on the global behavior, except perhaps during the beginning of the cracking stage where the structural stiffness is smaller for the simulation using the bond stress—slip law.

Fig. 17

Force—deflection curve. Experimental and numerical results

Figure 18 shows the evolution of the vertical displacements in the constant moment zone obtained from the vertical sensors and a comparison with the simulations. Experimentally, classical results are obtained. From the simulations, it is possible in both cases to reproduce the evolution of the displacement in a correct way (maximum relative difference of about 20 %). Once again, no clear difference can be highlighted between simulations using, or not, the bond model.

As a conclusion, both simulations are able to reproduce quite well the experimental global behavior and the bond model does not seem to influence it.

Fig. 18

Deformed shape (vertical displacement) for a force equal to 36 kN. Experimental and numerical results

4.2 Horizontal displacements

First, experimental comparisons are performed on the horizontal displacements in order to validate the image correlation technique. Results obtained from the horizontal sensors are compared to the distribution given by the image correlation for different values of the force (Fig. 19). A zero horizontal displacement is supposed at the midspan to correct the rigid body displacement. A good agreement is observed between the two techniques which validates the methodology. The differences can be explained by a non-totally symmetric cracking behavior in the depth of the beam.

Fig. 19

Horizontal displacement. Experimental comparisons between LVDT sensors and image correlation

Moreover, as previously mentioned, the image correlation technique is able to provide “continuous” information on the front face while the sensors provide only localized information (cumulated displacement along the sensors). Especially, the image correlation technique enables to precisely locate the jumps in the displacement that characterize the crack opening. In this sense, it represents a real advantage compared to classical measurement methods. In the following, only results from image correlation technique will be presented.

A comparison on the horizontal displacement is proposed between the experiment and the simulations for two values of the force (25 kN for Fig. 20 and 36 kN for Fig. 21). Experimentally, two curves are proposed in the figure, one for each tested beam. Concerning the numerical results, both simulations are able to capture the values of the horizontal displacement. It validates the ability of the models to be globally representative of the cracking behavior. More precisely, the bond model seems to better estimate the horizontal displacements at the beginning of the cracking process (25 kN) for which the perfect relation underestimates the horizontal displacement. But, when the crack is developed (36 kN), the differences between the two simulations tend to decrease.

Fig. 20

Evolution of the horizontal displacement along the beam. Applied force equal to 25 kN

Fig. 21

Evolution of the horizontal displacement along the beam. Applied force equal to 36 kN

This evolution can probably be explained by the competition between two effects: the stress transfer associated to the bond effect at the beginning of the cracking process and the development of damage in concrete during loading which tends to limit the effect of the bond model.

4.3 Cracking properties

Image correlation gives access to local results on the front face. It thus enables to produce results concerning the crack opening and spacing. Table 5 summarizes the results for four characteristic values of the applied force concerning the number of cracks and the crack opening along the bottom line of the front face (cumulated, mean and maximum values). Experiment and simulations are compared. Experimental values correspond to the mean values measured on the two tested beams. That is why non integer values are obtained for the number of cracks for example.

Table 5 Crack properties for 4 values of the force

Concerning the crack spacing, the bond model seems better appropriate to represent the apparition of the cracks. With the perfect relation, the final number of cracks is correctly represented (13 cracks) but the initiation and the development of the cracks are not so well simulated (underestimation of the number of cracks for 20 kN). For the opening, this table confirms the tendency observed on the horizontal displacement curves. The introduction of the bond model improves the simulation of the cracking behavior in the active cracking phase (20 and 25 kN). The difference tends to decrease with the development of the cracks. Nevertheless, the simulation using the bond model gives crack openings which are generally higher than those obtained with the perfect relation.

It is to be noted that the experimental initiation of crack seems faster than the simulated one. It is especially visible for a force of 20 kN for which the maximum and cumulated values are higher than the simulated ones. This difference at the very beginning of the cracking phase could be explained by the choice of the constitutive law (as the crack opening is in our approach a direct function of the strain which depends on the chosen constitutive law) or by the approximate evaluation of the structural tensile strength (see Sect. 3.2) (as the value of the tensile strength directly influences the end of the initial linear elastic phase). This point would need a further study to quantitatively investigate the influence of both effects on both global (small overestimation of the experimental curve) and local results. Figure 22 shows the evolution of the cumulated crack opening on the bottom line of the front face with the force. A good agreement is achieved between experiment and simulations. As already mentioned, the introduction of the bond model tends to increase the crack opening and to improve the response. Especially, during the active cracking phase at the beginning of the loading. It is more or less the same for the maximum value of the crack opening (Fig. 23). Globally, a good agreement is obtained with the simulations.

Fig. 22

Force—cumulated crack opening (bottom line of the beam) curve

Fig. 23

Force—maximum value of the crack opening (bottom line of the beam) curve

One of the main advantages of the correlation technique is to give access to cracking results in every point of the considered face. It becomes possible to investigate local results. For example, Figs. 24 and 25 give the cumulated crack opening in the height of the beam for two values of the force (25 and 36 kN). In the first figure, the influence of the bond model is clearly underlined. Taking into account the bond effects improves significantly the simulation of the crack opening. When the cracking is developed, the differences between the two simulations tend to decrease and the results are more or less the same. It is also interesting to notice that in both cases the position of the “neutral axis” (zero crack opening) is correctly reproduced.

Fig. 24

Cumulated crack opening in the height at a force of 25 kN

Fig. 25

Cumulated crack opening in the height at a force of 36 kN

To conclude the comparison between the simulations, Figs. 26 and 27 give the tensile damage distribution ($d^{+}$ in Eq. (1)) for a force equal to 36 kN along two lines. The first line corresponds to the external bottom line at the width of the tensile steel bar while the second one includes the concrete element surrounding the tensile steel reinforcement.

Fig. 26

Damage evolution along the bottom line at mid-depth (F = 36 kN)

Fig. 27

Damage evolution along the concrete element surrounding the tensile steel bar (F $=$ 36 kN)

Damage is equal to zero in the safe parts of the structure and equal to one at the position of the cracks. If the external behavior is considered (Fig. 26), as already mentioned, no real difference is observed between the two simulations. The failure mode is similar. But if the internal behavior is observed (i.e. near the steel reinforcement, Fig. 27), the perfect relation involves a total degradation of the surrounding concrete elements (damage almost equal to one along the whole line) whereas with the bond model, the degradation is more progressive and certainly more representative of the experimental behavior. This effect is directly influenced by the introduction of a bond slip with the bond model as illustrated in Fig. 28. As expected (Au and Bai 2007), the crack location (damage equal to one) coincides with a “discontinuity” in the slip distribution which cannot be captured, by definition, with the perfect relation (same displacements between steel and concrete). It is to be noted that the maximum values of the slip reached around 45 $\upmu \text{ m}$. It validates the definition of the numerical bond stress—bond slip law only in the hardening phase, as the bond model is only used in the very beginning of the law.

Fig. 28

Evolution of the damage in tension and of the bond slip along the concrete element surrounding the steel bar (F $=$ 36 kN)

Figures 29 and 30 give the evolution of the steel stress along the tensile steel bar for two values of the force (active cracking phase—25 kN and stabilized phase—36 kN). In the constant moment zone, the steel stress is directly influenced by the distribution of the shear stress. During the active cracking phase (Fig. 29), the steel stress obtained with the bond model is higher. This difference can be explained by two effects:

• The introduction of the bond slip, instead of the perfect relation, which “releases” the concrete at the position of the crack, especially when the cracks appear

• The decreasing slope at each side of the crack which is influenced by the bond model (stiffer behavior with the perfect relation)

After the apparition of the cracks, the differences in the stress distribution (Fig. 30) tend to decrease as the stress distribution is rather influenced by the development of concrete damage than by the stress transfer due to the bond.

Fig. 29

Evolution of the axial steel stress along the tensile steel bar (F $=$ 25 kN). Comparison between the perfect relation hypothesis and the bond model

Fig. 30

Evolution of the axial steel stress along the tensile steel bar (F $=$ 36 kN). Comparison between the perfect relation hypothesis and the bond model

5 Conclusions

In this contribution, experimental and numerical results were presented in order to characterize the cracking behavior of two reinforced concrete beams loaded in four point bending. The objective was to provide experimental results concerning the cracks and to numerically evaluate the influence of taking into account a steel-concrete bond model for the simulation of a four point reinforced concrete beam.

Experimentally, the use of image correlation technique enabled to obtain local results concerning the cracking. Maximum, mean and cumulated crack openings were measured especially. The data obtained from the correlation technique were compared to classical sensors and validated the chosen method. Compared to more usual approaches, this technique gave access to the distribution of the displacement field on the whole instrumented face. In this sense, this contribution provides interesting results for numerical comparisons and benchmarking activities.

Numerically, two approaches were compared, taking into account the bond slip effect between steel and concrete or considering the classical perfect relation hypothesis. The comparison between the two simulations leads to the following conclusions:

• Concerning the global behavior, on the force-deflection curve (global behavior), no significant difference was noticed considering or not the bond model and a good agreement with experimental results was achieved in both cases.

• Concerning the cracking behavior (studied on the external instrumented face) :

• the introduction of the bond model enables to improve the description of the “active cracking phase” (beginning of crack apparition) with, especially, a better agreement on the crack spacing.

• After the apparition of the main cracks, the local behavior is rather governed by the concrete damage and the bond model does not influence any more the results with similar crack properties obtained with both simulations

• Concerning the cracking behavior (studied inside the concrete, near the tensile steel bar), taking into account the steel-concrete bond has a high impact in the neighborhood of the steel bars. It avoids the well-known localization of the damage along the bar. This point may be of great interest, especially when local damages inside the structure are needed (evaluation of the transfer properties for example).

As a conclusion, taking into account numerically the steel – concrete bond for this particular example (i.e. for this geometry and for this four point bending loading) presents an interest for the description of the active cracking phase and for the local mechanical degradation. If global or “stabilized” results are needed, the perfect relation is sufficient to provide acceptable results. It is to be noted that this conclusion is highly dependent on the shape of the bond stress – bond slip law which has been calibrated in this present study from experimental results. Moreover, further studies on different cases (influence of the concrete cover for example) or loadings (three point bending for example) should be performed in order to generalize these conclusions.