1 Introduction

In recent years, increased demand for using performance-based design methods has made researchers to intensify their efforts to modify and enhance the accuracy of nonlinear static procedures on a variety of structural models. A number of those methods have been implemented in different design codes and guidelines. These procedures apply constant load patterns, such as equivalent lateral force, first mode shape and response combination load patterns in performing pushover analyses [1].

The preliminary methods consist of decomposition of axial force into two parts. Each part of the axial force is considered with one of the moments which are applied in the two main directions of the section. After separate sets of calculations are made, the computed stresses are superimposed [2]. These simplified models do not reflect the nonlinearity of materials. Richard Yen [3] has proposed a model to calculate “Reinforced Concrete” (RC) sections under biaxial-bending moment based on the position of the neutral axis and the percentage of longitudinal reinforcement. In this method, many simplifications are used that have a detrimental effect on the precision of the results. Yau et al. [4] have proposed a method to calculate the ultimate strength of the sections under biaxial-bending moment using the percentage of longitudinal reinforcement and the distance between the neutral axis and the point with maximum compressive stress, as main parameters. Alnoury et al. [5] have proposed a method using the tangent of the force–displacement curve and the local rigidity in the section level. The model proposed by Hsu et al. [6], which uses the developed Newton–Raphson method and simplified models of strain–stress curves for concrete and reinforcement, is not applicable for the descending branch of the “moment–curvature” (M–ϕ) curve. Brondum-Nielsen [7, 8] has proposed a method to calculate the ultimate strength of the sections under biaxial-bending moment using the developed Newton–Raphson method and the simplified rectangular model of strain–stress for concrete recommended by the CEB-FIP code. Zak [9] has also proposed a method to calculate the ultimate strength of the sections under biaxial-bending moment using the developed Newton–Raphson method. The Newton–Raphson method yields a fast solution, but presents problems while descending the response curve and near the inflection point that causes the divergence of the solution. Newton’s method, well adapted for monotonic curves, needs to be transformed at each relative extreme point occurrence. The maxima have to be evaluated anyway. The Ricks method, derived from Newton’s, allows the user to cross over the peaks. Newton and Ricks processes could be considered as “auto-blind methods”, and must be used with caution in the numerical simulation. Hashemi and Vaghefi [10] have investigated the effect of bond-slip on the bearing capacity of reinforced concrete columns subjected to axial force and biaxial-bending moment. They concluded that, although the ACI318-11 criteria is based on the perfect bond assumption, the global results using ACI assumption are conservative anyway due to the fact that the beneficial effect of stirrups confinement on the concrete compressive strength is neglected.

Among several existing techniques, to analyze the RC sections under “Biaxial-Bending Moment and Axial Loading” (BBMAL), two of them are the most common: direct search procedure to obtain the strain equilibrium plane and direct search procedure to find the location of the neutral axis.

The direct search procedure can be divided into two main approaches. Except for the case of the linear approach where exact integration rules can be used, the section is generally discretized into parallel layers rotating with the neutral axis. This method can be applied only in the monotonic loading case. Another way consists in discretizing the cross section into FRFE. This method can be used under any loading mode.

The aim of this paper is to propose a simulation method to assess the RC columns under “Oriented Pushover Force and Axial Loading” (OPFAL) in any direction (i.e., sections under BBMAL) using VOFE in the discretization of the sections and the advantages of the nonlinear real behavior of materials.

2 Mechanical Equilibrium of Sections

2.1 Basis of the Proposed Numerical Simulation Method

The column is decomposed into two segments (Macro-Elements) that are positioned between the inflection point (zero moment) in the middle of the column and the critical sections (maximum moments) at the column’s two ends. The nonlinear behavior of each Macro-Element (as Base Model) is analyzed. A Base Model is a half-column under OPFAL applied in any direction. To find the status of a full-scale column, the secondary moments due to P-∆ effect are also considered in the analysis of the entire column.

2.2 Discretization Principles

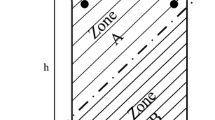
In the proposed simulation, the sections of column are discretized into VOFE that always stay parallel to the neutral axis. Two different widths are adopted for VOFE in a section. The frontier between two zones A and B which can have different oblique element widths are selected to pass a fixed point M at the corner of section, as shown in Fig. 1. In this case, the number of elements is limited to “m + n”, while if using FRFE discretization, the section is divided into “m·n” elements (m and n are numbers of elements along the larger and smaller sides of the section, respectively).

Fig. 1
figure 1

Discretization of a section into VOFE

Full size image

Since, zone A is usually under tension or under low compression stresses and its contribution in resisting axial force and bending moments is low, the width of elements situated in zone A can be selected to be greater than the width of elements situated in zone B. This reduces the number of elements.

Using this type of VOFE discretization, the time of calculation is significantly decreased, and since the proposed oblique elements always stay parallel to the neutral axis, there is a uniform stress distribution along each oblique element, which increases the accuracy of the results.

Figures 1, 4, 5, and 6 show schematically the principal notations used in the proposed model.

In this method, the inclinations of the oblique finite elements and the position of their respective centers of gravity are variable. To calculate structural members under monotonic pushover loading, there is no need to save the previous steps of loading, which significantly saves the calculation time.

As confirmed by Abbasnia et al. [11], it is to be noted that VOFE and fiber discretization approaches are able to consider the simultaneous effects of axial load and flexural moment in more precise stress distribution along the member length and cross-sectional area. In addition, because materials in terms of steel and concrete are defined as stress–strain constitutive behavior in these approaches, the transverse confinement effect as a key factor in concrete deformability could conveniently be incorporated into the analytical procedures.

2.3 Fundamental Assumptions

In the proposed method for each concrete and reinforcement element, a uniaxial behavior is considered and their strain distributions are assumed to form a plane, which remains a plane during deformation (Kinematics Navier’s hypothesis). The basic equilibrium is justified over a critical hypothetical cross section assuming the Navier’s hypothesis with an average curvature. A perfect bond condition between reinforcing steel bars and surrounded concrete is assumed in the proposed method.

2.4 Concrete Behavior Modeling

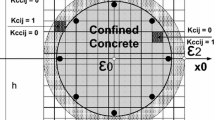
For compressive confined and unconfined concrete elements, the monotonic parts of cyclic stress–strain models proposed by the author [12] have been used. Equations (1) and (2) present the used models that are valid for concretes with the strengths within the range of 20 MPa < \(f_{c}^{\prime }\) < 50 MPa:

$$\sigma = \frac{{f_{c}^{\prime } }}{{A\left( {\frac{\varepsilon }{{\varepsilon_{0} }}} \right)^{2} + B\left( {\frac{\varepsilon }{{\varepsilon_{0} }}} \right) + C + D\left( {\frac{\varepsilon }{{\varepsilon_{0} }}} \right)^{ - 1} }}\quad \left( {{\text{for}}\,{\text{unconfined}}\,{\text{concrete}}} \right)$$
(1)
$$\sigma = \frac{{f_{cc}^{\prime } }}{{A_{L} \left( {\frac{\varepsilon }{{\varepsilon_{c0} }}} \right)^{2} + B_{L} \left( {\frac{\varepsilon }{{\varepsilon_{c0} }}} \right) + C_{L} + D_{L} \left( {\frac{\varepsilon }{{\varepsilon_{c0} }}} \right)^{ - 1} }}\quad \left( {{\text{for}}\,{\text{confined}}\,{\text{concrete}}} \right) .$$
(2)

The values of \(f_{cc}^{\prime }\) and ɛ c0 [12, 13] are given as:

$$f_{cc}^{'} = f_{c}^{'} \left( {1.000 + 2.5a.\omega_{w} } \right)\quad \left( {{\text{for}}\;\sigma /f_{c}^{\prime } < 0.05\;{\text{or}}\;a.\omega_{w} < 0.1} \right)$$
(3)
$$f_{cc}^{'} = f_{c}^{'} \left( {1.125 + 1.25a.\omega_{w} } \right)\quad \left( {{\text{for}}\;\sigma /f_{c}^{\prime } \ge 0.05\;{\text{or}}\;a.\omega_{w} \ge 0.1} \right)$$
(4)
$$\varepsilon_{c0} = \varepsilon_{0} \left( {\frac{{f_{cc}^{\prime } }}{{f_{c}^{\prime } }}} \right)^{2}$$
(5)
$${\text{with: }}\omega_{w} = k \left( {\frac{{A_{\text{t}} }}{{b_{\hbox{max} } . S_{\text{t}} }}} \right)\left( {\frac{{f_{\text{yt}} }}{{f_{c}^{'} }}} \right)$$
(6)
$$a = a_{n} . a_{\text{s}}$$
(7)
$$a_{n} = 1 - \frac{8}{3\eta }\quad \left( {{\text{P}} . {\text{S.: }}a_{n} = 1\;{\text{for}}\;{\text{circular}}\;{\text{sections}}} \right)$$
(8)
$$a_{\text{s}} = \left( {1 - \frac{{S_{\text{t}} }}{{2 b_{0} }}} \right)^{2} \quad \left( {{\text{for}}\;{\text{rectangular}}\;{\text{and}}\;{\text{circular}}\;{\text{sections}}} \right)$$
(9)
$$a_{\text{s}} = \left( {1 - \frac{{S_{\text{t}} }}{{2b_{0} }} } \right)\quad \left( {{\text{for}}\;{\text{circular}}\;{\text{sections}}\;{\text{with}}\;{\text{spiral}}\;{\text{transverse}}\;{\text{reinforcements}}} \right)$$
(10)

where σ represents the stress; ɛ represents the strain; \(f_{c}^{'}\) and \(f_{cc}^{'}\) represent compression strengths of unconfined and confined concretes at 28 days, respectively; ɛ 0 and ɛ c0 represent the strains related to \(f_{c}^{'}\) and \(f_{cc}^{'}\), respectively; A t represents the cross-sectional area of a transverse reinforcement; f yt represents the yield stress of transverse reinforcement; b max represents the larger dimension of the section; S t represents the longitudinal spacing between transverse reinforcements; a represents the confinement efficiency factor defined as the ratio of the confined area over the total area; a n represents the transverse reinforcement form factor; \(a_{\text{s}}\) represents the transverse reinforcements spacing factor; b 0 represents the distance between extreme longitudinal reinforcements in the two sides of the column section. The factors k and η and also the method to find the unknown coefficients A, B, C, D, A L , B L , C L, and D L are given in [12].

The concrete tensile stress is assumed to be linear up to the concrete ultimate tensile strength.

Figure 2 shows an example of the application of the compression stress–strain model proposed by the author [12] for confined concrete (\(f_{c}^{'}\) = 42 MPa) under monotonic loading.

Fig. 2
figure 2

Example of monotonic stress–strain curve for confined concrete

Full size image

2.5 Reinforcement Behavior Modeling

For the monotonic stress–strain model of reinforcements, the following expressions have been used. Typical graph to determine the behavior of steel bars under monotonic tension loading has the following four phases:

Phase 1—Linear elastic phase:

$$\sigma_{\text{s}} \left( \varepsilon \right) = E_{\text{s}} \varepsilon \quad \left( {{\text{for}}\;\varepsilon \le \varepsilon_{\text{y}} } \right)$$
(11)

where ɛ y represents the strain at starting point of plastic phase (yielding); E s represents the modulus of elasticity of steel bar.

Phase 2—Constant plastic phase:

$$\sigma_{\text{s}} \left( \varepsilon \right) = F_{\text{y}} \quad \left( {{\text{for}}\;\varepsilon_{\text{y}} < \left| \varepsilon \right| \le \varepsilon_{\text{sh}} } \right)$$
(12)

where ɛ sh represents the strain at starting point of strain hardening phase; F y represents yielding stress of steel bar.

Phase 3—Strain hardening phase:

In this phase, a relationship is employed to obtain a curve passing two known points A(x 0, y 0) and B(x 1, y 1) with two slopes m 0 and m 1 as follows:

$$y = y_{0} + m_{0} \left( {x - x_{0} } \right) + \mu \left( {x - x_{0} } \right)^{\beta }$$
(13)
$${\text{with: }}\mu = \frac{{y_{1} - y_{0} - m_{0} \left( {x_{1} - x_{0} } \right)}}{{\left( {x_{1} - x_{0} } \right)^{\beta } }}$$
(14)
$$\beta = \frac{{(x_{1} - x_{0} )\left( {m_{1} - m_{0} } \right)}}{{y_{1} - y_{0} - m_{0} \left( {x_{1} - x_{0} } \right)}} .$$
(15)

Therefore, for this phase, Eq. (16) is used [13]:

$$\sigma_{\text{s}} \left( \varepsilon \right) = {\text{Sign}}\left( \varepsilon \right)\left[ {F_{\text{y}} + E_{\text{sh}} \left( { \left| {\varepsilon - \varepsilon_{\text{sh}} } \right|} \right) - \frac{{\left| {\varepsilon - \varepsilon_{\text{sh}} } \right|^{{\left( {R_{1} } \right)}} }}{{R_{1} \left( {\varepsilon_{U} - \varepsilon_{\text{sh}} } \right)^{{\left( {R_{1} - 1} \right)}} }}} \right]$$
(16)

where F U represents ultimate strength of steel bar; ɛ U represents the strain at the peak point of the stress–strain curve and \(R_{1} = \left| {\frac{{E_{\text{sh}} \left( {\varepsilon_{U} - \varepsilon_{sh} } \right)}}{{F_{\text{U}} - F_{\text{y}} - E_{\text{sh}} \left( {\varepsilon_{U} - \varepsilon_{\text{sh}} } \right)}}} \right|\).

Phase 4—Final phase up to failure:

During this phase, in a monotonic loading case after peak point (ɛ U , F U), elongation increases up to failure without increasing any load.

Figure 3 shows an example of application of the stress–strain model used for reinforcements (F y = 470 MPa) under monotonic loading.

Fig. 3
figure 3

Example of the stress–strain curve for steel elements

Full size image

2.6 Materials Failure Criteria

For the maximum compression strain value (ɛ CU) of unconfined concrete of compression resistance \(f_{c}^{'}\), Eq. (17) given by CEB Code [14] is used. This equation is particularly applicable, where there is a loss of concrete cover outside the stirrups:

$$\varepsilon_{\text{CU}} = \left( {4 - 0.02f_{c}^{'} } \right)/1000\quad \left( {f_{c}^{\prime } \;{\text{in}}\;{\text{MPa}}} \right) .$$
(17)

For confined concrete constrained within stirrups, a different formula is used. In those cases in which the concrete is efficiently confined by the stirrups, the maximum strain of concrete is very big and failure normally occurs due to the first fracture in a stirrup. Equation (18) proposed by Sheikh [15] is used in the proposed simulation to determine the failure of confined concrete:

$$\varepsilon_{\text{CU}} = 0.004 + \left( {0.9\rho_{\text{s}} .f_{\text{yh}} } \right)/300\quad \left( {f_{\text{yh}} \;{\text{in}}\;{\text{MPa}}} \right)$$
(18)

where ρ s represents the ratio of transversal reinforcement volume per concrete volume situated inside the stirrups and f yh represents the yielding stress of the stirrups.

2.7 Sections Equilibrium

The fundamental relationships determining the equilibrium state of the sections are as follows:

  1. a)

    Equilibrium equation of axial forces in the center of the column section;

  2. b)

    Equilibrium equations of bending moments at the column section.

The general equilibrium system of each section consists of three nonlinear relations equating external and internal effects:

$$P_{\text{ext}} = P_{\text{int}}$$
(19)
$$Mx_{\text{ext}} = Mx_{\text{int}}$$
(20)
$$My_{\text{ext}} = My_{\text{int}}$$
(21)
$${\text{with: }}P_{\text{int}} = \mathop \sum \limits_{i}^{m} \sigma_{i} A_{i} + \mathop \sum \limits_{j}^{n} \sigma_{j} A_{j} + \mathop \sum \limits_{k}^{ns} \sigma s_{k} As_{k}$$
(22)
$$Mx_{\text{int}} = \mathop \sum \limits_{i}^{m} \sigma_{i} A_{i} y_{i} + \mathop \sum \limits_{j}^{n} \sigma_{j} A_{j} y_{j} + \mathop \sum \limits_{k}^{ns} \sigma s_{k} As_{k} y_{k}$$
(23)
$$My_{\text{int}} = \mathop \sum \limits_{i}^{m} \sigma_{i} A_{i} x_{i} + \mathop \sum \limits_{j}^{n} \sigma_{j} A_{j} x_{j} + \mathop \sum \limits_{k}^{ns} \sigma s_{k} As_{k} x_{k}$$
(24)

where P ext and P int represent the external and internal axial forces, respectively; Mx ext and My ext represent the external bending moments about x 0 and y 0 axes, respectively (see Fig. 4); Mx int and My int represent the internal bending moments about x 0 and y 0 axes, respectively; A i , A j, and As k are the areas of concrete element i (at zone A), concrete element j (at zone B), and steel elements, respectively (see Fig. 1).

Fig. 4
figure 4

Position and inclination of neutral axis on a section

Full size image

The moment equilibrium Eqs. (20), (21), (23), and (24) are considered about the orthogonal x 0 and y 0 axes passing through the center of the section [16] (see Fig. 4).

The proposed method requires the resolution of a quasi-static simultaneous equations system using a triple iteration process over the strains which depends on the position of the neutral axis. It is based also on the nonlinear stress–strain relationships for concrete finite elements and reinforcements. To reach equilibrium, three main characteristic parameters ɛ C (the strains in the extreme compression point of the section), X n, and Y n (coordinates of two points E and F at the intersections of the neutral axis with X and Y axes located on two perpendicular edges of the section), as shown in Fig. 4, are used as the three main variables.

2.8 Determination of Strains

The strain values of the elements are determined by taking into consideration the Kinematics Navier’s hypothesis (see Sect. 2.3). An equation is established for the strain plane based on strains of three nonaligned characteristic points on the section: C, the point representing maximum compression stress, and two points E and F at the intersections of the neutral axis with X and Y axes. The origin of XY Cartesian coordinates system is located at point C (see Fig. 4). The strain plane equation is given as follows:

$$\varepsilon = \varepsilon_{c} \left( {1 - \frac{x}{{X_{n} }} - \frac{y}{{Y_{n} }}} \right)$$
(25)

where x and y represent the coordinates of any point on the strain plane and ε represents its strain; ɛ c represents the strain at point C; X n and Y n represent coordinates of points E and F, respectively (see Fig. 4).

The strains of concrete and steel elements are determined by applying Eq. (25).

2.9 Determination of Neutral Axis Position

To find the solution of the equilibrium Eqs. (19), (20) and (21), four cases of movements for each position of neutral axis, composed of two cases of displacement and two cases of rotation, are considered (see Fig. 5). For two cases of displacements, two sets of increments of (+Δx, +Δy) and (−Δx, −Δy) are applied, and for two cases of rotations, two sets of increments of (+Δx, −Δy) and (−Δx, +Δy) are applied. Based on these four movements and by applying a comparative step-by-step method during the successive steps, the solution of equilibrium state for forces and bending moments is found. To complete these steps, the differences between external and internal forces and also the differences between external and internal bending moments are reduced to satisfy the acceptance criteria given in Sect. 3, below. The minimum differences allow one to determine the position of the neutral axis. To find the minimum differences, a linear combination of the resultant-bending moment and axial force which are normalized to their maximal values are used.

Fig. 5
figure 5

Four cases depicting increments of neutral axis position

Full size image

Based on \(M_{\text{ext}} \left( {k, l} \right)\) and \(\phi \left( {k, l} \right)\) (i.e., the applied external moment and relative curvature on the section l for loading step k), the parameters dM1 and dM2 (in the imposed force case) or dϕ1 and dϕ2 (in the imposed displacement case) are defined as follows:

$$dM1 = M_{\text{ext}} \left( {k - 1, l} \right) - M_{\text{ext}} \left( {k - 2, l} \right)\quad {\text{or}}\quad d\phi 1 = \phi \left( {k - 1, l} \right) - \phi \left( {k - 2, l} \right)$$
(26)
$$dM2 = M_{\text{ext}} \left( {k, l} \right) - M_{\text{ext}} \left( {k - 1, l} \right)\quad {\text{or}}\quad d\phi 2 = \phi \left( {k, l} \right) - \phi \left( {k - 1, l} \right) .$$
(27)

These parameters enable one to follow up the different phases of loading history on the sections. The typical trajectory of static pushover loading is described by the following expression:

$$\left[ {dM1 \ge 0\;{\text{and}}\;dM2 > 0} \right]\quad {\text{or}}\quad \left[ {d\phi 1 \ge 0\;{\text{and}}\;d\phi 2 > 0} \right] .$$
(28)

2.10 Determination of Curvatures

The strains at points 0, 1, and 2 (ɛ 0, ɛ 1 and ɛ 2) on the section shown in Fig. 6 are calculated by applying the strain of characteristic point C (ɛ C ), and X n and Y n parameters of neutral axis position in Eq. (25). Then, using these stras, the curvatures in directions x and y are calculated as follows:

$$\phi_{x} = \frac{{2\left( {\varepsilon_{2} - \varepsilon_{0} } \right)}}{b}$$
(29)
$$\phi_{y} = \frac{{2\left( {\varepsilon_{1} - \varepsilon_{0} } \right)}}{h} .$$
(30)

The maximum curvature is given as:

$$\phi = \frac{{\varepsilon_{C} }}{{h^{\prime}}}$$
(31)

where h ′ represents the distance between extreme compression point C and neutral axis.

Fig. 6
figure 6

Characteristic strains and parameters to find curvatures

Full size image

It can be proved that this maximum curvature can also be presented as:

$$\phi = \sqrt {\phi_{x}^{2} + \phi_{y}^{2} } .$$
(32)

3 Convergence Criteria

To achieve acceptable accuracy within a reasonable calculation time, the convergence tolerances are considered as:

$$\left| {\varOmega_{\text{ext}} - \varOmega_{\text{int}} } \right| \le 0.1^\circ$$
(33)
$$\left| {P_{\text{ext}} - P_{\text{int}} } \right| \le 0.001 P_{\text{ext}}$$
(34)
$$\left| {M_{\text{ext}} - M_{\text{int}} } \right| \le 0.001 M_{\text{ext}}$$
(35)

where \(\varOmega_{\text{ext}} = \varOmega = { \tan }^{ - 1} \left( {My_{\text{ext}} /Mx_{\text{ext}} } \right)\); \(\varOmega_{\text{int}} = { \tan }^{ - 1} \left( {My_{\text{int}} /Mx_{\text{int}} } \right)\); M ext = [(Mx ext)2 + (My ext)2]1/2 and M int = [(Mx int)2 + (My int)2]1/2.

4 Calculation of Deflections

In general, two methods are used to calculate deflections: “Curvatures Numerical Double Integration Method” (CNDIM) and “Elasto-Plastic Method” (EPM). In the first method, the equilibrium state is calculated in each cross section discretized along the length of the column and then a numerical double integration of curvatures φ x and φ y is performed to evaluate the deflection. To apply CNDIM, Eqs. (36)–(39) proposed by Lamirault and Bresse [17] are used to calculate the deflections and rotations in two principal directions of the sections along the length of the column.

$$\delta_{xl} = \mathop \sum \limits_{i = 1}^{i = l} {\text d}h\left[{\theta_{xi} + \left({\phi_{xi} + 2\phi_{{x\left({i - 1} \right)}}} \right){\text d}h/6} \right]$$
(36)
$$\delta_{yl} = \mathop \sum \limits_{i = 1}^{i = l} {\text d}h\left[{\theta_{yi} + \left({\phi_{yi} + 2\phi_{{y\left({i - 1} \right)}}} \right){\text d}h/6} \right]$$
(37)
$$\theta_{xl} = \mathop \sum \limits_{i = 1}^{i = l} {\text d}h\left[{\left({\phi_{xi} + 2\phi_{{x\left({i - 1} \right)}}} \right)/2} \right]$$
(38)
$$\theta_{yl} = \mathop \sum \limits_{i = 1}^{i = l} dh\left[ {\left( {\phi_{yi} + 2\phi_{{y\left( {i - 1} \right)}} } \right)/2} \right]$$
(39)

where dh = L/p; L represents the length of column; p represents the number of sections considered along the column); ϕ xi and ϕ yi represent the curvatures in two principal directions of section i; δ xl and δ yl represent the deflections of section l in x and y directions, respectively; θ xl and θ yl represent rotations of section l in x and y directions, respectively.

The deflections in two principal directions (δ xl and δ yl ) are calculated, and then, the resultant of their projections on the applied force direction is calculated. This method is time consuming in comparison with EPM.

The second method (EPM) is based on the evidence that a column is highly affected in the critical zone when a lateral load is applied. The main bending effect is due to the curvature registered at critical sections.

In the proposed method, the column deflections are determined using the EPM [18] considering mainly the curvature at the critical section and the length of the column. Immediately following the peak value of the M–ϕ curve of the critical section, a very important local effect occurs at the critical section where a pseudo-plastic hinge appears. Once the peak has passed, curvature enhancement is concentrated in the critical zone. While in the other regions, the curvatures decrease rapidly to near zero. In simulation, when applying EPM to calculate deflections, Eqs. (40) and (41) are used:

$$\delta = \left( {\frac{\phi }{3} L^{2} } \right)\quad \left( {{\text{for}}\;\phi \le \phi_{p} } \right)$$
(40)
$$\delta = \left( {\frac{{\phi_{p} }}{3} L^{2} } \right) + \left( {\phi - \phi_{p} } \right)\left( {L_{p} } \right)\left( {L - 0.5 L_{p} } \right)\quad \left( {{\text{for}}\;\phi \ge \phi_{p} } \right)$$
(41)

where \(\delta\) represents the deflection at the top of Macro-Element (half-column); \(\phi\) represents the curvature at critical section and ϕ p represents its value at the plastic hinge performance phase, respectively; L and L p represent the lengths of Macro-Element (half column) and the length of plastic hinge, respectively.

In Fig. 7, two methods of deflection calculation (CNDIM and EPM) and experimental values for pushover loading applied in the direction of Ω = 45° are compared. In this figure, the numerical simulation results, obtained by applying SADEP (see Sect. 5, below) and using FRFE option are shown. For CNDIM, the calculation up to the ultimate strength of the section is shown. As Fig. 7 shows, there is good agreement between simulated deflections by applying both mentioned methods and the experimental results in the elastic phase. In post-elastic phase, CNDIM underestimates the deflection values, while there is good agreement between the experimental results and simulated deflections using EPM.

Fig. 7
figure 7

Comparison of deflections using CNDIM and EPM, Ω = 45°

Full size image

5 Developed Computer Program

Computer program entitled “Structural Analysis and Damage Evaluation Program” (SADEP) has been developed by the author [19] to simulate numerically the behavior of RC structures under monotonic (pushover) and cyclic loading. SADEP has some sub-programs, such as BBCS (Biaxial-Bending Column Simulation), which is used as the Base Model and considers FRFE in the discretization of sections, SOPA (Static-Oriented Pushover Analysis) which is used as the Base Model and considers VOFE in the discretization of sections, CCS (Confined Concrete Simulation), UCS (Unconfined Concrete Simulation), SBS (Steel Bars Simulation), NAPS (Neutral Axis Position Simulation), DC (Deflection Calculation), and DIC (Damage Index Calculation).

In the recently added sub-program SOPA, behavior models for confined and unconfined concretes generated using CCS and UCS are considered and the behavior models of the columns are specified.

In SOPA, each section of the column is discretized into VOFE. In fact, in SADEP, two options for discretization of sections are applied: in BBCS, sections are discretized into FRFE, and in SOPA, the sections are discretized into VOFE.

SADEP deals with the numerical simulation of RC members under cyclic loading and OPFAL in any direction (i.e., BBMAL applied on sections), considering the nonlinear behavior of materials.

For compressive confined and unconfined concrete elements, the monotonic and cyclic stress–strain models proposed by the author [12], and for reinforcements, the expressions proposed by Park and Kent [13] based on the Ramberg–Osgood monotonic and cyclic models have been used. The concrete tensile stress is assumed to be linear up to the concrete tensile strength. The CEB code specification [14] is used for the maximum compression strain value of unconfined concrete, and the value proposed by Sheikh [15] is employed for confined concrete.

The basic equilibrium is justified over a critical hypothetical cross section, assuming the Kinematics Navier’s hypothesis with an average curvature. The method used qualifies as a “Strain Plane Control Process” that requires the resolution of quasi-static simultaneous equations system using a triple iteration process over the strains when the FRFE option is applied [19] and an iteration process to find the neutral axis position when the VOFE option is applied.

The program takes into account the confining effect of the transverse reinforcement and simulates the loss of the concrete cover. It allows the determination of the failure, the local internal behavior of critical sections (i.e., strains, stresses, neutral axis position, moment–curvature curve, cracks positions, loss of material, microscopic damage index, etc.) and the global external behavior of the column (deflection, average rigidity, equivalent viscous damping ratio, macroscopic damage index, etc.). The simulated results, obtained using SADEP, are confirmed by the full-scale experimental results obtained by other researchers [13, 20, 21].

6 Experimental Data and Reference Column

The proposed numerical simulation has mainly been validated by the experimental test results carried out at the University of Nantes [20–22]. Over 20 tests performed by Garcia Gonzalez [20] on full-scale columns under OPFAL are used. The horizontal loads through different horizontal directions of angles (orientations) Ω with the main axis of cross section have been applied on the top of the columns.

In this paper, the column tested by Garcia Gonzalez [20] is called “reference column” and its section is called “reference section”. Column dimensions and characteristics used in numerical simulations are as follows: rectangular section (18 cm × 25 cm), column height = 1.75 m, four longitudinal reinforcement with a diameter of 12 mm (ϕ12), concrete of strength \(f_{c}^{'}\) = 42 MPa, stirrup ties of diameter 6 mm with a longitudinal spacing of 9 cm (ϕ6@9cmc/c), yielding stress of steel bars: F y = 470 MPa. This column (i.e., Macro-Element, Base Model or half column) is fixed at the bottom, free at the top and is under an axial force of 500 kN and a monotonic or cyclic oriented lateral force at the top.

7 Analysis of the Obtained Results

In Fig. 8, the results of the proposed numerical simulation using VOFE and FRFE are compared with experimental test results for OPFAL with the orientation of Ω = 45°. As this figure shows for loading up to 85 % of the ultimate strength of the section, there is a better agreement between simulated results using VOFE discretization and experimental results than when the FRFE discretization model is employed.

Fig. 8
figure 8

Comparison of experimental values, VOFE-based and FRFE-based simulations, Ω = 45°

Full size image

Variations in neutral axis inclination (α) of the reference section for different pushover force orientations (Ω) are shown in Fig. 9. As this figure shows, the inclination of the neutral axis is not equal to pushover force orientation, except for the orientations of 0° and 90°. The neutral axis inclination is constant for low pushover force values and it has a deviation when approaching the maximum value of the applied pushover force.

Fig. 9
figure 9

Neutral axis inclinations (α) of the reference section for different values of Ω

Full size image

Figure 10 shows the variations of X n and Y n as a function of oriented pushover force applied on the top of the column with an orientation of Ω = 45°. As this figure shows by increasing pushover load, X n and Y n are reduced and Tan−1(Y n /X n ), which equals the inclination of neutral axis (α), first remains constant and then varies when ultimate pushover load is applied. This is reflected in Fig. 9.

Fig. 10
figure 10

Variations of X n and Y n for the reference section, Ω = 45°

Full size image

Figure 11 shows the variations of the position of the neutral axis at the critical section of the reference column when the oriented pushover force with the orientation of Ω = 45° is increased to its maximum value. It should be noted that according to the coordinate systems shown in Fig. 4, X n values are positive, but for illustration purposes only, they are shown in the negative form in Fig. 11. As shown in this figure, by increasing the pushover load (or moment), the neutral axis moves from outside the section to point T (with an inclination of about α = 55°) and then shifts toward the center of the section when the maximum load is applied (ultimate strength of the section) with an inclination of α = 60°. As it can be seen from Fig. 11, when the load is increased, the neutral axis moves with an approximately constant inclination up to the ultimate strength of the section. This indicates that there is no rotation of the section, while following the peak (ultimate strength of the section), there is a deviation in the direction of the neutral axis. This is mainly due to the loss of concrete cover and the yielding of compression steel. This deviation indicates a slight rotation of the section that occurs after the mentioned loading peak, which is normally ignored in the calculations.

Fig. 11
figure 11

Neutral axis positions of the reference section, Ω = 45°

Full size image

Based on the measurements on the full-scale experimental tests of Garcia Gonzalez [20], the evaluated neutral axis position when peak load is applied to the critical section of the reference column is shown by the dashed lines in Fig. 11. Garcia Gonzalez’s experimental results showed an inclination of α = 59° for the neutral axis when peak load was applied on the section for an orientation of Ω = 45°. Figure 11 shows there is a good agreement between simulated values and experimental results. Comparison of the simulated and experimental values shows a slight dislocation that is mainly due to the experimental procedure. The presence of only three strain gages in an experimental test can be accepted, but they were not positioned at the most sensitive points of the section to determine the strains at point C “maximum compression” and point T “maximum tension”.

The variations of the strains at the corners C, T, and M versus the applied moment on the critical section of the reference column under OPFAL of orientation Ω = 45° are shown in Fig. 12. The variations of ɛ M are very limited, and the greatest variation is in ɛ T .

Fig. 12
figure 12

Variations of strains at corners C, T, and M of critical section of reference column, Ω = 45°

Full size image

Figure 13 shows the variations of the M–ϕ curves of the critical section of the reference column under OPFAL for different values of axial force “Pext” for the pushover orientation of Ω = 30°. As this figure indicates, the rigidity and ultimate strength of the column are increased by increasing the axial force. In addition, it shows that the failure of the column occurs earlier by increasing the axial force, meaning a heavy axial load makes the column fragile, imposing a big loss of material, and reducing the ductility of the column. This type of fragility, reduction of ductility, and loss of material needs to be carefully considered in prestressed structural members design. Similarly, care needs to be taken in the design of structures being designed for seismic zones having a significant vertical force component of earthquake loading.

Fig. 13
figure 13

Effect of axial force on the response of the critical section, Ω = 30°

Full size image

Figure 14 shows the variations of M–ϕ curves of the critical section of the reference column under OPFAL for different values of longitudinal reinforcement for the pushover orientation of Ω = 30°. As this figure indicates, the rigidity and ultimate strength of the column are increased by increasing the percentage of the longitudinal reinforcements.

Fig. 14
figure 14

Effect of steel percentage on the response of the critical section, Ω = 30°

Full size image

Figure 15 presents the axial force-moment interaction diagram for the critical section of the reference column under the applied pushover force with the orientation of Ω = 0° for different slenderness ratios of the column.

Fig. 15
figure 15

Interaction diagram for different slenderness ratios of full-size columns (P-∆ effect), Ω = 0°

Full size image

8 Verification of the “Components Effects Combination Method” (CECM)

In seismic zones, the building codes generally accept the use of the combination of the components’ effects in linear and equivalent linear calculations. As an example, according to AFPS [23], in nonlinear calculations, the three components are to be considered simultaneously in calculation, but in linear and equivalent linear calculations, the maximum effect of each component can be determined separately and then combined according to the following formulation:

$$S = \mp S_{x} \mp \lambda S_{y} \mp \mu S_{z}$$
(42)
$$S = \mp \lambda S_{x} \mp S_{y} \mp \mu S_{z}$$
(43)
$$S = \mp \lambda S_{x} \mp \mu S_{y} \mp S_{z}$$
(44)

where S x , S y, and S z represent the deformations or loading due to horizontal and vertical components, respectively; and S represents their resultant values.

In general cases, λ and μ are taken equal to 0.4. The effect of the vertical component can be neglected (μ = 0 and the third equation “Eq. (44)” is neglected).

The application of this simplified method (CECM) is compared with the proposed “Simultaneous Direct Method” (SDM). To carry out this comparison, the responses of the critical section of the reference column under OPFAL for different orientations have been studied. Figure 16 shows the M–ϕ curves of the critical section of the reference column under OPFAL with orientations of Ω = 15°, 30°, and 60° for both the cases of calculation methods: CECM (according to AFPS) and SDM. Note that only the calculations up to the ultimate strength of the section are shown in Fig. 16.

Fig. 16
figure 16

Comparison between CECM and SDM for pushover orientations of 15°, 30°, and 60°

Full size image

Table 1 and Fig. 17 show the differences between the curvatures at peak points of the moment–curvature curves (ϕ max, M max) using SDM and CECM for different values of pushover orientation Ω.

Table 1 Comparison of curvatures at peak point (ϕ max, M max) when applying CECM and SDM
Full size table
Fig. 17
figure 17

Underestimation of curvature at peak of loading when using CECM

Full size image

It can be seen from the polynomial best fit curve shown in Fig. 17 that the maximum underestimation of the response is observed when the pushover force is applied in the direction of the diagonal of the section (diagonal orientation of reference section: Ω = Tan−1 (h/b) = 36°).

The following conclusions are obtained from the simulated columns (see also Figs. 16 and 17):

  • In the linear phase, there is a very good agreement between the results obtained from SDM and CECM for all orientations of applied pushover loads (Ω) (as confirmed by AFPS).

  • In the post-elastic phase, the difference between the calculated results using SDM and CECM increases when the load is increased.

  • In the post-elastic phase, CECM presents an underestimation of the response, which is not conservative. This underestimation is maximum at the peak of the M–ϕ curve for all orientations (Ω) of applied pushover loads.

  • In the case of applied force in the direction of the diagonal of the section, CECM gives a maximum error of around 50 %.

  • The obtained results show the necessity of applying SDM for nonlinear calculations. Especially, during the post-elastic phase, which occurs frequently during earthquake loading. In this case, the calculations performed by CECM give non-conservative results.

9 Conclusions

A nonlinear numerical simulation method using VOFE to simulate the behavior of RC columns subjected to OPFAL (i.e., BBMAL on sections) is proposed. A sub-program entitled SOPA, which employs VOFE, has been added to SADEP. In the proposed method, sections of the column are discretized into VOFE which always stay parallel to the neutral axis. To minimize the number of elements, two different widths are adopted for VOFE in a section. In this case, the number of elements in each section is limited to “m + n”. While in the case of FRFE discretization, the section is discretized into “m·n” elements. Using this type of VOFE discretization, the time of calculation is significantly decreased, and since VOFE always stay parallel to the neutral axis, variations of stress distribution along the element are significantly decreased. Therefore, the proposed method using VOFE presents more accurate results and is faster compared to the method using FRFE. The proposed numerical simulation method has been validated by experimental test results obtained from full-scale columns in the laboratory. The obtained results show that there is a very good agreement between SDM and CECM, in the elastic phase for all orientations of applied pushover loads. In the post-elastic phase, CECM presents an underestimated response and thus should be used with due caution. The obtained results demonstrate the significant benefits of applying SDM for nonlinear calculations.