Performance Evaluation of Grid-Connected Photovoltaic System Using EHO-Tuned VPTIDF and DQC-Based SPWM

Abstract

This manuscript presents the design of elephant herding optimization algorithm-tuned variable parameter tilt integral derivative with filter (EHO-tuned VPTIDF) controller to reduce the harmonic distortion and improve performance of grid-connected solar micro-inverter. Classical controllers with optimization techniques are seen to improve performance, but it failed to make the system robust. Robustness can be improved by considering control parameter as a function of error. This is utilized in the proposed novel control technique. The nonlinearities present in photovoltaic system framework cause power quality issues and occasional faults. The use of Levenberg–Marquardt algorithm (LMA)-based machine learning technique efficiently detects a fault condition from standard operating conditions efficiently. EHO-tuned VPTIDF along with direct and quadrature control (DQC)-based sinusoidal pulse width modulation (SPWM) technique is implemented in this manuscript. This proposed model is analyzed for reduction in harmonic, improved system performance and fault classification.

1 Introduction

The proposed system consists of components like photovoltaic (PV) array, boost converter, micro-inverter and EHO-tuned VPTIDF. The boost converter is realized using non-ideal boost converter model. The boost converter uses an insulated gate bipolar transistor (IGBT) and a diode as a switch (Sadaf et al. 2020; Padmanaban et al. 2018; Hu et al. 2019; Ayop and Tan 2018). The triggering pulse to the converter is provided by the proposed control technique (EHO-tuned VPTIDF). However, many researchers proposed various control techniques for generating gate pulses. Some of the prominent control techniques includes second-order generalized integrators-based phase locked loops (SOGI-PLL) (Xu et al. 2019; Ahmad and Singh 2017), proportional resonant controller (PRC) (Keddar et al. 2019; Huang et al. 2018; Sattianadan et al. 2020), hysteresis current controller (HCC) (Zhao et al. 2018), H bridge-based sinusoidal pulse width modulation (HB-SPWM) (Zeb et al. 2019), PLL-feed forward (Wang et al. 2020), proportional integral derivative controller (PIDC) (Khan et al. 2019).

The choice of fractional-order controller is done as most modern systems are slowly migrating toward fractional-order system structure (Sahu et al. 2016; Patra 2020; Patra and Nanda 2021). The reason behind the choice of migration is fractional-order system design creates a distribution of time constant, which in turn improves system responses. Fractional-order controllers are seen to demonstrate capabilities of suppressing chaotic behavior in mathematical models. While being used as controllers it serves various purposes. The basic purpose of fractional-order controllers is to mend the large stability of the proposed system, improve robustness, disturbance rejection ability against parameter uncertainties, better performance under abnormal operating condition and improved power quality. This proposed controller is a modification of Tilt Integral Derivative Controller (TIDC). The research gap is TIDC is it is not robust as their control parameters (tilt gain ($K_{{\text{t}}}$), integral gain ($K_{{\text{i}}}$), derivative gain ($K_{{\text{d}}}$), coefficient of tilt (n) and prefilter gain ($N$)) are considered as independent gain. The robustness of the controller can be improved by considering the control parameters as a function of error. The proposed approach proposes an answer to the research gap by proposing variable parameter tilt integral derivative controller. EHO-tuned VPTIDF controller combines the advantages of fractional-order calculus, control system and robustness (control parameter as a function of error). The control parameters of EHO-tuned VPTIDF are tuned for better response. This optimization of control parameters is achieved by using elephant herding optimization (EHO) algorithm technique (Li et al. 2020; Wang et al. 2015; Meena et al. 2017). The choice of EHO is because of its superior performance, faster convergence rate, more consistent and accurate results and easier implementation.

The voltage of boost converter is DC in nature and is fed directly to low power micro-inverter. The main advantage of using a micro-inverter is while micro-inverters for the most part have a lower proficiency than string inverters, the general effectiveness is expanded because of the way that each inverter unit acts freely (Razi et al. 2021; Çelik et al. 2020; Yaqoob et al. 2021). The micro-inverter system is tuned using DQC-based SPWM technique (Kalavalli et al. 2021; Chaithanakulwat et al. 2021; Missula et al. 2021). The stability analysis of the proposed control technique is done by analyzing Matignon stability theorem (Ben et al. 2017). IEEE-519 provides the standard for Total Harmonic Distortion ($THD$) measurement (Marrero et al. 2022). The occurrence of fault is integral to all power systems. Identifying the difference between a normal and a faulty system is critical for any fault detecting system. It is imperative to go for fault classification as it improves system response. The fault identification is achieved by using machine learning techniques (Fazai et al. 2019; Bilski et al. 2020). The use of Levenberg–Marquardt algorithm (LMA) improves the ability of fault detection. The choice of LMA, because it is an effective nonlinear approach for nonlinear regression problems, more steady, reduces mean square error (MSE) more effectively and short training time that results from a significant reduction of complexity of Jacobian matrix which in turn improves its implementation. The improved accuracy and stability, enhanced robustness, harmonic suppression and ability of fault detection, and better capability to handle uncertainties are the novelty of the proposed PV system. The proposed model along with MO-tuned VPTIDF provides the noteworthy contributions which are summarized below.

• Designing of a single-phase PV model in a MATLAB/SIMULINK environment for performance analysis.

• To design a novel control strategy EHO-tuned VPTIDF with DQC-SPWM for the PV system to enhance the performance and reduction in harmonic distortions.

• Assessment of harmonic distortion in proposed PV system to justify its better performance.

• Enhancement of robustness and improvement in fault identification ability of the proposed PV model.

• In order to validate overall superior performance a relative exploration of proposed photovoltaic model with pre-existing techniques is carried out.

The remaining of the manuscript is prearranged in the following order. Section 2 states the basis of photovoltaic cell, non-ideal boost converter, DQC-SPWM, micro-inverter and open-circuit analysis of the proposed model. Section 3 presents the details about the proposed control strategy (EHO-tuned VPTIDF). Section 4 displays the simulation results for performance, stability and robustness. The concluding remarks are presented in Sect. 5.

2 Problem Formulations

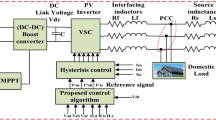
The PV system comprises of micro-inverter, PV cell, DQC-SPWM, triggering mechanisms, EHO-tuned VPTIDF and non-ideal boost converter. The framework for the proposed model is presented in Fig. 1a. Figure 1b presents single-diode model of solar PV cell. Figure 1c represents the circuit diagram of boost converter, Fig. 1d represents the non-ideal model of the boost converter and the detail model of the proposed PV system is represented in Fig. 1e. The voltage generated by solar or PV cell is very low in magnitude and it cannot be used. Hence, before inverting it to AC it is step up to higher DC level. This step up of voltage is achieved by using non-ideal boost converter. The detailed modeling of the PV system is presented in the subsequent subsections. The detailed parameters of the proposed PV system are placed in Table 1.

Fig. 1

a Block diagram of closed-loop PV system, b single-diode model of solar PV cell, c circuit diagram of ideal boost converter, d non-ideal model of boost converter and e block diagram model of proposed PV system

Table 1 Specification and parameter of the proposed PV system

2.1 PV Cell

To understand the basic behavior of PV cell it’s imperative to model it in electrical elementary terms. Under idyllic conditions PV cell behaves as a current source which has a diode connected in parallel to it. Under real-world conditions, the idyllic conditions do not stand a place. So to model the PV cell as per practical conditions series and shunt resistances are connected to the PV cell (Sadaf et al. 2020; Padmanaban et al. 2018; Hu et al. 2019; Ayop and Tan 2018). PV cell is realized by using its mathematical equivalences. The single-diode model of PV cell is represented in Fig. 1b. The current from PV cell is represented by $J$. The series and shunt resistances are $R_{{{\text{sh}}}}$&$R_{{\text{s}}}$, respectively. The current through diode, series resistance and shunt resistances are $J_{{\text{d}}}$, $J_{{\text{l}}}$ and $J_{{{\text{sh}}}}$, respectively. The voltage across shunt resistance and output voltage is $V_{{\text{j}}}$ and $V_{{{\text{in}}}}$, respectively. Reverse saturation current in amperes is represented by $J_{0}$, respectively. Thermal voltage and temperature are represented by $V_{{\text{t}}}$ and $T$.The mathematical expressions for $J$, $J_{{\text{d}}}$, $J_{{{\text{sh}}}}$ and $V_{j}$ is represented by Eqs. (1–4), respectively.

$$J = J_{{\text{l}}} - J_{{\text{d}}} - J_{{{\text{sh}}}}$$

(1)

$$J_{{\text{d}}} = J_{{\text{o}}} \left( {e^{{\frac{{V_{j} }}{{nV_{t} }}}} - 1} \right)$$

(2)

$${{J}}_{{{\text{sh}}}} { = }\frac{{{{V}}_{{\text{j}}} }}{{{{R}}_{{{\text{sh}}}} }} \,$$

(3)

$$V_{{\text{j}}} = V_{{{\text{in}}}} + J_{l} R_{s} .$$

(4)

The solar panel used in the scope of the manuscript has a maximum power rating of 60 Watt, voltage at maximum power is 33.54 V, current at maximum power is 1.89 A, open-circuit voltage is 39.66 V and short-circuit current is 1.99 A, respectively.

2.2 Boost Converter

Figure 1c represents the model for ideal boost converter. The non-ideal boost converter consists of two switches (one controlled and one uncontrolled), one capacitor ($C_{{{\text{out}}}}$) and one inductor ($L_{{{\text{in}}}}$). The controlled switch is insulated gate bipolar transistor ($IGBT$), while the uncontrolled switch is diode ($D$). The specification for diode to be used in converter is maximum reverse voltage is 100 V, maximum forward current is 40 A, forward bias voltage is 0.8 V, resistance of diode should be 1 mΩ. Similarly the specification for IGBT maximum collector current is 30 A, collector emitter voltage (saturation) is 1.95 V, maximum collector emitter voltage is 650 V and resistance of IGBT should be less than 1 mΩ. In order to investigate the steady state and dynamical behavior, it is essential to model the boost converter dynamically. There are many methods to mathematically model the boost converter. Some of the populous methods include switching flow graph, averaging technique, state space technique, current injection technique and bond graph method. All of these methods have their share of advantages and disadvantages. However, in most of these techniques all elements of boost converter are considered ideal. Hence an ideal control strategy is never formulated. When the elements are not considered ideal then an effective and ideal switching technique will be formulated. The boost converter is modeled by using non-ideal state space averaging technique.

2.2.1 Non-ideal Boost Converter

The exact model for non-ideal model of boost converter is represented in Fig. 1d. The parasitic resistance and equivalent resistances are also represented in the circuit. $R_{{{\text{SP}}}}$ represents the internal resistance of PV system. $R_{{{\text{in}}}}$ represents the Equivalent Series Resistance (ESR) of inductor. ESR value of inductor is less than 1 Ω. The internal resistance of IGBT is represented by $R_{{{\text{ONIGBT}}}}$. The ESR resistance connected in series with $C_{{{\text{out}}}}$ is $R_{{{\text{Co}}}}$. The typical value of $R_{{{\text{Co}}}}$ is less than 1 Ω. The Resistance of diode $D$ is represented by $R_{{{\text{Diode}}}}$. The forward voltage drop of diode is represented by a voltage source which is named as $V_{{{\text{fb}}}}$. The switching operation of IGBT present in boost converter is divided into two time frames. The time frames are on time and off time. The analysis is done separately for both on time and off time (Hu et al. 2019).

2.2.1.1 During IGBT on Time

The input loop equation of boost converter is represented by Eq. (5).

$$L_{{{\text{in}}}} \frac{{{\text{d}}I_{{{\text{SP}}}} \left( t \right)}}{{{\text{d}}t}} = - (R_{{{\text{lin}}}} + R_{{{\text{ONIGBT}}}} + R_{{{\text{SP}}}} )I_{{{\text{SP}}}} \left( t \right) + V_{j} (t).$$

(5)

In order to analyze the non-ideal modeling of boost converter, a small perturbation is applied to the boost converter. This current perturbation is $I_{{{\text{RLPE}}}}$. The non-ideal model of boost converter is represented in Fig. 1d. The current across capacitor $C_{{{\text{out}}}}$ is represented in Eq. (6).

$$I_{{{\text{Cout}}}} \left( t \right) = \frac{{C_{{{\text{out}}}} {\text{d}}V_{{{\text{Cout}}}} \left( t \right)}}{{{\text{d}}t}} = \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {R_{L} + R_{Co} } \right)}}V_{{{\text{Cout}}}} \left( t \right) - \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{R_{Co} }}I_{{{\text{RLPE}}}} \left( t \right).$$

(6)

The output voltage is represented by Eq. (7).

$$V_{{\text{b}}} \left( t \right) = \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {R_{Co} } \right)}}V_{{{\text{Cout}}}} \left( t \right) - \left( {R_{L} \left\| {R_{{{\text{Co}}}} } \right.} \right)I_{{{\text{RLPE}}}} \left( t \right).$$

(7)

Equations (5–7) can be written in state space equation form. The state variables are

$$\begin{aligned}& z_{2} \left( t \right) = \left| {\begin{array}{*{20}c} {I_{{{\text{SP}}}} \left( t \right)} & {V_{{{\text{Cout}}}} \left( t \right)} \\ \end{array} } \right|^{T},\\ &u\left( t \right) = \left| {\begin{array}{*{20}c} {V_{{\text{b}}} \left( t \right)} & {I_{{{\text{RLPE}}}} \left( t \right)} \\ \end{array} } \right|^{T} \end{aligned}$$

and $y\left( t \right) = \left| {\begin{array}{*{20}c} {V_{b} \left( t \right)} & {I_{J} \left( t \right)} \\ \end{array} } \right|^{T}$. The state equations are expressed by Eqs. (8–9), respectively.

$$\dot{z}_{2} \left( t \right) = A_{{w1}} z_{2} \left( t \right) + B_{{w1}} u\left( t \right) + G_{{w1}} V_{{{\text{fb}}}}$$

(8)

$$y\left( t \right) = C_{w1} z_{2} \left( t \right) + E_{w1} u\left( t \right) + H_{w1} V_{fb}$$

(9)

The state space matrices are represented below.

$$A_{w1} = \left| {\begin{array}{*{20}c} {\frac{{ - \left( {R_{{{\text{ONIGBT}}}} + R_{{{\text{in}}}} + R_{{{\text{SP}}}} } \right)}}{{L_{{{\text{in}}}} }}} & 0 \\ 0 & { - \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {C_{out} R_{L} R_{Co} } \right)}}} \\ \end{array} } \right|;\begin{gathered} G_{w1} = \left| {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \right|^{T} ; \hfill \\ H_{w1} = \left| {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \right|^{T} ; \hfill \\ \end{gathered}$$

$$B_{w1} = \left| {\begin{array}{*{20}c} {\frac{1}{{L_{in} }}} & 0 \\ 0 & { - \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {C_{out} R_{Co} } \right)}}} \\ \end{array} } \right|; C_{w1} = \left| {\begin{array}{*{20}c} 0 & {\frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {R_{Co} } \right)}}} \\ 1 & 0 \\ \end{array} } \right|; E_{w1} = \left| {\begin{array}{*{20}c} 0 & { - \left( {R_{L} \left\| {R_{Co} } \right.} \right)} \\ 0 & 0 \\ \end{array} } \right|;$$

2.2.1.2 During IGBT off Time

When IGBT is turned off and diode D is conducting, the input equation of boost converter is expressed by Eq. (10).

$$L_{{{\text{in}}}} \frac{{dI_{{{\text{SP}}}} \left( t \right)}}{dt} = - \left( {\left( {R_{{\text{L}}} + R_{{{\text{Diode}}}} + R_{{{\text{SP}}}} } \right) + \left( {R_{L} \left\| {R_{{{\text{Cout}}}} } \right.} \right)} \right)I_{{{\text{SP}}}} \left( t \right) - \frac{{\left( {R_{L} \left\| {R_{{{\text{Cout}}}} } \right.} \right)}}{{R_{{{\text{Cout}}}} }}V_{{{\text{Cout}}}} \left( t \right) + V_{{\text{j}}} \left( t \right) + \left( {R_{L} \left\| {R_{{{\text{Cout}}}} } \right.} \right)I_{{{\text{RLPE}}}} \left( t \right) - V_{{\text{f}}} .$$

(10)

nThe current across capacitor $C_{{{\text{out}}}}$ is represented in Eq. (11).

$$I_{{{\text{Cout}}}} \left( t \right) = \frac{{C_{{{\text{out}}}} {\text{d}}V_{{{\text{Cout}}}} \left( t \right)}}{{{\text{d}}t}} = \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {R_{Co} } \right)}}I_{{{\text{RL}}}} \left( t \right) - \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{R_{L} R_{Co} }}V_{{{\text{Cout}}}} \left( t \right) - \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {R_{Co} } \right)}}I_{{{\text{RLPE}}}} \left( t \right).$$

(11)

The output voltage is represented by Eq. (12).

$$V_{b} \left( t \right) = \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {R_{Co} } \right)}}V_{Cout} \left( t \right) - \left( {R_{L} \left\| {R_{Co} } \right.} \right)I_{RLPE} \left( t \right) + \left( {R_{L} \left\| {R_{Co} } \right.} \right)I_{RL} \left( t \right)$$

(12)

Equation (10–12) can be written in state space equation form. The state variables are $z_{2} \left( t \right) = \left| {\begin{array}{*{20}c} {I_{{{\text{SP}}}} \left( t \right)} & {V_{{{\text{Cout}}}} \left( t \right)} \\ \end{array} } \right|^{T},$ $u\left( t \right) = \left| {\begin{array}{*{20}c} {V_{{\text{b}}} \left( t \right)} & {I_{{{\text{RLPE}}}} \left( t \right)} \\ \end{array} } \right|^{T}$ and $y\left( t \right) = \left| {\begin{array}{*{20}c} {V_{b} \left( t \right)} & {I_{J} \left( t \right)} \\ \end{array} } \right|^{T}$. The modified state equations are represented by Eqs. (13–14).

$$\dot{z}_{2} \left( t \right) = A_{{w2}} z_{2} \left( t \right) + B_{{w2}} u\left( t \right) + G_{{w2}} V_{{{\text{fb}}}}$$

(13)

$$y\left( t \right) = C_{w2} z_{2} \left( t \right) + E_{w2} u\left( t \right) + H_{w2} V_{fb}$$

(14)

The state space matrices are represented below.

$$A_{w2} = \left| {\begin{array}{*{20}c} {\frac{{ - \left( {R_{{{\text{Diode}}}} + R_{{{\text{SP}}}} + R_{L} } \right) + \left( {\left( {R_{L} \left\| {R_{Co} } \right.} \right)} \right)}}{{L_{{{\text{in}}}} }}} & 0 \\ 0 & { - \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {C_{{{\text{out}}}} R_{L} R_{Co} } \right)}}} \\ \end{array} } \right|; \begin{gathered} G_{w2} = \left| {\begin{array}{*{20}c} {\frac{ - 1}{{L_{in} }}} & 0 \\ \end{array} } \right|^{T} ; \hfill \\ H_{w2} = \left| {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \right|^{T} ; \hfill \\ \end{gathered}$$

$$B_{w2} = \left| {\begin{array}{*{20}c} {\frac{1}{{L_{{{\text{in}}}} }}} & {\frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{L_{{{\text{in}}}} }}} \\ 0 & { - \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {C_{{{\text{out}}}} R_{Co} } \right)}}} \\ \end{array} } \right|; C_{w2} = \left| {\begin{array}{*{20}c} {\left( {R_{L} \left\| {R_{Co} } \right.} \right)} & {\frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {R_{Co} } \right)}}} \\ 1 & 0 \\ \end{array} } \right|; E_{w2} = \left| {\begin{array}{*{20}c} 0 & { - \left( {R_{L} \left\| {R_{Co} } \right.} \right)} \\ 0 & 0 \\ \end{array} } \right|;$$

The overall averaged non-ideal state space model of boost converter is obtained by using Eqs. (8, 9, 13 &14). The overall averaged non-ideal state space matrices are represented below.

$$\begin{gathered} \begin{array}{*{20}c} {A_{{{\text{avg}}}} = DA_{w1} + \mathop D\limits^{\sim } A_{w2} ;} & {B_{{{\text{avg}}}} = DB_{w1} + \mathop D\limits^{\sim } B_{w2} ;} & {C_{{{\text{avg}}}} = DC_{w1} + \mathop D\limits^{\sim } C_{w2} ;} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {E_{{{\text{avg}}}} = DE_{w1} + \mathop D\limits^{\sim } E_{w2} ;} & {G_{{{\text{avg}}}} = DG_{w1} + \mathop D\limits^{\sim } G_{w2} ;} & {H_{{{\text{avg}}}} = DH_{w1} + \mathop D\limits^{\sim } H_{w2} ;} \\ \end{array} \hfill \\ \end{gathered}$$

where $D$ is duty cycle and $\mathop D\limits^{\sim } = 1 - D$. The overall state space matrices of the averaged non-ideal model of boost converter are represented below.

$$A_{{{\text{avg}}}} = \left| {\begin{array}{*{20}c} {\frac{{ - \left( {\left( {DR_{{{\text{ONIGBT}}}} + \mathop D\limits^{\sim } R_{{{\text{Diode}}}} + R_{{{\text{SP}}}} + R_{{{\text{in}}}} } \right)\left( {R_{L} + R_{{{\text{Cout}}}} } \right) + D\mathop D\limits^{\sim } R_{L} RC_{{{\text{out}}}} } \right)}}{{L_{{{\text{in}}}} }}} & {\frac{{\mathop D\limits^{\sim } \left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {L_{{{\text{in}}}} R_{Co} } \right)}}} \\ {\frac{{\mathop D\limits^{\sim } \left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {C_{{{\text{out}}}} R_{Co} } \right)}}} & { - \frac{{\left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{\left( {C_{{{\text{out}}}} R_{L} R_{Co} } \right)}}} \\ \end{array} } \right|;B_{{{\text{avg}}}} = \left| {\begin{array}{*{20}c} {\frac{1}{{L_{{{\text{in}}}} }}} & {\frac{{\mathop D\limits^{\sim } \left( {R_{L} \left\| {R_{Co} } \right.} \right)}}{{L_{{{\text{in}}}} }}} \\ 0 & { - \frac{{\left( {R_{L} \left\| {R_{{{\text{Co}}}} } \right.} \right)}}{{\left( {C_{{{\text{out}}}} R_{{{\text{Co}}}} } \right)}}} \\ \end{array} } \right|; C_{{{\text{avg}}}} = \left| {\begin{array}{*{20}c} {\mathop D\limits^{\sim } \left( {R_{L} \left\| {R_{{{\text{Co}}}} } \right.} \right)} & {\frac{{\left( {R_{L} \left\| {R_{{{\text{Co}}}} } \right.} \right)}}{{\left( {R_{{{\text{Co}}}} } \right)}}} \\ 1 & 0 \\ \end{array} } \right|; E_{{{\text{avg}}}} = \left| {\begin{array}{*{20}c} 1 & { - \left( {R_{L} \left\| {{\text{R}}_{{{\text{Co}}}} } \right.} \right)} \\ 0 & 0 \\ \end{array} } \right|;$$

$$G_{{{\text{avg}}}} = \left| {\begin{array}{*{20}c} { - \frac{{\tilde{D}}}{{L_{{{\text{in}}}} }}} \\ 0 \\ \end{array} } \right|; H_{avg} = \left| {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right|;$$

The ratio between Laplace transform of output to Laplace transform of input is the transfer function. The transfer function ($TF\left( s \right)$) for non-ideal boost converter is the ratio between output voltage to input voltage. This can be obtained by doing small signal analysis of the non-ideal boost converter. Mathematically, it is expressed by Eq. (15).

$$TF\left( s \right) = \frac{{V_{b} \left( s \right)}}{{V_{j} \left( s \right)}} = C_{{{\text{avg}}}} \left( {sI - A_{{{\text{avg}}}} } \right)^{ - 1} B_{{{\text{avg}}}} + E_{{{\text{avg}}}}$$

(15)

$I$ is the unitary matrix. $s$ is the Laplace operator. The specifications of components used in non-ideal boost converter are $L_{in}$ is 0.0391mH, $R_{L}$ is 50 and $C_{out}$ is 400 µF.

2.2.2 Loss Analysis of Non-ideal Boost Converter

The model for boost converter is represented in Fig. 1(c). Under ideal conditions, the equation governing boost converter is represented mathematically by Eqs. (16–17).

$$\begin{array}{*{20}c} {V_{{\text{L}}} = L_{{{\text{in}}}} \frac{{{\text{d}}I_{{{\text{SP}}}} }}{{{\text{d}}t}} = \left\{ \begin{gathered} V_{j} \hfill \\ V_{j} - V_{{\text{b}}} \hfill \\ \end{gathered} \right.} & \begin{gathered} 0 < t < DT \hfill \\ DT < t < T \hfill \\ \end{gathered} \\ \end{array}$$

(16)

$$V_{b} = \frac{{V_{j} }}{{\tilde{D}}}$$

(17)

where $T$ is the switching period. The exact non-ideal model of boost converter is represented in Fig. 1(d). The parasitic resistance and equivalent resistances for all components are also represented in the circuit. The power balance equation for the non-ideal boost converter is represented by Eq. (18).

$$P_{in} = P_{out} + P_{{R_{in} }} + P_{{R_{Co} }} + P_{Diode} + P_{IGBT}$$

(18)

where $P_{{{\text{in}}}}$, $P_{{{\text{out}}}}$, $P_{{R_{{{\text{in}}}} }}$, $P_{{R_{{{\text{Co}}}} }}$, $P_{{{\text{Diode}}}}$ and $P_{{{\text{IGBT}}}}$ represent the input power, output power, power loss in inductor, power loss in capacitor, power loss in diode and power loss in IGBT, respectively. The mathematical equivalence for all power components are expressed in Eq. (19).

$$\left. \begin{gathered} P_{{{\text{in}}}} = \frac{{V_{{\text{b}}} \times V_{j} }}{{R_{L} \times \tilde{D}}};P_{{{\text{out}}}} = \frac{{V_{b}^{2} }}{{R_{L} }};P_{{R_{{{\text{in}}}} }} = R_{{{\text{in}}}} \times \frac{{V_{b}^{2} }}{{\tilde{D}^{2} \times R_{L}^{2} }}; \hfill \\ P_{{R_{{{\text{Co}}}} }} = R_{{{\text{Co}}}} \times \frac{{V_{{\text{b}}}^{2} \times D}}{{\tilde{D} \times R_{L}^{2} }};P_{{{\text{Diode}}}} = \frac{{DR_{{{\text{Diode}}}} V_{b}^{2} }}{{\tilde{D}^{2} R_{L}^{2} }} + \frac{{V_{F} V_{b} }}{{R_{L} }}; \hfill \\ P_{{{\text{IGBT}}}} = \frac{{D \times R_{{{\text{ONIGBT}}}} \times V_{b}^{2} }}{{\tilde{D}^{2} \times R_{L}^{2} }} + \frac{1}{2}f_{s} C_{{{\text{out}}}} V_{b}^{2} \hfill \\ \end{gathered} \right\}$$

(19)

The efficiency is defined as the ratio between output power ($P_{{{\text{out}}}}$) to input power ($P_{{{\text{in}}}}$). Mathematically, it is expressed by Eq. (20).

$$\eta = \frac{{P_{{{\text{out}}}} }}{{P_{{{\text{in}}}} }} = \frac{{P_{{{\text{out}}}} }}{{P_{{{\text{out}}}} + P_{{R_{{{\text{in}}}} }} + P_{{R_{{{\text{Co}}}} }} + P_{{{\text{Diode}}}} + P_{{{\text{IGBT}}}} }}.$$

(20)

Substituting the values from Eq. (19) in (20), the modified expression for Eq. (20) is expressed by Eq. (21).

$$\eta = \frac{{P_{o} }}{{1 + \frac{{R_{{{\text{in}}}} + DR_{{{\text{ONIGBT}}}} }}{{\tilde{D}^{2} R_{L} }} + \frac{{R_{{{\text{Diode}}}} + DR_{{{\text{Co}}}} }}{{\tilde{D}^{2} R_{L} }} + \frac{{V_{F} }}{{V_{{\text{b}}} }} + \frac{1}{2}f_{s} C_{{{\text{out}}}} R_{L} }}.$$

(21)

2.3 Micro-inverter

The voltage from non-ideal boost converter is DC in nature and this is fed directly to low power micro-inverter. The main advantage of using micro-inverter is, while micro-inverters for the most part have a lower proficiency than string inverters, the general effectiveness is expanded because of the way that each inverter unit acts freely. A further benefit is found in the panel output quality. The panel output of any two panels made from a same base can shift by as much as 10% or more. This is alleviated with a micro-inverter arrangement. However, this is not really in a string setup. The outcome is most extreme force reaping from a micro-inverter exhibit (Razi et al. 2021; Çelik et al. 2020; Yaqoob et al. 2021). Systems with micro-inverters additionally can be changed simpler, when power demands develop or decline after some time. In opposite, with string-based inverters, the inverter size should be as per the quantity of boards or the measure of pinnacle power. Picking a larger than usual string-inverter is conceivable, when future expansion is anticipated. However, such an arrangement for a dubious future builds the expenses regardless. Checking and upkeep are additionally simpler as numerous micro-inverter makers give applications or sites to screen their units. The specification for diode to be used in micro-inverter is maximum reverse voltage is 100 V, maximum forward current is 40 A, forward bias voltage is 0.8 V, resistance of diode should be 1 mΩ. Similarly the specification for IGBT maximum collector current is 30 A, collector emitter voltage (saturation) is 1.95 V, maximum collector emitter voltage is 650 V and resistance of IGBT should be less than 1 mΩ. The micro-inverter system is tuned using DQC-based SPWM technique.

2.3.1 Harmonic

Total harmonic distortion calculated for current signal ($thd_{i}$) is a measure of all harmonics found in an electrical signal. It is mostly induced by the use of high frequency power electronics-based switching devices. The ratio of all summation of all powers of harmonic components to the power of fundamental component is known as total harmonic distortion. Harmonics affects the power systems in many possible ways like heating effects, electromagnetic emissions and reduction of power factors among many others. It is the basic outcome of doing Fourier analysis of a periodic signal. Low peak current, high power factor, high efficiency is indicated by lower values of harmonic distortions. It is always desirable to maintain low values of harmonic in a power circuit. Hence, for better performance of our proposed model harmonic needs to be reduced to very low values. IEEE-519 has predefined standards for harmonic values depending upon number of phases and voltage magnitude (Marrero et al. 2022).

2.4 Direct and Quadrature Control-based Sinusoidal Pulse Width Modulation (DQC-SPWM)

A computational model of the proposed PV system is used for designing of the DQC strategy (Kalavalli et al. 2021; Chaithanakulwat et al. 2021; Missula et al. 2021; Ben et al. 2017). Let the grid side voltage and current be represented by $V_{grid}$ and $i_{2}$, respectively. The inverter side voltage and current be represented by $V_{inv}$ and $i_{1}$, respectively. The inverter side and grid side filter resistances are $R_{1}$ and $R_{2}$, respectively. The inverter side and grid side filter inductance are $l_{1}$ and $l_{2}$, respectively.$C_{f}^{{}}$ represents the parallel capacitance. The dynamic equation of the AC (grid and inverter) side is given by Eqs. (22–24).

$$V_{inv} = R_{1} i_{1} + sL_{1} i_{1} + V_{cf}$$

(22)

$$V_{{{\text{cf}}}} = R_{2} i_{2} + sL_{2} i_{2} + V_{{{\text{grid}}}}$$

(23)

$$i_{1} = i_{2} + \frac{{V_{cf} }}{S}$$

(24)

Thus, upon neglecting the influence of capacitor in the design of current controller. Equation (22) can be drafted as Eqs. (25–26) for $\alpha \beta$ frame where $V_{{{\text{inv}}\_\alpha }}$ and $V_{{{\text{inv}}\_\beta }}$ represents the $\alpha$ and $\beta$ component of $V_{{{\text{inv}}}}$

$$V_{{{\text{inv}}\_\alpha }} = \left( {R_{1} + R_{2} } \right)i_{\alpha } + s\left( {L_{1} + L_{2} } \right)i_{\alpha } + V_{{{\text{grid}}\_\alpha }}$$

(25)

$$V_{inv\_\beta } = \left( {R_{1} + R_{2} } \right)i_{\beta } + s\left( {L_{1} + L_{2} } \right)i_{\beta } + V_{grid\_\beta }^{{}}$$

(26)

Further applying stationary to Rotating Reference Frame (RRF) transformation to Eqs. (25–26) according to $X_{dq} = X_{\alpha \beta } e^{ - j\omega t}$ where $X_{dq}$ represents the reactance for $dq$ axis and $X_{\alpha \beta }$ represents the reactance for the $\alpha \beta$ frame and $\omega$ represents angular frequency. The dynamics of combined grid and inverter variable in rotating frame are represented by Eq. (27).

$$\left. \begin{gathered} V_{{{\text{inv}}\_d}} = \left( {R_{1} + R_{2} } \right)i_{d} + s\left( {L_{1} + L_{2} } \right)i_{d} - \omega_{{{\text{ff}}}} (L_{1} + L_{2} )i_{q} + V_{{{\text{grid}}\_d}} \hfill \\ V_{{{\text{inv}}\_q}} = \left( {R_{1} + R_{2} } \right)i_{q} + s\left( {L_{1} + L_{2} } \right)i_{q} - \omega_{{{\text{ff}}}} (L_{1} + L_{2} )i_{d} + V_{{{\text{grid\_}}q}} \hfill \\ \end{gathered} \right\}.$$

(27)

The above system in RRF contains both decoupling and compensating expressions. The nominal angular frequency (rad/sec) of the grid is represented by $\omega_{ff}$. Equation (28) represents the relationships between the $dq$ axis components of $V_{{{\text{inv}}}}$, $V_{grid}$ and the voltage control signals ($V_{c\_d}$ and $V_{c\_q}$) of $dq$ axis. This is done in order to achieve $i_{d}$ and $i_{q}$, respectively.

$$\left. \begin{gathered} V_{inv\_d} = V_{c\_d} - \omega_{ff} (L_{1} + L_{2} )i_{q} + V_{grid\_d} \hfill \\ V_{inv\_q} = V_{c\_q} - \omega_{ff} (L_{1} + L_{2} )i_{d} + V_{grid\_q} \hfill \\ \end{gathered} \right\}$$

(28)

The values of $V_{c\_d}$ and $V_{c\_q}$ is denoted in Eq. (29).

$$\left. \begin{gathered} V_{c\_d} = \left( {R_{1} + R_{2} } \right)i_{d} + s\left( {L_{1} + L_{2} } \right)i_{d} \hfill \\ V_{c\_q} = \left( {R_{1} + R_{2} } \right)i_{q} + s\left( {L_{1} + L_{2} } \right)i_{q} \hfill \\ \end{gathered} \right\}$$

(29)

The use of $\alpha \beta$ to $dq$ transformation is not possible as there is only a single variable while it requires a minimum of two variables. In order to formulate the above transformation a frictious component needs to be created. This frictious component is created by phase shifting the measured signal. The measured and phase shifted components form the reference frame for $\alpha \beta$ frame. The $\alpha$ component of grid current is $i_{a}$ and its phase shifted component is $i_{\alpha }^{*}$, respectively. The system response becomes slower and fluctuating due to insertion of delay, this can be rectified by using the error signal ($i_{\alpha }^{*} - i_{a}$) to generate the steady-state errors in $dq$ frame, where $\varepsilon d$ represents error for $d - axis$(direct axis) and $\varepsilon q$ represents error for $q - axis$(quadrature axis), respectively. The relation between stationary and the rotating frame is expressed by Eq. (30) and vice versa by Eq. (31), respectively.

$$\left| {\begin{array}{*{20}c} d \\ q \\ \end{array} } \right| = \left| {\begin{array}{*{20}c} {\cos (\theta )} & {\sin (\theta )} \\ { - \sin (\theta )} & {\cos (\theta )} \\ \end{array} } \right|.\left| {\begin{array}{*{20}c} \alpha \\ \beta \\ \end{array} } \right|$$

(30)

$$\left| {\begin{array}{*{20}c} \alpha \\ \beta \\ \end{array} } \right| = \left| {\begin{array}{*{20}c} {\cos (\theta )} & { - \sin (\theta )} \\ {\sin (\theta )} & {\cos (\theta )} \\ \end{array} } \right|.\left| {\begin{array}{*{20}c} d \\ q \\ \end{array} } \right|$$

(31)

Equation (31) will not be applicable as there is only one variable $i_{\alpha }^{{}}$. This is averted by using phase locked loop (PLL) angle ($\theta_{PLL}$) to find $i_{\alpha }^{*}$ and $i_{\beta }^{*}$, respectively. This is represented in Eq. (32).

$$\left. \begin{gathered} i_{\alpha }^{*} = I^{*} = I_{m}^{*} \cos \left( {\theta_{PLL} } \right) \hfill \\ i_{\beta }^{*} = I_{m}^{*} \sin \left( {\theta_{PLL} } \right) \hfill \\ \end{gathered} \right\}$$

(32)

Appling $dq$ transformation with $\theta = \theta_{PLL}$ the two reference currents ($i_{\alpha }^{*}$ and $i_{\beta }^{*}$) are expressed in Eq. (33).

$$\left. \begin{gathered} i_{d}^{*} = I_{m}^{*} \left( {\cos^{2} (\theta_{PLL} ) + \sin^{2} (\theta_{PLL} )} \right) = I_{m}^{*} \hfill \\ i_{q}^{*} = I_{m}^{*} \left( { - \cos (\theta_{PLL} ).\sin (\theta_{PLL} ) + \sin (\theta_{PLL} ).\cos (\theta_{PLL} )} \right) = 0 \hfill \\ \end{gathered} \right\}$$

(33)

The measured real current ($i_{\alpha }$) is given by Eq. (34).

$$i_{\alpha } = i = I_{m} \cos (\theta_{PLL} )$$

(34)

The frictious component of current ($i_{\beta }$) is represented by Eq. (35).

$$i_{\beta } = i = I_{m} \sin (\theta_{PLL} )$$

(35)

Assuming $i_{\beta } = i_{\beta }^{*}$ at steady state. The steady-state error in $dq$ frame ($\varepsilon d$ and $\varepsilon q$) are given by Eqs. (36–37).

$$\left. \begin{gathered} \varepsilon d = i_{d}^{*} - i_{d}^{{}} \hfill \\ \varepsilon d = \left[ {i_{\alpha }^{*} \cos \left( {\theta_{PLL} } \right) + i_{\beta }^{*} \sin \left( {\theta_{PLL} } \right) - i_{\alpha }^{{}} \cos \left( {\theta_{PLL} } \right) + i_{\beta }^{{}} \sin \left( {\theta_{PLL} } \right)} \right] \hfill \\ \varepsilon d = \left[ {\left( {i_{\alpha }^{*} - i_{\alpha } } \right)\cos \left( {\theta_{PLL} } \right) + \left( {i_{\beta }^{{}} - i_{\beta }^{*} } \right)\sin \left( {\theta_{PLL} } \right)} \right] \hfill \\ \varepsilon d = \left[ {\left( {i_{\alpha }^{*} - i_{\alpha } } \right)\cos \left( {\theta_{PLL} } \right)} \right] \hfill \\ \end{gathered} \right\}$$

(36)

$$\left. \begin{gathered} \varepsilon q = i_{q}^{*} - i_{q}^{{}} \hfill \\ \varepsilon q = \left[ { - i_{\alpha }^{*} \sin \left( {\theta_{PLL} } \right) + i_{\beta }^{*} \cos \left( {\theta_{PLL} } \right) - i_{\alpha }^{{}} \sin \left( {\theta_{PLL} } \right) + i_{\beta }^{{}} \cos \left( {\theta_{PLL} } \right)} \right] \hfill \\ \varepsilon q = \left[ { - \left( {i_{\alpha }^{*} - i_{\alpha } } \right)\sin \left( {\theta_{PLL} } \right) + \left( {i_{\beta }^{{}} - i_{\beta }^{*} } \right)\cos \left( {\theta_{PLL} } \right)} \right] \hfill \\ \varepsilon q = \left[ { - \left( {i_{\alpha }^{*} - i_{\alpha } } \right)\sin \left( {\theta_{PLL} } \right)} \right] \hfill \\ \end{gathered} \right\}$$

(37)

From the above two equations $\varepsilon d$ and $\varepsilon q$ are determined based on the values of real current error $\varepsilon \alpha$ and by the use of $dq$ current controller. This $dq$ is applied to generate the sinusoidal reference which is used in SPWM. The intersection of SPWM reference sinusoidal wave ($V_{{{\text{ref}}}}$) and carrier wave ($V_{{{\text{car}}}}$) determines the operating point. When $V_{{{\text{ref}}}}$ > $V_{{{\text{car}}}}$ the resultant voltage is positive and converse is true for negative peak. Equation (22–37) helps to formulate control strategy for micro-inverter, which is established in the simulation model as shown in Fig. 1. The carrier wave frequency controls the load frequency and modulation index. Root mean square value of output voltage ($V_{inv}$) is dependent upon the modulation index. Equation (38–39) gives the value of modulation index and output voltage, where $T$ is the total time period, $T_{on}$ is the width of the $n^{th}$ pulse then, respectively.

$$V_{inv} = V_{s} \sqrt {\left( {\sum\limits_{b = 1}^{2n} {\frac{{2T_{on} }}{T \times \pi }} } \right)}$$

(38)

$$m_{a} = \frac{{V_{c} }}{{V_{car} }}$$

(39)

2.5 Filter

The current and voltage signals from micro-inverters often contain disturbances and harmonic components. The purpose of filter is to filter out unwarranted disturbances coming from micro-inverter. The L–C–L-type filter is used in the scope of the paper. The proposed filter has better response as compared to other type of filter. The base impedance ($Z_{b}$) for the proposed L–C–L-type filter is expressed by Eq. (40). Equations (41) and (42) represent the mathematical formularies for base capacitance ($V_{f}$) and maximum values of load current ($I_{\max }$).

$$z_{b} = V_{bn}^{2} p_{l}^{ - 1}$$

(40)

$$C_{b} = \left( {\omega_{g} z_{b} } \right)^{ - 1}$$

(41)

$$I_{\max } = 0.333*P\sqrt 2 *\left( {V_{f} } \right)^{ - 1}$$

(42)

The active power is represented by $P_{l}$, while the filter voltage is represented by $V_{f}$, respectively. A tolerance of 10% is accommodated in the values of design parameters for robustness purposes. The change in load current accommodating 10% variation and the value of inverter side inductance is given by Eqs. (43, 44) separately. The switching frequency and DC link voltage is represented by $f_{s}$ and $V_{b}$.

$$\Delta I_{\max } = 0.10 \times I_{\max }$$

(43)

$$L_{1} = \frac{{V_{b} }}{{6 \times f_{s} \times \Delta I_{\max } }} = \frac{{V_{b} }}{{0.6 \times f_{s} \times I_{\max } }}$$

(44)

After allowing a 5% variation in the capacitance of the filter. Equation (45) represents the capacitance of the filter ($C_{f}$). The DC link side inductor ($L_{2}$) is expressed mathematically by Eq. (46).

$$C_{f} = 0.05 \times C_{b}$$

(45)

$$L_{2} = \frac{{\sqrt {\left( {k_{a}^{ - 2} + 1} \right)} }}{{C_{f} \times \left( {f_{{{\text{sw}}}} } \right)^{2} }}$$

(46)

The attenuation factor is represented by $k_{a}$. In order to compensate for the ripple effects, electromagnetic interference and resonance, a resistor with resistance ($R_{f}$) is inserted in series with filter capacitor. The resonant frequency is given by $f_{{{\text{res}}}}$. The value of $R_{f}$ is expressed mathematically by Eq. (47).

$$R_{f} = \left( {3C_{f} \times \omega_{res} } \right)^{ - 1}$$

(47)

Equations (40–47) help to formulate filter strategy for PV system, which is established in simulation model as shown in Fig. 1.

2.6 Fault Classification

Faults are broadly defined as abnormal working conditions. The faults that are considered in the scope of this manuscript are grid open-circuit fault, grid short-circuit fault, load open-circuit fault, load short-circuit fault, inverter open-circuit fault, inverter device fault and converter device fault. The fault classification is a machine learning-based mechanism where the neural network is trained to identify the types of fault occurring in a PV system. The machine learning-based neural network for eight kinds of operating conditions. The operating conditions include seven types of fault and normal operating condition. The fault classification is achieved by using LMA which is realized by using a Feed forward Neural Network (FNN). There is no formation of loops in FNN-based ANN. The information flows from input node to the output node via the hidden nodes. The mathematical optimization is carried out in the hidden layer. The hidden layer also pre-processes data and prepares the data. The FNN-based ANN is realized using 22 hidden layers and fourteen inputs and one output (Fazai et al. 2019; Bilski et al. 2020).

2.6.1 Levenberg–Marquardt Algorithm (LMA)

The choice of algorithm for fault detection is a machine learning-based algorithm which is Levenberg–Marquardt Algorithm (LMA). LMA works effectively by reducing the cost function or loss function values. LMA uses computing gradient and Jacobian matrix techniques to optimize the response (Bilski et al. 2020). The cost function is represented by $f$. It is defined as

$$f = \sum\limits_{i = 1}^{m} {e_{i}^{2} }$$

(48)

where number of data samples is represented by $m$. The performance index is integral time absolute error. This performance index is utilized as a cost function. Mathematically it is expressed as

$$f = \sum\limits_{{{\text{peak}} = 1}}^{m} {t_{{{\text{peak}}}} } *\left| {e_{{{\text{peak}}}} } \right|$$

(49)

The Jacobian matrix is expressed in terms of error vector ($e_{i}$) and parameter vector ($w_{j}$) by Eq. (50)

$$J_{i.j} = \frac{{\partial e_{i} }}{{\partial w_{j} }}$$

(50)

The instances of dataset and number of parameters are represented by $i$ and $j$, respectively. The slope of the vector field is calculated by the gradient vector ($\nabla f$) while the determination of local minima and maxima is carried out by using hessian approximation ($H_{f}$). Gradient vector in addition to hessian approximation of the cost function is expressed mathematically by Eq. (51).

$$\left. \begin{gathered} \nabla f = 2J^{T} .e \hfill \\ H_{f} \approx 2J^{T} .J + \lambda I \hfill \\ \end{gathered} \right\}$$

(51)

Damping factor and identity matrix are represented by $\lambda$ and $I$, respectively. The progress in response is calculated by computing the next set of weights ($w^{(i + 1)}$) is expressed mathematically in Eq. (52).

$$w^{(i + 1)} = w^{i} = - (J^{(i)T} .J^{(i)} + \lambda^{(i)} I)^{ - 1} .(2J^{(i)T} .e^{(i)} )$$

(52)

The failure of iteration is predicted by increase or decrease in damping factor values. If $\lambda$ increases then the iteration fails but when $\lambda$ decreases then the value of cost function decreases and in turn this speeds up the iteration.

2.7 Open-Loop Response

The solar PV system traits are probed underneath working conditions in the appending sections.

2.7.1 Open-Loop Non-ideal Boost Converter

The triggering of the IGBT is achieved through a simple pulse generator. IGBT is switched at a frequency of 30,000 Hertz. The converter is based on the basics of boost converter. The input voltage of 24 V is from solar subsystem; it is stepped up to 44.48 V. There is a ripple of 1.02 V. The voltage fluctuates between 43.98 V and 45 V. Figure 2a represents the output voltage of non-ideal boost converter. Nonlinearities present in PV system are the main source of ripple in the output voltage. The input power to non-ideal boost converter is 60 W, and the output power is 47.5 W. The power loss in non-ideal boost converter is 10 W. The non-ideal boost converter is seen to operate at an efficiency of 79.16%. The Efficiency versus output power plot for non-ideal boost converter is presented in Fig. 2b.

Fig. 2

Performance of open-loop PV system: a non-ideal boost converter output voltage; b efficiency of non-ideal boost converter with respect to output power; c micro-inverter output voltage; d micro-inverter output current; e micro-inverter output power; and f $thd_{i}$ plot

2.7.2 Open-Loop Micro-inverter

The micro-inverter is a basic bridge converter with 4 IGBTs. The switching frequency in open-loop mode is 30 kHz and it is being provided by DC Pulse Width Modulation (DCPWM) Modules. The magnitude of voltage inverted by micro-inverter is 226 V. This is depicted in Fig. 2c. The AC current is 1.5 A. This is depicted in Fig. 2d. The apparent power is 340 watts. This is depicted in Fig. 2e. The current THD was found out to be 1.35%. This is depicted in Fig. 2f. The open-loop analysis suggests the use of control technique for better results.

3 Control Algorithms

The EHO-tuned VPTIDF control action algorithm is evidently established in appending subsections. The PV system performance with EHO-tuned VPTIDF controller as far as robustness, accuracy and stability are studied. The control performance indices current harmonic distortion, voltage harmonic distortion, PV system voltage, PV system current, PV system power and boost converter output voltage are also evaluated as well as investigated with apposite validation of the EHO-tuned VPTIDF control actions (Sahu et al. 2016; Patra 2020; Patra and Nanda 2021; Li et al. 2020; Wang et al. 2015; Meena et al. 2017). The proposed control approach uses EHO-tuned VPTIDF which is described in the sections appended below.

3.1 EHO-tuned VPTIDF

Figure 3a exemplifies the PV structure with EHO-tuned VPTIDF. In this control strategy, the output of EHO-tuned VPTIDF ($u(t)$) is formulated by using the input of the controller. The input to the controller is error signal $e(t)$. The Transfer Function ($TF$) of the EHO-tuned VPTIDF controller is expressed as (Sahu et al. 2016; Patra 2020):

$$TF = \left( {K_{t} \times s^{ - n} } \right) + \left( {\frac{{K_{i} }}{s}} \right) + K_{d} \left( {\frac{Ns}{{N + s}}} \right)$$

(53)

Fig. 3

a Block diagram of EHO-tuned VPTIDF and b flowchart of EHO algorithm

where the control parameters are represented by tilt gain ($K_{{\text{t}}}$), integral gain ($K_{{\text{i}}}$), derivative gain ($K_{{\text{d}}}$), coefficient of tilt (n) and prefilter gain ($N$). The evaluation of control parameters is based on the response of proposed model for the lowest value of the fitness function like Integral Time Absolute Error ($ITAE$). Equation (54) highlights the mathematical equivalence of $ITAE$_. The lowest value of fitness function is responsible for better performance such as less harmonic and better system voltage of the proposed model.

$$ITAE = \int\limits_{0}^{\infty } {|e(t)|} tdt$$

(54)

where the magnitude of the error signal is denoted by $|e(t)|$. Aimed at improved PV system performance, the control parameters are estimated by assistance of the EHO method.

3.2 Optimization Algorithm

The advent of optimization algorithms provides better tuning methods. The optimization algorithms used is Elephant Herding Optimization (EHO). This is explained in sections appended below.

3.2.1 Elephant Herding Optimization (EHO)

Elephants unlike most animals exhibit social behavior. An elephant clan, which is called as herd is headed by matriarch. The herd of elephants mostly consists of female and calves. The male elephants mostly reside in seclusion at places far away from their families. The following assumptions are made in EHO.

• 1. Some clans with fixed number of elephants consist of the elephant population.

• 2. A fixed number of male elephants in their generations will leave the group and would reside in faraway places unsociably.

• 3. A matriarch will lead the group in each clan.

There are two basic operations that are carried out in EHO. Those are the clan updating operation and separating operation.

• (i) Clan Updating Operator

  As per the natural habitats of elephants, a matriarch heads the clan and new position of each elephant is influenced by matriarch. The elephant’s $j$ position in each clan $c_{i}$ can be calculated as shown in Eq. (55).

  $$x_{{new,c_{i} ,j}} = x_{{c_{i} ,j}} + a \times r \times \left( {x_{{best,c_{i} }} - x_{{c_{i} ,j}} } \right)$$

  (55)

  where$x_{{new,c_{i} ,j}}$ is the present new position of elephant $j$ in clan $c_{i}$, $x_{{{\text{best}},c_{i} }}$ is the position for the fittest elephant (matriarch) in the clan $c_{i}$, $x_{{c_{i} ,j}}$ is the old position of elephant $j$ in clan $c_{i}$,$a$ and $r$ are scaling factors whose values are lies between 0 and 1 expressed mathematically by Eq. (56).

  $$a,r \in \left[ {0,1} \right]$$

  (56)

  The fittest elephant in each clan $c_{i}$ cannot be updated by Eq. (55). It is calculated as shown in Eq. (57).

  $$x_{{{\text{new}},c_{i} ,j}} = \beta \times x_{{{\text{center}},c_{i} }}$$

  (57)

  where $\beta$ is the factor with values lying between 0 and 1 represents the influence of $x_{{{\text{center}},c_{i} }}$ on $x_{{{\text{new}},c_{i} ,j}}$ its value lies within the limits as expressed by Eq. (2). $x_{{{\text{center}},c_{i} }}$ is the center elephant of the clan $c_{i}$. Its position is given by Eq. (58).

  $$x_{{{\text{center}},c_{i} ,d}} = \frac{1}{{n_{{c_{i} }} }} \times \sum\limits_{j = 1}^{{n_{{c_{i} }} }} {x_{{c_{i} ,j,d}} }$$

  (58)

  where $d$ is the number of dimension which lies between $1 \le d \le D$. $D$ is the total dimension. $n_{{c_{i} }}$ is the number of elephant in each clan $c_{i}$. $x_{{c_{i} ,j,d}}$ is the $d^{th}$ dimension of elephant $j$ in clan $c_{i}$.

• (ii) Separating Operator

  The separation of male elephant from the herd is modeled mathematically for solving the optimization problem. The separating operator is implemented by the elephant individual with the worst fitness function in each generation. The worst position ($x_{{{\text{worst}},c_{i} }}$) in the clan $c_{i}$ is represented by Eq. (59).

  $$x_{{{\text{worst}},c_{i} }} = x_{\min } + \left( {x_{\max } - x_{\min } + 1} \right) \times r$$

  (59)

  where $x_{\min }$ and $x_{\max }$ represents the lower and upper bounds of the elephant individual.

The optimization is carried till the limit of maximum generation ($\max_{{{\text{gen}}}}$) is reached or the iteration limits are reached. The optimal EHO-tuned VPTIDF control parameters are implemented centered on the EHO approach as stated in Table 2. The optimization (EHO) is achieved through reduction in the cost function ($ITAE$). The structure of EHO-tuned VPTIDF is depicted in Fig. 3a, this control strategy is designed centered on Eqs. (55) and (59). The working principle of the proposed optimization technique (EHO) is clearly described through a flow chart as shown in Fig. 3b. Table 2 highlights the control parameter values of variable parameter EHO-tuned VPTIDF.

Table 2 EHO-tuned VPTIDF optimized parameter values

4 Outcomes and Deliberations

The purpose of this section is to analyze the outcomes of the proposed model and to justify the superiority of the proposed approach by justifying the control action robustness, stability and performance of the proposed PV system. System performance is dependent upon controller parameter settings. The proposed technique treats the control parameters ($K_{t}$,$K_{i}$,$K_{d}$, $n$ and $N$) as variable, which varies as a function of error.

4.1 Control Action

The control action is verified by doing the control parameter sensitivity analysis.

4.1.1 Control Parameter Sensitivity Analysis

System performance is dependent upon controller parameter settings; hence setting the parameter plays a significant role. The use of optimization technique essentially uses a cost function which minimizes the error and optimizes the parameters. This results in optimizing the control parameters, but not the response of the controller. In order to make a system robust, its controller must be robust in nature. However, in practice gain values are seen to vary as a function of error. It is evident that when the control parameters are treated as variables. It is seen to provide a better response. Hence, the EHO-tuned VPTIDF is modeled for variable control parameters. The variable parameter tends to give better oscillation rejection, accelerate system response and is seen to reduce overlapping. The error function $f\left( e \right)$ that is used to determine the variable control parameters is represented by Eq. (60).

$$f\left( e \right) = \sqrt {\frac{2}{\pi }} \int\limits_{0}^{t} {\left| {e^{{ - \frac{{t^{2} }}{2}}} } \right|} dt$$

(60)

The error function is utilized to evaluate the variable control parameters. The control parameters tilt gain ($K_{t}$), integral gain ($K_{i}$), derivative gain ($K_{d}$), coefficient of tilt ($n$) and prefilter gain ($N$) are all treated as variables. Tilt gain aids in accelerating system response and decreasing system settling time and it sometimes tends to increase system oscillations. The variation of tilt gain is represented by Eq. (61). Where $t^{\max }$ or $c_{1}$ and $t^{\min }$ or $c_{2}$ are boundary constants of tilt gain. The values of $c_{1}$ and $c_{2}$ are 0.357165 and 0.123708, respectively. The parameter variations are plotted in Fig. 4a.

$$K_{t} = c_{1} + f(e)*c_{2}$$

(61)

Fig. 4

EHO-tuned VPTIDF controller parameter variation plot: a the variation of tilt gain; b the variation of integral gain; c the variation of derivative gain; d the variation of coefficient of tilt; e the variation of prefilter gain; f the variation of output voltage of boost converter; and g the variation of $thd$ tilt gain

The integral gain aids in reducing steady-state error but if varied vigorously it sometimes tends to induce oscillations and induces overshoot. Where $c_{3}$ and $c_{4}$ are boundary constants of integral gain. The values of $i^{\max }$ or $c_{3}$ and $i^{\min }$ or $c_{4}$ are 0.003539 and 0.003174, respectively. The variation of integral gain is represented by Eq. (62). The parameter variations are plotted in Fig. 4b.

$$K_{i} = c_{3} - f(e)*c_{4}$$

(62)

The derivative gain aids in reducing steady-state error but if varied vigorously it sometimes tends to induce oscillations and induces overshoot. Where $d^{\max }$ or $c_{5}$ and $d^{\min }$ or $c_{6}$ are boundary constants of derivative gain. The values of $c_{5}$ and $c_{6}$ are 0.480264 and 0.13067, respectively. The variation of derivative gain is represented by Eq. (63). The parameter variations are plotted in Fig. 4c.

$$K_{d} = c_{5} + f(e)*c_{6}$$

(63)

The coefficient of tilt aids in reducing steady-state error but if varied vigorously it sometimes tends to induce oscillations and induces overshoot. Where $n^{\max }$ or $c_{7}$ and $n^{\min }$ or $c_{8}$ are boundary constants of coefficient of tilt. The values of $c_{7}$ and $c_{8}$ are 0.485354 and 0.042968, respectively. The variation of coefficient of tilt is represented by Eq. (64). The parameter variations are plotted in Fig. 4d.

$$n = c_{7} + f(e)*c_{8}$$

(64)

The prefilter gain helps in prefiltering any disturbance present across the derivative component of the proposed controller. It is a low pass filter. Where $c_{9}$ and $c_{10}$ are boundary constants of prefilter gain. The values of $p^{\max }$ or $c_{9}$ and $p^{\min }$ or $c_{10}$ are 100.43 and 263.53, respectively. The variation of prefilter gain is represented by Eq. (65). The parameter variations are plotted in Fig. 4e.

$$n = c_{9} + f(e)*c_{10}$$

(65)

The variation in boost converter output voltage with variation in control parameters is plotted in Fig. 4f. It is eminent from Fig. 4f that the parameters variation induces a fluctuation of 0.173399. This is 0.346798%. This is under tolerance limits. The variation of $thd$ is plotted in Fig. 4g. It can be seen from the figure that the fluctuations in $thd$ is 0.000744. Table 3 highlights the minimum and maximum values for all the control parameters.

Table 3 The range of various control parameters

4.2 Closed-Loop Boost Converter

The voltage developed by solar panels is very low in magnitude, which cannot be used. Hence there is a requirement to increase the magnitude of the voltage. This is achieved by using a boost converter. The voltage is boosted to 50 V. This is depicted in Fig. 5a. IGBTs present in the boost converter are provided triggering pulses by the proposed controller at 8500 Hz. The average output voltage of low rating converter is about 48 V. 50 V is a serious output voltage in case of the low rating converter. This 50 V is taken as a standard output voltage of the low rating converter Hence, for the verification of proposed PV system performance, 50 V is taken as the output voltage of the converter, as shown in Fig. 5a. The input power to non-ideal boost converter is 60 W, and the output power is 50 W. The power loss in non-ideal boost converter is 10 W. The non-ideal boost converter is seen to operate at an efficiency of 83.33%. The Efficiency versus output power plot for non-ideal boost converter is presented in Fig. 5b.

Fig. 5

a DC voltage output of non-ideal boost converter and b efficiency of non-ideal boost converter with respect to output power

4.3 Closed-Loop Micro-inverter

This stepped up voltage is then fed to micro-inverter. This in turn inverts this voltage to AC. The magnitude of this induced voltage is 220 V. This is depicted in Fig. 6. The inverter is connected to an impedance of 100 + 240e⁻³j Ω. The current developed by the load is 1.6 A in steady state. This is depicted in Fig. 7. The electrical power consumed by the load is 360 watts. This is depicted in Fig. 8.

Fig. 6

Output voltage of micro-inverter

Fig. 7

Output current of micro-inverter

Fig. 8

Output power of micro-inverter

A Load of 12 KW is to be fed from both grid and renewable source (solar micro-inverter). The grid and renewable source (solar micro-inverter) are connected to a three terminal transformer which feeds to the 12KW load. The contribution from the grid, renewable source (solar micro-inverter) and the energy consumption from load are represented in Fig. 9. It takes a RMS voltage of 162.5 V from the inverter and grid. It draws a current of 6.3 A from grid while it draws a current of 11.63 A from the inverter. The load voltage is 169.5 and current is 8.134 A.

Fig. 9

a Grid current plot; b grid voltage plot; c micro-inverter current plot; d micro-inverter voltage plot; e load current plot; and f load voltage plot

4.4 Robustness Analysis

Robustness of any system is the ability of the system to tolerate any kind fluctuations in the input parameters. Robustness is analyzed by variation of input parameters to the solar array. The variation in temperature, irradiance should not alter the responses of the system. The system under variations is studied for changes in boost converter output voltage, boost converter output current, RMS value of micro-inverter output voltage, RMS value of micro-inverter output current, RMS value of load current, RMS value of load voltage and RMS value of grid current and voltages. Figure 10 represents the robustness plot for the proposed system.

Fig. 10

Robustness performance of PV system with respect to variation in temperature and irradiance: a variation in temperature; b variation in irradiance; c non-ideal boost converter voltage; d non-ideal boost converter current; e grid current plot; f grid voltage plot; g micro-inverter current; h micro-inverter voltage; i load current plot; and j load voltage plot

In Fig. 10, the input parameters to the solar PV system (temperature and irradiance) are varied and the system is observed for variation in parameters. Irradiance is varied between 800 W/m² and 1200 W/m². This is depicted in Fig. 10a. The temperature varies between 25 and 45 °C. This is depicted in Fig. 10b. It is seen that the boost converter output voltage is varying between 49 and 52 V. This is depicted in Fig. 10c. While boost converter output current is varied between 1.0 and 1.2 A. This is depicted in Fig. 10d. Grid current is shown to vary between 6.11 and 6.4 amp. Grid variations are characterized in Fig. 10e–f, respectively. Figure 10e represents the current fed by grid while Fig. 10f represents the voltage fed by grid. There is no variation in grid fed voltage while current change is minuscule. The micro-inverter fed grid current is seen to vary between 11 and 15 amperes. This is depicted in Fig. 10g. The micro-inverter fed voltage varies between 158 and 162 V. It is well inside tolerance levels. This is depicted in Fig. 10h. The consumption pattern of load is more or less same. As there is a fluctuation in micro-inverter level the load current and voltage show very minute variations. The load current varies between 8 and 8.12 amperes. This is depicted in Fig. 10i, while load voltage fluctuates between 179 and 184 V.

4.4.1 System Performance Under Variations in Irradiance and Temperature

The variation in temperature, irradiance should not alter the responses of system. The system under variations is studied for changes in RMS value of output voltage, current and power. In Fig. 11, the temperature is varied from 20 degree centigrade (°C) to 48 °C. The irradiance is varied from 700 Watt/ square Meter (W/M²) to 1361 W/M². The output voltage of micro-inverter for both variations in temperature and irradiance varies between 160.98 and 161.24 V. The variation is 0.26 V, this is 0.162%, which is under tolerance limits of ± 5%. The output voltage versus temperature is plotted in Fig. 11a, while Fig. 11b represents the output voltage versus irradiance is plot. The output current of micro-inverter for variation in temperature is between 1.4125 and 1.4135 amp. The variation is 0.001 amp this is 0.074% which is under tolerance limits of ± 5%. This is depicted in Fig. 11c. The output current of micro-inverter for variation in irradiance is between 1.4125 and 1.4155 amp. The variation is 0.003 amp this is 0.022% which is under tolerance limits of ± 5%. This is depicted in Fig. 11d. The output power of micro-inverter for variation in temperature is between 248.3 and 249.8 watts. The variation is 1.6 watts this is 0.645% which is under tolerance limits of ± 5%. This is depicted in Fig. 11e. The output power of micro-inverter for variation in irradiance is between 245 and 255 watts. The variation is 10 watts this is 4.03% which is under tolerance limits of ± 5%. This is depicted in Fig. 11f. The impact of solar irradiance on the control parameters is reflected through the boost converter output voltage ($V_{{\text{b}}}$). Figure 11g, h reflects the variation of $V_{{\text{b}}}$ with variation in temperature and irradiance. It is evident from Fig. 11g, h that there is no variation of converter output voltage ($V_{{\text{b}}}$). It is possible due to the adaptive optimal control technique (EHO-tuned VPTIDF), which is able to adjust itself, such that the impact of variation in temperature and irradiance on the system output is minimized. As there is miniscule fluctuation in micro-inverter level the load current and voltage show very minute variations. The proposed system is seen to tolerate rapid fluctuations in temperature and irradiance. The proposed system exhibits robustness.

Fig. 11

Performance of PV system: a output voltage of micro-inverter with respect to temperature; b output voltage of micro-inverter with respect to irradiance; c output current of micro-inverter with respect to temperature; d output current of micro-inverter with respect to irradiance; e output power of micro-inverter with variation in temperature; f output power of micro-inverter with variation in irradiance; g output voltage of non-ideal boost converter with respect to temperature; and h output voltage of non-ideal boost converter with respect to irradiance

4.5 Stability of Variable Parameter Tilt Integral Derivative with Filter Controller

Stability analysis is used as a method to validate the proposed model. The proposed model is analyzed under a wide range of frequencies spectrum (Ben et al. 2017). Matignon stability theorem is used for the stability analysis of the proposed model. Dynamic system stability analysis of linear time invariant system suggests that all the all roots of the characteristic equation should lie on left and side of the s-plane and should be away from origin. However, it is not the case in the fractional-order controllers. The stability of the fractional-order system is based on Matignon stability theorem. Which states that a fractional-order system G(s) is stable if it satisfies Eq. (66). Where $\sigma$ can be seen as a symbol for the Laplace variable $s$, $i$ represents $i^{th}$ root of characteristic equation and $q$ represents order of integral, respectively.

$$\left| {\arg \left( {\sigma_{i} } \right)} \right| = q\frac{\pi }{2},\left\{ {\sigma = s^{q} :q \mathrel\backepsilon \left( {0 \le q \le 2} \right):\forall \sigma_{i} \in C} \right\}$$

(66)

Stability of the fractional-order system is analyzed by the help of the Matignon Stability Theorem. This theorem extensively tilts the vertical axis by some value $\theta$. This angle is dependent on the fractional order of system. Figure 12 represents the stability curve for the fractional-order (EHO-tuned VPTIDF) closed-loop system, evidently the proposed model is stable as there are no poles or zeros present between the angle $\theta$ whereas for open-loop response there are poles in the unstable region.

Fig. 12

Root locus plot for PV system: a open-loop plot; b closed-loop plot for all $s$; and c closed-loop plot for all $s = j\omega$

4.6 Fault Classification

Figure 13a–d represents the analysis plots for LMA. Figure 13a represents the performance validation plot for LMA. It is evident from the plot that at 953 epochs the best performance of 1.3206 × 10^–9 is achieved. Figure 13b represents the error histogram plot. From the plot, it is evident that the error is very small with higher accuracy. The parameters of LMA are highlighted in Table 4.

Fig. 13

Performance analysis for LMA: a performance validation plot; b error histogram analysis plot; c training validation analysis plot; and d regression analysis plot

Table 4 Parameters of LMA

Error histogram indicates the number of instances of occurrence of error. Conditionally paramount instances obligate minimal error at that time the training is deemed fit and with minutest incongruities. The failures in data training are highlighted by the training failure plot. A best fit solution is indicated by no or minimum number of failures. Figure 13c represents the pool training failures. The information about scattering of data is obtained from regression plot. It has a value ranging from − 1 to 1 through 0. A value of − 1 indicates reverse fit, while a value of 1 indicates perfect fit. A value of 0 indicates no fit. The regression plot is indicated in Fig. 13d. The inputs to the machine learning-based fault classifier are the RMS values of load current($iload$), grid current ($vload$), inverter current ($inv$), load voltage ($vload$), grid voltage ($vgrid$), inverter voltage ($vinv$), irradiance ($irradiance$), Frequency ($freq$), temperature ($temp$), boost converter output voltage ($vdc$), boost converter output current ($idc$), total harmonic distortion ($thdloadi$), solar panel voltage ($vpanel$) and solar panel current ($ipanel$). The output predicts the type of fault. There are three output variables ($Y_{1}$,$Y_{2}$ and $Y_{3}$) for classification of faults. The three output variables are used to classify the eight types of fault. The details of which are placed in Table 5.

Table 5 Binary equivalence of various operating conditions

Figure 14a–c represents the plot for normal operating condition or the no fault condition. The values of output variables $Y_{1}$,$Y_{2}$ and $Y_{3}$ is zero. Under grid open-circuit fault condition, the values of output variable $Y_{1} = Y_{2} = 0$ and $Y_{3}$ is 1. This is depicted in Fig. 14d–f.

Fig. 14

a No fault condition classification by output identifier ($Y_{1}$); b no fault condition classification by output identifier ($Y_{2}$); c no fault condition classification by output identifier ($Y_{3}$); d grid open-circuit fault condition classification by output identifier ($Y_{1}$); e grid open-circuit fault condition classification by output identifier ($Y_{2}$); and f grid open-circuit fault condition classification by output identifier ($Y_{3}$)

Figure 15a–c represents the plot for grid short-circuit fault condition. The values of output variables $Y_{1} = 0$,$Y_{2} = 1$ and $Y_{3} = 0$, respectively. Under load open-circuit fault condition, the values of output variable $Y_{1} = 0$ and $Y_{2} = Y_{3} = 1$. This is depicted in Fig. 15d–f.

Fig. 15

a Grid short-circuit fault condition classification by output identifier ($Y_{1}$); b grid short-circuit fault condition classification by output identifier ($Y_{2}$); c grid short-circuit fault condition classification by output identifier ($Y_{3}$); d load open-circuit fault condition classification by output identifier ($Y_{1}$); e load open-circuit fault condition classification by output identifier ($Y_{2}$); and f load open-circuit fault condition classification by output identifier ($Y_{3}$)

Figure 16a–c represents the plot for load short fault condition. The values of output variables $Y_{1} = 1$,$Y_{2} = Y_{3} = 0$, respectively. Under inverter open-circuit fault condition, the values of output variable $Y_{1} = 1$, $Y_{2} = 0$ and $Y_{3}$ is 1. This is depicted in Fig. 16d–f.

Fig. 16

a Load short-circuit fault condition classification by output identifier ($Y_{1}$); b load short-circuit fault condition classification by output identifier ($Y_{2}$); c load short-circuit fault condition classification by output identifier ($Y_{3}$); d inverter open-circuit fault condition classification by output identifier ($Y_{1}$); e inverter open-circuit fault condition classification by output identifier ($Y_{2}$); and f inverter open-circuit fault condition classification by output identifier ($Y_{3}$)

Figure 17a–c represents the inverter fault condition. The values of output variables $Y_{1} = Y_{2} = 1$ and $Y_{3} = 0$. Under converter fault condition, the values of output variable $Y_{1} = Y_{2} = Y_{3} = 1$. This is depicted in Fig. 17d–f.

Fig. 17

a Inverter fault condition classification by output identifier ($Y_{1}$); b inverter fault condition classification by output identifier ($Y_{2}$); c inverter fault condition classification by output identifier ($Y_{3}$); d converter fault condition classification by output identifier ($Y_{1}$); e converter fault condition classification by output identifier ($Y_{2}$); and f converter fault condition classification by output identifier ($Y_{3}$)

In order to mitigate the fault quickly efficient detection of fault plays a vital role. The duration of fault chosen here is 5 cycles of frequency. The frequency is 50 Hz which is 50 cycles completed in 1 s. The time required to complete 5 cycles is 0.1 s. The fault duration is chosen as 0.1 s because it is the minimum duration for any kind of fault. The classifier is tested with both small duration faults. It is to be noted that fault is applied to the system at 0.3 and mitigated at 0.4 s. The classifier detects the fault by the end of 2^nd cycle.

4.7 Comparative Analysis

It is evident from the comparative study presented in Table 6 that the proposed EHO-tuned VPTIDF-based PV system is having better results as compared to others state of the art controllers. IEEE standards provide a benchmark for accepting a new technique. As per IEEE-519, the harmonic should be below 5% for a period of 30 cycles but for the proposed model for a period of 30 cycles the current harmonic is found out to be 0.61%. This is depicted in Fig. 18.

Table 6 Comparative analysis of proposed technique with others state of art control techniques

Fig. 18

Current harmonic plot proposed system

5 Conclusions

In the scope of this paper, a grid-connected PV system is studied. The proposed system used a variable parameter fractional controller (EHO-tuned VPTIDF) and DQC-SPWM. In the proposed framework the implemented control procedure is utilized to diminish harmonic effects, improve robustness of the system and it also improved the stability of the overall system. The use of variable parameter EHO-tuned VPTIDF and DQC-SPWM improved the harmonic rejection ability, improved robustness of the system and it also improved the stability of the overall system. Variable parameter EHO-tuned VPTIDF not only improves system response to disturbances, but also is seen to improve system robustness and stability. This justified through simulated results. The faults are integral part of any system. The fault detection mechanism employed by using machine learning techniques is seen to be potent enough to capture the fault. This justified through simulated results. The improved performance, fault detection ability, robustness and stability of closed loop system is implemented and the results presented validates its real time implementation.