Oppositional Krill Herd Algorithm-Based RLNN Controller for Discrete-Mode AGC in Deregulated Hydrothermal Power System Using SMES

Abstract

This paper presents the application of oppositional krill herd algorithm (OKHA)-based reinforced learning neural network (RLNN) controller to study the discrete-mode automatic generation control (AGC) problems in the deregulated environment considering superconducting magnetic energy storage (SMES) system for three-area hydrothermal power system. The dynamic responses using OKHA-based RLNN controller for various loading conditions are compared with the proportional–integral–derivative (P–I–D) controllers whose gains are also optimized using OKHA. Area control error (ACE) is used as input to both P–I–D and RLNN controllers, and the weights of neural networks have been adjusted online for RLNN controllers. Sensitivity analyses have been performed to investigate the robustness of the controllers that are subject to change in SMES parameters and loading conditions. Investigation reveals that OKHA-based RLNN controllers give better dynamic performances compared to gains of P–I–D controllers obtained using OKHA considering SMES units for different loading conditions.

1 Introduction

Traditional power system structure has gone through many changes after deregulation of power sector, and most of the countries in the world have power regulating authorities who have set up restructured rules to improve power supply, which has resulted in the deregulation of AGC. The generation companies (GENCOs), distribution companies (DISCOs), transmission companies (TRANSCOs) and independent system operator (ISO) autonomously play a role in the competitive market. So, consumers have the opportunity to choose the providers of electricity and GENCOs that sell power to various DISCOs at competitive prices and each DISCO in an area has the freedom to have a contract with any GENCO in any other area to buy power. The total agreement is represented in a matrix called DISCO participation matrix (DPM) (Donde et al. 2001). More research works on the deregulation system have been incorporated in the literature (Christie and Bose 2001; Kumar et al. 1997; Tan et al. 2012; Demiroren and Zeynelgil 2007; Sinha et al. 2012; Arya and Kumar 2016; Balamurugan and Lekshmi 2016; Sahu et al. 2016; Nizamuddin and Bhatti 2014). The changes of the tie-line power flow and frequency deviations have occurred due to sudden load perturbation of demands from the customer side in the areas of power system. In this context, fixed gain controllers are not capable of handling the changes of the operating points.

Moreover, in case of load disturbances, the oscillations in the power–frequency and tie-line power flow persist for a long duration even with the supplementary controller. To compensate the sudden load changes, an active power source with first response such as superconducting magnetic energy storage (SMES) can take measuring action most effectively. In the literature Banerjee et al. (1990a, b), Tripathy et al. (1991), Tripathy et al. (1994) and Bhatt et al. (2011), the SMES is located in each area of the two-area system for AGC. Demroren (2003, 2004) has investigated the performance of a neural network controller for automatic generation control of a power system including the SMES unit. Abraham et al. (2007) have incorporated SMES unit as an active power source with fast response of frequencies and tie-power responses in an interconnected hydrothermal power system to compensate the sudden change of load.

Mostly integral controllers are used for AGC controllers, these types of controllers are slow acting, and nonlinearities cannot be taken into account to control the generating units using these controllers. The inherent nonlinearities in the system have led researchers to consider neural network techniques, and a nonlinear artificial neural network (ANN) controller is built with high efficiency of performance (Djukanovic et al. 1995). Supervised ANN controllers have been used by the investigators (Djukanovic et al. 1995; Beaufays et al. 1994) for better dynamic performance in the AGC system. But a considerable computational time is required for the database for training of the neural network controller using supervised learning algorithm. Reinforced learning algorithms (Ahamed et al. 2002, 2006) have also been used to get the optimal control output for the AGC system. The limitations in Djukanovic et al. (1995), Beaufays et al. (1994) and Ahamed et al. (2002, 2006) are the schemes offline and training sets are generated a priori by random variations of load and as a result the control action is discrete in nature. A back propagation through time algorithm (Zeynelgil et al. 2002) is used as neural network learning rule, and a multilayer perception neural network (MLPNN) controller for each area is used to overcome the limitations. MATLAB/Simulink model (Saikia et al. 2011) has been used to simulate the AGC system using reinforced learning neural network (RLNN) controller, and in both cases, the deregulated environment and SMES unit have not been considered. The fixed values of parameters have been considered while designing the RLNN controller based on trial and error method. Recently developed bio-inspired optimization techniques such as particle swarm optimization (Gozde et al. 2011), cuckoo search algorithm (Dash et al. 2014), firefly algorithm (Padhan et al. 2014; Sekhar et al. 2016), ant lion optimizer algorithm (Raju et al. 2016), bacterial foraging algorithm (Dhillon et al. 2016), grey wolf optimization (Guha et al. 2015) have been successfully applied for designing the controller parameters for load frequency control of interconnected power system. Also, krill herd algorithm (KHA) (Gandomi and Alavi 2012; Guha 2015, 2016), biogeography-based optimization (Guha 2014) and oppositional krill herd algorithm (OKHA) (Tizhoosh 2005; Dutta et al. 2016; Alam 2016) have been successfully applied in the various fields of power system including AGC. However, no literature has investigated the optimization of RLNN parameters for improving the dynamic responses of AGC system including the SMES unit. The present work has incorporated the physical constraints of SMES unit in the AGC while designing the RLNN controller, and the parameters of RLNN controller have been optimized using OKHA to improve its performance. The discrete-mode power system model of AGC with SMES unit has been used for designing the OKHA-based RLNN controller to make it more realistic.

In view of the above, the present work considers SMES unit in a discrete-mode AGC of three-area deregulated hydrothermal power system, and the main contributions of the present work are:

• (i) to optimize the gains of proportional–integral–derivative (P–I–D) controllers for a discrete-mode AGC of three-area deregulated hydrothermal power system using OKHA considering SMES unit.

• (ii) to design OKHA-based RLNN controller for the same power system and compare its performance with that obtained in step (i) for different loading conditions.

• (iii) to perform the sensitivity analysis for investigating the robustness of the OKHA-based RLNN controller that is subject to change in SMES parameters and loading conditions.

2 Dynamic Models of Three-Area Deregulated Power System

In the present work, two reheat thermal units and one hydrothermal unit with two GENCOs and two DISCOs have been considered in area 1, area 2 and area 3, respectively, as shown in Fig. 1.

Fig. 1

Three-area restructured power system

In Fig. 1, three areas have been connected through tie-lines so that any GENCO can supply power to any DISCO of any area. In this deregulated environment, DISCOs of any area can buy power from different GENCOs of any area at competitive prices and the whole transaction can be presented using DISCO participation matrix (DPM) as follows:

$${\text{DPM = }}\left[ \begin{aligned} {\text{cpf}}_{ 1 1} {\text{ cpf}}_{ 1 2} {\text{ cpf}}_{ 1 3} {\text{ cpf}}_{ 1 4} {\text{ cpf}}_{ 1 5} {\text{ cpf}}_{ 1 6} \hfill \\ {\text{cpf}}_{ 2 1} {\text{ cpf}}_{ 2 2} {\text{ cpf}}_{ 2 3} {\text{ cpf}}_{ 2 4} {\text{ cpf}}_{ 2 5} {\text{ cpf}}_{ 2 6} \hfill \\ {\text{cpf}}_{ 3 1} {\text{ cpf}}_{ 3 2} {\text{ cpf}}_{ 3 3} {\text{ cpf}}_{ 3 4} {\text{ cpf}}_{ 3 5} {\text{ cpf}}_{ 3 6} \hfill \\ {\text{cpf}}_{ 4 1} {\text{ cpf}}_{ 4 2} {\text{ cpf}}_{ 4 3} {\text{ cpf}}_{ 4 4} {\text{ cpf}}_{ 4 5} {\text{ cpf}}_{ 4 6} \hfill \\ {\text{cpf}}_{ 5 1} {\text{ cpf}}_{ 5 2} {\text{ cpf}}_{ 5 3} {\text{ cpf}}_{ 5 4} {\text{ cpf}}_{ 5 5} {\text{ cpf}}_{ 5 6} \hfill \\ {\text{cpf}}_{ 6 1} {\text{ cpf}}_{ 6 2} {\text{ cpf}}_{ 6 3} {\text{ cpf}}_{ 6 4} {\text{ cpf}}_{ 6 5} {\text{ cpf}}_{ 6 6} \hfill \\ \end{aligned} \right]$$

(1)

Here cpf is the contract participation factor and the total number of entries of column for DISCO_j in the DPM is $\sum\nolimits_{i = 1}^{6} {{\text{cpf}}_{ij} = 1}$.

For example, in the above DPM matrix, cpf₄₂ is the fraction of the total load power contracted by DISCO₂ from GENCO₄. In the case of more than one GENCO in each area, area control error (ACE) signal must be shared by the GENCOs in proportion to their contributions in each area and it can be represented by the coefficients, called ACE participation factors (ap) and for each area $\sum\nolimits_{i = 1}^{n} {{\text{ap}}_{i} = 1}$ where n is the number of GENCOs in each area. The scheduled steady-state power flow through the three tie-lines, i.e. $\Delta P_{\text{tie12}}^{\text{scheduled}}$, $\Delta P_{\text{tie23}}^{\text{scheduled}}$ and $\Delta P_{\text{tie31}}^{\text{scheduled}}$, can be expressed as follows (Demiroren and Zeynelgil 2007; Arya and Kumar 2016):

$$\Delta P_{\text{tie12}}^{\text{scheduled}} = \, \left[ \begin{aligned} \hfill \left( {{\text{cpf}}_{13} \Delta {\text{PL}}_{3} + {\text{cpf}}_{14} \Delta {\text{PL}}_{4} + {\text{cpf}}_{23} \Delta {\text{PL}}_{3} + {\text{cpf}}_{24} \Delta {\text{PL}}_{4} } \right) \\ \hfill - \left( {{\text{cpf}}_{31} \Delta {\text{PL}}_{1} + {\text{cpf}}_{32} \Delta {\text{PL}}_{2} + {\text{cpf}}_{41} \Delta {\text{PL}}_{1} + {\text{cpf}}_{42} \Delta {\text{PL}}_{2} } \right) \\ \end{aligned} \right]$$

(2)

$$\Delta P_{\text{tie23}}^{\text{scheduled}} = \left[ \begin{aligned} \left( {{\text{cpf}}_{ 3 5} \Delta{\text{PL}}_{ 5} + {\text{cpf}}_{ 3 6} \Delta{\text{PL}}_{ 6} + {\text{cpf}}_{ 4 5} \Delta{\text{PL}}_{ 4} + {\text{cpf}}_{ 4 6} \Delta{\text{PL}}_{ 6} } \right) \hfill \\ - \left( {{\text{cpf}}_{ 5 3} \Delta{\text{PL}}_{ 3} + {\text{cpf}}_{ 5 4} \Delta{\text{PL}}_{ 4} + {\text{cpf}}_{ 6 3} \Delta{\text{PL}}_{ 3} + {\text{cpf}}_{ 6 4} \Delta{\text{PL}}_{ 4} } \right) \hfill \\ \end{aligned} \right]$$

(3)

$$\Delta P_{\text{tie31}}^{\text{scheduled}} = \left[ \begin{aligned} \left( {{\text{cpf}}_{ 5 1} \Delta{\text{PL}}_{ 1} + {\text{cpf}}_{ 5 2} \Delta{\text{PL}}_{ 2} + {\text{cpf}}_{ 6 1} \Delta{\text{PL}}_{ 1} + {\text{cpf}}_{ 6 2} \Delta{\text{PL}}_{ 2} } \right) \hfill \\ - \left( {{\text{cpf}}_{ 1 5} \Delta{\text{PL}}_{ 5} + {\text{cpf}}_{ 1 6} \Delta{\text{PL}}_{ 1} + {\text{cpf}}_{ 2 5} \Delta{\text{PL}}_{ 5} + {\text{cpf}}_{ 2 6} \Delta{\text{PL}}_{ 6} } \right) \hfill \\ \end{aligned} \right]$$

(4)

where ΔPL is the change in load demand. The tie-line power flow errors are given as (Demiroren and Zeynelgil 2007; Arya and Kumar 2016):

$$\Delta P_{\text{tie12}}^{\text{error}} \, = \, \Delta P_{\text{tie12}}^{\text{actual}} - \Delta P_{\text{tie12}}^{\text{scheduled}} \,$$

(5)

$$\Delta P_{\text{tie23}}^{\text{error}} = \Delta P_{\text{tie23}}^{\text{actual}} - \Delta P_{\text{tie23}}^{\text{scheduled}} \,$$

(6)

$$\Delta P_{\text{tie31}}^{\text{error}} = \Delta P_{\text{tie31}}^{\text{actual}} - \Delta P_{\text{tie31}}^{\text{scheduled}} \,$$

(7)

The ACE signals in the three areas can then be expressed as follows:

$${\text{ACE}}_{1} = B_{1} \Delta F_{1} + \Delta P_{\text{tie12}}^{\text{error}}$$

(8)

$${\text{ACE}}_{2} = B_{2} \Delta F_{2} + \Delta P_{\text{tie23}}^{\text{error}}$$

(9)

$${\text{ACE}}_{3} = B_{3} \Delta F_{3} + \Delta P_{\text{tie31}}^{\text{error}}$$

(10)

where B₁, B₂ and B₃ are the bias factors, ΔF₁, ΔF₂ and ΔF₃ are the frequency deviations for area 1, area 2 and area 3, respectively, and contracted power supplied by ith GENCO is given by:

$$\Delta P_{i \, } = \sum\limits_{j = 1 \, }^{6} {{\text{cpf}}_{ij} \Delta {\text{PL}}_{j} }$$

(11)

The aforesaid three-area deregulated hydrothermal power system has been represented in the state space form for the analysis of the dynamic performance of the system. Figure 2 shows the block diagram of the above system, and the SMES blocks have been incorporated in each area. The system parameters are given in “Appendix”.

Fig. 2

Three-area deregulated hydrothermal power system with the SMES

3 SMES Configuration in the Power System

The thyristor-controlled SMES unit configuration is shown in Fig. 3. The SMES unit has a DC superconducting coil and 12-pulse converter which are connected through a star–delta or star–star transformer to the AC grid through a power conversion system (PCS). The superconducting coils have current of hundreds of thousands of amperes, and no ac power system normally operates at these current levels. During the normal operation of the power system, the superconducting coil may be charged to a set value from the grid and also conducts current with negligible losses because it is maintained at very low temperatures (Banerjee et al. 1990a, b; Tripathy et al. 1991; Tripathy et al. 1994; Bhatt et al. 2011; Demroren 2003; Demiroren and Yesil 2004). The stored energy is almost released through the PCS to the power system as alternating current during the sudden rise of load demand. When the governor as well as other control mechanisms starts working to set the new equilibrium condition of the power system, the coil current changes back to its initial value. Similar action also occurs during the sudden release of loads. The excess energy of some portion is absorbed as the system returns to its steady state because the coil immediately gets charged towards its full value.

Fig. 3

(Reproduced with permission from Abraham et al. 2007; Tripathy et al. 1992)

SMES circuit diagram

So, the DC voltage across the inductor varies continuously within a certain range of positive and negative values by the control of the converter firing angle. The inductor is initially charged to its rated current by applying a small positive voltage, and the coil is superconducting because the rated value of current is maintained constant by reducing the voltage across the inductor to zero. Neglecting the transformer and converter losses, the DC voltage is given by (Tripathy et al. 1994):

$$E_{\text{d}} = 2V_{\text{do}} \cos \phi - 2I_{\text{d}} R_{\text{c}}$$

(12)

where $E_{\text{d}}$ = inductor dc voltage in kV, $\phi$ = firing angle in degrees, $I_{\text{d}}$ = inductor current in kA, $R_{\text{c}}$ = equivalent resistance in ${\text{k}}\Omega$ and $V_{\text{do}}$ = maximum circuit bridge voltage in kV. The change of commutation angle $\phi$ is controlled by charging and discharging of the SMES. Converter acts in the converter mode (charging mode) when $\phi < 90^{ \circ }$, as well as the converter acts in the inverter mode (discharging mode) when $\phi > 90^{ \circ }$.

4 Control of SMES Unit

When sudden changes of loading occur in any of the three areas, the frequency falls, power is to be pumped back, and the control voltage $E_{\text{d}}$ becomes negative since the current through the inductor and the thyristors cannot change its direction. The change of incremental voltage applied to the inductor is expressed as:

$$\Delta E_{\text{d}} = \left[ {{{K_{\text{smes}} } \mathord{\left/ {\vphantom {{K_{\text{smes}} } {1 + sT_{\text{dc}} }}} (\right. \kern-0pt} {1 + sT_{\text{dc}} }}} )\right]\Delta E_{\text{r}}$$

(13)

where $\Delta E_{\text{d}}$ = incremental change in converter voltage, T_dc = converter time delay, K_smes = gain of control loop, and $\Delta E_{\text{r}}$ = input signal to the SMES control logic. The inductor current deviation is given by:

$$\Delta I_{\text{d}} = {{\Delta E_{\text{d}} } \mathord{\left/ {\vphantom {{\Delta E_{\text{d}} } {sL}}} \right. \kern-0pt} {sL}}$$

(14)

In this work, ACE of ith area is considered as the input signal to the SMES control logic (i.e. $\Delta E_{\text{di}} = {\text{ACE}}_{i}$). Thus, from Eq. (13),

$$\Delta E_{\text{di}} = \frac{{K_{\text{smesi}} }}{{1 + sT_{\text{dci}} }}(B_{i} \Delta F_{i} + \Delta P_{\text{tieij}}^{\text{error}} )$$

(15)

If Eq. (15) is used, the inductor current in the SMES unit will return to its nominal value very slowly. Figure 4 shows the block diagram representation of SMES incorporating the negative inductor current deviation, and the dynamic equations for both the inductor voltage and current deviation of the SMES unit area are given below:

Fig. 4

(Reproduced with permission from Abraham et al. 2007)

SMES block diagram with negative inductor current deviation feedback

$$\Delta E_{\text{di}} = \frac{1}{{1 + sT_{\text{dci}} }}\left[ {K_{\text{smesi}} (B_{i} \Delta F_{i} + \Delta P_{\text{tieij}}^{\text{error}} ) - K_{\text{idi}} \Delta I_{\text{di}} } \right]$$

(16)

5 State Space Representation of the System

For the present analysis, the dynamic model in state space form can be written as:

$$\mathop X\limits^{ \bullet } = AX + BU + \varGamma P_{1} + \varUpsilon P_{2}$$

(17)

where X, U, $P_{1}$ and $P_{2}$ are the state, control, load disturbance vectors and un-contracted power demand vectors, respectively, and A, B, $\varGamma$ and $\varUpsilon$ are the real constant matrices depending on the system parameters and operating points.

The discrete time analysis of the above continuous time system is modelled by the first-order linear difference equation (Kothari et al. 1989):

$$X(k + 1) = \varPhi X(k) + \varPsi U(k) + \varLambda P_{1} (k) + \lambda P_{2} (k)$$

(18)

where $\varPhi = e^{AT}$; $\varPsi = (e^{AT} - I)A^{ - 1} B$; $\varLambda = (e^{AT} - I)A^{ - 1} \varGamma$; $\lambda = (e^{AT} - I)A^{ - 1} \varUpsilon$; T = sampling period; t = KT, K = 0, 1, 2….

In the present work, the value of T has been considered as 0.01 s.

6 Oppositional Krill Herd Algorithm (OKHA)

Gandomi and Alavi (2012) have proposed the krill herd algorithm (KHA) based on the herding behaviour of krill individuals where in the search process, an individual krill always tries to move towards the highest density of food. The position of the individual krill is updated towards the value of objective function, i.e. the distance of the food from the highest density of the krill swarm by the process of induced movement foraging and random diffusion (Guha 2015, 2016).

6.1 Induced Movement

The movement of the ith krill can be defined as (Gandomi and Alavi 2012):

$$M_{i}^{\text{new}} = M_{i}^{\hbox{max} } \xi_{i} + \omega_{n} M_{i}^{\text{old}}$$

(19)

and

$$\xi_{i} \, = \, \xi_{i}^{\text{new}} + \, \xi_{i}^{\text{target}}$$

(20)

where $M^{\hbox{max} }$ = maximum induced speed and it is taken 0.01 m/s, $\omega_{n}$ = inertia weight of motion induced in the range [0, 1]. $M_{i}^{\text{old}}$ = last motion induced, $\xi_{i}^{\text{new}}$ = local effect provided by the neighbours, $\xi_{i}^{\text{target}}$ = effect of target direction provided by the best krill individual.

The effect of the neighbours in a krill movement individual can be expressed as follows (Gandomi and Alavi 2012):

$$\xi_{i}^{\text{new}} = \sum\limits_{z = 1}^{p} {Q_{iz} G_{iz} } \,$$

(21)

$$G_{iz} = {{(G_{z} - G_{i} )} \mathord{\left/ {\vphantom {{(G_{z} - G_{i} )} {(\left\| {G_{z} - G_{i} } \right\| + \tau )}}} \right. \kern-0pt} {(\left\| {G_{z} - G_{i} } \right\| + \tau )}}$$

(22)

$$Q_{iz} = {{(Q_{i} - Q_{z} )} \mathord{\left/ {\vphantom {{(Q_{i} - Q_{z} )} {(Q^{\text{w}} - Q^{\text{b}} )}}} \right. \kern-0pt} {(Q^{\text{w}} - Q^{\text{b}} )}}$$

(23)

where $Q^{\text{b}}$ = best fitness values of the krill individuals, $Q^{\text{w}}$ = worst fitness values of the krill individuals, $Q_{i}$ = fitness value of the ith krill individual, $Q_{z}$ = fitness value of the zth neighbour, p = total number of neighbours, G = relative position of the krill, τ = small positive number.

The sensing distance for each krill individual is determined as follows (Gandomi and Alavi 2012):

$$d_{i} = \frac{1}{5N} \, \sum\limits_{z = 1}^{N} {\left\| {G_{i} - G_{z} } \right\|} \,$$

(24)

where $d_{i}$ = sensing distance for the ith krill individual, N = no of krill individual.

The lowest fitness of an individual krill is known target vector and the effect of the individual krill with the best fitness on the ith individual krill have been incorporated in the following formula which leads to global optima and is expressed as (Gandomi and Alavi 2012):

$$\xi_{i}^{\text{target}} = \, C^{\text{b}} Q_{{i{\text{b}}}} G_{{i{\text{b}}}}$$

(25)

where $C^{\text{b}}$ = coefficient with the best fitness to the ith krill individual and is expressed as:

$$C^{\text{b}} = 2\left( {R + ({I \mathord{\left/ {\vphantom {I {I_{\hbox{max} } }}} \right. \kern-0pt} {I_{\hbox{max} } }})} \right)$$

(26)

where R = random values between 0 and 1, I = no of actual iteration, I_max = maximum no of iterations.

6.2 Foraging Motion

The food location and previous experience about food locations are the main effective parameters of foraging motion, and it can be expressed for the ith krill individual as follows (Gandomi and Alavi 2012):

$$F_{i} = V_{\text{f}} \gamma_{i} + \omega_{\text{f}} F_{i}^{\text{old}}$$

(27)

and

$$\gamma_{i} = \gamma_{i}^{\text{f}} + \gamma_{i}^{\text{b}}$$

(28)

where $V_{\text{f}}$ = foraging speed and it is taken 0.02 m/s, $\omega_{\text{f}}$ = inertia weight of foraging motion in the range [0, 1], $\gamma_{i}^{\text{f}}$ = attractive of food, $\gamma_{i}^{\text{b}}$ = effect of the best fitness of the ith krill.

The iteration of food centre is expressed as (Gandomi and Alavi 2012):

$$G^{\text{f}} {{\sum\limits_{i = 1}^{N} {(G_{i} /Q_{i} )} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{N} {(G_{i} /Q_{i} )} } {\sum\limits_{i = 1}^{N} {(1/Q_{i} } )}}} \right. \kern-0pt} {\sum\limits_{i = 1}^{N} {(1/Q_{i} } )}}$$

(29)

The food attraction for the ith krill individual is expressed as:

$$\gamma_{i}^{\text{f}} = C^{\text{f}} Q_{{i{\text{f}}}} G_{{i{\text{f}}}}$$

(30)

where food coefficient, $C^{\text{f}} = 2\left( {1 - ({I \mathord{\left/ {\vphantom {I {I_{\hbox{max} } }}} \right. \kern-0pt} {I_{\hbox{max} } }})} \right)$.

The best fitness effect of the ith krill individual is defined as:

$$\gamma_{i}^{\text{b}} = Q_{{i{\text{b}}}} G_{{i{\text{b}}}}$$

(31)

where $Q_{{i{\text{b}}}}$ = previously best position of the ith krill individual.

6.3 Physical Diffusion

It can be expressed as:

$$D_{i} = D^{\hbox{max} } \delta$$

(32)

where $D^{\hbox{max} }$ = maximum diffusion speed in the range [0.002, 0.010] m/s, $\delta$ = random directional vector and its arrays are random values between − 1 and 1.

Equation (32) has decreased the random speed linearly with the time and works on the basis of a geometrical annealing schedule as follows (Gandomi and Alavi 2012):

$$D_{i} = D^{\hbox{max} } \left( {1 - ({I \mathord{\left/ {\vphantom {I {I_{\hbox{max} } }}} \right. \kern-0pt} {I_{\hbox{max} } }})} \right)\delta$$

(33)

6.4 Motion Process of the KHA

The foraging motion and motion induced by other krill individuals work together to make KHA a powerful algorithm (Gandomi and Alavi 2012). The position vector of a krill individual during the interval t to ($t + \Delta t$) is given by,

$$G_{i} (t + \Delta t) = G_{i} (t) + \Delta t\frac{{dG_{i} }}{dt}$$

(34)

$\Delta t$ completely depends on the search space and it seems it can be expressed as (Gandomi and Alavi 2012):

$$\Delta t = C_{t} \sum\limits_{j = 1}^{n} {({\text{Ub}}_{j} - {\text{Lb}}_{j} )}$$

(35)

where n = total number of variables, ${\text{Ub}}_{j}$ = upper bounds of the jth variables, ${\text{Lb}}_{j}$ = lower bounds of the jth variables, $C_{t}$ = constant number between [0, 2].

6.5 Application of the Genetic Operators

The genetic reproduction mechanisms such as crossover and mutation are incorporated into KHA for improving the performance of the algorithm (Gandomi and Alavi 2012). The jth components of the ith krill may be updated by,

$$M_{ij} = \left\{ {\begin{array}{*{20}c} {M_{{{\text{r}}j}} } & {R_{ij} < \, C_{\text{r}} } \\ {M_{ij} } & {\text{else}} \\ \end{array} } \right.$$

(36)

where $r = 1,2, \ldots ,i - 1,\;i + 1, \ldots ,N$ and crossover probability, $C_{\text{r}} = 0.2Q_{{i{\text{b}}}}$.

The adaptive mutation operation is expressed as:

$$M_{ij} = \left\{ {\begin{array}{*{20}l} {M_{gj} + \mu (M_{pj} - M_{qj} )} \hfill & {R_{ij} < {\text{Mu}}} \hfill \\ {M_{ij} } \hfill & {\text{else}} \hfill \\ \end{array} } \right.$$

(37)

where $p,q = 1,2, \ldots ,i - 1,\;i + 1, \ldots ,K \,$ and mutation probability, ${\text{Mu}} = 0.05/Q_{{i{\text{b}}}}$, $\mu = 0\;{\text{to}}\;1$.

6.6 Opposition-Based Learning

Tizhoosh (2005) has incorporated the opposition-based learning (OBL) in computational intelligence which enhances the search abilities of the conventional population-based optimization techniques for solving nonlinear optimization problem. The main idea behind OBL is to consider the opposite of an assumption or a guess and compare it with the original assumption, thereby improving the chances to find a solution faster. The OBL concepts have been developed depending on two factors, opposite number and opposite point. Let $x \in [a,b]$ be the real number and $P\left( {x_{1} ,x_{2} , \ldots x_{n} } \right)$ be a point in n-dimensional coordinate system with $x_{i} \in [a_{i} ,b_{i} ]$, then,

$${\text{The}}\;{\text{opposition}}\;{\text{number}}\;{\text{is,}}\quad \hat{x} = \, a + b - x$$

(38)

$${\text{And}}\;{\text{the}}\;{\text{opposite}}\;{\text{point}}\;{\text{is}},\quad \hat{x}_{i} = \, a_{i} + b_{i} - x_{i}$$

(39)

For fitness function f(x), if $x \in [a,b]$ is an initial (random) guess and $\hat{x}$ is its opposite value, then in every iteration we calculate f(x) and $f(\hat{x})$. If $f(\hat{x}) > f(x)$, then update the value of x with $\hat{x}$; otherwise keep it the same. Therefore, the population proceeds towards the best solution through simultaneous computation and evaluation of the current point.

7 Optimization of Gains of P–I–D Controllers Using OKHA

In the present work, the following objective function is proposed for optimizing the P–I–D gains using OKHA (Gandomi and Alavi 2012; Tizhoosh 2005; Alam 2016):

$$J = \sum\limits_{k = 0}^{ \propto } {\left[ {\left( {\Delta f_{1} (k)} \right)^{2} + \left( {\Delta f_{2} (k)} \right)^{2} + \left( {\Delta f_{3} (k)} \right)^{2} + \left( {\Delta P_{\text{tie12}}^{\text{error}} (k)} \right)^{2} + \left( {\Delta P_{\text{tie23}}^{\text{error}} (k)} \right)^{2} + \left( {\Delta P_{\text{tie31}}^{\text{error}} (k)} \right)^{2} } \right]}$$

(40)

In this case, inertia weight of motion induced ($\omega_{n}$) and inertia weights of foraging motion ($\omega_{f}$) have been considered 0.9 and 0.8, respectively, at the beginning of search process. The value of maximum induced speed ($M^{\hbox{max} }$), foraging speed ($V_{\text{f}}$) and maximum diffusion speed ($D^{\hbox{max} }$) are 0.01, 0.02 and 0.004 m/s, respectively. Also, the population size is taken as 50 and the number of iterations has been considered as 100. The optimal set of P–I–D controller gains has been investigated by OKHA to reduce the value of the above objective function, and the ranges of K_P, K_I and K_D have been considered $0 \le K_{\text{P}} \le 1$, $0 \le K_{\text{I}} \le 1$ and $0 \le K_{\text{D}} \le 1$, respectively.

8 Design of OKHA-Based RLNN Controller

In the present work, there are three control areas and each area has one OKHA-based RLNN controller. Figure 5 shows the OKHA-based RLNN controller structure with associated signals as well as the plant which represents state space blocks of a particular control area, and this figure also shows the error signals in the tie-lines that are used to bring up the RLNN controller weights. In this case, one neuron in the input layer, four numbers of neurons in the hidden layer and one neuron in the output layer have been considered and the tie-line error signals given by Eqs. (5, 6, 7) are used as error signals and the learning rates, $\alpha$ and $\sigma$, control the convergence speed and stability of the weights during learning. Similarly, the momentum constant $\beta$ is also used to improve the convergence. $\Delta W1_{ij}^{\text{old}}$ and $\Delta W2_{ij}^{\text{old}}$ are the one step previous updates for the weights.

Fig. 5

(Reproduced with permission from Saikia et al. 2011)

Construction of OKHA-based RLNN controller with plant

The initial values of all the weights in this AGC problem are considered as ‘0’, and $\alpha$, $\sigma$ and $\beta$ have been optimized using OKHA by optimized the objective function given by Eq. (40). The ranges of $\alpha$, $\sigma$ and $\beta$ have been considered $0 \le \alpha \le 0.02$, $- 1 \le \beta \le 0$ and $0 \le \sigma \le 1$, respectively. The log-sigmoidal activation functions have been used at the hidden layer.

The RLNN controllers input in the ith area are given by:

$$Y_{i} = {\text{ACE}}_{i} ,\quad i = 1,2,3.$$

(41)

The hidden layers input neurons for ith area are given by:

$$u_{ij} = Y_{i} \times W_{ij} ,\quad \, j = 1, \ldots ,N_{h} .$$

(42)

where N_h = hidden number of neuron (here, N_h = 4), W_ij = hidden layers input weight vector.

The output from the hidden layer after passing through the log-sigmoid activation function is given by:

$$h_{ij} = {1 \mathord{\left/ {\vphantom {1 {\left\{ {1 + \exp \left( { - u_{ij} } \right)} \right\}}}} \right. \kern-0pt} {\left\{ {1 + \exp \left( { - u_{ij} } \right)} \right\}}},\quad j = 1, \ldots ,4.$$

(43)

The control signal generated from the output layer is calculated as:

$$z = \sum\limits_{j = 1}^{4} {h_{ij} W2_{ij} }$$

(44)

where W2_ij = hidden layers output weight vector.

The weights of the output layer are then updated through the least mean square rule as given below:

$$\Delta W2_{ij} = - \alpha \times \Delta P_{\text{tie ij}}^{\text{error}} + \beta \times \Delta W1_{\text{ij}}^{\text{old}} ,\quad \, j = 1, \ldots ,4.$$

(45)

The back propagated error to the hidden layer from the output layer is as follows:

$${\text{EB2}}_{ij} = \Delta P_{\text{tie ij}}^{\text{error}} \times \Delta W2_{ij} ,\quad \, j = 1, \ldots ,4.$$

(46)

The derivative of output of log-sigmoid function with respect to its associated input weights is given by:

$${\text{EB}}1_{ij} = h1_{ij} \times \left( {1 - h1_{ij} } \right) \times {\text{EB}}2_{ij} , \, j = 1, \ldots ,4.$$

(47)

Therefore, the weights of hidden layer are updated using the following equation,

$$\Delta W1_{ij} = - \sigma \times {\text{EB}}1_{ij} \times Y_{i} + \beta \times \Delta W1_{ij}^{old} , \quad j = 1, \ldots, 4.$$

(48)

The MATLAB functions have been developed using the above equations, and the algorithm is given below:

• Step-1: Read $N_{h}$ and initialize $\alpha ,\beta \;{\text{and}}\;\sigma$ parameters for RLNN controller.

• Step-2: Initialize $W1_{ij} = 0,\;W2_{ij} = 0,\;\Delta W_{1} = 0\;{\text{and}}\;\Delta W_{2} = 0$.

• Step-3: Set iteration count $j = 1$.

• Step-4: Obtain ACE, Y_i from the system, $j = 1$.

• Step-5: If $j = N_{h}$, go to Step-7,

  • Else calculate $u_{ij} ,h_{ij} \;{\text{and}}\;z$ from Eqs. (42, 43) and (44), respectively.

• Step-6: Advance $j = j + 1$.

• Step-7: Out control signal ‘z’ to the system and $j = 1$.

• Step-8: If $j = N_{h}$, go to Step-10,

  • Else calculate ${\text{EB}}2_{ij} ,\;{\text{EB}}1_{ij} \;{\text{and}}\;\Delta W1_{ij}$ from Eqs. (46), (47) and (48), respectively.

• Step-9: Advance $j = j + 1$.

• Step-10: Initialize $j = 1$.

• Step-11: If $j = N_{h}$, go to Step-4,

  • Else calculate ${\text{EB}}2_{ij} \;{\text{and}}\;\Delta W1_{ij}$ from Eqs. (46) and (48), respectively.

• Step-12: Advance $j = j + 1$ and go to Step-11.

• Step-13: Simulate Eq. (18) and calculate J using Eq. (40).

• Step-14: Calculate induced motion using Eq. (19), foraging motion using Eq. (27) and physical diffusion using Eq. (32).

• Step-15: Implement the genetic operation using Eqs. (36) and (37).

• Step-16: Implement the opposition-based learning using Eqs. (38) and (39).

• Step-17: Update krill position, i.e. the value of $\alpha ,\;\beta \;{\text{and}}\;\sigma$ using Eq. (34).

• Step-18: If stop criterion is not reached, go to Step-13.

• Step-19: Find the optimal value of $\alpha ,\;\beta \;{\text{and}}\;\sigma .$

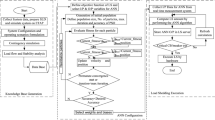
The flow chart for finding out the $\alpha ,\;\beta \;{\text{and}}\;\sigma$ parameters of RLNN controller using OKHA is shown in Fig. 6.

Fig. 6

Flow chart for finding optimized value of $\alpha ,\;\beta \;{\text{and}}\;\sigma$ for RLNN controller using OKHA

9 Results and Discussion

Three different cases for analysing the performance of AGC system using both RLNN controller and P–I–D controller have been considered as follows:

Case 1:

In this case, the load has been changed in area 1 and ACE participation factors are taken as ap₁₁ = 0.65, ap₁₂ = 0.35, ap₂₁ = 0.65, ap₂₂ = 0.35, ap₃₁ = 0.5, ap₃₂ = 0.5. The load demand value is considered in this case as ∆PL₁ = 0.05 pu MW, ∆PL₂ = 0.05 pu MW, ∆PL₃ = 0.0, ∆PL₄ = 0.0, ∆PL₅ = 0.0, ∆PL₆ = 0.0. The DISCO participation matrix (DPM) is considered as follows:

$${\text{DPM = }}\left[ {\begin{array}{*{20}l} { 0. 3} \hfill & { 0. 4} \hfill & { 0. 5} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.3} \hfill & {0.3} \hfill & {0.1} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.2} \hfill & {0.1} \hfill & {0.2} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.1} \hfill & {0.0} \hfill & {0.1} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.1} \hfill & {0.1} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.0} \hfill & {0.1} \hfill & {0.1} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill \\ \end{array} } \right]$$

Case 2:

For the second case, the ACE participation factors are considered as ap₁₁ = 0.75, ap₁₂ = 0.25, ap₂₁ = 0.55, ap₂₂ = 0.45, ap₃₁ = 0.35, ap₃₂ = 0.65 and the load demands are considered as ∆PL₁ = 0.05 pu MW, ∆PL₂ = 0.05 pu MW, ∆PL₃ = 0.05 pu MW, ∆PL₄ = 0.05 pu MW, ∆PL₅ = 0.05 pu MW, ∆PL₆ = 0.05 pu MW. The DISCO participation matrix (DPM) values are assumed as follows:

$${\text{DPM = }}\left[ {\begin{array}{*{20}l} {0.5} \hfill & {0.4} \hfill & {0.4} \hfill & {0.1} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.3} \hfill & {0.0} \hfill & {0.3} \hfill & {0.4} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.2} \hfill & {0.4} \hfill & {0.0} \hfill & {0.1} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.0} \hfill & {0.2} \hfill & {0.3} \hfill & {0.4} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.0} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill \\ {0.0} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill & {0.0} \hfill \\ \end{array} } \right]$$

Case 3:

In this case, the DISCO infringes an agreement by demanding additional power than the pre-specified value. Then, the GENCOs must supply the extra load demand in the same area to that DISCO. So, the agreement violation occurs under second operation case and in this case it is considered that DISCO₁ stipulates 0.05 p.u MW extra power. So, the full amount of local load for the area-1 is 0.15 p.u MW, i.e. [(DISCO₁ load + DISCO₂ load) = (0.05 + 0.05) + 0.05 = 0.15 p.u MW]. Similarly, the full amount of load for area-2 is 0.1 p.u MW, i.e. (DISCO₃ load + DISCO₄ load = 0.1 p.u MW). The full amount of load for area-3 is the same as that area-2. The loads without agreement of DISCO₁ are reproduced in generations both of GENCO₁ and GENCO₂, for the same area.

In this work, the gains of P–I–D controllers in deregulated operation are optimized using OKHA for each area in the three-area power system. For AGC after deregulation, for case-2, OKHA is used for both optimizing the gains of P–I–D controllers and the parameters of RLNN controller, and the values of gains of P–I–D controllers and the parameters of RLNN controller are given in Table 1. The P–I–D controller for each area designed using OKHA is substituted by RLNN controller, and the values of objective function J are given in Table 2 for case-2. The convergent characteristics of objective functions using OKHA for P–I–D and RLNN controllers are shown in Fig. 7. From Fig. 7, it is seen that the smooth curve for change of the value of objective function for both P–I–D and RLNN controller using OKHA ensures consistency in the convergence.

Table 1 Optimum values of gains of P–I–D controllers and RLNN controller parameters using OKHA for case-2

Table 2 Values of objective function considering OKHA-based P–I–D and RLNN controllers

Fig. 7

Convergent characteristics of objective functions using OKHA

Figure 8 shows the comparison of dynamic responses with and without SMES considering P–I–D controllers for case-1. It is clearly seen that SMES has great effect in terms of peak deviation and settling time. So SMES should be incorporated while analysing the dynamic performance of the system. Figure 9 shows the comparison of dynamic responses of frequency deviation for the first case for area-1 with RLNN controller and ANN controller using back propagation through time algorithm, and from this figure, it is seen that RLNN controller gives better dynamic response in terms of peak deviation and settling time. A transport time delay of feedback signal, i.e. area control error (ACE) of 50 ms has been incorporated into the system to find out its impact in the dynamic performance of the system. Figure 10 shows the comparison of responses with and without time delay in the feedback control for the OKHA-based RLNN controller for case-1. It is seen that the effect of time delay on the dynamic responses of the system is negligible.

Fig. 8

Dynamic response of frequency deviation for area-1, P–I–D controller with and without considering SMES unit

Fig. 9

Dynamic response of frequency deviation for the first case for area-1 with SMES

Fig. 10

Dynamic response of frequency deviation for the first case for area-1 with SMES

The comparison of frequency deviations in each area ($\Delta F_{1} ,\;\Delta F_{2} \;{\text{and}}\;\Delta F_{3}$) and the deviations of three tie-line powers ($\Delta P_{\text{tie12}}^{\text{error}} ,\;\Delta P_{\text{tie23}}^{\text{error}} \;{\text{and}}\;\Delta P_{\text{tie31}}^{\text{error}}$) for the first case considering SMES with P–I–D and RLNN controller are shown in Fig. 11, and Fig. 12 shows the comparison of the same variables for the second case. For the case of agreement violation, extra load occurs in area-1 and Fig. 13 shows the comparison of the same variables for case-3. From Figs. 11, 12 and 13, it is seen that the performance of OKHA-based RLNN controller gives better responses in terms of peak overshoot and settling time as compared to P–I–D controller designed using OKHA for frequency deviations in each area and the deviations of three tie-line powers.

Fig. 11

Dynamic responses of $\Delta F_{1} ,\;\Delta F_{2} ,\;\Delta F_{3} ,\;\Delta P_{\text{tie12}}^{\text{error}} ,\;\Delta P_{\text{tie23}}^{\text{error}} \;{\text{and}}\;\Delta P_{\text{tie31}}^{\text{error}}$ for case-1 considering SMES with P–I–D and RLNN controller

Fig. 12

Dynamic responses of $\Delta {F}_{ 1} ,\, \Delta {F}_{ 2} ,\, \Delta {F}_{ 3} ,\, \Delta {P}_{\text{tie12}}^{\text{error}} ,\, \Delta {P}_{\text{tie23}}^{\text{error}}\; {\text{and}} \; \Delta_{\text{tie31}}^{\text{error}}$ for case-2 considering SMES with P–I–D and RLNN controller

Fig. 13

Dynamic responses of $\Delta F_{1} ,\;\Delta F_{2} ,\;\Delta F_{3} ,\;\Delta P_{\text{tie12}}^{\text{error}} ,\;\Delta P_{\text{tie23}}^{\text{error}} \;{\text{and}}\;\Delta P_{\text{tie31}}^{\text{error}}$ for case-3 considering SMES with P–I–D and RLNN controller

The effect of variations of system parameters of SMES (L, T_dc, K_smes, I_do and K_id) and loading conditions on the dynamic responses have been observed for sensitivity analysis of the considered SMES-based deregulated three-area hydrothermal power system. The loading conditions for case-2 and system parameters of SMES are changed by ± 40% from their nominal values taking one at a time and the peak overshoot, settling time (2%) and the values of objective function J are calculated, and the results are given in Table 3. From Table 3, it is clear that the effects of variations on system parameters and loading conditions are negligible on the performances of the system.

Table 3 Sensitivity analysis of deregulated hydrothermal power system with SMES

10 Conclusions

In the present work, RLNN controllers and P–I–D controllers have been analysed in discrete-mode AGC of a three-area deregulated hydrothermal power system considering SMES unit in each area. The gains of P–I–D controllers and the parameters of RLNN controllers for the considered power system have been optimized using OKHA. The results reveal that the OKHA-based RLNN controllers give better dynamic responses than P–I–D controllers in terms of peak deviations and settling times for different loading conditions. Sensitivity analyses have also been performed to investigate the robustness of the RLNN controllers by changing loading conditions and parameters of SMES units. From the sensitivity analysis, it is seen that OKHA-based RLNN controllers are quite robust. Discrete-mode analyses have been performed for the practical realization of the RLNN controllers.

Appendix

State space model matrices:

For the considered three-area deregulated hydrothermal power system, the system matrix [A] is of the order of $24 \times 24$ and its nonzero elements are given below:

$$\begin{aligned} A_{1,1} & = - \frac{1}{{T_{p1} }},\quad A_{1,4} = - \frac{{K_{p1} }}{{T_{p1} }},\quad A_{1,6} = - a_{31} \frac{{K_{p1} }}{{T_{p1} }},\quad A_{1,7} = \frac{{K_{p1} }}{{T_{p1} }},\quad A_{1,10} = \frac{{K_{p1} }}{{T_{p1} }}, \\ A_{2,2} & = - \frac{1}{{T_{p2} }},\quad A_{2,4} = - a_{12} \frac{{K_{p2} }}{{T_{p2} }},\quad A_{2,5} = \frac{{K_{p2} }}{{T_{p2} }},\quad A_{2,10} = \frac{{K_{p2} }}{{T_{p2} }},\quad A_{2,13} = \frac{{K_{p2} }}{{T_{p2} }}, \\ A_{3,3} & = - \frac{1}{{T_{p3} }},\quad A_{3,5} = - a_{23} \frac{{K_{p3} }}{{T_{p3} }},\quad A_{3,6} = - \frac{{K_{p2} }}{{T_{p2} }},\quad A_{3,19} = \frac{{K_{p3} }}{{T_{p3} }},\quad A_{3,22} = \frac{{K_{p3} }}{{T_{p3} }}, \\ A_{4,1} & = 2\pi T_{12} ,\quad A_{4,2} = \, - \, 2\pi T_{12} , \\ A_{5,2} & = 2\pi T_{23} ,\quad A_{5,3} = \, - \, 2\pi T_{23} , \\ A_{6,1} & = \, - \, 2\pi T_{31} ,\quad A_{6,3} = 2\pi T_{31} , \\ A_{7,7} & = - 1/T_{r1} ,\quad A_{7,8} = \left( {\frac{1}{{T_{r1} }} - \frac{{K_{r1} }}{{T_{t1} T_{r1} }}} \right),A_{7,9} = \frac{{K_{r1} }}{{T_{t1} T_{r1} }}, \\ A_{8,8} & = - \frac{1}{{T_{t1} }},\quad A_{8,9} = \frac{1}{{T_{t1} }}, \\ A_{9,1} & = - \frac{1}{{R_{1} T_{g1} }},\quad A_{9,9} = - \frac{1}{{T_{g1} }}, \\ A_{10,10} & = - 1/T_{r2} ,\quad A_{10,11} = \left( {\frac{1}{{T_{r2} }} - \frac{{K_{r2} }}{{T_{t2} T_{r2} }}} \right),\quad A_{10,12} = \frac{{K_{r2} }}{{T_{t2} T_{r2} }}, \\ A_{11,11} & = - \frac{1}{{T_{t2} }},\quad A_{11,12} = \frac{1}{{T_{t2} }}, \\ A_{12,1} & = - \frac{1}{{R_{2} T_{g2} }},\quad A_{12,12} = - \frac{1}{{T_{g2} }}, \\ A_{13,13} & = - \frac{1}{{T_{r3} }},\quad A_{13,14} = \left( {\frac{1}{{T_{r3} }} - \frac{{K_{r3} }}{{T_{r3} T_{t3} }}} \right),\quad A_{13,15} = \frac{{K_{r3} }}{{T_{r3} T_{t3} }}, \\ A_{14,14} & = - \frac{1}{{T_{t3} }},\quad A_{14,15} = \frac{1}{{T_{t3} }}, \\ A_{15,2} & = - \frac{1}{{R_{3} T_{g3} }},\quad A_{15,15} = - \frac{1}{{T_{g3} }}, \\ A_{16,16} & = - \frac{1}{{T_{r4} }},\quad A_{16,17} = \left( {\frac{1}{{T_{r4} }} - \frac{{K_{r4} }}{{T_{r4} T_{t4} }}} \right),\quad A_{16,18} = \frac{{K_{r4} }}{{T_{r4} T_{t4} }}, \\ A_{17,17} & = - \frac{1}{{T_{g4} }},\quad A_{17,18} = \frac{1}{{T_{r4} }}, \\ A_{185,2} & = - \frac{1}{{R_{4} T_{g4} }},\quad A_{18,18} = - \frac{1}{{T_{g4} }}, \\ A_{19,3} & = - \frac{{2T_{r5} }}{{R_{5} T_{g5} T_{t5} }},\quad A_{19,19} = - \frac{2}{{T_{w1} }},\quad A_{19,20} = \left( {\frac{2}{{T_{w1} }} - \frac{2}{{T_{t5} }}} \right),\quad A_{19,21} = \left( {\frac{2}{{T_{t5} }} - \frac{{2T_{r5} }}{{T_{t5} T_{g5} }}} \right), \\ A_{20,3} & = - \frac{{T_{r5} }}{{R_{5} T_{g5} T_{t5} }},\quad A_{20,20} = - \frac{1}{{T_{t5} }},\quad A_{20,21} = \left( {\frac{1}{{T_{t5} }} - \frac{{T_{r5} }}{{T_{t5} T_{g5} }}} \right), \\ A_{21,3} & = - \frac{1}{{R_{5} T_{g5} }},\quad A_{21,21} = - \frac{1}{{T_{g5} }}, \\ A_{22,3} & = - \frac{{2T_{r6} }}{{R_{6} T_{g6} T_{t6} }},\quad A_{22,22} = - \frac{2}{{T_{w2} }},\quad A_{22,23} = \left( {\frac{2}{{T_{w2} }} - \frac{2}{{T_{t6} }}} \right),\quad A_{22,24} = \left( {\frac{2}{{T_{t6} }} - \frac{{2T_{r6} }}{{T_{t6} T_{g6} }}} \right), \\ A_{23,3} & = - \frac{{T_{r6} }}{{R_{6} T_{g6} T_{t6} }},\quad A_{23,23} = - \frac{1}{{T_{t6} }},\quad A_{23,24} = \left( {\frac{1}{{T_{t6} }} - \frac{{T_{r6} }}{{T_{t6} T_{g6} }}} \right), \\ A_{24,3} & = - \frac{1}{{R_{6} T_{g6} }},\quad A_{24,24} = - \frac{1}{{T_{g6} }} \\ \end{aligned}$$

The control matrix [B] is of the order of $24 \times 3$ and its nonzero elements are given below:

$$\begin{aligned} B_{9,1} = \frac{{A_{11}^{\prime } }}{{T_{g1} }},\quad B_{12,1} = \frac{{A_{12}^{\prime } }}{{T_{g2} }},\quad B_{15,2} = \frac{{A_{21}^{\prime } }}{{T_{g3} }},\quad B_{18,2} = \frac{{A_{22}^{\prime } }}{{T_{g4} }},\quad B_{19,3} = \frac{{2T_{r5} A_{31}^{\prime } }}{{T_{g5} }},\quad B_{20,3} = \frac{{T_{r5} A_{31}^{\prime } }}{{T_{g5} }},\quad B_{21,3} = \frac{{A_{31}^{\prime } }}{{T_{g5} }}, \hfill \\ B_{22,3} = \frac{{2T_{r6} A_{32}^{\prime } }}{{T_{g6} }},\quad B_{23,3} = \frac{{T_{r6} A_{32}^{\prime } }}{{T_{g6} }},\quad B_{24,3} = \frac{{A_{32}^{\prime } }}{{T_{g6} }} \hfill \\ \end{aligned}$$

The disturbance matrix [$\varGamma$] is of the order of $24 \times 6$, and its nonzero elements are given below:

$$\begin{aligned} \varGamma_{1,1} & = - \frac{{K_{p1} }}{{T_{p1} }},\quad \varGamma_{1,2} = - \frac{{K_{p1} }}{{T_{p1} }},\quad \varGamma_{2,3} = - \frac{{K_{p2} }}{{T_{p2} }},\quad \varGamma_{2,4} = - \frac{{K_{p2} }}{{T_{p2} }},\quad \varGamma_{3,5} = - \frac{{K_{p3} }}{{T_{p3} }},\quad \varGamma_{3,6} = - \frac{{K_{p3} }}{{T_{p3} }},\quad \varGamma_{9,1} = \frac{{cpf_{11} }}{{T_{g1} }},\quad \varGamma_{9,2} = \frac{{cpf_{12} }}{{T_{g1} }}, \\ \varGamma_{9,3} & = \frac{{cpf_{13} }}{{T_{g1} }},\quad \varGamma_{9,4} = \frac{{cpf_{14} }}{{T_{g1} }},\quad \varGamma_{9,5} = \frac{{cpf_{15} }}{{T_{g1} }},\quad \varGamma_{9,6} = \frac{{cpf_{16} }}{{T_{g1} }},\quad \varGamma_{12,1} = \frac{{cpf_{21} }}{{T_{g2} }},\quad \varGamma_{12,2} = \frac{{cpf_{22} }}{{T_{g2} }},\quad \varGamma_{12,3} = \frac{{cpf_{23} }}{{T_{g2} }}, \\ \varGamma_{12,4} & = \frac{{cpf_{24} }}{{T_{g2} }},\quad \varGamma_{12,5} = \frac{{cpf_{25} }}{{T_{g2} }},\quad \varGamma_{12,6} = \frac{{cpf_{26} }}{{T_{g2} }},\quad \varGamma_{15,1} = \frac{{cpf_{31} }}{{T_{g3} }},\quad \varGamma_{15,2} = \frac{{cpf_{32} }}{{T_{g3} }},\quad \varGamma_{15,3} = \frac{{cpf_{33} }}{{T_{g3} }},\quad \varGamma_{15,4} = \frac{{cpf_{34} }}{{T_{g3} }}, \\ \varGamma_{15,5} & = \frac{{cpf_{35} }}{{T_{g3} }},\quad \varGamma_{15,6} = \frac{{cpf_{36} }}{{T_{g3} }},\quad \varGamma_{18,1} = \frac{{cpf_{41} }}{{T_{g4} }},\quad \varGamma_{18,2} = \frac{{cpf_{42} }}{{T_{g4} }},\quad \varGamma_{18,3} = \frac{{cpf_{43} }}{{T_{g4} }},\quad \varGamma_{18,4} = \frac{{cpf_{44} }}{{T_{g4} }},\quad \varGamma_{18,5} = \frac{{cpf_{45} }}{{T_{g4} }}, \\ \varGamma_{18,6} & = \frac{{cpf_{46} }}{{T_{g4} }},\quad \varGamma_{19,1} = \frac{{2T_{r5} cpf_{51} }}{{T_{t5} T_{g5} }},\quad \varGamma_{19,2} = \frac{{2T_{r5} cpf_{52} }}{{T_{5} T_{g5} }},\quad \varGamma_{19,3} = \frac{{2T_{r5} cpf_{53} }}{{T_{t5} T_{g5} }},\quad \varGamma_{19,4} = \frac{{2T_{r5} cpf_{54} }}{{T_{t5} T_{g5} }}, \\ \varGamma_{19,5} & = \frac{{2T_{r5} cpf_{55} }}{{T_{t5} T_{g5} }},\quad \varGamma_{19,6} = \frac{{2T_{r5} cpf_{56} }}{{T_{t5} T_{g5} }},\quad \varGamma_{20,1} = \frac{{T_{r5} cpf_{51} }}{{T_{t5} T_{g5} }},\quad \varGamma_{20,2} = \frac{{T_{r5} cpf_{52} }}{{T_{5} T_{g5} }},\quad \varGamma_{20,3} = \frac{{T_{r5} cpf_{53} }}{{T_{t5} T_{g5} }}, \\ \varGamma_{20,4} & = \frac{{T_{r5} cpf_{54} }}{{T_{t5} T_{g5} }},\quad \varGamma_{20,5} = \frac{{T_{r5} cpf_{55} }}{{T_{t5} T_{g5} }},\quad \varGamma_{20,6} = \frac{{T_{r5} cpf_{56} }}{{T_{t5} T_{g5} }},\quad \varGamma_{21,1} = \frac{{cpf_{51} }}{{T_{g5} }},\quad \varGamma_{21,2} = \frac{{cpf_{52} }}{{T_{g5} }},\quad \varGamma_{21,2} = \frac{{cpf_{52} }}{{T_{g5} }},\quad \varGamma_{21,3} = \frac{{cpf_{53} }}{{T_{g5} }}, \\ \varGamma_{21,4} & = \frac{{cpf_{54} }}{{T_{g5} }},\quad \varGamma_{21,5} = \frac{{cpf_{55} }}{{T_{g5} }},\quad \varGamma_{21,6} = \frac{{cpf_{56} }}{{T_{g5} }},\quad \varGamma_{22,1} = \frac{{2T_{r6} cpf_{61} }}{{T_{t6} T_{g6} }},\quad \varGamma_{22,2} = \frac{{2T_{r6} cpf_{62} }}{{T_{6} T_{g6} }},\quad \varGamma_{22,3} = \frac{{2T_{r6} cpf_{63} }}{{T_{t6} T_{g6} }}, \\ \varGamma_{22,4} & = \frac{{2T_{r6} cpf_{64} }}{{T_{t6} T_{g6} }},\quad \varGamma_{22,5} = \frac{{2T_{r6} cpf_{65} }}{{T_{t6} T_{g6} }},\quad \varGamma_{22,6} = \frac{{2T_{r6} cpf_{66} }}{{T_{t6} T_{g6} }},\quad \varGamma_{23,1} = \frac{{T_{r6} cpf_{61} }}{{T_{t6} T_{g6} }},\quad \varGamma_{23,2} = \frac{{T_{r6} cpf_{62} }}{{T_{6} T_{g6} }}, \\ \varGamma_{23,3} & = \frac{{T_{r6} cpf_{63} }}{{T_{t6} T_{g6} }},\varGamma_{23,4} = \frac{{T_{r6} cpf_{64} }}{{T_{t6} T_{g6} }},\quad \varGamma_{23,5} = \frac{{T_{r6} cpf_{65} }}{{T_{t6} T_{g6} }},\varGamma_{23,6} = \frac{{T_{r6} cpf_{66} }}{{T_{t6} T_{g6} }},\quad \varGamma_{24,1} = \frac{{cpf_{61} }}{{T_{g6} }},\quad \varGamma_{24,2} = \frac{{cpf_{62} }}{{T_{g6} }}, \\ \varGamma_{24,3} & = \frac{{cpf_{63} }}{{T_{g6} }},\quad \varGamma_{24,4} = \frac{{cpf_{64} }}{{T_{g6} }},\quad \varGamma_{24,5} = \frac{{cpf_{65} }}{{T_{g6} }},\quad \varGamma_{24,6} = \frac{{cpf_{6} }}{{T_{g6} }}, \\ \end{aligned}$$

The matrix [$\gamma$] is of the order of $24 \times 3$, and its nonzero elements are given below:

$$\gamma_{1,1} = - \, (K_{p1} /T_{p1} ),\quad \gamma_{2,2} = - (K_{p2} /T_{p2} ),\quad \gamma_{3,3} = - (K_{p3} /T_{p3} ).$$

The parameters values of the power system (Arya and Kumar 2016):

$$\begin{aligned} R_{1} & = R_{2} = R_{3} = R_{4} = R_{5} = R_{6} = 2.40\;{\text{Hz/pu MW}}, \\ K_{p1} & = K_{p2} = K_{p3} = K_{p4} = K_{p5} = K_{p6} = 120\;{\text{Hz/pu MW}}, \\ T_{p1} & = T_{p2} = T_{p3} = T_{p4} = T_{p5} = T_{p6} = 20\;{\text{s}}, \\ T_{g1} & = T_{g2} = T_{g3} = T_{g4} = T_{g5} = T_{g6} = 0.08\;{\text{s}}, \\ T_{t1} & = T_{t2} = T_{t3} = T_{t4} = T_{t5} = T_{t6} = 0.30\,{\text{s}} \\ K_{r1} & = K_{r2} = K_{r3} = K_{r4} = 0.5, \\ T_{r1} & = T_{r2} = T_{r3} = T_{r4} = T_{r5} = T_{r6} = 5\,{\text{s}}, \\ T_{w1} & = T_{w2} = 1\,{\text{s}} \\ T_{12} & = 0.086630\,{\text{s}}, \\ B_{1} & = 0.66,\;B_{2} = 0.61,\;B_{3} = 0.60, \\ a_{12} & = - 1,\;a_{23} = - 1,\;a_{31} = - 1. \\ \end{aligned}$$

SMES unit data (Abraham et al. 2007): L = 13.65 H, T_dc = 0.03 s, K_smes = 100 kV/unit MW, K_id = 0.2 kV/kA, I_d0 = 0.45 kA.