1 Introduction

Passive bistatic radars (PBRs) are known by some characteristics and benefits that make them unsubstitutable in some applications. They do not require dedicated transmitters and so are inexpensive, invulnerable to jamming, covert and without frequency allocation requirements. Moreover, frequency and space diversity are provided. But as the transmitter’s location and the transmission properties cannot be controlled by the radar designer, processing, synchronization and system challenges are increased (Cherniakov 2008).

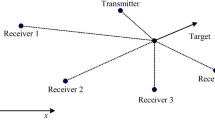
The general geometry of a PBR is shown in Fig. 1. The transmitter of opportunity is assumed to have a wide beam antenna in azimuth, propagating the transmitting signal in a wide sector. The receiver’s antenna is an array antenna with several directional surveillance beams produced by a suitable beamforming method and a separate beam toward the transmitter (reference beam) for the reception of directly transmitted signal. So, the PBR depicted in Fig. 1 has \(M\) surveillance channels and one reference channel. The surveillance channels collect the target echoes. Unfortunately, the strong unwanted returns of direct signal and clutter/multipath are also received in the surveillance channels which degrade or deny the capability to detect the targets (Cherniakov 2008; Colone et al. 2009a; Radmard and Nayebi 2015). For each surveillance channel, time-domain signal processing and target detection are done independently. The algorithms to allow for the detection of targets can be categorized into “adaptive” and “non-adaptive”. For PBRs, the non-adaptive approach has been researched vastly, while the theory of adaptive approach is still immature. The analytical discussion of PBR “adaptive” detection problem is the main subject of this paper. Before introducing the works which have already been presented in the literature and demonstrating our contribution, let us explain some required concepts for future discussions.

Fig. 1
figure 1

PBR general geometry

Full size image

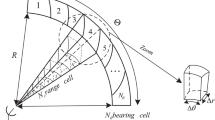
Throughout this paper as shown in Fig. 2a, the total clutter scatterers within a given surveillance beam and between two ellipses of constant range sums (bistatic isorange contours) corresponding to \(R_{r}\) and \(R_{r} + \Delta R\) are defined as the rth “clutter cell” where \(\Delta R\) is chosen according to the range resolution. The clutter cells adjacent to the rth clutter cell are also shown in Fig. 2a, b. Hence, there are several clutter cells corresponding to successive range cells. The clutter scatterers within a given clutter cell have different bistatic velocities. If we divide the total possible bistatic velocity interval into some velocity cells, the total scatterers whose bistatic velocities belong to each velocity cell are called “clutter patch”. For example, a zoomed view of the clutter cells of Fig. 2a is given in Fig. 2b, where each clutter patch is shown with a distinct dash type. In this illustration, there are three clutter patches for each clutter cell as depicted in Fig. 2c. The total bistatic range and velocity intervals covered by the clutter patches of clutter cells are defined as “clutter scatterers range-velocity region”.

Fig. 2
figure 2

Categorizing clutter scatterers: a clutter cells, b zoomed view of clutter cells and c clutter patches of clutter cells (scatters and their velocities are denoted by points and arrows, respectively)

Full size image

In the non-adaptive category of algorithms, it is assumed that each clutter cell’s complex radar cross section (RCS) has a narrow spectrum around zero Doppler frequency and Doppler frequencies of targets of interest are higher than the bandwidth of this spectrum. Hence, clutter cancellation methods are firstly exploited and then target detection is performed by forming the cross ambiguity function which acts as a matched filter and provides the necessary integration gain as well as target bistatic range and Doppler estimation (Cherniakov 2008). Transversal adaptive filters such as the least mean squares (LMS) and recursive least squares (RLS) (Cherniakov 2008; Colone et al. 2007), the extensive cancellation algorithm (ECA) (Colone et al. 2006), the sequential cancellation algorithm (SCA) (Colone et al. 2006), the multistage processing algorithm (Colone et al. 2009a), the generalized likelihood ratio test (GLRT) (Zaimbashi et al. 2013) and OFDM-specific methods (Colone et al. 2014; Palmer et al. 2013; Zhao et al. 2012) are some of the main works presented in the literature. This category of algorithms is generally used for passive ground-based radars. It is noteworthy to mention that for such radars an alternative approach is using clutter map for adaptation of threshold to be applied to cross ambiguity function.

For the situations such as airborne and maritime PBRs where each clutter cell’s RCS spectrum overlaps with the target’s RCS spectrum and its parameters such as bandwidth and center frequency vary rapidly and within a wide range, the slowly varying clutter maps do not provide sufficient adaptation to the environment and also the non-adaptive approach is not feasible. Considering these issues and especially for maritime and airborne passive radars, there is a vital need for developing data-adaptive methods based on the estimation of unknown spectral properties of clutter cell’s RCS. This is the case of interest in this work.

Adaptive processing is a fully developed theory for active pulse radars. In this theory, two sets of data vectors known as primary and secondary (training) data are exploited. The primary data, which are the output of the receiver’s matched filter in a given range cell (range cell under test), contain the target echoes, returns of its corresponding clutter cell and noise. The set of target-free secondary data, which are the outputs of the receiver’s matched filter in range cells adjacent to the range cell under test, are assumed to have the same covariance matrix as the primary data. It is satisfied under the assumption that the neighboring clutter cells corresponding to the primary and secondary data sets are homogenous, i.e., their RCSs have the same spectral properties. In addition, due to the statistical independence of clutter cells’ RCSs, it is readily concluded that the secondary data set are independent of each other and are also independent of the primary data. The unknown covariance matrix of the primary data can be estimated using the independent and identically distributed (iid) secondary data and then target detection proceeds. While sample matrix inversion (SMI) (Reed et al. 1974) is probably the most basic work in this theory, Kelly’s GLR (generalized likelihood ratio) (Kelly 1986) replaces this ad-hoc procedure by a likelihood ratio test which has the constant false alarm rate (CFAR) behavior. In Robey et al. (1992), the adaptive matched filter (AMF) has been introduced which is the simplified version of Kelly’s GLR and is less computationally intensive, slightly underperformed and less robust in non-Gaussian interferences than its counterpart. The Doppler domain localized GLR (DDL–GLR) (Wang and Cai 1991) and the per-symmetric GLR (PGLR) (Wang and Cai 1992) have been presented which require a reduced size of iid training data set by exploiting localized adaptive processing and by considering a per-symmetric structure for the interference covariance matrix, respectively. Through years of studies, there are numerous works done in this field, all of which share the same basis as the mentioned methods and also investigate specific problems such as nonhomogeneous secondary data (Gao et al. 2014; Melvin 2000; Shahraki et al. 2007).

In passive radars, due to the continuous-wave nature of transmitting signals, the reflected signals from all clutter cells and targets overlap in the surveillance channel signal. Hence, the generalization of adaptive processing concepts in active pulse radars to PBRs is not straightforward and has been a subject of recent researches. In this regard (Neyt et al. 2006), the feasibility of PBR adaptive processing is shown through the definition of mixing product for the first time. The simulation-based and experimental results of applying space–time adaptive processing (STAP) based on SMI for a GSM-based PBR have been reported. A similar work has been done in (Raout et al. 2007) but for a DVB-T (digital video broadcast-terrestrial)-based PBR. A number of other spatio-temporal filtering methods such as PC (principal components), JDL (joint domain localized), D3 (direct data domain) and the hybrid JDL-D3 have also been investigated by the same authors in (Raout and Preaux 2008; Raout 2008a, b). They are implemented based on the mixing product, too. The mixing product has also been used in a novel method which does not estimate the covariance matrix but iteratively rejects the components of the clutter using the amplitude and phase estimation (APES) (Raout et al. 2010a) which is later followed by a work which combines the Wiener filtering and the APES (Raout et al. 2010b). The implementation of STAP in PBRs has also been investigated in (Tan et al. 2010, 2011, 2012, 2014) in which the snapshot modeling approach is based on the separate matched filtering of several segments of the surveillance channel signal and joint processing of them is proposed. It is also shown that before applying STAP algorithms such as SMI, a prior cancellation of direct signal and strong clutter signals of closer ranges by the ECA leads to a superior performance (Tan et al. 2014).

Most literature about adaptive approach for PBRs, as mentioned earlier, is based on designing adaptive weights to filter out the interference and maximize the signal-to-interference-plus-noise ratio. The aim of this paper is to consolidate the theory of existing methods and, in contrast to them, organize the study based on a detection performance measure. In this regard, the previous works are ad-hoc. So, in this paper, with a detailed statistical analysis of the mixing product approach including the distribution and also the covariance matrix, adaptive target detection as a hypothesis test and modification of the conventional secondary data generation which leads to a suitable secondary data generation scheme to have iid secondary data are studied. It is also established that adaptive detectors from active pulse radar area can be generalized for use in passive radars and their detection performances can be theoretically obtained using the derivations of this paper. In this regard, the generalizations of Kelly’s GLR, DDL-GLR and PGLR are presented. The analysis of detection performance and performance comparison with cross ambiguity function processing is another contribution of this paper.

The adopted detectors estimate the unknown spectral specifications of clutter cell’s RCS and by using the spectral differences between the complex RCSs of target and clutter cell make target detection possible even in the clutter scatterers range-velocity region. This is in contrast to non-adaptive algorithms like the ECA (Colone et al. 2006) and the GLRT (Zaimbashi et al. 2013) where the clutter scatterers range-velocity region should be defined a priory. In such algorithms, for the purpose of proper clutter cancellation a high detection loss occurs in the clutter scatterers range-velocity region (Zaimbashi et al. 2013) and no target detection is possible within this region. So, non-adaptive and adaptive algorithms are used in different categories of applications and it is not accurate to compare them in terms of detection performance. However, in the PBR literature, a logical solution for the problem of target detection in the presence of clutter with unknown clutter scatterers range-velocity region is known to be the cross ambiguity function processing, without interference cancellation. Hence, the detection performances of the adopted detectors are compared to the conventional cross ambiguity function processing with CFAR thresholding, and their superiority, in most situations, is shown by several simulations.

This paper is organized as follows. In Sect. 2, the signal model is described and its statistical properties are introduced. The procedure for formulating adaptive detection problem as statistical hypothesis testing is also given through some lemmas. Section 3 discusses some adaptive detectors for the desired hypothesis test. Simulation results are reported in Sect. 4. Finally, some conclusions are given in Sect. 5. For the purpose of shortening the main body of the paper while preserving its integrity, most excess explanations, math expressions, and proofs of the important lemmas in Sect. 2 are moved to the appendices. These appendices include some of the novelties of this work.

In this paper, superscripts, \((.)^{*}\), \((.)^{T}\) and \((.)^{H}\) are exploited to represent complex conjugate, transpose, and complex conjugate transpose, respectively, and \(\odot\) denotes Hadamard product. The symbols used for statistical expectation and covariance matrix of a random vector are \(\text{E} \{.\}\) and \({\mathbf{R}}\{.\}\), respectively. The operator \(\text{dig} (.)\) converts a vector to a diagonal matrix whose main diagonal entries are the elements of the vector. It must be noted that we have attempted to keep the symbols and notations used within this paper consistent with (Raout and Preaux 2008; Raout 2008a, b; Raout et al. 2010a) for ease of understanding and referral.

2 Signal Model and its Statistical Property

Let us denote the lth sample of the surveillance channel and reference channel signals after baseband demodulation by \(x(l)\) and \(x_{\rm ref} (l)\), respectively. The vector representations of these samples of the surveillance channel signal, \({\mathbf{x}}\), and the reference channel signal, \({\mathbf{x}}_{\rm ref}^{{}}\), during the integration time are given by

$$\begin{aligned} {\mathbf{x}} & = [x(0)\;x(1) \ldots \;x(N_{i} - 1)]^{T} \\ {\mathbf{x}}_{\rm ref} & = [x_{\rm ref} (0)\;x_{\rm ref} (1) \ldots \;x_{\rm ref} (N_{i} - 1)]^{T} \\ \end{aligned}$$
(1)

where the number of samples to be coherently processed within the integration time is \(N_{i}\).

It is assumed that target detection is to be performed in a given delay (range) interval, and targets, direct signal and clutter cells corresponding to previous and forthcoming delays (outside of detection range interval) have been canceled using a least square approach such as the ECA (Colone et al. 2006). In fact, \({\mathbf{x}}\) presents the surveillance channel signal after this preprocessing. In general, \({\mathbf{x}}\) includes the signal returns of targets, contributions of clutter/multipath and additive white Gaussian noise (AWGN) which are symbolized by \({\mathbf{x}}_{t}\), \({\mathbf{x}}_{c}\), and \({\mathbf{w}}\), respectively:

$${\mathbf{x}} = {\mathbf{x}}_{t} + {\mathbf{x}}_{c} + {\mathbf{w}}$$
(2)

It is assumed that \({\mathbf{x}}_{\rm ref}^{{}}\) is a delayed replica of transmitting signal and is free of multipath (Colone et al. 2009a, b; Zaimbashi et al. 2013). By assuming that the direct signal to noise ratio (DNR) in the reference channel is much larger than the DNR in the surveillance channel, the thermal noise in the reference channel can be neglected (Colone et al. 2009a; Zaimbashi et al. 2013). Under these assumptions, the signal model is developed.

The delayed version of the reference channel signal with sample delay \(n\) is computed by \({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}\) where \({\mathbf{D}}\) is a 0/1 permutation matrix that applies a delay of single sample and is expressed by (Colone et al. 2009a):

$${\mathbf{D}} = \{ d_{ij} \}_{{i,j = 1, \ldots ,N_{i} }} ,\quad d_{ij} = \left\{ {\begin{array}{*{20}l} 1 &\quad {i = j + 1} \\ 0 &\quad {\text{otherwise}} \\ \end{array} } \right.$$
(3)

Let us consider \(N_{t}\) targets, \({\mathbf{x}}_{{t_{k}}}\), (\(k = 1,\ldots,N_{t}\)) with sample delays \(n_{{t_{k}}}\) (with respect to the reference channel signal), normalized Doppler frequencies \(\bar{f}_{{t_{k}}} = f_{{t_{k}}}/f_{s}\) (\(f_{{t_{k}}}\) is Doppler frequency and \(f_{s}\) denotes the sampling frequency) and complex amplitudes \(\alpha_{{t_{k}}}\). The temporal steering vector of the kth target corresponding to \(\bar{f}_{{t_{k}}}\) is denoted by \({\mathbf{s}}_{{t_{k}}}\). So, we can formulate \({\mathbf{x}}_{t}\) by (Colone et al. 2006; Zaimbashi et al. 2013; Raout 2008b):

$${\mathbf{x}}_{t} = \sum\limits_{k = 1}^{{N_{t}}} {{\mathbf{x}}_{{t_{k}}}}$$
(4)

where

$${\mathbf{x}}_{{t_{k}}} = \alpha_{{t_{k}}} ({\mathbf{D}}^{{n_{{t_{k}}}}} {\mathbf{x}}_{\rm ref}) \odot {\mathbf{s}}_{{t_{k}}}$$
(5)

and

$${\mathbf{s}}_{{t_{k} }} = \left[ {1\;{\text{e}}^{{j2\pi \bar{f}_{{t_{k} }} }} \ldots \;{\text{e}}^{{j2\pi \bar{f}_{{t_{k} }} (N_{i} - 1)}} } \right]^{T}$$
(6)

It should be remembered that in this paper, sample delays, ranges, velocities and Doppler frequencies are all based on bistatic measurements. The clutter, in the detection range interval, is composed of \(N_{r}\) clutter cells with \(N_{c}\) clutter patches for each clutter cell and its signal contribution, \({\mathbf{x}}_{c}\), can be expressed as (Colone et al. 2006; Zaimbashi et al. 2013; Raout 2008b):

$$\begin{aligned} {\mathbf{x}}_{c} & = \sum\limits_{r = 1}^{{N_{r} }} {\sum\limits_{i = 1}^{{N_{c} }} {\gamma_{{c_{i,r} }} ({\mathbf{D}}^{{n_{{c_{r} }} }} {\mathbf{x}}_{\text{ref}} )} } \odot {\mathbf{s}}_{{c_{i} }} \\ & = \sum\limits_{r = 1}^{{N_{r} }} {\left[ {({\mathbf{D}}^{{n_{{c_{r} }} }} {\mathbf{x}}_{\text{ref}} ) \odot \sum\limits_{i = 1}^{{N_{c} }} {\gamma_{{c_{i,r} }} } {\mathbf{s}}_{{c_{i} }} } \right]} \\ \end{aligned}$$
(7)

in which the complex amplitude, sample delay (with respect to the reference channel signal) and normalized Doppler frequency of the ith clutter patch within the rth clutter cell are symbolized by \(\gamma_{{c_{i,r}}}\), \(n_{{c_{r}}}\) and \(\bar{f}_{{c_{i}}}\), respectively, and the temporal steering vector, \({\mathbf{s}}_{{c_{i}}}\), of this clutter patch with normalized Doppler frequency \(\bar{f}_{{c_{i}}}\) is given by

$${\mathbf{s}}_{{c_{i} }} = \left[ {1\;{\text{e}}^{{j2\pi \bar{f}_{{c_{i} }} }} \ldots \;{\text{e}}^{{j2\pi \bar{f}_{{c_{i} }} (N_{i} - 1)}} } \right]^{T}$$
(8)

As Eq. (4), \({\mathbf{x}}_{c}\) can also be written based on its components:

$${\mathbf{x}}_{c} = \sum\limits_{r = 1}^{{N_{r}}} {\sum\limits_{i = 1}^{{N_{c}}} {{\mathbf{x}}_{{c_{i,r}}}}}$$
(9)

where

$${\mathbf{x}}_{{c_{i,r}}} = \gamma_{{c_{i,r}}} ({\mathbf{D}}^{{n_{{c_{r}}}}} {\mathbf{x}}_{\rm ref}) \odot {\mathbf{s}}_{{c_{i}}}$$
(10)

In the PBR literature, this is the most general modeling used for clutter signal contribution (Colone et al. 2006; Zaimbashi et al. 2013; Raout 2008b), and is shown to be practically applicable to real scenarios (Zaimbashi et al. 2013). The complex amplitudes of clutter patches, \(\gamma_{{c_{i,r}}}\), are assumed to have complex zero-mean Gaussian distributions (Skolnik 2005; Theodoridis and Chellappa 2013; Stergiopoulos 2009) with variances of \(G_{i,r}\), and to be independent and hence uncorrelated. Therefore, we have:

$${\text{E}}\left\{ {\gamma_{{c_{i,r} }} \gamma_{{c_{j,t} }}^{*} } \right\} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad i \ne j\quad {\text{or}}\quad r \ne t} \hfill \\ {{\text{E}}\{ |\gamma_{{c_{i,r} }} |^{2} \} = G_{i,r} } \hfill & {\quad i = j\quad {\text{and}}\quad r = t} \hfill \\ \end{array} } \right.$$
(11)

Considering these assumptions, we study the statistical characteristics of the surveillance channel signal, \({\mathbf{x}}\), in Appendix A. According to this appendix, \({\mathbf{x}}\) has a complex Gaussian distribution with mean \({\mathbf{x}}_{t}\) and covariance matrix \({\mathbf{R}}_{c} + \sigma_{w}^{2} {\mathbf{I}}\) where \({\mathbf{I}}\) denotes the identity matrix, \(\sigma_{w}^{2}\) is the variance of AWGN, and the clutter covariance matrix, \({\mathbf{R}}_{c}\), is presented in Appendix A (see Eqs. (40) and (41)). The representation used for this distribution is \({\mathbf{x}}\mathop \sim \limits^{d} N({\mathbf{x}}_{t},{\mathbf{R}}_{c} + \sigma_{w}^{2} {\mathbf{I}})\).

The mixing product corresponding to sample delay n, which mixes the surveillance channel signal with the complex conjugate of the nth sample delayed version of the reference channel signal, is defined as (Neyt et al. 2006; Stein 1981):

$${\tilde{\mathbf{x}}}(n) = {\mathbf{x}} \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*})$$
(12)

It can be considered as a vector of length \(N_{i}\) for each sample delay \(n\) as follows and is called “mixed signal” throughout this manuscript.

$$\begin{aligned} {\tilde{\mathbf{x}}}(n) & = [\tilde{x}(0;n)\; \tilde{x}(1;n) \ldots\; \tilde{x}(N_{i} - 1;n)]^{T} , \\ \tilde{x}(l;n) & = x(l)x_{\rm ref}^{*} (l - n),\quad l = 0,\ldots,N_{i} - 1 \\ \end{aligned}$$
(13)

The mixed signal can also be decomposed into its components using a similar procedure to Eq. (2):

$$\begin{aligned} {\tilde{\mathbf{x}}}(n) & = {\tilde{\mathbf{x}}}_{t} (n) + {\tilde{\mathbf{x}}}_{c} (n) + {\tilde{\mathbf{w}}}(n) \\ {\tilde{\mathbf{x}}}_{t} (n) & = {\mathbf{x}}_{t} \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*} ) = \sum\limits_{k = 1}^{{N_{t} }} {\alpha_{{t_{k} }} {\mathbf{s}}_{{t_{k} }} \odot ({\mathbf{D}}^{{n_{{t_{k} }} }} {\mathbf{x}}_{\rm ref} ) \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*} )} = \sum\limits_{k = 1}^{{N_{t} }} {{\tilde{\mathbf{x}}}_{{t_{k} }} (n)} \\ {\tilde{\mathbf{x}}}_{c} (n) & = {\mathbf{x}}_{c} \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*} ) = \sum\limits_{r = 1}^{{N_{r} }} {\sum\limits_{i = 1}^{{N_{c} }} {\gamma_{{c_{i,r} }} {\mathbf{s}}_{{c_{i} }} \odot ({\mathbf{D}}^{{n_{{c_{r} }} }} {\mathbf{x}}_{\rm ref} )} } \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*} ) \\ {\tilde{\mathbf{w}}}(n) & = {\mathbf{w}} \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*} ) \\ \end{aligned}$$
(14)

In Appendix A, it is shown that the distribution of the mixed signal is Gaussian with mean \({\tilde{\mathbf{x}}}_{t} (n)\), and its covariance matrix which is dependent on the sample delay \(n\) is given by

$${\mathbf{R}}\{{\tilde{\mathbf{x}}}(n)\} = ({\mathbf{R}}_{c} + \sigma_{w}^{2} {\mathbf{I}}) \odot (({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*})({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref})^{T})$$
(15)

The adaptive approach is based on the mixed signal (Neyt et al. 2006; Raout et al. 2007; Raout and Preaux 2008; Raout 2008a, b), and the mixed signal is then applied to a low-pass filter and subsampled. In the following, we consolidate the theory regarding why this decimation maintains the target signal contribution and then statistically analyze the subsampled mixed signal.

Using Eq. (14), for any target with index k and sample delay \(n_{{t_{k}}} = n\), we have

$${\tilde{\mathbf{x}}}_{{t_{k}}} (n) = {\mathbf{x}}_{{t_{k}}} \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*}) = \alpha_{{t_{k}}} {\mathbf{s}}_{{t_{k}}} \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}) \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*})$$
(16)

Considering \(({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}) \odot ({\mathbf{D}}^{n} {\mathbf{x}}_{\rm ref}^{*})\mathop = \limits^{\Delta} {\mathbf{e}}(n)\), we have: \(e(l;n) = |x_{\rm ref} (l - n)|^{2}\) where \(e(l;n)\), the lth sample of \({\mathbf{e}}(n)\), is also a sample of the square of envelope of transmitting signal. To better understand Eq. (16), let us firstly consider the special case of constant envelope transmitting signals like phase shift keying (PSK) and frequency modulated (FM) signals. For this case, in which \(e(l;n) = {\text{cte}},\quad \forall l,n\), \({\mathbf{e}}(n)\) is a scalar multiple of unit vector so that \({\tilde{\mathbf{x}}}_{{t_{k}}} (n) \propto \alpha_{{t_{k}}} {\mathbf{s}}_{{t_{k}}}\) is a pure tone with target Doppler frequency. So, if a target with sample delay \(n\) is present, \({\tilde{\mathbf{x}}}(n)\) will be a pure tone with target Doppler frequency immersed in a colored Gaussian interference. As a result, it is reasonable to use \({\tilde{\mathbf{x}}}(n)\) as decision data for the detection of targets with sample delay \(n\). Using this idea, since the Doppler frequencies of targets of interest are noticeably smaller than the sampling frequency, according to the irrelevance theorem (Proakis and Salehi 2008), the out-of-band Doppler components of \({\tilde{\mathbf{x}}}(n)\) can be filtered and \({\tilde{\mathbf{x}}}(n)\) can be subsampled. Let us assume that the magnitudes of Doppler frequencies of targets, \(f_{{t_{k}}}\), are at most \(2S\) times smaller than the sampling frequency, or more exactly are such that:

$$\left|f_{{t_{k}}} \pm \frac{{f_{s}}}{{N_{i}}}\right| \le \frac{{f_{s}}}{2S}, \quad \left|\bar{f}_{{t_{k}}} \pm \frac{1}{{N_{i}}}\right| \le \frac{1}{2S} \quad (\forall k)$$
(17)

Then, the mixed signal, \({\tilde{\mathbf{x}}}(n)\), can be decimated to \(N_{d} = \left\lfloor {N_{i}/S} \right\rfloor\) samples by the subsampling factor \(S\) to yield \({\tilde{\mathbf{y}}}(n)\). This can be implemented by an integrate-and-dump filter in its simplest form (Raout et al. 2010a, b), i.e.,

$$\begin{aligned} {\tilde{\mathbf{y}}}(n) & = [\tilde{y}(0;n)\;\tilde{y}(1;n) \ldots\; \tilde{y}(N_{d} - 1;n)]^{T} , \\ \tilde{y}(b;n) & = \sum\limits_{l = bS}^{bS + S - 1} {\tilde{x}(l;n)} ,\quad b = 0,\ldots,N_{d} - 1 \\ \end{aligned}$$
(18)

The sampling frequency is now reduced to \(f^{\prime}_{s} = f_{s}/S\). It is noted that Eq. (17) ensures that the mentioned pure tone is within the low-pass filter bandwidth (\(1/S\) in the normalized frequency domain).

In general, since the square of the envelope of any transmitting signal (as a positive function) has a non-zero dc component and an ac component, \({\tilde{\mathbf{x}}}_{{t_{k}}} (n)\) is the sum of a pure tone with target Doppler frequency and an ac component. Using the idea of constant envelope case, if Eq. (17) is satisfied, the subsampling can be performed by Eq. (18) and the ac component of \({\tilde{\mathbf{x}}}_{{t_{k}}} (n)\) after decimation can be ignored.

Equation (18) implies that each element of \({\tilde{\mathbf{y}}}(n)\) is proportional to the average of \(S\) successive elements of \({\tilde{\mathbf{x}}}(n)\). If the filtered and subsampled versions of \({\tilde{\mathbf{x}}}_{t} (n)\), \({\tilde{\mathbf{x}}}_{c} (n)\), and \({\tilde{\mathbf{w}}}(n)\) are represented by \({\tilde{\mathbf{y}}}_{t} (n)\), \({\tilde{\mathbf{y}}}_{c} (n)\), and \({\tilde{\mathbf{z}}}(n)\), respectively, we have

$$\begin{aligned} {\tilde{\mathbf{y}}}(n) & = {\tilde{\mathbf{y}}}_{t} (n) + {\tilde{\mathbf{y}}}_{c} (n) + {\tilde{\mathbf{z}}}(n) \to \\ \tilde{y}(b;n) & = \tilde{y}_{t} (b;n) + \tilde{y}_{c} (b;n) + \tilde{z}(b;n),\quad b = 0,\ldots,N_{d} - 1, \\ \tilde{y}_{t} (b;n) & = \sum\limits_{l = bS}^{bS + S - 1} {\tilde{x}_{t} (l;n)} \\ \tilde{y}_{c} (b;n) & = \sum\limits_{l = bS}^{bS + S - 1} {\tilde{x}_{c} (l;n)} \\ \tilde{z}(b;n) & = \sum\limits_{l = bS}^{bS + S - 1} {\tilde{w}(l;n)} \\ \end{aligned}$$
(19)

It is noteworthy to emphasize that, for instance, \(\tilde{y}(b;n)\) denotes the bth element of \({\tilde{\mathbf{y}}}(n)\). Using Eq. (14) in Eq. (19) and by a change of variable \(l^{\prime} = l - bS\), it can be shown that

$$\begin{aligned} {\tilde{\mathbf{y}}}_{t} (n) & = \sum\limits_{k = 1}^{{N_{t} }} {\alpha_{{t_{k} }} {\varvec{\uppsi}}(n - n_{{t_{k} }} , - \bar{f}_{{t_{k} }} )} \odot {\mathbf{v}}_{{t_{k} }} \\ {\tilde{\mathbf{y}}}_{c} (n) & = \sum\limits_{r = 1}^{{N_{r} }} {\sum\limits_{i = 1}^{{N_{c} }} {\gamma_{{c_{i,r} }} {\varvec{\uppsi}}(n - n_{{c_{r} }} , - \bar{f}_{{c_{i} }} )} } \odot {\mathbf{v}}_{{c_{i} }} \\ \end{aligned}$$
(20)

where \({\mathbf{v}}_{{t_{k}}}\) and \({\mathbf{v}}_{{c_{i}}}\) are the reduced steering vectors of the kth target and the ith clutter patch corresponding to the reduced normalized Doppler frequencies \(\upsilon_{{t_{k}}}\) and \(\upsilon_{{c_{i}}}\), respectively:

$${\mathbf{v}}_{{t_{k} /c_{i} }} = \left[ {1\;{\text{e}}^{{j2\pi \upsilon_{{t_{k} /c_{i} }} }} \ldots\; {\text{e}}^{{j2\pi \upsilon_{{t_{k} /c_{i} }} (N_{d} - 1)}} } \right]^{T} ,\quad \upsilon_{{t_{k} /c_{i} }} = \bar{f}_{{t_{k} /c_{i} }} S = \frac{{f_{{t_{k} /c_{i} }} S}}{{f_{s} }} = \frac{{f_{{t_{k} /c_{i} }} }}{{f_{s}^{\prime } }}$$
(21)

and \({\varvec{\uppsi}}(n - n_{{t_{k}}}, - \bar{f}_{{t_{k}}})\) and \({\varvec{\uppsi}}(n - n_{{c_{r}}}, - \bar{f}_{{c_{i}}})\) are vectors of dimension \(N_{d}\) whose bth elements, \(b = 0,1,\ldots,N_{d} - 1\) are defined as:

$$\begin{aligned} {\varvec{\uppsi}} \left( {n - n_{{t_{k} /c_{r} }} , - \bar{f}_{{t_{k} /c_{i} }} } \right) & = \left[ {\psi_{0} \left( {n - n_{{t_{k} /c_{r} }} , - \bar{f}_{{t_{k} /c_{i} }} } \right) \ldots\; \psi_{{N_{d} - 1}} \left( {n - n_{{t_{k} /c_{r} }} , - \bar{f}_{{t_{k} /c_{i} }} } \right)} \right]^{T} \\ \psi_{b} \left( {n - n_{{t_{k} /c_{r} }} , - \bar{f}_{{t_{k} /c_{i} }} } \right) & = \sum\limits_{{l^{\prime } = 0}}^{S - 1} {x_{\rm ref} \left( {l^{\prime } + bS - n_{{t_{k} /c_{r} }} } \right)x_{\rm ref}^{*} (l^{\prime } + bS - n)} {\rm e}^{{j2\pi \bar{f}_{{t_{k} /c_{i} }} l^{\prime } }} \\ \end{aligned}$$
(22)

Suppose that the reference channel signal is divided into \(N_{d}\) segments of length \(S\), for large enough \(S\) (with respect to the maximum sample delay of detection range interval) it can be shown that \(\psi_{b} (n - n_{{t_{k}/c_{r}}}, - \bar{f}_{{t_{k}/c_{i}}})\) is approximately the S-sample complex self-ambiguity function of the bth (\(b = 0,\ldots,N_{d} - 1\)) segment of the reference channel signal, computed in sample delay \(n - n_{{t_{k}/c_{r}}}\) and normalized Doppler frequency \(- \bar{f}_{{t_{k}/c_{i}}}\). For each segment of the reference channel signal, the magnitude of its corresponding S-sample complex self-ambiguity function generally has a single correlation lobe peaking at zero delay and zero normalized Doppler frequency. The width of correlation lobe is \(2\left\lfloor {f_{s}/(2B)} \right\rfloor + 1\mathop = \limits^{\Delta} 2c - 1\) samples in the delay domain (\(B\) denotes the transmitting signal bandwidth) and \(1/S\) in the normalized Doppler frequency domain. Hence, we have

$$\begin{aligned} |\psi_{b} (n - n_{{t_{k}/c_{r}}}, - \bar{f}_{{t_{k}/c_{i}}})| &\cong 0, \quad |n - n_{{t_{k}/c_{r}}} | \ge c,\forall b \to \hfill \\ {\varvec{\uppsi}}(n - n_{{t_{k}/c_{r}}}, - \bar{f}_{{t_{k}/c_{i}}}) &\cong {\mathbf{0}}, \quad |n - n_{{t_{k}/c_{r}}} | \ge c \hfill \\ \end{aligned}$$
(23)

Since \({\tilde{\mathbf{y}}}(n)\) is the subsampled version of output of an LTI filter whose input is the Gaussian vector \({\tilde{\mathbf{x}}}(n)\), it is also normally distributed with mean \({\tilde{\mathbf{y}}}_{t} (n)\), and it can be shown that its covariance matrix is given by

$${\mathbf{R}}\{ {\tilde{\mathbf{y}}}(n)\} = \sum\limits_{r = 1}^{{N_{r}}} {\sum\limits_{i = 1}^{{N_{c}}} {G_{i,r}}} ({\varvec{\uppsi}}(n - n_{{c_{r}}}, - \bar{f}_{{c_{i}}}){\varvec{\uppsi}}^{H} (n - n_{{c_{r}}}, - \bar{f}_{{c_{i}}})) \odot ({\mathbf{v}}_{{c_{i}}} {\mathbf{v}}_{{c_{i}}}^{H}) + \sigma_{w}^{2} {\mathbf{I}}$$
(24)

where without loss of generality we presume that: \(\psi_{b} (0,0) = |\psi_{b} (0,0)| \cong 1, \quad \forall b\).

As also mentioned before, the idea is to use \({\tilde{\mathbf{y}}}(n)\) (the subsampled version of \({\tilde{\mathbf{x}}}(n)\)) as decision (primary) data for target detection at sample delay \(n\). In the literature, it is suggested that the subsampled mixed signals with sample delays adjacent to \(n\) are exploited as secondary data (Neyt et al. 2006; Raout et al. 2007; Raout and Preaux 2008; Raout 2008a). For adaptive detection which is the subject of this paper, one may use \({\tilde{\mathbf{y}}}(k), \quad k \in D\) as target-free secondary (training) data provided that the secondary data set \(D\) is generated such that some requirements are met. The secondary data should be iid and have the same distribution as the background of the primary data, and be independent of it. Hence, by the statistical analysis of this paper, the following lemmas are demonstrated in which a suitable secondary data generation scheme is established and the corresponding hypothesis test is formulated.

Lemma 1

If a target exists in sample delay n with complex amplitude \(\alpha_{t}\) and reduced normalized Doppler frequency \(\upsilon_{t}\), and there is no other target in the delay interval \([n - c + 1,n + c - 1]\), we have

$${\tilde{\mathbf{y}}}_{t} (n) = \alpha {\mathbf{v}}_{t}$$
(25)

where \({\mathbf{v}}_{t}\) is the target reduced steering vector corresponding to \(\upsilon_{t}\), \(\alpha\) is a complex scalar proportional to \(\alpha_{t}\) and \(2c - 1\) is the sample width of main lobe of S-sample complex self-ambiguity function in the delay domain.

Lemma 2

Let \(k - k^{\prime} \ge 2c - 1\) and the clutter patches be range homogenous (\(G_{i,r} = G_{i}, \quad \forall r\)), then \({\tilde{\mathbf{y}}}_{c} (k) + {\tilde{\mathbf{z}}}(k)\) and \({\tilde{\mathbf{y}}}_{c} (k^{\prime}) + {\tilde{\mathbf{z}}}(k^{\prime})\) (interference plus noise components of \({\tilde{\mathbf{y}}}(k)\) and \({\tilde{\mathbf{y}}}(k^{\prime})\), respectively) will be iid and have zero-mean Gaussian distributions with covariance matrix \({\mathbf{R}}_{y}\), given by

$${\mathbf{R}}_{y} = \sum\limits_{i = 1}^{{N_{c} }} {\left[ {G_{i} ({\mathbf{v}}_{{c_{i} }} {\mathbf{v}}_{{c_{i} }}^{H} ) \odot \left( {\sum\limits_{{r^{\prime } = 1 - c}}^{c - 1} {{\varvec{\uppsi}}(r^{\prime } , - \bar{f}_{{c_{i} }} ){\varvec{\uppsi}}^{H} (r^{\prime } , - \bar{f}_{{c_{i} }} )} + {\mathbf{R}}_{\psi } } \right)} \right]} + \sigma_{w}^{2} {\mathbf{I}}$$
(26)

where \(G_{i}\) is the power of the ith clutter patch in each clutter cell and \({\mathbf{R}}_{\psi}\) as expressed by Eq. (47) corresponds to the side-lobe region of complex self-ambiguity functions.

Regarding Lemmas 1 and 2, if the clutter patches are range homogenous, the detection problem of a target with reduced normalized Doppler frequency \(\upsilon_{t}\) and sample delay n, where there are no other targets in the delay interval \([n - L - c + 1,n + L + c - 1]\) (the sample delay under test \(n\) and its \(2L + 2c - 1\) surrounding sample delays), can be formulated as the following hypothesis test:

$$\left\{ {\begin{array}{*{20}l} {H_{0} :\quad {\tilde{\mathbf{y}}}(n)\mathop \sim \limits^{d} N({\mathbf{0}},{\mathbf{R}}_{y} ),\quad {\tilde{\mathbf{y}}}(k)\mathop \sim \limits^{d} N({\mathbf{0}},{\mathbf{R}}_{y} ),\quad k \in D} \hfill \\ {H_{1} :\quad {\tilde{\mathbf{y}}}(n)\mathop \sim \limits^{d} N(\alpha {\mathbf{v}}_{t} ,{\mathbf{R}}_{y} ),\quad {\tilde{\mathbf{y}}}(k)\mathop \sim \limits^{d} N({\mathbf{0}},{\mathbf{R}}_{y} ),\quad k \in D} \hfill \\ \end{array} } \right.$$
(27)

where

$$\begin{aligned} {\mathbf{v}}_{t} & = \left[ {1\;{\rm e}^{{j2\pi \upsilon_{t} }} \ldots \;{\rm e}^{{j2\pi \upsilon_{t} (N_{d} - 1)}} } \right]^{T} \\ {\mathbf{R}}_{y} & = \sum\limits_{i = 1}^{{N_{c} }} {\left[ {G_{i} ({\mathbf{v}}_{{c_{i} }} {\mathbf{v}}_{{c_{i} }}^{H} ) \odot \left( {\sum\limits_{{r^{\prime } = 1 - c}}^{c - 1} {{\varvec{\uppsi}}(r^{\prime } , - \bar{f}_{{c_{i} }} ){\varvec{\uppsi}}^{H} (r^{\prime } , - \bar{f}_{{c_{i} }} )} + {\mathbf{R}}_{\psi } } \right)} \right]} + \sigma_{w}^{2} {\mathbf{I}}, \\ \end{aligned}$$
(28)

\(\alpha\) is a deterministic and unknown complex scalar, \({\tilde{\mathbf{y}}}(n)\) and \({\tilde{\mathbf{y}}}(k), \quad k \in D\) are independent, the training data set \(D\) is given by

$$D = \left\{ {k|k = n \pm (2c - 1)d,\quad d = 1, \ldots ,\left\lfloor {\frac{L}{2c - 1}} \right\rfloor } \right\},$$
(29)

and the total number of training data is \(K = 2\left\lfloor {L/(2c - 1)} \right\rfloor\).

Proofs

See Appendix B.

So, using the proposed secondary data generation scheme of Eq. (29) and under the mentioned assumptions, the theory of adaptive target detection can be generalized to passive radars. In the next section, we continue the investigation of adaptive detection problem in passive radars and express the detection tests based on the derived hypothesis test of Eq. (27).

3 Detection Algorithms

The hypothesis test given by Eq. (27) is the same as the general hypothesis test of adaptive detection problem in active pulse radars (Kelly 1986). So, all adaptive detectors from active pulse radar theory based on this hypothesis test can potentially be generalized for use in passive radars. In this section, we investigate the generalizations of Kelly’s GLR, the DDL-GLR and the PGLR. In addition, we can use the theoretical performance expressions of these detectors using the derived covariance matrix (Eq. (28)) to predict their performances in passive radars.

When the interference covariance matrix \({\mathbf{R}}_{y}\) is totally unknown and the target reduced normalized Doppler frequency \(\upsilon_{t}\) is known (equivalent to known reduced steering vector \({\mathbf{v}}_{t}\)), the GLR solution of Eq. (27) is the same as Kelly’s GLR (Kelly 1986) with the following decision test:

$$L_{\rm Kelly} (n) = \frac{{|{\mathbf{v}}_{t}^{H} \; {\hat{\mathbf{R}}}_{y}^{- 1} {\tilde{\mathbf{y}}}(n)|^{2}}}{{\text{(}{\mathbf{v}}_{t}^{H} {\hat{\mathbf{R}}}_{y}^{- 1} {\mathbf{v}}_{t} \text{)(1 +}{\tilde{\mathbf{y}}}^{H} (n){\hat{\mathbf{R}}}_{y}^{- 1} {\tilde{\mathbf{y}}}(n)\text{)}}}\mathop > \limits^{{H_{1}}} \eta_{0}$$
(30)

where \({\hat{\mathbf{R}}}_{y}^{{}}\) is the sample covariance matrix using secondary data:

$${\hat{\mathbf{R}}}_{y}^{{}} = \sum\limits_{k \in D}^{{}} {{\tilde{\mathbf{y}}}(k){\tilde{\mathbf{y}}}^{H} (k)}$$
(31)

The presence of a target at sample delay \(n\) and with known reduced normalized Doppler frequency \(\upsilon_{t}\) is decided if \(L_{\rm Kelly} (n)\) exceeds the threshold \(\eta_{0}\). \(\eta_{0}\) is set to meet the desired probability of false alarm, \(p_{\rm fa}\), with the following theoretical expression (Kelly 1986):

$$\eta_{0} = 1 - (p_{\rm fa})^{{\frac{1}{{K - N_{d} + 1}}}}$$
(32)

where \(K\) is the total number of training data. The probability of detection, \(p_{d}\), is expressed by Kelly (1986):

$$p_{d} = 1 - (1 - \eta_{0} )^{{K - N_{d} + 1}} \sum\limits_{k = 1}^{{K - N_{d} + 1}} {\left( {\begin{array}{*{20}c} {K - N_{d} + 1} \\ k \\ \end{array} } \right)} \left( {\frac{{\eta_{0} }}{{1 - \eta_{0} }}} \right)^{k} H_{k} (\beta (1 - \eta_{0} ))$$
(33)

where

$$H_{k} (y) = \frac{K!}{{(K - N_{d} + 1)!(N_{d} - 2)!}}\int\limits_{0}^{1} {r^{{K - N_{d} + 1}} (1 - r)^{{N_{d} - 2}} {\rm e}^{- ry} \sum\limits_{n = 0}^{k - 1} {\frac{{(ry)^{n}}}{n!}} dr}$$
(34)

and

$$\beta = |\alpha |^{2} {\mathbf{v}}_{t}^{H} {\mathbf{R}}_{y}^{- 1} {\mathbf{v}}_{t}$$
(35)

As can be seen, the detection performance depends on \(N_{d}\), \(K\) and the signal-to-interference-plus-noise ratio parameter \(\beta\), where \(\beta\) is dependent on target Doppler frequency, target power and the true interference covariance matrix, \({\mathbf{R}}_{y}\).

Since the target Doppler frequency is unknown in practical applications, the GLR test is evaluated for a discrete set of Doppler frequencies, forming a Doppler detector bank. For an acceptable performance, we require that (Wang and Cai 1994):

$$K \ge 2N_{d} \sim 3N_{d}$$
(36)

It must be reminded that if Eq. (36) is not satisfied, i.e., we do not have enough iid training data as required, more data-efficient implementations such as the DDL-GLR and the PGLR can be utilized.

The DDL-GLR (Wang and Cai 1991) tries to find the GLR solution of Eq. (27) in the Doppler frequency domain. It is based on applying several GLR processors to the Doppler frequency domain data, divided into several localized processing regions (LPRs), separately (Wang and Cai 1991, 1994). The DDL-GLR reduces the required number of training data to \(K \ge 2N_{l} \sim 3N_{l}\), assuming that the lth LPR has \(N_{l}\) Doppler-bin coverage (Wang and Cai 1994).

Using Eq. (28), since the elements of \({\mathbf{R}}_{\psi}\) are smaller than the elements of \(\sum\nolimits_{{r^{\prime} = 1 - c}}^{c - 1} {{\varvec{\uppsi}}(r^{\prime}, - \bar{f}_{{c_{i}}}){\varvec{\uppsi}}^{H} (r^{\prime}, - \bar{f}_{{c_{i}}})}\) and if it can be assumed that the complex self-ambiguity functions of all segments of the reference channel signal are approximately equal in the main lobe region (\(r^{\prime} \in [1 - c,c - 1]\)), it can be shown that the interference covariance matrix has approximately per-symmetric property, i.e.,

$${\mathbf{R}}_{y} = {\mathbf{JR}}_{y}^{*} {\mathbf{J}}$$
(37)

where \({\mathbf{J}}_{{N_{d} \times N_{d}}}\) is the permutation matrix with unit cross-diagonal entries and zero elements elsewhere. The target steering vector has per-symmetric property, too:

$${\mathbf{v}}_{t} = {\mathbf{Jv}}_{t}^{*}$$
(38)

The PGLR detector uses this information about the structured form of \({\mathbf{R}}_{y}\) to reduce the secondary data size requirement by a factor of two (Wang and Cai 1992).

4 Simulation Results

In the preceding sections, the adaptive detection theory has been established for passive radars and it has been shown that regardless of the type and modulation of transmitting signal, this theory is applicable. Here, the detection performances of the adopted detectors are evaluated by Monte Carlo simulations and compared to the cross ambiguity function processing with CFAR thresholding.

It should be remembered that in some derivations of Sect. 2, we have made reasonable assumptions such as Eq. (23). If these assumptions are approximately satisfied, the detection performance of adaptive detectors will obey the theoretical performance expressions. To investigate these approximations, each simulation of this section also contains a comparison between the theoretical and simulation-based detection performances of Kelly’s GLR. As will be seen, the simulation-based and theoretical detection performances validate each other.

We suppose that the transmitting signal of opportunity is BPSK (binary PSK) with 192 kbit/s bit rate, and is received in the reference channel with DNR of \(63\;{\rm dB}\) (the transmitting waveforms of satellite-based PBR systems (Cristallini et al. 2010) are based on such digital modulations). The sampling frequency of 192 kHz (equal to the transmitting signal bandwidth) is considered.

In the first simulation set, the direct signal in the surveillance channel is canceled by preprocessing, and the detection range interval corresponds to 75 sample delays in time, containing range homogenous clutter patches. The input clutter to noise ratio (CNR) per sample delay (range cell) in this interval is assumed to be \(15\;{\rm dB}\). The power spectrum of each clutter cell’s RCS is a Gaussian function centered at zero Doppler frequency with \(\sigma = 1\;{\rm Hz}\) [\(\sigma\) denotes its standard deviation (STD)], which is frequent in maritime and airborne radar applications. To achieve this spectrum in the simulations, the Doppler frequencies of clutter patches of each clutter cell are very closely spaced in the interval of \([- 6,6]\;{\rm Hz}\) while their powers, \(\{G_{i} \}\), change as a Gaussian function with \(\sigma = 1\;{\rm Hz}\). Firstly, the detection performances of Kelly’s GLR and the cross ambiguity function processing with a CFAR thresholding algorithm are compared. The comparison depends on the target Doppler frequency. Hence, several simulation scenarios with different assumed target Doppler frequencies are arranged. In all of them, the target is located in the 50th sample delay. Other simulation parameters are listed in Table 1.

Table 1 Simulation parameters for the performance comparison of Kelly’s GLR and the cross ambiguity function processing
Full size table

In Kelly’s GLR, the subsampled mixed signals corresponding to the mentioned delay interval are used to generate training data according to the proposed scheme of Eq. (29) with \(2c - 1 = 2\left\lfloor {f_{s}/(2B)} \right\rfloor + 1 = 2\left\lfloor {192/384} \right\rfloor + 1 = 1\). The size of the training data set is \(K = 74\). For the integration time of 1 s, the Doppler resolution of \(1\;{\rm Hz}\) is expected, and the Doppler frequency bins for the GLR detector bank are selected as:

$$f_{t} \in \{ - 11, - 10, \ldots ,11\} {\text{Hz}},\quad \upsilon_{t} \in \left\{ { - 0.5 + \frac{1}{24}, - 0.5 + \frac{2}{24}, \ldots ,0.5 - \frac{1}{24}} \right\}$$
(39)

Kelly’s GLR has the embedded CFAR property with respect to the level and structure of interference covariance matrix (Kelly 1986), and a fixed threshold is assigned to the whole range-Doppler plane (75 sample delays and Doppler frequencies up to \(11\;{\rm Hz}\)) for the desired probability of false alarm (\(p_{\rm fa} = 10^{- 3}\)).

In the cross ambiguity function processing, a CFAR thresholding algorithm should be applied over the square of magnitude of the cross ambiguity function (equivalent to the Fourier transform of the subsampled mixed signals, Stein 1981) in the range-Doppler plane (75 sample delays and Doppler frequencies up to \(11\;{\rm Hz}\)) which is designed carefully based on the considered scenario. To do this, the square of magnitude of the cross ambiguity function, when no target is present, is shown in Fig. 3a. As depicted in Fig. 3a, due to the range homogeneity of the clutter patches in the detection range interval, for every cell in the range-Doppler plane its neighboring cells in the range dimension can be used as reference or training cells. Let us also illustrate a simple case in which the surveillance channel contains thermal noise and the return of a strong target at sample delay \(n = 50\) with Doppler frequency of \(0.25\;{\rm Hz}\) (no clutter) in Fig. 3b. As shown in Fig. 3b, a strong target can cause false targets around itself in the Doppler dimension due to the poor side-lobe property of cross ambiguity function and sampling phenomenon. This issue happens in the general case of simultaneous presence of target and clutter, too. To prevent false targets’ detection, the cells adjacent to the cell under test in the Doppler dimension should also be used as reference cells. But due to the non-uniform spectrum of clutter cell’s RCS (as shown in Fig. 3a), the number of these cells should be as low as possible. To consider these points, we propose that the CFAR algorithm be the combination (logical and) of two one-dimensional cell-averaging CFARs (CA-CFARs) in the range dimension and the Doppler dimension. The CA-CFAR in the range dimension for a reasonable and fair comparison utilizes the same number of reference cells as the number of training data used in Kelly’s GLR, which is 74 in this simulation. The CA-CFAR in the Doppler dimension, when the Doppler bins are selected in the same way as Eq. (39), is composed of only two reference cells. The thresholds of these CA-CFARs are chosen such that each yields approximately the same probability of false alarm, and also the combination of both CA-CFARs leads to \(p_{\rm fa} = 10^{- 3}\) in the whole considered range-Doppler plane.

Fig. 3
figure 3

Square of magnitude of cross ambiguity function (CAF) in dB for a target-free and b clutter-free surveillance channel signal

Full size image

In each of the considered scenarios (Table 1), the detection probability (\(p_{d}\)) of both methods versus input signal to clutter ratio (\({\rm SCR}_{i}\)) is depicted in Figs. 4 and 5. From Figs. 4 and 5, it is concluded that for such targets whose Doppler frequencies are far enough from the peak of clutter cell’s RCS spectrum (at zero Doppler frequency), the performance of Kelly’s GLR (the GLR) is considerably superior to the cross ambiguity function processing with CFAR thresholding (CFAR CAF). However, in the strong peak region of clutter cell’s RCS spectrum, the GLR underperforms the CFAR CAF to a much lesser extent. To clarify this, the required input SCRs of these methods (in decibels) for \(p_{d} = 0.8\) and their difference as a function of the target Doppler frequency are shown in Fig. 6a. An important observation in Fig. 6a is that at \(f_{t} = 4\;{\rm Hz}\) (four times the STD of Gaussian-shaped clutter cell’s RCS spectrum), the performance improvement of the GLR with respect to the CFAR CAF is maximum (about \(10.7\;{\rm dB}\)). To further investigate this observation, simulations are repeated without any change, except that the STD is selected \(\sigma = 0.5\;{\rm Hz}\). The results are shown in Fig. 6b which confirms that the most performance improvement is achieved around the edge of clutter cell’s RCS spectrum. In Figs. 4 and 5, the theoretical detection performance of Kelly’s GLR is also plotted which matches well with the simulation-based performance. It is noted that according to Eq. (33), the detection performance is a function of \(\beta\), defined by Eq. (35). To generate each plot, firstly \({\mathbf{R}}_{y}\) is computed by substituting the simulation parameters in Eq. (28) in which \({\mathbf{R}}_{\psi}\) is derived by Eq. (47) for \(n = n_{t} = 50\). Secondly, \(\beta\) and hence \(p_{d}\) is evaluated for the assumed target Doppler frequency and a set of input SCRs using the computed \({\mathbf{R}}_{y}\). It is also demonstrated that the computation of \({\mathbf{R}}_{\psi}\) with different values of \(n\) has very little effect on the theoretical performance.

Fig. 4
figure 4

Detection performance comparison of Kelly’s GLR and the CFAR CAF for target Doppler of a 0 Hz, b 1 Hz, c 2 Hz and d 3 Hz

Full size image
Fig. 5
figure 5

Detection performance comparison of Kelly’s GLR and the CFAR CAF for target Doppler of a 4 Hz, b 5 Hz, c 6 Hz and d 8 Hz

Full size image
Fig. 6
figure 6

Required input SCR (dB) versus target Doppler for \(p_{d} = 0.8\) in the case of a RCS power spectrum with \(\sigma = 1\;{\rm Hz}\) and b power spectrum with \(\sigma = 0.5\;{\rm Hz}\)

Full size image

The cross ambiguity function is the matched filter detector in a white interference scenario. For highly correlated interferences, its performance degradation compared to the adaptive detectors is increased. In addition, the GLR achieves better false alarm regulation than the CFAR CAF.

Let us also investigate the detection performance in the presence of a strong interfering target at the range cell under test for the GLR and the CFAR CAF. It is assumed that in the 50th sample delay, there is a strong target with Doppler frequency of \(0.25\;{\rm Hz}\) and \({\rm SCR}_{i} = 5.6\;{\rm dB}\) as well as the test target with \(f_{t} = 4\;{\rm Hz}\). The detection probability of both methods versus the input SCR for the test target is plotted in Fig. 7. If compared to Fig. 5a, the performance of the CFAR CAF in the presence of an interfering target is decreased while the GLR maintains its performance.

Fig. 7
figure 7

Detection performance comparison of Kelly’s GLR and the CFAR CAF for target Doppler of 4 Hz in the presence of an interfering target at the range cell under test with Doppler of 0.25 Hz and \({\rm SCR}_{i} = 5.6\;{\rm dB}\)

Full size image

In the next simulation, for the target Doppler frequency of \(f_{t} = 4\;{\rm Hz}\) and the previously considered detection range interval, the detection performances of the three adopted detectors and the CFAR CAF for \(p_{\rm fa} = 10^{- 3}\) and \(p_{\rm fa} = 10^{- 4}\) are shown in Fig. 8a, b, respectively. The considered LPR for the DDL-GLR and the number of training data used by the detectors are given in Table 2. Other simulation parameters are the same as the first simulation. The DDL-GLR unlike Kelly’s GLR and the PGLR can work well even in high training-limited case of \(K = 15\). Figure 8 also highlights the fact that the PGLR and the DDL-GLR outperform Kelly’s GLR for the same number of training data, lower than the secondary data size requirement of Kelly’s GLR. Obviously, the performance of Kelly’s GLR in this simulation with \(K = 36\) is degraded with respect to Fig. 5a with \(K = 74\). The cross ambiguity function processing uses a CFAR algorithm with the same structure as one used in the previous simulations, except that the CA-CFAR in the range dimension now employs \(K = 36\) reference cells. It has the worst performance among the investigated methods.

Fig. 8
figure 8

Detection performance comparison of the DDL-GLR, PGLR, CFAR CAF and Kelly’s GLR for target Doppler of 4 Hz a \(p_{\rm fa} = 10^{- 3}\) and b \(p_{\rm fa} = 10^{- 4}\)

Full size image
Table 2 Simulation parameters for the performance comparison of the adopted detectors
Full size table

An important model to depict nonhomogeneous environments is the variation of clutter cell’s RCS power in range (Gao et al. 2014). In the final simulation set, a practical nonhomogeneous scenario in which the input CNR per sample delay varies proportional to the inverse of target range is considered. The input CNR per sample delay changes over the interval \([10\;{\rm dB}, - 10\;{\rm dB}]\) in the sample delays between 1 and 100. The clutter cell’s RCS spectrum is a Gaussian function with \(\sigma = 1\;{\rm Hz}\). A target with \(f_{t} = 4\;{\rm Hz}\) is located in the 80th sample delay. Figure 9 depicts the detection probability of Kelly’s GLR with 32 training data and the CFAR CAF with 32 training cells in its range dimension CA-CFAR (corresponding to the sample delay interval [64,96]) versus input SCR in the sample delay under test (the 80th sample delay). The input CNR in this sample delay is \(- 9\;{\rm dB}\). Figure 9 also shows the detection performance in the case of ideally homogenous detection range interval consisting of 33 sample delays (32 training data) with input CNR per sample delay of \(- 9\;{\rm dB}\) (both theoretical and simulation-based). As we can see, the performance of Kelly’s GLR degrades in the practical nonhomogeneous environment with respect to the ideally homogenous one. So, the ECA is applied to eliminate the first 63 sample delays, where the clutter cells’ RCSs are stronger and encounter severe non-homogeneity. These interfering clutter cells degrade the performance of adaptive detection in the desired detection range interval (sample delays of 64–96). For reducing the computational cost of the ECA, the Doppler frequency interval of \([- 2,2]\;{\rm Hz}\) is selected for cancellation. Kelly’s GLR in the nonhomogeneous environment after performing the ECA has reasonably good performance, close to its performance in the homogeneous environment. The CFAR CAF, with or without the prior ECA, does not perform well. From the results of this simulation, we conclude that the sample delay under test and its adjacent sample delays usually correspond to range homogenous clutter patches, and the preprocessing of the surveillance channel signal helps to reduce the masking effects of the clutter patches outside of the detection range interval on the adaptive detection of desired targets. Similar conclusion has been made in (Tan et al. 2014) without the analysis of detection performance. If after this preprocessing the non-homogeneity is still severe, we could use the DDL-GLR or other detectors especially designed for such cases (Gao et al. 2014; Melvin 2000). It is noted that for the simulations of Fig. 9, the threshold is set for \(p_{\rm fa} = 10^{- 3}\) in the desired range-Doppler plane consisting of sample delay interval \([64,96]\) and Doppler frequency interval \([- 7,7]\;{\rm Hz}\). In addition, we have: \(N_{d} = 16\), \(K = 32\) and \(S = 12{,}000\).

Fig. 9
figure 9

Detection performance comparison of Kelly’s GLR (the GLR) and the CFAR CAF for a practical nonhomogeneous case with and without the prior ECA, and its corresponding homogeneous case for target Doppler of 4 Hz

Full size image

5 Conclusion

A formulation of adaptive target detection for passive radar systems as a hypothesis testing problem has been addressed in this paper. This has been facilitated by a detailed statistical analysis of the mixing product approach, including the distribution and also the covariance matrix. We have presented how the conventional secondary data generation should be modified based on the properties of the self-ambiguity function of transmitting signal to satisfy iid requirements. It has been established that adaptive detectors from active pulse radar area such as Kelly’s GLR, the DDL-GLR and the PGLR are applicable to the derived hypothesis test using the proposed secondary data generation scheme. We have provided the required information to use the theoretical performance expressions of these detectors to predict their performances in passive radars. Simulations have been performed to show the effectiveness of the adopted detectors which in most cases and especially around the edge of clutter cell’s RCS spectrum exhibit significantly better detection probability than the cross ambiguity function processing with CFAR thresholding.