1 Introduction

The classical theory of thermoelasticity assumes that thermal waves propagate at infinite velocity, however, this is contrary to the experimental observation that thermal waves propagate at finite velocity. To eliminate this difference, Lord and Shulman (1967) made the first revision of the classical thermoelastic theory. They introduced the flux rate expression into the Fourier's law of heat conduction equation, making it a heat transfer equation with hyperbolic properties, which ensures that the heat wave propagates at a finite velocity. Subsequently, several scholars introduced a series of generalized thermoelasticity theories, namely, Green and Lindsay (1972) thermoelasticity theory, Green and Naghdi (1991, 1992, 1993) thermoelasticity theory, two-phase lag thermoelasticity theory (Tzou 1995a), and three-phase lag thermoelasticity theory (Choudhuri 2007).

However, the lag behaviour within the heat conduction of solids deserves the attention of researchers when studying some practical problems. Especially during transient processes of solid heating, the number of slips is particularly small or the heat flow is very large (Singh et al. 2020). The three-phase lag model has important research value in problems such as heat conduction and heat diffusion. Zhang et al. (2021) used a three-phase lag model to analyse the thermoelastic response of biological tissues subjected to temperature loading. Zenkour (2022) discussed thermal diffusion vibrations in an infinite medium utilizing a three-phase lag G-N model. Abd-Elaziz et al. (2022) analysed the effect of diffusion and rotation on porous thermoelastic media in the context of a three-phase lag thermoelastic model.

With the wide application of fractional order calculus in various scientific fields such as viscoelasticity, bioengineering, and mechanics, scientists have gradually developed a strong interest in it (Ezzat 2011, 2013, 2016a, 2018; Stanisauskis et al. 2022; Ali and Katoch 2023; Abouelregal et al. 2022). Wang and Li (2011) proposed memory-dependent derivatives (MDD) inspired by fractional order derivatives. Compared with the fractional order derivative, the MDD can describe the memory effect more accurately and express its physical meaning more intuitively. Subsequently Ezzat et al. developed a generalised thermo-viscoelastic model with MDD (Ezzat et al. 2014) and a magneto-thermo-viscoelastic model with dual-temperature MDD (Ezzat and EI-Bary 2016b).

In recent years, some scholars have carried out a series of studies combining phase lag and memory-dependent models. Ezzat et al. (2017a) established a dual-phase lag generalised thermoelasticity model with MDD. Sarkar and Mukhopadhyay (2021) discussed thermal viscoelastic interactions in infinite space subject to moving heat sources using a generalized thermal viscoelastic dual-phase lag model with memory-related derivatives. Kumar et al. (2023) mathematically analysed a micropolar generalized thermoelastic plate with a three-phase lag model based on memory-related derivatives. Kaur et al. (2022) investigated the reflection and refraction of plane waves at the imperfect boundary between two dissimilar transversely isotropic piezo-thermoelastic (PT) solid half-spaces with diffusion and two-temperature using the three-phase lag thermal diffusion model of MDD. Tiwari et al. (2021) investigated the nonlocal behaviour of a piezoelectric half-space subjected to a magnetic field in the context of a three-phase lag heat conduction theory with memory-related derivatives by introducing a nonlocal theory.

It is well known that micron- and nanoscale structured materials have received widespread attention due to their excellent multifunctionality (Odegard et al. 2002). For some high-performance nanostructures such as nanoelectromechanical systems, accurate analysis of the intrinsic stress, strain, and heat conduction is essential during design or safe transportation (Kambali et al. 2017; Yu et al. 2016; Dehrouyeh-Semnani 2017, 2018, 2021). However, the characteristic sizes of nanostructured materials are so small that the intrinsic properties of nanoscale structured materials differ significantly from block materials (Li et al. 2014). To bridge this gap, scholars have proposed the following models of continuum media mechanics: strain gradient elasticity theory (Lam et al. 2003), coupled stress theory (Yang et al. 2002), and nonlocal elasticity theory (Eringen 2002). Among them, the nonlocal theory proposed by Eringen is more widely used. Pranavi et al. (2022) used Eringen's nonlocal theory for the analysis of functional gradient beams, plates, and shells and presented the nature of nonlocal moduli and their internal length scale dependence. Yang and Chen (2020) proposed a generalized uncoupled nonlocal thermal viscoelastic theory based on Eringen's nonlocal theory and applied it to finite plate 1D analysis subjected to thermal shock.

Studies have found that many materials that do not exhibit viscoelasticity at room temperature, or have insignificant viscoelasticity, both exhibit significant viscoelasticity at high temperatures. In engineering applications, large thermal stresses can be effectively avoided and the strength of structures can be improved by analyzing the thermo-viscoelastic behaviour of materials. Therefore, it is important to consider the viscoelastic behaviour of such materials when studying or designing them (Guo et al. 2022a). With the wide application of ultra-fast heating techniques in viscoelastic materials, the analysis of thermal stresses in viscoelastic materials has gradually become an important topic of interest for researchers in areas such as polymer science and the plastics industry (Abouelregal and Ahmad 2021; Ezzat et al. 2022a, 2022b, 2022c; Guo et al. 2021, 2022b; Li et al. 2019, 2021, 2023).

This paper aims to construct a new model of three-phase lag thermoviscoelasticity incorporating memory-dependent derivative by introducing Kelvin-Voigt viscoelasticity model. The model is applied to the analysis of the transient response of an elastic rod under the action of a magnetic field and a moving heat source. Modification of the classical theory of elasticity using Eringen's theory of nonlocal elasticity, taking into account size effects. The model is an improvement of the conventional coupled thermoelastic theory. Analytical solutions for temperature, displacement and stress are obtained by solving the governing equations by Laplace integral transform and its numerical inverse transform. The effects of time, heat source velocity, magnetic field, viscosity, and memory-dependent effects on the physical quantities inside the rod were investigated. The results of this work have certain reference value for the research of nonlocal material science researchers, low-temperature physicists and new material designers.

2 Eringen's Theory of Nonlocal Elasticity

In the theory of nonlocal elasticity, the stress–strain relationship is (Eringen 2002):

$$\sigma_{ij} \left( {\mathbf{x}} \right) = \int_{{\text{V}}} {\alpha^{ * } \left( {\left| {{\mathbf{x}} - {\mathbf{x}}^{\prime} } \right|} \right)} {\uptau }_{ij} \left( {{\mathbf{x}}^{\prime} } \right){\text{dV}}\left( {{\mathbf{x}}^{\prime} } \right)$$
(1)
$$\tau_{ij} \left( {{\mathbf{X}}^{\prime} } \right) = 2\mu e_{ij} \left( {{\mathbf{X}}^{\prime} } \right) + \left[ {\lambda e_{kk} \left( {{\mathbf{X}}^{\prime} } \right) - \gamma \theta \left( {{\mathbf{X}}^{\prime} } \right)} \right]\delta_{ij} ,\;\;i,j = 1,2,3$$
(2)
$$e_{ij} \left( {{\mathbf{x}}^{\prime} } \right) = \frac{1}{2}\left[ {\frac{{\partial {{u}}_{{{i}}} \left( {{\mathbf{x}}^{\prime} } \right)}}{{\partial {{x}}^{\prime}_{{{j}}} }} + \frac{{\partial {{u}}_{{{j}}} \left( {\mathbf{{x}}^{\prime} } \right)}}{{\partial {{x}}^{\prime}_{{{i}}} }}} \right]$$
(3)

where, \(\sigma_{ij}\) is the nonlocal stress tensor, \(\tau_{ij}\) is the local stress tensor, \(e_{ij}\) is the classical local strain tensor, \({{u}}_{{{i}}} \left( {{\mathbf{x}}^{\prime} } \right)\) is the local displacement component, \(\lambda\) and \(\mu\) are Lamé constants, \(\left| {{\mathbf{x}} - {\mathbf{x}}^{\prime} } \right|\) denotes the distance in Euclidean space. The nonlocal kernel function \(\alpha^{ * } \left( {\left| {{\mathbf{x}} - {\mathbf{x}}^{\prime} } \right|} \right)\) represents the effect of the strain at point \({\mathbf{x}}^{\prime}\) in the elastomer on the stress at point \({\mathbf{x}}\).

Equation (1) can be simplified to (Eringen 2002):

$$\tau_{ij} = [1 - \left( {e_{0} a} \right)^{2} \nabla^{2} ]\sigma_{ij}$$
(4)

where, \(e{}_{0}\) is the material constant, \(\nabla^{2}\) is the Laplace function, and \(e{}_{0}a\) is the nonlocal parameter.

3 Basic Equation of the Problem

In the present problem, we consider the initial magnetic field H in the elastic rod, as well as the induced magnetic field h, the induced electric field E and the Lorentz force F = J × H. For linear thermoelasticity, we take smaller values for h and E. However, due to the Lorentz force, half of the particles on the rod will be displaced through the displacement vector u. The Maxwell equation is:

$${\text{curl}} \, {\mathbf{h}}{ = }{\mathbf{J}}{ + }\varepsilon_{0} \frac{{\partial {\mathbf{E}}}}{\partial t}$$
(5)
$${\text{curl}} \, {\mathbf{E}}{ = } - \mu_{0} \frac{{\partial {\mathbf{h}}}}{\partial t}$$
(6)
$${\mathbf{E}} = - \mu_{0} \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} \times {\mathbf{H}}} \right)$$
(7)
$${\text{div}} \, {\mathbf{h}} = 0$$
(8)

where, J denotes the current density, \(\mu_{0}\) and \(\varepsilon_{0}\) denote the magnetic and electrical permeability. The motion equation is set up through the magnetic field defined in Maxwell’s equations:

$$\rho \ddot{u}_{i} = \tau_{ij,j} + \mu_{0} \left( {{\mathbf{J}} \times {\mathbf{H}}} \right)_{i}$$
(9)

When considering Kelvin-Voigt type viscoelasticity, the relationship between stress and strain is

$$\tau_{ij} = \lambda_{e} \left( {1 + \lambda_{0} \frac{\partial }{\partial t}} \right)e_{kk} \delta_{ij} + 2\mu_{e} \left( {1 + \mu_{0} \frac{\partial }{\partial t}} \right)e_{ij} - \gamma_{e} \left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\theta \delta_{ij} ,\;\;i,j = 1,2,3$$
(10)

where, \(\lambda_{0}\), \(\mu_{0}\) and \(\gamma_{0}\) are viscoelastic parameters, and \(\gamma_{e} = \left( {3\lambda_{e} + 2\mu_{e} } \right)\alpha_{t}\), \(\gamma_{0} = \left( {3\lambda_{e} \lambda_{0} + 2\mu_{e} \mu_{0} } \right)\alpha_{t} /\gamma_{e}\), \(\alpha_{t}\) is the coefficient of linear thermal expansion.

Substituting Eqs. (4) into (10) yields:

$$[1 - \left( {e_{0} a} \right)^{2} \nabla^{2} ]\sigma_{ij} = \lambda_{e} \left( {1 + \lambda_{0} \frac{\partial }{\partial t}} \right)e_{kk} \delta_{ij} + 2\mu_{e} \left( {1 + \mu_{0} \frac{\partial }{\partial t}} \right)e_{ij} - \gamma_{e} \left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\theta \delta_{ij}$$
(11)

The relationship between strain and displacement is given by:

$$e_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right)$$
(12)

Ezzat et al. (2015) notated the memory-dependent derivative Fourier's law of heat conduction as:

$$\left( {1 + \omega D_{\omega } } \right)q_{i} = - K\theta_{,i}$$
(13)

where, \(q_{i}\) is the heat flux component, \(K\) is the thermal conductivity, \(\theta_{,i}\) is the heat flux component. Simplifying Eq. (13) to the heat conduction equation of LS type (Lord and Shulman 1967):

$${\text{K}}\theta_{,ii} = \left( {1 + \tau_{\omega } D_{\omega } } \right)\left( {\rho C_{E} \dot{\theta } + T_{0} \gamma_{e} \left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\dot{u}_{,i} - \rho {\text{Q}}} \right)$$
(14)

where, \(\rho\) is the density, \(T_{0}\) is the reference temperature, \(C_{E}\) is the constant strain-specific heat, \(\tau_{\omega }\) is the time factor. Fourie's law of three-phase lag with memory-dependent derivatives in isotropic and homogeneous media is (Mondal et al. 2019):

$$- K\left( {1 + \tau_{\theta } D_{{\tau_{\theta } }} } \right)\dot{\theta }_{,i} - K^{ * } \left( {1 + \tau_{\upsilon } D_{{\tau_{\upsilon } }} } \right)\theta_{,i} = \left( {1 + \tau_{q} D_{{\tau_{q} }} + \frac{{\tau_{q}^{2} }}{2}D_{{\tau_{q} }}^{2} } \right)\dot{q}_{i}$$
(15)

where, \(K\) is the thermal conductivity, \(K^{*}\) is the additional material constant, \(\tau_{\theta }\) is the delay time of the temperature gradient, \(\tau_{\upsilon }\) is the delay time of the thermal displacement gradient, \(\tau_{q}\) is the delay time of the heat flow vector.

When the heat source is present, Eq. (15) can be simplified to the heat equation of the three-phase lag model as:

$$\begin{gathered} K\left( {1 + \tau_{\theta } D_{{\tau_{\theta } }} } \right)\dot{\theta }_{,ii} + K^{ * } \left( {1 + \tau_{\upsilon } D_{{\tau_{\upsilon } }} } \right)\theta_{,ii} = \left( {1 + \tau_{q} D_{{\tau_{q} }} + \frac{{\tau_{q}^{2} }}{2}D_{{\tau_{q} }}^{2} } \right) \hfill \\ *\left( {\rho C_{E} \ddot{\theta } + T_{0} \gamma_{e} \left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\ddot{u}_{,i} - \rho \dot{Q}} \right) \hfill \\ \end{gathered}$$
(16)

4 Formulation of the Problem

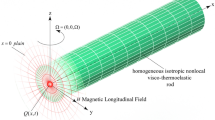
In this paper, a nonlocal thermo-viscoelastic rod of length l \(\left( {0 \le x \le l} \right)\) is studied. The rod is assumed to be subjected to a moving heat source and a magnetic field, where the initial magnetic field is H with component (0, 0, \(H{}_{0}\)). In addition, the induced magnetic and induced electric fields are h = (0, 0, h) and E = (0, E, 0), respectively. The dynamics of a rod can be viewed as a one-dimensional problem. Assuming that the length of the rod is along the positive direction of the x-axis, its physical field depends only on time \(t\) and space \(x\). Therefore, the displacement component has the following form:

$${\varvec{u}} = \left( {u\left( {x,t} \right),0,0} \right)$$
(17)

According to Maxwell's system of equations, the magnetic and electric fields in the one-dimensional case can be written as:

$${\mathbf{E}} = \left( {0,\mu_{0} H_{0} \frac{\partial u}{{\partial t}},0} \right)$$
(18)
$${\mathbf{h}} = \left( {0,0, - H_{0} \frac{\partial u}{{\partial x}}} \right)$$
(19)
$${\mathbf{J}} = \left( {0, - \left( {\frac{\partial h}{{\partial x}} + \varepsilon_{0} \mu_{0} H_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }}} \right),0} \right)$$
(20)

Equations (9), (11) and (16) can be simplified as:

$$\beta \left( {1 - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\frac{{\partial^{2} u}}{{\partial t^{2} }} = \left( {\frac{{\lambda_{e} + 2\mu_{e} + \left( {\lambda_{e} \lambda_{0} + 2\mu_{e} \mu_{0} } \right)\frac{\partial }{\partial t}}}{\rho }} \right)\frac{{\partial^{2} u}}{{\partial x^{2} }} - \frac{{\gamma_{e} }}{\rho }\left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\frac{\partial \theta }{{\partial x}}$$
(21)
$$[1 - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}]\sigma = \left( {\lambda_{e} + 2\mu_{e} + \left( {\lambda_{e} \lambda_{0} + 2\mu_{e} \mu_{0} } \right)\frac{\partial }{\partial t}} \right)\frac{\partial u}{{\partial x}} - \gamma_{e} \left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\theta$$
(22)
$$\begin{gathered} \left( {1 + \tau_{q} D_{{\tau_{q} }} + \frac{{\tau_{q}^{2} }}{2}D_{{\tau_{q} }}^{2} } \right)\left( {\rho C_{E} \ddot{\theta } + T_{0} \gamma_{e} \left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\frac{{\partial \ddot{u}}}{\partial x} - \dot{Q}} \right) = K\left( {1 + \tau_{\theta } D_{{\tau_{\theta } }} } \right)\frac{{\partial^{2} \dot{\theta }}}{{\partial x^{2} }} \hfill \\ + K^{ * } \left( {1 + \tau_{\upsilon } D_{{\tau_{\upsilon } }} } \right)\frac{{\partial^{2} \theta }}{{\partial x^{2} }} \hfill \\ \end{gathered}$$
(23)

where, \(\beta = 1 + \frac{{\alpha_{0}^{2} }}{{c^{2} }}\), \(c^{2} = \frac{1}{{\varepsilon_{0} \mu_{0} }}\), \(\alpha_{0}^{2} = \frac{{H_{0}^{2} \mu_{0} }}{\rho }\) it is Alfven speed.

We introduce the following dimensionless variables to Eqs. (21–23):

$$\left( {x^{\prime} ,u^{\prime} } \right) = c_{0} \eta \left( {x,u} \right),\;\left( {t^{\prime} ,\tau^{\prime} ,\tau_{q}^{\prime} ,\tau_{\theta }^{\prime} ,\tau_{\upsilon }^{\prime} ,\lambda_{0}^{\prime} ,\mu_{0}^{\prime} ,\gamma_{0}^{\prime} } \right) = c_{0}^{2} \eta \left( {t,\tau ,\tau_{q} ,\tau_{\theta } ,\tau_{\upsilon } ,\lambda_{0} ,\mu_{0} ,\gamma_{0} } \right),\;\theta^{\prime} = \frac{{\gamma_{e} \theta }}{{\rho c_{0}^{2} }},$$
$$E^{\prime} = \frac{E}{{\mu_{0} H_{0} C_{0} }},\;\sigma^{\prime} = \frac{\sigma }{{\lambda_{e} + 2\mu_{{\text{e}}} }},\;K^{ * ^{\prime}} = \frac{{K^{ * } }}{{Kc_{0}^{2} \eta }},\;Q^{\prime} = \frac{{\gamma_{e} Q}}{{K\rho c_{0}^{4} \eta^{2} }},\;J^{\prime} = \frac{J}{{\mu_{0} H_{0} C_{0} }},\;h^{\prime} = \frac{h}{{H_{0} }}$$

After omitting the primes, the Eqs. (21–23) can be taken in the following dimensionless form:

$$E = \frac{\partial u}{{\partial t}}$$
(24)
$$h = - \frac{\partial u}{{\partial x}}$$
(25)
$$J = - \left( {\frac{\partial h}{{\partial x}} + V^{2} \frac{{\partial^{2} u}}{{\partial t^{2} }}} \right)$$
(26)
$$\left( {1 + \left( {\frac{{\lambda_{e} \lambda_{0} + 2\mu_{e} \mu_{0} }}{{\lambda_{e} + 2\mu_{e} }}} \right)\frac{\partial }{{\partial {\text{t}}}}} \right)\frac{{\partial^{2} u}}{{\partial x^{2} }} = \beta \left[ {1 - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{{\partial^{2} u}}{{\partial t^{2} }} + \left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\frac{\partial \theta }{{\partial x}} \,$$
(27)
$$\left[ {1 - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\sigma = \left( {1 + \left( {\frac{{\lambda_{e} \lambda_{0} + 2\mu_{e} \mu_{0} }}{{\lambda_{e} + 2\mu_{e} }}} \right)\frac{\partial }{{\partial {\text{t}}}}} \right)\frac{\partial u}{{\partial x}} - \left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\theta$$
(28)
$$\begin{gathered} \left( {1 + \tau_{q} D_{{\tau_{q} }} + \frac{{\tau_{q}^{2} }}{2}D_{{\tau_{q} }}^{2} } \right)\left( {\ddot{\theta } + \varepsilon_{1} \left( {1 + \gamma_{0} \frac{\partial }{\partial t}} \right)\frac{{\partial \ddot{u}}}{\partial x} - \dot{Q}} \right) = \left( {1 + \tau_{\theta } D_{{\tau_{\theta } }} } \right)\frac{{\partial^{2} \dot{\theta }}}{{\partial x^{2} }} \hfill \\ + K^{ * } \left( {1 + \tau_{\upsilon } D_{{\tau_{\upsilon } }} } \right)\frac{{\partial^{2} \theta }}{{\partial x^{2} }} \hfill \\ \end{gathered}$$
(29)

where

\(K^{ * } = \frac{{C_{E} \left[ {\lambda_{e} + 2\mu_{e} + \left( {\lambda_{e} \lambda_{0} + 2\mu_{e} \mu_{0} } \right)s} \right]}}{4}\), \(\varepsilon_{1} = \frac{{T_{0} \gamma_{e}^{2} }}{{\rho c_{0}^{2} \eta K}}\), \(\eta = \frac{{\rho C_{E} }}{K}\), \(c_{0}^{2} = \frac{{\lambda_{e} + 2\mu_{e} }}{\rho }\),and \(V = c_{0} /c\). The mobile heat source can take the following dimensionless form:

$$Q = Q_{0} \delta \left( {x - \upsilon t} \right)$$
(30)

Since the ends of the rod are fixed and insulated, the boundary conditions can be written as:

$$\left. {u\left( {x,{\text{t}}} \right)} \right|_{x = 0,l} = 0,\;\left. {\frac{{\partial \theta \left( {x,t} \right)}}{\partial x}} \right|_{x = 0,l} = 0$$
(31)

Ezzat et al. (2014) used the definition of a selection kernel function to reflect the memory effect (instantaneous rate of change depending on the past state):

$$K\left( {t - \zeta } \right) = 1 - \frac{2b}{\omega }\left( {t - \xi } \right) + \frac{{a^{2} \left( {t - \xi } \right)^{2} }}{{\omega^{2} }} = \left\{ {\begin{array}{*{20}c} {1,} & {{\text{a}} = 0, \, b = 0,} \\ {1 - \frac{t - \xi }{\omega },} & {a = 0, \, b = \frac{1}{2},} \\ {1 - (t - \xi ),} & {a = 0, \, b = \frac{\omega }{2},} \\ {\left( {1 - \frac{t - \xi }{\omega }} \right)^{2} ,} & {a = 1, \, b = 1,} \\ \end{array} } \right.$$
(32)

where, a and b are constants.

5 Solving Method

The Laplace transform is defined as shown below:

$$\overline{f}\left( {x,s} \right) = L\left\{ {f\left( {x,t} \right)} \right\} = \int_{0}^{\infty } {f\left( {x,t} \right)e^{ - st} } dt,\;{\text{Re}} \left( s \right) > 0$$
(33)

Using the Eq. (33), we perform Laplace transform on Eqs. (27) and (28), and then obtain:

$$\left( {A + \beta \left( {e_{0} a} \right)^{2} s^{2} } \right)D^{2} \overline{u} = \beta s^{2} \overline{u} + CD\overline{\theta }$$
(34)
$$\left[ {1 - \left( {e_{0} a} \right)^{2} D^{2} } \right]\overline{\sigma } = AD\overline{u} - C\overline{\theta }$$
(35)

where, \({\text{A}} = 1 + \left( {\frac{{\lambda_{e} \lambda_{0} + 2\mu_{e} \mu_{0} }}{{\lambda_{e} + 2\mu_{e} }}} \right)s\), \(C = \left( {1 + \gamma_{0} s} \right)\), \(D = \frac{\partial }{\partial x}\).

Applying Laplace transform to memory dependent derivative, we get

$$L\left\{ {\omega D_{\omega } f\left( t \right)} \right\} = L\left\{ {\int_{t - \omega }^{t} {K\left( {t - \xi } \right)f^{i} \left( \xi \right)} d\xi } \right\} = L\left\{ {f\left( t \right)} \right\}G\left( {s,\omega } \right)$$
(36)

The expression of the function \(G\left( {s,\omega } \right)\) is:

$${\text{G}}\left( {{\text{s,}}\omega } \right) = \left( {1 - e^{ - s\omega } } \right)\left( {1 - \frac{2b}{{\omega s}} + \frac{{2a^{2} }}{{\omega^{2} s^{2} }}} \right) - e^{ - s\omega } \left( {a^{2} - 2b + \frac{{2a^{2} }}{\omega s}} \right)$$
(37)

where, \(\omega = \tau_{q} ,\;\tau_{\upsilon }\) or \(\tau_{\theta }\)

Applying the Laplace transform of Eqs. (36–29) yields:

$$\begin{gathered} \left[ {1 + G\left( {s,\tau_{q} } \right) + \frac{{\tau_{q} s}}{2}G\left( {s,\tau_{q} } \right)} \right]\left[ {s^{2} \overline{\theta } + \varepsilon_{1} CDs^{2} \overline{u} - \varepsilon_{2} se^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)x}} } \right] \hfill \\ = \left[ {s\left\{ {1 + G\left( {s,\tau_{\theta } } \right)} \right\} + K^{ * } \left\{ {1 + G\left( {s,\tau_{\upsilon } } \right)} \right\}} \right]D^{2} \overline{\theta } \hfill \\ \end{gathered}$$
(38)

where, \(\varepsilon_{2} = \frac{{Q_{0} }}{\upsilon }\).

If we substitute \(s\tau_{\theta }\) for \(G\left( {s,\tau_{\theta } } \right)\), \(s\tau_{q}\) for \(G\left( {s,\tau_{q} } \right)\), and \(s\tau_{\upsilon }\) for \(G\left( {s,\tau_{\upsilon } } \right)\) in Eq. (38), the heat conduction equation in the Laplace transform domain, when not affected by memory-dependent effects, is obtained as follows:

$$\left[ {1 + s\tau_{q} + \frac{{\tau_{q}^{2} s^{2} }}{2}} \right]\left[ {s^{2} \overline{\theta } + \varepsilon_{1} CDs^{2} \overline{u} - \varepsilon_{2} se^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)x}} } \right] = \left[ {s\left( {1 + s\tau_{\theta } } \right) + K^{ * } \left( {1 + s\tau_{\upsilon } } \right)} \right]D^{2} \overline{\theta }$$
(39)

When \(K^{ * } = 0\), we can obtain the heat conduction equation for the dual-phase lag:

$$\left[ {1 + s\tau_{q} + \frac{{\tau_{q}^{2} s^{2} }}{2}} \right]\left[ {s\overline{\theta } + \varepsilon_{1} CsD\overline{u} - \varepsilon_{2} e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)x}} } \right] = \left( {1 + s\tau_{\theta } } \right)D^{2} \overline{\theta }$$
(40)

For the LS model (as a special case of the dual-phase lag model with \(\tau_{\theta } = 0\) and retaining the first term of \(\tau_{q}\)), Eq. (38) can be written as:

$$\left[ {1 + s\tau_{q} } \right]\left[ {s\overline{\theta } + \varepsilon_{1} CsD\overline{u} - \varepsilon_{2} e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)x}} } \right] = D^{2} \overline{\theta }$$
(41)

In the Laplace transformation domain, the boundary condition for this problem is:

$$\left. {\overline{u}\left( {x,{\text{t}}} \right)} \right|_{x = 0,l} = 0,\;\left. {\frac{{\partial \overline{\theta }\left( {x,t} \right)}}{\partial x}} \right|_{x = 0,l} = 0$$
(42)

6 Solution in the Laplace Transform Domain

Combining Eqs. (34) and (38), and eliminating \(\overline{\theta }\), it follows that:

$$\left( {D^{4} - m_{1} D^{2} + m_{2} } \right)\overline{u}(x) = m_{3} e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)x}}$$
(43)

where

$$m_{1} = \frac{{s^{2} \left[ {\beta + M(G)\left( {A + \beta (e_{0} a)^{2} s^{2} - C^{2} \varepsilon_{1} } \right)} \right]}}{{A + \beta (e_{0} a)^{2} s^{2} }},\;m_{2} = \frac{{M\left( G \right)\beta s^{4} }}{{A + \beta (e_{0} a)^{2} s^{2} }},\;\eta_{4} = \frac{{\left( {Ak_{2} - C\psi_{4} } \right)}}{{1 - \left( {e_{0} a} \right)^{2} k_{2}^{2} }}$$

\(m_{3} = \frac{{M\left( G \right)\varepsilon_{1} C}}{{A + \beta (e_{0} a)^{2} s^{2} }}\frac{{s^{2} }}{\upsilon },\;M\left( G \right) = \frac{{1 + G\left( {s,\tau_{q} } \right) + \frac{{\tau_{q} s}}{2}G\left( {s,\tau_{q} } \right)}}{{s\left( {1 + G\left( {s,\tau_{\theta } } \right)} \right) + K^{ * } \left( {1 + G\left( {s,\tau_{\upsilon } } \right)} \right)}}\)

The general solution of \(\overline{u} \left( {x,s} \right)\) is expressed in the following form:

$$\overline{u} \left( {x,s} \right) = u_{1} e^{{ - k_{1} x}} + u_{2} e^{{k_{1} x}} + u_{3} e^{{ - k_{2} x}} + u_{4} e^{{k_{2} x}} + u_{5} e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)x}}$$
(44)

where \(u_{5} = {{m_{3} } \mathord{\left/ {\vphantom {{m_{3} } {\left[ {\left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)^{4} - m_{1} \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)^{2} + m_{2} } \right]}}} \right. \kern-0pt} {\left[ {\left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)^{4} - m_{1} \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)^{2} + m_{2} } \right]}}\), \(k_{1}\) and \(k_{2}\) are the roots of the characteristic equation \(k^{4} - m_{1} k^{2} + m_{2} = 0\). The expression of the characteristic root is:

$$k_{1} = \sqrt {\frac{{m_{1} + \sqrt {m_{1}^{2} - 4m_{2} } }}{2}} ,\;k_{2} = \sqrt {\frac{{m_{1} - \sqrt {m_{1}^{2} - 4m_{2} } }}{2}}$$
(45)

Similarly, the general solution for \(\overline{\theta }\left( {x,s} \right)\) and \(\overline{\sigma }\left( {x,s} \right)\) takes the following form:

$$\overline{\theta }\left( {x,s} \right) = \theta_{1} e^{{ - k_{1} x}} + \theta_{2} e^{{k_{1} x}} + \theta_{3} e^{{ - k_{2} x}} + \theta_{4} e^{{k_{2} x}} + \theta_{5} e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)x}}$$
(46)
$$\begin{gathered} \overline{\sigma }\left( {x,s} \right) = \sigma_{1} e^{{ - k_{1} x}} + \sigma_{2} e^{{k_{1} x}} + \sigma_{3} e^{{ - k_{2} x}} + \sigma_{4} e^{{k_{2} x}} + \sigma_{5} e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)x}} \hfill \\ \hfill \\ \end{gathered}$$
(47)

Substituting Eqs. (44), (46) and (47) into (34) and (35), respectively, it follows that:

$$\sigma_{i} = \eta_{i} u_{i} ,\;\theta_{i} = \psi_{i} u_{i}$$
(48)

where

\(\psi_{1} = \frac{{ - \left( {Fk_{1}^{2} - \beta s^{2} } \right)}}{{Ck_{1} }}\), \(\psi_{2} = \frac{{\left( {Fk_{1}^{2} - \beta s^{2} } \right)}}{{Ck_{1} }}\), \(\psi_{3} = \frac{{ - \left( {Fk_{2}^{2} - \beta s^{2} } \right)}}{{Ck_{2} }}\), \(\psi_{4} = \frac{{\left( {Fk_{2}^{2} - \beta s^{2} } \right)}}{{Ck_{2} }}\),

$$\eta_{1} = \frac{{ - \left( {Ak_{1} + C\psi_{1} } \right)}}{{1 - \left( {e_{0} a} \right)^{2} k_{1}^{2} }},\;\eta_{2} = \frac{{\left( {Ak_{1} - C\psi_{2} } \right)}}{{1 - \left( {e_{0} a} \right)^{2} k_{1}^{2} }},\;\eta_{3} = \frac{{ - \left( {Ak_{2} + C\psi_{3} } \right)}}{{1 - \left( {e_{0} a} \right)^{2} k_{2}^{2} }},\;\eta_{4} = \frac{{\left( {Ak_{2} - C\psi_{4} } \right)}}{{1 - \left( {e_{0} a} \right)^{2} k_{2}^{2} }}$$
(49)
$$\theta_{5} = \frac{{u_{5} s\left( {\beta \upsilon^{2} - F} \right)}}{C\upsilon },\;\sigma_{5} = \frac{{ - \left( {A\left( {{{\text{s}} \mathord{\left/ {\vphantom {{\text{s}} \upsilon }} \right. \kern-0pt} \upsilon }} \right)u_{5} + C\theta_{5} } \right)}}{{1 - \left( {e_{0} a} \right)^{2} ({s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon })^{2} }},\;F = A + \beta \left( {e_{0} a} \right)^{2} s^{2}$$

Now, applying the boundary condition (42) to determine \(u_{i} \left( {i = 1,2,3,4} \right)\), bringing the boundary condition into Eqs. (44) and (46) yields:

$$\begin{gathered} \left( {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ {e^{{ - k_{1} l}} } & {e^{{k_{1} l}} } & {e^{{ - k_{2} l}} } & {e^{{k_{2} l}} } \\ {\frac{{\left( {Fk_{1}^{2} - \beta s^{2} } \right)}}{C}} & {\frac{{\left( {Fk_{1}^{2} - \beta s^{2} } \right)}}{C}} & {\frac{{\left( {Fk_{2}^{2} - \beta s^{2} } \right)}}{C}} & {\frac{{\left( {Fk_{2}^{2} - \beta s^{2} } \right)}}{C}} \\ {\frac{{\left( {Fk_{1}^{2} - \beta s^{2} } \right)}}{C}e^{{ - k_{1} l}} } & {\frac{{\left( {Fk_{1}^{2} - \beta s^{2} } \right)}}{C}e^{{k_{1} l}} } & {\frac{{\left( {Fk_{2}^{2} - \beta s^{2} } \right)}}{C}e^{{ - k_{2} l}} } & {\frac{{\left( {Fk_{2}^{2} - \beta s^{2} } \right)}}{C}e^{{k_{2} l}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ {u_{3} } \\ {u_{4} } \\ \end{array} } \right) \hfill \\ = - u_{5} \left( {\begin{array}{*{20}c} 1 \\ {e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)l}} } \\ {\frac{{s^{2} \left( {F - \beta \upsilon^{2} } \right)}}{{C\upsilon^{2} }}} \\ {\frac{{s^{2} \left( {F - \beta \upsilon^{2} } \right)}}{{C\upsilon^{2} }}e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)l}} } \\ \end{array} } \right) \hfill \\ \end{gathered}$$
(50)

By solving Eq. (50), we can obtain:

$$\begin{gathered} u_{1} = \frac{{\left( {e^{{k_{1} l}} - e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)l}} } \right)\left( {k_{2}^{2} - {{s^{2} } \mathord{\left/ {\vphantom {{s^{2} } {\upsilon^{2} }}} \right. \kern-0pt} {\upsilon^{2} }}} \right)}}{{\left( {e^{{k_{1} l}} - e^{{ - k_{1} l}} } \right)\left( {k_{1}^{2} - k_{2}^{2} } \right)}}u_{5} ,\;\;\;\;\;u_{2} = - \frac{{\left( {e^{{ - k_{1} l}} - e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)l}} } \right)\left( {k_{2}^{2} - {{s^{2} } \mathord{\left/ {\vphantom {{s^{2} } {\upsilon^{2} }}} \right. \kern-0pt} {\upsilon^{2} }}} \right)}}{{\left( {e^{{k_{1} l}} - e^{{ - k_{1} l}} } \right)\left( {k_{1}^{2} - k_{2}^{2} } \right)}}u_{5} , \hfill \\ u_{3} = - \frac{{\left( {e^{{k_{2} l}} - e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)l}} } \right)\left( {k_{1}^{2} - {{s^{2} } \mathord{\left/ {\vphantom {{s^{2} } {\upsilon^{2} }}} \right. \kern-0pt} {\upsilon^{2} }}} \right)}}{{\left( {e^{{k_{2} l}} - e^{{ - k_{2} l}} } \right)\left( {k_{1}^{2} - k_{2}^{2} } \right)}}u_{5} ,\;\;\;\;\;u_{4} = \frac{{\left( {e^{{ - k_{2} l}} - e^{{ - \left( {{s \mathord{\left/ {\vphantom {s \upsilon }} \right. \kern-0pt} \upsilon }} \right)l}} } \right)\left( {k_{1}^{2} - {{s^{2} } \mathord{\left/ {\vphantom {{s^{2} } {\upsilon^{2} }}} \right. \kern-0pt} {\upsilon^{2} }}} \right)}}{{\left( {e^{{k_{2} l}} - e^{{ - k_{2} l}} } \right)\left( {k_{1}^{2} - k_{2}^{2} } \right)}}u_{5} , \hfill \\ \end{gathered}$$
(51)

7 Laplace Inverse Transform

To obtain the distribution of temperature, displacement, and stress in the physical domain, Laplace inverse transformations of \(\overline{\theta }\), \(\overline{u}\), and \(\overline{\sigma }\) are required. Since the expressions for \(\overline{\theta }\), \(\overline{u}\), and \(\overline{\sigma }\) are complex, we use the Riemann-sum (Tzou 1995b) approximation method for its numerical inverse transformation. With the help of this method, any function \(\overline{f} \left( {x,s} \right)\) in the Laplace domain can be transformed into the time domain with the following equation:

$$f\left( {x,t} \right) = \frac{{e^{\beta t} }}{t}\left[ {\frac{1}{2}\overline{f}\left( {x,\beta } \right) + {\text{Re}} \sum\limits_{n = 2}^{N} {\overline{f}\left( {x,\beta + \frac{in\pi }{t}} \right)} \left( { - 1} \right)^{n} } \right]$$
(52)

where, \({\text{Re}}\) is the real part, \(i\) is the imaginary unit. To be able to converge faster, a large number of numerical experiments have shown that \(\beta\) needs to satisfy the relation \(\beta t \approx 4.7\) (Tzou 1995b).

8 Numerical Results and Discussion

In this subsection, our main purpose is to illustrate the numerical results of the analytical expressions for each physical quantity after Laplace inverse transformation. Here, we consider the material properties of copper with the following relevant material parameters (Ezzat et al. 2017b):

$$K = 386{\text{N}} /Ks,\,\alpha_{t} = 1.78 \times 10^{ - 5} {\text{K}}^{ - 1} ,\;C_{E} = 383.1{\text{m}}^{2} /K,\;\rho = 8954{\text{kg}} /m^{3} ,\;T_{0} = 293{\text{K}} ,$$
$$\varepsilon_{0} = \frac{{10^{ - 9} }}{36\pi }{{{\text{C}}^{2} } \mathord{\left/ {\vphantom {{{\text{C}}^{2} } {Nm^{2} }}} \right. \kern-0pt} {Nm^{2} }},\;e_{0} a = 0.045,\;\tau_{q} = 0.05{\text{s}} ,\;\tau_{\theta } = 0.07{\text{s}} ,\;\tau_{\upsilon } = 0.09{\text{s}} ,\;Q_{0} = 10,\;l = 10,$$
$$\mu_{e} = 3.86 \times 10^{10} {\text{Nm}}^{ - 1} ,\;\lambda_{e} = 7.76 \times 10^{10} {\text{Nm}}^{ - 1} ,\;\mu_{0} = 0.1{\text{s}},\;\lambda_{0} = 0.05{\text{s}} ,\;H_{0} = \frac{{10^{ - 7} }}{4\pi }Am^{ - 1}$$

8.1 Numerical Verification

In Sect. 1, we simplify the model of this paper to that of Bayones et al. (2023) to verify the accuracy of the proposed model.

In this section, we have chosen to compare the present study with Bayones et al. (2023) in the absence of viscosity and magnetic fields. From Fig. 1 we can see that when the material study parameters, boundary conditions, and study objects are the same as in Bayones et al. (2023), the distributions of dimensionless temperatures and dimensionless stresses in Fig. 1 are the same as in Bayones et al. (2023).

Fig. 1
figure 1

The values of temperature \(\theta\) and stress \(\sigma\) are comparison with those of Bayones et al. (2023). a temperature distribution, b stress distribution

Full size image

Next, the paper is divided into the following five subsections that discuss the variation of dimensionless temperature, displacement and stress for each case.

8.2 Effect of Viscosity and MDD in the Absence of a Magnetic Field

In Sect. 2, the first case (Fig. 2) we study the effects of MDD and viscosity, when no magnetic field is present and time remains constant. From Fig. 2 we can see that the speed of the moving heat source plays an important role in all distributions. At the same time, due to the increase in the speed of the moving heat source, the time to release heat per unit length of the rod is shorter, so less heat is released, and the temperature inside the rod decreases. As the temperature inside the rod decreases, the thermal expansion and deformation of the rod are reduced, and therefore the displacement and compressive stress in the rod are subsequently reduced. However, since the ends are fixed, this results in the greatest deformation from thermal expansion near the rod end. As a result, the displacements and compressive stress achieve their maximum values close to the end of the rod. In addition to this, we can see from Fig. 2 that the temperature inside the rod decreases in the presence of memory-dependent effect as compared to the case where memory-dependent effect is not present. On the contrary, when viscosity is present, the temperature inside the rod increases, and the thermal expansion deformation and thermal compressive stresses of the rod increase consequently.

Fig. 2
figure 2

Effect of MDD and viscosity in the absence of magnetic field at \(t = 1\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image

In the second case (Fig. 3), we investigated the effects of MDD and viscosity, when no magnetic field is present and the velocity of the moving heat source remains constant. From Fig. 3 we can see that time plays an equally important role in all distributions. With the velocity held constant, the longer the time the slower the heat source and the deeper the region of thermal disturbance develops in the rod. Therefore, the temperature increases with time. However, due to the action of the applied heat source, thermal expansion and deformation occur in the rod. With the increase of time, the thermal expansion and deformation inside the rod increase, and the displacement becomes larger. Since the ends of the rod are fixed, the compressive stress in the rod increases with the displacement. It is also clear from Fig. 3 that temperature, displacement, and stress are all reduced when memory-dependent effect are present compared to when they are absent. On the contrary, the presence of viscosity increases the value of the physical quantity in the rod.

Fig. 3
figure 3

Effect of MDD and viscosity in the absence of magnetic field at \(\upsilon = 1\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image

8.3 Effect of Viscosity and MDD in the Presence of a Magnetic Field

In Sect. 3, the first case (Fig. 4) demonstrates the effect of MDD and viscosity, when the magnetic field is present and time is kept constant. From Fig. 4 we can see that as the speed of the moving heat source increases, the temperature inside the rod gradually increases, which leads to an increase in the thermal expansion and deformation of the rod, and a gradual increase in the displacement and stress in the rod. Similarly, it is evident from Fig. 4 that the MDD predicts smaller temperatures, displacements, and stresses when a magnetic field is present. Conversely, the presence of viscosity has a tendency to increase the distribution of physical quantities within the rod compared to the absence of viscosity.

Fig. 4
figure 4

Effect of MDD and viscosity in the presence of magnetic field at \(t = 1\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image

In the second case (Fig. 5), we investigated the effect of MDD and viscosity when the magnetic field is present and the speed of the moving heat source is kept constant. From Fig. 5, it can be seen that temperature, displacement and strain show a positive correlation with time, respectively. It is also evident that smaller physical field distributions can be obtained when MDD are present. In addition, the presence of viscosity is able to obtain a larger physical quantity.

Fig. 5
figure 5

Effect of MDD and viscosity in the presence of magnetic field at \(\upsilon = 1\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image

8.4 Effect of Viscosity and Magnetic Field in the Presence of MDD

In Sect. 4, for the first case (Fig. 6) we investigate the influence of the magnetic field and viscosity on each physical quantity when there is a memory-dependent effect and time is kept constant. From Fig. 6 we can see that faster heat source speeds result in smaller temperatures. This is because in as the speed of the moving heat source increases, the time per unit length of the rod to release heat is short, the less heat the rod releases, the smaller the rod temperature rises. Due to the decrease in rod temperature, the thermal expansion deformation of the rod becomes smaller, and the displacement and hot compressive stress in the rod also decrease. We can also see from Fig. 6 that the presence of an applied magnetic field has no significant effect on the temperature. In addition, it is not difficult to see that the presence of magnetic fields has a significant effect on displacement and stress. Compared to the absence of a magnetic field, the presence of a magnetic field can significantly reduce the displacement and thermal stress within the rod. Similarly, from Fig. 6, it is clear that the presence of viscosity tends to significantly increase the physical quantity in the rod compared to the absence of viscosity.

Fig. 6
figure 6

Effect of magnetic field and viscosity in the presence of memory-dependent effects at \(t = 1\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image

In the second case (Fig. 7), we study the effect of the magnetic field and viscosity when the MDD is present and the speed of the moving heat source is kept constant. From Fig. 7, we can clearly see that the heat absorbed by the unit rod increases at longer times, and the thermal expansion and deformation in the rod increases, so the displacement and thermal compressive stresses in the rod increase. As can be seen in Fig. 7, when the speed of the moving heat source is constant, the variation of the temperature inside the rod is almost unaffected by the magnetic field. However, the presence of magnetic field significantly affects the displacement and thermal stress inside the rod. The presence of magnetic field was able to obtain smaller displacements and thermal stresses. On the contrary, the presence of viscosity has a tendency to increase the physical quantity under study.

Fig. 7
figure 7

Effect of magnetic field and viscosity in the presence of memory-dependent effects at \(\upsilon = 1\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image

8.5 Impact of Delay Time

In Sect. 5, we examine the effects of three delay times in memory-dependent TPL models, as shown in Figs. 8, 9 and 10. From Figs. 8, 9 and 10 we can clearly see that in all the distributions, the variation of the delay time has a significant effect on the distribution of each physical field.

Fig. 8
figure 8

Effect of delay time \(\tau_{\theta }\) in absence of magnetic field at \({\text{t}} = 2\), \(\upsilon = 2\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image
Fig. 9
figure 9

Effect of delay time \(\tau_{\upsilon }\) in the absence of magnetic field at \({\text{t}} = 2\), \(\upsilon = 2\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image
Fig. 10
figure 10

Effect of delay time \(\tau_{q}\) in absence of magnetic field at \({\text{t}} = 2\), \(\upsilon = 2\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image

From Fig. 8 we can see that the physical field inside the rod varies with the delay time of the temperature gradient \(\tau_{\theta }\). As the delay time of the temperature gradient increases, the temperature and compressive stresses in the rod increase. From Fig. 9 we can clearly see that the physical quantities inside the rod fluctuate significantly with the delay time of the thermal displacement gradient \(\tau_{\upsilon }\). As the delay time of the heat displacement gradient increases, the physical quantity inside the rod decreases significantly. On the contrary, we can see from Fig. 10 that the physical quantity inside the rod increases significantly with the increase of the delay time of the heat flow vector \(\tau_{q}\).

8.6 Impact of Nonlocal Effects

For Sects. 2–5 (Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10) we take \(e_{0} a = 0\), i.e., the local thermoelasticity model. In Sect. 6, we study the effect of nonlocal effects when there is no memory-dependent effect, viscosity, and magnetic field (the nonlocal parameter \({\text{e}}_{0} {\text{a}}\) is taken to be 0.045).

In this section, in the first case we study the influence of nonlocal effects under different moving heat sources. From Fig. 11 we can clearly see that the physical quantities in the rod increase with the speed of the moving heat source. In addition, from Fig. 11 we can also see that the values of displacements and stresses in the nonlocal elasticity theory are smaller than those under the local theory. In addition to this, we can also observe that there is almost no difference in the distribution of temperature under the influence of nonlocal effects. This is due to the fact that we have introduced the nonlocal terms into the constitutive equations rather than into the heat conduction equations, and hence there is no significant difference in the temperature distribution within the rod.

Fig. 11
figure 11

The influence of non-local effects, in the absence of magnetic field and memory-dependent effects at \({\text{t}} = 1\), \(\upsilon = 1\). a temperature distribution, b displacement distribution, c stress distribution

Full size image

In the second case, we investigate the influence of non-local effects when time is different. From Fig. 12 we can clearly see that the physical quantities in the rod change significantly with increasing time. As time increases, the values of temperature, displacement and stress in the rod gradually increase. What is also evident is that non-local effects have little effect on the change in temperature. In addition, the values of displacements and stresses are smaller under the non-localised theory as compared to the localised theory.

Fig. 12
figure 12

Influence of non-local effects in the absence of magnetic fields and memory-dependent effects at \({\text{t}} = 1\), \(\upsilon = 1\). a temperature distribution, b displacement distribution, and c stress distribution

Full size image

9 Conclusions

In this paper, the thermoelastic response of a viscoelastic rod subjected to a magnetic field and thermal shock is analysed using the Kelvin-Voigt viscoelastic model, three-phase lag heat transfer model, and the Eringen nonlocal theory. The control equations of the problem are solved by using the Laplace transform and the inverse numerical transformation, and the dimensionless temperature, displacement and stress are obtained and displayed graphically. The results show that:

  1. (1)

    Moving heat source velocity and time had a significant effect on all distributions. At smaller moving heat source velocities and larger times, the physical quantities in the rods increased significantly.

  2. (2)

    Magnetic fields and non-local effects have almost no effect on temperature, but significantly affect displacement and thermal stresses. The presence of magnetic field significantly reduces the displacement and stress in the rod. On the contrary the presence of non-local effects significantly enhances the displacement and stress in the rod.

  3. (3)

    The presence of viscosity has a tendency to increase the distribution of physical quantities within the rod compared to the absence of viscosity.

  4. (4)

    Memory-dependent effects reduce the distribution of the physical quantities considered compared to the absence of memory-dependent effects.

  5. (5)

    Changes in the three delay times of the memory-dependent TPL model will have different effects on all distributions.