1 Introduction

Todays, new materials such as functionally graded materials (FGMs), smart materials, smart composites, and nanofluids are the focus of many articles (Ahmad et al. 2019; Ahmad et al. 2021a, b; Ahmad 2023). FGM is one of these that has attracted a lot of attention in recent years and many articles have been published in this field (Singh and Harsha 2020; Alibeigloo 2021; Saadatfar et al. 2023a, b; Saadatfar et al. 2023a, b). Functionally graded magneto-electro-elastic material is a type of smart composite structure that can convert the energy from mechanical to magnetic or electric type and vice versa. These materials have many potential applications in important industries, such as aerospace, turbine rotor designing, magnetic storage, smart structures, and many other fields (Chang et al. 2020; Saadatfar and Zarandi 2020a, b; Saadatfar 2021a, b; Ly et al. 2022).

Several reported articles investigate the stresses and deformation of rotating disks. Sahni and Sahni (2015) examined a rotating FGM disk with variable thickness and considered external pressure. Thermoelastic analysis of an FGM rotating disk has been done by Dai and Dai (2016). In this analysis, the thickness and angular speed of the disk have been considered to be variable. Hosseini et al. (2016) analyzed the stress of rotating FGM nanodisks with variable thickness profiles. Rattan et al. (2016) investigated the creep behavior of an isotropic disk made of composite. In this work, the thermal residual stress has been considered. Dai et al. (2017) investigated a rotating functionally graded piezoelectric disk located in a hygrothermal field. Creep analysis of an FGM rotating disk considering the Tresca criteria has been done by Khanna et al. (2017). The results of this analysis have been compared to von Mises criteria results. Thawait et al. (2017) used the element-based material grading for the elastic analysis of an FGM rotating disk with non-constant thickness. Bose and Rattan (2018) investigated the influence of thermal gradation on the creep behavior of an FGM rotating disk. Designing FGM rotating disks by weight optimization has been done by Khorsand and Tang (2018). The designed disks have been examined under thermomechanical loads. Considering the rule of mixture, the stress and deformation of an FGM rotating disk have been analyzed by Madan et al. (2018). Hayat et al. (2018) examined the flow of a nanofluid due to a rotating disk. In this analysis, the influences of chemical reaction and heat generation have been considered and the final ordinary differential equation has been solved using homotopy analysis method. Hosseini et al. (2019) studied rotating FGM micro/nanodisks considering a variable thickness profile. Li et al. (2019) studied the transient response of a rotating turbine disk experimentally. In this examination, the thermal loading management strategy has been used. Madan et al. (2019) investigated the limit of angular speed of a rotating disk made of functionally graded material using temperature-dependent/independent mechanical properties. The deformation of a rotating composite disk due to the thermal gradient has been analyzed by Kaur et al. (2020). Saadatfar and Zarandi (2020a, b) examined the mechanical behaviors of a rotating annular plate made of FGPM considering variable thickness. Sondhi et al. (2020) analyzed the stress and deformation of an FGM disk with variable thickness considering orthotropic structure and rotation. Ahmad et al. (2021a, b) modeled the effect of the magnetic field on a rotating disk flow considering heat transfer. The effects of angular deceleration on the behaviors of multilayer disks made of functionally graded material have been investigated by Eldeeb et al. (2021). Responses of an FGPM cylinder considering hygrothermal loading have been examined by Saadatfar (2021a, b). Saber and Abd_Elsalam (2022) presented a theoretical model for the investigation of the performance of FGM rotating disks.

There are many works on stress analysis of FGMEE structures in the literature. Akbarzadeh and Chen (2012) analyzed FGMEE rotating cylinders resting on an elastic foundation. The considered cylinders were analyzed under hygrothermal loading. Gupta and Singh (2016) modeled the creep of an FGM rotating disk mathematically considering the variable thickness. Dai and Dai (2017) analyzed a rotating FGMEE disk in thermal environment. Dai et al. (2019) examined a porous FGMEE disk in hygrothermal environment and analyzed its mechanical behaviors. Ebrahimi et al. (2019) studied the effect of porosity on dynamic characteristics of the heterogeneous FGMEE plates. Investigation of influences of porosity, thickness profile, and rotational acceleration on the behaviors of an FGMEE rotating disk has been done by Saadatfar et al. (2021). The analyzed disk was located in a constant magnetic field. Zhang et al. (2022) studied the static and dynamic behaviors of FGMEE shells and plates. Zhou et al. (2022) analyzed the static behaviors of inhomogeneous FGMEE plates in thermal environment. The element-free Galerkin method has been used in this analysis.

The literature review shows stress analysis of rotating variable thickness FGMEE disks with a convection heat transfer, an internal heat source, and solar radiation for the case that heat convection and conduction coefficients are dependent on temperature and radius has not been analyzed. So, the novelties of this article are considering conduction and convection heat transfer coefficients as functions of temperature and radius, and considering the effects of heat transfer including the conduction, convection, solar radiation, and internal heat source. The power-law function of the radius was considered for material properties. The obtained nonlinear differential equation was solved using DTM. Then, the equilibrium equation was derived and solved analytically to achieve stresses, displacement, electric and magnetic potential distributions.

2 Thermal Equations

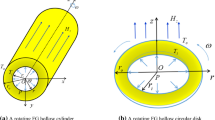
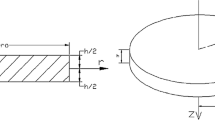
In this article, a variable thickness FGMEE disk has been considered as shown in Fig. 1. The rotation of the disk is around its Z-axis. Four types of heat transfer phenomena are considered: conduction, convection, internal heat generation, and solar radiation. Regarding symmetry and plane stress conditions, nonzero components of displacement and temperature are functions of radius. A power-law function of the radius has been used for the thickness profile of the disk:

$$h\left( r \right) = y_{0} r^{ - \Omega } .$$
(1)
Fig. 1
figure 1

Schematic of the rotating FGMEE disk

Full size image

2.1 Thermal Equations Derivation

In thermal analysis, there are four methods for heat exchange, which are heat conduction, heat convection, internal heat generation, and solar radiation. It is important to mention that convective and conductive heat transfer coefficients change with temperature and radius. According to the energy balance equation, we have (Incropera et al. 1996):

$$\frac{{\text{d}}}{{{\text{d}}r}}\left( {{\text{KA}}_{c} \frac{{{\text{d}}T}}{{{\text{d}}r}}} \right){\text{d}}r - h\left( {T - T_{{\text{a}}} } \right){\text{d}}A_{s} + \alpha_{s} G_{s} {\text{d}}A_{s} - \varepsilon \sigma \left( {T^{4} - T_{a}^{4} } \right){\text{d}}A_{s} + \dot{q}{\text{d}}V = 0.$$
(2)

where

$$K = k_{0} r^{\gamma } \left( {1 + \beta \theta } \right),$$
(3)
$$h = h_{0} \theta^{\Gamma } \left( {a + b\omega r} \right),$$
(4)
$$\dot{q} = q_{0} \left( {1 + e_{0} \theta } \right).$$
(5)

For the simplification, the following variable change is considered:

$$\theta = \frac{{T - T_{b} }}{{T_{{\text{a}}} - T_{b} }},$$
(6)
$$\eta = \frac{{r - r_{i} }}{{r_{o} - r_{i} }}.$$
(7)

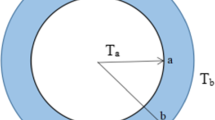
where Tb and Ta are the inner radius temperature of the disk and ambient air temperature, respectively. The expression (αsGsdAs) indicates the amount of solar radiation received by the disk. Also, the expression (εσ(T4− Ta4)dAs) refers to the reflected radiation of the disk. Using the introduced parameters and simplifying, Eq. (2) can be written as:

$$\begin{aligned} \frac{{\left( {T_{{\text{a}}} - T_{b} } \right)}}{{\left( {r_{o} - r_{i} } \right)^{2} }} & \cdot \frac{{\text{d}}}{{{\text{d}}\eta }}\left\{ {y_{0} \left( {1 + \beta \theta } \right)\left( {r_{i} + \eta \left( {r_{o} - r_{i} } \right)} \right)^{\gamma + 1 - \Omega } \frac{d\theta }{{d\eta }}} \right\} \\ & - \frac{{h_{0} }}{{k_{0} }}\theta^{\Gamma } \left( {\theta - 1} \right)\left( {T_{{\text{a}}} - T_{b} } \right)\left( {r_{i} + \eta \left( {r_{o} - r_{i} } \right)} \right)\left( {a + b\omega \left( {r_{i} + \eta \left( {r_{o} - r_{i} } \right)} \right)} \right) \\ & + \left( {r_{i} + \eta \left( {r_{o} - r_{i} } \right)} \right)\left( {\frac{{\alpha_{s} G_{s} }}{{k_{0} }} - \frac{\varepsilon \sigma }{{k_{0} }}\left( {\left( {\theta \left( {T_{a} - T_{b} } \right) + T_{b} } \right)^{4} - T_{{\text{a}}}^{4} } \right)} \right) \\ & + \frac{{q_{0} y_{0} }}{{k_{0} }}\left( {r_{i} + \eta \left( {r_{o} - r_{i} } \right)} \right)^{1 - \Omega } \left( {1 + e_{0} \theta } \right) = 0. \\ \end{aligned}$$
(8)

The obtained differential equation (Eq. (8)) is a second-order type. Therefore, it will be important to use two boundary conditions:

$$r = r_{i} :\eta = 0 \to T = T_{b} :\theta = 0,$$
(9)
$$r = r_{o} :\eta = 1 \to T = T_{o} :\left( {T_{a} - T_{b} } \right)\theta + T_{b} = T_{o} .$$
(10)

According to the introduced boundary conditions, the internal and external temperature of the disk will be constant.

2.2 Solution of Nonlinear Thermal Differential Equation

The well-known DTM was used for solving the nonlinear heat transfer differential equation in Eq. (8). This method creates a polynomial analytical approach for differential equations. DTM is an iterative procedure for gaining analytical Taylor series solutions for differential equations. The necessary functions of this method are presented in Appendix. Now, the final differential transformation of Eq. (8) can be expressed as:

$$\begin{gathered} \left\{ {\sum\limits_{x = 0}^{k} {\sum\limits_{v = 0}^{x} {H_{1} \left[ v \right]} } \left( {\beta \theta \left[ {x - v} \right] + \delta \left( {x - v} \right)} \right)\left( {\left( {k - x + 1} \right)\theta \left[ {k - x + 1} \right]} \right)} \right\} \hfill \\ \quad + \left\{ {\sum\limits_{x = 0}^{k} {\sum\limits_{v = 0}^{x} {H_{2} \left[ v \right]} } \left( {\left( {x - v + 1} \right)\theta \left[ {x - v + 1} \right]} \right)\left( {\left( {k - x + 1} \right)\theta \left[ {k - x + 1} \right]} \right)} \right\} \hfill \\ \quad - \left\{ {\sum\limits_{x = 0}^{k} {\sum\limits_{v = 0}^{x} {H_{3} \left[ v \right]} } \left( {\beta \theta \left[ {x - v} \right] + \delta \left( {x - v} \right)} \right)\left( {\left( {k - x + 1} \right)\theta \left[ {k - x + 1} \right]} \right)} \right\} \hfill \\ \quad + \left\{ {\sum\limits_{x = 0}^{k} {\sum\limits_{v = 0}^{x} {H_{4} \left[ v \right]} } \left( {\beta \theta \left[ {x - v} \right] + \delta \left( {x - v} \right)} \right)\left( {\left( {k - x + 1} \right)\left( {k - x + 2} \right)\theta \left[ {k - x + 2} \right]} \right)} \right\} \hfill \\ \quad - \left\{ {\sum\limits_{x = 0}^{k} {\sum\limits_{v = 0}^{x} {\sum\limits_{r = 0}^{v} {\sum\limits_{w = 0}^{r} {H_{7} \left[ w \right]} } } } \theta \left[ {r - w} \right]\theta \left[ {v - r} \right]\theta \left[ {x - v} \right]\left( {\theta \left[ {k - x} \right] - \delta \left( {k - x} \right)} \right)} \right\} \hfill \\ \quad + \left\{ {H_{5} \left[ k \right]} \right\} \hfill \\ \quad - \left\{ {\sum\limits_{x = 0}^{k} {\sum\limits_{v = 0}^{x} {\sum\limits_{r = 0}^{v} {\sum\limits_{w = 0}^{r} {H_{6} \left[ w \right]\left( {\left( {T_{a} - T_{b} } \right)\theta \left[ {r - w} \right] + T_{b} \delta \left( {r - w} \right)} \right)\left( {\left( {T_{a} - T_{b} } \right)\theta \left[ {v - r} \right] + T_{b} \delta \left( {v - r} \right)} \right)} } } } } \right. \hfill \\ \quad \left. {\left( {\left( {T_{a} - T_{b} } \right)\theta \left[ {x - v} \right] + T_{b} \delta \left( {x - v} \right)} \right)\left( {\left( {T_{a} - T_{b} } \right)\theta \left[ {k - x} \right] + T_{b} \delta \left( {k - x} \right)} \right)} \right\} \hfill \\ \quad + \left\{ {T_{a}^{4} H_{6} \left[ k \right]} \right\} + \left\{ {\sum\limits_{x = 0}^{k} {H_{8} \left[ x \right]} \left( {\delta \left( {k - x} \right) + e_{0} \theta \left[ {k - x} \right]} \right)} \right\} = 0. \hfill \\ \end{gathered}$$
(11)

where

$$\begin{aligned} H_{1} \left[ t \right] & = y_{0} \frac{{T_{a} - T_{b} }}{{\left( {r_{o} - r_{i} } \right)}}\left( {\gamma + 1} \right)\left( {r_{i} + t\left( {r_{o} - r_{i} } \right)} \right)^{\gamma - \Omega } , \\ H_{2} \left[ t \right] & = y_{0} \beta \frac{{T_{a} - T_{b} }}{{\left( {r_{o} - r_{i} } \right)^{2} }}\left( {r_{i} + t\left( {r_{o} - r_{i} } \right)} \right)^{\gamma - \Omega + 1} , \\ H_{3} \left[ t \right] & = y_{0} \Omega \frac{{T_{a} - T_{b} }}{{\left( {r_{o} - r_{i} } \right)}}\left( {r_{i} + t\left( {r_{o} - r_{i} } \right)} \right)^{\gamma - \Omega } , \\ H_{4} \left[ t \right] & = y_{0} \frac{{T_{a} - T_{b} }}{{\left( {r_{o} - r_{i} } \right)^{2} }}\left( {r_{i} + t\left( {r_{o} - r_{i} } \right)} \right)^{\gamma - \Omega + 1} , \\ H_{5} \left[ t \right] & = \frac{{\alpha_{s} G_{s} }}{{k_{0} }}\left( {r_{i} + t\left( {r_{o} - r_{i} } \right)} \right), \\ H_{6} \left[ t \right] & = \frac{\varepsilon \sigma }{{k_{0} }}\left( {r_{i} + t\left( {r_{o} - r_{i} } \right)} \right), \\ H_{7} \left[ t \right] & = \frac{{h_{0} }}{{k_{0} }}\left( {T_{a} - T_{b} } \right)\left( {r_{i} + t\left( {r_{o} - r_{i} } \right)} \right)\left( {a + b\omega \left( {r_{i} + t\left( {r_{o} - r_{i} } \right)} \right)} \right), \\ H_{8} \left[ t \right] & = \frac{{y_{0} q_{0} }}{{k_{0} }}\left( {r_{i} + t\left( {r_{o} - r_{i} } \right)} \right)^{1 - \Omega } . \\ \end{aligned}$$
(12)

where δ is the Dirac delta function and x, k, w, v, and r are the sigma boundaries used in the DTM method. The transformed boundary conditions can be expressed as:

$$\begin{aligned} \theta \left[ 0 \right] & = 0, \\ \theta \left[ 1 \right] & = \mu_{0} . \\ \end{aligned}$$
(13)

In the next step, the coefficients of the main dimensionless temperature function will be obtained using the iterative procedure; such as:

$$\begin{aligned} \theta \left[ 2 \right] & = \frac{ - 1}{{2r_{i}^{\gamma + 1} }}\{ \beta r_{i}^{\gamma + 1} \mu^{2} + r_{i}^{\gamma + 1} \Omega \mu - r_{i}^{\gamma } r_{o} \Omega \mu - r_{i}^{\gamma + 1} \gamma \mu + r_{i}^{\gamma } r_{o} \gamma \mu - r_{i}^{\gamma + 1} \mu + r_{i}^{\gamma } r_{o} \mu \\ & \quad + \frac{{\left( {r_{o} - r_{i} } \right)^{2} }}{{\left( {T_{a} - T_{b} } \right)y_{0} }}\frac{\varepsilon \sigma }{{k_{0} }}T_{a}^{4} r_{i}^{\Omega + 1} - \frac{{\left( {r_{o} - r_{i} } \right)^{2} }}{{\left( {T_{a} - T_{b} } \right)y_{0} }}\frac{\varepsilon \sigma }{{k_{0} }}T_{b}^{4} r_{i}^{\Omega + 1} \\ & \quad + \frac{{\left( {r_{o} - r_{i} } \right)^{2} }}{{\left( {T_{a} - T_{b} } \right)}}\frac{{q_{0} }}{{k_{0} }}r_{i} + \frac{{\left( {r_{o} - r_{i} } \right)^{2} }}{{\left( {T_{a} - T_{b} } \right)y_{0} }}\frac{{\alpha_{s} G_{s} }}{{k_{0} }}r_{i}^{\Omega + 1} \} . \\ \end{aligned}$$
(14)

Finally, we have:

$$\theta \left( \eta \right) = \sum\limits_{i = 1}^{U} {\theta \left[ i \right]} .\eta^{i} = \theta_{0} + \theta_{1} \eta + \theta_{2} \eta^{2} + \theta_{3} \eta^{3} + \theta_{4} \eta^{4} + \theta_{5} \eta^{5} .$$
(15)

Now, substituting θ and η, the temperature function was derived as:

$$T\left( r \right) = a_{0} + a_{1} r + a_{2} r^{2} + a_{3} r^{3} + a_{4} r^{4} + a_{5} r^{5} .$$
(16)

3 Stress Field Equations

3.1 Basic Equations

Stress–strain relations of FGMEE disk can be expressed as (Saadatfar 2019; Saadatfar et al. 2021):

$$\sigma_{r} = c_{11} \varepsilon_{rr} + c_{12} \varepsilon_{\theta \theta } + c_{13} \varepsilon_{zz} - e_{11} E_{r} - q_{11} H_{r} - \lambda_{1} T,$$
(17)
$$\sigma_{\theta } = c_{12} \varepsilon_{rr} + c_{22} \varepsilon_{\theta \theta } + c_{23} \varepsilon_{zz} - e_{12} E_{r} - q_{12} H_{r} - \lambda_{2} T,$$
(18)
$$\sigma_{z} = c_{13} \varepsilon_{rr} + c_{23} \varepsilon_{\theta \theta } + c_{33} \varepsilon_{zz} - e_{13} E_{r} - q_{13} H_{r} - \lambda_{3} T,$$
(19)
$$D_{r} = e_{11} \varepsilon_{rr} + e_{12} \varepsilon_{\theta \theta } + e_{13} \varepsilon_{zz} + \beta_{11} E_{r} + \varepsilon_{11} H_{r} + p_{1} T,$$
(20)
$$B_{r} = q_{11} \varepsilon_{rr} + q_{12} \varepsilon_{\theta \theta } + q_{13} \varepsilon_{zz} + \varepsilon_{11} E_{r} + d_{11} H_{r} + m_{1} T.$$
(21)

Considering the plane stress condition, we have:

$$\sigma_{z} = 0 \Rightarrow \varepsilon_{zz} = - \frac{{c_{13} }}{{c_{33} }}\varepsilon_{rr} - \frac{{c_{23} }}{{c_{33} }}\varepsilon_{\theta \theta } + \frac{{e_{13} }}{{c_{33} }}E_{r} + \frac{{q_{13} }}{{c_{33} }}H_{r} + \frac{{\lambda_{3} }}{{c_{33} }}T.$$
(22)

Replacing Eq. (22) in Eqs. (17), (18), (20), and (21) yields to:

$$\sigma_{r} = c^{\prime}_{11} \frac{\partial u}{{\partial r}} + c^{\prime}_{12} \frac{u}{r} + e^{\prime}_{11} \frac{\partial \phi }{{\partial r}} + q^{\prime}_{11} \frac{\partial \psi }{{\partial r}} - \lambda^{\prime}_{1} T,$$
(23)
$$\sigma_{\theta } = c^{\prime}_{12} \frac{\partial u}{{\partial r}} + c^{\prime}_{22} \frac{u}{r} + e^{\prime}_{12} \frac{\partial \phi }{{\partial r}} + q^{\prime}_{12} \frac{\partial \psi }{{\partial r}} - \lambda^{\prime}_{2} T,$$
(24)
$$D_{r} = e^{\prime}_{11} \frac{\partial u}{{\partial r}} + e^{\prime}_{12} \frac{u}{r} - \beta^{\prime}_{11} \frac{\partial \phi }{{\partial r}} - \varepsilon^{\prime}_{11} \frac{\partial \psi }{{\partial r}} + p^{\prime}_{1} T,$$
(25)
$$B_{r} = q^{\prime}_{11} \frac{\partial u}{{\partial r}} + q^{\prime}_{12} \frac{u}{r} - \varepsilon^{\prime}_{11} \frac{\partial \phi }{{\partial r}} - d^{\prime}_{11} \frac{\partial \psi }{{\partial r}} + m^{\prime}_{1} T.$$
(26)

where

$$\begin{aligned} c^{\prime}_{11} & = c_{11} - \frac{{c_{13}^{2} }}{{c_{33} }},\,\,\,\,\,\,\,\,\,\,\,\,c^{\prime}_{12} = c_{12} - \frac{{c_{13} c_{23} }}{{c_{33} }},\,\,\,\,\,\,\,\,\,\,c^{\prime}_{22} = c_{22} - \frac{{c_{23}^{2} }}{{c_{33} }}, \\ e^{\prime}_{11} & = e_{11} - \frac{{c_{13} e_{13} }}{{c_{33} }},\,\,\,\,\,\,\,e^{\prime}_{12} = e_{12} - \frac{{c_{23} e_{13} }}{{c_{33} }},\,\,\,\,\,\,\,\,\,\,q^{\prime}_{11} = q_{11} - \frac{{c_{13} q_{13} }}{{c_{33} }},\,\,\,\,\,q^{\prime}_{12} = q_{12} - \frac{{c_{23} q_{13} }}{{c_{33} }}, \\ \lambda^{\prime}_{1} & = \lambda_{1} - \frac{{c_{13} \lambda_{3} }}{{c_{33} }},\,\,\,\,\,\,\,\lambda^{\prime}_{2} = \lambda_{2} - \frac{{c_{23} \lambda_{3} }}{{c_{33} }},\,\,\,\,\,\,\,\,\,\,\,\,m^{\prime}_{1} = m_{1} + \frac{{\lambda_{3} q_{13} }}{{c_{33} }},\,\,\,\,\,\,\,\,\,\,\,d^{\prime}_{11} = d_{11} + \frac{{q_{13}^{2} }}{{c_{33} }}, \\ \beta^{\prime}_{11} & = \beta_{11} + \frac{{e_{13}^{2} }}{{c_{33} }},\,\,\,\,\,\,\varepsilon^{\prime}_{11} = \varepsilon_{11} + \frac{{e_{13} q_{13} }}{{c_{33} }},\,\,\,\,\,\,\,\,\,p^{\prime}_{1} = p_{1} + \frac{{e_{13} \lambda_{3} }}{{c_{33} }}. \\ \end{aligned}$$
(27)

For simplicity, all of the material properties are supposed to change based on a power-law function:

$$P = \overline{P}r^{\gamma } .$$
(28)

where \(\overline{P }\) is the material constant. Finally, the nonzero terms of the equilibrium equation of the rotating FGMEE disk are (Saadatfar 2021a, b):

$$\frac{{\partial \left( {h(r)\sigma_{r} } \right)}}{\partial r} + h(r)\frac{{(\sigma_{r} - \sigma_{\theta } )}}{r} + h(r)\rho r\omega^{2} = 0.$$
(29)

Also, the electrostatic and magnetostatic equations are in the following form:

$$\frac{{\partial \left( {h(r)D_{r} } \right)}}{\partial r} + \frac{{h(r)D_{r} }}{r} = 0,$$
(30)
$$\frac{{\partial \left( {h(r)B_{r} } \right)}}{\partial r} + \frac{{h(r)B_{r} }}{r} = 0.$$
(31)

The solution of Eqs. (30) and (31) can be introduced as:

$$D_{r} = \frac{{A_{1} }}{{r^{ - \Omega + 1} }} = e^{\prime}_{11} \frac{\partial u}{{\partial r}} + e^{\prime}_{12} \frac{u}{r} - \beta^{\prime}_{11} \frac{\partial \phi }{{\partial r}} - \varepsilon^{\prime}_{11} \frac{\partial \psi }{{\partial r}} + p^{\prime}_{1} T,$$
(32)
$$B_{r} = \frac{{A_{2} }}{{r^{ - \Omega + 1} }} = q^{\prime}_{11} \frac{\partial u}{{\partial r}} + q^{\prime}_{12} \frac{u}{r} - \varepsilon^{\prime}_{11} \frac{\partial \phi }{{\partial r}} - d^{\prime}_{11} \frac{\partial \psi }{{\partial r}} + m^{\prime}_{1} T.$$
(33)

where A1 and A2 are unknown constants. According to Eqs. (32) and (33), we can recognize the electric and magnetic potential equations as:

$$\frac{\partial \phi (r)}{{\partial r}} = L_{1} \frac{\partial u}{{\partial r}} + L_{2} \frac{u}{r} + L_{3} \frac{{A_{2} }}{{r^{\gamma - \Omega + 1} }} - L_{5} \frac{{A_{1} }}{{r^{\gamma - \Omega + 1} }} + L_{4} T,$$
(34)
$$\frac{\partial \psi (r)}{{\partial r}} = P_{1} \frac{\partial u}{{\partial r}} + P_{2} \frac{u}{r} + P_{3} \frac{{A_{1} }}{{r^{\gamma - \Omega + 1} }} - P_{5} \frac{{A_{2} }}{{r^{\gamma - \Omega + 1} }} + P_{4} T.$$
(35)

where

$$\begin{aligned} L_{1} & = \frac{{e^{\prime}_{11} d^{\prime}_{11} - q^{\prime}_{11} \varepsilon^{\prime}_{11} }}{{d^{\prime}_{11} \beta^{\prime}_{11} - \varepsilon_{11}^{^{\prime}2} }},\,\,\,\,\,L_{2} = \frac{{e^{\prime}_{12} d_{11}^{\prime} - q^{\prime}_{12} \varepsilon^{\prime}_{11} }}{{d_{11}^{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{^{\prime}2} }},\,\,\,\,\,\,L_{3} = \frac{{\varepsilon_{11}^{\prime} }}{{d_{11}^{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{^{\prime}2} }}, \\ L_{4} & = \,\frac{{p^{\prime}_{11} d_{11}^{\prime} - m^{\prime}_{1} \varepsilon^{\prime}_{11} }}{{d_{11}^{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{^{\prime}2} }},\,\,\,\,\,L_{5} = \frac{{d_{11}^{\prime} }}{{d_{11}^{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{^{\prime}2} }}, \\ P_{1} & = \frac{{q^{\prime}_{11} \beta_{11}^{\prime} - \varepsilon^{\prime}_{11} e^{\prime}_{11} }}{{d_{11}{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{^{\prime}2} }},\,\,\,\,\,\,P_{2} = \,\frac{{q_{12}^{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{\prime} e^{\prime}_{12} }}{{d_{11}^{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{^{\prime}2} }},\,\,\,\,\,\,\,P_{3} = \,\frac{{\varepsilon_{11}^{\prime} }}{{d_{11}^{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{^{\prime}2} }}, \\ P_{4} & = \,\frac{{m^{\prime}_{1} \beta_{11}^{\prime} - \varepsilon^{\prime}_{11} p^{\prime}_{1} }}{{d_{11}^{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{^{\prime}2} }},\,\,\,\,\,\,\,\,P_{5} = \frac{{\beta_{11}^{\prime} }}{{d_{11}^{\prime} \beta_{11}^{\prime} - \varepsilon_{11}^{^{\prime}2} }}. \\ \end{aligned}$$
(36)

Using Eqs. (34) and (35), the stress equations become simpler:

$$\sigma_{r} = C_{1} r^{\gamma } \frac{\partial u}{{\partial r}} + C_{2} r^{\gamma } \frac{u}{r} + C_{3} \frac{{A_{2} }}{{r^{ - \Omega + 1} }} + C_{4} \frac{{A_{1} }}{{r^{ - \Omega + 1} }} + C_{5} r^{\gamma } T - \lambda^{\prime}_{1} r^{2\gamma } T,$$
(37)
$$\sigma_{\theta } = E_{1} r^{\gamma } \frac{\partial u}{{\partial r}} + E_{2} r^{\gamma } \frac{u}{r} + E_{3} \frac{{A_{2} }}{{r^{ - \Omega + 1} }} + E_{4} \frac{{A_{1} }}{{r^{ - \Omega + 1} }} + E_{5} r^{\gamma } T - \lambda^{\prime}_{2} r^{2\gamma } T.$$
(38)

where:

$$\begin{gathered} C_{1} = c^{\prime}_{11} + e^{\prime}_{11} L_{1} + q^{\prime}_{11} P_{1} ,\,\,\,\,\,\,\,C_{2} = c^{\prime}_{12} + e^{\prime}_{11} L_{2} + q^{\prime}_{11} P_{2} ,\,\,\,\,\,C_{3} = e^{\prime}_{11} L_{3} - q^{\prime}_{11} P_{5} , \hfill \\ C_{4} = q^{\prime}_{11} P_{3} - e^{\prime}_{11} L_{5} ,\,\,\,\,\,\,\,\,\,C_{5} = e^{\prime}_{11} L_{4} + q^{\prime}_{11} P_{4} , \hfill \\ \end{gathered}$$
(39)
$$\begin{gathered} E_{1} = c^{\prime}_{12} + e^{\prime}_{12} L_{1} + q^{\prime}_{12} P_{1} ,\,\,\,\,\,\,\,E_{2} = c^{\prime}_{22} + e^{\prime}_{12} L_{2} + q^{\prime}_{12} P_{2} ,\,\,\,\,\,\,\,\,\,\,E_{3} = e^{\prime}_{12} L_{3} - q^{\prime}_{12} P_{5} , \hfill \\ E_{4} = q^{\prime}_{12} P_{3} - e^{\prime}_{12} L_{5} ,\,\,\,\,\,\,\,\,\,E_{5} = e^{\prime}_{12} L_{4} + q^{\prime}_{12} P_{4} . \hfill \\ \end{gathered}$$
(40)

Substituting Eqs. (37) and (38) in Eq. (29) yields:

$$\begin{aligned} \frac{{\partial^{2} u}}{{\partial r^{2} }} & + \frac{{M_{1} }}{r}\frac{\partial u}{{\partial r}} + \frac{{M_{2} }}{{r^{2} }}u = M_{3} r^{\gamma - 1} T + M_{4} \frac{T}{r} + \left( {M_{6} r^{\gamma } - M_{5} } \right)\frac{\partial T}{{\partial r}} + M_{7} \frac{{A_{2} }}{{r^{\gamma - \Omega + 2} }} \\ & + M_{8} \frac{{A_{1} }}{{r^{\gamma - \Omega + 2} }} - M_{13} r. \\ \end{aligned}$$
(41)

where:

$$\begin{gathered} M_{1} = \frac{{\left( {\gamma - \Omega + 1} \right)C_{1} + C_{2} - E_{1} }}{{C_{1} }}\,\,,\,\,M_{2} = \frac{{\left( {\gamma - \Omega } \right)C_{2} - E_{2} }}{{C_{1} }}, \hfill \\ M_{3} = \frac{{\left( {2\gamma - \Omega + 1} \right)\lambda^{\prime}_{1} - \lambda^{\prime}_{2} }}{{C_{1} }}\,\,,\,\,M_{4} = \frac{{E_{5} - \left( {\gamma - \Omega + 1} \right)C_{5} }}{{C_{1} }}\,\,,\,\,M_{5} = \frac{{C_{5} }}{{C_{1} }}, \hfill \\ M_{6} = \frac{{\lambda^{\prime}_{1} }}{{C_{1} }}\,\,,\,\,M_{7} = \frac{{E_{3} }}{{C_{1} }}\,\,,\,\,M_{8} = \frac{{E_{4} }}{{C_{1} }}\,\,,\,\,\,\,M_{13} = \frac{{\rho \omega^{2} }}{{C_{1} }}. \hfill \\ \end{gathered}$$
(42)

Substituting the temperature function (Eq. (16)) in Eq. (41) gives:

$$\begin{aligned} \frac{{\partial^{2} u}}{{\partial r^{2} }} & + \frac{{M_{1} }}{r}\frac{\partial u}{{\partial r}} + \frac{{M_{2} }}{{r^{2} }}u = \left( {M_{3} a_{0} } \right)r^{\gamma - 1} + \left( {M_{3} a_{1} + M_{6} a_{1} } \right)r^{\gamma } \\ & + \left( {M_{3} a_{2} + 2M_{6} a_{2} } \right)r^{\gamma + 1} + \left( {M_{3} a_{3} + 3M_{6} a_{3} } \right)r^{\gamma + 2} + \left( {M_{3} a_{4} + 4M_{6} a_{4} } \right)r^{\gamma + 3} \\ & + \left( {M_{3} a_{5} + 5M_{6} a_{5} } \right)r^{\gamma + 4} + \left( {M_{4} a_{0} } \right)r^{ - 1} + \left( {M_{4} a_{1} - M_{5} a_{1} } \right) \\ & + \left( {M_{4} a_{2} - 2M_{5} a_{2} - M_{13} } \right)r + \left( {M_{4} a_{3} - 3M_{5} a_{3} } \right)r^{2} + \left( {M_{4} a_{4} - 4M_{5} a_{4} } \right)r^{3} \\ & + \left( {M_{4} a_{5} - 5M_{5} a_{5} } \right)r^{4} + M_{7} \frac{{A_{2} }}{{r^{\gamma - \Omega + 2} }} + M_{8} \frac{{A_{1} }}{{r^{\gamma - \Omega + 2} }}. \\ \end{aligned}$$
(43)

We can write the solution of Eq. (43) in the following form:

$$\begin{aligned} u & = B_{1} r^{{m_{1} }} + B_{2} r^{{m_{2} }} + B_{3} r^{\gamma + 1} + B_{4} r^{\gamma + 2} \, + B_{5} r^{\gamma + 3} + B_{6} r^{\gamma + 4} + B_{7} r^{\gamma + 5} + B_{8} r^{\gamma + 6} \\ & \quad + B_{9} r\, + B_{10} r^{2} + B_{11} r^{3} + B_{12} r^{4} + B_{13} r^{5} + B_{14} r^{6} + B_{15} A_{2} r^{ - \gamma + \Omega } + B_{16} A_{1} r^{ - \gamma + \Omega } , \\ \end{aligned}$$
(44)
$$\begin{aligned} m_{1} & = \frac{1}{2}\left( { - \left( {M_{1} - 1} \right) + \sqrt {\left( {M_{1} - 1} \right)^{2} - 4M_{2} } } \right), \\ m_{2} & = \frac{1}{2}\left( { - \left( {M_{1} - 1} \right) - \sqrt {\left( {M_{1} - 1} \right)^{2} - 4M_{2} } } \right). \\ \end{aligned}$$
(45)

where:

$$\begin{aligned} B_{3} & = \frac{{M_{3} a_{0} }}{{\left( {\gamma + 1} \right)^{2} + \left( {M_{1} - 1} \right)\left( {\gamma + 1} \right) + M_{2} }},B_{4} = \frac{{\left( {M_{3} + M_{6} } \right)a_{1} }}{{\left( {\gamma + 2} \right)^{2} + \left( {M_{1} - 1} \right)\left( {\gamma + 2} \right) + M_{2} }}, \\ B_{5} & = \frac{{\left( {M_{3} + 2M_{6} } \right)a_{2} }}{{\left( {\gamma + 3} \right)^{2} - \left( {\gamma + 3} \right) + M_{1} \left( {\gamma + 3} \right) + M_{2} }},\,B_{6} = \frac{{\left( {M_{3} + 3M_{6} } \right)a_{3} }}{{\left( {\gamma + 4} \right)^{2} + \left( {M_{1} - 1} \right)\left( {\gamma + 4} \right) + M_{2} }}, \\ B_{7} & = \frac{{\left( {M_{3} + 4M_{6} } \right)a_{4} }}{{\left( {\gamma + 5} \right)^{2} - \left( {\gamma + 5} \right) + M_{1} \left( {\gamma + 5} \right) + M_{2} }},\,B_{8} = \frac{{\left( {M_{3} + 5M_{6} } \right)a_{5} }}{{\left( {\gamma + 6} \right)^{2} - \left( {\gamma + 6} \right) + M_{1} \left( {\gamma + 6} \right) + M_{2} }}, \\ B_{9} & = \frac{{M_{4} a_{0} }}{{M_{1} + M_{2} }},\,B_{10} = \frac{{\left( {M_{4} - M_{5} } \right)a_{1} }}{{2 + 2M_{1} + M_{2} }},\,B_{11} = \frac{{\left( {M_{4} - 2M_{5} } \right)a_{2} - M_{13} }}{{6 + 3M_{1} + M_{2} }},\, \\ B_{12} & = \frac{{\left( {M_{4} - 3M_{5} } \right)a_{3} }}{{12 + 4M_{1} + M_{2} }},\,B_{13} = \frac{{\left( {M_{4} - 4M_{5} } \right)a_{4} }}{{20 + 5M_{1} + M_{2} }},\,B_{14} = \frac{{\left( {M_{4} - 5M_{5} } \right)a_{5} }}{{30 + 6M_{1} + M_{2} }}, \\ B_{15} & = \frac{{M_{7} }}{{\left( {1 - M_{1} } \right)\left( {\gamma - \Omega } \right) + \left( { - \gamma + \Omega } \right)^{2} + M_{2} }},\,B_{16} = \frac{{M_{8} }}{{\left( {1 - M_{1} } \right)\left( {\gamma - \Omega } \right) + \left( { - \gamma + \Omega } \right)^{2} + M_{2} }}. \\ \end{aligned}$$
(46)

B1 and B2 are unknown constants. By Substituting Eq. (44) in Eqs. (34) and (35), and integrating, the electric and magnetic potential functions can be obtained as:

$$\begin{aligned} \phi (r) & \quad = \frac{{\left( {L_{1} m_{1} + L_{2} } \right)B_{1} }}{{m_{1} }}r^{{m_{1} }} + \frac{{\left( {L_{1} m_{2} + L_{2} } \right)B_{2} }}{{m_{2} }}r^{{m_{2} }} + \frac{{\left( {L_{1} \left( {\gamma + 1} \right) + L_{2} } \right)B_{3} }}{\gamma + 1}r^{\gamma + 1} \\ & \quad + \frac{{\left( {L_{2} + L_{1} \left( {\gamma + 2} \right)} \right)B_{4} }}{\gamma + 2}r^{\gamma + 2} + \frac{{\left( {L_{2} + L_{1} \left( {\gamma + 3} \right)} \right)B_{5} }}{\gamma + 3}r^{\gamma + 3} + \frac{{\left( {L_{2} + L_{1} \left( {\gamma + 4} \right)} \right)B_{6} }}{\gamma + 4}r^{\gamma + 4} \\ & \quad + \frac{{\left( {L_{2} + L_{1} \left( {\gamma + 5} \right)} \right)B_{7} }}{\gamma + 5}r^{\gamma + 5} + \frac{{\left( {L_{2} + L_{1} \left( {\gamma + 6} \right) + } \right)B_{8} }}{\gamma + 6}r^{\gamma + 6} + \left( {\left( {L_{1} + L_{2} } \right)B_{9} + L_{4} a_{0} } \right)r \\ & \quad + \frac{{\left( {\left( {2L_{1} + L_{2} } \right)B_{10} + L_{4} a_{1} } \right)}}{2}r^{2} + \frac{{\left( {\left( {3L_{1} + L_{2} } \right)B_{11} + L_{4} a_{2} } \right)}}{3}r^{3} \\ & \quad + \frac{{\left( {\left( {4L_{1} + L_{2} } \right)B_{12} + L_{4} a_{3} } \right)}}{4}r^{4} + \frac{{\left( {\left( {5L_{1} + L_{2} } \right)B_{13} + L_{4} a_{4} } \right)}}{5}r^{5} \\ & \quad + \frac{{\left( {\left( {6L_{1} + L_{2} } \right)B_{14} + L_{4} a_{5} } \right)}}{6}r^{6} - \frac{{\left( {\left( {L_{2} - L_{1} \left( {\gamma - \Omega } \right)} \right)B_{15} A_{2} + \left( {L_{2} - L_{1} \left( {\gamma - \Omega } \right)} \right)B_{16} A_{1} } \right)}}{\gamma - \Omega }r^{ - \gamma + \Omega } \\ & \quad - \frac{{L_{3} A_{2} }}{\gamma - \Omega }r^{ - \gamma + \Omega } + \frac{{L_{5} A_{1} }}{\gamma - \Omega }r^{ - \gamma + \Omega } + Z_{1} , \\ \end{aligned}$$
(47)
$$\begin{aligned} \psi (r) & \quad = \frac{{\left( {P_{1} m_{1} + P_{2} } \right)B_{1} }}{{m_{1} }}r^{{m_{1} }} + \frac{{\left( {P_{1} m_{2} + P_{2} } \right)B_{2} }}{{m_{2} }}r^{{m_{2} }} + \frac{{\left( {P_{1} \left( {\gamma + 1} \right) + P_{2} } \right)B_{3} }}{\gamma + 1}r^{\gamma + 1} \\ & \quad + \frac{{\left( {P_{2} + P_{1} \left( {\gamma + 2} \right)} \right)B_{4} }}{\gamma + 2}r^{\gamma + 2} + \frac{{\left( {P_{2} + P_{1} \left( {\gamma + 3} \right)} \right)B_{5} }}{\gamma + 3}r^{\gamma + 3} + \frac{{\left( {P_{2} + P_{1} \left( {\gamma + 4} \right)} \right)B_{6} }}{\gamma + 4}r^{\gamma + 4} \\ & \quad + \frac{{\left( {P_{2} + P_{1} \left( {\gamma + 5} \right)} \right)B_{7} }}{\gamma + 5}r^{\gamma + 5} + \frac{{\left( {P_{2} + P_{1} \left( {\gamma + 6} \right)} \right)B_{8} }}{\gamma + 6}r^{\gamma + 6} + \left( {\left( {P_{1} + P_{2} } \right)B_{9} + P_{4} a_{0} } \right)r \\ & \quad + \frac{{\left( {\left( {2P_{1} + P_{2} } \right)B_{10} + P_{4} a_{1} } \right)}}{2}r^{2} + \frac{{\left( {\left( {3P_{1} + P_{2} } \right)B_{11} + P_{4} a_{2} } \right)}}{3}r^{3} \\ & \quad + \frac{{\left( {\left( {4P_{1} + P_{2} } \right)B_{12} + P_{4} a_{3} } \right)}}{4}r^{4} + \frac{{\left( {\left( {5P_{1} + P_{2} } \right)B_{13} + P_{4} a_{4} } \right)}}{5}r^{5} \\ & \quad + \frac{{\left( {\left( {6P_{1} + P_{2} } \right)B_{14} + P_{4} a_{5} + P_{6} b_{5} } \right)}}{6}r^{6} - \frac{{\left( {\left( {P_{2} - P_{1} \left( {\gamma - \Omega } \right)} \right)B_{15} A_{2} + \left( {P_{2} - P_{1} \left( {\gamma - \Omega } \right)} \right)B_{16} A_{1} } \right)}}{\gamma - \Omega }r^{ - \gamma + \Omega } \\ & \quad - \frac{{P_{3} A_{1} }}{\gamma - \Omega }r^{ - \gamma + \Omega } + \frac{{P_{5} A_{2} }}{\gamma - \Omega }r^{ - \gamma + \Omega } + Z_{2} . \\ \end{aligned}$$
(48)

where, Z1 and Z2 are unknown coefficients. Since the radial displacement is known, the radial and hoop stresses can be calculated using Eqs. (44) in (37) and (38):

$$\begin{aligned} \sigma_{r} & \quad = \left( {C_{1} m_{1} + C_{2} } \right)B_{1} r^{{\gamma + m_{1} - 1}} + \left( {C_{1} m_{2} + C_{2} } \right)B_{2} r^{{\gamma + m_{2} - 1}} + \left( {\left( {\left( {\gamma + 1} \right)C_{1} + C_{2} } \right)B_{3} - \lambda^{\prime}_{1} a_{0} } \right)r^{2\gamma } \\ & \quad + \left( {\left( {\left( {\gamma + 2} \right)C_{1} + C_{2} } \right)B_{4} - \lambda^{\prime}_{1} a_{1} } \right)r^{2\gamma + 1} + \left( {\left( {\left( {\gamma + 3} \right)C_{1} + C_{2} } \right)B_{5} - \lambda^{\prime}_{1} a_{2} } \right)r^{2\gamma + 2} \\ & \quad + \left( {\left( {\left( {\gamma + 4} \right)C_{1} + C_{2} } \right)B_{6} - \lambda^{\prime}_{1} a_{3} } \right)r^{2\gamma + 3} + \left( {\left( {\left( {\gamma + 5} \right)C_{1} + C_{2} } \right)B_{7} - \lambda^{\prime}_{1} a_{4} } \right)r^{2\gamma + 4} \\ & \quad + \left( {\left( {\left( {\gamma + 6} \right)C_{1} + C_{2} } \right)B_{8} - \lambda^{\prime}_{1} a_{5} } \right)r^{2\gamma + 5} + \left( {B_{9} \left( {C_{1} + C_{2} } \right) + C_{5} a_{0} } \right)r^{\gamma } \\ & \quad + \left( {B_{10} \left( {2C_{1} + C_{2} } \right) + C_{5} a_{1} } \right)r^{\gamma + 1} + \left( {B_{11} \left( {3C_{1} + C_{2} } \right) + C_{5} a_{2} } \right)r^{\gamma + 2} \\ & \quad + \left( {B_{12} \left( {4C_{1} + C_{2} } \right) + C_{5} a_{3} } \right)r^{\gamma + 3} + \left( {B_{13} \left( {5C_{1} + C_{2} } \right) + C_{5} a_{4} } \right)r^{\gamma + 4} \\ & \quad + \left( {B_{14} \left( {6C_{1} + C_{2} } \right) + C_{5} a_{5} } \right)r^{\gamma + 5} + \left( {\left( {C_{2} - \left( {\gamma - \Omega } \right)C_{1} } \right)A_{2} B_{15} + \left( {C_{2} - \left( {\gamma - \Omega } \right)C_{1} } \right)A_{1} B_{16} } \right)r^{\Omega - 1} \\ & \quad + C_{3} \frac{{A_{2} }}{{r^{ - \Omega + 1} }} + C_{4} \frac{{A_{1} }}{{r^{ - \Omega + 1} }}, \\ \end{aligned}$$
(49)
$$\begin{aligned} \sigma_{\theta } & = \left( {E_{1} m_{1} + E_{2} } \right)B_{1} r^{{\gamma + m_{1} - 1}} + \left( {E_{1} m_{2} + E_{2} } \right)B_{2} r^{{\gamma + m_{2} - 1}} + \left( {\left( {\left( {\gamma + 1} \right)E_{1} + E_{2} } \right)B_{3} - \lambda^{\prime}_{2} a_{0} } \right)r^{2\gamma } \\ & \quad + \left( {\left( {\left( {\gamma + 2} \right)E_{1} + E_{2} } \right)B_{4} - \lambda^{\prime}_{2} a_{1} } \right)r^{2\gamma + 1} + \left( {\left( {\left( {\gamma + 3} \right)E_{1} + E_{2} } \right)B_{5} - \lambda^{\prime}_{2} a_{2} } \right)r^{2\gamma + 2} \\ & \quad + \left( {\left( {\left( {\gamma + 4} \right)E_{1} + E_{2} } \right)B_{6} - \lambda^{\prime}_{2} a_{3} } \right)r^{2\gamma + 3} + \left( {\left( {\left( {\gamma + 5} \right)E_{1} + E_{2} } \right)B_{7} - \lambda^{\prime}_{2} a_{4} } \right)r^{2\gamma + 4} \\ & \quad + \left( {\left( {\left( {\gamma + 6} \right)E_{1} + E_{2} } \right)B_{8} - \lambda^{\prime}_{2} a_{5} } \right)r^{2\gamma + 5} + \left( {B_{9} \left( {E_{1} + E_{2} } \right) + E_{5} a_{0} } \right)r^{\gamma } \\ & \quad + \left( {B_{10} \left( {2E_{1} + E_{2} } \right) + E_{5} a_{1} } \right)r^{\gamma + 1} + \left( {B_{11} \left( {3E_{1} + E_{2} } \right) + E_{5} a_{2} } \right)r^{\gamma + 2} \\ & \quad + \left( {B_{12} \left( {4E_{1} + E_{2} } \right) + E_{5} a_{3} } \right)r^{\gamma + 3} + \left( {B_{13} \left( {5E_{1} + E_{2} } \right) + E_{5} a_{4} } \right)r^{\gamma + 4} \\ & \quad + \left( {B_{14} \left( {6E_{1} + E_{2} } \right) + E_{5} a_{5} } \right)r^{\gamma + 5} + \left( {\left( {E_{2} - \left( {\gamma - \Omega } \right)E_{1} } \right)A_{2} B_{15} + \left( {E_{2} - \left( {\gamma - \Omega } \right)E_{1} } \right)A_{1} B_{16} } \right)r^{\Omega - 1} \\ & \quad + E_{3} \frac{{A_{2} }}{{r^{ - \Omega + 1} }} + E_{4} \frac{{A_{1} }}{{r^{ - \Omega + 1} }}. \\ \end{aligned}$$
(50)

So, there are six unknown coefficients (B1, B2, A1, A2, Z1, Z2) that can be evaluated using the mechanical, electrical, and magnetic boundary conditions. Here, the boundary conditions are considered as:

$$\begin{aligned} r & = r_{i} \Rightarrow \sigma_{r} = 0\,\,,\,\,\phi = \phi_{i} \,\,,\,\,\psi = \psi_{i} , \\ r & = r_{o} \Rightarrow \sigma_{r} = 0\,\,,\,\,\phi = \phi_{o} \,\,,\,\,\psi = \psi_{o} . \\ \end{aligned}$$
(51)

4 Results and Discussion

Several numerical examples were considered in this part to disclose the effects of different parameters on the distribution of stresses, displacement, electric and magnetic potentials, and temperature. The used material constants are given in Table 1. Otherwise is states, the used parameters in the numerical examples are as Table 2. The following dimensionless parameters were used in the results:

$$\begin{aligned} R & = \frac{{r - r_{i} }}{{r_{o} - r_{i} }},\,\,\sigma_{r,\theta }^{*} = \frac{{\sigma_{r,\theta } }}{{c_{11} }},\,\,u_{r}^{*} = \frac{{u_{r} }}{{r_{i} }},\,\,\phi^{ * } = \frac{{\phi \sqrt {{{\beta_{11} } \mathord{\left/ {\vphantom {{\beta_{11} } {c_{11} }}} \right. \kern-0pt} {c_{11} }}} }}{{r_{o} }}, \\ \psi^{*} & = \frac{{\psi \sqrt {{{d_{11} } \mathord{\left/ {\vphantom {{d_{11} } {c_{11} }}} \right. \kern-0pt} {c_{11} }}} }}{{r_{o} }},\,\,D_{r}^{*} = \frac{{D_{r} }}{{\sqrt {c_{33} \varepsilon_{11} } }},\,\,B_{r}^{*} = \frac{{B_{r} }}{{\sqrt {c_{33} \mu } }}. \\ \end{aligned}$$
(52)
Table 1 Material properties
Full size table
Table 2 Used parameters for the FGMEE disk
Full size table

4.1 Validation

4.1.1 Thermal Analysis

Since there are no comparable results in the literature, to validate the accuracy of the solution method used for the heat transfer equation, a numerical solution was performed using the FlexPDE software for the heat transfer equation. According to Fig. 2, the results show good agreement.

Fig. 2
figure 2

Validation of results in thermal analysis

Full size image

4.1.2 Stress Analysis

The obtained results for radial stress, hoop stress and radial displacement of the FGMEE disk were compared with the reported research about static behaviors of an FGM disk. The used material constants are listed in Refs. (Çallioğlu et al. 2011) and (Dai and Dai 2016). The obtained results have a good accuracy according to Fig. 3.

Fig. 3
figure 3

Validation of the stress and deformation results

Full size image

4.2 Effective Parameters Investigation

The influences of key parameters on the radial and circumferential stresses, radial deformation, electric and magnetic potentials, and temperature were analyzed in this section.

4.2.1 Grading Index

The inhomogeneity index is the first parameter to disclose its influence. Figure 4 illustrates the effects of the inhomogeneity index on the response of the disk. As shown, the outward radial displacement, radial stress, absolute hoop stress, and temperature reduce by an increase in the inhomogeneity index, whereas the electric potential and magnetic potential increase for a higher grading index. So, by selecting the proper grading index, the stress and displacement can be controlled.

Fig. 4
figure 4

Effect of the inhomogeneity index

Full size image

4.2.2 Different Profiles of Thickness

For the next example, the effect of the inner and outer thickness of the disk was disclosed. The findings can be observed in Fig. 5. Regarding Fig. 5, the outward displacement, electric potential, magnetic potential, maximum of electric displacement, and maximum of magnetic induction are smaller for the case ho < hi comparison with the case ho > hi. Also, the positive circumferential stress at the interior radius has a smaller value, and negative hoop stress at the exterior radius has a higher absolute value for the case ho < hi comparison with the case ho > hi. It should be noted that FGMEEs usually have brittle behavior. So, high tensile hoop stress can increase the chance of crack growth and must be avoided. Also, the graphs show that changes in the inner and outer thickness have a slight effect on the radial stress. Generally, Fig. 5 shows that using a non-uniform thickness disk with an outer thickness smaller than the inner thickness can reduce the radial displacement, maximum tensile hoop stress, and electromagnetic potentials.

Fig. 5
figure 5

Influence of the different profiles of thickness

Full size image

4.2.3 Thickness Coefficient

The changes in the stresses, radial displacement, and electromagnetic potentials for different thickness coefficients were investigated in this example. Figure 6 shows a higher value of the thickness coefficient leads to a reduction in radial displacement, electric potential, magnetic potential, electric displacement, and magnetic induction. Also, the graph of hoop stress shifts down for a higher thickness coefficient. As shown, the radial stress shows no significant change for different thickness coefficients. Moreover, the temperature increases at the same radius for a higher thickness index. It should be noted that higher thickness coefficients mean disks with thicker thickness.

Fig. 6
figure 6

Influence of the thickness profile coefficient

Full size image

4.2.4 Temperature Difference

In the next example, the effect of temperature difference was explored. Figure 7 shows the influence of the temperature difference between the inside and outside of the disk on stresses, displacement, electric and magnetic potentials, and electric and magnetic displacement. As shown, the radial stress, outward deformation, electric potential, magnetic potential, electric displacement, and magnetic induction increase for the higher temperature difference. Moreover, there are two points through the thickness in which the circumferential stress shows no change by a change in temperature difference. The trend of changes before and after these two points is in contrast with the trend of changes between them. Also, the maximum tensile circumferential stress increases for a higher temperature difference.

Fig. 7
figure 7

Influence of the temperature difference

Full size image

4.2.5 Angular Velocity

Figure 8 indicates the influence of the angular speed on the stress behavior of the disk. As observed, higher angular speed results in higher radial stress and deformation. The rate of change is incremental. Also, the tensile hoop stress at the interior radius increases, and compressive circumferential stress at the exterior radius decreases for higher angular speed. Since these smart materials show brittle behavior, a high tensile circumferential stress can yield crack growth. So, the high tensile hoop stress must be avoided. In addition, in the second half of thickness, the temperature graph shows an increase in temperature for a higher angular speed. It should be noted that the convection heat transfer is a function of angular velocity according to Eq. (4). Therefore, this effect is observed due to the effect of convection heat transfer.

Fig. 8
figure 8

Effect of the angular velocity

Full size image

4.2.6 Solar Radiation

For the next parameter, changes in the mechanical response due to solar radiation are illustrated in Fig. 9. Here, we have: Tb = 303(K), To = 288(K), k0 = 4.5(W/mK), h0 = 0, ω = 20 π(Rad/s), and β = 3. The graph shows that the tensile radial stress, radial deformation, electric displacement, and magnetic induction decrease for higher values for coefficients Gs and αs. Also, it results in more reduction in the temperature distribution graph. However, the coefficient ε exhibits an opposite effect on stresses, displacement, temperature, electric displacement, and magnetic induction. Besides, there exist two points in which the circumferential stress is independent of solar radiation. Also, the location of maximum hoop stress changes from inside radius to a point between these two fixed points for higher values for coefficients Gs and αs.

Fig. 9
figure 9

Effect of solar radiation coefficients on the temperature distributions

Full size image

4.2.7 Internal Heat Generation

The effects of the internal heat source were disclosed in the next example. Here, we have: Tb = 303(K), To = 288(K), k0 = 4.5(W/mK), h0 = 0, ω = 20π(Rad/s), and β = 3. The internal heat generation is temperature dependent according to Eq. (5). So, the power of the heat source depends on two parameters q0 and e0 that are investigated in Fig. 10. Concerning Fig. 10, the tensile radial stress, radial deformation, electric displacement, and magnetic induction decrease for higher source powers. Moreover, the location of maximum tensile hoop stress changes from the inside radius to a radius through the thickness. Also, more reduction can be observed in the temperature distribution for the higher values of source power. According to Fig. 10, the temperature dependency coefficient e0 has reverse effects in comparison with power source q0.

Fig. 10
figure 10

Effect of internal heat generation coefficients on the temperature distributions

Full size image

4.2.8 Convection Heat Transfer

The influence of convection heat transfer was disclosed in this part. In this case, we have: Tb = 303(K), To = 288(K), k0 = 4.5(W/mK), ε = 0.1, αs = 0.8, and β = 3. According to Eq. (4), the convection heat transfer constant is temperature-dependent, and it depends on three parameters h0, b, and a. The effects of these constants are indicated in Fig. 11. According to Fig. 11, the radial stress, outward deformation, electric displacement, and magnetic induction increase for the higher values of h0, a, and b. Also, it results in an increase in the maximum tensile hoop stress at the inner radius. Furthermore, less reduction can be observed in the temperature distribution for the higher values of h0, a, and b.

Fig. 11
figure 11

Effect of convection heat transfer coefficients on the temperature distributions

Full size image

4.2.9 Conduction Heat Transfer

The effect of heat conduction constant and heat conduction temperature dependency should be investigated in the next example. Here, Tb = 303(K), To = 288(K), h0 = 0, ε = 0.1, and αs = 0.8. According to Eq. (3), the thermal conductivity constant is temperature-dependent, and it depends on two constants k0 and β. Figure 12 shows the effects of these two constants. As observed, the tensile radial stress, radial displacement, electric displacement, and magnetic induction increase for a higher conductivity constant k0. Besides, the location of maximum hoop stress changes from a point through the thickness to the interior radius for a higher conductivity constant. Also, less reduction can be observed in the temperature distribution graph for the higher values of the conductivity constant. Figure 12 indicates that the effects of temperature dependency constant β are opposite to the effects of conductivity constant k0.

Fig. 12
figure 12

Effect of conduction heat transfer coefficients on the temperature distributions

Full size image

5 Conclusions

The thermoelastic response of a rotating functionally graded magneto-electro-elastic disk with non-constant thickness was investigated considering internal heat generation, convection, and radiation heat transfer. The heat conduction and convection coefficients are functions of temperature and radius. The differential transformation method was used for solving the obtained nonlinear differential equation of heat transfer. Then, the equilibrium equation of the disk was derived and solved analytically. The radial stress, circumferential stress, radial deformation, electric and magnetic potential, electric displacement, and magnetic induction can be obtained. The following findings can be expressed based on the results:

  • The displacement, radial stress, absolute hoop stress, and temperature reduce by an increase in the inhomogeneity index, whereas the electric potential and magnetic potential increase for the higher grading indexes.

  • Using a non-uniform thickness disk with an outer thickness smaller than the inner thickness can reduce the radial displacement, maximum tensile hoop stress, and electromagnetic potentials.

  • The radial stress, displacement, electric and magnetic potentials, electric displacement, and magnetic induction increase for the higher temperature difference.

  • The tensile radial stress, radial deformation, electric displacement, and magnetic induction decrease for higher values of coefficients of solar flux intensity and absorption coefficient of solar radiation. However, the emission coefficient exhibits an opposite effect.

  • The tensile radial stress, radial deformation, electric displacement, and magnetic induction decrease for higher source powers. Also, the location of maximum tensile hoop stress changes from the inside radius to a radius through the thickness. The temperature dependency coefficient has reverse effects in comparison with the power source.

  • The radial stress and displacement, electric displacement, and magnetic induction increase for the higher values of the convection coefficients.

  • The tensile radial stress, radial displacement, electric displacement, and magnetic induction increase for a higher conductivity constant. Also, the location of maximum hoop stress changes from a point through the thickness to the interior radius for a higher conductivity constant. The effects of the temperature-dependency constant are opposite to the effects of the conductivity constant.