1 Introduction

Investigations on improving the thermal efficiency of different heating and cooling devices have been ongoing over the past few decades (Murshed and de Castro 2016; Wang et al. 2012). With the advancement of modern engineering technology, the miniaturisation of electronic components has seen major improvements. For example, a microprocessor is a component which drastically increases power consumption. Therefore, an effective method to improve the thermal efficiency by understanding the mechanism of heat dissipation will be required. Therefore, researchers have been emphasising more on improving cooling system by analysing heat transfer characteristics of coolants (air, liquid, gas, to name a few) (Murshed and de Castro 2016; Wang et al. 2012; Palm et al. 2006; Swalmeh et al. 2018). The concept of considering small metal particles to form a suspension by mixing with common fluids has been proven to significantly improve the thermal conductivity of the fluid as well as the thermal efficiency of the electronic equipment. The idea of ferrofluid came into being from these investigations.

A ferrofluid is a colloidal suspension or is sometimes referred to as a magnetic colloid. It consists of monodomain magnetic particles with dimensions usually between 10 to 100 nm suspended within an electrically non-conductive fluid (Kefayati 2014; Marin and Malaescu 2020; Afsana et al. 2021). The smaller fraction of fluid particles ensures higher stability in the suspension, making ferrofluid an ideal candidate in multifarious industrial applications (Shojaeizadeh et al. 2020; Vasilakaki et al. 2020; Kole and Khandekar 2021; Sints et al. 2022). In addition, the impact of ferrofluids in environmental or agricultural science has been described in terms of vegetation and micro-organisms, removal of contaminated particles from drinking water streams, recovery of hazardous and toxic materials from the environment, and heat transfer/dissipation, to name a few (Cotae and Creanga 2005; Scherer 2005; Meng et al. 2019; Oehlsen et al. 2022). The liquid can either be polar or non-polar. Ferrofluid was developed by NASA in 1960 when natural magnetite was required for liquid transportation through space (weightless environment). In general, ferrofluids consist of either iron salts or iron oxides. The composition of ferrofluid has been reported as \(85\%\) liquid, \(10\%\) surfactant, and \(5\%\) magnetic particles (Waqas 2020). Both fluid viscosity and Brownian motion of the particles play significant roles in restricting the deposition of the magnetic particles throughout the fluid; hence, the essential impact of fluid viscosity cannot be ignored in any industrial application. One of the major issues faced by industries is the interruption of thermomagnetic convection due to the presence of a magnetic field in the heat transfer unit or relevant devices. Although qualitatively acceptable results have been reported in the literature with marginal magnetic field either as a variable or constant, the approach is not realistic (Sints et al. 2015). While the magnetic field has a negative impact on applications more aligned with the separation process, the inclusion of permeable walls in the considered geometry has been attributed to resolving the concerns, particularly in heat transfer applications (Blums 2004). As a result, researchers have been trying to analyse the behaviour of fluids in different regular or irregular geometries for the last few decades. Among different geometries, vertical permeable cones, flat plates, exponentially accelerated radiative Riga plates, thin cylinders, wavy-walled cavities, and regular cubic or square enclosures with adiabatic walls are the most popular (Himika et al. 2021; Hassan et al. 2022; Djebali et al. 2021; Asogwa et al. 2022; Mebarek-Oudina 2019; Madasu and Bucha 2020; Abouelregal et al. 2021). Many studies mostly determined Nusselt numbers (\(\text{ Nu }\)) to understand the heat transfer characteristics of fluid under the influence of magnetic field including the effect of variable thermal conductivity, radiation, velocity and thermal slip effects and other thermophoresis aspects (Himika et al. 2021; Rashidi et al. 2014; Hassan et al. 2019; Himika et al. 2020; Swain et al. 2021).

In heat transfer applications, natural convection is widely considered in the numerical study of physical sciences. The behaviour of ferrofluid under natural convective conditions has been considered in the past (Kefayati 2014; Mehryan et al. 2018; Siddiqui and Turkyilmazoglu 2020; Chu et al. 2020). However, most of the published works focused on square cavities. In general, studies of fluid flow along a cylinder are conducted in two-dimension due to the consideration of radius being more extensive than the boundary layer thickness. Thin cylinders or any thin-walled geometries are mostly used for low-pressure processing equipment. Some of the previous works done by researchers on cones or cylinders are worth mentioning. Hossain et al. (2002) studied natural convective flow along a vertical circular cone with uniform surface heat flux and temperature in a thermally stratified medium, but elaborate discussions on different fluids or various Prandtl numbers (\(\text{ Pr }\)) are still required. Hossain and Alim (1997) included the effect of radiation within the boundary layer of a thin vertical cylinder for fixed \(\text{ Pr }\), but the findings were limited to the uniform surface temperature. The presentation of Gori et al. (2006) was a much-improved version as they considered both high (\(\text{ Pr }=730\)) and low (\(\text{ Pr }=0.7\)) \(\text{ Pr }\) to demonstrate the versatility of their approach. Nevertheless, the changes in viscosity required more attention. In a typical numerical analysis, \(\text{ Pr }\) can also provide information on the type of fluids by correlating viscosity with thermal conductivity. A higher \(\text{ Pr }\)(\(>5\)) indicates the heat transfer influenced by the fluid momentum rather than by the thermal diffusion (Smith et al. 2013). Therefore, varying \(\text{ Pr }\) at different scales establishes more confidence in accepting a numerical approach to the relevant industry. Furthermore, the viscosity is a function of temperature in the presence of a magnetic field to make the applicability of ferrofluid more pragmatic. Hasan et al. (2022) recently worked with vertical permeable cones within the boundary layer and provided threefold solutions by varying fluid characteristics and associated parameters. The implications of temperature-dependent viscosity provided more options for state-of-the-art research in applied sciences. However, the work of Hasan et al. (2022) only considered regular fluids. Under the influence of the magnetic field, the correlation between the electromagnetic and viscous forces should be considered. This relation is defined by the Hartmann number (\({\text{ Ha }}\)), and by varying \({\text{ Ha }}\), the strength of the magnetic field could be observed. Numerous works are available in the literature where researchers shifted their focus to different types of nanofluids (Kefayati and Bassom 2021; Sadeghi et al. 2021; Rostami et al. 2020; Reddy et al. 2022; Sivaraj et al. 2018; Hassan et al. 2022) or implications in state-of-the-art technology in an industrial setup such as for the manufacturing of viscoelastic functionally graded nanostructures (Jalaei et al. 2022; Dastjerdi et al. 2020; Civalek et al. 2022). Sivaraj and Sheremet (2018) investigated natural convection in a cavity under the influence of magnetohydrodynamics (MHD) by considering the finite volume method. Reddy et al. (2022) recently studied the heat transfer characteristics of magnetic nanofluid inside a square cavity with a smaller range of Rayleigh (Ra) numbers. The inclusion of carbon nanotubes outlines interesting findings for industrial applications. Hamzah et al. (2021) also investigated magnetic nanofluid behaviour inside a rotating conductive cylinder by finite element analysis and proposed further research directions in this field. In most cases, much literature did not widely investigate the effect of temperature-dependent viscosity. In practical applications, the temperature variations are evident, and hence viscosity of the fluids will change. Therefore, it is necessary to investigate the significant role of temperature in industrial applications. Furthermore, there should be a clear understanding on mixing ferroparticles into the base fluid. An arbitrary mixing of ferroparticles to form the suspension may do more harm than good such as clogging engineering equipment, loss of efficiency, and erosion of other physical components. Therefore, the effects of varying the volume fraction of ferroparticles needs to be comprehensively investigated to analyse the characteristics. In order to reach this milestone, a standard and efficient numerical method needs to be selected.

A numerical analysis requires selecting an appropriate method to solve a problem based on advantages and efficacy. The implicit finite difference method through the Keller box scheme is considered to be robust, reliable, numerically efficient, and unconditionally convergent in obtaining a second-order spatio-temporal solution of a boundary layer problem (Esfahanian and Torabi 2006; Hussain et al. 2018; Habib et al. 2018). In addition, the Keller box method also uses a non-uniform step size of the spatio-temporal equation which makes solving parabolic partial differential equations more efficient and appropriate (Habib et al. 2018). It also has the ability to handle high-performance computing on fluid flow equations containing heterogeneous clusters. Some of the complex grid requires working with unknown functions and their associated derivatives at each node concurrently. This process can be simplified numerically by implementing the Keller box method through defining boundary conditions as well as interface conditions, if needed (Esfahanian and Torabi 2006; Hussain et al. 2018; Habib et al. 2018).

Based on the above discussions, it could be inferred that there is still a requirement to investigate the heat transfer characteristics of ferrofluid and associated phenomena to manifest a theoretical understanding for the purpose of integrating into engineering applications. This requirement could be obtained by conducting sensitivity analyses of the influential parameters on the heat transfer parameters by choosing an efficient numerical method. The current study aims to answer the aforementioned shortcomings in the literature by considering the efficient Keller box technique as a representative method of implicit finite difference. A vertical thin cylinder has been considered as the geometry for the investigation which could be aligned with the configuration of a simple heat exchanging device. Ferrofluid is considered as the subject fluid to test the attributes and effects to represent a more pragmatic approach to tune the volume fraction of ferroparticles. In addition, \({\text{ Ha }}\) is included in the study to incorporate the effect of the magnetic field strength as well as the Lorentz force. For the ease of numerical analysis, the governing boundary layer equations were non-dimensionalised. The conducted numerical study shows the results in illustrative descriptions with streamlines and isotherms, as well as the velocity and temperature profiles within the considered geometric boundary. Numerical code validation was conducted at both low and high \(\text{ Pr }\) (0.72 and 10) to determine the non-dimensional \(\text{ Nu }\). The obtained results showed a good comparison with well-cited literature.

2 Theoretical Formulation

2.1 Problem Statement

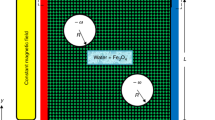
The geometry considered in this study is a two-dimensional vertical thin cylinder immersed in a ferrofluid, which is shown in Fig. 1. Here, the viscosity of the fluid is a function of fluid temperature. The fluid flow is assumed to be laminar and incompressible with \({\text{ Pr }} = 6.2\), and the fluid is a mixture of water and Fe\(_3\)O\(_4\) ferroparticles. It is assumed in the present study that the nanofluid is a single-phase fluid, where the nanoparticles are added to the base fluid in order to change its thermal properties, e.g. changes of viscosity, thermal conductivity, rate of heat transfer as well as other basic characteristic. The pertinent thermophysical properties are given in Table 1.

Fig. 1
figure 1

Schematic diagram of a vertical thin cylinder immersed in ferrofluid

Full size image
Table 1 Thermophysical properties of the base fluid and solid ferroparticles (Sivaraj and Sheremet 2018; Dogonchi 2019; Shenoy et al. 2016; Sheikholeslami et al. 2015)
Full size table

The coupled momentum and energy equations govern the flow by temperature or mass gradient for natural convection. Under the Boussinesq approximation, the density variation occurs only in the buoyant force, which introduces in the body force term. Therefore, the effective density, heat capacitance, and thermal expansion of nanofluid can be expressed as:

$$\begin{aligned}{} & {} \rho _{ff} = (1-\phi )\rho _{f} +\phi \rho _s \end{aligned}$$
(1)
$$\begin{aligned}{} & {} (\rho c_p)_{ff} = (1-\phi )(\rho c_p)_f +\phi (\rho c_p)_s \end{aligned}$$
(2)

and

$$\begin{aligned} \beta _{ff} = (1-\phi )\beta _f +\phi \beta _s \end{aligned}$$
(3)

The empirical formula for temperature dependent viscosity (Ling and Dybbs 1987; Molla et al. 2005) is combined with Brinkman model (Brinkman 1952) for the ferrofluid is given as follows:

$$\begin{aligned} \mu _{ff} = \frac{\mu _f}{(1-\phi )^{2.5}\left[ 1+\gamma (T-T_{\infty })\right] } \end{aligned}$$
(4)

The Maxwell-Garnetts (MG) models (Afsana et al. 2021) are used for the thermal conductivity \(k_{ff}\) and electric conductivity \(\sigma _{ff}\), respectively, as follows:

$$\begin{aligned}{} & {} k_{ff} = k_f \frac{k_{s} + 2k_{f} - 2\phi (k_{f} - k_{s})}{k_{s} + 2k_{f} + \phi (k_{f} - k_{s})} \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \sigma _{ff} = \sigma _f \left[ 1 + \frac{3\left( \frac{\sigma _s}{\sigma _f} - 1\right) \phi }{\left( \frac{\sigma _s}{\sigma _f} + 2\right) -\left( \frac{\sigma _s}{\sigma _f} - 1\right) \phi } \right] \end{aligned}$$
(6)

Here, \(\phi\) is the particle volume fraction, subscripts f and s are, respectively, represented the base fluid and solid particle. Therefore, the thermal diffusivity of the nanofluid is

$$\begin{aligned} \alpha _{ff} = \frac{k_{ff}}{(\rho c_p)_{ff}} \end{aligned}$$
(7)

2.2 Governing Dimensional Equations and Boundary Conditions

For the boundary layer problem, the dimensional governing equations under the Boussinesq approximation are the equations for continuity (8), momentum (9) and energy (10), which are as follows (Hossain and Alim 1997):

$$\begin{aligned}{} & {} \frac{\partial }{\partial x}\left( r u\right) + \frac{\partial }{\partial r}\left( r v\right) = 0 \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \rho _{ff}\left( u\frac{\partial u}{\partial x} + v \frac{\partial u}{\partial r}\right) \nonumber \\{} & {} \quad = \frac{1}{r}\frac{\partial }{\partial r}\left( r\mu _{ff} \frac{\partial u}{\partial r}\right) + g \left( \rho \beta \right) _{ff}\left( T-T_\infty \right) - \sigma _{ff}B_o^2u \end{aligned}$$
(9)
$$\begin{aligned}{} & {} u \frac{\partial T}{\partial x}+ v \frac{\partial T}{\partial r}= \alpha _{ff}\frac{1}{r}\frac{\partial }{\partial r}\left( r \frac{\partial T}{\partial r}\right) \end{aligned}$$
(10)

where u and v are the velocity components in the x and \(r-\)directions, respectively, T is the temperature of the ferrofluid, \(T_\infty\) is the ambient temperature, \(B_o\) is the magnetic field imposed normal to the plate, and g is the acceleration due to gravity.

The appropriate boundary conditions to solve (8)-(10) are

$$\begin{aligned}{} & {} u=v=0, \quad T=T_w \quad \text {at} \quad r= 0 \end{aligned}$$
(11a)
$$\begin{aligned}{} & {} u\rightarrow 0, v\rightarrow 0, T\rightarrow T_\infty \quad \text {as} \quad r\rightarrow \infty \end{aligned}$$
(11b)

To non-dimensionalise the above equations, the following non-dimensional variables are used

$$\begin{aligned}{} & {} \begin{aligned}&x= \frac{{\overline{x}}}{L}, \xi =\frac{2L}{R}{Gr}^{-1/4}{x}^{1/4}, \\&\quad \eta =\frac{r^2-R^2}{R^2\xi }, \frac{r^2}{R^2}=1+\xi \eta ,\\&\psi =4\nu _f{R}{Gr}^{1/4}{x}^{3/4}f(\eta ,\xi ), \theta =\frac{T-T_\infty }{T_\omega -T_\infty },\\&\quad \nu _f=\frac{\mu _f}{\rho _f},\\&Gr=\frac{g\beta (T_\omega -T_\infty )L^3}{4\nu _f}, Ha=\sqrt{\frac{\sigma _f}{4\mu _f}}{B_0 R} \end{aligned} \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \begin{aligned} u&=\frac{1}{r}{\frac{\partial \psi }{\partial r}}=\frac{4\nu _f}{L}{Gr}^{1/2}{x}^{1/2}f'\\ \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \begin{aligned} v&=-\frac{1}{r}{\frac{\partial \psi }{\partial {\overline{x}}}}=-\frac{\nu _f}{L}\left( \frac{R}{r}\right) {Gr}^{1/4}{x}^{-1/4}\left[ \xi \frac{\partial f}{\partial \xi }-f'\eta +3f\right] \\ \end{aligned} \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \begin{aligned} \frac{\partial {u}}{\partial {x}} =\frac{\nu _0}{L^2}{Gr}^{1/2}{x}^{-1/2}\left[ \xi \frac{\partial f'}{\partial \xi }-\eta f''+2f'\right] \end{aligned} \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \begin{aligned} \frac{\partial u}{\partial r} =\frac{4\nu _0}{L^2}{Gr}^{3/4}{x}^{1/4}\left( \frac{r}{R}\right) f'' \end{aligned} \end{aligned}$$
(16)
$$\begin{gathered} \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\mu _{{ff}} \frac{{\partial u}}{{\partial r}}} \right) = \frac{{\mu _{{\epsilon}} }}{{(1 - \phi )^{{2.5}} }}\frac{{4\nu _{f} Gr}}{{L^{3} }}. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \left[ {\left( {1 + \epsilon\theta } \right)^{{ - 1}} \left( {1 + \xi \eta } \right)f^{{\prime \prime \prime }} + \left( {1 + \epsilon\theta } \right)^{{ - 1}} Gr^{{1/4}} } \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \left. {\frac{{2L}}{R}x^{{1/4}} f^{{\prime \prime }} - \epsilon\left( {1 + \xi \eta } \right)\left( {1 + \epsilon\theta } \right)^{{ - 2}} f^{{\prime \prime }} \theta ^{\prime}} \right] \hfill \\ \end{gathered}$$
(17)
$$\begin{aligned}{} & {} \begin{aligned} \frac{\partial {T}}{\partial {x}}&=\frac{\Delta T}{L}\frac{1}{4x}\left( \xi \frac{\partial \theta }{\partial \xi }-\eta \theta '\right) \end{aligned} \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \begin{aligned} \frac{\partial {T}}{\partial r} =\left( \frac{r}{R}\right) \frac{\Delta T}{L}{Gr}^{1/4}{x}^{-1/4}\theta ' \end{aligned} \end{aligned}$$
(19)
$$\begin{aligned} \frac{\partial }{{\partial r}}\left( {r\frac{{\partial T}}{{\partial r}}} \right) = & \frac{{\Delta T}}{L}Gr^{{1/4}} x^{{ - 1/4}} \frac{{2r^{3} }}{{R^{3} \xi }}\theta ^{{\prime \prime }} \\ + & 2\left( {\frac{r}{R}} \right)\frac{{\Delta T}}{L}Gr^{{1/4}} x^{{ - 1/4}} \theta ^{\prime } \\ \end{aligned}$$
(20)

The non-dimensional governing equations become as follows:

$$\begin{aligned} {} \begin{aligned}&\frac{\rho _f}{\rho _{ff}}.\frac{1}{\left( 1-\phi \right) ^{2.5}}\left[ \left( 1+\epsilon \theta \right) \left( 1+\xi \eta \right) f'''\right. \\&\left. +\xi \left( 1+\epsilon \theta \right) f''-\epsilon \left( 1+\xi \eta \right) f''\theta '\right] +\left( 1+\epsilon \theta \right) ^{2}.\\&\left[ 3ff''-2f'+\frac{\left( \rho \beta \right) _{ff}}{\left( \rho \beta \right) _{f}}.\frac{\rho _f}{\rho _{ff}}\theta -\frac{\sigma _{ff}}{\sigma _{f}}.\frac{\rho _f}{\rho _{ff}}Ha^2\xi ^2f'\right] \\& \quad \quad \; =\left( 1+\epsilon \theta \right) ^2\xi \left[ f'\frac{\partial f'}{\partial \xi }-f''\frac{\partial f}{\partial \xi }\right] \end{aligned} \end{aligned}$$
(21)
$$\begin{aligned} {} \begin{aligned} \frac{1}{Pr}.\frac{\alpha _{ff}}{\alpha _f}\left[ \left( 1+\xi \eta \right) \theta ''+\xi \theta '\right] +3f\theta '=\xi \left[ f'\frac{\partial \theta }{\partial \xi }-\theta '\frac{\partial f}{\partial \xi }\right] \\ \end{aligned} \end{aligned}$$
(22)

where \(\epsilon =\gamma (T_w-T_{\infty })\) is the viscosity variation parameter.

The non-dimensional boundary conditions are

$$\begin{aligned}{} & {} f'=0, \quad \theta =1 \quad \text {at} \quad \eta = 0 \end{aligned}$$
(23a)
$$\begin{aligned}{} & {} f'\rightarrow 0, \theta \rightarrow 0 \quad \text {as} \quad \eta \rightarrow \infty \end{aligned}$$
(23b)

The calculation of the shearing stress in terms of the skin-friction coefficient and the rate of heat transfer in terms of the Nusselt number, which can be expressed in non-dimensional form as the following:

$$\begin{aligned} C_{f}=\frac{R Gr^{-3/4}L}{4 \mu _{f}\nu _{f}}T_{w}, Nu=\frac{R Gr^{-1/4}L}{k_{f}\Delta T}q_{w} \end{aligned}$$
(24)

where

$$\begin{aligned} T_{w}=\mu _{f}\left( \frac{\partial u}{\partial {\overline{r}}}\right) _{{\hat{r}}=R}, q_{w}=-k_{ff}\left( \frac{\partial T}{\partial {\overline{r}}}\right) _{{\hat{r}}=R} \end{aligned}$$
(25)

Therefore, the obtained boundary conditions using variables are:

$$\begin{aligned} \frac{C_{f}L}{x^{1/4}r}=f''\left( \xi , 0 \right) \end{aligned}$$
(26)
$$\begin{aligned} \frac{Nu}{x^{-1/4}r}=\frac{k_{ff}}{k_f}\theta '\left( \xi , 0 \right) \end{aligned}$$
(27)

2.3 Numerical Methods

The implicit finite difference method (Keller box method 1978) is considered in this study to solve the non-linear method of partial differential equations (21)–(22) that control the flow. The set of equations (21)–(22) are written in terms of a system of first-order equations in \(\eta\), which are then presented in finite difference form (FDF) by their derivatives and approximating the functions given the principal variations in the direction of both coordinates. Signifying the net scores in the (\(\xi\),\(\eta\)) plane by \(\xi _i\) and \(\eta _j\), where i=1, 2, 3, 4,...., M and j=1, 2, 3, 4,...., N, principle variation guesses are prepared such that the equalisations concerning \(\xi\) explicitly are gathered at \((\xi _{i-1/2}, \eta _{j-1/2})\) and the rest at \((\xi _i, \eta _{j-1/2})\), where \(\eta _{j-1/2}\)= \((\eta _j+\eta _{j-1})/2\). This creates a set of non-linear differential equations in \(\xi _{i-1}\) in terms of their value for strangers in \(\xi _i\). Then, Newton’s semi-linearisation technique is used to linearise these equations and take the converged solution at \(\xi =\xi _{i-1}\) as the primary repetition. To start the method at \(\xi\) = 0, first, we implement the inferential forms for the five variables and apply the Keller box method to determine the absolute common differential equations. It is effective to proceed step by step along the boundary zone after getting the solution to the low stagnation event. For a supplied value of \(\xi\), the repetitive system is closed when the variation in velocity and temperature calculations in the subsequent repetition is smaller than \(10^{-5}\) when \(|\delta f^i|\le 10^{-5}\), where the superscript expresses the repetition quantity. The calculations were not accomplished by applying an equal layer in the direction of y, but a non-stable layer \(\eta _j=\sinh ((j-1)/p)\) was applied with j=1,2,3,4,.....,301 and p=100. This method was elaborately explained by Molla et al. (2006a, 2006b, 2009). A brief summary of the Keller box method is presented in Fig. 2.

Fig. 2
figure 2

Flowchart of the Keller box method demonstrating the steps

Full size image

3 Model Validation

The present FORTRAN 90 code is validated with available results of Aziz and Na (1982), Wang and Kleinstreuer (1989) and Takhar et al. (2002) in terms of the ratio of local Nusselt number to local Nusselt number at the leading edge, as shown in Table 2. This table shows that the present results agree well with the above-mentioned results.

Table 2 The results of \(Nu/(Nu)_\xi =0\) for different Pr
Full size table

4 Results and Discussion

The magnetohydrodynamic natural convection of ferrofluid with temperature-dependent viscosity along a heated vertical thin cylinder has been investigated using the implicit finite difference method. In this section, computational results of streamline, isotherms, local skin friction, local Nusselt number, velocity and temperature distribution with the effect of various parameters such as nanoparticle volume fraction, \(\phi\) (=0.0, 0.02, 0.04, 0.06), viscosity variation parameter \(\epsilon\)(=0.0, 0.2, 0.5, 0.8), Hartmann number, \({\text{ Ha }}\) (=0, 1, 2, 3, 4, 5), and Prandtl number at \({\text{ Pr }} =6.2\) are presented and analysed in the following subsections.

4.1 Effect of \({\text{ Ha }}\) Number

The effect of \({\text{ Ha }}\) has an adverse effect on natural convection. As \({\text{ Ha }}\) increases, the magnitude corresponding to heat transfer should decrease due to the weakened convective flow inside the geometry. In addition, an increased \({\text{ Ha }}\) also increases the thickness of the boundary layer.

4.1.1 Changes in Local Skin Friction and \(\text{ Nu }\) Number

In Fig. 3, computed values of local skin friction (\(C_{\text{ f }}\)) and local Nusselt number (Nu) against axial coordinate \(\xi\) for different values of \({\text{ Ha }}\) (=0, 1, 2, 3, 4, 5) are represented. The analysis was conducted under homogeneous conditions with \(\phi =0.04\). In general, it was found that as \({\text{ Ha }}\) increased from a non-zero value, the local skin friction decreased concurrently, thus confirming the statement mentioned earlier. However, the complete absence of \({\text{ Ha }}\) from the system (\({\text{ Ha }}=0\)) caused \(C_{\text{ f }}\) to increase continuously, which confirms the negative impact of increasing boundary thickness if \({\text{ Ha }}\) is present in any system. This behaviour is attributed to the fact that with increasing \({\text{ Ha }}\), the Lorentz force opposes the flow, and the magnetic force is an obstacle to the velocity. As a result, the thickness of the momentum boundary layer decreases. The continuous increase in \({\text{ Ha }}\) is anticipated to increase further restriction to the fluid within the boundary layer, thereby leading to a further reduction in the \(C_{\text{ f }}\) values as \(\xi\) increased concurrently. On the other hand, the local \(\text{ Nu }\) also decreased with increasing \({\text{ Ha }}\). If \({\text{ Ha }}=0\) was considered from the beginning, \(\text{ Nu }\) increased linearly. However, an increase in \({\text{ Ha }}\) from a non-zero value decreased \(\text{ Nu }\) up to one stage before increasing abruptly. The sharp changes are attributed to the position where the thickest boundary is overcome. As the fluid overcame the thickest position within the boundary layer and approached a comparatively thinner layer, \(\text{ Nu }\) increased concurrently, as if \({\text{ Ha }}\) was absent from the system. This change occurs much earlier for higher \({\text{ Ha }}\). For example, at \({\text{ Ha }}=5\), in Fig. 3b, \(\text{ Nu }\) started to increase around \(\xi =1\), whereas it was observed at a much later stage for \({\text{ Ha }}=1\), which was at approximately \(\xi =4\). The observed results from this section suggest that the increasing \(C_f\) has an adverse impact on \(\text{ Nu }\), i.e., numerical representative of heat transfer. Therefore, as \(C_{\text{ f }}\) started to decrease at the initial stage due to the impact of \({\text{ Ha }}\), \(\text{ Nu }\) started to decrease gradually. Nevertheless, at \(\xi >1\), the effect of \(C_{\text{ f }}\) diminished from the system, providing more degrees of freedom for \(\text{ Nu }\) to increase. In the absence of \({\text{ Ha }}\), \(C_{\text{ f }}\) does not change significantly because the magnetic field is non-existent; however, \(\text{ Nu }\) increases rapidly due to the absence of the obstacles to the heat transfer that were generated due to the Lorentz force.

Fig. 3
figure 3

Effect of \({\text{ Ha }}\) on a local skin friction (\(C_{\text{ f }}\)), and b local Nusselt numbers (\(\text{ Nu }\)) at \(\epsilon =0.5\), \(\phi =0.04\)

Full size image

4.1.2 Influence on Velocity and Temperature Profiles

Fig. 4
figure 4

Effect of \({\text{ Ha }}\) on a velocity profile (\(f'\)) and b temperature profile (\(\theta\)) at \(\epsilon =0.5\), \(\phi =0.04\)

Full size image

The effects of \({\text{ Ha }}\) were later subjected to analysis concerning velocity (\(f'\)) and temperature (\(\theta\)) profiles against a pseudo-similarity variable (\(\eta\)) as depicted in Fig. 4. The influence of magnetic parameters on both profiles has different trends, as the temperature is more affected by the presence of \({\text{ Ha }}\). At the same time, the velocity profile corresponding to the highest \({\text{ Ha }}\) in the analysis is less affected.

As per Fig. 4a, the local maxima for each curve representing velocity profiles were found to be between \(0.025\le \eta \le 0.135\) at different \({\text{ Ha }}\), with \(Ha_{max}\) on the input leading to the lowest peak value of velocity. In other words, the peak with the highest value was found to be the fluid without the influence of any \({\text{ Ha }}\), i.e., \({\text{ Ha }}=0\). This behaviour can be linked with the discussion of the Lorentz force earlier, which eventually hinders the fluid velocity. Therefore, as \(\eta\) increased, \(f'\) decreased simultaneously before heading towards the quasi-static condition at \(\eta =8\). Meanwhile, no peak was recorded in terms of the temperature profile, as illustrated in Fig. 4b. The temperature profiles were found to be improved under the presence of magnetic parameter, and the temperature profile corresponding to \({\text{ Ha }}=0\) exhibited the lowest values before reaching almost 0 at \(\eta =3\). While \(\theta =0.45\) was obtained at \(\eta =2\) for \({\text{ Ha }}=5\), the value was around 0.05 for \({\text{ Ha }}=0\) and 0.1 for \({\text{ Ha }}=1\), which are much lower. In other words, with an increase in \({\text{ Ha }}\) from 1 to 5, at \(\eta =2\), the value of \(\theta\) increased almost \(350\%\), which represents the significant impact of \({\text{ Ha }}\) on the temperature profile. The velocity distribution cannot be uniform within the boundary layer due to the shape of the geometry and the boundary conditions. The separation due to the thermal boundary layer and momentum boundary layer are also evident. A peak velocity will be developed regardless of the \({\text{ Ha }}\) values. However, it could be understood from the aforementioned analysis that the absence of \({\text{ Ha }}\) provides more mobility to the fluid flow. Therefore, the velocity curve representing \({\text{ Ha }}=0\) exhibited the highest peak value. It can also be postulated from this analysis that a further increase in \({\text{ Ha }}\) will eventually impose a higher degree of restrictions and eventually the mobility of the fluid flow will be close to 0, i.e., static flow condition. Meanwhile, the temperature profiles will continue to demonstrate a consistent trend in the values due to heat dissipation. As \(\eta\) increases, the distribution of temperature will continue to plummet due to the dominance of variable viscosity as well as the inclusion of \({\text{ Ha }}\). In the absence of magnetic field strength, the temperature profile will not be able to create the distribution and eventually, it will reach 0 quicker than any other curve representing a non-zero \({\text{ Ha }}\). Therefore, in order to prolong the temperature distribution within the boundary layer, it is recommended to consider a non-zero \({\text{ Ha }}\)that will be adequate to face the obstacles created by the Lorentz force as well as \(\eta\) to show a complete temperature profile. As per the results from Fig. 4a, b, \({\text{ Ha }}=1-3\) seems to be an appropriate choice.

4.2 Influence of Volume Fraction (\(\phi\)) Number

This section aims to discuss the results in terms of the effect of the volume fraction parameter (\(\phi\)), which distinguishes between the carrier fluid (\(\phi =0\)) and ferrofluid (\(\phi >0\)). At first, the effect of \(\phi\) on \(C_{\text{ f }}\) and \(\text{ Nu }\) will be discussed (Fig. 5), and then both velocity (\(f'\)) and temperature (\(\theta\)) profiles (Fig. 6) will be analysed. In all circumstances, \({\text{ Ha }}\) has been kept constant at 2, and \(\epsilon =0.5\) were considered.

4.2.1 Impact on Local Skin Friction and \(\text{ Nu }\) Number

Figure 5 (a) examines the effect of \(\phi\) on \(C_{\text{ f }}\). In general, it was found that \(C_{\text{ f }}\) continued to decrease as \(\xi\) increased, regardless of the rheology of the fluid. However, carrier fluid or pure fluid, i.e., fluid with \(\phi =0\) had the highest peak value of \(C_{\text{ f }}\), indicating the negative impact of ferromagnetic particles on the boundary layer. The inclusion of \(\phi\) effectively reduced the local maxima of \(C_{\text{ f }}\) marginally due to the higher density of ferromagnetic particles. The highest \(\phi\) was considered 0.06 in this segment, and the corresponding curve exhibited the lowest peak value as seen in Fig. 5a. The consideration of \(\phi\) eventually improved the fluid viscosity within the system; hence, the surface shear stress got reduced, leading to decreasing \(C_{\text{ f }}\) values. Combining this situation, it was expected that an enhancement in the effective heat transfer would take place, which was manifested at the later stage.

Fig. 5
figure 5

Impact of \(\phi\) on a local skin friction (\(C_{\text{ f }}\)), and b local Nusselt (\(\text{ Nu }\)) at \({\text{ Ha }}=2\), \(\epsilon =0.5\)

Full size image

On the other hand, different trends were observed for \(\text{ Nu }\) as \(\phi\) varied as illustrated in Fig. 5b. In general, it was observed that initially, \(\text{ Nu }\) increased and reached peak values as \(\xi\) increased from 0, irrespective of \(\phi\) values. However, after reaching the peak, the values of \(\text{ Nu }\) started to decrease continuously, indicating the reduction in the heat transfer due to the dominance of the ferromagnetic particles. Including ferromagnetic particles tends to restrict fluid mobility inside the cylinder, which eventually decreases \(\text{ Nu }\), representing heat transfer. However, the maximum peak value of \(\text{ Nu }\) was observed in the absence of a ferromagnetic particle, i.e., at \(\phi =0\), indicating the negative impact of \(\phi\) on the heat transfer. The findings from this segment suggest that the inclusion of \(\phi\) can eventually be good to overcome the hindrance created by \(C_{\text{ f }}\); however, that should also decrease the heat transfer phenomena marginally. Nevertheless, it will be prudent to tune \(\phi\) as per the requirement of a device containing ferrofluid as coolant. The marginal inclusion of \(\phi\) could improve the heat transfer characteristics within the boundary layer.

4.2.2 Influence on Velocity and Temperature Profiles

As mentioned earlier, the inclusion and increasing values of \(\phi\) restrict the fluid movement. Further evidence was observed while studying the response of the velocity (\(f'\)) as depicted in Fig. 6a. The increasing \(\phi\) values indicate the increasing viscosity, which also increased concurrently with the thermal conductivity. Therefore, as \(\eta\) increased initially from 0, the fluid exhibited mobility from the complete static condition. Once the values of \(\eta\) increased and crossed \(\eta > 1\), the velocity dropped sharply due to increased restriction of fluid movement inside the cylinder. It was also observed that the peak value of \(f'\) corresponding to \(\phi =0\) was marginally more significant than any of the peak \(f'\) values representing other non-zero values of \(\phi\). Since only one \({\text{ Ha }}\) was considered in this part of study, the bigger difference was not noticed. However, the impact of \({\text{ Ha }}\) was already discussed while explaining Fig. 4.

Fig. 6
figure 6

Effect of \(\phi\) on a velocity and b temperature profiles for different values of \(\phi\) while \({\text{ Ha }}=2\), \(\epsilon =0.5\)

Full size image

The impact of \(\phi\) on the temperature profile has been included by observing the changes in temperature representative \(\theta\), as shown in Fig. 6b. While the difference was not completely visible at first glance, the magnified image of a specific area of interest has been added inside a frame for a better visualisation. As per the magnified image, the increased values of \(\phi\) increased the temperature of the ferrofluid. In other words, at a specific value of \(\eta\), the temperature was higher for \(\phi =0.06\) than for \(\phi =0\). The increasing \(\phi\) values indicate the ferrofluid’s improved thermal conductivity; hence, \(\theta\) will be higher as \(\phi\) increases. However, it was also observed that as \(\eta\) increased, \(\theta\) decreased continuously, regardless of the values of \(\phi\), due to the increased viscosity. If \(\eta\) increased, the temperature started to fall; therefore, \(\theta\) started to decrease rapidly. The observed results from this analysis showed that the inclusion of \(\phi\) within the boundary layer impacted the \(C_{\text{ f }}\) and \(\text{ Nu }\), the velocity and temperature distribution are seldom impacted. Any electronic cooling device containing ferrofluid can benefit from this observation as the heat transfer capability can be improved or downgraded as per the requirement, without creating any major change in the fluid velocity or temperature profile. Improving heat transfer at the cost of increased fluid velocity is not advantageous, as it may cause the whole system to become unstable, which will create another challenge to tackle. Therefore, the mixing of nanoparticles or ferromagnetic particles should be performed by observing the aforementioned sensitivity analyses.

4.3 Impact of Viscosity

The parametric sensitivity analyses so far have been conducted in terms of varying \({\text{ Ha }}\) and \(\phi\). This section will explore the behavioural changes in the target variables as a function of viscosity.

4.3.1 Impact on Local Skin Friction and \(\text{ Nu }\) Number

The influence of \(\epsilon\) was demonstrated in Fig. 7 by observing the changes in local skin-friction coefficient (\(C_{\text{ f }}\)) and local \(\text{ Nu }\) in Fig. 7a and b, respectively. It was observed that the \(C_{\text{ f }}\) values decreased as \(\xi\) increased. However, at a fixed \(\phi =0.04\), the inclusion of \(\epsilon\) accelerated the peak values of fluid with the highest \(\epsilon\) value (in this case \(\epsilon =0.8\)). While the local maximum of the curve corresponding to fluid with \(\epsilon =0.8\) was observed to be around 0.65, the value plummeted to around 0.42 in the absence of \(\epsilon\). The increasing values of \(\epsilon\) reinforced the reduction of the \(C_{\text{ f }}\) values as the reduced shear stress accelerated resistance within the cylinder. Technically, \(\epsilon =0\) does not exist in practical fluid, as the second law of thermodynamics requires fluids to have positive viscosity. However, fluid with \(\epsilon =0\) is generally defined as ideal fluid/superfluid or inviscid.

Fig. 7
figure 7

Influence of viscosity on a local skin friction (\(C_{\text{ f }}\)), and b local Nusselt numbers (\(\text{ Nu }\)) at \({\text{ Ha }}=2\), \(\phi =0.04\)

Full size image

Similar behaviour was observed regarding local \(\text{ Nu }\) with fluid with the maximum \(\epsilon\) exhibiting the highest peak value. This behaviour was linked with the previous observation where the increasing fluid viscosity reduced the boundary layer thickness and shear stress leading to improved viscosity, which is also responsible for increasing the heat transfer. However, as the peak values were overcome, the curves representing \(\text{ Nu }\) started to fall to local minima before increasing again. Since the effect viscosity initially decreased, \(\text{ Nu }\) began to increase due to the dominance of natural convection. The graphs obtained from the numerical simulation describe the significant contribution of temperature-dependent viscosity on \(C_{\text{ f }}\) and \(\text{ Nu }\). Because of the consistent value of \({\text{ Ha }}\) within the system, the Lorentz force played a key role in increasing the peak values of both \(C_{\text{ f }}\) and \(\text{ Nu }\). It could also be observed that the presence of \(\phi\) along with \({\text{ Ha }}\) in fact increased the peaks of \(\text{ Nu }\), which was the highest for an increased viscosity. The increased viscosity values within the boundary layer would have restricted the fluid mobility in the absence of \({\text{ Ha }}\) and if only carrier fluid was present in the system, i.e., \(\phi =0\). However, due to the presence of those parameters, the increasing \(\epsilon\) in fact improved the heat transfer of the fluid within the boundary layer. The findings highlight the need to consider the temperature-dependent viscosity within a system rather than considering it as a constant, where the latter does not necessarily represent a practical example.

4.3.2 Behavioural Changes in Velocity and Temperature Profiles

In Fig. 8, the effects of varying viscosity, \(\epsilon\) (\(=0.0, 0.2, 0.5, 0.8\)), on the velocity (\(f'\)) and temperature (\(\theta\)) profiles against the pseudo-similarity variable (\(\eta\)) are displayed in Fig. 8a and b, respectively. As observed in Fig. 8a, the velocity profiles increased at the leading edge, and after that, they started to decrease with increasing values of \(\eta\). Viscosity is inversely equivalent to dimensional viscosity. Therefore, as a result of increasing the viscosity parameter, the non-dimensional viscosity decreased, and as a consequence, the viscous energy decreased, which was responsible for opposing the fluid flow. This consequence eventually affected the viscous forces and translated into inertia energy; therefore, the liquid mobility was accelerated. On the other hand, in Fig. 8b, the \(\theta\) values decreased with increasing \(\epsilon\). Like the previous sections, it was also observed in Fig. 8 that for each value of \(\epsilon\), there exists local maxima in velocity near the leading edge, and later the corresponding parametric values started to decrease. This behaviour can be explained by the fact that the reduction of excess viscosity is interpreted as a reduction in viscous energy. As a result, this viscous energy reduced friction between the liquid and the surface, leading to reduced heat wastage within the boundary layer. The characteristic curves illustrated in Fig. 8a, b accord with the findings described in Fig. 7a, b, where the increased \(\epsilon\) increased the velocity peak marginally. However, the temperature profiles remained almost unchanged. The changes could only be observed through magnification on a specific point. Based on this part of the analysis, the implications of variable viscosity should be conducted in such a way that the thermal efficiency is improved within the system and at the same time, the fluid mobility remains stable. The constant input values of \({\text{ Ha }}\) and \(\phi\) played the pivotal role in maintaining such consistency. Therefore, in order to improve the heat transfer phenomena at a variable viscosity, it is recommended to keep constant magnetic field strength and volume fraction of ferromagnetic particle. However, the velocity is likely to plummet consequently as fluid flow crosses the thermal boundary layer and approaches the end point of the momentum boundary layer.

Fig. 8
figure 8

Effect of viscosity on a velocity and b temperature profiles at \({\text{ Ha }}=2\),\(\phi =0.04\)

Full size image

4.4 Streamlines and Isotherms

The impact of different parameters on the streamlines and isotherms is visualised here. Therefore, the analyses in this section will be discussed in terms of varying viscosity (\(\epsilon\)), volume fraction of nanoparticles (\(\phi\)) and \({\text{ Ha }}\). In all cases, the differences in the patterns of streamlines and isotherms are observed keeping pseudo-similarity variable or representative viscosity \(\eta\) as a dependent variable.

4.4.1 Impact on Streamlines and Isotherms at Variable Viscosity

The focus of this section is the influence of the streamwise axial parameter (\(\xi\)) on the streamlines and isotherms of the ferrofluid within the boundary layer. At first, the role of \(\xi\) under the influence of varying viscosity (\(\epsilon\)) has been observed under constant \({\text{ Ha }}\) and \(\phi\). It was anticipated that under the lower values of \(\xi\), there would not be a significant impact on \(\eta\), regardless of the presence of \(\epsilon\) near the wall. It was observed that in terms of streamlines, as \(\xi\) increased further, the starting values of \(\eta\) continued to increase before plummeting or exhibiting constant values of 1. It was also found that at lower \(\xi\) when fluid particles are near the wall, it sharply fell from the starting value and maintained consistent values throughout regardless of the increasing values of \(\xi\). However, at \(\xi \ge 6\), the steady values were not observed immediately due to the impact of the free-stream surface. The isotherms obtained in Fig. 9b show the streamline patterns, as it was observed that the isotherms began from \(\eta =1\) since \(\xi\) was 0. However, as \(\xi\) increased from 0, the isotherms began to spread out, and the difference between each module started to increase from the top. Nevertheless, the differences were not significant. To summarise, the obtained graphs in Fig. 9 suggest that the variation of flow rate or temperature is insignificant to \(\phi\). However, marginal difference in the streamlines could be noticed at \(\xi \ge 8\), yet those do not represent any dominance or impact of \(\epsilon\). Further explanations could be included in the light of the discussion above. Because of the constant \({\text{ Ha }}\) and \(\phi\) values within the boundary layer, the values of stream function remained almost identical at the beginning because they were close to the wall. However, as \(\xi\) increased gradually, the flow edged away from the boundary layer and consequently, marginal differences in the stream function (flow rate) values could be observed at \(\xi >8\). While peak values representing different \(\epsilon\) increased the peak values of \(\text{ Nu }\) before, the stream function does not change significantly regardless of the \(\epsilon\) value due to the less influential impact on fluid mobility and temperature profile as depicted in Fig. 8. Since \({\text{ Ha }}\) remained constant, the thickness of the boundary layer did not increase. Therefore, the changes in the stream function values and isotherms could only be impacted due to the variable viscosity (\(\epsilon\)).

Fig. 9
figure 9

Effect of \(\xi\) on a streamlines and b isotherms at \(\epsilon =0\) (solid lines), \(\epsilon =0.8\) (dashed lines) while \({\text{ Ha }}=2\), \(\phi =0.04\)

Full size image

4.4.2 Impact on Streamlines and Isotherms Due to Ferroparticles

Meanwhile, the immediate impact of \(\phi\) was noticed as \(\xi\) increased to a significantly higher value (for example, \(\xi \ge 8\)) near the free-stream surface under a constant \(\epsilon\) since it was found that porosity variation was not influential in varying \(\eta\). Figure 10 supports the aforementioned theory as illustrated for both streamlines (Fig. 10a) and isotherms (Fig. 10b). It was expected that the effect of \(\phi\) would have less influence near the wall, regardless of the condition implied within the geometry. However, as \(\xi\) increased further to 3, the impact of \(\phi\) was observed. In fact, at \(\xi =4\), the streamline exhibited twice the value at \(\phi =0.06\) than that at \(\phi =0.0\). It was anticipated that the difference would keep expanding at further increased \(\xi\) as well, indicating the simultaneous effect of \(\phi\) on the flow rate. Nevertheless, the influence of \(\phi\) or \(\epsilon\) will still have less influence than \(\xi\) due to less impact on the temperature variation. According to Fig. 10b, the obtained curves support the hypothesis. Compared to the findings from Fig. 9, it could be seen that the changes in the stream function are more visible in this analysis. This evidences the impact of \(\phi\) on the stream function which was more influential than \(\epsilon\). The increasing value of \(\phi\) means the fraction of the ferromagnetic particles increased which eventually increased the skin-friction coefficient. Therefore, the fluid mobility is restricted and the stream function decreases. Initially, there was no difference in the stream function. However, as \(\xi\) increased gradually, the distance from the wall increased and difference in the stream function value increased. As \(\xi\) continued increasing, the difference in the stream function values between the curves corresponding to \(\phi =0\) and \(\phi =0.06\) continued increasing.

Fig. 10
figure 10

Effect of \(\phi\) on a streamlines and b isotherms for \(\phi =0\) (solid lines), \(\phi =0.06\) (dashed lines) while \({\text{ Ha }}=2\), \(\epsilon =0.5\)

Full size image

4.4.3 Changes in Streamlines and Isotherms Due to \({\text{ Ha }}\) Number

Finally, the effect of varying \({\text{ Ha }}\) is observed in Fig. 11. The presence of \({\text{ Ha }}\) always creates an obstacle or downgrades the streamlines and temperature to a greater extent due to the presence of the magnetic field. As per Fig. 11a, at lower \(\xi\) (\(\le 1\)), there was no prominent impact of \({\text{ Ha }}\). However, as \(\xi\) increased, the curves representing \({\text{ Ha }}=0\) and \({\text{ Ha }}=5\) started to lose alignment. The curves of \({\text{ Ha }}\) started to exhibit quasi-horizontal characteristics. In contrast, the curves of \({\text{ Ha }}=0\) remained in a consistent state at the beginning due to the presence of the wall. This behaviour could be attributed to the fact that in the presence of \({\text{ Ha }}\) inside the cylinder, the ferrofluid is influenced significantly by the magnetic field, which decreases the flow rate. Because of this, it was also expected that the temperature variation would be substantially different at the free-stream surface due to the weakened convective flow. The curves illustrated in Fig. 11b confirm these characteristics. It can be seen that the differences in the isothermal lines at \(\xi \ge 3\) are so wide that two different colours were obtained separately instead of overlapped curves, implying the significant role of \({\text{ Ha }}\) in the isothermal lines as well as \(\eta\). At \(\xi =3\) and \(\xi =4\), the differences (\(\%\)) in the peak values of the curve representing \({\text{ Ha }}=0\) and \({\text{ Ha }}=5\) were \(46.66\%\) and \(52.63\%\), respectively. In other words, the viscosity increased to a large extent, which eventually restricted the flow movement leading to comparatively less-significant convective flow inside the boundary layer of the thin cylinder. The impact of \({\text{ Ha }}\) within the thin cylinder suggests that the magnetic field strength significantly downgrade the stream flow of the fluid if \(\epsilon\) and \(\phi\) remain constant. This negative impact could be overcome by imposing variable viscosity within the system as described earlier. On the other hand, if it is a necessity to keep stream function lower within the system, increasing magnetic field strength should suffice which could provide an option on the controlling mechanism of the ferrofluid within a system.

Fig. 11
figure 11

Influence of varying \({\text{ Ha }}\) numbers on a streamlines and b isotherm for \({\text{ Ha }}=0\) (solid lines), \({\text{ Ha }}=5\) (dashed lines) while \(\epsilon =0.5\), \(\phi =0.04\)

Full size image

5 Conclusions

In this research, the natural convection of ferrofluid along a vertical thin cylinder with temperature-dependent viscosity has been studied by implicit finite difference by considering the Keller box method. The viscosity function is inversely proportional to temperature. The study has been conducted by varying four key parameters, namely, ferroparticle volume fraction \(6\%\), (\(\phi \in [0,0.06]\)), temperature-dependent viscosity, \(\epsilon \in [0, 0.8]\), and Hartmann number (\(0\le\)Ha\(\le 5\)). The computational code was written in the FORTRAN language, and model validation was conducted by comparing the obtained results with three well-cited literature studies. The physical correlations among the ferroparticles, heat transfer, and the influence of the external magnetic field were investigated by sensitivity analyses. The concepts within this study can be used in industries working with nanofluids, where stabilising the fluid flow within the defined geometries poses an inherent challenge. With the further addition of \({\text{ Ha }}\), the flow can be stabilised within geometry, and at the same time, elevated temperature can be recorded. The major outcomes of the study are listed below:

  • The inclusion of \({\text{ Ha }}\) weakens the convective heat transfer within the thin cylinder. As a result, the local skin friction (\(C_{\text{ f }}\)), Nusselt number (\(\text{ Nu }\)), and velocity distribution (\(f'\)) will decrease concurrently if \({\text{ Ha }}\) increases. By increasing \({\text{ Ha }}\), the Lorentz force is free to dominate the ferrofluid flow within the thin boundary layer, and hence the momentum is hindered.

  • As the volume fraction of ferroparticles (\(\phi\)) increases, the local skin friction decreases due to the reduction in particle mobility due to the increased viscosity and decreasing surface shear stress. A similar trend is also seen in terms of \(\text{ Nu }\) at the leading edge, but after a local minimum, it starts to increase. However, if \({\text{ Ha }}\) remains constant throughout, there is no significant impact of \(\phi\) on velocity (\(f'\)) and temperature (\(\theta\)) distributions.

  • Increasing viscosity (\(\epsilon\)) leads to increasing the peak values of \(C_{\text{ f }}\) and \(\text{ Nu }\) under the presence of \({\text{ Ha }}\). However, \(f'\) exhibits a similar behaviour at the edge of the cylinder and later plummets to quasi-static conditions.

  • A significant variation is observed in the free-stream surface for varying \({\text{ Ha }}\) within the geometry. The inclusion of the magnetic parameter almost doubles the pseudo-similarity variable (\(\eta\)) at a constant \(\epsilon\) and \(\phi\) (non-zero).