A Revamped Element-Free Galerkin Algorithm for Accelerated Simulation of Fracture and Fatigue Problems in Two-Dimensional Domains

Abstract

This work presented a revamped element-free Galerkin method algorithm for two-dimensional fracture problems subjected to mechanical/thermoelastic loads. The conventional element-free Galerkin (EFG) technique is modified at the level of approximation along with a novel blended basis enrichment criterion together with parametric optimization at computational level. Further an optimized quadrature point criteria is embedded in the EFGM algorithm to accelerate its computational capability. The modified EFG method exhibits a higher computational efficiency and accuracy than the existing one based on moving least-squares approximation which is susceptible to generation of an ill-conditioned system of equations. The modified algorithm utilizes lesser number of nodes from the problem domain compared to the conventional EFG method for the construction of shape function. A variety of two-dimensional fracture/fatigue problems, have been modelled and simulated with the revamped algorithm. Results reveal that the revamped element-free Galerkin (REFG) method is a robust and efficient technique for modelling two-dimensional fracture problems under both mechanical and thermoelastic loads. Moreover, a significant reduction in computational time is achieved with the proposed algorithm which adds to the prowess of the proposed REFG method.

1 Introduction

Computational methods provide an edge over analytical and experimental methods by saving manpower, experimentation time and need of prototype testing. Finite element method (FEM) being one of the earliest and robust numerical tool still holds its position when it comes to solution of engineering problems. It holds the credit of being the backbone of countless engineering analysis software. This was the earliest development in computational methods for analysis of variety of problems linked with design and analysis (Afsar and Go 2010; Kaddouri et al. 2006; Ju and Hsu 2014; Chao and Chow 2002). Finite element method is a mesh-based technique hence it does not remains untouched from the limitations associated with mesh itself, for example, problems of moving mesh boundary, phase change problems and problems involving continuous remeshing. Moreover, element distortion and low-quality mesh produce spurious results which consequentially require intensive manpower and excessive time. Mesh-free methods have been developed by the continuous improvements in the procedures of mesh-based methods. Mesh-free methods approximations are built with the use of nodal points only, and this helps in eliminating the limitations associated with mesh-based methods.

Element-free Galerkin Method (EFGM) (Belytschko et al. 1994a) is one of the mesh-free method that has been applied for analysis of a variety of problems(Belytschko et al. 1994b; Belytschko et al. 1995; Chen and Wang 2000; Xuan 2002; Li et al. 2015; Singh et al. 2003; Pathak et al. 2014). Modelling and simulations performed with EFGM depends on predefined EFG parameters like nodal density in problem geometry, Gauss quadrature used, support domain size, polynomial function used for defining the weight functions, and technique for imposing essential boundary conditions (Garg and Pant 2016).

EFGM chalks up other mesh-free techniques used in fracture problems by eliminating the demand of remeshing and redistribution of nodal data. EFGM also enables high convergence rates and high adaptivity, and can also be applied to large distortion problems (Nguyen et al. 2008). The application of EFGM for modelling and simulating fracture problems (Pant et al. 2010, 2011a; Pathak et al. 2012; Pant and Bhattacharya 2016; Salari-Rad et al. 2011; Garg and Pant 2018a) has enabled the researchers to perform the crack analysis with a more versatile and robust tools. EFGM has emerged out as an outstanding tool for analysis of variety of problems (Garg and Pant 2018b) as it has the capability to blend with other techniques (Pathak 2017; Pathak et al. 2016, 2015, 2017). As EFGM established itself as a novel technique in the area of design and analysis, the further focus was concerned toward its modification and enhancements, so that it can be made more flexible and efficient in comparison to its conventional form.

The first advancement in EFG method started with use of moving least-square (MLS) method (Shepard 1968) for constructing the shape function and applying boundary conditions with the help of Lagrange's multiplier (Yagawa and Furukawa 2000; Belytschko et al. 1993; Günther and Liu 1998) approach. Further, there have been continuous efforts to improve the procedure for constructing the shape function (Lu et al. 1994; Wen et al. 2008) and implementing boundary conditions (Gavete et al. 2000; Lee and Yoon 2004). Ramp function was used to blend EFGM with FEM (Belytschko et al. 1995; Asadpoure et al. 2006) and fractal finite element methods (FFEM)(Rajesh and Rao 2010; Reddy and Rao 2008) to remove some inherent flaws of EFGM. Later, truly meshless technique emerged on blending EFGM with radial point interpolation method RPIM (Cao et al. 2013) as compared to coupled FEM-EFG approach. Such hybrid techniques inherited the advantages of both parent techniques to fulfil Kronecker delta property simultaneously with high-order continuity and smoothness of shape functions. Improved element-free Galerkin (IEFG) method was purposed (Kaljevic and Saigal 1997) for eliminating the singularities linked to weight functions where basis function was achieved by normalization process. An increase in computation speed in IEFG (Zhang et al. 2008) was achieved compared to the standard EFG method as lesser nodes are required for defining the domain geometry. While few researchers demonstrated the improvement of EFG method by engaging on specific parameters (Valencia et al. 2008, 2009), they did not remark on values or standards of these parameters. Wenterodt and Estorff (2011) carried out parametric analysis of various EFGM parameters like weight function, influence domain size and gauss quadrature in order to decrease the effect of dispersion in acoustics. Meshless Galerkin least-square method (MGLS) (He et al. 2011) was employed for problem based on L-shaped cavity acoustics by varying the EFGM parameters and was found that there is a significant decrement in computational time in comparison to EFGM. Computational speed was significantly increased by applying extended parametric meshless Galerkin method (Musivand-Arzanfudi et al. 2007) for simulating elastostatics problems as this method involved enrichments of approximation functions with discontinuous fields through partition of unity method. Sheng et al. (2015) proposed a criteria by employing uniform number of nodes in support domain but failed to comment about optimum number of nodes in the support domain, instead their criteria increased the total computational time of problem. The changes made in domain radius selection were flawed due to the presence of a scaling parameter (Belytschko et al. 1994a; Sheng et al. 2015; Dolbow and Belytschko 1998; Liu and Tu 2002). To the best of author’s knowledge, very limited work has been emphasized on the optimum range of EFG parameters ideal for efficient simulations with least computational time. Previously performed parametric studies varied the range of EFG parameters rather than using optimization technique for multiple simulations variations.

In the present work, a novel revamped structure of element-free Galerkin algorithm has been proposed by the authors which includes:

• Use of improved moving least-square (IMLS) approximation method rather than conventional moving least-square (MLS) approximation method.

• Optimization of EFGM parameters using Taguchi’s optimization to reduce the actual number of simulations required.

• Employing a newly proposed blended basis enrichment criterion rather than using conventional full basis enrichment function.

• Use of newly proposed optimized quadrature criteria for integration purpose.

The novelty of present work lies in enhancing the conventional element-free Galerkin method by blending it with Improved moving least-square method (IMLS) (Liew et al. 2005, 2006) along with optimization of EFGM parameters using Taguchi's technique into a unified EFG algorithm wherein the proposed algorithm can be used as a generic tool to model and simulate a wide variety of fracture problems with high accuracy and least computational time.

Optimization will help to choose a suitable predetermined value of the nodes (under domain of influence) thereby eliminating the confusion about suitable value of scaling parameter. Moreover, the algorithm has been blended with newly proposed enrichment criteria in order to enhance computational efficiency of the method. Algebraic equations in case of IMLS approximation are not ill conditioned and can be solved with the use of inverse matrix. Moreover, fewer coefficients in IMLS approximation further enhance the computation speed of algorithm. The simulation so performed using the optimized parameters blended with new enrichment criteria along with improved moving least-square method (IMLS) will drastically decrease the computational time (T_EFGM) of EFGM analysis while keeping the accuracy intact. The new proposed algorithm is tested for various fracture problem simulations under different loadings and also in complex geometry problems. Further, the method has been extended to simulate the fatigue life estimation where the simulation needs to run for a very high number of repetitive cycles, and thus the total computational time becomes a significant parameter to be worked upon. Results reveal that the modified algorithm proposed in this article works efficiently with significantly lesser number of nodes and provide nearly 75% reduction in the computational time required for simulation.

2 EFGM Formulation for Two-Dimensional Elasticity Problems

Figure 1 shows a 2D domain bounded by $\Gamma$, subjected to various forces.

Fig. 1

Domain representation with boundary conditions

The governing equilibrium equations (Nguyen et al. 2008) are as follows:

$$\nabla .\,{{\varvec{\upsigma}}} + {\mathbf{b}} = 0\quad {\text{over}}\,\Omega$$

(1)

Subjected to boundary conditions mentioned below:

$${\mathbf{u}} = {\overline{\mathbf{u}}}\quad {\text{over}}\,\Gamma_{u} \,\left( {{\text{Essential}}} \right)$$

(2)

$${{\varvec{\upsigma}}}.\,{\overline{\mathbf{n}}} = {\overline{\mathbf{t}}}\quad {\text{over}}\,\Gamma_{t} \left( {{\text{Natural}}} \right)$$

(3)

here ${{\varvec{\upsigma}}}$ represents the stress tensor, as ${{\varvec{\upsigma}}} = {\mathbf{D}}({\mathbf{x}})\,[{{\varvec{\upvarepsilon}}}]$, ${\mathbf{D}}({\mathbf{x}})$ is the material matrix, ${{\varvec{\upvarepsilon}}}$ is the strain vector,${\mathbf{b}}$ is the body force vector, ${\mathbf{u}}$ is the displacement vector, ${\overline{\mathbf{t}}}$ is the traction force and ${\overline{\mathbf{n}}}$ is the unit normal. Now, using Lagrange multiplier approach (Belytschko et al. 1994a) to enforce boundary conditions and applying variational principle (Belytschko et al. 1994b; Nguyen et al. 2008), discrete equations as mentioned below is obtained from Eq. (1)

$$\left[ \begin{gathered} {\mathbf{K}}\,\,\,\,\,\,\,\,\,{\mathbf{G}} \hfill \\ {\mathbf{G}}^{T} \,\,\,\,\,\,\,0 \hfill \\ \end{gathered} \right]\left\{ \begin{gathered} {\mathbf{u}} \hfill \\ {{\varvec{\uplambda}}} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} {\mathbf{f}} \hfill \\ {\mathbf{q}} \hfill \\ \end{gathered} \right\}$$

(4)

where,

$$K_{I\,J} = \int\limits_{\Omega } {{\mathbf{B}}_{I}^{T} \,{\mathbf{D}}} \,{\mathbf{B}}_{I} \,d\Omega$$

(5)

$$f_{I} = \int\limits_{{\Gamma_{t} }} {{\overline{\mathbf{t}}}} \,\Phi_{I} \,d\Gamma_{t} ,\quad q_{K} = - \int\limits_{{\Gamma_{u} }} {{\mathbf{N}}_{K} \,\overline{u}\,d\Gamma_{u} }$$

(6)

where $\,\Phi_{I} \,$denotes the mesh-free shape function whose expression is derived in next section.

${\mathbf{N}}_{K}$ is a 1D Lagrange interpolant

$${\mathbf{B}}_{I} = \left[ {\begin{array}{*{20}l} {\Phi_{I,x} } \hfill & 0 \hfill \\ 0 \hfill & {\Phi_{I,y} } \hfill \\ {\Phi_{I,y} } \hfill & {\Phi_{I,x} } \hfill \\ \end{array} } \right],\quad {\mathbf{N}}_{K} = \left[ {\begin{array}{*{20}l} {N_{K} } \hfill & 0 \hfill \\ 0 \hfill & {N_{K} } \hfill \\ \end{array} } \right],$$

(7)

$$\begin{aligned} {\mathbf{D}} & = \frac{E}{1 - \nu }\left[ {\begin{array}{*{20}l} 1 \hfill & \nu \hfill & 0 \hfill \\ \nu \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\left( {1 - \nu } \right)/2} \hfill \\ \end{array} } \right]\quad \left( {\text{for plane stress}} \right) \\ & = \frac{E}{{\left[ {1 + \nu } \right]\,\left[ {\left( {1 - 2\nu \,} \right)} \right]}}\left[ {\begin{array}{*{20}l} {1 - \nu } \hfill & \nu \hfill & 0 \hfill \\ \nu \hfill & {1 - \nu } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\left( {1 - 2\nu } \right)/2} \hfill \\ \end{array} } \right]\quad \left( {\text{for plane strain}} \right) \\ \end{aligned}$$

(8)

3 Shape Function Evaluation Using Moving Least-Square (MLS) Approximation

MLS approximation used in EFGM for nodal point interpolation (Belytschko et al. 1994a, b) has been developed by Lancaster and Salkauskas (Lancaster and Salkauskas 1981). Interpolation of displacement u by MLS approximation, u^h(x) is given as:

$$u^{h} ({\mathbf{x}}) = \sum\limits_{j = 1}^{m} {p_{j} ({\mathbf{x}})\,a_{j} } ({\mathbf{x}}) \equiv {\mathbf{p}}^{T} {(}{\mathbf{x}}{)}\,{\mathbf{a}}{(}{\mathbf{x}}{)}$$

(9)

where m is the total number of nodes in problem domain and

p^T(x) a vector of complete basis functions (usually polynomial) is given as:

$${\mathbf{p}}^{T} ({\mathbf{x}}) = [1,\,\,\,x,\,\,\,y,\,\,\,xy,\,\,...\,\,\,\,x^{{k^{\prime}}} ,\,\,\,y^{{k^{\prime}}} ]$$

(10)

and a^T(x) is a vector of unidentified coefficients

$${\mathbf{a}}^{T} ({\mathbf{x}}) = [a_{1} ({\mathbf{x}}),\,\,\,a_{2} ({\mathbf{x}}),\,\,\,a_{3} ({\mathbf{x}}), \ldots \,\,a_{m} ({\mathbf{x}})]$$

(11)

a(x) for any location of point x can be obtained by minimizing the weighted least-square sum of the difference between local approximation, $u^{h} \left( x \right)$ and field function nodal parameters, ${u}_{I}$. This can be expressed as:

$${\mathcal{L}}\left( x \right) = \mathop \sum \limits_{I = 1}^{n} w\left( {x - x_{I} } \right)\left[ {p^{T} \left( x \right)a\left( x \right) - u_{I} } \right]^{2}$$

(12)

$w(x - x_{I}$) is the weight function linked to support domain of node I, and n represents the number of nodes within domain of influence corresponding to point x, i.e., $w(x-{x}_{I}$) $\ne 0$

By minimization of $\mathcal{L}\mathrm{w}.\mathrm{r}.\mathrm{t}. a$, we get:

$${M}^{0}\left(x\right)a\left(x\right)= {B}^{0}(x)u$$

(13)

$$a\left(x\right)= {\left({M}^{0}\right)}^{-1}(x){B}^{0}(x)u$$

(14)

where ${M}^{0}\left(x\right)$ and ${B}^{0}(x)$ are defined as:

$$M^{0} ({\mathbf{x}}) = \sum\limits_{i = 1}^{n} {w(x - x_{I} )} \,{\mathbf{p}}(x_{I} )\,{\mathbf{p}}^{T} (x_{I} ) = w(x - x_{1} )\left[ {\begin{array}{*{20}l} 1 \hfill & {x_{1} } \hfill \\ {x_{1} } \hfill & {x_{1}^{2} } \hfill \\ \end{array} } \right] + \cdots + w(x - x_{n} )\left[ {\begin{array}{*{20}l} 1 \hfill & {x_{n} } \hfill \\ {x_{n} } \hfill & {x_{n}^{2} } \hfill \\ \end{array} } \right]$$

(15)

$$B^{0} ({\mathbf{x}}) = [w(x - x_{1} ){\text{p}}(x_{1} ), \ldots ,w(x - x_{n} ){\text{p}}(x_{n} )] = \left\{ {w(x - x_{1} )\left[ {\begin{array}{*{20}c} 1 \\ {x_{1} } \\ \end{array} } \right], \ldots ,w(x - x_{n} )\left[ {\begin{array}{*{20}c} 1 \\ {x_{n} } \\ \end{array} } \right]} \right\}$$

(16)

By using Eqs. (9) and (13), the approximation function is generated as:

$$u^{h} ({\mathbf{x}}) = \sum\limits_{I = 1}^{n} {\Phi_{I} ({\mathbf{x}})u_{I} } = \Phi^{T} ({\mathbf{x}}){\mathbf{u}}$$

(17)

where,

$$\Phi^{T} ({\mathbf{x}}) = \left\{ {\Phi_{1} ({\mathbf{x}}),\,\,\,\Phi_{2} ({\mathbf{x}}),\,\,\,\Phi_{3} ({\mathbf{x}}),\,\,\,...\,\,\Phi_{n} ({\mathbf{x}})} \right\}$$

(18)

$${\mathbf{u}}^{T} = [u_{1} ,\,\,\,\,u_{2} ,\,\,\,\,u_{3} ,\,\,\,...\,\,\,u_{n} ]$$

(19)

The mesh-free shape function $\Phi_{I} ({\mathbf{x}})$ is defined as:

$$\Phi_{I} ({\mathbf{x}}) = \sum\limits_{j = 1}^{m} {p_{j} ({\mathbf{x}})\left( {\left( {M^{0} } \right)^{ - 1} (x)B^{0} (x)} \right)_{jI} } = {\mathbf{p}}^{T} \left( {M{}^{0}} \right)^{ - 1} B_{I}^{0}$$

(20)

Choice of weight function greatly affects the approximation function $u^{h} ({\mathbf{x}}_{I} )$ in EFG method.

4 EFGM shape Function Using Improved Moving Least-Square (IMLS) Approximation

In the MLS approximation, Eq. (13) because of ill-conditioned matrix, it sometimes becomes difficult to get the numerical solution correctly. To prevent this, Liew et al. (2005) the IMLS approximation as follows.

For $\forall f\left({\varvec{x}}\right), g\left({\varvec{x}}\right)\in \mathrm{span}(p)$, define

$$\left(f,g\right)=\sum_{I=1}^{n}w({\varvec{x}}-{{\varvec{x}}}_{{\varvec{I}}})f({{\varvec{x}}}_{I})g({{\varvec{x}}}_{I}).$$

(21)

(f, g) represents the inner product, and span(p) represents a Hilbert space.

For the set of points $\left\{{{\varvec{x}}}_{{\varvec{i}}}\right\}$ and the weight functions $\left\{{\mathbf{w}}_{\mathbf{i}}\right\}$, if the functions ${p}_{1}({\varvec{x}})$, ${p}_{2}({\varvec{x}})$,….. ${p}_{m}\left({\varvec{x}}\right)$ in the Hilbert space span(p) satisfies the conditions:

$$\left({p}_{k},{p}_{j}\right)=\sum_{i=1}^{n}{w}_{i}{p}_{k}({{\varvec{x}}}_{i}){p}_{j}({{\varvec{x}}}_{i})$$

(22)

$$= \left\{ {\begin{array}{*{20}l} 0 \hfill & {k \ne j} \hfill \\ {A_{k} } \hfill & {k = j} \hfill \\ \end{array} } \right.\quad \left( {k, \, j = 1, \, 2, \ldots , \, m} \right),$$

Then the function set ${p}_{1}({\varvec{x}})$, ${p}_{2}({\varvec{x}})$,….. ${p}_{m}({\varvec{x}})$ can be termed as weighted orthogonal function set with a weighted function $\left\{{\mathbf{w}}_{\mathbf{i}}\right\}$ about points $\left\{{{\varvec{x}}}_{{\varvec{i}}}\right\}$. If ${p}_{1}({\varvec{x}})$, ${p}_{2}({\varvec{x}})$,….. ${p}_{m}({\varvec{x}})$ are polynomials, then the function set ${p}_{1}({\varvec{x}})$, ${p}_{2}({\varvec{x}})$,….. ${p}_{m}\left({\varvec{x}}\right)$ is known as a weighted orthogonal polynomial set with weighted functions $\left\{{\mathbf{w}}_{\mathbf{i}}\right\}$ about points $\left\{{{\varvec{x}}}_{{\varvec{i}}}\right\}$.

From Eqs. (21) and (13) are written as

$$\left[ {\begin{array}{*{20}c} { (p_{{\begin{array}{*{20}c} {1, } \\ \end{array} }} p_{1} ) \left( {p_{1,} p_{2} } \right) \ldots \ldots \ldots . \left( {p_{1,} p_{m} } \right)} \\ {\left( {p_{2,} p_{1} } \right)\left( {p_{2,} p_{2} } \right) \ldots \ldots \ldots \ldots \left( {p_{2, } p_{m} } \right)} \\ { \vdots \vdots \ddots \vdots } \\ {\left( {p_{m, } p_{1} } \right)\left( {p_{m,} p_{2} } \right) \ldots \ldots \ldots \ldots \left( {p_{m,} p_{m} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {a_{1} \left( {\varvec{x}} \right)} \\ {a_{2} \left( {\varvec{x}} \right)} \\ . \\ \vdots \\ {a_{m} \left( x \right)} \\ \end{array} } \right] \cdots = \left[ {\begin{array}{*{20}c} {\left( {p_{1, } u_{1} } \right)} \\ {\left( {p_{2, } u_{I} } \right)} \\ . \\ \vdots \\ {\left( {p_{m, } u_{I} } \right)} \\ \end{array} } \right]$$

(23)

If the basis function set ${p}_{\begin{array}{c}i\end{array}}$(x) $\in span\left(p\right), i=\mathrm{1,2},\dots \dots ., m,$ is a weighted orthogonal function set about points $\left\{{{\varvec{x}}}_{{\varvec{i}}}\right\}$, i.e., if (${p}_{i}, {p}_{j}$) = 0, (i $\ne j$),

Then Eq. (23) becomes

$$\left[ {\begin{array}{*{20}l} {\left( {p_{1,} p_{1} } \right)} \hfill & {0 \cdots } \hfill & 0 \hfill \\ 0 \hfill & \begin{gathered} \left( {p_{2,} p_{2} } \right) \cdots \, \cdots \hfill \\ \vdots \vdots \ddots \vdots \hfill \\ \end{gathered} \hfill & 0 \hfill \\ {00} \hfill & { \cdots \, \cdots } \hfill & {\left( {p_{m,} p_{m} } \right)} \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {a_{1} \left( {\varvec{x}} \right)} \\ {a_{2} \left( {\varvec{x}} \right)} \\ . \\ \vdots \\ {a_{m} \left( x \right)} \\ \end{array} } \right] \cdots \cdots = \cdots \left[ {\begin{array}{*{20}c} {\left( {p_{1, } u_{1} } \right)} \\ {\left( {p_{2, } u_{I} } \right)} \\ . \\ \vdots \\ {\left( {p_{m, } u_{I} } \right)} \\ \end{array} } \right]$$

(24)

We ${a}_{i}({\varvec{x}})$ can be obtained directly as:

$$a_{i} \left( {\varvec{x}} \right) = \frac{{\left( {p_{i,} u_{I} } \right)}}{{\left( {p_{i, } p_{i} } \right)}}; \ldots i = 1,2, \ldots m,$$

$${\text{i.e.}},\quad {\varvec{a}}\left( {\varvec{x}} \right) \, = \overline{\varvec{A}}\left( {\varvec{x}} \right){\varvec{B}}\left( {\varvec{x}} \right){\varvec{u}},$$

(25)

where,

$$\overline{{\varvec{A}} }\left({\varvec{x}}\right)=\left[\begin{array}{c}\frac{1}{{(p}_{1},{p}_{1})} 0 \dots \dots 0 \\ 0 \frac{1}{\left({p}_{2,}{p}_{2}\right)}\dots \dots 0\\ \vdots \vdots \ddots \vdots \\ 0 0 \dots .\dots \frac{1}{({p}_{m},{p}_{m})}\\ \end{array}\right]$$

From Eqs. (25) and (9), approximation function $u^{h}$(x) can be obtained as:

$$u^{h} \left( {\varvec{x}} \right) = \overline{\phi }\left( {\varvec{x}} \right)u = \mathop \sum \limits_{I = 1}^{n} \overline{\phi }_{I} \left( {\varvec{x}} \right)u_{I}$$

(26)

where $\overline{\phi }$(x)is the shape function and

$$\overline{\phi }\varvec{ }\left( {\varvec{x}} \right) = \left( {\left( {\overline{\phi }_{1} \left( {\varvec{x}} \right),\overline{\phi }_{2} \left( {\varvec{x}} \right), \ldots .., \overline{\phi }_{n} \left( {\varvec{x}} \right)} \right) } \right) = {\varvec{p}}^{{\varvec{T}}} \left( {\varvec{x}} \right)\overline{\varvec{A}}\left( {\varvec{x}} \right){\varvec{B}}\left( {\varvec{x}} \right).$$

(27)

As coefficients $a_{i} \left( {\varvec{x}} \right)$ are obtained directly and simply, which eliminates the scope of obtaining an ill conditioned or singular equation system, and thus we obtain a correct solution.

From Eq. (27), we have

$$\overline{\phi }_{I} \left( {\varvec{x}} \right) = \mathop \sum \limits_{j = 1}^{m} p_{j} \left( {\varvec{x}} \right)[\overline{\varvec{A}}\left( {\varvec{x}} \right){\varvec{B}}\left( {\varvec{x}} \right)]_{jI} ,$$

(28)

which represents the shape function of the IMLS approximation for the corresponding node I. We can then obtain the partial derivatives of $\overline{\phi }_{I} \left( {\varvec{x}} \right)$ as

$$\overline{\phi }_{I,i} \left( x \right) = \mathop \sum \limits_{j = 1}^{m} [ p_{j,i} \left( {\overline{\varvec{A}}\varvec{B})_{{{\varvec{jI}}}} + p_{j} (\overline{\varvec{A}}_{,i} \varvec{B } + \varvec{ \overline{A}B}_{,i} )_{jI} } \right] .$$

(29)

The weighted orthogonal basis function set ${{\varvec{p}}=(p}_{i})$ can be formed with the Schmidt method

$$\begin{aligned} p_{1} & = 1 , \\ p_{i} & = r^{i - 1} - \mathop \sum \limits_{k = 1}^{i - 1} \frac{{\left( {r^{i - 1} ,p_{k} } \right)}}{{\left( {p_{k,} p_{k} } \right)}}p_{k} ,\quad i = 2,3 \ldots \\ \end{aligned}$$

(30)

With $r={x}_{1}$ for one-dimensional problem, $r=\sqrt{{x}_{1}^{2 }+ {x}_{2}^{2}}$ or $r={x}_{1}+{x}_{2}$ for two-dimensional problems, and $r={x}_{1}^{2}+{x}_{2}^{2}+{x}_{3}^{2}$ or $r={x}_{1}+{x}_{2}+{x}_{3}$ for three-dimensional problems.

In addition, the Schmidt method can be used to for the weighted orthogonal basis function set ${\varvec{p}}=({p}_{i})$

$$\overline{{\varvec{p}} }=\left({\overline{p} }_{i}\right)=(1,{x}_{1,}{x}_{2, }{x}_{1}^{2}, {x}_{1}{x}_{2, }{x}_{2}^{2},\dots ),$$

(31)

Weighted orthogonal basis function set can be obtained by relation:

$${p}_{i}={\overline{p} }_{i}-\sum_{k=1}^{i-1}\frac{\left({\overline{p} }_{i},{p}_{k}\right)}{\left({p}_{k},{p}_{k}\right)}{p}_{k} , i=\mathrm{1,2},3\dots$$

(32)

Because of weighted orthogonal basis functions, the total number of coefficients in the trial function are reduced. Less number of nodes are required in influence domain for IMLS approximation as compared to MLS approximation. This provides an edge to the IMLS approximation over the MLS approximation.

5 Blended Basis Enrichment Criteria

A new enrichment criterion has been proposed in order to enhance the computational efficiency of element-free Galerkin method (EFGM). The new enrichment criteria will be a blend of full intrinsic basis enrichment function and a linear basis function. For this, two concentric circular areas are created in the proximity of crack tip as represented in Fig. 2a. The degree of enrichment will be decided by the location of evaluation point (gauss point) under consideration, within these areas. Figure 2a demonstrates the methodology of newly proposed criteria with a schematic diagram. Two circular zones are defined having the same center. The radius of inner circle is equal to the length of crack $a$, while the outer circle is of radius ($c \times a)$. The value of area ratio, i.e., $c^{2}$, will be determined by performing a parametric optimization analysis for area ratio as discussed later. The three different regions are marked as $A$,$B$ and $C$, respectively. Firstly, the location of evaluation point is obtained by calculating the distance of that evaluation point from the crack tip. If the evaluation point lies in the inner most region $A$, then a full intrinsic enrichment basis will be employed for imparting contribution to global stiffness matrix $[{\mathbf{KG}}]$ For all evaluation points lying in region $C$, a linear basis is used for constituting stiffness matrix.

Fig. 2

Blended basis enrichment criteria a geometry definition and b degree of enrichment

But if, the evaluation point lies in the transition zone, i.e., region $B$, then instead of a sudden truncation of enrichment basis, the contribution to global stiffness matrix will be calculated using a blend of both linear and full enriched basis as follows:

$$[{\mathbf{KG}}]_{{{\text{Total}}}} = [{\mathbf{KG}}]_{{{\text{Enriched}}\,{\text{basis}}}} \times R\, + \,[{\mathbf{KG}}]_{{{\text{Linear}}\,{\text{basis}}}} \times (1 - R)$$

(33)

where the parameter $R$ will decide the contribution of each basis function to the global stiffness matrix. The value of $R$ can be obtained as:

$$R = \frac{{(c \times \,a\,\, - \,r_{g} )}}{(c - 1) \times a}$$

(34)

where$c$ is a parameter which determines the area bounded within region $B$, $a$ is the crack length and $r_{g}$ is distance between evaluation point and crack tip. Contribution of enriched basis to the global stiffness matrix will be maximum for those points (in region B) which are nearer to the boundary of region A while contribution of linear basis will be minimum for these points. The contribution of enrichment basis continuously decreases as the location of evaluation point shifts from region $A$ to region $B$. At the outer boundary of region $B$, the contribution of linear basis to the global stiffness matrix will be maximum. Figure 2b clearly illustrates the use of linear basis, full enriched basis or a combination these two according to the zone in which an evaluation point lies. The proposed criterion not only reduces the computational time of algorithm but is also capable of simulation crack tip fields in both convex and non convex domains. Figure 3 presents a flowchart for the above mentioned criterion that has been embedded in the revamped EFGM algorithm.

Fig. 3

Flowchart for the blended basis enrichment criteria

6 Optimized Quadrature Criteria for Integration

Stiffness matrix (${\mathbf{K}}$), displacement matrix (${\mathbf{G}}$), and force vector (${\mathbf{f}}$) are evaluated by area integration over domain in two dimensions. Gauss quadrature is required for evaluation of stiffness matrix and force vector which subdivides the domain and helps in numerical integration. Unlike finite elements, mesh-free methods do not subdivide the domain into finite elements. In order to cope with this situation, element quadrature (background mesh) is the widely used criteria for element-free Galerkin method. In conventional EFG method, a uniform Guass quadrature is employed for the entire domain. In the present work, a new optimized quadrature criteria have been proposed and employed for revamping the conventional EFG method. The proposed optimized quadrature criteria are embedded in EFG algorithm such that it is efficient in simulation both straight and kinked crack. The proposed criterion is as follows:

• 1. In element quadrature method, the nodal locations itself are utilized to form a background mesh of virtual elements for generation of gauss points within them. Figure 4a shows the uniformly distributed nodes over the entire problem domain along with a crack of length a.

• 2. For a single crack, define one circular region with center at the midpoint of crack length and radius as half the crack length.

• 3. Define second circular region with center at the crack tip and radius as half the length of crack.

• 4. Select all nodes lying within these two circular domains and name them as ${N}_{E}$.

• 5. For all the virtual elements having at least one of the nodes as ${N}_{E}$, define a higher-order quadrature compared to the rest of domain.

Fig. 4

Optimized quadrature criteria for straight crack

As shown in Figs. 4a and 5a, the circular domains are defined by circle 1 and circle 2 and circle 3. All the virtual element lying within these two circular domains are used to define a higher-order gauss quadrature. Also the virtual elements (highlighted with star) which share at least one of the nodes from ${N}_{E}$ are also embedded with a higher-order Gaussian quadrature compared to rest of domain. Figures 4b and 5b shows the variable gauss quadrature generated inline with the above mentioned criteria. Figure 6 presents the flowchart for the proposed optimized quadrature criteria that has been embedded in revamped EFGM algorithm.

Fig. 5

Optimized quadrature criteria for kinked crack

Fig. 6

Flowchart for optimized quadrature criteria

7 Modelling of Kinked Crack Segments

Near-tip asymptotic displacement field (Nguyen et al. 2008) functions are used to intrinsically enrich (Nguyen et al. 2008) the basis function of EFGM, for simulation of crack tip stress fields in fracture mechanics problems. An enriched basis (Nguyen et al. 2008) used in the present work is given as:

$${\mathbf{P}}^{T} \left( {\mathbf{x}} \right) = \left[ {1,x,y,\sqrt r \cos \frac{\theta }{2},\sqrt r \sin \frac{\theta }{2},\sqrt r \sin \frac{\theta }{2}\sin \theta ,\sqrt r \cos \frac{\theta }{2}\sin \theta } \right]$$

(35)

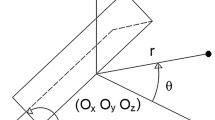
where $r$ is the distance of evaluation point form the crack tip, and $\theta$ is the angle with respect to a coordinate system located at crack tip as shown in Fig. 7.

Fig. 7

Local coordinate system ($\overline{x},\overline{y}$) at crack tip

Discontinuity along $\theta = \pm \pi$ from the crack line is simulated by Eq. (35). In case of kinked crack, mapping is required for aligning the discontinuous fields with the segments of actual crack. Modification in the angular orientation of an evaluation point has been carried out, for modelling a kinked crack in the present analysis. The proposed method for modelling a kinked crack is based on the modification in angular orientation of an evaluation point. Angular orientations are modified such that all the evaluation points in the proximity of crack segments exhibits a discontinuity along $\theta = \pm \pi$. RS and ST are segments of kinked crack as shown in Fig. 8. Alignment of the local coordinate system is done along the leading crack segment such that ST is aligned with x-axis having origin at the tip. Now, Consider an evaluation point P which is located in the vicinity of crack having the angular position $\alpha$. This angular position $\alpha$ will require a mapping to new coordinate system where $\alpha \to \pm \pi$, in order to exhibit a discontinuity along the crack line. Mapping the angular positions of evaluation points to new coordinate system is done in way that there is discontinuity in displacement fields along the points lying near to crack line.

Fig. 8

Scheme for kinked crack mapping

7.1 Methodology for Mapping a Kinked Crack

Consider a kinked crack as shown in Fig. 9. Following steps are to be followed for mapping the near-tip stress field in a kinked crack:

• 1. Divide the domain (containing the kinked crack) into segments like RS, ST where T is tip of leading crack.

• 2. Draw normal at common point of both segments in order to discretize the region above the crack, i.e., point B, on which normal are drawn as SQ and SP which are perpendicular to crack segments RS and ST, respectively.

• 3. Draw normal at tip of leading crack segment ST.

• 4. Draw the bisector of angle RST in order to divide the region below the crack into two parts such that a total of six regions are formed in the vicinity of kinked crack and similar procedure must be applied for cracks having multiple kinks.

• 5. Apply proposed geometrical and mathematical expressions to obtain the new mapped orientation of evaluation point.

Fig. 9

Domain description for modelling kinked crack

In region 1 which is after the tip of leading crack, all angular measurements are done with respect to local coordinate axis, such that:

$$\,\theta^{\prime}\,\, = \,\theta \,\,\,{\text{for}} - \frac{\pi }{2} \le \theta \le \frac{\pi }{2}$$

(36)

Proposed modified angular orientation of evaluation points lying in regions 2, 3, 4 and 5 is as follows:

$$\left\{ \begin{gathered} \pi - \,{\text{Sin}}^{ - 1} \left( {\frac{{h^{\prime}}}{r}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{above}}\,\,{\text{the}}\,\,{\text{crack}} \hfill \\ - \pi + \,{\text{Sin}}^{ - 1} \left( {\frac{{h^{\prime}}}{r}} \right)\,\,\,\,\,\,\,\,\,\,{\text{above}}\,\,{\text{the}}\,\,{\text{crack}} \hfill \\ \end{gathered} \right\}$$

(37)

where $r$ signifies the distance between tip of the leading crack i.e. Point T and the evaluation point, $h^{\prime}$ signifies the normal distance between the crack segment in that region and the evaluation point. For points inside the region QSP and $h^{\prime}$ is calculated as the distance between the evaluation point and point representing that region, i.e., Point S. In performing so, a transformation achieved as point approaches to the crack line such that $h^{\prime} \to 0$ then $\theta^{\prime} \to \pm \pi$, and thus clear discontinuity is achieved along the crack line.

Hence, the new enriched basis function in term of modified angular orientation $\theta^{\prime}$ becomes:

$${\mathbf{P}}^{T} ({\mathbf{x}}) = \left[ {\underbrace {1,\,\,\,x,\,\,y}_{\begin{gathered} {\text{standard}} \\ {\text{basis}} \\ \end{gathered} },\underbrace {{\sqrt r \cos \frac{{\theta^{^{\prime}} }}{2},\sqrt r \sin \frac{{\theta^{^{\prime}} }}{2},\sqrt r \sin \frac{{\theta^{^{\prime}} }}{2}\sin \theta^{^{\prime}} ,\sqrt r \cos \frac{{\theta^{^{\prime}} }}{2}\sin \theta^{^{\prime}} }}_{{{\text{enrichment}}\,{\text{terms}}}}} \right]$$

(38)

where, (1, $x,$$y$) that is the first three terms represents standard basis and the rest four terms composes of enrichment part for the kinked crack.

8 Interaction Integral Approach for Calculating Stress Intensity Factors

The J-integral for a isotropic cracked body is as follows (Rao and Rahman 2003):

$$J= {\int }_{\Gamma }\left({W{\delta }_{ij}-\sigma }_{ij}\frac{\partial {u}_{i}}{\partial {x}_{1}}\right){n}_{j}d\Gamma$$

(39)

where $W= {\int }_{0}^{\varepsilon }\sigma \mathrm{d}\varepsilon$ is the strain energy density, $\sigma$ is the stress and n is outward unit normal vector to a discretional curve surrounding the crack tip as shown in Fig. 10. For linear elastic materials,$W= {\sigma }_{ij}{\varepsilon }_{ij}/2$. Green’s theorem (Rao and Rahman 2003) can be applied to covert contour integral in Eq. 39 into area integral.

$$J= {\int }_{A}\left({\sigma }_{ij}\frac{\partial {u}_{i}}{\partial {x}_{1}}-W{\delta }_{ij}\right)\frac{\partial q}{\partial {x}_{j}}\mathrm{d}A$$

(40)

where A represents the area under the curve and q is a weight function, which has zero value along the boundary of domain and unity at the crack. Now assume two states for a cracked body, State 1 which is primary state or real state having some predefined boundary conditions and the other state 2 which is a secondary or auxiliary state. The J-integral in the superimpose states is as follows:

$${J}^{U}= {\int }_{A}\left[\left({\sigma }_{ij}^{(1)}+{\sigma }_{ij}^{(2)}\right)\frac{\partial \left({u}_{i}^{(1)}+{u}_{i}^{(2)}\right)}{\partial {x}_{i}}-{W}^{U}{\delta }_{ij}\right]\frac{\partial q}{\partial {x}_{j}}\mathrm{d}A$$

(41)

where i, j = 1, 2, and U specifies fields and quantities associated with primary, secondary and unified states, respectively.

Fig. 10

Crack surrounded by area A_o

On expanding Eq. (41):

$${J}^{U}= {J}^{(1)}+{J}^{(2)}+{M}^{(U)}$$

(42)

where

$${M}^{(U)}= {\int }_{A}\left[{\sigma }_{ij}^{(1)}\frac{\partial {u}_{i}^{(2)}}{\partial {x}_{1}}+{\sigma }_{ij}^{(2)}\frac{\partial {u}_{i}^{(1)}}{\partial {x}_{1}}-{W}^{U}{\delta }_{ij}\right]\frac{\partial q}{\partial {x}_{j}}\mathrm{d}A$$

(43)

This is interaction integral which is employed for computing stress intensity factors (SIFs) under mechanical loads. Thermal interaction integral for homogeneous materials under the thermal loading is precisely elaborated by Pant et al. (2010) as follows:

$$M^{\left( U \right)} = \mathop \smallint \limits_{A} \left[ {\sigma_{ij}^{\left( 1 \right)} \frac{{\partial u_{i}^{\left( 2 \right)} }}{{\partial x_{1} }} + \sigma_{ij}^{\left( 2 \right)} \frac{{\partial u_{i}^{\left( 1 \right)} }}{{\partial x_{1} }} - W^{U} \delta_{ij} } \right]\frac{\partial q}{{\partial x_{j} }}{\text{d}}A + \alpha \mathop \smallint \limits_{A} \frac{\partial T}{{\partial x_{1} }}\sigma_{kk}^{2} q{\text{d}}A$$

(44)

Here, the terms represented in bold are the additional terms that are needed for thermal interaction integral calculation. T represents Temperature applied, $\alpha$ is thermal expansion coefficient and ${\sigma }_{kk}$ is the thermal stress.

9 Results and Discussion

This section presents optimization of EFGM parameter along with implementation of proposed algorithm to model and simulate few numerical problems of fracture and fatigue life estimation. The revamped EFG algorithm incorporates:

• IMLS approximation.

• Blended enrichment criteria.

• Optimized quadrature criteria

• Criteria for modelling kinked crack.

The application of the revamped EFGM algorithm has been demonstrated for a variety of fracture problems with different geometric and loading conditions. Finally, proposed the method has been extended to simulate fatigue crack growth problem in order to establish its worth and robustness for efficiently reducing the computation time.

9.1 Parametric Optimization

The number of nodes in problem domain $({n}_{d})$, order of Gauss quadrature, scaling factor (d_max) and area ratio (c²) influences the total time of EFGM simulation. Earlier parametric studies (Musivand-Arzanfudi et al. 2007; Sheng et al. 2015) on EFGM were mainly focused on multiple number of simulations (range 600–1000) instead of using some optimization technique. Taguchi optimization (Kosaraju et al. 2012) technique has been applied in current work and L16 orthogonal array has been selected for the analysis which in turn reduces the actual number of simulations required for finding the optimum parameters, thus providing the computationally efficient form of EFGM.

Optimization technique is applied here for analysis of an edge crack problem with different EFGM parameters. In this Taguchi analysis (Kosaraju et al. 2012; Mahapatra and Patnaik 2007; Wang et al. 2016; Elizalde-Gonzalez and Garcia-Diaz 2010) relative deviation has be considered as the response value for the analysis. In the current optimization analysis, four parameters namely, total number of nodes, gauss quadrature type, scaling factor ${(d}_{\mathrm{max}})$, and area ratio (A_r) are selected as the input parameters for finding the optimum combination of these parameters for simulations.

For finding the optimum values of these parameters, a cracked rectangular domain having height (H) = 2 units and width (W) = 1 units and having mechanical properties $\left(E=1\times {10}^{6} \mathrm{units}, \nu =0.3\right)$ subjected to tensile load of ${\sigma }_{0}$ = 1 unit, under plane stress conditions is selected for this study as shown in Fig. 11.

Fig. 11

Problem geometry along with boundary conditions

Crack orientation is parallel to the horizontal axis located at coordinates x = 0 and y = H/2 and a size of a = 0.4 units.

The variable range of parameters used in the present analysis are: Number of nodes ranging from 200–300, gauss quadrature ranging from order of 2*2 to 8*8, Scaling factor (d_max) from 1.5 to 3 and area ratio (c²) ranging from 1.5 to 3. Table 1 represents the various control parameters along with their respective levels. Sixteen simulations analysis have been performed as per the Taguchi’s L-16 orthogonal array (Elizalde-Gonzalez and Garcia-Diaz 2010). Results of simulation are shown in Table 2. The values of Mode-I stress intensity factor (SIF) values thus obtained, are compared with Ref. 1 (Salari-Rad et al. 2011) results and the relative deviation is calculated using: $\left(\mathrm{RD}=\left|\left(\frac{{K}_{1}^{\mathrm{Ref}.1}-{K}_{1}^{\mathrm{EFGM}}}{{K}_{1}^{\mathrm{Ref}.1}}\right)\times 100\right|\right)$.

Table 1 Process parameters and their levels for Taguchi design of experiments

Table 2 L16 Orthogonal array for experimentation along with response outputs

MINITAB 17 software has been used for the Taguchi’s design of experiments and optimization analysis. All EFGM simulations are performed using algorithm written in MATLAB coding platform with HP workstation having Xeon (Quad-core)-CPU with 16 GB RAM.

Signal-to-noise (S/N) ratio for the results have been calculated using MINITAB 17 software. Taguchi’s characteristic of “minimum is better” is applied in the present analysis, as a less relative deviation is required for our simulations, to obtain optimum results. The loss function L for objective is defined as follows:

$${L}_{\mathrm{LB}}= \frac{1}{n}\sum_{i=1}^{n}{y}_{\mathrm{RD}}^{2}$$

(45)

where y_RD is the value of relative deviation (RD) and n is number of experiments.

Signal-to-noise ratio can also be calculated by logarithmic transformation as follows:

$${\text{S/N}}\,{\text{ratio}}\,{\text{for}}\,{\text{relative}}\,d{\text{eviation}} = - 10\log_{10} \left( {L_{{{\text{LB}}}} } \right)$$

(46)

The effect of control parameters on relative deviation is shown in Table 2. Figure 12 shows the mean of S/N ratio with the condition that minimum is better. Plot reveals that the control factors at levels A₂, B₃, C₃, and D₂ contribute maximum in obtaining low relative deviations, and thus, they may be regarded as the optimum levels for carrying out further simulations.

Fig. 12

Plot for mean of S/N ratios

Next, the simulations at these corresponding optimum levels have been performed; using proposed revamped element-free Galerkin method (REFGM), to calculate the values of K_I and relative deviation. Value of K_I = 2.3365 units and a relative deviation of 0.85% were observed and time consumed for this simulations was found to be 22 s.

In order to have a relative comparison of the computational time, the same problem was simulated using conventional EFGM approach. All other simulation parameters were kept same as shown in Table 3. A relative comparison of computational time predicts that the revamped element-free Galerkin method (REFGM) is faster than the conventional method by 80% with nearly equal accuracy of results.

Table 3 Computational time comparison

The revamped EFG method is further employed for modelling of a variety of fracture and fatigue problem to ensure and establish its accurate simulation capabilities with least computational time.

9.2 Bimetallic Interfacial Cracks

Both conventional EFGM and revamped EFGM have been employed for solving bimaterial interface crack problems. Jump function (Pant et al. 2011b) has been used to model the material discontinuity, i.e., weak discontinuity and intrinsic enrichment (Nguyen et al.2008 ) has been used to model the strong discontinuities. Interaction integral (Sukumar et al. 2004; Yau et al. 1980) in domain form has been used for calculating the stress intensity factors as follows:

$$M = - \int\limits_{A} {\left( {\sigma_{ik} \varepsilon_{ik}^{aux} \delta_{1j} - \sigma_{ij} u_{i,1}^{aux} - \sigma_{ij}^{aux} u_{i,1} } \right)} \,\overline{q}_{,j} \,{\text{d}}A$$

(47)

where, $\overline{q}$ is a weight function which has zero value on the contour C and unity at the tip of crack. Relation between stress intensity factor and integration integral is given as (Sukumar et al. 2004):

$$M_{i} = \frac{2}{{E^{*} \cosh^{2} (\pi \tilde{\varepsilon })}}(K_{{\text{I}}} K_{{{\text{II}}}}^{{{\text{aux}}}} + K_{{\text{I}}} K_{{{\text{II}}}}^{{{\text{aux}}}} )\,\quad \,{\text{with}}\,\,i = 1,\,2$$

(48)

$K_{{\text{I}}}^{{{\text{aux}}}}$ and $K_{{{\text{II}}}}^{{{\text{aux}}}}$ are auxiliary stress intensity factors and $E^{*}$ is equivalent Young’s Modulus (${{E^{*} = 2E_{1} E_{2} } \mathord{\left/ {\vphantom {{E^{*} = 2E_{1} E_{2} } {\left( {E_{1} + E_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {E_{1} + E_{2} } \right)}}$) and $\tilde{\varepsilon }$ is the bimaterial constant (Sukumar et al. 2004). $K_{{\text{I}}}^{{{\text{aux}}}}$ can be calculated by considering $K_{{\text{I}}}^{{{\text{aux}}}} = 1$ and $K_{{{\text{II}}}}^{{{\text{aux}}}} = 0$, and similarly $K_{{{\text{II}}}}$ can also be calculated.

A bimetallic rectangular plate having a Width W = 100 mm and Height, H = 200 mm, with an interface crack located at the center has been considered for analysis, as shown in Fig. 13a. Horizontal material interface is located at a distance of ${H \mathord{\left/ {\vphantom {H 2}} \right. \kern-\nulldelimiterspace} 2}$ from the bottom of plate. A tensile load of 9.8 MPa has been applied perpendicular to the interface of the crack. A nodal density of (20 × 50) nodes is used to define the problem domain. Near-tip nodal arrangement and selection of higher quadrature regions are shown in Fig. 13b. As per the optimized quadrature criteria discussed in previous section, all the cells lying within the circular regions along with partially intersected cells (highlighted with star) will employ a higher Gaussian quadrature (6 × 6) as compared to the rest of domain having a (4 × 4) Gaussian quadrature.

Fig. 13

a Bimetallic plate with an interface crack, b nodes and optimized quadrature cells

Cracks with different lengths, i.e., 40 mm and 60 mm, are considered in the present analysis. Poisson’s ratio for both materials is taken as 0.3 and value of Young’s modulus (E₁) for lower material is fixed at 205.8 GPa while that of upper material (E₂) is varied. For different ratio of Young’s modulus, i.e., $E_{2} /E_{1}$ = 1, 2, 3, 4, 10, 100, the values of stress intensity factors are calculated.

The normalized stress intensity factor is defined as ${{K_{i} } \mathord{\left/ {\vphantom {{K_{i} } {\sigma \sqrt {\pi a} }}} \right. \kern-\nulldelimiterspace} {\sigma \sqrt {\pi a} }}$ ($i$ = 1, 2). This is done so as to get a non-dimensional value of stress intensity factor corresponding to both mode-I and mode-II stress intensity factors. The results were compared with those obtained by Ref. 2 (Miyakazi et al. 1993; Nagashima et al. 2003). Variation of normalized stress intensity factors corresponding to varying modular ratio $E_{2} /E_{1}$ for a crack length of 40 mm is shown in Fig. 14. A good agreement has been found between the REFGM results and the reference results. Next simulation has been performed for a crack length of 60 mm, and the results were compared with the Ref. 2 (Miyakazi et al. 1993; Nagashima et al. 2003) as shown in Fig. 15. Tables 4 and 5 show comparison of the values of normalized stress intensity factors for various material mismatch ratios with the reference values along with comparison of simulation time of the proposed REFGM algorithm with the conventional EFGM results.

Fig. 14

SIFs variation for $2a = 40\,{\text{mm}}$

Fig. 15

SIFs variation for $2a = 60\,{\text{mm}}$

Table 4 Normalized of stress intensity factors for crack length 40 mm

Table 5 Normalized of stress intensity factors for crack length 60 mm

Further, the revamped EFGM algorithm was utilized to generate the contours of $\sigma_{YY}$ and $\varepsilon_{YY}$ for large material mismatch ratio at the interface, i.e., ${{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {E_{1} }}} \right. \kern-\nulldelimiterspace} {E_{1} }} = 100$. In this case, the stress contours of $\sigma_{YY}$ is almost continuous as shown in Fig. 16a while strain contours of $\varepsilon_{YY}$ shows a discontinuity at the interface as shown in Fig. 16b. Table 6 presents a comparison of average computational time of REFGM algorithm for simulation of bimetallic interfacial crack problem with respect to conventional EFGM technique. It can be clearly observed that the revamped EFGM algorithm is capable of reducing the average computational time by 76%.

Fig. 16

$\sigma_{xx}$ and $\varepsilon_{xx}$ contours for ${{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {E_{1} }}} \right. \kern-\nulldelimiterspace} {E_{1} }} = 100$

Table 6 Computational time comparison for crack in bimaterial domain

9.3 Fracture in Functionally Graded Material

A cracked plate made of functionally graded material with properties varying as hyperbolic tangent function have been analyzed in this section. Dimensions of this functionally graded plate having an edge crack of length a are width = 2 units and height = 4 units as shown in Fig. 17a. Constraints are applied in y-direction for both top and bottom edges. Steady state thermal loadings in form of temperatures $T_{1} = - 10\,^{ \circ } {\text{C}}$ and $T_{2} = 0\,^{ \circ } {\text{C}}$ is applied to the plate. Top and bottom edges are considered to be insulated so that there is no heat flux across them. Plane strain condition has been assumed to simulate this problem along a uniform distribution of 1250 nodes. The values of Young's modulus $\left( E \right)$, Poisson's ratio $\left( \nu \right)$, thermal expansion coefficient $\left( \beta \right)$, and thermal conductivity (k) are obtained by its hyperbolic tangent function as:

$$E(X_{1} ) = \frac{{E^{ - } + E^{ + } }}{2} + \frac{{E^{ - } - E^{ + } }}{2}\tanh \left[ {\tilde{\delta }\left( {X_{1} + d} \right)} \right]$$

(49)

$$\nu (X_{1} ) = \frac{{\nu^{ - } + \nu^{ + } }}{2} + \frac{{\nu^{ - } - \nu^{ + } }}{2}\tanh \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta } \left( {X_{1} + d} \right)} \right]$$

(50)

$$\beta (X_{1} ) = \frac{{\beta^{ - } + \beta^{ + } }}{2} + \frac{{\beta^{ - } - \beta^{ + } }}{2}\tanh \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta } \left( {X_{1} + d} \right)} \right]$$

(51)

$$k(X_{1} ) = \frac{{k^{ - } + k^{ + } }}{2} + \frac{{k^{ - } - k^{ + } }}{2}\tanh \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta } \left( {X_{1} + d} \right)} \right]$$

(52)

where $\left( {E^{ - } ,E^{ + } } \right) = \left( {1,\,3} \right)$, $\left( {\nu^{ - } ,\nu^{ + } } \right) = \left( {0.3,\,0.1} \right)$, $\left( {\beta^{ - } ,\beta^{ + } } \right) = \left( {0.01,\,0.03} \right)$, $\left( {k^{ - } ,k^{ + } } \right) = \left( {1,\,3} \right)$$\tilde{\delta } = 15$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta } = 5$, $d = 0$. The steady state temperature distribution over the problem domain has been generated and shown in Fig. 17b. The near-tip nodal distribution along with optimized quadrature cells for defining higher quadrature is shown in Fig. 17c. As proposed by the optimized quadrature criteria, the cells lying within the circular regions along with the boundary cells (highlighted with star) will employ a higher Gaussian quadrature compared to the rest of domain. Equations (49–52) are plotted to visualize the gradation of material properties across the width and a sharp jump in these material properties has been observed at the mid of width as shown in Figs. 18 and 19.

Fig. 17

a Problem geometry, b temperature distribution over the domain, c nodes and optimized quadrature cells

Fig. 18

Gradation of coefficient of thermal expansion and thermal conductivity across the width

Fig. 19

Gradation of modulus of elasticity and Poisson’s ratio across the width

By analyzing the displaced nodal positions from Fig. 20a, it has been observed that edge crack exhibited only mode 1 displacements under these prescribed loading and boundary conditions.

Fig. 20

Displaced nodal positions and variation of stress intensity factor

For different $\left( \frac{a}{W} \right)$ ratios, the mode-I stress intensity factor has been plotted as shown in Fig. 20b, a good agreement can be seen between the obtained REFGM results and reference FEM solution (Kc et al. 2008). A decrement in the value of $K_{{\text{I}}}$, with increasing crack length (due to the gradation in material properties) has been observed. Table 7 shows a comparison of mode-I stress intensity factors and computational time for both EFGM and REFGM algorithm with the FEM reference values. It can be clearly observed that REFGM algorithm is capable of generating accurate results with least computational time for simulation of interfacial crack domain problem in comparison to conventional EFGM scheme. Moreover, a comparison of average computational time reveals that revamped EFGM algorithm is faster than its predecessor EFGM method by around 75% as shown in Table 8.

Table 7 Comparison of stress intensity factors and computational time

Table 8 Comparison of average computational time

9.4 Thermoelastic Fracture

This section describes the application of REFGM for simulation of fracture problems under thermoelastic loading. At first, the temperature distribution over the cracked domain is obtained by solving the heat transfer equation across the domain. The temperature field so obtained is then employed as an input to determine the nodal displacements and near-tip stress fields.

In the present simulation, a rectangular plate of dimensions width = 5 units and height = 1 units containing inclined adiabatic crack (Pant et al. 2010) as shown in Fig. 21a has been analyzed. Uniform discretization of the plate geometry has been done by taking 32 nodes in x direction and 64 nodes in y-direction. Top and bottom edges of this rectangular plate were kept at equal and opposite temperatures $(T_{1} = 10\,^{ \circ } {\text{C}})$, while right and left edges were kept insulated so that there is not heat flow across them and crack surface is considered adiabatic. Discontinuous temperature field is observed at the center of the plate as shown in Fig. 21b.

Fig. 21

Adiabatic inclines crack: a problem geometry, b temperature profile

Next, a rectangular plate of dimensions width = 1 units and height = 2 units containing isothermal center crack (Pant et al. 2010) as shown in Fig. 22a has been analyzed. Uniform nodal density has been used to define the domain by considering 32 nodes in x direction and 64 nodes in y-direction. All edges of the rectangular plate has been kept at same temperature $(T_{2} = 10^{ \circ } {\text{C}}))$, while temperature of the crack surface has been kept at $(T_{1} = 0^{ \circ } {\text{C}}))$ such that $T_{1} < T_{2}$. As can be seen from Fig. 22b continuous temperature field has been observed since the crack surface having a prescribed temperature value is considered as a part of essential boundary.

Fig. 22

Isothermal inclines crack: a problem geometry, b temperature profile

The value of stress intensity factors $K_{I}$ and $K_{II}$ have been calculated using the modified thermal interaction integral (Pant et al. 2010). The normalization of stress intensity factors is done by by $\beta \,\Theta \,\left( {{W \mathord{\left/ {\vphantom {W H}} \right. \kern-\nulldelimiterspace} H}} \right)E\sqrt {2W}$ for the adiabatic crack and $\beta \,\left( {T_{2} - T_{1} } \right)\,E\sqrt {2W}$ for the isothermal crack (Pant et al. 2010), where $E$ is the Young's modulus of elasticity, $\nu$ is the Poisson's ratio, $\beta$ is the coefficient of linear expansion, $\Theta = T_{o} - T$ with $T_{o}$ is the applied temperature and $T$ is the ambient temperature.

Figures 21c and 22c represent the near crack tip arrangements of nodes and implementation of optimized quadrature criteria for both adiabatic and isothermal crack modelling, respectively. For a particular angular orientation of the crack circular regions are defined as stated in optimized quadrature criteria. For this particular case all the cells lying within circular regions along with partially intersected cells (highlighted with star) are determined as shown in Figs. 21c and 22c. A higher Gaussians quadrature is employed for all such cells, while a lower Gaussian quadrature is used for rest of the domain.

Variation of normalized stress intensity factor for an adiabatic crack with respect to inclination angle is shown in Fig. 23a. Figure 23a shows that value of mode-I stress intensity factor is zero at inclination angle $\alpha = 0^{ \circ }$ and $90^{ \circ }$ and maximum at inclination angle of 45°, while value of mode-II stress intensity factor is found maximum at inclination angle of 0° and decreases to zero for inclination angle 90°. It has been seen that the calculated values of $K_{{\text{I}}}$ and $K_{{{\text{II}}}}$ are in good agreement with the results of literature Ref. 3 (Prasad and Aliabadi 1994; Duflot 2008). Table 9 represents the variation of normalized stress intensity factors with varying crack inclination along with a comparison of simulation time for conventional EFG technique and proposed REFG algorithm.

Fig. 23

Variation of normalized stress intensity factor with crack inclination

Table 9 Variation of normalized stress intensity factors with crack inclination for adiabatic crack

Variation of normalized stress intensity factor for an isothermal crack with respect to inclination angle is shown in Fig. 23b.Value of both mode-I stress intensity factor and mode-II stress intensity factors has been calculated. Figure 23b shows that the value of mode-I stress intensity factor decreases from its maximum value at angle $\alpha = 0^{ \circ }$ to a minimum value at $90^{ \circ }$, while value of mode-II stress intensity factor is found maximum at inclination angle of 45º and decreases to zero for inclination angle $\alpha = 0^{ \circ }$ and $90^{ \circ }$. It has been seen that the calculated values of $K_{I}$ and $K_{II}$ are found in good agreement with the results of literature Ref. 3 (Prasad and Aliabadi 1994; Duflot 2008). Table 10 represents the variation of normalized stress intensity factors with varying crack inclination along with a comparison of conventional EFGM technique and proposed REFGM algorithm in terms of computational efficiency. Results show that algorithm is quiet faster than the EFGM technique without any compromise in accuracy of results.

Table10 Variation of normalized stress intensity factors with crack inclination for isothermal crack

Table 11 represents a comparison of average computational time for thermoelastic problems simulated using both EFGM and REFGM algorithm with same parameters. The proposed REFGM algorithm has an edge over the computational time by about 76% as compared to EFGM algorithm.

Table 11 Comparison of average computational time for thermoelastic problems

9.5 Fatigue Crack Growth

Finally, a fatigue crack growth analysis for a two-dimensional homogeneous cracked domain is performed under a cyclic mechanical loading of fixed amplitude. Paris law has been used to calculate fatigue life cycles for each crack increments. The change in stress intensity factor $(\Delta K)$ for constant cyclic loads is as follows:

$$\Delta K = K_{{{\text{maximum}}}} - K_{{{\text{minimum}}}}$$

(53)

where$K_{{{\text{maximum}}}}$ is the stress intensity factor corresponding to maximum applied load $(\sigma_{\max } )$ and $K_{{{\text{minimum}}}}$ is the stress intensity factor corresponding to minimum applied load $(\sigma_{\min } )$.Small linear increments of crack have been used in current work for modelling quasistatic crack growth. At the crack tip, the local direction of crack growth $\theta_{c}$ is determined on the basis of maximum principal stress theory (Sukumar and Prevost 2003). So, direction for the crack growth $\theta_{c}$ is obtained from relation:

$$K_{I} \sin \theta_{c} + K_{II} (3\sin \theta_{c} - 1) = 0$$

(54)

Simplifying above equation, we obtain

$$\theta_{c} = 2\tan^{ - 1} \left( {\frac{{K_{{\text{I}}} - \sqrt {K_{{\text{I}}}^{2} + 8K_{{{\text{II}}}}^{2} } }}{{4K_{{{\text{II}}}} }}} \right)$$

(55)

From Eq. (55), we get two values of $\theta_{c}$, out of which one is the maximum value. $\Delta K_{{{\text{Ieq}}}}$ can be calculated using Eq. (54) by using the value of $\theta_{c}$ corresponding to maximum equivalent stress intensity factor and is written as follows:

$$\Delta K_{{{\text{Ieq}}}} \, = \,\Delta K_{{\text{I}}} \,\cos^{3} \left( {\frac{{\theta_{{\text{c}}} }}{2}} \right)\, - \,3\Delta K_{{{\text{II}}}} \cos^{2} \left( {\frac{{\theta_{c} }}{2}} \right)\,\,\sin \left( {\frac{{\theta_{c} }}{2}} \right)\,$$

(56)

Paris law is applied for calculating fatigue life of a propagating quasi-static crack under cyclic loading using the following expression:

$$\frac{{{\text{d}}a}}{{{\text{d}}N}} = C(\Delta K_{{{\text{Ieq}}}} )^{{\text{m}}}$$

(57)

where a represents length of crack, N is number of load cycle, m and C are material constants of Paris model. Crack length is modified after obtaining the direction and magnitude of crack increment. For crack growth simulations we require optimum value of crack extension as larger crack increments will not represent real path of crack. Simulations for fatigue crack growth problems are provided with increment of 1 mm (optimum increment size). Table 12 shows the material properties considered for calculation of fatigue life.

Table 12 Material properties for fatigue life calculation

9.5.1 Fatigue Crack Growth an Inclined Edge Crack

A problem domain with dimensions $100\,\,{\text{mm}} \times 200\,\,{\text{mm}}$ with an inclined edge crack has been considered for fatigue life simulation. A uniform nodal density of $(30 \times 60)$ nodes is considered. An edge crack length $a$ = 10 mm have been considered for this simulation. Orientation of this initial crack is kept at $40^{o}$ with the horizontal axis. The boundary conditions along with other geometrical parameters are shown in Fig. 24a. Constant amplitude mechanical load of $\sigma {}_{\max } = 100\;{\text{N/mm}}$ and $\sigma {}_{\min } = 0\;{\text{N/mm}}$ is applied at the top edge of the plate whereas the bottom edge is constrained in y-direction. The quasi static crack growth is modelled using the REFGM algorithm which is also capable of simulating kinked cracks. With each incremental crack growth the crack path is determined and updated automatically within the algorithm. Figure 24b shows the stress $(\sigma {}_{yy})$ contours in the vicinity of crack tip before failure. For a particular crack configuration before failure, Fig. 24c represents the near-tip arrangement of nodes along with application of optimized quadrature criteria to determine cell for employing higher Gaussian quadrature compared to the rest of problem domain. All the boundary cells (highlighted with star) along with cells lying in the interior of circular regions are predetermined by algorithm as shown on Fig. 24c. The final fatigue life is estimated using Paris law. Fatigue life and critical crack length obtained by revamped EFG algorithm are found to be 910 cycles and 28.23 mm, whereas the same obtained by conventional EFGM approach are found as 918 cycles  and 28.70 mm.

Fig. 24

Plate with inclined crack a problem geometry, b stress contours $(\sigma {}_{yy})$, c Near-tip nodes and optimized quadrature cells

A comparison of average computational time for estimating fatigue life of cracked domain is presented in Table 13. It can be clearly observed that, for similar algorithm parameters, the proposed REFG algorithm is capable of estimating the fatigue life faster than the EFGM algorithm by about 77%. Moreover, the proposed criteria for modelling kinked crack is capable of simulating the near-tip stress field in quiet accurate and efficient manner.

Table 13 Comparison of average simulation time for fatigue life estimation

9.6 Crack Emanating from Annular Disc

In order to establish the efficiency and modeling capabilities of the proposed algorithm for different domain geometry, an annular disc with a crack emanating from the inner edge is considered. The problem is simulated with both revamped element-free Galerkin method (REFGM) and conventional EFG method. Figure 25 shows an annular metallic disc ($r_{i}$ = 100 mm and $r_{o}$ = 300 mm) having an edge crack of length $a$ with modulus of elasticity ($E$) = 200 GPa and Poisson’s ratio ($\nu$) = 0.3. A far-field stress, $\sigma$ = 100 MPa is applied at the outer boundary. The domain has been discretized with a total of 666 nodes which are defined in form of concentric circles. This is achieved by defining nine equally spaced nodes along the radial direction and 77 equally spaced nodes along angular direction. The nodal distribution along with crack orientation is clearly shown in Fig. 25. The distribution of nodes is represented in Fig. 26. The initial Gaussian distribution over the annular disc is represented in Fig. 27. In order to visualize the implementation of optimized quadrature criteria, a region near the crack tip has been zoomed in and shown separately in Fig. 27. Again, the optimized quadrature criterion helps in determining the regions where a higher Gaussian quadrature will be utilized as compared to the rest of domain. These higher quadrature regions are predetermined by algorithm are highlighted with blue stars as shown in Fig. 27.

Fig. 25

Annular disc with an interior edge crack

Fig. 26

Nodal distribution over domain

Fig. 27

Gaussian points over the domain, Optimized quadrature criteria

Fig. 28

Contours of stress component $\sigma_{xx}$

For a better understanding of the results obtained by Revamped EFG algorithm and conventional EFG method, the contours of stress components are plotted as shown in Figs. 28 and 29.

Fig. 29

Contours of stress component $\sigma_{yy}$

Fig. 30

Stress intensity factor (K_I) values for different crack lengths

Figure 28 shows the contour of stress component $\sigma_{xx}$ over the problem domain using the proposed REFGM algorithm. This contour plot shows that the crack surfaces are almost traction-free in $x$-direction as expected. In contrast, the stress contour of $\sigma_{xx}$ generated using conventional EFGM shows a nearly zero stress level over the domain accompanied by a compressive stress zone to the opposite side of the crack as shown in Fig. 28b, which is misleading and incorrect.

Next, the stress contours of $\sigma_{yy}$ are plotted and analyzed. Figure 29a presents the contour of $\sigma_{yy}$ using REFGM algorithm. The crack surfaces are almost traction-free in y-direction as per theoretical expectation. A high stress level is generated at the crack tip (compared to the rest of domain), which is a unique feature of stress singularity at the crack tip. In comparison to that, EFGM is incapable of simulating the crack tip singularity as shown in Fig. 29b.

The values of stress intensity factor K_I are evaluated for different crack lengths. Figure 30 shows a relative comparison of stress intensity factor (SIFs) K_I, for different crack lengths, varying from 5 to 15 mm, obtained using both revamped EFG algorithm and conventional EFGM. Both the results are compared with Finite Element Method (FEM) solution obtained using ANSYS-14 software. It can be clearly seen that for all values of crack length, the results obtained by REFGM are in good agreement with those obtained by FEM, whereas the results obtained by conventional EFGM are absurd and deviating with the reference FEM solution.

Moreover, a comparison of average computational time for simulating crack tip field in annular disc is presented in Table 14. This computational time simulation is performed for a crack length of 12 mm. Table 14 shows that for similar algorithm parameters the proposed REFGM algorithm is capable of estimating the results faster than the EFG method by around 75% in this case. Moreover, the proposed REFGM algorithm is capable of modelling the near-tip stress field quiet accurately and efficiently along with obtaining accurate values of stress Intensity factors at the crack tip.

Table 14 Comparison of average simulation time for cracked annular disc

10 Conclusion

Element-free Galerkin method has been successfully revamped within its framework by incorporating improved moving least-square method together with blended enrichment criteria and optimized quadrature criteria. Moreover, suitable parametric optimization has been performed for the selection of EFGM algorithm parameters thereby improving its robustness and accelerating the overall computational time of the algorithm. The revamped EFGM algorithm so developed is tested for a variety of fracture problems involving mechanical/thermal loads and compared with conventional EFGM algorithm. An average of 70–80% reduction in computational time is achieved with the proposed algorithm. The revamped EFGM algorithm outscores not only in terms of computational efficiency but also in terms of its robustness and flexibility to simulate variety of problems. The proficiency of revamped EFGM algorithm can be further extended for modelling of 3D fracture problems in complex geometries which requires the use of voluminous nodal data thereby increasing the computational time in an exponential way.