Nonlinear Thermal Stress Analysis of Functionally Graded Thick Cylinders and Spheres

Abstract

Nonlinear thermal stress analysis in a functionally graded hollow thick cylinders and spheres under the effect of high temperatures and temperature differences is considered by taking into account the material properties of the body both temperature dependent and radially graded, except Poisson’s ratio which is taken to be constant for simplicity. These conditions result in nonlinear governing differential equation that is adopted to solve numerically. The effect of the temperature-dependent material properties on the temperature distribution, radial displacement, and thermal stresses is presented in a graphical form. The importance of the effect of temperature on the material is shown in functionally graded materials manufactured to be exposed to high temperature and temperature difference. Benchmark solutions available in the literature are used to validate the results and to emphasize the convergence of the numerical solutions.

1 Introduction

Thick cylinders and spheres are widely used in many engineering design applications as common structural components. These structures are generally subject to thermal stresses, temperature, and environmental factors. Therefore, their material design is an important issue, not only to withstand high pressures, radial loads, and radial temperature, but also high temperatures, corrosion, erosion, and high fracture. In this context, functionally graded materials (FGMs) that are resistant to both internal and environmental conditions have been started to be developed and used in many areas (Koizumi 1997; Miyamoto et al. 1999). So, the thermal stress analysis of these intelligent materials has been an important issue addressed by many scientists in recent years.

Even though it is based on mainly the principle of producing material resistant to high temperatures and temperature changes, in many theoretical studies on the thermal stress of cylinder and sphere in the literature, material properties are handled independently of temperature. Some of them are given in chronological order as follows. Obata and Noda (1994) examined thermal stresses in hollow functionally graded cylinders and spheres using the perturbation technique. The analytical solution of the thick-walled hollow functionally graded sphere and cylinder is given by Lutz and Zimmerman (1996) and Zimmerman and Lutz (1999), respectively, using the Frobenius series method. They also obtained a precise statement for the effective thermal expansion coefficient. One-dimensional transient temperature distribution and thermal stress analysis of the functionally graded hollow cylinder consisting of ceramic-metal-based material is investigated numerically (Awaji and Sivakumar 2001) by exposing the ceramic inner surface to high temperature and the metallic outer surface to low temperature. The effect of temperature on the material is neglected. The exact analysis of the hollow cylinder, which is functionally graded according to the power-law function in the radial direction, under the radial symmetrical loads and non-axisymmetric steady-state loads, is presented in Jabbari et al. (2002, 2003), respectively. Liew et al. (2003) proposed a technique that could be obtained by a novel limiting process using the solution of the homogeneous cylinder, without resorting to non-homogeneous thermoelasticity equations to study the thermomechanical behavior in the functionally graded hollow cylinder. The stress analysis of a functionally graded simply supported circular hollow cylinder with finite length subjected to axisymmetric pressure loadings is solved analytically (Shao et al. 2004). A general solution is provided for thermal and mechanical stresses under general thermal and mechanical boundary conditions in a one-dimensional steady state in a hollow thick-walled sphere made of functionally graded material (Eslami et al. 2005). By using a multi-layered approach based on laminated composites theory, solutions of temperature, displacements, and thermal/mechanical stresses in a cylinder with a functionally graded circular hollow finite length are given in Shao (2005). Thermal stress analysis of the hollow sphere and cylinder, whose material properties are graded according to the exponential function in the radial direction, is presented in Celebi et al. (2016) and Celebi et al. (2017), respectively. Besides, some studies focus only on certain material properties depending on both coordinate and temperature. However, temperature dependency in all material properties should be considered to describe the thermal and mechanical stresses in functionally graded materials accurately, especially in the case of large temperature differences. In other words, the temperature dependency in the material properties can be neglected at low-temperature differences, whereas in applications with high-temperature differences, dependence on temperature has to be taken into account. These conditions result in a complicated nonlinear governing differential equations, which cannot be solved analytically except for some special cases.

Although there are many works on the functionally graded materials, studies with temperature-dependent material properties are barren in the literature, especially in the spherical bodies. A transfinite element method for transient analysis of thermal stresses in a functionally graded hollow cylinder with temperature-dependent material properties is presented by Azadi and Azadi (2009). Moosaie (2016) investigated the solution of the nonlinear thermal and thermoelastic problem for an FGM thick-walled cylindrical shell with temperature-dependent material properties by using the perturbation method. However, in this study, the power series of the temperature in the perturbation method does not have a defined threshold expansion degree for higher temperature values.

In this research, apart from the studies in the literature, a practical unified method that combines the Chebyshev pseudospectral collocation (CPS) and the fixed-point iteration methods is applied to the thermal stress distributions in a functionally graded hollow thick cylinders and spheres under the effect of high temperatures and temperature difference. It is assumed that the material properties of the bodies are both temperature dependent and radially graded, except Poisson’s ratio which is taken to be constant for simplicity. These conditions are produced a nonlinear ordinary differential equation that cannot be solved analytically with conventional methods except for some simple grading functions. Therefore, a numerical solution becomes essential to solve the problem. First, the ordinary differential equation is transformed into a nonlinear system by using the pseudospectral Chebyshev collocation method (Gottlieb and Orszag 1977; Trefethen 2000; Yarımpabuç 2019); then, the nonlinear system is solved iteratively by fixed-point iteration method (Burden and Faires 1993). The effect of the temperature-dependent material properties on temperature distribution, radial displacement, and thermal stresses is presented in the graphical form. The CPS procedure is validated by comparing the solutions of thick hollow bodies for functionally graded temperature-independent materials (Jabbari et al. 2002; Eslami et al. 2005). Compared with other numerical methods, CPS method is easy to implement and has a high accuracy with low computational cost. This is due to the structure of the mesh size, which is dense mesh near the boundary and coarse towards the center points. For this reason, CPS collocation method is preferred in this study. It is shown that temperature-dependent material properties at high temperatures and temperature differences have a great effect on temperature, displacement, and stress distributions.

2 Nonlinear Analysis

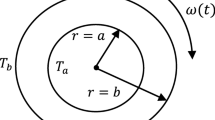
Nonlinear thermal stress distributions of a functionally graded hollow thick cylinder and sphere under axisymmetric conditions are calculated numerically. The inner and outer radii of the thick hollow bodies are taken as $r_\mathrm{i}$ and $r_\mathrm{o}$, respectively. A separable model (Moosaie 2016) is used for material properties that are both functions of temperature and graded along the radial direction and assumed to obey a simple power law as:

$$\begin{aligned} E(r,T)&=E_\mathrm{i}r^{m_1}T^{n_1}, \end{aligned}$$

(1a)

$$\begin{aligned} \alpha (r,T)&=\alpha _\mathrm{i}r^{m_2}T^{n_2} \end{aligned}$$

(1b)

$$\begin{aligned} k(r,T)&=k_\mathrm{i}r^{m_3}T^{n_3}, \end{aligned}$$

(1c)

Here, $T,~k,~E,~\alpha ,~(k_\mathrm{i},E_\mathrm{i},\alpha _\mathrm{i})$ and $m_{i}-n_{i},~i=1,2,3$ are the temperature distribution, thermal conductivity, modulus of elasticity, thermal expansion coefficient, material constants in the inner boundary and power-law indices of the material, respectively. It is assumed that the body is exposed to high temperature on the outer surface with high temperature difference between the inner and the outer boundaries. The boundary conditions for temperatures are prescribed as

$$\begin{aligned} {T\vert _{r=r_\mathrm{i}} }&={T_\mathrm{i},} \end{aligned}$$

(2a)

$$\begin{aligned} {T\vert _{r=r_\mathrm{o}}}&={T_\mathrm{o}} \end{aligned}$$

(2b)

where $T_\mathrm{i}$ and $T_\mathrm{o}$ are the temperature in the inner and outer surface of the body, respectively. It is supposed that the thick hollow body has a pressure on its inner surface, so the boundary conditions for the radial stress are

$$\begin{aligned} {\sigma _\mathrm{rr}\vert _{r=r_\mathrm{i}}}&={-P_\mathrm{i},} \end{aligned}$$

(3a)

$$\begin{aligned} {\sigma _\mathrm{rr}\vert _{r=r_\mathrm{o}}}&={0.} \end{aligned}$$

(3b)

Here, $\sigma _\mathrm{rr}$ is radial stress of the body and $P_\mathrm{i}$ is the pressure in the inner surface.

2.1 Thick Hollow Cylindrical Body

Consider the nonlinear distribution of temperature and thermal stresses for a thick hollow cylinder in a one-dimensional steady-state conditions. The nonlinear steady-state axisymmetric heat conduction equation without heat generation for the one-dimensional problem (Hetnarski and Eslami 2009; Carslaw and Jaeger 1959) is given as

$$\begin{aligned} \frac{1}{r}\frac{\text {d}}{\text {d}r}\left( rk(r,T)\frac{\text {d}T}{\text {d}r} \right) =0 \end{aligned}$$

(4)

Using Eq. (1c), the nonlinear heat conduction equation becomes

$$\begin{aligned} T''+\left( \frac{m_3+1}{r}+n_3 T^{-1}T'\right) T'=0. \end{aligned}$$

(5)

Let u be displacement component in the radial direction. Under the plain strain assumption and axisymmetry, the strain–displacement relations (Hetnarski and Eslami 2009)

$$\begin{aligned} { \varepsilon _\mathrm{rr} }&={\frac{\text {d}u}{\text {d}r},} \end{aligned}$$

(6a)

$$\begin{aligned} {\varepsilon _{\theta \theta }}&={\frac{u}{r}} \end{aligned}$$

(6b)

and the stress–strain relations (Hetnarski and Eslami 2009) are

$$\begin{aligned} \sigma _\mathrm{rr}&=\left( C_{11}\varepsilon _\mathrm{rr}+C_{12} \varepsilon _{\theta \theta }-\frac{1}{1-2\nu }{\int _{T_\mathrm{i}}^{T}\alpha (r,T) \text {d}T}\right) E(r,T), \end{aligned}$$

(7a)

$$\begin{aligned} \sigma _{\theta \theta }&=\left( C_{11}\varepsilon _{\theta \theta }+C_{12}\varepsilon _\mathrm{rr} -\frac{1}{1-2\nu }{\int _{T_\mathrm{i}}^{T}\alpha (r,T) \text {d}T}\right) E(r,T), \end{aligned}$$

(7b)

where

$$\begin{aligned} C_{11}&=\frac{(1-\nu )}{(1+\nu )(1-2\nu )}, ~~C_{12}=\frac{\nu }{(1+\nu )(1-2\nu )} \end{aligned}$$

Here, $\sigma _{\theta \theta }$ is the hoop stress and $\varepsilon _\mathrm{rr},~\varepsilon _{\theta \theta }$ are the strain tensors. And, $\nu$ is the Poisson’s ratio, which is taken constant for simplicity (Jabbari et al. 2015; Yıldırım et al. 2019). The equilibrium equation in the radial direction, disregarding the body force and inertia term (Hetnarski and Eslami 2009), is

$$\begin{aligned} \frac{\text {d} \sigma _\mathrm{rr}}{\text {d} r}+\frac{\sigma _\mathrm{rr}-\sigma _{\theta \theta }}{r}=0 \end{aligned}$$

(8)

Substituting Eqs. (6, 7a, and 7b) into stress equilibrium equation (8), and by using the temperature-dependent material properties (1a, 1b), one can get the nonlinear ordinary differential equation in terms of radial displacement, u as

$$\begin{aligned}&u''+P(r,T)u'+Q(r,T)u=R(r,T) \nonumber \\&P(r,T)=\left( \frac{m_1+1}{r} +n_1\frac{T'}{T} \right) ,\nonumber \\&Q(r,T)=\left( \frac{\nu n_1}{1-\nu } \frac{T'}{T}\frac{1}{r}+\frac{\nu m_1}{1-\nu }\frac{1}{r^2}-\frac{1}{r^2}\right) \nonumber \\&{R(r,T)}=\frac{1+\nu }{1-\nu }\alpha _\mathrm{i} r^{m_2}\nonumber \\&\quad \left( (n_1+n_2+1)T^{n_2}T'-n_1\frac{T'}{T}T_\mathrm{i}^{n_2+1}\right. \nonumber \\&\quad \left. \frac{m_1+m_2}{r}\left( T^{n_2+1}-T_\mathrm{i}^{n_2+1}\right) \right) . \end{aligned}$$

(9)

The boundary conditions in terms of displacement, derived from stress–strain relation (7a) and boundary conditions (3), can be written as

$$\begin{aligned} \left[ (1-\nu )u'+\frac{\nu }{r}u \right] _{r=r_\mathrm{i}}&={\left[ (1+\nu )\frac{\alpha _\mathrm{i}r^{m_2}}{n_2+1} \left( T^{n_2+1}-T_\mathrm{i}^{n_2+1} \right) \right. } \nonumber \\&\quad -\left. \dfrac{P_\mathrm{i}(1+\nu )(1-2\nu )}{E_\mathrm{o}T^{n_1}r^{m_1}} \right] _{r=r_\mathrm{i}} \nonumber \\ \left[ (1-\nu )u'+\frac{\nu }{r}u \right] _{r=r_\mathrm{o}}&={\left[ \frac{(1+\nu )\alpha _\mathrm{i}r^{m_2}}{n_2+1} \left( T^{n_2+1}-T_\mathrm{i}^{n_2+1} \right) \right] _{r=r_\mathrm{o}}} \end{aligned}$$

(10)

2.2 Thick Hollow Spherical Body

Consider the nonlinear distribution of temperature and thermal stresses for a thick hollow sphere in a one-dimensional steady-state conditions. The nonlinear steady-state axisymmetric heat conduction without heat generation for the one-dimensional problem (Hetnarski and Eslami 2009; Carslaw and Jaeger 1959) is given as

$$\begin{aligned} \frac{1}{r^2}\frac{\text {d}}{\text {d}r}\left( r^2k(r,T)\frac{\text {d}T}{\text {d}r} \right) =0 \end{aligned}$$

(11)

Using Eq. (1c), the nonlinear heat conduction equation becomes

$$\begin{aligned} T''+\left( \frac{2+m_3}{r}+n_3 T^{-1}T'\right) T'=0. \end{aligned}$$

(12)

Let u be displacement component in the radial direction. Then, the strain–displacement relations (Hetnarski and Eslami 2009)

$$\begin{aligned} { \varepsilon _\mathrm{rr} }&={\frac{\text {d}u}{\text {d}r},} \end{aligned}$$

(13a)

$$\begin{aligned} {\varepsilon _{\theta \theta }}&={\varepsilon _{\phi \phi }=\frac{u}{r}} \end{aligned}$$

(13b)

and the stress–strain relations (Hetnarski and Eslami 2009) are

$$\begin{aligned} \sigma _\mathrm{rr}&=\left( C_{11}\varepsilon _\mathrm{rr}+2C_{12} \varepsilon _{\theta \theta }-\frac{1}{1-2\nu }{\int _{T_\mathrm{i}}^{ T}\alpha (r,T) \text {d}T} \right) E(r,T), \end{aligned}$$

(14a)

$$\begin{aligned} \sigma _{\theta \theta }&=\sigma _{\phi \phi }=\left( \frac{C_{12}}{\nu }\varepsilon _{\theta \theta }+C_{12}\varepsilon _\mathrm{rr} -\frac{1}{1-2\nu }{\int _{T_\mathrm{i}}^{T}\alpha (r,T) \text {d}T}\right) E(r,T), \end{aligned}$$

(14b)

The equilibrium equation in the radial direction, disregarding the body force and inertia term (Hetnarski and Eslami 2009), is

$$\begin{aligned} \frac{\text {d}\sigma _\mathrm{rr}}{\text {d} r}+\frac{2(\sigma _\mathrm{rr}-\sigma _{\theta \theta })}{r}=0 \end{aligned}$$

(15)

Substituting Eqs. (13, 14a, and 14b) into stress equilibrium equation (15), and by using the temperature-dependent material properties (1b, 1c), one can get the nonlinear ordinary differential equation in terms of radial displacement, u as

$$\begin{aligned}&u''+P(r,T)u'+Q(r,T)u=R(r,T) \nonumber \\&P(r,T)=\left( \frac{m_1+2}{r}+n_1\frac{T'}{T} \right) ,\nonumber \\&Q(r,T)=\left( \frac{\nu n_1 }{1-\nu }\frac{T'}{T}\frac{2}{r} +\frac{\nu m_1}{1-\nu }\frac{2}{r^2}-\frac{2}{r^2}\right) \nonumber \\&{R(r,T)}=\frac{1+\nu }{1-\nu }\alpha _\mathrm{i} r^{m_2}\nonumber \\&\quad \left( (n_1+n_2+1)T^{n_2}T'-n_1\frac{T'}{T}T_\mathrm{i}^{n_2+1}\right. \nonumber \\&\quad \left. \frac{m_1+m_2}{r}\left( T^{n_2+1}-T_\mathrm{i}^{n_2+1}\right) \right) . \end{aligned}$$

(16)

The boundary conditions in terms of displacement, derived from stress–strain relation (14a) and boundary conditions (3), can be written as

$$\begin{aligned} \left[ (1-\nu )u'+\frac{2\nu }{r}u \right] _{r=r_\mathrm{i}}&={\left[ (1+\nu )\frac{\alpha _\mathrm{i}r^{m_2}}{n_2+1} \left( T^{n_2+1}-T_\mathrm{i}^{n_2+1} \right) \right. } \nonumber \\&\quad -\left. \dfrac{P_\mathrm{i}(1+\nu )(1-2\nu )}{E_\mathrm{o}T^{n_1}r^{m_1}} \right] _{r=r_\mathrm{i}}\nonumber \\ \left[ (1-\nu )u'+\frac{2\nu }{r}u \right] _{r=r_\mathrm{o}}&={\left[ \frac{(1+\nu )\alpha _\mathrm{i}r^{m_2}}{n_2+1} \left( T^{n_2+1}-T_\mathrm{i}^{n_2+1} \right) \right] _{r=r_\mathrm{o}}} \end{aligned}$$

(17)

3 Solution Procedure

The Chebyshev pseudospectral method is used to convert the nonlinear differential equation to a nonlinear system that can easily be solved by any iterative methods. In this study, due to the ease of implementation, fixed-point iteration, see, e.g., Burden and Faires (1993), is used to solve the nonlinear system iteratively.

3.1 Chebyshev Pseudospectral Method

The Chebyshev pseudospectral method is based on Chebyshev polynomials of the first kind, see, e.g., Gottlieb and Orszag (1977), Trefethen (2000), and Yarımpabuç (2019). It is a commonly preferred method due to its high accuracy, low computational cost, and the ease in implementation. For this reason, CPS collocation method is used to convert the nonlinear heat conduction equations (5, 12) to nonlinear system of equations. The first-order $(N+1)\times (N+1)$ Chebyshev differentiation matrix associated with the collocation points

$$\begin{aligned} 0=r_{0}<r_{1} \cdots < r_{N}, ~~\text {with}~~ r_{j}=\frac{1}{2}[1-\cos (j \pi /N)], \end{aligned}$$

(18)

$(j=0,1,\ldots ,N)$ will be denoted by D. First-order Chebyshev differentiation matrix D provides highly accurate approximation to $T'(r_{j}),~ T''(r_{j}), \ldots ,$ simply by multiplication differential matrix with corresponding data vector $T'(r_{j})= (D T)_{j}, ~ T''(r_{j})= (D^{2} T)_{j}$, such like that $T=[T_{0}, \ldots , T_{n} ]^{T}$ discrete vector data at positions $r_{j}.$

The computation procedure of the Chebyshev differentiation matrix and codes as m-file can be found in notable references, see, e.g., Trefethen (2000), where the collocation points $r_j$ are numbered from right to left and defined in $[-1,1]$. With a small adaptation, the m-file of the differentiation matrix D can be transcribed to any desired range [a, b].

Efficiency, accuracy, and the ease of implementation of the method are explained in detail in the study of Trefethen (2000) and Yarımpabuç (2019). Therefore, the nonlinear heat conduction equation for the thick hollow cylinder (4) is simply converted into a nonlinear system by using the pseudospectral Chebyshev collocation method as follows:

$$\begin{aligned} M_TT_\mathrm{new}=\text {RHS}(r,T_\mathrm{old}) \end{aligned}$$

(19)

where

$$\begin{aligned} M_T=D^2 \end{aligned}$$

(20)

and

$$\begin{aligned} \text {RHS}(r,T_\mathrm{old})=-\left( \frac{m_3+1}{r}+n_3 T_\mathrm{old}^{-1}(DT_\mathrm{old})\right) (DT_\mathrm{old}) \end{aligned}$$

(21)

Boundary conditions for temperature (2) are imposed to this linear system (19) by only replacing the first and last row of the system matrix $M_T$ with the first and last row of the identity matrix, respectively, and the corresponding RHS values with $T_\mathrm{i}$ and $T_\mathrm{o}$. Then, the nonlinear system (19) can be iterative solved by selecting a random prediction vector for temperature using the fixed-point method in the following way:

$$\begin{aligned} T_\mathrm{new}=M_T^{-1}\text {RHS}(r,T_\mathrm{old}) \end{aligned}$$

(22)

Here, $T_\mathrm{{old}}$ and $T_\mathrm{new}$ are the temperature value in previous and current iteration, respectively. After that, the radial displacement of the thick hollow cylinder can be discretized by using calculated temperature (22) with the combination of the Chebyshev differentiation matrix in the following way:

$$\begin{aligned} M_uu=R(r,T_\mathrm{new}) \end{aligned}$$

(23)

where

$$\begin{aligned} M_u=D^2+P(r,T_\mathrm{new})D+Q(r,T_\mathrm{new}) \end{aligned}$$

(24)

Boundary conditions for the radial displacement (10) are imposed in a similar way. Therefore, radial displacement can simply be found by inverting $M_u$ as:

$$\begin{aligned} u= M_u^{-1}R(r,T_\mathrm{new}) \end{aligned}$$

(25)

The same solution procedure is followed for the solution of the thick hollow sphere.

4 Results

The effect of the temperature-dependent material properties on temperature, radial displacement, and stresses on the thick hollow bodies is presented for $r_\mathrm{i}=1$, $r_\mathrm{o}=1.2$, $E_\mathrm{i}=200~\text {GPa}$, $\alpha _\mathrm{i}=1.2\times 10^{-6}/ ^{\circ }\text {C}$, $T_\mathrm{i}=40^{\circ }C,$ $T_\mathrm{o}=400^{\circ }\text {C}$, $P_\mathrm{i}=50\,\text {MPa}$, $\nu =0.3$. The material properties of the thick hollow bodies are assumed to be a function of temperature and graded along the radial direction with a power-law function, while the Poisson’s ratio is taken to be constant.

The CPS procedure is validated by comparing the solutions of thick hollow bodies for functionally graded temperature-independent materials $(n_{i}=0,~m_{i}=-2)$ (Jabbari et al. 2002; Eslami et al. 2005) in Tables  1 and 2. It can be noticed from Tables  1 and 2 that the results are in good agreement and have a substantial amount of accuracy.

Before going to the numerical calculations, the grid refinement tests are performed for the current approach for thick hollow cylinders and spheres with temperature-dependent material properties and presented in Tables 3 and 4. It can be observed from Tables 3 and 4 that eleven ($N=10$ interval ) collocation points are enough for six-digit accuracy. Therefore, the present solutions are calculated at eleven $(N=10)$ collocation points.

Table 1 Comparison of the present solutions of thick hollow cylinder for temperature-independent material properties with Jabbari et al. (2002) $(n_{i}=0,~m_{i}=-2,~i=1,2,3)$

Table 2 Comparison of the present solutions of thick hollow sphere for temperature-independent material properties with Eslami et al. (2005) $(n_{i}=0,~m_{i}=-2,~i=1,2,3)$

Table 3 Mesh refinement test of the present solutions for thick hollow cylinder at $r=1.1,~n_1=-0.1,$ $n_{2,3}=0.1$, $m_{i}=-2,~i=1,2,3$

Table 4 Mesh refinement test of the present solutions for thick hollow sphere at $r=1.1,~n_1=-0.1,$ $n_{2,3}=0.1$,      $m_{i}=-2,~i=1,2,3$

A comparison between the results of the linear and nonlinear models for temperature distribution of cylinder and sphere is presented in Tables 5 and 6 to show the importance of the second one.

Table 5 Comparison between the results of the linear $(n_{i}=0)$ and nonlinear models $(n_1=-0.1,~n_{2,3}=0.1)$ for temperature distribution of cylinder $(m_{i}=-2,~i=1,2,3)$

Table 6 Comparison between the results of the linear $(n_{i}=0)$ and nonlinear models $(n_1=-0.1,~n_{2,3}=0.1)$ for temperature distribution of sphere $(m_{i}=-2,~i=1,2,3)$

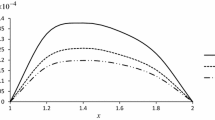
The effect of the temperature-dependent material properties on temperature distribution, radial displacement, and thermal stresses for the thick-walled functionally graded cylinder and sphere at a high temperature and temperature differences is also presented in Figs. 1, 2, and 3. Solid line $(n_{i}=0,~m_{i}=-2)$ and dashed-dot line $(n_1=-0.1,~n_{2,3}=0.1,~m_{i}=-2)$ correspond to functionally graded (temperature-independent) and both radial and temperature-dependent material properties, respectively. The nonlinearity parameter of the modulus of elasticity $(n_1=-0.1)$ is taken negative due to the decrease in elastic modulus with temperature increase.

Fig. 1

The effect of the temperature-dependent material properties on temperature distribution

It is found that the temperature (Fig. 1) and the displacement (Figs. 2a, 3a) along the radial direction are higher when the material properties have a temperature effect for both cylindrical and spherical geometry. Accordingly, it is shown in Figs. 2b and 3b that the radial stresses are lower compared to temperature-independent functionally graded model. The hoop stresses (Figs.  2c, 3c) along the radius take higher values on the inner wall and lower values on the outer wall compared to only radially dependent material. It can be observed from Figs.  1, 2, and 3 that temperature-dependent material properties at high temperatures have great effect on temperature, displacement, and stress distributions.

5 Conclusions

In this study, nonlinear thermal stress analysis of the functionally graded hollow thick cylinder and sphere in the interval from 40 to $400^{\circ }C$ is solved numerically with combination of the Chebyshev pseudospectral collocation method (CPS) and the fixed-point iteration method. The material properties of the hollow thick cylinder and sphere are both temperature dependent and radially graded except the Poisson’s ratio, which is taken to be constant. The CPS procedure is validated by comparing the solutions of thick hollow bodies for functionally graded temperature-independent materials (Jabbari et al. 2002; Eslami et al. 2005). It is shown that all results are in good agreement. Finally, it can be deduced that:

• Temperature-dependent material properties at high temperatures and temperature differences have a great effect on temperature, displacement, and stresses. Therefore, the effect of temperature on material properties should be considered in studies requiring high accuracy.

• The combination of the Chebyshev pseudospectral collocation method (CPS) and the fixed-point iteration method can efficiently be used for both nonlinear heat conduction problems and thermal stress analysis.

• The solution procedure has high accuracy, low calculation cost, and ease in implementation.

Fig. 2

The effect of the temperature-dependent material properties on cylindrical geometry

Fig. 3

The effect of the temperature-dependent material properties on spherical geometry