1 Introduction

Many studies have been carried out from past to present regarding the static, dynamic and stability analysis of buildings, and different numerical analysis methods have been developed. Although the finite element method has become widespread in practice, another practical method has been developed to be used, especially in the pre-sizing phase. One of these is the continuous system calculation model. In this model, a multi-story building is idealized as an equivalent continuous media.

The first study on the continuous system calculation model was made by Chity (1947). In the study conducted by Chity, the shear beam and the flexural beam were combined with bars with joints at both ends and their static analyses were carried out. In a later work, Chitty and Wan (1948) applied the continuous method to buildings but neglected axial strain in vertical elements. Skattum (1971) proposed an approach for the dynamic analysis of coupled shear walls. Reinhorn (1978) used the continuous method and the Tansfer matrix method to present an approximate analytical model for the static and dynamic analysis of tall buildings where it included the axial deformations. Miranda (1999) used the flexural-shear beam model to calculate the displacements of buildings under different static loading situations. Potzta and Kollár (2003) used the sandwich beam model for the dynamic analysis of buildings and proposed an approach to calculate the equivalent stiffness of load-bearing systems located in different planes. Bozdoğan (2010) developed Transfer matrices to be used in static, dynamic and stability analyses of multi-story symmetrical and asymmetrical buildings. In the study, the contributions of shear displacements in the walls and axial loads in the vertical elements to the horizontal displacement were also considered. Zalka (2001, 2002, 2003, 2009, 2013) developed closed form solutions for the calculation of displacements of symmetrical and asymmetrical buildings under static loads, calculation of periods and critical buckling loads. Bozdogan (2012) proposed the Transfer matrix method for free vibration analysis of shear-frame systems placed asymmetrically in plan.

Aydın and Bozdogan (2016) proposed a method for stability analysis in shear-frame systems according to the sandwich beam model. In the method, the critical buckling load was obtained by solving the differential equation system written in accordance with the continuous system calculation model with the differential transformation method. Faridani and Capsoni (2016) proposed a modified flexural-shear beam model for the analysis of damping systems. Mohammadnejad and Kazemi (2018) used the bending beam model for the analysis of buildings whose structural system is a tube system. Sgambi (2020) examined multi-beam models used in modeling buildings. Kara et al. (2021) proposed a practical approach using the continuous system calculation model to find the soil-structure interaction periods of the buildings. Laier (2021) used the improved continuous system calculation model developed for the analysis of three-dimensional buildings.

One of the models used in the analysis of buildings with a continuous system is to represent the buildings as an equivalent Timoshenko beam. The studies in the literature related to the modeling of Timoshenko beams used for analysis and identification of structures are summarized below.

Köpecsiri and Kollar (1998), for the determination of displacement and internal forces by means of modal response analysis of tall building, used the Timoshenko beam model. In their study, for the first two modes, the base shear force, bending moment, maximum displacements and maximum drift ratio between floors are practically available with the help of graphs. Design forces and displacements are determined using the mode superposition method.

Lord and Ventura (2002) compared the results by finding periods of an experimental and analytical method of a 48-story and core wall bearing system with tuned mass damper. As an analytical method, they modeled the structure as an equivalent Timoshenko beam.

Rahgozar et al. (2004) investigated the analytical solution of the variable section Timoshenko beam for free vibration analysis of tall building. They obtained an analytical solution for the polynomial and exponential exchange of inertia moment, sectional area and mass. In this study, change functions were selected specifically to allow an analytical solution.

Boutin et al. (2005) showed that regular structures with on-site period measurements could be successfully represented by the Timoshenko beam model. Michel et al. (2006) proposed a method in which the ambient vibration and Timoshenko beam model were used together to determine modal parameters of reinforced concrete structures.

Xie and Wen (2008) used model buildings as an equivalent Timoshenko beam for determining the interstory drift ratio of multi-story buildings and presented a measurement of the seismic demands of ground motion considering the non-uniform distribution of drift demands.

Koehler et al. (2013) benefited from the Timoshenko beam model in the approach they developed for the identification of buildings. Rahgozar et al. (2004) used the Timoshenko vogue model to determine the natural periods of multi-story buildings.

Ebrahimian and Todorovska (2014) analyzed the wave propagation of a tall building excited by seismic ground motion. In a later work, Ebrahimian and Todorovska (2015) have used a non-uniform Timoshenko beam model for system identification of tall buildings. Damage assessment of the buildings can be carried out with the presented model. Su et al. (2015) used the Timoshenko beam model to assess seismic behaviors of existing buildings in Malaysia quickly.

Cheng and Heaton (2015) utilized from the Timoshenko beam model to determine the linear elastic behavior of buildings, by considering the soil effect. The building behavior can be considerably determined by measuring the first two horizontal modes. The suitability of the method presented at the end of the study is shown on the Caltech Millikan library building.

Su et al. (2016a), in the low moderate seismic region, for determination of earthquake behaviors of buildings, used the two-zone Timoshenko beam model to clarify the seismic behavior of the structures. In a subsequent investigation, Su et al. (2016b), for the reinforced concrete, benefited from the Timoshenko beam model to quickly and practically determine the mode shapes of tall buildings. In the method presented, graphs were used to determine mode shapes.

Taciroglu et al. (2017) used the Timoshenko beam model to determine the dynamic stiffness of the soil foundations system. Ozmutlu et al. (2018) studied wave propagation in rigid slab periodical structures using the Timoshenko beam model. Feretti (2018) benefited from the three-dimensional Timoshenko beam model to find a critical buckling load for structures consisting of columns and rigid slabs. Davari et al. (2019) developed closed equations for the static analysis of tall buildings using the Timoshenko beam model. Gungor and Bozdogan (2021) proposed the Timoshenko beam model for the spectral analysis of steel plate shear wall systems. In the study, they used the differential transformation method to determine the dynamic characteristics of the Timoshenko beam model.

The size of the Transfer matrix method, which was previously developed in the literature (Bozdogan 2010) for static, dynamic and stability solution of all types of systems, was 6*6 for the symmetric buildings case and 12*12 for the asymmetric building. In this study, symmetric systems consisting of pure frames and pure shear walls are represented by the equivalent Timoshenko beam model, which is a special case of the general case, and the Transfer matrices are obtained. In this case, the dimension of the Transfer matrices is 4*4, and unlike the literature, the contribution of local bending of columns and shear walls to the horizontal displacement is neglected. In this study, Transfer matrices were created for the static, dynamic and stability analysis of buildings that can be modeled as Timoshenko beams, and the Transfer matrix method was proposed for the analysis of these systems. The following assumptions were made in the study.

  1. 1.

    The material shows linear elastic behavior.

  2. 2.

    P-Δ and P-δ effects are negligible.

  3. 3.

    The buildings are placed symmetrically in the plan, and the torsional and translational movements are uncoupled.

  4. 4.

    The effect of axial displacements in the beams on the horizontal translational displacements has been neglected.

  5. 5.

    Slabs show rigid diaphragm behavior.

2 Timoshenko Replacement Beam

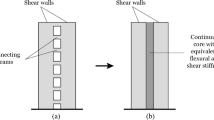
Buildings consisting of only shear walls and only frame systems can be modeled as an equivalent Timoshenko beam under static and dynamic loads. The Timoshenko replacement beam (Fig. 1) consists of the series coupling of a bending beam and a shear beam. The representation of the Timoshenko beam model with springs is shown in Fig. 1. In the Figure, Kb shows the bending stiffness and Ks shows the shear stiffness.

Fig. 1
figure 1

Timoshenko beam. a-c Equivalent replacement beam and d Schematic representation of the mechanism

Full size image

3 Static Analysis

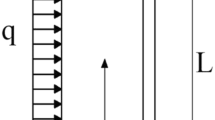
In the continuous system calculation model, the loads are considered as distributed along the system as it is known. In this study, in order to comply with the finite element method, the loads are applied at the floor levels. In Fig. 2, the distributed loads are shown acting on the floor levels in a discrete manner.

Fig. 2
figure 2

Discretization process of the continuous model. a General distributed lateral load and b Point loads acting on floor levels

Full size image

The differential equation system of the Timoshenko beam under static loads is written as in Eq. (1), using Hamilton’s principle.

$$\begin{gathered} K_{{\text{b}}} \theta_{(x)}^{\prime \prime } + K_{s} \left[ {u_{(x)}^{\prime } - \theta_{(x)} } \right] = 0 \hfill \\ K_{{\text{s}}} \left[ {u_{(x)}^{\prime \prime } - \theta_{(x)}^{\prime } } \right] + f_{(x)} = 0 \hfill \\ \end{gathered}$$
(1)

where \(H\) is the total height of the continuous model, \({f}_{(x)}\) is the distributed lateral load, \({u}_{(x)}\) is the lateral displacement and \({\theta }_{(x)}\) is the rotation due to bending.

Assuming that the external loads are not distributed throughout the element but only effect the nodes at the floor levels, the differential equation system is written as follows.

$$\begin{gathered} K_{{\text{b}}} \theta_{(x)}^{\prime \prime } + K_{s} \left[ {u_{(x)}^{\prime } - \theta_{(x)} } \right] = 0 \hfill \\ K_{{\text{s}}} \left[ {u_{(x)}^{\prime \prime } - \theta_{(x)}^{\prime } } \right] = 0 \hfill \\ \end{gathered}$$
(2)

If the differential equation system (2) is solved by any method known from the theory of differential equations, the \({u}_{(x)}\) and \({\theta }_{(x)}\) functions are found with Eqs. (3).

$$\begin{aligned} u_{(x)} = & C_{0} + C_{1} x + C_{2} x^{2} + C_{3} x^{3} \\ \theta_{(x)} = & C_{1} + C_{2} \left( {2x} \right) + C_{3} \left( {3x^{2} + 6\frac{{K_{{\text{b}}} }}{{K_{{\text{s}}} }}} \right) \\ \end{aligned}$$
(3)

Using the displacement functions (3), the bending moment and shear force functions are found with Eq. (4) as follows.

$$\begin{aligned} M_{(x)} = & K_{{\text{b}}} \theta_{(x)}^{\prime } = C_{2} \left( {2K_{{\text{b}}} } \right) + C_{3} \left( {6K_{{\text{b}}} x} \right) \\ V_{(x)} = & K_{{\text{s}}} \left[ {u_{(x)}^{\prime } - \theta_{(x)} } \right] = C_{3} \left( { - 6K_{{\text{b}}} } \right) \\ \end{aligned}$$
(4)

Equations (3) and (4) can be written in matrix form as Eq. (5):

$$\left\{ {\begin{array}{*{20}c} {u_{i} \left( {x_{i} } \right)} \\ {\theta_{i} \left( {x_{i} } \right)} \\ {M_{i} \left( {x_{i} } \right)} \\ {V_{i} \left( {x_{i} } \right)} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 1 & {x_{i} } & {x_{i}^{2} } & {x_{i}^{3} } \\ 0 & 1 & {2x_{i} } & {3x_{i}^{2} + 6\frac{{K_{{\text{b}}} }}{{K_{{\text{s}}} }}} \\ 0 & 0 & {2K_{{\text{b}}} } & {6K_{{\text{b}}} x} \\ 0 & 0 & 0 & { - 6K_{{\text{b}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\} = {\mathbf{A}}_{i} \left( {x_{i} } \right)\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\}$$
(5)

At the base of the i-th floor, Eq. (5) is written as follows.

$$\left\{ {\begin{array}{*{20}c} {u_{i} \left( 0 \right)} \\ {\theta_{i} \left( 0 \right)} \\ {M_{i} \left( 0 \right)} \\ {V_{i} \left( 0 \right)} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & {6\frac{{K_{{\text{b}}} }}{{K_{{\text{s}}} }}} \\ 0 & 0 & {2K_{{\text{b}}} } & 0 \\ 0 & 0 & 0 & { - 6K_{{\text{b}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\} = {\mathbf{A}}_{{\mathbf{i}}} \left( {\mathbf{0}} \right)\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\}$$
(6)

At the top point of the i-th floor, Eq. (5) is written as follows.

$$\left\{ {\begin{array}{*{20}c} {u_{i} \left( {h_{i} } \right)} \\ {\theta_{i} \left( {h_{i} } \right)} \\ {M_{i} \left( {h_{i} } \right)} \\ {V_{i} \left( {h_{i} } \right)} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 1 & {h_{i} } & {h_{i}^{2} } & {h_{i}^{3} } \\ 0 & 1 & {2h_{i} } & {3h_{i}^{2} + 6\frac{{K_{{\text{b}}} }}{{K_{{\text{s}}} }}} \\ 0 & 0 & {2K_{b} } & {6K_{{\text{b}}} h_{i} } \\ 0 & 0 & 0 & { - 6K_{{\text{b}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\} = {\mathbf{A}}_{i} \left( {{\text{h}}_{{\text{i}}} } \right)\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\}$$
(7)

Matrix Eq. (8) is obtained from matrix Eqs. (6) and (7).

$$\left\{ {\begin{array}{*{20}c} {u_{i} \left( {h_{i} } \right)} \\ {\theta_{i} \left( {h_{i} } \right)} \\ {M_{i} \left( {h_{i} } \right)} \\ {V_{i} \left( {h_{i} } \right)} \\ \end{array} } \right\} = {\mathbf{A}}_{{\mathbf{i}}} \left( {h_{i} } \right){\mathbf{A}}_{{\mathbf{i}}} \left( 0 \right)^{ - 1} \left\{ {\begin{array}{*{20}c} {u_{i} \left( 0 \right)} \\ {\theta_{i} \left( 0 \right)} \\ {M_{i} \left( 0 \right)} \\ {V_{i} \left( 0 \right)} \\ \end{array} } \right\} = {\mathbf{T}}_{{\mathbf{i}}} \left\{ {\begin{array}{*{20}c} {u_{i} \left( 0 \right)} \\ {\theta_{i} \left( 0 \right)} \\ {M_{i} \left( 0 \right)} \\ {V_{i} \left( 0 \right)} \\ \end{array} } \right\}$$
(8)

where Ti is the Transfer matrix of the i-th floor and is calculated with the following equation:

$${\mathbf{T}}_{{\mathbf{i}}} = {\mathbf{A}}_{{\mathbf{i}}} \left( {h_{i} } \right){\mathbf{A}}_{{\mathbf{i}}} \left( 0 \right)^{ - 1}$$
(9)

For static analysis under horizontal loads acting on floors, floor Transfer matrices and external load vectors (f) created by external loads acting on floor levels can be used. The following relation is written as a result of successive operations between the top point of the building and its base.

$$\left\{ {\begin{array}{*{20}c} {u_{{{\text{top}}}} } \\ {\theta_{{{\text{top}}}} } \\ {M_{{{\text{top}}}} } \\ {V_{{{\text{top}}}} } \\ \end{array} } \right\} = {\mathbf{t}}\left\{ {\begin{array}{*{20}c} {u_{{{\text{base}}}} } \\ {\theta_{{{\text{base}}}} } \\ {M_{{{\text{base}}}} } \\ {V_{{{\text{base}}}} } \\ \end{array} } \right\} + {\mathbf{f}}$$
(10)

where

$${\mathbf{t}} = \prod\limits_{k = 1}^{n} {{\mathbf{T}}_{{\mathbf{k}}} } ,{\mathbf{f}} = - \sum\nolimits_{s = 0}^{n} {\left[ {\prod\limits_{k = s + 1}^{n} {{\mathbf{T}}_{{\mathbf{k}}} } } \right]{\mathbf{F}}_{s} - {\mathbf{F}}_{{\mathbf{n}}} }$$
(11)

As seen here, the size of the system Transfer matrix is the same as the size of the element Transfer matrices and is 4*4.

Boundary conditions must be defined for the solution of matrix Eq. (10). These are briefly summarized below.

  • Translation and rotation at the base of the building are zero.

  • At the top of the building, the bending moment and shear force are zero.

These four conditions are mathematically shown by Eqs. (12), (13), (14) and (15).

$$u_{{{\text{base}}}} = 0$$
(12)
$$\theta_{{{\text{base}}}} = 0$$
(13)
$$M_{{{\text{top}}}} = 0$$
(14)
$$V_{{{\text{top}}}} = 0$$
(15)

If these four conditions are substituted in matrix Eq. (10), matrix Eq. (16) is obtained.

$$\left\{ {\begin{array}{*{20}c} {u_{{{\text{top}}}} } \\ {\theta_{{{\text{top}}}} } \\ 0 \\ 0 \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {t_{1,1} } & {t_{1,2} } & {t_{1,3} } & {t_{1,4} } \\ {t_{2,1} } & {t_{2,2} } & {t_{2,3} } & {t_{2,4} } \\ {t_{3,1} } & {t_{3,2} } & {t_{3,3} } & {t_{3,4} } \\ {t_{4,1} } & {t_{4,2} } & {t_{4,3} } & {t_{4,4} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {M_{{{\text{base}}}} } \\ {V_{{{\text{base}}}} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ {f_{3} } \\ {f_{4} } \\ \end{array} } \right\}$$
(16)

By solving the matrix Eq. (16), the bending moment and shear force at the base can be found with Eq. (17), and the translation and rotation values at the top can be found with Eq. (18).

$$\left\{ {\begin{array}{*{20}c} {M_{{{\text{base}}}} } \\ {V_{{{\text{tase}}}} } \\ \end{array} } \right\} = - \left[ {\begin{array}{*{20}c} {t_{3,3} } & {t_{34} } \\ {t_{4,3} } & {t_{4,4} } \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} {f_{3} } \\ {f_{4} } \\ \end{array} } \right\}$$
(17)
$$\left\{ {\begin{array}{*{20}c} {u_{{{\text{top}}}} } \\ {\theta_{{{\text{top}}}} } \\ \end{array} } \right\} = - \left[ {\begin{array}{*{20}c} {t_{1,3} } & {t_{14} } \\ {t_{2,3} } & {t_{2,4} } \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ \end{array} } \right\}\left[ {\begin{array}{*{20}c} {t_{3,3} } & {t_{34} } \\ {t_{4,3} } & {t_{4,4} } \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} {f_{3} } \\ {f_{4} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ \end{array} } \right\}$$
(18)

4 Dynamic Analysis

Assuming that the masses are lumped at floor level, the inertia force at i. floor level is written as follows:

$$F_{i} = m_{{_{i} }} \mathop u\limits^{..} = m_{{_{i} }} w^{2} u_{i}$$
(19)

where mi is the mass of the floor.

For equilibrium:

$$V_{i + 1} = V_{i} + m_{i} w^{2} u_{{_{i} }}$$
(20)

The relationship between forces and displacements between two consecutive floors is obtained by taking into account the Transfer matrix and the vector of external point forces. For the j-th floor:

$$\left\{ {\begin{array}{*{20}c} {u_{i + 1} \left( {h_{i} } \right)} \\ {\theta_{i + 1} \left( {h_{i} } \right)} \\ {M_{i + 1} \left( {h_{i} } \right)} \\ {V_{i + 1} \left( {h_{i} } \right)} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ {m_{i} w^{2} } & 0 & 0 & 1 \\ \end{array} } \right]{\mathbf{T}}_{i} \left\{ {\begin{array}{*{20}c} {u_{i} \left( 0 \right)} \\ {\theta_{i} \left( 0 \right)} \\ {M_{i} \left( 0 \right)} \\ {V_{i} \left( 0 \right)} \\ \end{array} } \right\}$$
(21)

Rewriting:

$$\left\{ {\begin{array}{*{20}c} {u_{i + 1} \left( {h_{i} } \right)} \\ {\theta_{i + 1} \left( {h_{i} } \right)} \\ {M_{i + 1} \left( {h_{i} } \right)} \\ {V_{i + 1} \left( {h_{i} } \right)} \\ \end{array} } \right\} = {\mathbf{T}}_{{{\mathbf{wi}}}} \left\{ {\begin{array}{*{20}c} {u_{i} \left( 0 \right)} \\ {\theta_{i} \left( 0 \right)} \\ {M_{i} \left( 0 \right)} \\ {V_{i} \left( 0 \right)} \\ \end{array} } \right\}$$
(22)

where Twi is the dynamic Trasfer matrix of the i-th story and is defined as follows:

$${\mathbf{T}}_{{{\mathbf{wi}}}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ {m_{i} w^{2} } & 0 & 0 & 1 \\ \end{array} } \right]{\mathbf{T}}_{i}$$
(23)

If the matrix relation (21) is applied sequentially for all building floors, the matrix Eq. (24) is obtained.

$$\left\{ {\begin{array}{*{20}c} {u_{top} } \\ {\theta_{top} } \\ {M_{top} } \\ {V_{top} } \\ \end{array} } \right\} = \prod\limits_{k = 1}^{n} {{\mathbf{T}}_{{{\mathbf{wk}}}} } \left\{ {\begin{array}{*{20}c} {u_{top} } \\ {\theta_{top} } \\ {M_{top} } \\ {V_{top} } \\ \end{array} } \right\} = {\mathbf{t}}_{{\mathbf{w}}} \left\{ {\begin{array}{*{20}c} {u_{top} } \\ {\theta_{top} } \\ {M_{top} } \\ {V_{top} } \\ \end{array} } \right\}$$
(24)

where

$${\mathbf{t}}_{{\mathbf{w}}} = \prod\limits_{k = 1}^{n} {{\mathbf{T}}_{{{\mathbf{wk}}}} }$$
(25)

If the boundary conditions given in Eqs. (12), (13), (14) and (15) are applied to the matrix Eq. (24), Eq. (26) is obtained.

$$\left\{ {\begin{array}{*{20}c} {u_{top} } \\ {\theta_{top} } \\ 0 \\ 0 \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {t_{w1,1} } & {t_{w1,2} } & {t_{w1,3} } & {t_{w1,4} } \\ {t_{w2,1} } & {t_{w2,2} } & {t_{w2,3} } & {t_{w2,4} } \\ {t_{w3,1} } & {t_{w3,2} } & {t_{w3,3} } & {t_{w3,4} } \\ {t_{w4,1} } & {t_{w4,2} } & {t_{w4,3} } & {t_{w4,4} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {M_{{{\text{base}}}} } \\ {V_{{{\text{base}}}} } \\ \end{array} } \right\}$$
(26)

From matrix Eq. (26), matrix Eq. (27) can be obtained:

$$\left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {t_{w3,3} } & {t_{w3,4} } \\ {t_{w4,3} } & {t_{w4,4} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {M_{{{\text{base}}}} } \\ {V_{{{\text{base}}}} } \\ \end{array} } \right\}$$
(27)

The necessary and sufficient condition for the bending moment and shear force to be non-zero in the given equation is that the determinant of the matrix is zero. The values of ω that make the determinate zero give the angular frequencies.

5 Stability Analysis

Several studies have been carried out in the literature (Hegedűs and Kollár, 1984; Bozdogan and Ozturk 2010) on the stability analysis of buildings according to the continuous system calculation model. In their study, Bozdogan and Ozturk proposed the Transfer matrix method for the stability analysis of buildings in the most general way. In the study, all effects on shear walls and frames were considered, and the size of the Transfer matrix was considered as 6 * 6. In this study, stability Transfer matrices of size 4 * 4 were obtained according to the Timoshenko beam model for the stability analysis of pure frame and pure shear walls, which are a special case of the general case. has been made. In the continuous system calculation model in stability analysis, axial loads are assumed to be distributed along the height of the building. However, in this study, to comply with the finite element method, axial loads are assumed to act at floor levels (Fig. 3). In this section, in obtaining the stability Transfer matrix, the stability Transfer matrix obtained for columns in the literature (Li 2001) is used.

Fig. 3
figure 3

Structural plan of the building of shear walls and core

Full size image

Using the total potential energy, the differential equation system in stability for the Timoshenko beam is written as follows.

$$\begin{array}{*{20}c} {K_{{\text{b}}} \theta_{(x)}^{\prime \prime } + K_{{\text{s}}} \left[ {u_{(x)}^{\prime } - \theta_{(x)} } \right] = 0} \\ { - K_{{\text{s}}} \left[ {u_{(x)}^{\prime \prime } - \theta_{(x)}^{\prime } } \right] + Nu_{(x)}^{\prime \prime } = 0} \\ \end{array}$$
(28)

where N is the axial load of the i-th story. From the solution of the differential equation system given above, the lateral translation \({u}_{(z)}\) and rotation \({\theta }_{(z)}\) functions are found as follows (Li 2001).

$$\begin{aligned} u(x) = & c_{0} + c_{1} x + c_{2} \cos (ax) + c_{3} \sin (ax) \\ \theta \left( x \right) = & c_{1} - c_{2} a\left( {1 + \frac{N}{{K_{s} }}} \right)\sin (ax) + c_{3} a\left( {1 - \frac{N}{{K_{s} }}} \right)\cos (ax) \\ \end{aligned}$$
(29)

where

$$b = \left[ {1 - \frac{N}{{K_{{\text{s}}} }}} \right]$$
(30)
$$a = \sqrt {\frac{N}{{bK_{{\text{b}}} }}}$$
(31)

Internal forces such as bending moment and shear force associated with lateral displacement result in:

$$\begin{aligned} M(x) = & EI\theta^{\prime } = c_{2} N\cos (ax) + c_{3} N\sin (ax) \\ V\left( x \right) = & EI\theta^{\prime \prime } + Nu(x)^{\prime } = c_{1} N \\ \end{aligned}$$
(32)

Writing the equations in matrix form:

$$\left\{ {\begin{array}{*{20}c} {u_{i} \left( {x_{i} } \right)} \\ {\theta_{i} \left( {x_{i} } \right)} \\ {M_{i} \left( {x_{i} } \right)} \\ {V_{i} \left( {x_{i} } \right)} \\ \end{array} } \right\} = {\mathbf{B}}_{{\mathbf{i}}} \left( {x_{i} } \right)\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\}$$
(33)

where

$$B_{i} \left( {x_{i} } \right) = \left[ {\begin{array}{*{20}c} 1 & {x_{i} } & {\cos \left( {a_{i} x_{i} } \right)} & {\sin \left( {a_{i} x_{i} } \right)} \\ 0 & 1 & {a_{i} \left( {1 + \frac{{N_{i} }}{{K_{si} }}} \right)\sin \left( {a_{i} x_{i} } \right)} & {a_{i} \left( {1 - \frac{{N_{i} }}{{K_{si} }}} \right)\cos \left( {a_{i} x_{i} } \right)} \\ 0 & 0 & { - N_{i} \cos \left( {a_{i} x_{i} } \right)} & { - N_{i} \sin \left( {a_{i} x_{i} } \right)} \\ 0 & {N_{i} } & 0 & 0 \\ \end{array} } \right]$$
(34)

At the top of the I-th floor, Eq. (33) is written as follows.

$$\left\{ {\begin{array}{*{20}c} {u_{i} \left( {h_{i} } \right)} \\ {\theta_{i} \left( {h_{i} } \right)} \\ {M_{i} \left( {h_{i} } \right)} \\ {V_{i} \left( {h_{i} } \right)} \\ \end{array} } \right\} = {\mathbf{B}}_{{\mathbf{i}}} \left( {h_{i} } \right)\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\}$$
(35)

where

$$B_{i} \left( {h_{i} } \right) = \left[ {\begin{array}{*{20}c} 1 & {h_{i} } & {\cos \left( {a_{i} h_{i} } \right)} & {\sin \left( {a_{i} h_{i} } \right)} \\ 0 & 1 & {a_{i} \left( {1 + \frac{{N_{i} }}{{K_{si} }}} \right)\sin \left( {a_{i} h_{i} } \right)} & {a_{i} \left( {1 - \frac{{N_{i} }}{{K_{si} }}} \right)\cos \left( {a_{i} h_{i} } \right)} \\ 0 & 0 & { - N_{i} \cos \left( {a_{i} h_{i} } \right)} & { - N_{i} \sin \left( {a_{i} h_{i} } \right)} \\ 0 & {N_{i} } & 0 & 0 \\ \end{array} } \right]$$
(36)

At the base of the i-th floor, Eq. (33) is written as follows.

$$\left\{ {\begin{array}{*{20}c} {u_{i} \left( 0 \right)} \\ {\theta_{i} \left( 0 \right)} \\ {M_{i} \left( 0 \right)} \\ {V_{i} \left( 0 \right)} \\ \end{array} } \right\} = {\mathbf{B}}_{{\mathbf{i}}} \left( 0 \right)\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\}$$
(37)

where

$${\mathbf{B}}_{{\mathbf{i}}} \left( 0 \right) = \left[ {\begin{array}{*{20}c} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & {a_{i} \left( {1 - \frac{{N_{i} }}{{K_{si} }}} \right)} \\ 0 & 0 & { - N_{i} } & 0 \\ 0 & {N_{i} } & 0 & 0 \\ \end{array} } \right]_{i}$$
(38)

From matrix Eqs. (35) and (37), matrix Eq. (39) is obtained.

$$\left\{ {\begin{array}{*{20}c} {u_{i} \left( {h_{i} } \right)} \\ {\theta_{i} \left( {h_{i} } \right)} \\ {M_{i} \left( {h_{i} } \right)} \\ {V_{i} \left( {h_{i} } \right)} \\ \end{array} } \right\} = {\mathbf{B}}_{{\mathbf{i}}} \left( {h_{i} } \right){\mathbf{B}}_{{\mathbf{i}}} \left( 0 \right)^{ - 1} \left\{ {\begin{array}{*{20}c} {u_{i} \left( 0 \right)} \\ {\theta_{i} \left( 0 \right)} \\ {M_{i} \left( 0 \right)} \\ {V_{i} \left( 0 \right)} \\ \end{array} } \right\} = {\mathbf{S}}_{{\mathbf{i}}} \left\{ {\begin{array}{*{20}c} {u_{i} \left( 0 \right)} \\ {\theta_{i} \left( 0 \right)} \\ {M_{i} \left( 0 \right)} \\ {V_{i} \left( 0 \right)} \\ \end{array} } \right\}$$
(39)

It is seen that the Transfer matrix obtained is compatible with the literature (Li 2001).

If relation (39) is applied successively from the base to the top of the building, Eq. (40) is obtained:

$$\left\{ {\begin{array}{*{20}c} {u_{{{\text{top}}}} } \\ {\theta_{{{\text{top}}}} } \\ {M_{{{\text{top}}}} } \\ {V_{{{\text{top}}}} } \\ \end{array} } \right\} = \left[ {\prod\limits_{k = 1}^{n} {{\mathbf{S}}_{{\mathbf{k}}} } } \right]\left\{ {\begin{array}{*{20}c} {u_{{{\text{base}}}} } \\ {\theta_{{{\text{base}}}} } \\ {M_{{{\text{base}}}} } \\ {V_{{{\text{base}}}} } \\ \end{array} } \right\} = {\mathbf{s}}\left\{ {\begin{array}{*{20}c} {u_{{{\text{base}}}} } \\ {\theta_{{{\text{base}}}} } \\ {M_{{{\text{base}}}} } \\ {V_{{{\text{base}}}} } \\ \end{array} } \right\}$$
(40)

where

$${\mathbf{s}} = \prod\limits_{k = 1}^{n} {{\mathbf{S}}_{{\mathbf{k}}} }$$
(41)

If the boundary conditions defined in Eqs. (12), (13), (14) and (15) are applied to matrix Eq. (40), matrix Eq. (42) is obtained.

$$\left\{ {\begin{array}{*{20}c} {u_{{{\text{top}}}} } \\ {\theta_{{{\text{top}}}} } \\ 0 \\ 0 \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {s_{1,1} } & {s_{1,2} } & {s_{1,3} } & {s_{1,4} } \\ {s_{2,1} } & {s_{2,2} } & {s_{2,3} } & {s_{2,4} } \\ {s_{3,1} } & {s_{3,2} } & {s_{3,3} } & {s_{3,4} } \\ {s_{4,1} } & {s_{4,2} } & {s_{4,3} } & {s_{4,4} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {M_{{{\text{base}}}} } \\ {V_{{{\text{base}}}} } \\ \end{array} } \right\}$$
(42)

From Eq. (42), matrix Eq. (43) is obtained.

$$\left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {s_{3,3} } & {s_{3,4} } \\ {s_{4,3} } & {s_{4,4} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {M_{{{\text{base}}}} } \\ {V_{{{\text{base}}}} } \\ \end{array} } \right\}$$
(43)

For Eq. (43) to have a non-zero solution, the determinant of the coefficient’s matrix must be zero. Hence, relation Eq. (44) is obtained.

$${\mathbf{s}}_{{{\mathbf{3,3}}}} {\mathbf{s}}_{{{\mathbf{4,4}}}} - {\mathbf{s}}_{{{\mathbf{3,4}}}} {\mathbf{s}}_{{{\mathbf{4,3}}}} = 0$$
(44)

Axial load N, which makes the given equation zero, gives the critical load factor.

6 Application

In this section, we present the results of typical tall buildings in the practice of structural engineering. In this section, three different examples are solved, and the results are compared to demonstrate the suitability of the Transfer matrix method presented in this paper to the finite element method. SAP2000 is used for the finite element method. The software required for the implementation of the Transfer matrix method presented in this study was created in MATLAB.

6.1 Building of Shear Walls and a Central Core with Uniform Properties Throughout Height

In the first application, a building with shear walls and a central core is considered (Fig. 3).

The geometric and material characteristics are detailed below. The modulus of elasticity is \(E=25000\) MN/m2, the shear modulus is \(G=10416.67\) MN/m2, the height of the story is \(3\) m, the width of the shear walls and cores is \(0.4\) m, the uniform lateral load in height is \(1.00\) kN/m2 and the uniform vertical load is \(12.00\) kN/m2.

The building will be analyzed in its main directions X and Y. The building has a flexural stiffness \({K}_{b{\text{x}}}=975792500\) kN m2 and \({K}_{by}=692717500\) kNm2 and a shear stiffness \({K}_{s{\text{x}}}=179585416.7\) kN and \({K}_{s{\text{y}}}=171252083.3\) kN.

Tables 1, 2, 3, 4, 5 and 6 show the results of static, dynamic (free vibration) and stability analysis of the building. From the tables, it can be seen that the results obtained with the proposed method are consistent with the results obtained with finite elements.

Table 1 Maximum lateral displacement (mm)—X direction
Full size table
Table 2 Maximum lateral displacement (mm)—Y direction
Full size table
Table 3 First period of vibration (s)—X direction
Full size table
Table 4 First period of vibration (s)—Y direction
Full size table
Table 5 Ratio of global buckling critical load—X direction
Full size table
Table 6 Ratio of global buckling critical load—Y direction
Full size table

6.2 Building of Shear Walls and a Central Core With Non-Uniform Properties Throughout Height

To verify the results of the proposed method (Transfer matrix method) with the finite element analysis, 15- and 30-story buildings with shear walls and central core presented in Fig. 3, whose geometry characteristics vary along the building height, are analyzed.

Table 7 shows the equivalent stiffnesses of the 15-story building, and Table 8 shows the equivalent stiffnesses of the 30-story building.

Table 7 Equivalent stiffness of the 15-story building
Full size table
Table 8 Equivalent stiffness of the 30-story building
Full size table

Tables 9, 10, 11, 12, 13 and 14 show the results of static, dynamic and stability analysis of the building. It shows that the proposed method (Transfer Matrix Method) gives results that are compatible with the finite element method when the building geometry characteristics are variable along the height of the building.

Table 9 Maximum Lateral displacement (mm)—X direction
Full size table
Table 10 Maximum Lateral displacement (mm)—Y direction
Full size table
Table 11 First period of vibration (s)—X direction
Full size table
Table 12 First period of vibration (s)—Y direction
Full size table
Table 13 Ratio of global buckling critical load—X direction
Full size table
Table 14 Ratio of global buckling critical load—Y direction
Full size table

6.3 Frame Building with Uniform and Variable Properties

In order to demonstrate the suitability of the proposed method, a 10-story building consisting of frames (Fig. 4) is considered as the third application. The modulus of elasticity is 25,000 MN/m2, the shear modulus is 10,416.67 MN/m2 and the story height is 3 m. The vertical distributed load is 12.00 kN/m2.

Fig. 4
figure 4

Structural plan of the building of frames

Full size image

In case of uniform and variable cross-section, static loads were calculated according to the equivalent static load method. According to the equivalent static load method, the Peruvian seismic code was taken into account for the calculation of the base shear force and the loads acting on the floors. Assuming that the given building was built for office purposes in Lima, Peru, on a type of soil considered intermediate, the base shear force was calculated as 1540 kN, and the floor forces acting on the floors were calculated and shown in Fig. 5.

Fig. 5
figure 5

Variation of loads acting on floors along building heights

Full size image

In this example discussed in the study, two situations were taken into account. In the first case, it is assumed that the columns are 0.5 m/0.5 m and are uniform throughout the building height. In the second case, it is assumed that the column cross-sections vary from 0.5 m/0.5 m to 0.3 m/0.3 m along the building height. Both In this case, beam dimensions are accepted as 0.3 m/0.5 m. In Tables 15 and 16, equivalent bending stiffnesses and equivalent shear stiffnesses with the changes in column sections are given for both cases.

Table 15 Equivalent stiffness of 10-story building with uniform properties
Full size table
Table 16 Equivalent stiffness of the 10-story building with variable properties
Full size table

Figure 6a and b shows the lateral displacement profile of the uniform and variable building, respectively. A good estimate is observed using the proposed model and method. Tables 17, 18 and 19 show the results obtained for the static, dynamic (Free vibration) and stability analyses. In both cases excellent results were obtained with good convergence.

Fig. 6
figure 6

Lateral displacement profile. a Building with uniform properties and b Building with variable properties

Full size image
Table 17 Maximum lateral displacement (mm)
Full size table
Table 18 First period of vibration(s)
Full size table
Table 19 Ratio of global buckling critical load
Full size table

7 Conclusion

In this study, the Transfer matrices previously developed in the literature for the static, dynamic and stability analysis of shear-frame systems for sandwich beams are developed for the Timoshenko beam model, which is a special case of the sandwich beam model. The presented approach is suitable for the behavior of buildings consisting of pure shear walls and pure frames.

The presented approach has the advantages of the Transfer matrix method. As is known, the most important advantage of the Transfer matrix method is that the size of the system Transfer matrix is independent of the number of elements. In the proposed approach, the size of the element Transfer matrix and the size of the system Transfer matrix are fixed and are 4*4. Thus, both size and time savings can be achieved compared to the classical finite element method.

From the two examples presented at the end of the study, it is observed that the proposed approach gives results compatible with the classical finite element method. As a result, it can be said that the presented method can be used safely especially in the pre-dimensioning stage. The main advantage of the presented method is that it saves time due to the small matrix size.