System Reliability Analysis of Site Slope Using the Conditional Spatial Variability of Soil Properties

Abstract

In slope stability projects, in order to better investigate the site, the boreholes are distributed between different parts of the site. In this paper, the location of their known data is considered by conditional spatial variability of soil properties by coupling the geostatistical and finite element methods. For this purpose, a real site with fifteen boreholes is considered. The reliability index of the global safety factor and maximum horizontal displacement safety factor of the slope was determined. In addition, the system reliability index of these components was calculated. This study shows that considering the conditional spatial variability of soil properties, the reliability indices are different for the global safety factor and the maximum horizontal displacement safety factor. Also, the system reliability index was smaller than all other indices, which indicates that the analyses without considering the location of the known data give a higher-confidence reliability index than real values.

1 Introduction

It is well known that the inherent spatial variability of properties of soil layers can significantly influence the reliability analysis of slope stability (Cho 2007; Jiang et al. 2014; Xiao et al. 2016; Li et al. 2017a, b). Thus, researchers have exerted increasing effort to investigate the reliability of slopes in the spatial variable of soil layers in recent years (Griffiths et al. 2009; Cho 2010; Javankhoshdel et al. 2017; Qi and Li 2018; Nguyen et al. 2019; Jiang et al. 2020a, b; Jiang et al. 2022).

In the stochastic analysis, the conditional and unconditional simulation methods are employed in the slope stability (Griffiths and Fenton 2004; Li et al. 2016a, b, c, d; Li et al. 2016a, b, c, d; Li et al. 2017a, b; Cheng et al. 2018; Jiang et al. 2020a, 2020b; Shadabfar et al. 2020; Ou-Yang et al. 2021).

In a stochastic analysis by the RFEM, the effects of the known data locations are not implemented. In other words, the extracted data from the boreholes are used in stochastic slope stability analysis without considering their known data location. This is while in the application of the conditional simulation method (CSM), three steps should be taken by geostatistical methods (Webster and Oliver 2007). First, the soil parameters at each specified depth are interpolated based on known other boreholes at the same level. In the second step, the soil properties at each depth are predicted in the section of analysis based on the known data location of the boreholes. In the third step, the soil properties are predicted from the data obtained in the previous step for all elements in the specified section of analysis.

There are limited studies that have been made to apply CSM for stochastic analysis of slope. Liu et al. (2017) evaluated the reliability analysis of a cohesive-frictional slope using a conditional random field (based on the Cholesky decomposition technique and kriging method) and considered the spatial variability of soil properties in the analysis. The numerical simulation showed that the autocorrelation and sample distances are effective in the conditional random fields. Yang et al. (2017) investigated conditional random fields of modeling the spatial variability of soils taking into account the actual site-specific data obtained. The results showed that the inclusion of this data could be an essential factor in determining slope reliability. Huang et al. (2019) considered the influence of rotated anisotropy in the reliability analysis of slope stability by conditional random field. They represented that when the sampling points are distributed along with the base orientation, the probability of failure (Pf) is high. Li et al. (2016a, b, c, d) obtained the uncertainty in the Factor of Safety (FS) and Pf of a slope considering the geological uncertainty via borehole data. The results showed that the borehole within the zone of influence of slope has the most effect on the stochastic analysis of slope. Deng et al. (2017) assessed the reliability analysis of slope considering soil parameters variability and geological uncertainty by coupling the Markov chain.

On the other hand, in the system reliability analysis, considerable research has been done (Zai et al. 2021). Johari and Kalantari (2020) investigated the system reliability analysis of a soldier-piled excavation in unsaturated soil using random finite element and sequential compounding methods. The result showed that the unsaturated state's reliability analysis increases the mean value and decreases the standard deviation (std.) value of the Peng et al. (2020) investigated the reinforced slope failure probability using system reliability analysis. The global probability of the reinforced slope was determined by system analysis between local reinforcement and conditional failures of a slope. Liu et al. (2020) applied the system reliability analysis of slope stability by limit equilibrium and adaptive Monte Carlo Simulation (MCS) methods and considered a large number of circular and non-circular slip surfaces. Liu et al. (2018) assessed the system reliability analysis of the c–ϕ slope using the Multiple Response Surface Method (MRSM) and MCS. The results indicate that the spatial variability of soil properties has a variation in the results of the system reliability analysis of slope.

The soil structure is such that the spatial variation and shear resistance parameters of the soil properties should be considered. If these soil characteristics are considered correctly, the output of the model and the answers are more accurate. Generally, considering a section in a site (two-dimensional) cannot consider the spatial diversity of all directions. In fact, in a two-dimensional slope stability analysis because of borehole scattering, certain cross-sectional areas cannot lead to a reliable answer. The various sections of analysis can be considered as system components to achieve more realistic solutions. The main objective of this study is to assess the effectiveness of the conditional spatial variability of soil properties in stochastic slope stability analysis. For this purpose, the real slope has been divided into 14 sections with equal distances. In each section, according to the location of known data, the soil parameters are predicted by geostatistical methods from the real boreholes into the mapped ones and at every mesh element. Then, the stochastic analysis of the sections are carried out using the finite element method (FEM). Finally, to obtain the global reliability index of the slope, the reliability indices of the sections will be combined as a series of system components.

2 Geostatistical Analysis

Geostatistics developed originally in the mining industry (Lee 1978), is now being applied widely in geotechnical projects (Kring and Chatterjee 2020). It is based on a model of spatially correlated random variation, and estimating the spatial autocorrelation is the first step in the geostatistical analysis.

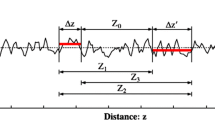
Estimation of the semivariogram is the first step in the geostatistical analysis, and the sample semivariogram can be represented by several curves corresponding to several directions. The semivariogram shows how the dissimilarity between Z(x) and Z(x + h) evolves with the separation h.

As mentioned earlier, the first step in the geostatistical approach is the variogram analysis. To draw a variogram, an experimental semivariogram must be drawn relative to their distance. The choice of the distance between two pairs of points is expressed based on the direction between them. These directions are 0°, 45°, 90°, and 135° with a tolerance of 22.5°. In fact, Z(x) is the first data value of the first point pair in the desired direction and Z(x + h) is the second data in the second point pair. For this purpose, the experimental semivariogram for a set of data Z(xi), i = 1,2,… in the kriging method is calculated as follows (Journel and Huijbregts 1978; Wackernagel 2003; Davison 2013):

$$\gamma (h) = \frac{1}{2N(h)}\sum\limits_{i = 1}^{N} {\left\{ {\left[ {Z(X_{i} ) - Z(X_{i} + h)} \right]^{{^{2} }} } \right\}}$$

(1)

where N(h) is the number of pairs of data points separated by the particular lag vector h, which is the backbone of any geostatistical estimation, which shows how the dissimilarity between Z(x) and Z(x + h) evolves with the separation h.

In the multivariate geostatistical analysis, the spatial structure of a pair of cross-correlated variables can be described by the cross-semivariogram. The experimental cross-semivariogram for random functions Z_j(x) and Z_k(x) is computed using the following equation (Journel and Huijbregts 1978; Wackernagel 2003; Davison et al. 2013):

$$\gamma_{ } (x) = \frac{1}{2N(h)}\sum\limits_{i = 1}^{N} {\left[ {\left\{ {Z_{u} (x) - Z_{u} (x + h)} \right\}\left\{ {Z_{v} (x) - Z_{v} (x + h)} \right\}} \right]}$$

(2)

where γ_jk(h) is the experimental cross-semivariogram, and N(h) is the number of pairs of data points, separated by h, which have measured values of both random functions Z_j(x) and Z_k(x).

The experimental semivariograms are replaced by a fitted mathematical function as a model or approximation to the theoretical model to have a physical meaning. Generally, the choice of the type of semivariogram functions (linear, Gaussian, exponential, and spherical) depends on the Residual Sums of Squares (RSS) and the coefficient of determination (R²) values; So, a function is selected based on the maximum value of the RSS and the minimum value of the R². With more meaning, the lag distances indicate the distance between pairs of points. These pairs of points are selected based on the direction between them (0 °, 45°, 90°, and 135°). On the other hand, The lag distance at which the semivariogram reaches the sill value. Presumably, autocorrelation is essentially zero beyond the range. Generally, to estimate the data of a point, the characteristics of all points around it should be used. In general, to be able to use the features of the entire environment, semivariograms must be used in all directions. In fact, an omnidirectional semivariogram is more effective in estimating unknown data than reality.

2.1 Kriging Analysis

The kriging method was developed during the 1960s and 1970s and has been acknowledged as a good univariate geostatistical interpolator tool for interpolation between known borehole data (Matheron 1963; Isaaks and Srivastava 1989; Der Kiureghian 2005; Ang and Tang 2007). In this paper, it was assumed that the global means of variables are unknown. Generally, the mean value (Z^*(x₀)) as the linear unbiased estimator and the standard deviation value (σ_ok) of the ordinary kriging estimator are defined as follows (Matheron 1963; Isaaks and Srivastava 1989; Der Kiureghian 2005; Ang and Tang 2007; Webster and Oliver 2007):

$$Z^{*} (x_{0} ) = \sum\limits_{i = 1}^{N} {\lambda_{i} Z(x_{i} )}$$

(3)

$$\sigma_{OK}^{2} = \beta_{OK} - \gamma (x_{i} ,x_{j} ) + \sum\limits_{i = 1}^{N} {\lambda_{i} \gamma (x_{i} ,\,x_{0} )}$$

(4)

where Z (x_i), i = 1,2,…, N, is the known data, x₀ is the unknown field point and λ is the ordinary Kriging coefficient, respectively. γ(x_i, x_j) and γ(x₀, x_i), i = 1,2,…, N are the semivariogram between known points and the semivariogram between known points and unknown points, respectively (Matheron 1963; Isaaks and Srivastava 1989; Der Kiureghian 2005; Ang and Tang 2007; Webster and Oliver 2007). Overall, continue the parameters of the equations in the kriging method which are defined in Appendix 2.

2.2 Cokriging Analysis

Cokriging is the multivariate extension of kriging to several correlated variables whereby several variables are estimated jointly utilizing a best linear unbiased estimator. Between V correlated variables, the linear ordinary cokriging estimator for variable u at an unknown field point x₀ is (Matheron 1963; Isaaks and Srivastava 1989; Der Kiureghian 2005; Ang and Tang 2007; Webster and Oliver 2007):

$$Z_{u}^{*} (x_{0} ) = \sum\limits_{l = 1}^{V} {\sum\limits_{i = 1}^{{n_{l} }} {\lambda_{il} Z_{i} (x_{i} )} }$$

(5)

where Z* and Z are, respectively, denoted the estimated and measured values of the considered variable. The subscript i refers to the n_l locations, of which the variable l is measured. The λ_il are cokriging weights. The minimized cokriging estimation variance is (Matheron 1963; Isaaks and Srivastava 1989; Der Kiureghian 2005; Ang and Tang 2007; Webster and Oliver 2007):

$$\sigma_{CK}^{2} = \sum\limits_{l = 1}^{V} {} \sum\limits_{j = 1}^{nl} {\lambda_{jl} \gamma (x_{j} ,x_{0} ) + \beta_{u} - \gamma_{uu} (x_{0} ,x_{0} )}$$

(6)

where β_u is Lagrange multipliers, and γ_uu is the direct semivariogram. Generally, continue the parameters of the equations in cokriging method which are defined in Appendix 2.

3 Strength Reduction Technique in Slope Stability Analysis

The FEM with the Mohr–Coulomb failure criterion is a model for the simulations and solves many problems. In the present study, according to the Mohr–Coulomb criterion, the soil behavior is modeled as elastic perfectly plastic and used as the strength reduction method to solve the problem (Matsui and San 1992; Nian et al. 2012; Tschuchnigg et al. 2015; Arvin et al. 2019). In this method, the soil shear strength parameters (effective cohesion and effective friction angle) decrease at each stage of analysis. The cohesion and friction angle of the strength reduction technique are defined as follows:

$$c_{r} = \frac{{c^{\prime}}}{\text{SRF}}$$

(7)

$$\phi_{r} = \arctan \left( {\frac{{\tan \phi^{\prime } }}{{{\text{SRF}}}}} \right)$$

(8)

where c′ and ϕ′ are effective cohesion and effective friction angle (shear strength parameters) of soil; the SRF is the strength reduction factor. In fact, the value of SRF is usually set to a reasonably low value and then increases in each step of analysis until slope failure occurs, and this failure value is assumed as the FS of the slope.

4 Development and Verification of a Coded Program

No software is a combination of FEM and geostatistics; therefore, in this research, a finite element-based program was coded in MATLAB for deterministic analysis of the slope and then extended for stochastic analysis by geostatistics. The program was provided for the two-dimensional, plane strain condition using eight-node quadrilateral elements of elastic viscoplastic soil with the Mohr–Coulomb failure criterion and a non-associated flow rule. The coded program was verified with the presented model by Smith et al. (2013). The model consisted of 355 elements, each having eight nodes and each of which with two degrees of freedom in the horizontal and vertical directions. The boundary conditions are defined by fully restraining the bottom side and horizontally restraining the left and right sides of the soil domain. The finite element discretization of the slope with boundary conditions is presented in Fig. 1. The soil parameters are selected by Smith et al. (2013) and were used for verification of the coded program. These parameters are summarized in Table 1. The maximum shear strain of the soil in the assessed slope by the proposed model and FLAC is shown in Figs. 2 and 3, respectively. In this study, an example from Smith et al. (2013) has been selected to verify the validity of the program. Once this example was done using the program coded by MATLAB and another time using FLAC software. In the end, the simulation results of Smith et al. (2013), the code, and the FLAC soft program were compared with each other.

Fig. 1

The finite element discretization and boundary conditions of the assessed slope

Table 1 The selected soil parameters for coded program verification (Smith et al. 2013)

Fig. 2

The maximum shear strain of the slope

Fig. 3

The maximum shear strain of the slope by FLAC

Also, the comparison of the safety factor of slope stability for the three models is presented in Table 2. It can be seen that the obtained results by the proposed model are close to the results of Smith et al. (2013).

Table 2 Comparison of the results

5 Procedure for Slope Stability Reliability Analysis of the Site

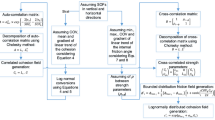
In the previous sections, the methodologies for implementing the geostatistical method to interpolate soil properties from sparse sampling points into continuous surfaces were described. The main target of this section is to present the procedure for the performance of the CSM in slope stability reliability analysis of a real site (Johari and Fooladi 2020, 2022). The methodology is shown in Fig. 4. The procedure includes two parts to soil parameter prediction (i.e., geostatistical estimations and stochastic analysis), which are repeated by the application of the MCS (Malkawi et al. 2001; Tang et al. 2020) and are analyzed by FEM. Finally, the safety factor reliability index of the global stability and maximum horizontal displacement is determined, and the system reliability index of these components is calculated. For this purpose, a computer program in MATLAB has been developed for combining the FEM with the geostatistical method.

Fig. 4

Flowchart of the system reliability analysis of slope by the CSM

6 Characteristic and Geotechnical Parameters of the Site

For evaluating the reliability index of the CSM in slope stability stochastic analysis, a site with real data, which is located in the Shiraz City of Iran, is considered (Johari and Fooladi 2020, 2022). The satellite overview of the site is shown in Fig. 5. To investigate the subsurface layer's properties, fifteen boreholes were drilled to a depth of approximately 25.0 m from the ground surface. In Fig. 5, the locations of boreholes and locations of the upper and lower lines of the slope are demonstrated. Also, the depth and characteristics of the boreholes are expressed in Table 6 (Appendix 1). On the other hand, for each borehole, several tests such as grain size, direct shear, and unit weight were performed. Based on Table 6, the soil types are mainly fine grain size, and a significant part of the soil's site is composed of lean clay and silty clay.

Fig. 5

The satellite overview of the site and boreholes arrangement

On the other hand, the boundary conditions are defined by fully restraining the bottom and horizontally restraining the left and the right sides of the soil domain. Figure 6 shows the finite element discretization of the real slope with boundary conditions.

Fig. 6

Finite element discretization and boundary conditions

7 Stochastic Analysis

To compare the slope stability reliability index by CSM, a stochastic analysis based on the same soil properties was performed (Li et al. 2016a, b, c, d; Xiao et al. 2017). The unit weight, cohesion, and friction angle were considered stochastic parameters, and the Poisson's ratio and modulus of elasticity were considered deterministic parameters. The model consisted of 1080 elements (Fig. 6), each having eight nodes and each of which with two degrees of freedom in the horizontal and vertical directions. The details of a stochastic analysis by the mentioned method are presented in the next subsections.

7.1 Stochastic analysis of the slope using the CSM

• In situ experiments can supply soil parameters at the location where the experiments are executed, but unavoidable uncertainty remains at locations that are not examined. As a solution, geostatistical approaches are employed for considering the effect of uncertainties in soil parameter estimation (Johari and Gholampour 2018a, b). The main purpose of using the geostatistical technique is to provide the best estimate of the soil properties between known data. For stochastic analysis by the CSM, the soil parameters are predicted by the geostatistical method in the following three steps.

• First, the soil parameters of each specified depth are interpolated based on known data from other boreholes at the same level. This procedure is shown in Fig. 7 for typical BH3. The results of this step are summarized in Table 6 of Appendix 1.

• In the second step, the soil properties at each depth are predicted in the selected section of analysis based on the known data locations of the boreholes. For example, based on Fig. 8 for the prediction of the friction angle of the soil in the depth of 2.0 m in BH9, all real and predicted friction angles in BH1 to BH15 at depth 2.0 m are utilized.

• In the third step, the soil properties are predicted from the data obtained in the second step for all elements in the section of analysis. Figure 9 shows a typical procedure for the prediction of the soil parameters based on the borehole’s data in Sections 5–5. For this purpose, only a certain number of near neighbors' known data are used for estimation. These neighbors need to be within a region (e.g., circular or elliptical) around the estimation location.

Fig. 7

Prediction of unknown soil parameters in each depth of an arbitrary borehole, BH3 (first step)

Fig. 8

Prediction of soil parameters in an arbitrary Section 5–5 for virtual boreholes, BH’9 (second step)

Fig. 9

Typical elliptical region for prediction of soil parameters in elements from predicted data of the second step parameters in an arbitrary Section 5–5 (third step)

For geostatistical analysis, four anisotropic models (i.e., linear, spherical, exponential, and Gaussian) were examined to obtain the best fitting of semivariograms. For this purpose, two statistical formulations, RSS and R² were determined to aid the interpolation of model output. Based on these statistics formulations, the exponential model was selected for cohesion and friction angle, and the linear model was selected for unit weight because of its accuracy. It should be noted that semivariogram analysis makes it possible to estimate the spatial dependence between samples in horizontal, vertical, and oblique directions. For instance, the semivariogram model parameters for cohesion, friction angle, and unit weight are given in Table 3.

Table 3 The semivariogram parameters of different models for c, ϕ, and γ

In the next step, the geostatistical methods were used for the prediction of the mean values of the uncertainties parameters (the cohesion, friction angle, and unit weight). The results of the three mentioned steps are illustrated in Figs. 10, 11, 12 for typical Sections 5–5. Figures 10 and 12 illustrate the variation of estimated cohesion and angle of friction. These figures indicate that the cohesion and friction angle values are the stand-in inverse relationship to each other.

Fig. 10

The predicted mean value of the cohesion in an arbitrary Section 5–5 by the CSM (kN/m²)

Fig. 11

The predicted mean value of the friction angle in an arbitrary Section 5–5 by the CSM ("°")

Fig. 12

The predicted mean value of the unit weight in an arbitrary Section 5–5 by the CSM (kN/m³)

8 Slope Stability Reliability Analysis

For reliability analysis of the slope stability, the Probability Density Function (PDF) of the global safety factor and maximum horizontal displacement must be determined. To obtain the PDFs, the developed coded program was extended for iterative calculations based on MCS. In this way, 2000 generations were used. In the MCS, the more the number of simulations, the more accurate the statistical output. In solving geotechnical problems based on the limit equilibrium method, due to the simplicity of the solution, the number of simulations can be increased up to 1,000,000. But in solutions based on finite element methods, due to the complexity of the solution and the length of the output determination process, the number of simulations cannot be large. For this reason, it is tried to cover a smaller number of simulations with proper fitting on the outputs. Of course, in this way, methods with fewer simulations such as subset simulation can be used.

On the other hand, since the position of the section analysis affects the results of stochastic analysis by the CSM, 14 sections (including Sections 1–1 to 14–14) for stochastic analysis and determination of PDF were considered. Figure 13 shows the locations of these sections.

Fig. 13

The locations of the different sections in the analysis by the CSM

Figure 14 shows the PDFs of the global safety factor (FS) for all sections. The PDFs were obtained by fitting a log–normal function based on the computed values of the mean and standard deviation. In this study, based on the obtained data from the boreholes, some values of cohesion are close to zero, and since these data have been used for geostatistical analysis, therefore, in some elements, the average value for cohesion is predicted to be close to zero. On the other hand, because in the normal distribution to cover the range of the data, the data should be considered up to four times the standard deviation on both sides of the mean, cohesion less than zero was included in the calculations, which is not geotechnically correct. Therefore, in this study, log-normal distribution is utilized for all random variables. Since the log-normal distributions were considered for stochastic soil parameters, it seems sensible to suppose that the PDFs of the global safety factor also have a log-normal distribution.

Fig. 14

The PDFs of the global safety factor

8.1 Maximum Horizontal Displacement Safety Factor

To determine the system reliability index of the slope, the FS of maximum horizontal displacements must be obtained. For this purpose, for the different methods, using the critical (allowable) maximum horizontal displacements (0.002H = 2.40 cm (Schlosser et al. 1991)), the values of maximum horizontal displacements were changed to maximum horizontal displacements safety factor based on Eq. (9). Also,

$${\text{FS}}_{{\max .{\kern 1pt} {\kern 1pt} {\text{hor}}.{\kern 1pt} {\kern 1pt} {\text{disp}}}} = \frac{{{\text{Allowable}}{\mkern 1mu} {\mkern 1mu} {\text{horizontal}}{\mkern 1mu} {\mkern 1mu} {\text{displacement}}}}{{{\text{Maximum}}{\mkern 1mu} {\mkern 1mu} {\text{horizontal}}{\mkern 1mu} {\mkern 1mu} {\text{displacement}}}}$$

(9)

Figure 15 shows the PDFs of the maximum horizontal displacement safety factor for all sections. The PDFs were obtained by fitting a log–normal function based on the computed values of the mean and standard deviation. Since the log-normal distributions were considered for stochastic soil parameters, it seems sensible to suppose that the PDFs of the maximum horizontal displacement safety factor also have a log-normal distribution.

Fig. 15

The PDFs of the maximum horizontal displacement safety factor

Based on the importance of the project, the value of the critical safety factor is 1.25 (FS_critical = 1.25). In fact, the critical safety factor indicates that a slope is on the boundary between stability and instability in this project. The reliability index (β) is an alternative measure of safety, or reliability, which is uniquely related to the Pf. This parameter can be determined from the log-normal distribution of the safety factor’s PDF as follows:

$$\beta = \frac{{\ln \left[ {1.25 - \frac{{\mu_{FS} }}{{\sqrt {1 + {\text{COV}}_{FS}^{2} } }}} \right]}}{{\sqrt {\ln \left( {1 + {\text{COV}}_{FS}^{2} } \right)} }}$$

(10)

Generally, the statistical results of the global and maximum horizontal displacement safety factors are determined and summarized in Table 4.

Table 4 The statistical parameters of global safety factor and a maximum horizontal displacement safety factor by the CSM

Figure 16 shows the reliability index by the CSM for different sections, respectively. The figure indicates that, due to the heterogeneity of the site soil, the reliability index sections of the analysis do not obey any harmonic trend.

Fig. 16

The comparison of the reliability index for the global and maximum horizontal displacement safety factors of the analysis sections

8.2 System Reliability Analysis of Slope Stability Using the SCM

The SCM combines system components two by two, and in this way, the complexity of the combination is reduced and it will be able to solve big problems in a shorter time. In order to determine the overall stability of the site, the system reliability index must be determined. For this purpose, the reliability index (β) of the global and maximum horizontal displacement safety factors, which are summarized in Table 4, must be compounded with each other. In this research, the sequential compounding method (SCM) (Kang and Song (2010); Zhang et al. 2017; Peng et al. 2020; Johari and Lari 2020) was utilized for jointing the components and determining the system reliability index. In this way, the system was taken as a series system, and correlation coefficients between the section (components) were determined using their PDF data.

For compounding a series system consisting of several components (E₁, E₂, E₃…) with reliability indices (β₁, β₂, β₃…), the reliability index (β_1or2) of the compound event E_1or2 = E₁ ∪ E₂ must be determined firstly by univariate normal integration of P(E₁ ∪ E₂) as follows (Kang and Song (2010); Thoft-Christensen and Murotsu 2012; Johari and Lari 2020):

$$\begin{aligned} \beta_{1 {\text{or}}2} = & - \Phi^{ - 1} \left[ {P(E_{1} UE_{2} )} \right] = - \Phi^{ - 1} \left[ {1 - \Phi_{2} (\beta_{1} ,\beta_{2} ;\rho_{1,2} )} \right] \\ = & - \Phi^{ - 1} \left[ {\Phi (\beta_{1} ) + \Phi (\beta_{2} ) + \int\limits_{0}^{{\rho_{1,2} }} {\varphi_{2} (\beta_{1} ,\beta_{2} ;\rho )d\rho } } \right] \\ \end{aligned}$$

(11)

$$\Phi \left( \beta \right) = \int\limits_{ - \infty }^{\beta } {\frac{1}{{\sqrt {2\pi } }}} e^{{ - \frac{1}{2}x^{2} }} {\text{d}}x$$

(12)

It is noteworthy that, in a series system, the failure of any component causes the failure of the system, and in joining the components (random variables), correlation specifies the association between two random variables. In another case, the correlation coefficient between the new compound event E_1or2 and other components events (ρ_(1or2),k) in the system is obtained. The mentioned steps must be repeated for all components to determine the reliability index of the system. Figure 17 shows an arbitrary example for obtaining a correlation between the global safety factor for Sections 1–1 and 4–4. In the same way, Fig. 18 indicates the correlation between maximum horizontal displacement safety factors for Sections 1–1 and 3–3. In fact, these correlations are analyzed based on MCS and are used for the system reliability analysis.

Fig. 17

Typical of the correlation coefficient between Sections 1–1 and 5–5 of The global safety factor

Fig. 18

Typical of the correlation coefficient between Sections 1–1 and 4–4 of the maximum horizontal displacement safety factor

Generally, the correlation matrix of the global and maximum horizontal displacement safety factor between each section based on Table 4 is shown in Fig. 19.

Fig. 19

The correlation matrix (a) Global safety factor and (b) Maximum horizontal Displacement safety factor for the system reliability analysis

The stepwise procedure for combining the global safety factor of sections by SCM is shown in Fig. 20. It can be seen, after the combination, the system reliability index of the global safety factor is equal to β_sys = 1.551. The same as the global safety factor, the stepwise procedure for combining the maximum horizontal displacement safety factor of sections by SCM is shown in Fig. 21. This figure shows, after combining the components, the system reliability index of the maximum horizontal displacement safety factor is equal to β_sys = 2.238.

Fig. 20

Determination stages of the system reliability index for the global safety factor

Fig. 21

Determination stages of the system reliability index for the maximum horizontal displacement safety factor

Using the global and maximum horizontal displacement safety factor, the system reliability index of the CSM was calculated and is shown in Table 5. Furthermore, the exertion of borehole characteristics (location of the known data) gives near-realistic safety factors and reliability indices.

Table 5 System reliability indices of the site

9 Conclusions

Slope stability analysis is a branch of geotechnical engineering that is highly amenable to probabilistic treatments. The reliability analysis of slope stability has received considerable attention in the past few years. In this field, there have been limited studies carried out in the literature implementing the effects of the conditional spatial variability of soil properties. This paper proposed a practical approach for obtaining a reliability index of slope stability considering the location of the known data. For this purpose, computer programing was developed in MATLAB for combining the FEM with the geostatistical approach and random field theory. To account for the practical aspect of the research, a real site with fifteen boreholes was considered, and the slope was analyzed by the CSM.

To implement the effect of the conditional spatial variability of soil properties, the real slope was divided into 14 sections with equal distances. In each section, according to its location, soil parameters were predicted by geostatistical methods from the actual boreholes based on the hypotheses boreholes and, finally, in the cross-sectional mesh elements. In the next stage of the research, to obtain the global reliability index of the slope, the reliability indices of the sections were combined with each other as a serial component of the system.

Due to the importance of the maximum horizontal displacement control of slope, the global and maximum horizontal displacement safety factors were determined, and the system reliability index was calculated. Results show that considering the effect of the conditional spatial variability of soil properties causes the different reliability indices of the global safety factor and maximum horizontal displacement in selected sections. In other words, the analyses without considering the location of the known data give a higher-confidence reliability index than real values. Furthermore, the exertion of the location of the known boreholes data gives near-realistic safety factors and reliability indices.

Appendices

Appendix 1

The depth and coordinates of boreholes and the result of the first step estimation by the geostatistic method are shown in Table 6.

Table 6 The results of the first-step prediction by the geostatistical method for analysis by the CSM

Appendix 2

The general equation of the geostatistical estimation in the kriging and cokriging methods is defined as follows:

2.1 Kriging Method

$$\Lambda \Gamma \, = \gamma$$

(13)

$$\Gamma = \left[ {\begin{array}{*{20}c} {\lambda_{1} } \\ {\lambda_{1} } \\ \vdots \\ {\lambda_{N} } \\ {\beta_{OK} } \\ \end{array} } \right]$$

(14)

$$\upgamma = \left[ {\begin{array}{*{20}c} {\upgamma _{{{(x}_{{0}} {,x}_{{1}} {)}}} } \\ {\upgamma _{{{(x}_{{0}} {,x}_{{2}} {)}}} } \\ \vdots \\ {\upgamma _{{{(x}_{{0}} {,x}_{{N}} {)}}} } \\ {1} \\ \end{array} } \right]$$

(14)

$$\Lambda = \left[ {\begin{array}{*{20}c} {\gamma_{{(x_{1} ,x_{1} )}} } & {\gamma_{{(x_{1} ,x_{2} )}} } & \cdots & {\gamma_{{(x_{1} ,x_{N} )}} } & 1 \\ {\gamma_{{(x_{2} ,x_{1} )}} } & {\gamma_{{(x_{2} ,x_{2} )}} } & \cdots & {\gamma_{{(x_{2} ,x_{N} )}} } & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\gamma_{{(x_{N} ,x_{1} )}} } & {\gamma_{{(x_{N} ,x_{2} )}} } & \cdots & {\gamma_{{(x_{N} ,x_{N} )}} } & 1 \\ 1 & 1 & 1 & 1 & 0 \\ \end{array} } \right]$$

(15)

$$\gamma \left( {x_{0} ,x_{i} } \right) = C_{0} + C\left[ {\left( \frac{h}{a} \right)} \right]$$

(16)

$$a = \sqrt {A_{1}^{2} \left[ {\cos^{2} (\theta - \varphi )} \right] + A_{2}^{2} \left[ {\cos^{2} (\theta - \varphi )} \right]}$$

(17)

where Γ and γ are the vector of the ordinary kriging coefficient and the semivariogram between known points and unknown points, respectively. In fact, γ(x₀, x_i) is a linear function in the geostatistical estimation for unit weight in this study. Λ is the matrix of the semivariogram between known points. c₀ and c are nugget and structural variance, respectively. ‘h’ and ‘a’ are the distance between two points and ranges, respectively. A₁ and A₂ are the larger effective length and smaller effective length, respectively. θ and φ are the angles corresponding to the maximum parameter changes and the angles between pairs of points relative to the vertical direction, respectively.

2.2 Cokriging Method

$$\Gamma_{uv} = \left[ {\begin{array}{*{20}c} {\gamma_{uv} (x_{1} ,x_{1} )} & {\gamma_{uv} (x_{1} ,x_{2} )} & { \ldots \ldots } & {\gamma_{uv} (x_{1} ,x_{nv} )} \\ {\gamma_{uv} (x_{2} ,x_{1} )} & {\gamma_{uv} (x_{2} ,x_{2} )} & \ldots & {\gamma_{uv} (x_{2} ,x_{nv} )} \\ \vdots & \vdots & \ldots & \vdots \\ {\gamma_{uv} (x_{nu} ,x_{1} )} & {\gamma_{uv} (x_{nu} ,x_{2} )} & \ldots & {\gamma_{uv} (x_{nu} ,x_{nv} )} \\ \end{array} } \right]$$

(18)

$$b_{uu} = \left[ {\begin{array}{*{20}c} {\gamma_{uu} (x_{1} ,x_{0} )} \\ {\gamma_{uu} (x_{2} ,x_{0} )} \\ \vdots \\ {\gamma_{uu} (x_{nu} ,x_{0} )} \\ \end{array} } \right]$$

(19)

$$b_{uv} = \left[ {\begin{array}{*{20}c} {\gamma_{uv} (x_{1} ,x_{0} )} \\ {\gamma_{uv} (x_{2} ,x_{0} )} \\ \vdots \\ {\gamma_{uv} (x_{nv} ,x_{0} )} \\ \end{array} } \right]$$

(20)

$$\left[ {\begin{array}{*{20}c} {\Gamma_{uu} } & {\Gamma_{uv} } & \begin{gathered} 1 \hfill \\ 1 \hfill \\ : \hfill \\ 1 \hfill \\ \end{gathered} & \begin{gathered} 0 \hfill \\ 0 \hfill \\ : \hfill \\ 0 \hfill \\ \end{gathered} \\ {\Gamma_{vu} } & {\Gamma_{vv} } & \begin{gathered} 0 \hfill \\ 0 \hfill \\ : \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} 1 \hfill \\ 1 \hfill \\ : \hfill \\ 1 \hfill \\ \end{gathered} \\ {11....1} & {00....0} & 0 & 0 \\ {00....0} & {11....1} & 0 & 0 \\ \end{array} } \right]\left[ \begin{gathered} \lambda^{1}_{u} \hfill \\ \lambda^{2}_{u} \hfill \\ : \hfill \\ \lambda_{{n_{u} u}} \hfill \\ \lambda^{1}_{v} \hfill \\ \lambda^{2}_{v} \hfill \\ : \hfill \\ \lambda_{{n_{v} v}} \hfill \\ \Psi_{u} \hfill \\ \Psi_{v} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \hfill \\ \hfill \\ b_{uu} \hfill \\ \hfill \\ \hfill \\ \hfill \\ b_{uv} \hfill \\ \hfill \\ 1 \hfill \\ 0 \hfill \\ \end{gathered} \right]$$

(21)

$$\gamma \left( {x_{i} ,x_{n} } \right) = C_{0} + C\left[ {1 - \exp \left( {\frac{ - h}{a}} \right)^{{}} } \right]$$

(22)

where Γ_uv is the semivariogram matrix between two adjacent points. b_uu and b_uv the semivariogram vectors for variables u and cross-variograms, respectively. λ vector is the ordinary cokriging coefficient.