1 Introduction

Spillways are structures that transfer the excess water accumulated in the dam reservoir from upstream to downstream without damaging the dam. Stepped spillways, one type of spillway, have been used for more than 3500 years due to their ease of construction and design. According to the literature, it is estimated that the first example of a stepped spillway in the world is the Akarnanian stepped spillway in Greece, which was built around 1300 BC (Chanson 2000). In particular, from the beginning of the twentieth century, stepped spillways have begun to be designed more comprehensively to absorb the flow energy (Chanson 2004).

Stepped spillways can dissipate most of the flow energy in the discharge channel. The energy dissipated along the discharge channel is approximately 70–80% higher than in other spillways (Boes et al. 2000). For this reason, stepped spillways are more economical than conventional spillways since the size of the energy-dissipating structures at the downstream decreases by 30–40% with the shortening of the hydraulic jump formed at the end of the discharge channel in stepped spillways (Berkün 2007; Boes and Hager 2003a).

Experimental studies (Sorensen 1985; Peyras et al. 1992) have shown that the flow in stepped spillways is divided into two regimes: the nappe flow regime and the skimming flow regime. The nappe flow regime is defined as successively falling free nappes and occurs at low flow rates. The skimming flow regime occurs due to a stable flow of water at high flow rates (Chanson 1996). For the first time, Ohtsu and Yasuda (1991) mentioned a transition regime between these two regimes. Temporary hydrodynamic fluctuations in the transition regime can cause unstable flow behavior and expose the structure to unnecessary vibrations. Therefore, for safety reasons, designers do not recommend the transition regime (Chanson 1996).

Chanson (2001) defined the boundary between the nappe flow regime and the transition flow regime with Eq. (1) and defined the lower limit of the skimming flow regime with Eq. (2). On the other hand, Boes and Hager (2003b) defined the boundary between the transition flow regime and the skimming flow regime with Eq. (3).

$$\frac{{y_{{\text{c}}} }}{{h_{{\text{s}}} }} = 0.89 - 0.4\left( {\frac{{h_{{\text{s}}} }}{{l_{{\text{s}}} }}} \right)$$
(1)
$$\frac{{y_{{\text{c}}} }}{{h_{{\text{s}}} }} = 1.2 - 0.325\left( {\frac{{h_{{\text{s}}} }}{{l_{{\text{s}}} }}} \right)$$
(2)
$$\frac{{y_{{\text{c}}} }}{{h_{{\text{s}}} }} = 0.91 - 0.14\tan \left( \alpha \right)$$
(3)

where hs = step height (m), ls = step length (m), yc = critical flow depth, and α = chute angle.

Stepped spillways have attracted the attention of many researchers due to their practical and economical nature. In the first studies on stepped spillways, guidelines were formed for design criteria, development of fundamental equations, and their use in application areas (Sorensen 1985; Chanson 2001, 1993; Boes and Hager 2003b; Essery and Horner 1971). Some researchers studied the flow characteristics of stepped spillways using gabions (Peyras et al. 1992; Wuthrich and Chanson 2015; Zuhaira et al. 2020). Other researchers have also examined the scour downstream of stepped spillways (Aminpour and Farhoudi 2017; Eghlidi et al. 2020; Tuna and Emiroglu 2013). With the development of computer technology, the computational fluid dynamics (CFD) method has attracted the attention of researchers, and the number of numerical studies on stepped spillways has increased daily. In these studies, energy dissipation rates were investigated by using different step geometries, thresholds with different geometry, or different chute angles (Arjenaki et al. 2020; Ashoor and Riazi 2019; Stojnic et al. 2021; Tabbara et al. 2005; Thappeta et al. 2020; Zabaleta et al. 2020; Ikinciogullari 2023; Azman et al. 2020; Ghaderi et al. 2020, 2021; Hekmatzadeh et al. 2018; Li et al. 2020, 2018; Reeve et al. 2019; Shahheydari et al. 2015).

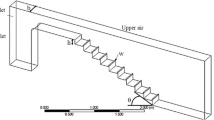
Based on a review of the literature, to the best of our knowledge, the effect of different turbulence methods on the results of a real dam has not been studied. The aim of this study is to use experimental data from a real dam prototype, and the most suitable turbulence model for the stepped spillway is determined using CFD for the discharge-water level relationship, pressure, energy dissipation rate, and velocity profile. In this context, the details of the turbulence equations used are given in the second section, and the details of the physical and numerical models are given in the third section. Then, the velocity, pressure, energy dissipation, and water surface profiles are compared with the experimental results (DSİ 2009) of Gökçeler Dam in the fourth section (Fig. 1).

Fig. 1
figure 1

Schematic representation of the FAVOR method (Oh et al. 2011)

Full size image

2 Governing Equations

Flow3D software, which uses Reynolds-averaged Navier–Stokes (RANS) and finite volume methods to solve continuity equations, was used for numerical simulations. TruVOF, an improved version of the finite volume method that provides extremely precise modeling of free surface flows, is used in Flow-3D software (Flow Science Incorporated 2022). In this software, calculations are carried out in mesh consisting of uniform cells with rectangular geometry. Although a network of this structure may seem like a problem or limitation initially, using this mesh type is an advantage because it is easy to manufacture, requires less memory, and uses two useful methods, VOF (volume of fluid) and FAVOR (fraction area-volume obstacle representation) (Harlow and Nakayama 2004).

In Flow-3D software, the problem geometry is obtained by closing some cells with obstacles. In this method, called FAVOR, two values obtained by calculating how much of an obstacle in the control volume covers the control volume and how much space this obstacle covers on each surface of the control volume are proportioned. This method is a gap technique used to identify the obstacles in the problem. If the solution cell is completely empty, this value is 1. If it is completely filled with an obstacle, this value is 0. If a cell is partially filled with an obstacle, this value takes a value between 0 and 1, depending on the volume occupied by the obstacle in the cell. Thanks to this method, even if models with complex geometry are modeled with coarse mesh, solution precision is provided (Flow Science Incorporated 2022).

The continuity equation used for three-dimensional, incompressible fluids can be expressed by Eq. (4).

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} + \frac{\partial w}{{\partial z}} = 0$$
(4)

where u = velocity in the x direction, v = velocity in the y direction, and w = velocity in the z direction. The Navier–Stokes equations for a three-dimensional flow is expressed in vectoral form as shown in Eq. (5).

$$\frac{{\partial \vec{V}}}{\partial t} + \vec{V} \cdot {\text{grad}}\vec{V} = - \frac{1}{\rho } {\text{grad}} P + \vec{F} + \nu \nabla^{2} \vec{V}$$
(5)

2.1 Turbulence Models

When there are inadequate stabilizing viscous forces, fluids move chaotically and unstably, which is known as turbulence. However, turbulence cannot be ignored in numerical modeling. The full spectrum of turbulent fluctuations can be simulated with mass and momentum conservation equations. This is conceivable only if the mesh resolution is high enough to capture such details. However, this is typically not feasible due to memory and processing time constraints. Therefore, to describe how turbulence affects the mean flow features, researchers must use simplified modeling. Six turbulence models are offered in FLOW-3D: the Prandtl mixing length model, the one-equation, the two-equation k–ε, RNG (renormalization group), k–ω, and LES (large eddy simulation) models (Flow Science Incorporated 2022). The Prandtl mixing length model is one of the earliest and simplest attempts to characterize three-dimensional turbulence effects, but it is no longer in widespread use (Turbulence Model 2022).

2.1.1 One-Equation (k) Model

The one-equation model is likewise a pioneering representation of turbulence. It requires a known turbulent mixing length (TLEN) at every site to compute the time-averaged turbulent kinetic energy k. The one-equation approach is inappropriate for simulating complicated flows since the TLEN is typically unknown beforehand (Turbulence Model 2022). The one-equation turbulence transport model consists of a transport equation for the kinetic energy linked to flow variations caused by turbulence, as shown in Eq. 6 (Flow Science Incorporated 2022).

$$k = \frac{1}{2}\left( {\overline{{u^{{\imath^{2} }} }} + \overline{{v^{{\imath^{2} }} }} + \overline{{w^{{\imath^{2} }} }} } \right)$$
(6)

where u′, v′, and w′ are the x, y, and z components of the fluid velocity associated with chaotic turbulent fluctuations. This corresponds to a turbulence intensity as calculated in Eq. 7.

$$I = \sqrt {\frac{k}{{\overline{K}}}}$$
(7)

where K is the mass-averaged mean kinetic energy in the domain (Flow Science Incorporated 2022).

The transport equation is calculated as follows:

$$\frac{\partial k}{{\partial T}} + \frac{1}{{V_{{\text{F}}} }}\left\{ {uA_{x} \frac{\partial k}{{\partial x}} + vA_{y} \frac{\partial k}{{\partial y}} + wA_{z} \frac{\partial k}{{\partial z}}} \right\} = P_{{\text{T}}} + G_{{\text{T}}} + {\text{Diff}}_{k} - \varepsilon$$
(8)

where VF, Ax, Ay, and Az are FLOW-3D’s FAVOR™ (fractional area/volume obstacle representation) functions, and PT is the turbulent kinetic energy production, calculated as Eq. 9.

$$P_{{\text{T}}} = {\text{CSPRO}}\left\{ {\frac{\mu }{{\rho V_{{\text{F}}} }}} \right\}\left\{ {\begin{array}{*{20}c} {2A_{x} \left( {\frac{\partial u}{{\partial x}}} \right)^{2} + 2A_{y} \left( {R\frac{\partial v}{{\partial y}} + \xi \frac{u}{x}} \right)^{2} + 2A_{z} \left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \\ { + \left( {\frac{\partial v}{{\partial x}} + R\frac{\partial u}{{\partial y}} - \xi \frac{v}{x}} \right)\left[ {A_{x} \frac{\partial y}{{\partial x}} + A_{y} \left( {R\frac{\partial u}{{\partial y}} - \xi \frac{v}{x}} \right)} \right] } \\ { + \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}}} \right)\left( {A_{z} \frac{\partial u}{{\partial z}} + A_{x} \frac{\partial w}{{\partial x}}} \right) + \left( {\frac{\partial v}{{\partial z}} + R\frac{\partial w}{{\partial y}}} \right)\left( {A_{z} \frac{\partial v}{{\partial z}} + A_{y} R\frac{\partial w}{{\partial y}}} \right)} \\ \end{array} } \right\}$$
(9)

where CSPRO is a turbulence parameter (default value is 1.0), and R and ξ are related to the cylindrical coordinate system (if used). The buoyancy production term is

$$G_{{\text{T}}} = - {\text{CRHO}}\left( {\frac{\mu }{{\rho^{3} }}} \right)\left( {\frac{\partial \rho }{{\partial x}}\frac{\partial P}{{\partial x}} + R^{2} \frac{\partial \rho }{{\partial y}}\frac{\partial P}{{\partial y}} + \frac{\partial \rho }{{\partial z}}\frac{\partial P}{{\partial z}}} \right)$$
(10)

where μ is the molecular dynamic viscosity, ρ is the fluid density, P is the pressure, and CRHO is another turbulence parameter (default value is 0.0). The diffusion term is

$${\text{Diff}}_{k} = \frac{1}{{V_{{\text{F}}} }}\left[ {\frac{\partial }{\partial x}\left( {u_{k} A_{x} \frac{\partial k}{{\partial x}}} \right) + R\frac{\partial }{\partial y}\left( {u_{k} A_{y} R\frac{\partial k}{{\partial y}}} \right) + \frac{\partial }{\partial z}\left( {u_{k} A_{z} \frac{\partial k}{{\partial z}}} \right) + \xi \frac{{u_{k} A_{x} k}}{x}} \right]$$
(11)

where υk is the diffusion coefficient of k and is computed based on the local value of the turbulent viscosity (Flow Science Incorporated 2022).

The rate of turbulent energy dissipation (ε) is calculated as shown in Eq. (12).

$$\varepsilon = {\text{CNU}}^{3/4} \frac{{k^{3/2} }}{{{\text{TLEN}}}}$$
(12)

where CNU is a parameter (0.09 by default), k is the turbulent kinetic energy. TLEN is a parameter that is 7% of the smallest domain dimension; however, it is recommended that this value should instead be 7% of the hydraulic diameter (Shojaee Fard and Boyaghchi 2007), which is a characteristic length scale of the flow (Flow Science Incorporated 2022).

2.1.2 k–ε Turbulence Model

The standard k–ε model (Harlow and Nakayama 1967) is a two-equation model that dynamically determines the turbulent mixing length TLEN while calculating the turbulent kinetic energy (k) and dissipation rate (ε). It serves as an industry standard and may be used to represent a variety of flows (Turbulence Model 2022; Rodi 1980). It has been demonstrated that the k–ε model can approximate a variety of flows with good accuracy. In this model, turbulent dissipation rate is calculated as shown in Eq. 13.

$$\frac{\partial \varepsilon }{{\partial T}} + \frac{1}{{V_{{\text{F}}} }}\left\{ {uA_{x} \frac{\partial \varepsilon }{{\partial x}} + vA_{y} R\frac{\partial \varepsilon }{{\partial y}} + wA_{z} \frac{\partial \varepsilon }{{\partial z}}} \right\} = \frac{{{\text{CDIS}}1 \cdot \varepsilon }}{k}\left( {P_{{\text{T}}} + {\text{CDIS}}3 \cdot G_{{\text{T}}} } \right) + {\text{Diff}}_{\varepsilon } - {\text{CDIS}}2\frac{{\varepsilon^{2} }}{k}$$
(13)

Here, the default values of the dimensionless parameters are CDIS1 = 1.44, CDIS2 = 1.92, and CDIS3 = 0.20. Diffε refers to the dissipation diffusion and is calculated as follows (Flow Science Incorporated 2022):

$${\text{Diff}}_{\varepsilon } = \frac{1}{{V_{{\text{F}}} }}\left[ {\frac{\partial }{\partial x}\left( {u_{\varepsilon } A_{x} \frac{\partial \varepsilon }{{\partial x}}} \right) + R\frac{\partial }{\partial y}\left( {u_{\varepsilon } A_{y} R\frac{\partial \varepsilon }{{\partial y}}} \right) + \frac{\partial }{\partial z}\left( {u_{\varepsilon } A_{z} \frac{\partial \varepsilon }{{\partial z}} + } \right) + \xi \frac{{u_{\varepsilon } A_{x} \varepsilon }}{x}} \right]$$
(14)

2.1.3 RNG Turbulence Model

The RNG k–ε model is a more robust version of the standard k–ε model. Equations comparable to those for the k–ε model are used in the RNG model. However, in the RNG model, equation constants discovered empirically in the standard k–ε model are determined formally. The RNG model generally provides more applications than the standard k–ε model. The RNG model is recognized to characterize flows with strong shear zones and low-intensity turbulence properly. The default values for CDIS1 and CNU are 1.42, and 0.085, respectively, instead of the numbers used in the k model. The turbulent kinetic energy (k) and turbulent production (PT) terms are used to calculate CDIS2 (Flow Science Incorporated 2022; Turbulence Model 2022).

The following formula is used to calculate the kinematic turbulent viscosity (νT) in all turbulence transport models:

$$\nu_{{\text{T}}} = {\text{CNU}}\frac{{k^{2} }}{\varepsilon }$$
(15)

The requirement to restrict the value of ε from below poses a unique numerical problem for both the k–ε model and the RNG model. While k should theoretically approach 0 in such circumstances as well, Eq. (13) has the potential to create values of ε that are unphysically huge due to numerical issues (Eq. 15). So the value of ε is set with a restriction for minimum value as follows (Flow Science Incorporated 2022):

$$\varepsilon_{\min } = {\text{CNU}}^{3/4} \frac{{k^{3/2} }}{{{\text{TLEN}}}}$$
(16)

2.1.4 k–ω Turbulence Model

No exception can be made for the k–ω model. Instead, it outperforms the k–ε and RNG models in several flow situations, particularly in flows with streamwise pressure gradients like jets, wakes, and close-to-wall borders (Flow Science Incorporated 2022). The k–ω is formulated as shown in Eq. 17.

$$\frac{\partial k}{{\partial T}} + \frac{1}{{V_{F} }}\left\{ {uA_{x} \frac{\partial k}{{\partial x}} + vA_{y} \frac{\partial k}{{\partial y}} + wA_{z} \frac{\partial k}{{\partial z}}} \right\} = P_{T} + G_{T} + {\text{Diff}}_{T} - \beta ^{*} k\omega$$
(17)

where ω ≡ ε/k, and \(\beta ^{*} = \beta _{0}^{*} f_{{\beta ^{*} }}\) (\(\beta _{0}^{*}\) = 0.09). The value of \(f_{{\beta ^{*} }}\) is calculated as follows:

$$f_{{\beta ^{*} }} = 1\;{\text{when}}\;x_{k} \le 0 \;{\text{and}}\;f_{{\beta ^{*} }} = \frac{{1 + 680x_{k}^{2} }}{{1 + 400x_{k}^{2} }}\;\quad {\text{when}}\;x_{k} > 0$$
(18)
$$x_{k} \equiv \frac{1}{{\omega^{3} }}\left\{ {\frac{\partial k}{{\partial x}}\frac{\partial \omega }{{\partial x}} + \frac{\partial k}{{\partial y}}\frac{\partial \omega }{{\partial y}} + \frac{\partial k}{{\partial z}}\frac{\partial \omega }{{\partial z}}} \right\}$$
(19)

For ω transport,

$$\frac{\partial \omega }{{\partial T}} + \frac{1}{{V_{{\text{F}}} }}\left\{ {uA_{x} \frac{\partial \omega }{{\partial x}} + vA_{y} \frac{\partial \omega }{{\partial y}} + wA_{z} \frac{\partial \omega }{{\partial z}}} \right\} = \alpha \frac{\omega }{k} \left( {P_{{\text{T}}} + {\text{CDIS}}3 \cdot G_{{\text{T}}} + {\text{Diff}}_{\omega } - \beta \omega^{2} } \right)$$
(20)

where \(\alpha\) = 13/25, and

$$\beta = \beta_{0} f_{\beta }$$
(21)

with β0 = 9/125 and

$$f_{\beta } = \frac{{1 + 70x_{w} }}{{1 + 80x_{w} }}$$
(22)

where

$$x_{w} \equiv \left| {\frac{{{{\varvec{\Omega}}}_{ij} {{\varvec{\Omega}}}_{jk} {\mathbf{S}}_{ki} }}{{\left( {\beta_{0}^{*} \omega } \right)^{3} }}} \right|$$
(23)

\({\Omega }_{ij}\) and Sij are the mean rotation and mean strain rate tensors, respectively, and the buoyancy term (Flow Science Incorporated 2022).

The viscosity is a sum of the molecular and turbulent viscosities as follows (Flow Science Incorporated 2022):

$$\mu = \rho \left( {\nu + \nu_{{\text{T}}} } \right)$$
(24)

2.1.5 Large Eddy Simulation (LES) Turbulence Model

The LES model of turbulence was developed through atmospheric modeling. The core principle is that any turbulent flow structures that the computational grid can resolve should be directly computed or approximately computed if it is not possible for direct computing. The LES model is time-dependent and three-dimensional by nature. Additionally, fluctuations must be initiated and/or input at inflow borders. LES findings frequently yield more information than those generated by models based on Reynolds averaging. However, this involves more work, and computations might be CPU-intensive due to the finer meshes required (Flow Science Incorporated 2022; Smagorinsky 1963).

Smagorinsky (1963) scales velocity fluctuations by L times the mean shear stress for the length scale and takes a geometric mean of the grid cell size. As indicated in Eq. (26), these values are combined to form the LES kinematic eddy viscosity.

$$L = \left( {\delta_{x} \delta_{y} \delta_{z} } \right)^{1/3}$$
(25)
$$\nu_{T} = \left( {cL} \right)^{2} \sqrt {2e_{ij} 2e_{ij} }$$
(26)

where eij stands for the components of the strain rate tensor, and c is the Smagorinsky coefficient, which typically has a value between 0.1 and 0.2. The dynamic viscosity utilized throughout Flow3D incorporates this kinematic eddy viscosity similarly to how turbulence transport models do (as Eq. 24):

$$\mu = \rho \left( {\nu + \nu_{{\text{T}}} } \right)$$
(27)

3 Materials and Methods

Gökçeler Dam is a facility built on Gökçeler Stream in the Gazipaşa district of Antalya, located in the south of Türkiye, for irrigation and drinking-use water supply purposes (Fig. 2). With the Gökçeler Dam project, 36,245 hm3/year of water is given to the Gazipaşa Plain as irrigation water and the Gazipaşa District as drinking-use water (DSİ 2009).

Fig. 2
figure 2

Location of Gazipaşa District and Gökçeler Dam (images taken from Google Earth on 30.11.2022)

Full size image

3.1 Physical Model

The Gökçeler Dam stepped spillway was modeled at a 1/40 scale by the State Hydraulic Works of Türkiye (DSİ) Technical Research and Quality Control Department. In this physical model (Fig. 3), they conducted studies to determine the discharge capacity, the flow velocities in the approach channel, and the flow conditions in the spillway discharge channel, and to measure the spillway profile and pressure in the discharge channel (DSİ 2009).

Fig. 3
figure 3

The physical model of Gökçeler Dam: a discharge channel, b approach channel (DSİ 2009)

Full size image

The Gökçeler Dam spillway is an uncontrolled spillway with a short approach channel located on the right bank of the dam body (Fig. 3b). This spillway has been designed as a stepped spillway and has 39 steps. The first six of these steps' dimensions gradually increase, and the remaining 33 steps have been designed as 1.50 m in horizontal and vertical dimensions (DSİ 2009).

It is an excellent approach to provide geometric simulation and Froude number to be the same in the model and prototype in terms of providing the necessary conditions for dynamic simulation. The velocity scale was obtained by equating the Froude numbers in the model and prototype to each other for the Froude analogy (Eq. 28). The discharge scale is obtained as Eq. (29), depending on the velocity scale and the length scale (DSİ 2009). Table 1 summarizes the length, velocity, and discharge scales required to achieve a geometrical and dynamical analogy (Froude) between the model and the prototype.

$$\frac{{V_{{\text{m}}} }}{{\sqrt {g \cdot L_{{\text{m}}} } }} = \frac{{V_{{\text{p}}} }}{{\sqrt {g \cdot L_{{\text{p}}} } }} \to \frac{{V_{{\text{m}}} }}{{V_{{\text{p}}} }} = \sqrt {\frac{{L_{{\text{m}}} }}{{L_{{\text{p}}} }}} \to V_{r} = L_{r}^{1/2}$$
(28)
$$Q_{r} = \frac{{Q_{{\text{m}}} }}{{Q_{{\text{p}}} }} = \frac{{V_{{\text{m}}} \cdot L_{{\text{m}}}^{2} }}{{V_{{\text{p}}} \cdot L_{{\text{p}}}^{2} }} = \sqrt {L_{r} } \frac{{L_{{\text{m}}}^{2} }}{{L_{{\text{P}}}^{2} }} \to Q_{r} = L_{r}^{5/2}$$
(29)

where Vm is the model velocity, Vp is the prototype velocity, Lr is the length scale, g is the acceleration of gravity, Qm is the model discharge, and Qp is the prototype discharge.

Table 1 Analogy relations and scale ratios between prototype and model (DSİ 2009)
Full size table

3.2 Numerical Model

The geometrical model of the Gökçeler Dam stepped spillway was designed to be 1.80 m high, 1.00 m wide, and 3.00 m long as the experimental model (Fig. 4). The solid model was designed using Solidworks software (Yalçın 2022).

Fig. 4
figure 4

Gökçeler Dam solid model a plan; b 3D view

Full size image

Uniform cells and the k–ε turbulence model were used in the trial analyses to determine the most suitable mesh domain for the Gökçeler Dam stepped spillway model (Fig. 5). In the first stage, analyses were carried out using 2,903,040 total cells 1.25 cm in size. Finally, the mesh size was reduced to 0.90 cm, and the total number of cells was increased to 7,725,600. In order to see the effect of the total cell on the results, the total hydraulic head was read on the 33rd step, where the flow parameters can be measured clearly. As shown in Table 2, since increasing the number of cells after a specific value has little effect on the energy level, it was concluded that the mesh domain 3, consisting of 7,725,600 solution cells with a cell size of 0.90 cm, is sufficient for this study. The analysis was continued for 30 s, although the results were steady at about 20 s.

Fig. 5
figure 5

Mesh domain

Full size image
Table 2 Effect of total cell on total hydraulic energy
Full size table

The boundary conditions used in the analyses were determined according to the experimental setup for the Gökçeler Dam physical model (DSİ 2009). A specified pressure (P) boundary condition was used on the xmin surface to determine the upstream water level using the discharge-level curve in the model report (DSİ 2009). Similarly, according to the model report (DSİ 2009), the specified pressure (P) boundary condition was utilized on the xmax surface to define the tail water level. The wall (W) boundary condition (no-slip) was used to define the right (ymin), left (ymax), and bottom (zmin) surfaces. The top surface of the model was determined as (zmax) a symmetry boundary condition (S) (Fig. 6).

Fig. 6
figure 6

Boundary conditions

Full size image

4 Results and Discussion

In this section, the numerical results of the Gökçeler Dam were investigated for discharge-reservoir water level, velocity profile, water surface profile, pressure, and energy dissipation rate on the spillway. Then the results were compared with the experimental results (DSİ 2009) for four turbulence models (k–ε, k–ω, RNG, LES). The obtained results are presented and discussed in the sections below.

4.1 Discharge-Reservoir Water Level

In the experimental study, reservoir water levels were measured for 14 different flow rates ranging from 42.25 to 592.85 m3/s. The experimental and numerical results obtained from four different turbulence methods are shown in Fig. 7. According to the obtained results, it is seen that all turbulence models are in good agreement with the experimental results, and the most suitable turbulence model for discharge-water level is the k–ω model with an average error of 2.76%. In addition, it is seen that the discharges obtained for high reservoir water levels in all turbulence models are closer to the experimental results (Table 3). The results are also consistent with the studies in the literature (Kumcu and Uçar 2020).

Fig. 7
figure 7

Variation of the discharge-reservoir water level

Full size image
Table 3 Comparison of the discharge-reservoir water level
Full size table

4.2 Pressure

The pressure values obtained for the maximum flow rate were compared with the numerical results by taking the positions as shown in Fig. 8. It is seen that the numerical results obtained for all turbulence models agree with the experimental results (DSİ 2009), and the most compatible turbulence model is k–ε, with an average relative error of 13.36% (Table 4 and Fig. 9). While the pressure heights obtained as a result of the analyses are compatible with the experimental pressure heights along the spillway discharge channel, it is seen that there is some difference at the points in the downstream basin (Table 4). This situation has also been observed in studies in the literature (Usta 2014; Yang et al. 2014).

Fig. 8
figure 8

Probes of the pressure: a the physical model; b the numerical model; c the location of the measuring point on the step

Full size image
Table 4 Pressure results and error
Full size table
Fig. 9
figure 9

Pressure distributions: a left axis, b center axis, and c right axis

Full size image

4.3 Water Surface Profile

In the physical model (DSİ 2009), the water surface profile formed in the center of the channel was examined numerically (for max discharge). The errors obtained in the comparison of the results are given in Table 5. Although the results are very close in all turbulence models (Fig. 10), it is seen that the most compatible turbulence model for the water surface profile is the LES model, with an average error of 0.15%.

Table 5 Water surface profiles and errors
Full size table
Fig. 10
figure 10

Water surface profile

Full size image

4.4 Velocity

Velocity measurements were taken from 25 points (for 5 plans × 5 longitudinal sections) on the spillway approach channel (Fig. 11). Flow velocity measurements in the approach channel were carried out for max discharge (592.85 m3/s). The flow velocities and relative error rates obtained from the numerical and experimental results (DSİ 2009) are given in Table 6 and Fig. 12. When the flow velocity profiles are examined, it is seen that the numerical results obtained at the second and fourth points are quite compatible with the experimental results. According to the results obtained, it is seen that the most compatible turbulence model is k–ε with an average relative error of 7.80%. In contrast, the measurements at the first, third, and fifth points are slightly different from the experimental results. In addition, it is seen that all turbulence models, except for the third point measurements, give very close results to each other. In the measurements at the third point, it is seen that the k–ε turbulence model is more compatible with the experimental results compared to the other models. It is thought that the difference between the experimental and numerical results is seen at the points close to the wall regions due to the y+ value. In numerical simulations, it is necessary to use much more sensitive solution networks to see the viscous effects occurring in the wall regions (SimScale CAE Forum 2022). However, because the total number of cells used in the current study is around 7 million and the geometry is comprehensive, it is thought that a much more comprehensive workstation is needed for a more precise solution network.

Fig. 11
figure 11

Plan view of flow velocity measurement points

Full size image
Table 6 Comparison of the flow velocity
Full size table
Fig. 12
figure 12

Measured velocities on the approach channel: a for probe 1; b for probe 2; c for probe 3; d for probe 4; e for probe 5

Full size image

4.5 Energy Dissipation

The energy dissipation rate can be calculated from the upstream (E0) and downstream energy (E1) values for stepped spillways as follows (Fig. 13):

$$E_{0} = H_{{{\text{dam}}}} + y_{{\text{c}}} + \frac{{V_{{\text{c}}}^{2} }}{2g}$$
(30)
$$\frac{{V_{{\text{c}}}^{2} }}{2g} = \frac{{Q^{2} }}{{2g*A^{2} }} = \frac{{q^{2} B^{2} }}{{2gy_{{\text{c}}}^{2} B^{2} }} = \frac{{q^{2} }}{{2gy_{{\text{c}}}^{2} }}$$
(31)
$$\frac{{V_{{\text{c}}}^{2} }}{2g} = \frac{{q^{2} }}{{2gy_{{\text{c}}}^{2} }} = \frac{{gy_{{\text{c}}}^{3} }}{{2gy_{{\text{c}}}^{2} }} = \frac{{y_{{\text{c}}} }}{2}$$
(32)
$$E_{0} = H_{{{\text{dam}}}} + y_{{\text{c}}} + \frac{{V_{{\text{c}}}^{2} }}{2g} = H_{{{\text{dam}}}} + 1.5y_{{\text{c}}}$$
(33)

where Hdam is the height of the dam, yc is the critical flow depth \((y_{c} = \sqrt[3]{{\frac{{q^{2} }}{g}}})\), Q is the discharge, q is the unit discharge (q = Q/B), Vc is the critical flow velocity, g is the gravitational acceleration, A is the area, and B is the channel width.

$$E_{1} = y_{1} + \frac{{V_{1}^{2} }}{2g}$$
(34)
Fig. 13
figure 13

Schematic view of a longitudinal section

Full size image

Then the energy dissipation difference (EL) is calculated as shown in Eq. (35). Then the energy dissipation rate (EL/E0) is calculated.

$$E_{L} = E_{0} - E_{1}$$
(35)

The energy dissipation rates for max discharge (592.85 m3/s) on the Gökçeler Dam stepped spillway were numerically examined using different turbulence methods and compared with the experimental results (DSİ 2009). The energy dissipation and relative error rates calculated according to the results obtained are given in Table 7 and Fig. 14. In general, the analysis results using different turbulence methods are quite close to the experimental results (DSİ 2009), while the k–ε turbulence model with a relative error rate of 0.13% is closer to the experimental results (Table 7).

Table 7 Comparison of the results for energy dissipation rates
Full size table
Fig. 14
figure 14

Total hydraulic head for different turbulence model

Full size image

5 Conclusions

One of the first steps that researchers have to decide on in numerical studies is to choose the appropriate turbulence model to overcome the closure problems in turbulent flows. Within the scope of this study, numerical modeling of the Gökçeler Dam stepped spillway, which was built in Antalya, located in the south of Türkiye, was investigated using the results of the physical model (DSİ 2009). This study examined discharge-reservoir water level, pressure, flow velocity in the approach channel, and the energy dissipation rate, and four turbulence models (k–ε, k–ω, LES, RNG) were tested using Flow3D software. The results of this study are listed below.

  • As a result of comparing the flow values corresponding to 14 reservoir water levels, all turbulence models agree with the experimental results (DSİ 2009). The turbulence model most compatible with the experimental results (DSİ 2009), with an error value of 2.76%, is the k–ω model. In addition, it was observed that the discharges obtained at high reservoir water levels in all turbulence models were more consistent with the experimental results (DSİ 2009).

  • It has been observed that close results are obtained for all turbulence models for pressure along the right axis, middle axis, and left axis of the spillway. However, the most suitable turbulence model was found to be the k–ε model, with an average relative error of 13.36%. In addition, in all turbulence models, numerical and experimental results (DSİ 2009) were consistent along the spillway channel, while some differences were observed in the downstream basin.

  • The water surface profiles obtained with all turbulence models were almost the same along the spillway discharge channel, but there was some difference in the downstream pool, and the most compatible turbulence model was the LES model, with an average relative error of 0.15%.

  • All turbulence models gave close results for the velocity at the approach channel except for the measurements at the third point. The turbulence model most compatible with the experimental results was the k–ε model, with an average relative error of 7.80%.

  • As a result of the comparison of the experimental (DSİ 2009) and numerical studies for energy dissipation rate, all turbulence models give close results. The turbulence model most compatible with the experimental results (DSİ 2009), with an average relative error of 0.13% is the k–ε model.