1 Introduction

The non-prismatic beams with thin-walled open cross sections have been commonly adopted in structural components ranging from civil engineering to aeronautical applications due to their ability to improve strength and stability and also utilize structural material more efficiently. With the development of manufacturing process, beams with varying cross section are now adopted with different materials such as wood, steel and composite materials. Functionally graded materials (FGMs) as a new class of advanced materials are made up by gradually and smoothly changing the composition of two or more different materials in any desired direction. Engineers can thus produce structural elements with favorable resistance and manage the distribution of material properties. Due to smooth variations in material properties, functionally graded materials (FGMs) can also overcome some disadvantages and weaknesses of laminated composites such as delamination and stress concentration. FGM possesses characteristics that can be acquired in accordance with the volume fraction of the phase material based on different theories such as polynomial, exponential and trigonometric volume fraction laws. Among these functions, power-law distribution (Yung and Munz 1996; Jin and Paulino 2001) and exponential function (Delale and Erdogan 1983; Jin and Noda 1994; Jin and Batra 1996; Erdogan and Wu 1996; Gu and Asaro 1997; Erdogan and Chen 1998) are extensively used to describe the material properties variation for FGM. The use of axially functionally graded (AFG) materials during past 20 years has been increasing in complicated engineering configurations such as nano-/microresonators (Li and Balachandran 2006), the outer surface of aircraft fuselages (Steinberg 1986; Lyu et al. 2008) and nanotubes (Sears and Batra 2004) due to their conspicuous characteristics such as high strength, thermal resistance and optimal distribution of weight. The exact estimation of stability limit state and vibration characteristics of this kind of members is of fundamental importance in the design. A large number of studies have been thus devoted by different researchers to accurately probe free vibration and static behavior of functionally graded beam with variable cross section.

Closed-form solutions for the flexural and lateral–torsional stability of thin-walled beams have been carried out since the early works of Timoshenko and Gere (1961), Vlasov (1959) as well as Bazant and Cedolin (1991) for I-beams under some representative load cases. Yang and Yau (1987) formulated a general finite element model to investigate the instability of a doubly symmetric tapered I-beam by considering the effect of geometrical nonlinearity. Kim and Kim (2000) proposed a finite element approach for the lateral–torsional buckling and vibration analyses of doubly symmetric I tapered thin-walled beams. Vibration and instability analyses of functionally graded thin-walled beam with circular cylindrical section were performed by Oh et al. (2005). Andrade and Camotim (2004,2005) and Andrade et al. (2007a, b, 2010; ) presented some useful works about the lateral–torsional stability analysis of thin-walled beams with doubly and singly symmetric I-section under different boundary conditions. A one-dimensional finite element solution was proposed by Lee (2006) and general laminate stacking sequences. Regarding deformation compatibilities of web and flanges, the total potential energy was obtained by Lei and Shu (2008) to present a finite element model for linear lateral stability analysis of web-tapered beams with doubly symmetric I-section. Zhang and Tong (2008) assessed the lateral stability capacity of web-tapered doubly symmetric I-beam subjected to fixed free and simply supported end conditions by formulating the strain energy according to deformation compatibilities of two flanges and web of I-section. An analytical approach was used by Sina et al. (2009) to study the free vibration of functionally graded beams based on a new beam theory different from traditional first-order shear deformation beam assumption. Huang and Li (2010) and Huang et al. (2013) studied free vibration of axially FG non-prismatic beam where assumptions of Euler–Bernoulli and Timoshenko beam theories were contemplated. In their studies, the governing motion equation of beam was transformed into Fredholm integral equations. The exact lateral–torsional stability criterion of cantilever strip beam subjected to combined effects of intermediate and end transverse point loads by means of Bessel functions was proposed by Challamel and Wang (2010). Based on first-order shear deformation theory, Mohanty et al. (2012) presented an investigation of static and dynamic behavior of functionally graded ordinary (FGO) beam and functionally graded sandwich (FGSW) beam having hinged–hinged boundary condition by utilizing a new finite element solution. Geometrical stiffness matrix of a thin-walled beam element with doubly symmetric I-section was derived by Yau and Kuo (2012) by applying rigid beam assemblage concept in conjunction with stiffness transformation method. Li et al. (2013) studied the free vibration behavior of exponentially functionally graded beams. Chen and Li (2013) proposed a new modified couple stress theory for vibration problem of microscale composite laminated Timoshenko beam (CLTB). Asgarian et al. (2013) studied the lateral–torsional behavior of tapered beams with singly symmetric cross sections and having different end conditions. The equilibrium equation was solved by the power series expansions. An analytical technique was proposed by Yuan et al. (2013) to obtain the lateral–torsional buckling load of steel web-tapered tee-section cantilevers subjected to a uniformly distributed load and/or a concentrated load at the free end. A nonlinear formula based on 1D model for lateral buckling analysis of simply supported tapered beams with doubly symmetric cross sections was proposed by Benyamina et al. (2013). Soltani et al. (2014) studied linear stability and free vibration behavior of non-prismatic thin-walled beams with arbitrary cross section using a new finite element solution. An investigation on transverse vibration characteristics of rotating functionally graded Timoshenko beam made of porous material via the semi-analytical differential transform method was accomplished by Ebrahimi and Mokhtari (2015). Kuś (2015) investigated a numerical procedure for the lateral buckling stability analysis of beams with doubly symmetric cross section. In his work, the Ritz method has been adopted and the effects of simultaneous changes in the web height and flange width are taken into consideration. Additionally, Ruta and Szybinski (2015) applied Chebyshev series to solve the torsion fourth-order differential equation obtained by Asgarian et al. (2013) and to determine the critical lateral–torsional buckling of simply supported and cantilever beams with arbitrary open cross sections. Based on Euler–Bernoulli beam model and Vlasov’s theory for torsion, the stability analysis of thin-walled FG sandwich box beams with various boundary conditions was carried out by Lanc et al. (2015). An efficient approach to derive dynamic stiffness matrix of AFG Timoshenko beams on viscoelastic foundation subjected to impulsive loads in the Laplace domain was introduced by Calim (2016). By contemplating the impact of elastic foundation and semirigid end conditions, buckling analysis of axially functionally graded Euler–Bernoulli beam having non-uniform cross section was performed in detail by Shvartsman and Majak (2016). Fang and Zhou (2016) investigated free vibration behavior of rotating axially functionally graded Timoshenko beams with varying cross section through a new hybrid approach based on combination of Chebyshev polynomials and Ritz method. The Eringen non-local elasticity was used by Vosoughi (2016) and Vosoughi et al. (2018) to investigate the behavior of nanobeam under different mechanical and thermal loadings. Based on Vlasov’s assumption, Chen et al. (2016) derived the element stiffness matrix of the pre-twisted thin-walled straight beam with elliptical section and I cross section. Based on six different shear deformation theories, Pradhan and Chakraverty (2017) surveyed free vibration behavior of functionally graded beam with various end restrains using Rayleigh–Ritz method. By using a mathematical approach, new optimization models for improving the dynamic performance of functionally graded beams with thin-walled box section were suggested by Maalawi (2017). Ebrahimi and Hashemi (2017) inspected thermo-mechanical vibration behavior of tapered beams made of functionally graded (FG) porous material subjected to different thermal loadings by applying the differential transform method. Nguyen et al. (2016a, b, 2017, 2019) and Nguyen and Lee (2018) published several important papers related to static, vibration and buckling analyses of beams with thin-walled cross section made from composite and/or FG materials. Effect of uniform Winkler–Pasternak elastic foundation on torsional post-buckling behavior of clamped beam with doubly symmetric I-section was investigated by Rao and Rao (2017). Based on the transformed-section method and Euler–Bernoulli beam theory, free vibration analysis for FG beams with a rectangular cross section is carried out by Chen and Chang (2017). In order to carry out the free vibration analysis of axially functionally graded Euler–Bernoulli beams with varying cross section, Ghazaryan et al. (2018) utilized the differential transform method (DTM). In the context of the surface elasticity theory of Gurtin–Murdoch, buckling analysis of thermally affected tapered nanowires with axially varying material properties was comprehensively conducted by Kiani (2018). Norouzzadeh et al. (2019) developed a comprehensive size-dependent model to survey the linear and geometrically nonlinear bending responses of Timoshenko nanobeams. Rezaiee-Pajand et al. (2018) performed lateral–torsional stability analysis of axially transversally functionally graded tapered I-beams. Through the BB-BC algorithm and Deb's constraint handling method, Ozbasaran and Yilmaz (2018) presented the shape optimization procedure of flange and/or web-tapered doubly symmetric I-beams subjected to bending about their strong axis. Soltani (2017) and Soltani and Asgarian (2019a, b) performed stability and free vibration analyses of axially functionally graded non-prismatic Euler–Bernoulli and Timoshenko beams through a new mathematical mythology based on power series approximation. Recently, Ghasemi and Meskini (2019) perused the free vibrational behavior of simply supported power-law FG circular cylindrical shells based on Love’s first approximation shell theory.

Based on Vlasov’s model (1959) and using small displacements theory, the lateral–torsional stability behavior of thin-walled beams with doubly symmetric cross section under bending about their strong axis is usually governed by two fourth-order differential equations coupled in terms of the lateral displacement and the torsion angle. Accordingly, the 8 * 8 static and buckling stiffness matrices are formulated based on eight displacement parameters, namely translation, twist, rotation and warping, at each of end node (Soltani et al. 2014).

Besides, to the best knowledge of the authors, the previous studies on the dynamic and static analyses of tapered thin-walled beams are exclusively restricted to members made from homogeneous materials or transversely FGMs. Although, in the last decades, a large number of studies have been performed to investigate stability and vibration behavior of AFG non-prismatic beams, they are capable of predicting free vibration characteristics and axial critical loads of members with rectangular and/or circular cross sections. Therefore, the lateral–torsional stability of axially functionally graded beams with axially varying thin-walled cross section needs more discussions.

Regarding this, the main purpose of this work is to exactly survey the lateral stability analysis of axially functionally graded non-uniform beams with doubly symmetric open cross section subjected to different boundary conditions. In this context, the present study intends to develop a new finite element solution using two-node four-degree-of-freedom element for linear stability analysis of AFG web and/or flanges tapered beams under different boundary conditions. The usual 8 * 8 elastic and buckling stiffness matrices for beam with doubly symmetric thin-walled cross section are thus condensed to 4 * 4 ones. The following are the gist of this paper:

  1. 1.

    Based on Vlasov’s model and using small displacements theory, the governing equilibrium equations are derived through the energy principle for functionally graded non-uniform beams with bi-symmetric I-section.

  2. 2.

    The acquired system of linear stability equations are coupled in terms of the lateral deflection and the angle of twist due to simultaneous bending and torsion deformations. In this stage, the differential equations are uncoupled and converted to a single fourth-order differential equation where only twist angle is present.

  3. 3.

    In the last section, the finite element equations using a two-node four-degree-of-freedom element are developed. For this, the resulting equilibrium equation is restated in an integral form called the weak form. The terms of elastic stiffness and buckling stiffness matrices are finally derived by means of the expressions of the shape functions of prismatic flexural elements made up of homogeneous material, known as the Hermitian functions. It is noteworthy that in the current finite element formulation, the variations of applied load, geometrical properties and material characteristics are exactly contemplated in the calculation procedure of the terms of structural and buckling stiffness matrices. By solving the eigenvalue problem, one can acquire the lateral–torsional buckling loads.

According to the steps mentioned above, for measuring the effects of non-uniformity ratio, load height position, end moment ratio and axial variation of material properties on lateral–torsional stability resistance of axially functionally graded tapered beam with doubly symmetric section subjected to various end conditions, three exhaustive numerical examples are used. It should be pointed out that material properties of functionally graded tapered I-beam are supposed to vary through longitudinal direction of the constituents according to simple power-law distribution (P-FGM) as well as exponential one (E-FGM). In the current study, Poisson’s ratio of the beams is assumed to be constant. In the case of homogenous beam with varying I-section, the exactness of the proposed finite element formulation is validated by comparing the obtained results with finite element simulations using ANSYS software and the available benchmarks. Comments and conclusions are presented toward the end of the manuscript.

2 Derivation of the Equilibrium Equations

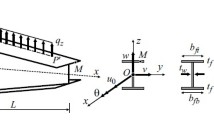
A straight tapered thin-walled beam as depicted in Fig. 1 is taken into account. It is assumed that the beam is made from non-homogeneous material with shear (G) and Young's (E) moduli which are variable along the beam’s length. The right-hand Cartesian coordinate system with x the initial longitudinal axis measured from the left end of the beam, the y-axis in the lateral direction and the z-axis along the thickness of the beam is considered. The origin of these axes (O) is located at the centroid of doubly symmetric I-section. The beam is initially subjected to arbitrary distributed force qz in z direction along with a line (PP′) on the section contour (Fig. 1). Based on small displacements assumption and Vlasov’s thin-walled beam theory for non-uniform torsion, the three displacement components of a point M on the section contour can be expressed as follows:

$$\begin{aligned} & U(x,y,z) = u_{0} (x) - y\frac{\partial v(x)}{{\partial x}} - z\frac{\partial w(x)}{{\partial x}} - \omega (y,z)\frac{\partial \theta (x)}{{\partial x}} \\ & V(x,y,z) = v(x) - z\theta (x) \\ & W(x,y,z) = w(x) + y\theta (x) \\ \end{aligned}$$
(1a, c)

In these equations, U is the axial displacement and displacement components V and W represent lateral and vertical displacements (in direction y and z). The term \(\omega (y,z)\) signifies a cross-sectional variable that is called the warping function, which can be defined based on Saint-Venant’s torsion theory and θ is twisting angle.

Fig. 1
figure 1

Beam with variable doubly symmetric I-section under external distributed loads: Coordinate system, notation for displacement parameters and definition of load eccentricities

Full size image

The equilibrium equations for beam with variable I-section are derived if the first variation of the total potential energy vanishes:

$$\delta \Pi = \delta \left( {U_{l} + U_{0} - W_{e} } \right) = 0$$
(2)

\(\delta\) illustrates a virtual variation in the last formulation. \(U_{l}\) represents the elastic strain energy and \(U_{0}\) expresses the strain energy due to effects of the initial stresses. \(\delta \Pi\) could be computed using the following:

$$ \begin{aligned}\delta \Pi &= \int_{0}^{L} {\int_{A} {\left( {\sigma_{xx} \delta \varepsilon_{xx}^{l} + \tau_{xy} \delta \gamma_{xy}^{l} + \tau_{xz} \delta \gamma_{xy}^{l} } \right){\text{d}}A{\text{d}}x} } \\&\quad+ \int_{0}^{L} {\int_{A} {\left( {\sigma_{xx}^{0} \delta \varepsilon_{xx}^{*} + \tau_{xy}^{0} \delta \gamma_{xy}^{*} + \tau_{xz}^{0} \delta \gamma_{xz}^{*} } \right){\text{d}}A{\text{d}}x} } \\&\quad- \int_{0}^{L} {q_{z} \delta w_{p} {\text{d}}x} = 0\end{aligned} $$
(3)

in which L and A express the element length and the cross-sectional area, respectively. (\(\delta \varepsilon_{xx}^{l}\),\(\delta \gamma_{xz}^{l}\),) and \(\delta \varepsilon_{xx}^{*}\) are the variation of the linear and the nonlinear parts of strain tensor, respectively. \(\sigma_{xx}\), \(\tau_{xy}\) and \(\tau_{xz}\) denote the Piola–Kirchhoff stress tensor components. Based on the assumption of the Green’s strain tensor, the linear and the nonlinear parts of strain–displacement relations and their first variation are:

$$\varepsilon_{xx}^{l} = u_{0}^{{\prime }} - yv^{{\prime \prime }} - zw^{{\prime \prime }} - \omega \theta^{{\prime \prime }} \to \delta \varepsilon_{xx}^{l} = \delta u_{0}^{{\prime }} - y\delta v^{{\prime \prime }} - z\delta w^{{\prime \prime }} - \omega \delta \theta^{{\prime \prime }}$$
(4a)
$$\varepsilon_{xx}^{*} = \frac{1}{2}\left[ {v^{{{\prime }2}} + w^{{{\prime }2}} + r^{2} \theta^{{{\prime }2}} } \right] + yw^{{\prime }} \theta^{{\prime }} - zv^{{\prime }} \theta^{{\prime }} \to \delta \varepsilon_{xx}^{*} = v^{{\prime }} \delta v^{{\prime }} + w\delta w^{{\prime }} + r^{2} \theta^{{\prime }} \delta \theta^{{\prime }} + y\theta^{{\prime }} \delta w^{{\prime }} + yw^{{\prime }} \delta \theta^{{\prime }} - z\theta^{{\prime }} \delta v^{{\prime }} - zv^{{\prime }} \delta \theta^{{\prime }}$$
(4b)
$$\gamma_{{_{xz} }}^{l} = 2\varepsilon_{{_{xz} }}^{l} = \left( {y - \frac{\partial \omega }{{\partial z}}} \right)\theta^{{\prime }} \to \delta \gamma_{xz}^{l} = \left( {y - \frac{\partial \omega }{{\partial z}}} \right)\delta \theta^{{\prime }}$$
(4c)
$$\gamma_{xz}^{*} = - \left( {v^{{\prime }} + \theta^{{\prime }} z} \right)\theta \to \delta \gamma_{xz}^{l} = - \theta \delta v^{{\prime }} - v^{{\prime }} \delta \theta - z\theta \delta \theta^{{\prime }} - z\theta^{{\prime }} \delta \theta$$
(4d)
$$\gamma_{{_{xy} }}^{l} = 2\varepsilon_{{_{xy} }}^{l} = - \left( {z + \frac{\partial \omega }{{\partial y}}} \right)\theta^{^{\prime}} \to \delta \gamma_{xy}^{l} = - \left( {z + \frac{\partial \omega }{{\partial y}}} \right)\delta \theta^{{\prime }}$$
(4e)
$$\gamma_{xy}^{*} = \left( {w^{{\prime }} + \theta^{{\prime }} y} \right)\theta \to \delta \gamma_{xy}^{*} = \theta \delta w^{{\prime }} + w^{{\prime }} \delta \theta + y\theta \delta \theta^{{\prime }} + y\theta^{{\prime }} \delta \theta$$
(4f)

In Eq. (3), \(\tau_{xy}^{0}\) and \(\tau_{xz}^{0}\) represent the mean value of the shear stress and \(\sigma_{xx}^{0}\) signifies initial normal stress in the cross section. According to Fig. 1, it is contemplated that the external bending moment occurs about the major principal axis (\(M_{y}^{*}\)). Therefore, the magnitude of bending moment with respect to z-axis is equal to zero. Regarding this, the most general case of normal and shear stresses associated with the external bending moment \(M_{y}^{*}\) and shear force Vz is considered as:

$$\sigma_{xx}^{0} = - \frac{{M_{y}^{*} }}{{I_{y} }}z,\quad \tau_{xz}^{0} = \frac{{V_{z} }}{A} = - \frac{{M_{y}^{{*{\prime }}} }}{A} \,$$
(5a, b)

In Eq. (3), wP is the vertical displacement of point P. According to kinematics used in Asgarian et al. (2013) and by adopting the quadratic approximation, the vertical displacement of the point P and its first variation are as:

$$w_{P} = w + y_{P} \theta - z_{P} \frac{{\theta^{2} }}{2} \to \, \delta w_{P} = \delta w + y_{P} \delta \theta - z_{P} \theta \delta \theta$$
(6)

In this equation, zP and yP are used to imply the eccentricities of the applied loads from the centroid of the cross section. Substituting Eqs. (4) to (6) into relation (3), the expression of the virtual potential energy can be carried out as:

$$\begin{aligned} \delta \Pi &= \int_{0}^{L} {\int_{A} {\sigma_{xx} \left( {\delta u_{0}^{{\prime }} - y\delta v^{{\prime \prime }} - z\delta w^{{\prime \prime }} - \omega \delta \theta^{{\prime \prime }} } \right){\text{d}}A{\text{d}}x} } \\ & \quad + \int_{0}^{L} {\int_{A} {\tau_{xy} \left( { - \left( {z + \frac{\partial \omega }{{\partial y}}} \right)\delta \theta^{{\prime }} } \right){\text{d}}A{\text{d}}x} } + \int_{0}^{L} {\int_{A} {\tau_{xz} \left( {\left( {y - \frac{\partial \omega }{{\partial z}}} \right)\delta \theta^{{\prime }} } \right){\text{d}}A{\text{d}}x} } \\ & \quad + \int_{0}^{L} {\int_{A} {\left( { - \frac{{M_{y}^{*} }}{{I_{y} }}z} \right)\left( {v^{{\prime }} \delta v^{{\prime }} + w\delta w^{{\prime }} + r^{2} \theta^{{\prime }} \delta \theta^{{\prime }} + y\theta^{{\prime }} \delta w^{{\prime }} + yw^{{\prime }} \delta \theta^{{\prime }} - z\theta^{{\prime }} \delta v^{{\prime }} - zv^{{\prime }} \delta \theta^{{\prime }} } \right){\text{d}}A{\text{d}}x} } \\ & \quad + \int_{0}^{L} {\int_{A} {\left( { - \frac{{M_{y}^{{*{\prime }}} }}{A}} \right)\left( { - \theta \delta v^{{\prime }} - v^{{\prime }} \delta \theta - z\theta \delta \theta^{{\prime }} - z\theta^{{\prime }} \delta \theta } \right){\text{d}}A{\text{d}}x} } - \int_{0}^{L} {\left( {q_{z} \delta w + \hat{M}_{t} \delta \theta - M_{t} \theta \delta \theta } \right){\text{d}}x} = 0 \\ \end{aligned}$$
(7)

in which \(\hat{M}_{t} = q_{z} y_{P}\) and \(M_{t} = q_{z} z_{P}\) denote the first- and the second-order torsion moments due to load eccentricities.

The variation of strain energy can be formulated in terms of section forces acting on cross-sectional contour of the elastic member in the buckled configuration. The section stress resultants are presented by the following expressions:

$$N = \int_{A} {\sigma_{xx} {\text{d}}A}$$
(8a)
$$M_{y} = \int_{A} {\sigma_{xx} z{\text{d}}A}$$
(8b)
$$M_{z} = - \int_{A} {\sigma_{xx} y{\text{d}}A}$$
(8c)
$$B_{\omega } = - \int_{A} {\sigma_{xx} \omega {\text{d}}A}$$
(8d)
$$M_{sv} = \int\limits_{A} {\left( {\tau_{xz} \left( {y - \frac{\partial \omega }{{\partial z}}} \right) - \tau_{xy} \left( {z + \frac{\partial \omega }{{\partial y}}} \right)} \right){\text{d}}A}$$
(8e)

where N is the axial force applied at end member. My and Mz denote the bending moments about major and minor axes, respectively. Bω is the bi-moment. Msv is the Saint-Venant torsion moment. In this stage, by integrating Eq. (7) over the cross-sectional area of the beam and using relations (8a)–(8e), the final form of the variation of total potential energy (\(\delta \Pi\)) is acquired as:

$$\begin{aligned} \delta \Pi &= \int_{L} {\left( {N\delta u_{0}^{{\prime }} + M_{z} \delta v^{{\prime \prime }} - M_{y} \delta w^{{\prime \prime }} + B_{\omega } \delta \theta^{{\prime \prime }} } \right){\text{d}}x} \\&\quad+ \int_{0}^{L} {\left( {M_{sv} \delta \theta^{{\prime }} } \right)} {\text{d}}x + \int_{0}^{L} {\left( {M_{y}^{*} (\theta^{{\prime }} \delta v^{{\prime }} + v^{{\prime }} \delta \theta^{{\prime }} )} \right){\text{d}}x}\\ & \quad + \int_{0}^{L} {\left( {M_{y}^{{*{\prime }}} (\theta \delta v^{{\prime }} + v^{{\prime }} \delta \theta )} \right){\text{d}}x} \\ & \quad- \int_{0}^{L} {\left( {q_{z} \delta w + \hat{M}_{t} \delta \theta - M_{t} \theta \delta \theta } \right){\text{d}}x} = 0 \\ \end{aligned}$$
(9)

Or

$$\begin{aligned} \delta \Pi &= \int_{L} {\left( {N\delta u_{0}^{{\prime }} + M_{z} \delta v^{{\prime \prime }} - M_{y} \delta w^{{\prime \prime }} + B_{\omega } \delta \theta^{{\prime \prime }} } \right){\text{d}}x} \\&\quad+ \int_{0}^{L} {\left( {M_{sv} \delta \theta^{{\prime }} } \right)} {\text{d}}x + \int_{0}^{L} {\left( { - M_{y}^{*} v^{{\prime \prime }} \delta \theta - M_{y}^{*} \theta \delta v^{{\prime \prime }} } \right)} {\text{d}}x \\&\quad- \int_{0}^{L} {\left( {q_{z} \delta w + \hat{M}_{t} \delta \theta - M_{t} \theta \delta \theta } \right){\text{d}}x} = 0 \\ \end{aligned}$$
(10)

According to the equation presented above, the first variation of total potential energy contains the virtual displacements (\(\delta u_{0} ,\delta v,\delta w,\delta \theta\)) and their derivatives. After appropriate integrations by parts, one gets an expression in terms of virtual displacements. After some calculations and needed simplifications, the following equilibrium equations in the stationary state are obtained:

$$N^{{\prime }} = 0$$
(11a)
$$- M_{y}^{{\prime \prime }} = q_{z}$$
(11b)
$$M_{z}^{{\prime \prime }} - (M_{y}^{*} \theta )^{{\prime \prime }} = 0$$
(11c)
$$B_{\omega }^{{\prime \prime }} - M_{y}^{*} v^{{\prime \prime }} - M_{sv}^{{\prime }} = \hat{M}_{t} - M_{t} \theta (x)$$
(11d)

The boundary conditions of the beam can be also expressed as:

$$\begin{array}{*{20}l} {N = 0} \hfill & {{\text{Or}}} \hfill & {\delta u_{0} = 0} \hfill \\ { - M_{y} = 0} \hfill & {{\text{Or}}} \hfill & {\delta w^{{\prime }} = 0} \hfill \\ {M_{y}^{{\prime }} = 0} \hfill & {{\text{Or}}} \hfill & {\delta w = 0} \hfill \\ {M_{z} - M_{y}^{*} \theta = 0} \hfill & {{\text{Or}}} \hfill & {\delta v^{{\prime }} = 0} \hfill \\ { - M_{z}^{{\prime }} + (M_{y}^{*} \theta )^{{\prime }} = 0} \hfill & {{\text{Or}}} \hfill & {\delta v = 0} \hfill \\ { B_{\omega } = 0} \hfill & {{\text{Or}}} \hfill & {\delta \theta^{{\prime }} = 0} \hfill \\ {-B_{\omega }^{{\prime }} + M_{sv} = 0} \hfill & {{\text{Or}}} \hfill & {\delta \theta = 0} \hfill \\ \end{array}$$
(12)

Assuming E and G to be the elastic parameters for an axially non-homogeneous material, which can be both variable through the longitudinal direction, the expressions of the stress components including the normal and shear ones are as:

$$\sigma_{xx} = E(x)\varepsilon_{xx}$$
(13a)
$$\tau_{xz} = G(x)\gamma_{xz}$$
(13b)
$$\tau_{xy} = G(x)\gamma_{xy}$$
(13c)

Substituting the strain–displacement relations defined in Eq. (4) into elastic stresses of Eq. (13) and integration over the cross-sectional area in the context of principal axes, the following components are derived:

$$ \begin{aligned}N &= \int_{A} {\sigma_{xx} {\text{d}}A} = \int_{A} {E(x)\varepsilon_{xx} {\text{d}}A} \\&= \int_{A} {E(x)(u_{0}^{{\prime }} - yv^{{\prime \prime }} - z^{{\prime \prime }} - \omega^{{\prime \prime }} ){\text{d}}A} = EAu_{0}^{{\prime }}\end{aligned} $$
(14a)
$$M_{y} = \int_{A} {E(x)(u_{0}^{{\prime }} - yv^{{\prime \prime }} - zw^{{\prime \prime }} - \omega \theta^{{\prime \prime }} )z{\text{d}}A} = - EI_{y} w^{{\prime \prime }}$$
(14b)
$$M_{z} = - \int_{A} {E(x)(u_{0}^{{\prime }} - yv^{{\prime \prime }} - zw^{{\prime \prime }} - \omega \theta^{{\prime \prime }} )y{\text{d}}A} = EI_{z} v^{{\prime \prime }}$$
(14c)
$$B_{\omega } = - \int_{A} {E(x)(u_{0}^{{\prime }} - yv^{{\prime \prime }} - zw^{{\prime \prime }} - \omega \theta^{{\prime \prime }} )\omega {\text{d}}A} = EI_{\omega } \theta^{{\prime \prime }}$$
(14d)
$$M_{sv} = \int\limits_{A} {G(x)\left( {\left( {y - \frac{\partial \omega }{{\partial z}}} \right)^{2} + \left( {z + \frac{\partial \omega }{{\partial y}}} \right)^{2} } \right)\theta^{{\prime }} {\text{d}}A} = GJ\theta^{{\prime }}$$
(14e)

In previous expressions, A is the cross-sectional area. \(I_{y}\) and \(I_{z}\) denote the second moments of area. J and \(I_{\omega }\) are the Saint-Venant torsion and warping constants. They are defined as:

$$\begin{aligned} & A = \int\limits_{A} {{\text{d}}A} ,\quad I_{y} = \int\limits_{A} {z^{2} {\text{d}}A} ,\quad I_{z} = \int\limits_{A} {y^{2} {\text{d}}A} {,}\quad I_{\omega } = \int\limits_{A} {\omega^{2} {\text{d}}A} \\ & J = \int\limits_{A} {\left( {\left( {y - \frac{\partial \omega }{{\partial z}}} \right)^{2} + \left( {z + \frac{\partial \omega }{{\partial y}}} \right)^{2} } \right){\text{d}}A} \\ \end{aligned}$$
(15a, e)

This model is also established in the context of small displacements and deformations. According to linear stability, nonlinear terms are also disregarded in the equilibrium equations. Based on these assumptions, the system of equilibrium equations for tapered I-beam is finally derived by replacing Eq. (14) into Eq. (11):

$$\left( {EAu_{0}^{{\prime }} } \right)^{{\prime }} = 0$$
(16a)
$$\left( {EI_{y} w^{{\prime \prime }} } \right)^{{\prime \prime }} = q_{z}$$
(16b)
$$\left( {EI_{z} v^{{\prime \prime }} } \right)^{{\prime \prime }} - \left( {M_{{_{y} }}^{*} \theta } \right)^{{\prime \prime }} = 0$$
(16c)
$$\left( {EI_{\omega } \theta^{{\prime \prime }} } \right)^{{\prime \prime }} - \left( {GJ\theta^{{\prime }} } \right)^{{\prime }} - M_{{_{y} }}^{*} v^{{\prime \prime }} = \hat{M}_{t} - M_{t} \theta$$
(16d)

In these differential equations, the successive x-derivatives are denoted by ()′, ()″. The last two equilibriums Eqs. (16c, d) are coupled differential equations due to the presence of lateral deflection and torsion component (v and θ) as well as bending moment (\(M_{y}^{*}\)), while the equation for the axial and vertical displacements (Eqs. 16a, b) are uncoupled from the others. Besides, they have no incidence on linear lateral–torsional buckling analysis of elastic beam with bi-symmetric thin-walled cross section. The associated boundary conditions are formulated as follows:

$$\begin{array}{*{20}l} {N = 0} \hfill & {{\text{Or}}} \hfill & {\delta u_{0} = 0} \hfill \\ { {EI_{y} w^{{\prime \prime }} } = 0} \hfill & {{\text{Or}}} \hfill & {\delta w^{{\prime }} = 0} \hfill \\ {-({EI_{y} w^{{\prime \prime }} })^{{\prime }} = 0} \hfill & {{\text{Or}}} \hfill & {\delta w = 0} \hfill \\ {({EI_{z} v^{{\prime \prime }} }) - M_{y}^{*} \theta = 0} \hfill & {{\text{Or}}} \hfill & {\delta v^{{\prime }} = 0} \hfill \\ { - ({EI_{z} v^{{\prime \prime }} })^{{\prime }} + (M_{y}^{*} \theta )^{{\prime }} = 0} \hfill & {{\text{Or}}} \hfill & {\delta v = 0} \hfill \\ {EI_{\omega } \theta^{{\prime \prime }} = 0} \hfill & {{\text{Or}}} \hfill & {\delta \theta^{{\prime }} = 0} \hfill \\ {-( EI_{\omega } \theta^{{\prime \prime }})^{{\prime }} + GJ\theta^{{\prime }}= 0} \hfill & {{\text{Or}}} \hfill & {\delta \theta = 0} \hfill \\ \end{array}$$
(17)

The governing equilibrium equation for lateral deformation (Eq. (16c)) can be transformed into:

$$v^{{\prime \prime }} = \frac{{M_{y}^{*} }}{{EI_{z} }}\theta$$
(18)

The last expression is incorporated in the fourth equilibrium equation Eq. (16d). After some simplifications, the mentioned equation is then uncoupled from the lateral displacement (v). The following differential equation is derived only in terms of the twist angle (θ):

$$\left[ {E(x)I_{{\omega }} (x)\theta^{{\prime \prime }} (x)} \right]^{{\prime \prime }} - \left[ {G(x)J(x)\theta^{{\prime }} (x)} \right]^{{\prime }} - \frac{{M_{y}^{2} (x)}}{{E(x)I_{z} (x)}}\theta (x) = - M_{t} (x)\theta (x) \,$$
(19)

Or

$$ \begin{aligned}&E(x)I_{z} (x)\left[ {E(x)I_{\omega } (x)\theta^{\prime \prime } (x)} \right]^{{\prime \prime }} - E(x)I_{z} (x)\left[ {G(x)J(x)\theta^{{\prime }} (x)} \right]^{{\prime }} \\&\quad- M_{y}^{2} (x)\theta (x) + E(x)I_{z} (x)M_{t} (x)\theta (x) = 0\end{aligned} $$
(20)

For simplicity, we assume that the distributed load is acted without any eccentricity in the lateral direction (yP = 0). Therefore, the value of first-order torsion moment (\(\hat{M}_{t}\)) is equal to zero. The characteristics of any geometrical properties of the beam are a function of the coordinate x due to the tapering of the web and/or flanges. Due to the presence of variable coefficients in the acquired fourth-order differential equation in terms of the angle of twist, closed-form solutions are not accessible. In order to overcome this difficulty, numerical and analytical techniques such as Rayleigh–Ritz method, finite element analysis (FEA), Galerkin’s method, finite difference method (FDM) and differential quadrature method (DQM) are possible. In the current work, the finite element method for linear lateral–torsional stability analysis of axially functionally graded web and/or flanges tapered doubly symmetric beams with various end conditions is employed. The finite element formulation using the exact shape functions for homogeneous beam elements with uniform cross section is developed in the remaining part of the current paper.

3 Finite Element Formulations

In the previous section, the formulation of differential equation along with the boundary conditions has been presented in a strong form, while, in the current section, the derivation of weak form of the equilibrium equation of AFG non-prismatic beam with tapered I-section is outlined to acquire approximate solution based on the finite element method. The weak form is an integral form of the equilibrium equation. In order to construct the weak form for the governing differential equation, it is essential that we multiply Eq. (20) by an arbitrary function (\(\psi\)) and integrate the result over the problem domain. The weak form of the equilibrium equation in terms of bending rotation is thus obtained by:

$$\int_{0}^{L} {\psi \left( {(EI_{z} )\left( {EI_{\omega } \theta^{\prime \prime } } \right)^{\prime \prime } - (EI_{z} )\left( {GJ\theta^{\prime } } \right)^{\prime } - M_{y}^{*2} \theta + (EI_{z} )M_{t} \theta } \right)} {\text{d}}x = 0$$
(21)

in which \(\psi\) is a test function which is continuous and satisfies the essential end conditions. Thus, the weak form for the equilibrium equation becomes:

$$ \begin{aligned}&\int_{0}^{L} ( {(EI_{z} )(EI_{\omega } )\psi^{\prime \prime } \theta^{\prime \prime } + 2(EI_{z} )^{\prime } (EI_{\omega } )\psi^{\prime } \theta }\\&\quad{+ (EI_{z} )^{\prime \prime } (EI_{\omega } )\psi \theta^{\prime \prime } + (EI_{z} )(GJ)\psi^{\prime } \theta^{\prime } }\\&\quad{+ (EI_{z} )^{\prime } (GJ)\psi \theta^{\prime }- M_{y}^{*2} \psi \theta + (EI_{z} )M_{t} \psi \theta ){\text{d}}x} = 0\end{aligned} $$
(22)

As can be seen in the above equation, the general quadratic functional form cannot be constructed in the presence of the second, third and fifth terms in the weak statement of the equilibrium equation which possesses a non-symmetric bi-linear form.

In the current finite element model, there are two nodes with two degrees of freedom per node for each element. The two nodes by which the finite element can be assembled into structure are located at its ends. According to finite element rules, it is essential to use local coordinate (\(\varepsilon = x/L_{e}\)). Le is the length of each segment. The local -axis is directed from node 1 to node 2. The considered degrees of freedom at the left and right nods of each element are: \(\theta^{1} ,\theta^{2}\) (the twist angle) and \(\theta^{{{\prime }1}} ,\theta^{{{\prime }2}}\) (the rate of twist, \({\raise0.7ex\hbox{${\partial \theta }$} \!\mathord{\left/ {\vphantom {{\partial \theta } {\partial \varepsilon }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial \varepsilon }$}}\)). The nodal displacements of the beam element in the local coordinate at \(\varepsilon = 0\) and \(\varepsilon = 1\) are illustrated in Fig. 2.

Fig. 2
figure 2

Nodal displacement vectors of a tapered I-beam element of length Le

Full size image

The terms of the element stiffness matrix can be found from the derivation of the interpolation functions. The shape functions define the deformation shape of the element by applying unit deformation at each of the four degrees of freedom, while constraining other nodal displacement. With these four interpolation functions, the exact deformed shape of the beam element can be expressed in terms of its nodal displacements. As it was previously pointed out, the exact shape functions of homogeneous and isotropic uniform flexural elements, known as Hermitian cubic interpolation (cubic spline) functions, are used in the current study. These shape functions are as follows:

$$\left\langle {\phi (\varepsilon )} \right\rangle = \left\langle {\begin{array}{*{20}c} {\phi_{1} (\varepsilon )} & {\phi_{2} (\varepsilon )} & {\phi_{3} (\varepsilon )} & {\phi_{4} (\varepsilon )} \\ \end{array} } \right\rangle$$
(23)

in which

$$\begin{gathered} \phi_{1} (\varepsilon ) = 2\varepsilon^{3} - 3\varepsilon^{2} + 1 \hfill \\ \phi_{2} (\varepsilon ) = \varepsilon^{3} - 2\varepsilon^{2} + \varepsilon \hfill \\ \phi_{3} (\varepsilon ) = - 2\varepsilon^{3} + 3\varepsilon^{2} \hfill \\ \phi_{4} (\varepsilon ) = \varepsilon^{3} - \varepsilon^{2} \hfill \\ \end{gathered}$$
(24a, d)

\(\phi_{i} (\varepsilon ),i = 1,2,3,4\) are the shape functions corresponding to the four degrees of freedom. Substituting the interpolation shape functions (Eq. (24)) into Eq. (22), the terms of elastic and buckling stiffness matrices of AFG tapered I-beam in the non-dimensional coordinate are derived as:

$$\begin{aligned} K_{ij}^{*} &= \frac{1}{{L_{e}^{3} }}\int_{0}^{1} {\left\{ {(E(\varepsilon )I_{z} (\varepsilon ))(E(\varepsilon )I_{\omega } (\varepsilon ))\phi_{i}^{{\prime \prime }} (\varepsilon )\phi_{j}^{{\prime \prime }} (\varepsilon )} \right\}{\text{d}}\varepsilon } \\&\quad+ \frac{2}{{L_{e}^{3} }}\int_{0}^{1} {\left\{ {(E(\varepsilon )I_{z} (\varepsilon ))^{{\prime }} (E(\varepsilon )I_{\omega } (\varepsilon ))\phi_{i}^{{\prime }} (\varepsilon )\phi_{j}^{{\prime \prime }} (\varepsilon )} \right\}{\text{d}}\varepsilon } \\ & \quad + \frac{1}{{L_{e}^{3} }}\int_{0}^{1} {\left\{ {(E(\varepsilon )I_{z} (\varepsilon ))^{{\prime \prime }} (E(\varepsilon )I_{\omega } (\varepsilon ))\phi_{i} (\varepsilon )\phi_{j}^{{\prime \prime }} (\varepsilon )} \right\}{\text{d}}\varepsilon }\\&\quad + \frac{1}{{L_{e} }}\int_{0}^{1} {\left\{ {(E(\varepsilon )I_{z} (\varepsilon ))(G(\varepsilon )J(\varepsilon ))\phi_{i}^{{\prime }} (\varepsilon )\phi_{j}^{{\prime }} (\varepsilon )} \right\}{\text{d}}\varepsilon } \\ & \quad +\frac{1}{{L_{e} }}\int_{0}^{1} {\left\{ {(E(\varepsilon )I_{z} (\varepsilon ))^{{\prime }} (G(\varepsilon )J(\varepsilon ))\phi_{i} (\varepsilon )\phi_{j}^{{\prime }} (\varepsilon )} \right\}{\text{d}}\varepsilon } \\ \end{aligned}$$
(25a)
$$ \begin{aligned}K_{{M_{ij} }}& = L_{e} \int_{0}^{1} {\left\{ {\left( {M_{y}^{*} (\varepsilon )M_{y}^{*} (\varepsilon )} \right)\phi_{i} (\varepsilon )\phi_{j} (\varepsilon ) }\right.}\\&\quad{\left.{+ (E(\varepsilon )I_{z} (\varepsilon ))M_{t} (\varepsilon )\phi_{i} (\varepsilon )\phi_{j} (\varepsilon )} \right\}{\text{d}}\varepsilon }\end{aligned} $$
(25b)

where \(K_{ij}^{*}\) and \(K_{{M_{ij} }}\) are, respectively, the usual elastic stiffness and the buckling stiffness matrices, which accounts for the effect of applied bending moment on the stiffness of the member.

At this stage, it is important to note that the elastic and buckling stiffness matrices [K*] and [KM] developed for an AFG beam with tapered I-section can be adopted to determine the similar stiffness matrices for a uniform beam made up of homogenous and isotropic materials. In this condition, the flexural rigidity (EIz) is constant over beam’s length and the elastic stiffness matrix is reduced to:

$$ \begin{aligned}K_{ij}^{*} &= \frac{1}{{L_{e}^{3} }}\int_{0}^{1} {\left\{ {(E(\varepsilon )I_{z} (\varepsilon ))(E(\varepsilon )I_{\omega } (\varepsilon ))\phi_{i}^{{\prime \prime }} (\varepsilon )\phi_{j}^{{\prime \prime }} (\varepsilon )} \right\}{\text{d}}\varepsilon } \\&\quad+ \frac{1}{{L_{e} }}\int_{0}^{1} {\left\{ {(E(\varepsilon )I_{z} (\varepsilon ))(G(\varepsilon )J(\varepsilon ))\phi_{i}^{{\prime }} (\varepsilon )\phi_{j}^{{\prime }} (\varepsilon )} \right\}{\text{d}}\varepsilon }\end{aligned} $$
(26)

By reviewing the above expression, it is important to mention that it is possible to construct the quadratic functional form for linear stability analysis of homogenous prismatic beam with thin-walled I-section. Thereafter, by assembling each element stiffness matrix based on its nodal displacements, the stiffness matrices of the whole structure can be achieved. In most finite element method textbooks (Zienkiewicz and Taylor 2005; Logan 2007), one can find the description of the process of assemblage in details.

It should be pointed out that only the linear lateral stability analysis is under consideration in the present study. In this regard, the buckling stiffness matrix is proportional to the initial stress forces. The critical buckling loads are thus evaluated by solving the following eigenvalue problem:

$$\left( {\left[ {K^{*} } \right] - \left[ {K_{M} } \right]} \right)\left\{ d \right\} = 0$$
(27)

in which \(\{ d\}\) are the eigenvectors related to eigenvalues. It is well known that for a system with n degrees of freedom, there exist n lateral–torsional buckling modes, but in practice only the lowest ones are of interest.

4 Numerical Results

In the previous sections, the equilibrium equation of axially functionally graded thin-walled beam with varying cross section was acquired; afterward, a new finite element model for lateral–torsional stability analysis was formulated. In the current section to demonstrate the effects of different parameters, namely load height position, moment gradient factor, tapering ratio, end conditions and axial variation, of material properties on the lateral–torsional critical load, three numerical examples are provided and solved through the proposed finite element methodology. It should be pointed out that material properties of functionally graded web and/or flanges tapered I-beam are supposed to vary through longitudinal direction of the constituents according to simple power-law distribution (P-FGM) as well as exponential one (E-FGM). Based on the studies presented by Delale and Erdogan (1983) and Li (2008), it is assumed that the Poisson’s ratio is constant through the length.

In the following, the mechanical properties at the left support (x = 0) and the right one (x = L) of the beam are, respectively, indicated with the subscripts 0 and 1. In order to simplify the solution procedure and the presentation of acquired results, the following non-dimensional parameters are defined as.

  • Buckling load for beam under concentrated load:

    $$\overline{P}_{cr} = \frac{{P_{cr} L^{2} }}{{E_{0} I_{z0} }}$$
    (28a)

  • Buckling load for beam under uniformly distributed load:

    $$\overline{q}_{cr} = \frac{{q_{cr} L^{3} }}{{E_{0} I_{z0} }}$$
    (28b)

  • Buckling moment for beam under gradient moment:

    $$\overline{M}_{cr} = \frac{{M_{cr} L}}{{E_{0} I_{z0} }}$$
    (28c)

4.1 Example 1: Lateral–Torsional Buckling of Cantilever Web-Tapered Beam Under Concentrated Load

The first example deals with the lateral stability analysis of a doubly symmetric web-tapered cantilever I-beam subjected to a concentrated lateral load. The beam exhibits a linear web tapering varying from the bigger section (d0) at the fixed end to the smaller one (d1) at the free end, as shown in Fig. 3, while the bottom and top flanges' width remain constant along the length. The web height is reduced at the free end with different tapering ratio \(\alpha = d_{0} /d_{1} ;\;0.1 \le \alpha \le 1\). In the current example, the tip load is applied at two different positions of the smaller section at the free end, namely at the top flange and at the centroid. The non-dimensional geometrical properties for the considered beam are shown in Fig. 3.

Fig. 3
figure 3

Cantilever web-tapered beam with doubly symmetric I-sections: geometry and loading properties

Full size image

The aim of the first part of the current example is to define the needed number of meshes (n) in the assemblage of the stiffness matrices of the considered beam to obtain an acceptable accuracy on elastic buckling loads. Regarding this, the lowest values of the lateral buckling load parameter (\(\overline{P}_{cr}\)) of the aforementioned web-tapered beam with thin-walled section for two load positions, on top flange and centroid, for different values of tapering ratios (α = 0.3, 0.5 and 1.0) are calculated with respect to the number of segments adopted in FE methodology. Through this part, the modulus of elasticity of the material and Poisson’s ratio are assumed to be 200 GPa and 0.3, respectively. The outcomes are verified with those obtained by finite element technique using ANSYS software and the semi-analytical method suggested by Asgarian et al. (2013). The web-tapered doubly symmetric beam has been modeled using BEAM188 in ANSYS software. This member is a two-node element with seven degrees of freedom—three translational UX, UY, UZ, three rotary ROTX, ROTY, ROTZ and warping of freedom at each node. By comparing our numerical results with FE simulations and with the existing ones (Asgarian et al. 2013) presented in Table 1, it can be stated that numerical results have rapid convergence. As n increases from 3 to 7, the relative errors between the evaluated results and others obviously diminish. Also, the acquired outcomes of the lowest lateral buckling parameters are identical to the exact results up to two decimal places. The efficiency and performance of the proposed finite element solution are thus confirmed. The precision and accuracy of the present methodology result from the contemplating the variations of external applied load, geometrical properties and material characteristics in the formulation of static and buckling stiffness matrices. In the following computations, we take n = 6 to calculate the first buckling load parameters, unless otherwise stated.

Table 1 Effect of number of elements (n) on linear lateral–torsional buckling parameter (\(\overline{P}_{{\rm cr}}\)) of cantilever tapered beams (centroid and top flange loading)
Full size table

In the following, to study the effects of material non-homogeneity on linear lateral–torsional stability, it is supposed that the material properties of the non-prismatic beam are graded smoothly along the beam axis by a power-law distribution of volume fractions of the constituents. The variation of Young’s modulus of elasticity along the longitudinal direction is thus defined with the following formulation:

$$E(x) = E_{0} + (E_{1} - E_{0} )\left( \frac{x}{L} \right)^{m}$$
(29)

in which E0 and E1 represent the values of Young’s modulus of the contemplated materials on the left and right support of the beam, respectively. m signifies the material non-homogeneity index indicating the material variation profile through the length of the beam. It is supposed that the web-tapered thin-walled beam is made of a mixture of ceramic phase and metal phase. Regarding this, two different materials specifically zirconia (ZrO2) and aluminum (Al) with the following characteristics are considered as:

$${\text{ZrO}}_{2}{:}\;E_{0} = 200\,{\text{GPa}};\; {\text{Al}}:\;E_{1} = 70\,{\text{GPa}};$$

According to the material property variation (Eq. (29)), the left side of AFG beam (x = 0) is intended pure ceramic (zirconia) and the right end (x = L) is pure metal (aluminum). By notifying Eq. (29), it can also be concluded that by raising the power-law index (m), the proportion of zirconia over the beam’s length increases. In this research, the power-law exponent (m) varies in the range of \(0.5 \le m \le 3\).

In this section, the first non-dimensional buckling load parameter (\(\overline{P}_{{\rm cr}}\)) for web-tapered I-beam made up of homogenous materials and axially functionally ones with different gradient indexes (m = 1, 2 and 3) are derived using the proposed finite element solution by dividing the beam into six equal segments. The dimensionless buckling loads for various tapering ratios and two different load height positions are arranged in Table 2.

Table 2 Critical buckling parameters (\(\overline{P}_{{\rm cr}}\)) of cantilever beam under tip load at the free end, for different power-law exponents, load height positions and tapering ratios
Full size table

Afterward, the lowest buckling load parameter variation versus the taper ratio (α) and the gradient index (m) for centroid and top flange loadings are presented in Fig. 4. Each of the depictions of Fig. 4a, b presents six different plots relating to m = 0.5, 1, 1.5, 2, 2.5 and 3.

Fig. 4
figure 4

Variation of lateral buckling parameter of cantilever I-beam under gradient moment, versus end tapering ratio (α) and the gradient index (m): a centroid loading, b top flange loading

Full size image

It is observable that increasing the gradient index leads to the enlargement of dimensionless buckling load for all values of tapering ratio. The reason is the higher portion of the ZrO2 phase as the value of the gradient index rises. For example, the magnitude of lateral buckling parameter of prismatic member when the tip load is applied at the centroid increases from 0.2272 to 0.2663 and then to 0.2872, when m increases from 1 to 3. It shows an increase by 17.21% and 26.41%, accordingly. Similar behavior can also be observed for the critical loads relating to web-tapered beams. It is found that for \(0.5 \le m \le 1.5\), the non-dimensional critical loads increase sharply, whereas, for m > 1.5, the buckling resistance increases slightly and approaches maximum magnitude. By pondering Fig. 4, one can remark that the variation of buckling parameter versus the tapering ratio is linear for centroid loading position, while this trend for top flange loading is nonlinear.

The table and figure indicate that non-uniformity parameter has a remarkable influence on the non-dimensional lateral–torsional buckling loads. The tapering parameter weakens the web-tapered beam subjected to a tip point load on the shear center due to decreasing the member stiffness, while the other results relating to web-tapered I-beams with a concentrated load at the top flange of the free end section do not follow the similar pattern. In other words, the lateral stability strength is enhanced with tapering ratio; for instance, the lateral buckling parameters of homogenous or AFG cantilevers with constant cross section (α = 1) are smaller than those of web-tapered with tapering ratio equal 0.1. This interesting reason is attributed to the fact that the torsion moment due to bending load height (Mt) is decreased by descending the taper ratio (α) from 1. Finally, it can be stated that this phenomenon is more predominant on lateral buckling resistance of cantilever beam subjected to a concentrated load than that of web non-uniformity ratio.

4.2 Example 2: Lateral–Torsional Buckling of Pinned–Fixed Double-Tapered Beam Under Uniformly Distributed Load

In the second numerical example, the linear lateral–torsional buckling load of power-law FG double-tapered I-beam under uniformly distributed load and subjected to pinned–fixed boundary condition is perused. As shown in Fig. 5, the geometrical properties of the left end section of the beam are constant; nevertheless, the flanges’ width and the web height for considered doubly symmetric I-sections are made to vary linearly from the pinned end to the fixed one. In the case of tapered web, the height of the beam’s section is (d0) at the left support and is linearly changed to \(d_{1} = (1 + \alpha )d_{0}\) at the other end. For the beam with tapered flanges, the width of flange is also made to vary linearly to \(b_{1} = (1 + \beta )b_{0}\) at the other end. The tapering parameters (β and α) can change from zero (prismatic beam) to a range of [0.1, 1] for non-uniform beams. In this example, lateral buckling loads are carried out for three different loading positions: the bottom flange, the centroid and the top flange. Moreover, the material features are identical to the first example.

Fig. 5
figure 5

a Schematic representation of double-tapered beam with I-section under uniformly distributed load, b configuration of AFG tapered beam with pinned–fixed boundary condition, c geometry properties and d loading positions

Full size image

The aim of the first section of this example is to investigate the influence of web and flanges tapering parameters on the lateral stability capacity of the contemplated beam made up of homogenous material. Hence, Fig. 6 illustrates the variation of the lowest lateral buckling parameters (\(\overline{q}_{{\rm cr}}\)) with respect to the web tapering ratio (α) and the flange tapering parameter (β), where the distributed transverse load is applied on the centroid of I-section through the length. According to this figure, it is found out that the lateral buckling parameter increases with an increase in web and/or flange non-uniformity ratios (β and α), as a result of the enhancement of all geometrical characteristics of cross section and consequently flexural stiffness and torsional rigidity of the elastic member. Moreover, it is easily evident that the impact of flanges width tapering parameter (β) on the magnitude of non-dimensional lateral–torsional buckling load is more predominant than that of web non-uniformity ratio (α).

Fig. 6
figure 6

Variation of lateral buckling parameter (\(\overline{q}_{{\rm cr}}\)) of homogenous beam with tapered I-section under a distributed load on the shear center for different web and flange tapering parameters

Full size image

The next set of results was derived to demonstrate the impact of the power-law exponent and distributed load position on the non-dimensional lateral buckling parameters (\(\overline{q}_{{\rm cr}}\)) of the power-law FG double-tapered I-beam. Variations of the acquired lateral buckling parameters of the aforementioned tapered beam for different values of tapering ratios (β  = α  = 0, 0.2, 0.5 and 0.5) and various gradient indices when uniformly transverse load is acted at three different locations along the beam’s length, namely top flange, mid-height and bottom flange, are tabulated in Table 3. Furthermore, for three different load height positions, Fig. 7 exhibits the effect of tapering ratio (α = β) on variation of lateral buckling parameters of pinned–fixed web and flanges tapered beam from homogenous material and axially functionally ones. To this end, the power-law exponent is taken m = 1, 2 and 3. It is noteworthy that the lowest normalized buckling parameters are derived using the proposed finite element solution by dividing the beam into six equal segments.

Table 3 First lateral buckling parameters (\(\overline{q}_{{\rm cr}}\)) for AFG double-tapered I-beam with various material non-homogeneity indexes (m) and three different loading positions
Full size table
Fig. 7
figure 7

Variation of lateral buckling parameter of pinned–fixed I-beam under gradient moment, versus end tapering ratio (α) and the gradient index (m): a top flange loading, b centroid loading, c bottom flange loading

Full size image

Figure 7 and Table 3 show that the variation of non-uniformity parameters has a remarkable influence on the lateral stability resistance of double-tapered beams subjected to pinned–fixed end conditions. It is also observed that the non-dimensional lateral buckling loads increase with the increase in the gradient index as expected because of the increase in the value of elasticity modulus and the value of flexural and torsion rigidities of the beam. In other words, the beam becomes stiffer and more stable by raising the power-law exponent (m).

By comparing the numerical outcomes presented in Table 3 and Fig. 7, it can be stated that the location of the applied load from the centroidal point of the cross section directly affects the lateral–torsional buckling capacity of the considered beam. For example, the non-dimensional lateral buckling parameter of homogenous prismatic member increases from 4.9136 to 6.7453 and then to 9.2043, when the load location is changed from top flange to shear center then bottom flange. It shows an increase by 37.28% and 36.46%, accordingly. In other words, the numerical outcomes reveal that the bottom flange loading enhances the stability characteristics of pinned–fixed beams with constant or variable cross section owing to the reduction the rotation of bi-symmetric I-section from its original.

4.3 Example 3: Lateral–Torsional Buckling of Simply Supported Web-Tapered Beam Under Gradient Moment

This example represents the linear buckling moments of simply supported web-tapered and prismatic thin-walled beams under bending moment gradient (M0, ψM0). The gradient moment factor (ψ) varies from + 1 to − 1. In the case of web-tapered beam, the web height is made to decrease linearly from (d0) at the left support to the (d1 =  α d0) at the right one, while the flanges’ width remains constant along the member’s length. In this example, tapering ratio α of web-tapered beams is varied from 0.1 to 1. The non-dimensional geometrical data of the considered beam are pictured in Fig. 8.

Fig. 8
figure 8

Simply supported tapered axially functionally graded beam under moment gradient: geometry properties

Full size image

In the first part of the current example, for homogenous beam with constant I-section (α = 1.0) and web-tapered one (α  = 0.4), the lowest buckling moment parameter (\(\overline{M}_{{\rm cr}}\)) variation versus the gradient moment factor (ψ) is shown in Fig. 9. After observing the results illustrated in Fig. 9a related to prismatic I-beam subjected to gradient moment, it can be concluded that there is an excellent agreement between the buckling moments calculated by proposed finite element formulation and those estimated by the semi-analytical technique based on the power series method suggested by Asgarian et al. (2013). In this loading condition, the relative difference between the proposed numerical approach and the benchmark is less than 1%. Besides, the maximum strength is reached when ψ=− 0.8 for the prismatic beam. These results are confirmed by Mohri et al. (2013).

Fig. 9
figure 9

Variation of buckling moment parameter of homogenous beam with doubly symmetric I-section under gradient moment, versus the gradient factor ψ: a prismatic beam (α = 1), b tapered beam (α = 0.4)

Full size image

For the beam with tapered I-section (α = 0.4), the critical buckling moment variation with ψ is depicted in Fig. 9b. It can be stated that under positive and negative gradient factors, the outcomes of proposed finite element method concord very well with the power series methodology (Asgarian et al. 2013). It is important to note that the buckling moments carried out from present numerical study underestimate beam strength (1% error). In the case of web-tapered beam with doubly symmetric I-section, the maximum lateral buckling capacity is achieved for ψ = − 0.8.

After validating the current technique, the variation of non-dimensional buckling moment versus the tapering ratio (α) and the gradient factor (ψ) is presented in Fig. 10 for first lateral–torsional buckling mode. According to Fig. 10 and for both uniform and web-tapered beams with I-section under variable bending moment, nonlinear variation of lateral buckling resistance of beam with gradient factor (ψ) is noticed. As shown in Fig. 10, for any value of end moment ratio the lateral stability strength of prismatic beam (α = 1) and tapered beam with α = 0.1 is most and least, respectively. This can be explained by the fact that a decrease in tapering ratio causes the reduction in torsion and bending rigidities. In other words, the beam becomes weaker and more unstable as the tapering ratio diminishes. It is also evident that for different non-uniformity parameters, the highest lateral–torsional strength is obtained about \(- 0.8 \le \psi \le - \,0.7\).

Fig. 10
figure 10

Variation of buckling moment parameters of simply supports tapered I-beam under gradient moment, versus end moment gradient factor (ψ) and tapering ratio (α)

Full size image

In this example, it is assumed that the Young’s modulus of elasticity varies continuously in the longitudinal direction according to an exponential function (E-FGM) of the volume fractions of the constituent materials, while the Poisson’s ratio is supposed to equal 0.3 along the beam axis:

$$E(x) = E_{0} e^{{\frac{\lambda x}{L}}} ;\quad \lambda = \ln \left( {\frac{{E_{1} }}{{E_{0} }}} \right)$$
(30a, b)

E0 and E1 represent values of Young’s modulus of the constituent materials. Note that E0 is root elastic modulus. λ signifies a dimensionless parameter defining the gradual variation of the material property along the longitudinal direction. In the case of an isotropic and homogenous material equals zero. The above expression is adopted in several papers (Suresh 2001; Aydogdu and Taskin 2007; Arshad et al. 2007; Atmane et al. 2011; Mohanty et al. 2012; Li et al. 2013, 2018; Şimşek 2015; Wang et al. 2016; Deng and Cheng 2016; Khaniki and Rajasekaran 2018; Soltani et al. 2019).

Afterward, the lowest buckling moment parameters (\(\overline{M}_{{\rm cr}}\)) for two different non-uniformity ratios (α = 1, 0.5), various gradient factors (ψ) with different material parameters (λ) are arranged in Table 4. Subsequently, for three different tapering ratios (α = 1, 0.7 and 0.4), Fig. 11 presents the impact of end moment gradient parameter (ψ) on variation of critical buckling moment of contemplated E-FG tapered I-beam with respect to gradient parameter (λ). Moreover, Fig. 12 illustrates the variation of buckling moments of E-FG web-tapered beam with respect to the tapering ratio (α) and the gradient parameter (λ) for pinned–pinned member subjected to end moment with two different moment gradient factors (ψ = − 1 and 1).

Table 4 Non-dimensional critical moment (\(\overline{M}_{{\rm cr}}\)) for exponentially FG web-tapered I-beam with different material non-homogeneity parameters (λ) and subjected to end moment
Full size table
Fig. 11
figure 11

Variation of dimensionless lateral buckling moment of simply supports I-beam under gradient moment, versus end moment gradient factor (ψ) and the gradient parameter (λ) a uniform beam (α = 1), b tapered beam (α = 0.7), c tapered beam (α =  0.4)

Full size image
Fig. 12
figure 12

Effects of the gradient parameter () on dimensionless lateral–torsional buckling moment (\(\overline{M}_{{\rm cr}}\)) of simply supported tapered I-beam with different tapering ratios subjected to end moment: a ψ = 1, b ψ = − 1

Full size image

As given in Table 3 and Figs. 11 and 12, for any value of gradient parameters (λ) and end moment ratio (ψ) the corresponding normalized buckling moment for the beam having constant cross section is the highest and that for tapered beam with the tapering ratio (0.1) is the lowest. Moreover, Figs. 11 and 12 show that the variation of non-homogeneity parameter has a significant influence on the lateral–torsional stability behavior of simply supported web-tapered beams under different circumstances. It can be also stated that the critical buckling moment parameters relating to the first mode are increased as the gradient parameter increases from − 1 to + 1. This statement is reasonable due to the fact that modulus of elasticity rises as the value of inhomogeneous constant increases over zero (λ > 0), and the gradient parameter under zero (λ < 0) indicates a decrease in Young’s moduli (see Eq. (30)).

In the following, comparison studies between the buckling resistance of ceramic–metal and metal–ceramic FG tapered beam having properties according to the power law with different gradient indexes and exponential law are carried out and presented in Fig. 13. In this regard, we have determined the first non-dimensional buckling moment for web-tapered beams, where in calculations ψ = 0 is chosen. Figure 13a reveals the influence of tapering ratio (α) on the critical moment of ceramic–metal FG beam with zirconia root and having properties corresponding to power law with indexes m = 1, 2 and 3 (Eq. (29)) as well as exponential law (Eq. (30)). The outcomes relating to homogenous beam are also plotted in this figure. It should be pointed out that the non-dimensional results are the same for pure ZrO2 and aluminum beams. Compared to Al, ZrO2 has superior mechanical properties. The material property distributions in AFG I-beam as power law with \(m \ge 1\) and exponential law make the volume fraction of ceramic in the longitudinal direction of beam highest and lowest, respectively. In other words, power-law distribution of properties makes the beam richer in ceramic content. Regarding this, the contemplated E-FGM beam has the lowest volume fraction of zirconia, and consequently, a weaker and more flexible member compared to a beam having properties according to power law is achieved. Since the lateral buckling resistance of beam is proportional to the stiffness of the members, it is evident from this illustration that the critical moment corresponding to any value of tapering ratios is the lowest for beam with exponential volume fraction law and highest for the homogenous beam from ceramic (ZrO2). Accordingly, the buckling moment of beam having properties corresponding to simple power law with three different power-law exponents (m = 1, 2, 3) is between the above-mentioned cases. In this case, the lateral buckling resistance is higher for higher value of volume fraction indexes.

Fig. 13
figure 13

Variation of dimensionless buckling moment with tapering parameter of beam with varying I-section: a metal–ceramic FG tapered I-beam with zirconia root, b ceramic–metal FG tapered I-beam with aluminum root

Full size image

The variation of the lowest normalized buckling moments for metal–ceramic tapered I-beams with aluminum root versus tapering parameters (α) is plotted in Fig. 13b, for simply supported beams having properties corresponding to power law with indexes m = 1, 2 and 3 (Eq. (29)) as well as exponential law (Eq. (30)). The critical buckling moments increase substantially with the increase in non-uniformity constant from 0.1 to 1, for both types of property distribution similar to the results of beam with zirconia root (Fig. 13a). In contrast to ceramic–metal FG beam, the non-dimensional critical moment of metal–ceramic member with aluminum root diminishes when the power-law index (m) is increased from 1 to 3. This phenomenon can be explained by the fact that the percentage content of aluminum increases over the beam axis and compared to zirconia, this component has got lower shear and Young's modulus, and as a result, more flexible beam is acquired. As reflected in this figure, the homogenous beam from aluminum and FG beam with properties corresponding to polynomial volume fraction law with m = 1 has the dimensionless critical moment with the smallest and largest values, respectively. Moreover, the presented outcomes also reveal that FG tapered I-beam with Al root with properties corresponding to power law with m = 2, m = 3 and exponential volume fraction law have intermediate stability.

5 Conclusions

In this study, lateral–torsional stability analysis of axially functionally graded beam with tapered doubly symmetric section under different boundary conditions is carried out via a new finite element model. For this purpose, a two-node element with two degrees of freedom, namely the twist angle and the rate of twist, at each node is introduced. The usual 8 * 8 elastic and lateral buckling stiffness matrices for beam with bi-symmetric I-section are thus condensed to 4 * 4 ones. In this regard, a fourth-order differential equation in terms of twist angle is obtained by uncoupling the system of equilibrium equations governing lateral stability behavior of non-prismatic thin-walled beam made up of isotropic functionally graded materials. Afterward, the element stiffness matrices including the elastic and buckling ones for linear stability analysis of AFG web and/or flanges tapered I-beam are derived by formulating the weak statement of the resulting equilibrium equation and using cubic Hermitian polynomials. It should be pointed out that the terms of structural and buckling stiffness matrices are determined by considering the influence of material gradient, varying cross section and applied load. It is also important to note that this numerical approach does not give the quadratic functional form due to the presence of a non-symmetric bi-linear term in the weak form. The impact of web and/or flanges tapering ratios, axial variation of mechanical properties, end conditions, load height parameter and end moment gradient factor on lateral buckling resistance of AFG tapered I-beam is comprehensively surveyed. It can be stated that the effects of linear variation in the cross section and axial inhomogeneity in material characteristics play important roles on the linear lateral stability capacity of AFG tapered beam. The numerical outcomes of this paper can serve as a benchmark for future studies for the determination of lateral–torsional buckling of axially functionally graded beams with varying doubly symmetric cross section and subjected to arbitrary load and various boundary conditions.