Determination of the Dynamic Characteristics of Frame Structures with Non-uniform Shear Stiffness

Abstract

Structures consisting of frames can be considered as shear structures under certain assumptions. The frame can be idealized as an equivalent shear beam in this case. In this study, the dynamic characteristics of non-uniform frames were investigated. For this purpose, the method of differential transform was used to solve the governing differential equation of the equivalent shear beam. This shear beam represented the structure of which shear stiffness varies along the height. In this study, the contribution of the axial deformation was taken into account with the help of equivalent shear stiffness. The least squares method was used in order to determine the parameter that defines the change of the shear stiffness. Thus, the dynamic characteristics were determined more realistically. Tables were prepared for use for the determination of the dynamic characteristics of frame structures with non-uniform shear stiffness. Response spectrum analysis can be easily conducted using these tables. The suitability of the approach was investigated through examples at the end part of the study. The suggested method could be used safely during the preliminary design stage. It is particularly easy to understand the structural behavior due to the usage of fewer parameters.

1 Introduction

Frame bearing systems are widely used in low-rise structures. An approach used in the analysis of structures under static and dynamic loads is the modeling of the structure as an equivalent cantilever beam. There are various models used for this, such as a shear beam, bending beam, Csonka’s beam, and sandwich beam. The literature contains important studies in this regard. The Following are some of the most significant of these studies: Heidebrecht and Stafford Smith (1973), Zalka (2001a), Potzta and Kollár (2003), Rahgozar et al. (2004), Kaviani et al. (2008) and Hoenderkamp (2001).

Frame-type structures, of which axial deformations may be neglected, are considered as shear structures under some assumptions. In this case, the structure may be considered as an equivalent shear beam. A set of studies have taken place in the literature on modeling and analyzing frames as continuous shear beams.

Baikov and Sigalov (1981) investigated the free vibration analysis of uniform frames of which axial deformations can be neglected. They based their solution on the shear beam’s differential equation.

Ertutar (1987) achieved the static analysis of frames of which structural properties change along the height of the structure, using the shear beam’s differential equation. In the study, the case of an exponential change in the shear stiffness along the height of the structure was investigated.

Li (2000) proposed a method for the free vibration analysis of shear beams of which mass and shear stiffness change along the length. In the presented method, the governing equation of the shear beam in case of free vibration was used. The solution of the differential equation was achieved with the help of Bessel equations. In the study, the changes in the mass and shear stiffness along the length of the beam were investigated for six different cases in the forms of exponential and polynomial.

Gulkan and Akkar (2002) suggested a practical equation to obtain drift spectrums. Dynamic behavior of the shear beam was taken as a basis to obtain the equation.

Rafezy et al. (2007) used the dynamic stiffness method to find the angular frequencies of asymmetrical structures of which bearing system consisting of frames and structural properties change along the height.

Kuang and Ng (2009) suggested an analytical method to determine the angular frequencies of asymmetrical frames of which structural properties do not change along the height. The structure in the study was modeled as an equivalent shear beam with St. Venant torsion.

Bozdogan and Ozturk (2010) suggested the Transfer Matrix Method for the dynamic analysis of asymmetrical structures that consist of frames. In the method, the analysis was achieved by the solution of a 6 × 6 matrix. The structure was modeled as an equivalent shear torsion beam. The method presented in the study could be used for the solution of structures of which the structural properties change along the height.

Zhang et al. (2013) investigated the shear beam-column systems to which axial load and elastically mass was applied.

Rodriguez and Miranda (2014) investigated the dynamic characteristics of cantilever shear beams with the uniform mass distribution of which lateral stiffness decreases along the length parabolically. Legendre polynomials were used in the study to solve the governing equation of the cantilever beam.

Tekeli et al. (2015) suggested a method to determine the ratios of displacement and inter-story drift ratio of uniform frames for the cases of loads that are distributed triangularly, uniformly, and point load applied on any level on the height of the structure. The frame system was modeled as an equivalent shear beam in the study.

Saffari and Mohammadnejad (2015) applied the weak form integral equations to the solution of non-prismatic shear, Timoshenko and Euler–Bernoulli beams and therefore got the period, modes and internal forces of high rise structures.

Hassan and Hadima (2015) applied Recursive Differentiation Method for static, dynamic and stability analysis of non-uniform beams resting on the elastic foundations.

Piccardo et al. (2015) developed an equivalent shear-St. Venant beam model for aeroelastic analysis of tower-type structures.

In this study, a practical method for the Response spectrum analysis of frame-type structures of which the shear stiffness changes along the height, was proposed. For this purpose, the dynamic parameters obtained by the solution of Differential Transform Method and the tables were prepared. With the proposed method, Response spectrum analysis can practically be done with the help of these tables. Differently, from the literature, the method does not require any software-code for the solution. In addition, the effect of axial deformations, which are particularly important in high and narrow structures, was taken into account in the study. Using the least squares method, a formula was developed to determine the change of the shear stiffness along the height of the structure.

The assumptions in the study are as the following:

• a. The material is linearly elastic,

• b. Geometric non-linear effects are ignored, therefore the first order theory is assumed,

• c. Mass of the structure is uniform along the height of the structure,

• d. Axial deformations of the beams and local bending deformation of columns are neglected,

• e. Torsion effects are neglected.

2 Physical and Mathematical Model of Presented Method

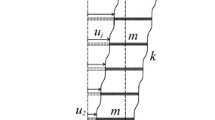
The multi-span planar frame can be represented as an equivalent shear beam as seen in Fig. 1, if axial deformations and local bending deformation are neglected.

Fig. 1

Modelling the frame system as an equivalent shear beam

Shear stiffness at the bottom of the equivalent shear beam is GA(O), while it is GA(H) at the top. H presents the height of the structure.

Different equations have been developed in the literature to determine the shear stiffness (Hosseini and Imagh-e-Naiini 1999; Caterino et al. 2013).

In this study, the following equations are used to determine the shear stiffness.

The equivalent shear stiffness of GA is calculated using the following equation for the first storey (Taranath 2010):

$${\text{GA}}_{1} = \frac{8}{{h\left( {\frac{1}{s} + \frac{1}{5*r}} \right)}}$$

(1)

For the other storeys, it is calculated by the following equation with the assumption that the bending moment is equal to zero at the midpoints of the columns and beams (Baikov and Sigalov 1981):

$${\text{GA}}_{i} = \frac{12}{{h\left( {\frac{1}{s} + \frac{1}{r}} \right)}}$$

(2)

here s and r are total rigidity values of the columns and beams respectively, and they are calculated with the equations below:

$$s = \sum\limits_{i = 1}^{e} {\frac{{EI_{ci} }}{h}}$$

(3)

$$r = \sum\limits_{i = 1}^{g} {\frac{{EI_{bi} }}{{l_{i} }}}$$

(4)

here E is the modulus of elasticity, I_ci is the moment of inertia of the ith column, e is the number of columns in the related storey, h is the height of the storey, I_bi is the moment of inertia of the ith beam, g is the number of beams in the related storey, and l_i is the length of the ith beam.

Especially in high-rise structures, the importance of axial deformations is increasing. Zalka (2001a) suggested an effective shear stiffness equation by taking account of axial deformations. The formula proposed by Zalka was only considering the first mode. In this study, the formula was developed by taking into account of four modes. For ith mode, the effective shear stiffness can be calculated as

$$({\text{GA}})_{\text{efi}} = \frac{{f_{\text{axi}}^{2} }}{{f_{\text{axi}}^{2} + f_{si}^{2} }}({\text{GA}})_{i} \quad \;i = 1,2,3,4$$

(5)

$$f_{si}^{2} = \frac{{({\text{GA}})_{i} (2*i - 1)^{2} }}{{(4H)^{2} \mathop m\limits^{ - } }}\quad \;i = 1,2,3,4$$

(6)

$$f_{\text{axi}}^{2} = \frac{{b_{i} D_{i} }}{{\mathop m\limits^{ - } H^{4} }}\quad \;(b_{1} = 0.313,\,b_{2} = 12.311,\,b_{3} = 96.117,\,b_{4} = 369.822)$$

(7)

where D_i is the global bending stiffness of ith story and can be calculated as below (Zalka 2001a, b; Potzta and Kollár 2003):

$$D_{i} = \sum\limits_{j = 1}^{m} {EA_{ji} d_{j} }^{2}$$

(8)

where A_ji is the area of the jth column in the ith story and d_j is the distance of jth column from the centroid of cross-section.

The change in the equivalent shear stiffness of the equivalent shear beam presenting the structure is taken as it is described in the literature (Rodriguez and Miranda 2014):

$${\text{GA}}_{\text{efi}} (z) = {\text{GA}}_{\text{efi}} (0)\left[ {1 - (1 - \delta_{i} )\frac{{z^{2} }}{{H^{2} }}} \right]$$

(9)

In this study, we obtained the following equation using the least squares method to determine the δ coefficient.

$$\delta_{i} = 1 - \frac{{H^{2} \sum\limits_{j = 1}^{n} {\left[ [{{\text{GA}}_{\text{efi}} (0)]^{2} *z_{j}^{2} - {\text{GA}}_{efi} (0)*GA_{\text{ef}} (z_{j} )z_{j}^{2} } \right]} }}{{\sum\limits_{j = 1}^{n} {\left[ [{{\text{GA}}_{\text{efi}} (0)]^{2}*z_{j}^{4} } \right]} }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i = 1,2,3,4$$

(10)

Using K_0i instead of GA_ef(0) from here on:

$$K_{0i} = {\text{GA}}_{\text{efi}} (0)$$

(11)

The differential equation of the equivalent shear beam in the case of free vibration is written as the following (Rodriguez and Miranda 2014, 2016):

$$\frac{\partial }{\partial z}\left[ {{\text{GA}}_{\text{efi}} (z)\frac{\partial u}{\partial z}} \right] - \mathop m\limits^{ - } \frac{{\partial^{2} u}}{{\partial t^{2} }} = 0$$

(12)

here $\mathop m\limits^{ - }$ shows the mass distributed along the height of the structure.

The partial differential Eq. (8) can be separated into its variables based on time and position like the following:

$$u(z,t) = y(z)q(t)$$

(13)

If the Eq. (13) is placed into the Eq. (12), the ordinary differential Eqs. (14) and (15) are obtained:

$$\frac{{{\text{d}}^{2} q}}{{{\text{d}}t^{2} }} + \omega_{i}^{2} q = 0$$

(14)

$$\frac{\text{d}}{{{\text{d}}z}}\left[ {{\text{GA}}_{\text{efi}} (z)\frac{{{\text{d}}y}}{{{\text{d}}z}}} \right] + \omega_{i}^{2} \mathop m\limits^{ - } y = 0$$

(15)

here ω_i represents the angular frequency.

If GA_efi(z) in the Eq. (9) is placed into the Eq. (15), the Eq. (16) is obtained:

$$K_{0i} \left[ {1 - (1 - \delta_{i} )\frac{{z^{2} }}{{H^{2} }}} \right]\frac{{{\text{d}}^{2} y}}{{{\text{d}}z^{2} }} - 2K_{0i} \frac{{(1 - \delta_{i} )}}{{H^{2} }}z\frac{{{\text{d}}y}}{{{\text{d}}z}} + \omega_{i}^{2} \mathop m\limits^{ - } y = 0$$

(16)

Displacement at the bottom and the shear force at the top of the equivalent shear beam are zero. In this case, the boundary conditions are defined with the Eqs. (17) and (18).

$$z = 0\quad \quad y = 0$$

(17)

$$z = H\quad \quad K_{0i} \delta_{i} \frac{{{\text{d}}y}}{{{\text{d}}z}} = 0$$

(18)

The transformation in Eq. (19) is used to make the given equations dimensionless.

$$\varepsilon = \frac{z}{H}$$

(19)

Applying the transformation (19), into the Eq. (16) results in the Eq. (20).

$$K_{0i} \left[ {1 - (1 - \delta_{i} )\varepsilon^{2} } \right]\frac{{{\text{d}}^{2} y}}{{{\text{d}}\varepsilon^{2} }} - 2K_{0i} (1 - \delta_{i} )\varepsilon \frac{{{\text{d}}y}}{{{\text{d}}\varepsilon }} + \omega_{i}^{2} \mathop m\limits^{ - } H^{2} y = 0$$

(20)

If both sides of the Eq. (20) are divided by K₀, the differential Eq. (21) is obtained:

$$\left[ {1 - (1 - \delta_{i} )\varepsilon^{2} } \right]\frac{{{\text{d}}^{2} y}}{{{\text{d}}\varepsilon^{2} }} - 2(1 - \delta_{i} )\varepsilon \frac{{{\text{d}}y}}{{{\text{d}}\varepsilon }} + \frac{{\omega_{i}^{2} \mathop m\limits^{ - } H^{2} }}{{K_{0i} }}y = 0$$

(21)

A shortened version of the Eq. (21) may be shown as the Eq. (22).

$$\left[ {1 - (1 - \delta_{i} )\varepsilon^{2} } \right]\frac{{{\text{d}}^{2} y}}{{{\text{d}}\varepsilon^{2} }} - 2(1 - \delta_{i} )\varepsilon \frac{{{\text{d}}y}}{{{\text{d}}\varepsilon }} + a_{i}^{2} y = 0$$

(22)

Here, the value of a is defined as the following for shortened representation of the equation.

$$a_{i}^{2} = \frac{{\omega_{i}^{2} \mathop m\limits^{ - } H^{2} }}{{K_{0i} }}$$

(23)

Similarly, if the transformation (19) is placed into the Eqs. (17) and (18), Eq. (24) and (25) are obtained.

$$\varepsilon = 0\quad \quad y = 0$$

(24)

$$\varepsilon = 1\quad \quad \frac{{K_{0i} \delta_{i} }}{H}\frac{{{\text{d}}y}}{{{\text{d}}\varepsilon }} = 0$$

(25)

The only solution of the Eq. (22) is the series solution.

3 A Solution of the Equation with Differential Transform Method

Differential Transform Method is a practical method used in the solution of differential equations (Kaya and Ozdemir Ozgumus 2010; Attarnejad et al. 2010). The differential transformation method has advantages such as simple applicability, computational efficiency, and high accuracy (Ahmad et al. 2015).

The differential transformation of function y can be defined as the following (Rajasekaran 2009):

$$Y[k] = \frac{1}{k!}\left[ {\frac{{{\text{d}}^{k} y(\varepsilon )}}{{{\text{d}}\varepsilon^{k} }}} \right]_{\varepsilon = 0} \quad \quad 0 \le \varepsilon \le 1$$

(26)

$$y(\varepsilon ) = \sum\limits_{k = 0}^{\infty } {\varepsilon^{k} } Y[k]$$

(27)

$$y(\varepsilon ) = \sum\limits_{k = 0}^{\infty } {\frac{{\varepsilon^{k} }}{k!}} \left[ {\frac{{{\text{d}}^{k} y(\varepsilon )}}{{{\text{d}}\varepsilon^{k} }}} \right]_{\varepsilon = 0}$$

(28)

From the equations given above, the differential transform equation can be shown practically by using the following arithmetic equation:

$$DT(\varepsilon^{\alpha } y^{\beta } ) = \left[ {\mathop \prod \limits_{i = 1}^{\beta } (k - \alpha + i)} \right]Y(k - \alpha + \beta )$$

(29)

here y^β shows the derivative as the following:

$$y^{\beta } = \frac{{{\text{d}}^{\beta } y}}{{{\text{d}}\varepsilon^{\beta } }}$$

(30)

Applying the transformation Eq. (29) in the Eq. (22) results in Eq. (31).

$$Y[k + 2] = \frac{{[(1 - \delta_{i} )(k - 1)k + 2(1 - \delta_{i} )k - a_{i}^{2} ]}}{(k + 1)(k + 2)}Y[k]$$

(31)

Applying differential transformation into the boundary conditions in Eqs. (24) and (25), results in Eqs. (32) and (33):

$$Y[0] = 0$$

(32)

$$\sum\limits_{i = 1}^{n} {iY[i]}=0$$

(33)

Taking Y[1] as unknown, showing the other coefficients in relation to Y[1] with the help of (31), and placing these into the Eq. (33) result in the following:

$$z(a_{i} )Y[1] = 0$$

(34)

In order to obtain a non-zero solution in the Eq. (34), a values are obtained from the solution of the Eq. (35).

$$z(a_{i} ) = 0$$

(35)

Using the a values and the Eq. (23), the ω values are found with the help of the Eq. (36) as the following:

$$\omega_{i} = a_{i} \sqrt {\frac{{K_{0i} }}{{\mathop m\limits^{ - } H^{2} }}}$$

(36)

In dynamic analysis, there is some difference between the results of the distributed model and the lumped mass model. In order to overcome this discrepancy, Zalka (2001a, b) proposed a coefficient of correction for the wall-frame systems. We developed this coefficient for frame-type structures.

In this case, the Eq. (36) is written as follows:

$$\omega_{i} = a_{i} r_{fi} \sqrt {\frac{{K_{0i} }}{{\mathop m\limits^{ - } H^{2} }}}$$

(37)

The coefficients of correction are calculated for the first four modes using the model shown in Fig. 2 and SAP2000 (2018) and are given in Table 1.

Fig. 2

Continuum and lumped mass models

Table 1 r_fi values for the first four modes

In the table n is the story number.

For the first four modes, a values are computed for different δ values and presented in Table 2.

Table 2 a_i values for the first four modes for different δ values

It can be seen from Table 2 that when δ = 0.01 situation is compared with δ = 1 which is the uniform shear stiffness case, the first natural vibration period value increases by 1.108 times. This increase is 1.345 for the second mode, 1.408 for the third mode and 1.435 for the fourth mode.

This change is graphically shown in Fig. 3.

Fig. 3

The change of natural period depending on δ values

If the a_i values found for each mode are written into the Eq. (31), the Y[k] values are obtained.

After finding the Y[k] values, y mode shapes for the ith mode are found using the Eq. (27).

4 Obtaining the Dynamic Characteristics

The parameters required for the spectral analysis can be found by the modal analysis. Using the y mode shapes, the effective mass is found using the following equation (Chopra 2016):

$$M_{i}^{*} = \frac{{\left[ {\sum\nolimits_{j = 1}^{n} {m_{j} *y_{ji} } } \right]^{2} }}{{\sum\nolimits_{j = 1}^{n} {m_{j} *y_{ji}^{2} } }}$$

(38)

The effective mass ratio is found using the ratio of the effective mass found with the Eq. (38) to the total mass of the structure. Table 3 shows the effective mass ratios for different values of δ. It is seen from Table 2, the variation in shear stiffness has little effect on effective mass ratios.

Table 3 The effective mass ratios for the first three modes for δ

Bottom shear force for the ith mode is calculated using the following equation:

$$V_{Ti} = M_{i}^{*} *S_{pa} (T_{i} )$$

(39)

here S_pa(T_i) shows the spectral acceleration for the ith mode.

Spectral acceleration ordinates corresponding to the periods are found from the acceleration spectrum obtained from the earthquake data or design spectrum.

The displacement of the top point of the non-uniform frame is calculated using the following equation for the ith mode:

$$d_{\hbox{max} i} = df_{i} *\frac{{S_{pa} (T_{i} )}}{{\omega_{i}^{2} }}$$

(40)

here df_i is the top point displacement coefficient and it is calculated using the following equation:

$$df_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {m_{j} *y_{ji} } }}{{\sum\nolimits_{j = 1}^{n} {m_{j} *y_{ji}^{2} } }}*y_{ni}$$

(41)

df_i values for different δ values are calculated for the first four modes and given in Table 4.

Table 4 df_i values for different δ values for the first four modes

The maximum value of the inter-story drift ratio occurs at the base of the structure due to the assumption of the shear beam and is calculated using the following equation:

$$Idr_{i} = \lambda_{i} *\frac{{S_{pa} (T_{i} )}}{{H*\omega_{i}^{2} }}$$

(42)

Table 5 shows the λ_i values for different δ values calculated for the first four modes.

Table 5 The λ_i values for different δ values for the first four modes

The values given in Table 5 show the inter-story drift ratio coefficients for the first four modes, at the position where the inter-story drift ratio is maximum for the first mode. In the high rise frames the maximum value of the inter-story drift ratio may occur in the middle stories, but considering the shear beam model it is assumed to occur at the base of the structure.

5 Response Spectrum Analysis

Response spectrum analysis can be conducted by utilizing an elastic spectrum created for certain earthquake data or design spectrums in earthquake codes. Steps for the process of the Response spectrum analysis are given below:

• GA values are computed using the Eqs. (1) and (2).

• For the first four modes, the effective shear stiffness involving the contribution of the axial deformations are calculated using Eqs. (5), (6) and (7).

• The values of δ, which show the change in shear stiffness, are calculated using Eq. (10) for the first four modes.

• Angular frequencies and periods for the first four modes are found for δ values, using Table 2 and the Eq. (37).

• Spectral acceleration ordinates corresponding to the periods are found from the acceleration spectrum obtained from the earthquake data or design spectrum.

• Dynamic coefficients are found from Tables 3, 4 and 5 for δ values for the first four modes.

• Base shear force for the ith mode is found by using the Eq. (39).

• The top point displacement for the ith mode is found by using the Eq. (40).

• The maximum inter-story drift value for the ith mode is found by using the Eq. (42).

• For each mode, the values (base shear force, top point displacement, maximum inter-story drift ratio) are found and combined by the rules of the method of the square root of the sum of the squares.

6 Numerical Examples

In this section, in order to show the suitability of the method, four examples were solved using the proposed method and the results were compared with the literature and the finite element method.

6.1 Example 1

In this example, the SAC 20 building of which the properties were used according to the literature (Rodriguez and Miranda 2014) was investigated. The δ value for the SAC 20 was taken as 0.34 as given in the literature. The ratios of the second and the third periods of this building to its first period were found with the method presented in this study and the results were compared with the literature in Table 6.

Table 6 Comparison of period ratios for Example 1

Table 6 shows that the proposed method provides results that are in accordance with the literature.

6.2 Example 2

The 9-story planar frame in Fig. 4 was investigated according to the Turkish Earthquake Code 2007, thus the local site class was taken as Z4, the seismic zone was second and the building that was designed as a residence. Column dimensions of the frame were shown in Table 7. The modulus of elasticity was E = 3 * 10⁷ kN/m², and all beams were in dimensions of 0.25 m/0.50 m. Story masses were taken as 15 t. Shear and global bending stiffness were given in Table 8. Calculated δ values were given in Table 9.

Fig. 4

9-storey planar frame

Table 7 Column sizes for Example 2

Table 8 Shear stiffness and global bending stiffness for Example 2

Table 9 The δ values for Example 2

Response spectrum analysis of the frame was conducted using the presented method, and the results were compared with the results obtained by using the SAP2000 (2018) package software.

The values of the periods for the first four modes were calculated using the method presented in this study, and compared with results of SAP2000 (2018) in Table 10.

Table 10 Comparison of the periods of the first four modes (Example 2)

Base shear force, top point displacement and maximum inter-story drift ratio were calculated and compared with SAP2000 (2018) results in Table 11.

Table 11 Base shear force, top point displacement and inter-story drift ratio comparison (Example 2)

As it was seen in Tables 10 and 11, the results obtained with the presented method were close to those of SAP2000 (2018).

6.3 Example 3

In this example, the Response spectrum analysis for the x-direction of a 12-story building in Fig. 5, was conducted by the presented method. Then the appropriateness of the method to the ETABS (2017) was investigated.

Fig. 5

The plan of 12 storey building

The height of the first story of the building was 4 m and the others were 3 m. The mass of the story was taken as 380 tons for the first 11 stories and 280 tons for the last story. The modulus of elasticity was E = 3.2 * 10⁷ kN/m² and the column and beam dimensions were presented in Table 12.

Table 12 Column and beam sizes for Example 3

The Response spectrum analysis was made according to the Turkish Earthquake Code 2007 and the building was built on the first seismic zone and on the Z2 soil class. The building importance factor was 1 and the structural behavior factor was 8.

The shear and global bending stiffness of the 12-story building were calculated and presented in Table 13.

Table 13 Shear and global bending stiffness values (Example 3)

The δ values calculated for the first four modes were given in Table 14.

Table 14 The δ values for Example 3

The same example was solved using ETABS (2017) and the results were compared in Tables 15 and 16. As it can be seen from the tables, the results obtained were suited for the preliminary design stage.

Table 15 Comparison of the periods of the first four modes (Example 3)

Table 16 Base shear force, top point displacement and drift comparison (Example 3)

6.4 Example 4

Moment-resisting steel frame in Fig. 6 was taken from the literature (Wong 2013) for the example. The periods were solved by the method presented in this study, and the results were compared. The column and beam dimensions of the six-story steel frame were given in Table 17.

Fig. 6

Moment-resisting steel frame

Table 17 Column and beam sizes for Example 4

The mass of each story was taken as 200. Shear stiffness and global bending stiffness values of the frame were calculated and given in Table 18.

Table 18 Shear and global bending stiffness values (Example 4)

The δ values were calculated and given in Table 19.

Table 19 The δ values for Example 4

Natural periods were calculated by the presented method and compared with the results obtained by the literature and SAP2000 (2018) in Table 20

Table 20 Comparison of the periods of the first four modes (Example 4)

7 Conclusion

In this study, a method was proposed for the dynamic analysis of frames of which shear stiffness changes non-uniformly along the height of the structure. The frame was modeled as an equivalent shear beam and the dynamic characteristics of the equivalent shear beam were determined with the Differential Transform Method. Therefore, a practical and fast method was proposed for the Response spectrum analysis by using tables. At the end of the study, four numerical examples were solved and the suitability of the method was analyzed. The results from the examples confirmed that the suggested method provides adequately suitable results fast and practically, thus it can be used safely in the stage of preliminary design. Moreover, the presented method provides a better understanding of structural behavior with a few parameters.