Estimating Discharge Coefficient of PK-Weir Under Subcritical Conditions Based on High-Accuracy Machine Learning Approaches

Abstract

This article adopts four high-accuracy machine learning-based approaches for the prediction of discharge coefficient of a Piano Key Weir (PK-weir) under subcritical condition located on the straight open-channel flume. These approaches consist of least-square support vector machine (LS-SVM), extreme learning machine (ELM), Bayesian ELM (BELM), and logistic regression (LR). For this purpose, 70 laboratory test results are used for determining discharge coefficient of PK-weir for a wide range of discharge values. Root-mean-squared error (RMSE), Nash–Sutcliffe model efficiency coefficient (NSE), the coefficient of correlation (R), threshold statistics (TS), and scatter index (SI) are used for comparing the performance of the models. The simulation results indicate that an improvement in predictive accuracy could be achieved by the ELM approach in comparison with LS-SVM and LR (RMSE of 0.016 and NSE of 0.986), while the BELM model’s generalization capacity enhanced, with RMSE of 0.011 and NSE of 0.989 in validation dataset. The results show that BELM is a simple and efficient algorithm which exhibits good performance; hence, it can be recommended for estimating discharge coefficient.

1 Introduction

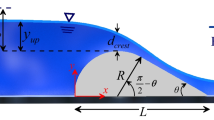
With rising demands for more reservoir water storage, increasing magnitudes of probable maximum flood (PMF) events, and the continuing need to improve dam safety, the capacities of many existing spillways are currently inadequate and in need of upgrade or replacement. Typically, reservoir spillways use weirs, gated or non-gated, as the flow control structure (Anderson and Tullis 2013). Piano key weir (abbreviated PK-weir) is a particular type of labyrinth weir which has been developed in the recent years as an alternative to the standard types. Figure 1 shows a longitudinal section and plan of a piano key weir for subcritical flow. As shown in Fig. 1, the PK-weir has a rectangular nonlinear weir crest layout (in platform), with sloped floors in the inlet and outlet cycles referred to as keys. In the innovative developed PKWs, the sloped floors produce cantilevered apex overhangs, which help to increase the overall crest length (L) relative to a rectangular labyrinth weir with the same weir footprint (Laugier 2007; Laugier et al. 2009; Leite Ribeiro et al. 2009). An accurate estimation of the discharge coefficient (C_d) of weirs is a significant factor in designing various hydraulic structures.

Fig. 1

Typical PK-weir geometries (top and bottom)

Some useful empirical discharge equations for these weirs have been proposed. PKW may consist of various cross sections depending on the flow requirements. There is a unique relationship between the unit discharge (the flow rate per unit width) and the upstream water depth measured relative to the weir crest, which is exploited for the purpose of flow measurement. As shown in Eq. (1), a common form of the weir head–discharge relationship (Eq. 5), the discharge capacity (Q) is proportional to L. The large value of L attainable with the PKW geometry is a significant factor in its high discharge capacity relative to linear weirs with the same channel width:

$$ Q = \frac{2}{3}C_{d} L\sqrt {2g} H_{T}^{3/2} $$

(1)

where C_d = dimensionless discharge coefficient; g = gravitational constant; and H_T= total head [piezometric head (H) measured relative to the elevation of the weir crest plus velocity head ($V^{2} /2$g)]. To describe the discharge capacity of a PK-weir, its discharge coefficient (C_d) is presented according to the common weir formulation referred to as the total developed crest length (L) as shown in Eq. (2)

$$ C_{d} = \frac{Q}{{LH^{{\frac{3}{2}}} \sqrt {2g} }} $$

(2)

Lempérière (Lempérière 2009) presented Eq. (3) as the head–discharge relationship specific to the recommended PK-weir design:

$$ q = 4.3h\sqrt {P_{m} } $$

(3)

In Eq. (3), P_m= a representative weir height measured in meters (Fig. 1); h = upstream head (piezometric or total head was not specified) measured relative to the weir crest elevation in meters (0.4P_m≤ h ≤ 2P_m); and q = weir discharge per unit spillway channel width (in cubic meters per second per meter). The form of Eq. (3) (linear, q ∝ h) is significantly different from the standard weir equation [Eq. (1)] (nonlinear, Q ∝ $H_{t}^{1.5}$). In Eq. (3), the constant, 4.3, is representative of a fixed-value discharge coefficient; published Cd values for other nonlinear weirs (e.g., labyrinth weirs) related to Eq. (1) are typically not constant but vary with H_t.

Recent works mainly focused on hydraulic behavior, flow conditions, and the discharge coefficient for different types of weirs. Kabiri-Samani and Javaheri (2012) carried out a set of laboratory experiments to investigate the effect of geometry on the discharge coefficient. Head–discharge data and visual observations were collected for PKW by Anderson (Logan 2011) over a wide range of discharges and compare the appropriateness of the recommended equations. Ribeiro et al. (2012) as a technical note reviewed the previous studies on the efficiency of planned and built PKW, and the results were evaluated by comparing an actual PK-weir’s discharge to that theoretically obtained for a sharp-crested spillway with crest length equal to the width of the PK-weir for a given hydraulic head.

Today by advancing the computational intelligence approaches in almost all areas of water engineering fields, especially in the water engineering studies, researchers have attempted to use these techniques for predicting and modeling the hydraulic or hydrologic phenomena (Tayfur 2014). As clear from the name of the computational intelligence approaches, developing these models is based on the data set; therefore, for developing the types of the computational intelligence models, investigators have tried to collect the related data set from the various reliable sources such as books, peer-reviewed articles and handbooks. During the data collection process defining the most affective independent parameters sometimes becomes difficult, therefore, to this purpose several mathematical approaches such as principal component analysis as multivariable analysis techniques have been proposed. Using these approaches leads to defining the most affective parameter on the desired phenomenon.

So far there have been several approaches of computational intelligence methods for application in prediction of discharge coefficient of weirs. For example, there has been an investigation of prediction discharge coefficient of weirs with artificial neural network (Bilhan et al. 2010). Some of the other applied intelligence methods in predicting discharge coefficient of weirs are: prediction of discharge coefficient for trapezoidal labyrinth side weir using a neuro-fuzzy approach by Emiroglu and Kisi (2013); predicting discharge coefficient of compound broad-crested weir by using genetic programming (GP) and artificial neural network (ANN) techniques by Salmasi et al. (2013); gene expression programming (GEP) to predict the discharge coefficient in rectangular side weirs by Ebtehaj et al. (2015); radial basis neural network and particle swarm optimization-based equations for predicting the discharge capacity of triangular labyrinth weirs by Zaji et al. (2015); prediction of lateral outflow over triangular labyrinth side weirs using soft computing approaches and two ANN techniques, that is, the radial basis neural network and GEP by Kisi et al. (2012); estimating discharge coefficient of semi-elliptical side weir using ANFIS by Dursun et al. (2012).

Recently machine learning (ML) technique is a popular learning technique for classification, regression, and other learning tasks. Unlike traditional artificial neural network technique, the quadratic programming (QP) with linear limitations is formulated in support vector machine (SVM) problems (Berthold and Hand 2003; Negnevitsky et al. 2005). Parsaie et al. (2018) used SVM to predict the discharge coefficient of cylindrical weir–gate. During the development of SVM model, it was found that the radial basis function as kernel function and hyperbolic tangent sigmoid as transfer function have a better accuracy compared to other tested functions. Also, simplifying the optimization processes of SVMs can be performed through a modification version of SVM, namely least-square support vector machine (LS-SVM) (Ahmadi et al. 2015a; 2015b). Researchers successfully applied LS-SVM for solving different problems in engineering (Sadri and Burn 2012; Wong et al. 2013; Goyal et al. 2014). Also, in recent years, there has been increasing interest in extreme learning machine (ELM), which is an extraordinary learning scheme for single hidden layer feed-forward neural network (SHLFN) (Huang et al. 2006, 2004). In ELM, the weights and biases of input layers are assigned randomly and the output weights are determined analytically. ELM produces high generalization performance at very high speed (Huang et al. 2011). There are different applications of ELM in the literature (Balbay et al. 2012; Du et al. 2014; Yu et al. 2013). In this study, a new version of ELM, called Bayesian ELM (BELM), which learns the output weights of basic ELM based on parametric Bayesian methods. BELM attempts to estimate the probability distribution of the output values, and hence the overfitting problem of conventional ELM is solved. Instead of fitting a curve to a set of data points, Bayesian methods try to estimate the probability distribution of output values and achieve higher generalization. The Bayesian approach involves taking advantage of some parameters (hyper parameters) that allow regularization. This regularization term is obtained from the distribution of model parameters and avoids the overfitting of the model. In the current literature (Soria-Olivas et al. 2011), many researches have already attempted to apply a BELM.

Logistic regression is another learning machine and statistical analysis method used for predicting and understanding categorical dependent variables (e.g., true/false, or multinomial outcomes) based on one or more independent variables (e.g., predictors, features, or attributes). Logistic regression is used to analyze the relationship between a single predictor, or several predictors, and an outcome that is dichotomous in nature (such as the presence or absence of an event). This form of regression analysis has become an increasingly employed statistical tool, especially over the last two decades (Oommen et al. 2011; Das et al. 2010; Wang et al. 2013; Shahabi et al. 2014). It is widely regarded as the statistic of choice for situations in which the occurrence of a binary (dichotomous) outcome is to be predicted (Hosmer and Lemeshow 2000; King and Zeng 2001).

In this study, we introduced an estimation model for discharge coefficient of a PK-weir by using the soft computing approach of machine learning. To the best knowledge of the authors, there is not any published study indicating the input–output mapping capability of computational intelligence techniques in modeling the discharge coefficient of PK-weirs. In addition, there is no report presenting the use of the soft computing approach based on machine learning in modeling discharge coefficient of any type of weir. Thus, the present study is focused on the introduction of different computational intelligence methods based on learning machine, such as LR, LS-SVM, ELM, and BELM to predict the discharge coefficient using a measured data set. These methods offer advantages over conventional modeling, including the ability to handle large amounts of noisy data from dynamic and nonlinear systems, especially when the underlying physical relationships are not fully understood. In addition, we discussed the accuracy of these techniques via the comparison of their performances. Our emphasis in this regard is simply from the point of view of obtaining higher accuracy. It is relevant to note that the models investigated in the present study are normally applied within deterministic frameworks in professional practices, which encouraged the practice of comparing the actual with predicted values. Therefore, the paper presents a comparative study on new generation computational intelligence approaches as a superior alternative to the linear and nonlinear regression models for predicting the discharge coefficient of a PK-weir located on a straight open channel under subcritical conditions.

2 Experimental Setup

The experiments were conducted on a smooth toughened glass-sided and smooth painted bed steel plate flume of 10 m working length. The flume cross-sectional area is 83 cm wide and 50 cm deep. The flume was equipped with a rolling point gauge (readability 0.01 cm) instrumentation carriage, which was used to measure water surface and crest elevations at various locations upstream of the PK-weir after the water level had been allowed to stabilize for a minimum of 5 min. All weir data were collected for flows ranging from 5 to 90 l/s. Flow rates were measured using calibrated ultrasonic flow meter. The channel was fed by a centrifuge pump delivering flow in an upstream stilling basin. The slope of the channel was considered zero in all the experiments. To dissipate large eddies, grid walls and wave suppressors were laid upstream along the channel. Water was pumped from the main tank to the flume. Experiments were performed for subcritical flow, stable flow conditions, and free overflow conditions. An elevation view of the flume is presented in Fig. 2. A total of 70 experiments were done for various hydraulic conditions to calculate C_d.

Fig. 2

Overview of weir test setup

Some statistical properties of the input and output variables in the training and validation datasets are given in Table 1, which include the mean, standard deviation (Sd), skewness coefficient (Csx), minimum, maximum of data. From this table, it could be observed that the extreme values of input data were in the training set.

Table 1 Statistics analysis of input and output data sets

When dividing the data set into training and validation subsets, it is essential to check that the data subsets represent the same statistical population. In general, Table 1 illustrates relatively similar statistical characteristics between training and validation sets in terms of mean, standard deviation and skewness coefficient. Skewness coefficients were low for both training and validation sets (see the Csx values). This is appropriate for modeling, because high skewness coefficient has a considerable negative effect on model performance (Altun et al. 2007). The skewness is not directly related to the relationship between the mean and median: A distribution with negative skew can have its mean greater than or less than the median, and likewise for positive skew.

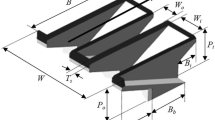
The weirs walls were fabricated using 6-mm-thick plexiglass acrylic sheeting. The weirs were assembled with acrylic glue, and the crest level was machined using a computer numerical controlled (CNC) milling machine. Models were designed with N = 4, and featured with a flat top crest. Weirs were sealed with silicon and other sealants. The weirs were installed in the flume on a short, adjustable base and leveled (± 0.5 mm) using surveying equipment. An overview of the test facility with the PKW installed is presented in Fig. 3. Table 2 presents the description of the weir configurations tested and their corresponding prefixes.

Fig. 3

Overview of Test flume (a) side view and (b) plan view

Table 2 Test weir dimensions

In this table, important geometric parameters for PK-weir design (most of which are shown in Fig. 1) include the total weir height (P), crest centerline length (L), inlet and outlet key width (Wi and Wo), PK-weir spillway width (W), footprint length (B_b), upstream (outlet key) and downstream (inlet key) apex cantilever lengths (Bo and Bi, respectively), inlet or outlet key length (B), weir wall thickness (T_s) and number of keys (N).

3 Methodology

3.1 Logistic Regression (LR)

Logistic regression is a statistical modeling method for data analysis, in which the dependent variable y has only two possible values, especially in the cases involving categorical response variables, such as yes/no or safe/unsafe. It is often used to find the relationship between probabilities and values of y. For simplicity, y is assigned to 1 in the case of positive outcome or success (i.e., yes or safe) and to 0 in the case of negative outcome (i.e., no or unsafe). For a set of p independent variables denoted by the vector $x' = x_{1} ,x_{2} , \ldots , x_{p}$, Hosmer and Lemeshow (2000) presented the following equation to represent the conditional mean of y in the logistic distribution (Cramer 2002; Wattimena et al. 2013):

$$ E\left( {\left. y \right|x} \right) = \pi \left( x \right) $$

(4)

The logistic regression model is formed as follows:

$$ \pi \left( x \right) = \frac{{e^{{\beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \cdots + \beta_{p} x_{p} }} }}{{1 + e^{{\beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \cdots + \beta_{p} x_{p} }} }} $$

(5)

where β₀, β₁, β₂,…, and β_p are the model’s parameters. Logistic regression is based on a linear model for the natural logarithm of the odds in favor of y = 1, which are simply the ratio of the proportions for the two possible outcomes (Moore et al. 2009):

$$ {\text{Odds}} = \frac{\pi \left( x \right)}{1 - \pi \left( x \right)} $$

(6)

A transformation of $\pi \left( x \right)$ is the logit transformation, which is defined as follows:

$$ \ln \left[ {\frac{\pi \left( x \right)}{1 - \pi \left( x \right)}} \right] = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \cdots + \beta_{p} x_{p} $$

(7)

This equation is also known as the logit transformation of p(x), and the related analysis is known as “logit analysis.”

3.2 Least-Square Support Vector Machine (LS-SVM)

Least-square support vector machine (LS-SVM) models are used to approximate the nonlinear relationship between input variables and output variables with certain accuracy (Suykens 2001; Smola and Bernhard 2004). The LS-SVM model is to use the least-square linear system as the loss function, and the inequality constraints are revised as the equality constraints in the LS-SVM model.

The given training sample is $S \, \left\{ {\left( {x_{i} , \, y_{i} } \right)| \, i = \, 1,2,3, \ldots ,m} \right\}, \, m$ is the number of samples, the set {x_i} $\in$R represents the input vector, y$\in$ {− 1,1} indicates the corresponding desired output vector, the input data are mapped into the high dimensional feature space by using nonlinear mapping function $\phi \left( \bullet \right)$. Then the existing optimal classification hyperplane must meet the following conditions:

$$ \left\{ {\begin{array}{*{20}c} {\omega^{T} x_{i} + b \ge 1, y_{i} = 1} \\ {\omega^{T} x_{i} + b \le - 1, y_{i} = - 1} \\ \end{array} } \right. $$

(8)

where $\omega$ is omega vector of superplane, b is offset quantity. Then the classification decision function is described as follows:

$$ f\left( {x_{i} } \right) = \text{sgn} \left( {\omega^{T} x_{i} + b} \right) $$

(9)

The classification model of LS-SVM is described by the optimization function $\begin{array}{*{20}c} {\hbox{min} } \\ {\omega , \xi ,b} \\ \end{array} J\left( {\omega ,\xi_{i} } \right){:}$

$$ \begin{array}{*{20}c} {\hbox{min} } \\ {\omega , \xi ,b} \\ \end{array} J\left( {\omega ,\xi_{i} } \right) = \frac{1}{2}\omega^{T} \omega + \frac{1}{2}\gamma \mathop \sum \limits_{i = 1}^{m} \xi_{i}^{2} $$

(10)

$$ s.t.\; y_{i} \left[ {\omega^{T} \phi \left( {x_{i} } \right) + b} \right] = 1 - \xi_{i} ,\quad i = 1,2,3, \ldots ,m $$

(11)

where $\xi_{i}$ is slack variable, b is offset, $\omega$ is support vector, $\xi = (\xi_{1} ,\xi_{2} , \ldots ,\xi_{m} ),\gamma$ is regression fiction parameter to balance the fitness error and model complexity.

The optimization problem is transformed into its dual space. Lagrange function is introduced to solve it. The corresponding optimization problem of LS-SVM model with Lagrange function is described as follows:

$$ L\left( {\omega ,b,\xi ,\alpha } \right) = \frac{1}{2}\omega^{T} \omega + \frac{1}{2}\gamma \mathop \sum \limits_{i = 1}^{m} \xi_{i}^{2} - \mathop \sum \limits_{k = 1}^{m} \alpha_{i} \left\{ {y_{i} \left[ {\omega^{T} \phi \left( {x_{k} } \right) + b} \right] - 1 + \xi_{i} } \right\} $$

(12)

where $\alpha_{i}$ is the Lagrange multiplier, and $\alpha_{i} \ge \; = \;0(i = 1,\;2,\;3,\; \ldots ,\;m)$. Then the classification decision function is described as follows:

$$ f\left( {x_{i} } \right) = \text{sgn} \left(\mathop \sum \limits_{i = 1}^{m} \alpha_{i} y_{i} K\left( {x,x_{i} } \right) + b\right) $$

(13)

3.3 Extreme Learning Machine

Extreme learning machine (ELM) is the modified version of single hidden layer feed-forward networks (SLFN) (Huang et al. 2004; Huang and Chen 2007). Due to the random determination of the input weights and hidden biases, ELM requires numerous hidden neurons. In practice, the number of hidden neurons should be larger than the number of the variables in dataset, since the useless neurons from the hidden layer will be pruned automatically. Figure 4 shows the topology of a single hidden layer feed-forward neural network based on ELM using the activation function, g(x) = sig(w_i. x_i+ b).

Fig. 4

Topology of single hidden layer feed-forward neural network using ELM

In SLFN, the relationship between input (x) and output (t) is given below:

$$ \mathop \sum \limits_{i = 1}^{L} \beta_{i} G\left( {a_{i} ,x_{j} ,b_{j} } \right) = t_{j} j = 1, \ldots ,N $$

(14)

where N is the number of samples, L is the number of hidden nodes, β_i is the output weight and (a_i, b_i) is the ith parameter of the ith hidden node. In this study, L_x and L_y are used as inputs of the ELM. The output of ELM is d. So, x = [L_x, L_y] and t = [d]. Equation (14) is written in Eq. (15):

$$ H\beta = T $$

(15)

where

$$ H = \left[ {\begin{array}{*{20}c} {G\left( {a_{1} ,x_{1} ,b_{1} } \right)} & \ldots & {G\left( {a_{L} ,x_{L} ,b_{L} } \right)} \\ \vdots & \ldots & \vdots \\ {G\left( {a_{1} ,x_{N} ,b_{1} } \right)} & \ldots & {G\left( {a_{L} ,x_{N} ,b_{L} } \right)} \\ \end{array} } \right]_{N \times L} , \quad \beta = \left[ {\begin{array}{*{20}c} {\beta_{1}^{T} } \\ \vdots \\ {\beta_{L}^{T} } \\ \end{array} } \right]_{L \times m} , \quad T = \left[ {\begin{array}{*{20}c} {t_{1}^{T} } \\ \vdots \\ {t_{L}^{T} } \\ \end{array} } \right]_{N \times m} $$

(16)

H is called the hidden layer output matrix of ELM (Ahmadi et al. 2015). The value of β is determined from Eq. (17):

$$ \beta = H^{\dag } T $$

(17)

where $H^{\dag }$ is the Moore–Penrose generalized inverse (Serre 2002).

3.4 Bayesian Extreme Learning Machine (BELM)

Combining ELM and Bayesian linear regression, BELM (Huang et al. 2006) learns the weights of the output layer in the Bayesian framework. In the single output case, BELM follows the relationship:

$$ t = h\beta + \varepsilon $$

(18)

where ε follows a Gaussian distribution with zero mean and variance $\sigma^{2} , h = [h\left( {x,o_{1} ,r_{2} } \right), \ldots ,h\left( {x,o_{M} ,r_{M} } \right)$ is the output vector of hidden layer with respect to the input x, and β is the output weights vector. Then, the conditional distribution of the output can be written as

$$ p\left( {\left. t \right|h,\beta , \sigma^{2} } \right) = {\rm N}\left( {h\beta ;\sigma^{2} } \right) $$

(19)

The corresponding conjugate prior is usually considered to be a Gaussian distribution (Bishop et al. 2006)

$$ p\left( {\left. {\beta_{i} } \right|a} \right) = {\rm N}\left( {0;a^{ - 1} } \right) i = 1, \ldots , M $$

(20)

where a is a hyper parameter. In this case, the posterior distribution is also Gaussian when both the prior distribution of β and the conditional distribution of the output are Gaussian. Then, the maximum likelihood estimation of the posterior mean $\hat{\beta }$ and the posterior variance S can be written as (Bishop et al. 2006; Soria-Olivas et al. 2011)

$$ \hat{\beta } = \sigma^{ - 2} SH^{T} t $$

(21)

$$ S = \left( {aI + \sigma^{ - 2} H^{T} H} \right)^{ - 1} $$

(22)

where t = [t₁,t₂,…,t_N] has the output vector and H has the same definition as in ELM. The regularization term a in (20) does not need to be specified by user, which differs from the conventional regularized approaches (Soria-Olivas et al. 2011; Oommen et al. 2011).

3.5 Model Performance Criteria

The results of the comparison between equation and those proposed models (LR, LS-SVM, ELM and BELM) in this study are presented herein, root-mean-square error (RMSE), the coefficient of correlation (R), the Nash–Sutcliffe model efficiency coefficient (NSE) and scatter index (SI), as defined below:

$$ R = \frac{{\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} \left( {xi - \bar{x}} \right)\left( {yi - \bar{y} } \right)}}{{\sqrt {\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} \left( {xi - \bar{x}} \right)^{2} } \times \sqrt {\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} \left( {yi - \bar{y}} \right)^{2} } }} $$

(23)

$$ {\text{NSE}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{i} - y_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{i} - \bar{x}} \right)^{2} }} $$

(24)

$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} (x_{i} - y_{i} )^{2} } $$

(25)

$$ {\text{SI}} = \frac{\text{RMSE}}{{\bar{x}}} $$

(26)

where y_i and x_i are the modeled and calculated C_d values, respectively, and $\bar{y}$ and $\bar{x}$ are the mean modeled and calculated C_d values, respectively. The afore-mentioned indexes represent the estimated values as prediction error average but provide no information on the prediction error distribution of the presented models. The RMSE index only indicates a model’s ability to predict a value away from the mean. Therefore, in order to test the effectiveness of the model developed, it is important to test the model using some other performance evaluation criteria such as threshold statistics (Jain et al. 2001; Jain and Ormsbee 2002). The threshold statistics (TS) not only give the performance index in terms of predicting C_d but also the distribution of the prediction errors.

The threshold statistic for a level of x % is a measure of the consistency in forecasting errors from a particular model. The threshold statistics are represented as TS_x and expressed as a percentage. This criterion can be expressed for different levels of absolute relative error from the model. It is computed for x% level (TL) as

$$ {\text{TS}}_{x} = \frac{{Y_{x} }}{n} \times 100 $$

(27)

where Y_x is the number of computed C_d (out of n total computed) for which the absolute relative error is less than x% from the model.

In the present study TS for absolute relative error levels of 5, 10 and 15 percent (TS5 and TS10) were used to measure the effectiveness of the models regarding their ability to accurately predict data from the calibrated model.

3.6 Data Preprocessing

In order to achieve effective training, the data are needed to be normally distributed using an appropriate transformation method. Luk et al. (2000) reported that networks trained on transformed data achieve better performance and faster convergence in general. Besides, Aqil et al. (2007) showed that the data preprocessing with log sigmoidal activation function before processing the black-box models. In this study, transformation is performed on all data independently using the following equation:

$$ z = a\log_{10} \left( {G + b} \right) $$

(28)

where z is the transformed value of C_d, a is an arbitrary constant, and b was set to 1 to avoid the entry of zero C_d in the log function. The final forecast results were then back transformed using the following equation:

$$ G = 10^{{{\raise0.7ex\hbox{$z$} \!\mathord{\left/ {\vphantom {z a}}\right.\kern-0pt} \!\lower0.7ex\hbox{$a$}}}} - b $$

(29)

4 Applications and Results

This part of the study focused on comparing the performance of LR, LS-SVM, ELM and BELM models for estimating discharge coefficient of the PK-weir. For this purpose, three input parameters, that is, the dimensionless upstream head H/P, the dimensionless parameter H/L, and discharge (Q) were considered in the study. For the same basis of comparison, the same training and validation sets, respectively, were used for all the above models developed, while the five quantitative standard statistical performance evaluation measures were employed to evaluate the performances of various models developed. The results are summarized in Tables 3 and 4. It was apparent that all of the performances of these models are almost similar during training as well as validation. In order to get an effective evaluation of the LR, LS-SVM, ELM, and BELM models performance, the best model structures have been used to compare the models. From the best-fit model, it was found that the difference between the values of the statistical indices of the training and validation set did not vary substantially. It was observed that all four models generally gave low values of the RMSE, and SI as well as high NSE, the performances of the LR, LS-SVM, ELM, and BELM models performance in the C_d estimation were satisfactory.

Table 3 Quantitative study of the presented models’ results in comparison with the experimental results using verification criteria (training period)

Table 4 Quantitative study of the presented models’ results in comparison with the experimental results using verification criteria (validation period)

In this study, three input parameters were used for the estimation of C_d. For modeling C_d, a three-layered architecture was adopted for ELM model development (Fig. 4). The first layer (input layer) used different input parameters. The output layer had one neuron representing the estimated discharge coefficient. For the hidden layer, a maximum of 40 neurons were tested for each model. For determining the optimum number of neurons in the hidden layer, initially 5 neurons were tested and subsequently the number of neurons was gradually increased to 40 by an interval of one. Radial basis activation function was employed for all the ELM models tested.

LS-SVM uses equality optimization constrains instead of inequalities constrains used in the traditional SVM. Equality optimization results in a direct least-square solution by avoiding quadratic programming. Choice of kernel functions and hyperparameters are some critical issues needed to be addressed before the application of LS-SVM. Radial basis function (RBF) a more compactly supported kernel function is able to reduce the computational complexity of the training process and provides a good performance. Hence, RBF kernel function was employed in this study. Different techniques for tuning the hyperparameters related to the regularization constant are available in the literature. In this study, the regularization parameter gamma (c) and kernel function parameter (σ²) were obtained by grid search technique based on leave-one-out cross-validation.

A model can be claimed to produce a perfect estimation if the NSE criterion is equal to 1. Normally, a model can be considered as accurate if the NSE criterion is greater than 0.8 (Shu and Ouarda 2008). Tables 3 and 4 show that the NSE values for various applied methods in this study are over 0.8. This indicated that they had good performance during both training and validation and these models achieved acceptable results. It also showed that the BELM model had the smallest value of the RMSE as well as higher value of NSE in the validation period, so it was selected as the best-fit model for predicting the C_d in this study. Also, the SI values for the BELM model that predict the C_d value were higher than those for the other models, which indicates that the overall quality of estimation of the BELM model is better than the LR, LS-SVM, and ELM models according to SI and NSE. Compared among models from the TS viewpoints, it was found that ELM and BELM models exhibited 100% estimates lower than 5% and 10% relative error. On the other hand, for LS-SVM and LR models, the estimates of relative error decreased to 83.84% and 56.6%, respectively, for TS₅. Therefore, the BELM and ELM models performed a bit better than the others. For analyzing the results during training phase, it can be observed that the BELM model outperformed all other models. Also, in the validation phase, the BELM model obtained the best RMSE, R, NSE and SI statistics of 0.011, 0.998, 0.989 and 0.009. Thus, in the validation phase, as shown in Tables 3 and 4, the values with the ELM and BELM models prediction were able to produce a good, near forecast as compared to those with other models. But the performance of BELM is slightly better than the ELM model. Furthermore, as shown in Tables 3 and 4 the virtues or defect degrees of forecasting accuracy are different in terms of different evaluation measures during the training phase and the validation phase. BELM model is able to obtain the better forecasting accuracy in terms of different evaluation measures, not only during the training phase but also during the validation phase.

It appears that while assessing the performance of any model for its applicability in predicting C_d, it is not only important to evaluate the average prediction error but also the distribution of prediction errors. The statistical performance evaluation criteria employed so far in this study are global statistics and do not provide any information on the distribution of errors. Therefore, in order to test the robustness of the model developed, it is important to test the model using some other performance evaluation criteria such as threshold statistics. On comparing the TS statistics for the models, it was found that the LR and LS-SVM models exhibited 56.6, 91.7 and 83.8%, 100% estimates lower than 5% and 10% relative error, respectively. On the other hand, for ELM and BELM model the estimates of relative error increased to 100%. The distribution of errors is presented in Fig. 5, which gives a clear indication of better performance by the BELM model. Figure 5 shows that all applied models perform almost similarly in terms of the distribution of the errors. According to this figure, nearly 92% and 98% of the discharge coefficients estimated using ELM and BELM have a relative error lower than 2%, respectively. However, according to Fig. 5, for LR and LS-SVM models, almost 88% and 98% of the estimated amounts have less than 8% error, respectively, and this is 100% for ELM and BELM. Based on the given explanations so far, it can be said that BELM is fairly accurate in estimating C_d.

Fig. 5

Distribution of forecast error across different error thresholds for all the models

Figure 6 displays the estimation discharge coefficients as presented by the four models in this study against the experimental results. This figure demonstrates that almost all applied model estimated the results fairly accurately, with all the discharge coefficient amounts estimated by this model having a relative error below 10%. It was obviously seen from these figures that the BELM and ELM estimates were closer to the corresponding observed flow values than those of the other models. As seen from the fit line equations (assume that the equation is y = ax + b) in the scatter plots that a and b coefficients for the ELM and BELM model are, respectively, closer to the 1 and 0 with a higher R² value of 0.099 than other models for C_d.

Fig. 6

Comparing the estimated results of the four models to the laboratory results

Overall, LS-SVM, ELM, and BELM models gave good prediction performance and were successfully applied to establish the forecasting models that could provide accurate and reliable C_d prediction. The results suggested that the BELM model was superior to the others in this forecasting. The reason for a better prediction accuracy of BELM model than other models lies, primarily, in the shortcoming of the models, e.g., slowly learning speed, overfitting, curse of dimensionality. and convergence to local minimum. Conversely, BELM model was based on the empirical risk minimization principle, which could attack the problem in theory.

The distributions of forecast errors by all models for C_d are given in Fig. 7 from which it was clearly evident that the ELM and BELM performed better than the other models. Figure 7 shows that for all developed models no specific clustering was observed.

Fig. 7

Distribution of forecast error across the full range of discharge coefficient

The data in Fig. 8 showed that the BELM was extremely closer to the experimental C_d values than other approaches used in this study. So it was evident that ELM and LS-SVM consistently performed better than LR.

Fig. 8

LR, LS-SVM, ELM, and BELM modeled C_d versus H_T/P data

C_d data for each model presented in Fig. 9 were normalized relative to modeled results to experimental data at a dimensionless upstream head, H_T/P in performance. As shown in Fig. 8, for BELM model, C_d (BELM)/C_d (experimental) was nearest to 1.0 and the results of C_d prediction demonstrated the effectiveness and efficiency of the LR, ELM, and LS-SVM models.

Fig. 9

LR, LS-SVM, ELM, and BELM C_d versus H_T/P data normalized to experimental data

Since four models had been developed to predict the discharge coefficient of piano key weir, a comparative study had been carried out between the adopted LR, LS-SVM, ELM, and BELM models (Fig. 10).

Fig. 10

Bar chart of R values of the different models

Figure 10 concludes that all four presented models provide fairly good results for discharge coefficient of a PK-weir. The only difference between the estimations of different models is their relative error distribution.

According to the basic concept of a Bayesian extreme learning machine, this type of learning machine has a high accuracy that may control the ill-posed problem, automatical selection problem of the hidden nodes and overfitting problem of ELM. This heuristic is essentially found to be true in the current study, as the BELM is found to perform better than the ELM in terms of most of the performance statistics. It can be concluded that the ELM and BELM algorithms have better generalization than LS-SVM and LR for the classification problem in the standard data sets. Moreover, the BELM algorithm is stable for different assignment of hidden node parameters. So the performance of the BELM as illustrated in earlier discussions confirms that it is able to preserve the advantages of the ELM. Accordingly, considering the given explanations, the fact that compared to other models the relative error by BELM was the lowest, and the RMSE and SI indexes presented for this model are good, it can be argued that compared to other models, BELM can serve as a replacement method. In general, BELM can be easily implemented by any flexible Bayesian prior distribution, and hence it is attractive for developing application. This suggests promising research areas for future studies.

5 Conclusion

In this paper, we have designed various high-accuracy machine learning techniques (e.g., LR, LS-SVM, ELM and BELM), to estimate discharge coefficient of a PK-weir. To achieve this objective, an experimental data set was employed to develop various models investigated in this study. The methods utilized the statistical properties of the data series. The obtained results indicated that computational intelligence methods were powerful tools to model C_d and could give good estimation performance. Therefore, the results of the study were highly encouraging and suggested that BELM and ELM approaches were promising in modeling C_d, and this might provide valuable reference for researchers and engineers who applied the methods for modeling long-term hydraulic parameters estimating. As the next step, comparing the results of the models, it was seen that the value of NSE of BELM models was higher than other models. Therefore, BELM and ELM models could improve the accuracy over the other applied models. Overall, the analysis presented in this study showed that the BELM method was superior to the LS-SVM, LR, and ELM in forecasting C_d of piano key weir. In general, the implementation of all intelligence models in the present study illustrated the flexibility of C_d modeling. It is hoped that future research efforts will focus in these directions, i.e., more efficient approach for learning machines, improve the prediction accuracy, especially for the high values of C_d, by combining or improving model parameters, saving computing time or more efficient optimization algorithms in searching optimal parameters of SVM model, to improve the accuracy of the forecasting models in terms of different evaluation measures for better planning, design, operation, and management of various engineering systems.