1 Introduction

In an extremely dense plasma, commonly referred to as the quantum plasma, where the interparticle distance reduces to a limit such that the wave functions of the constituent particles start overlapping, particles’ dynamics have to be treated quantum mechanically (Shukla and Eliasson 2011; Haas 2011; Bonitz et al. 2014). Not only in the extreme astrophysical environment where the presence of ultra-strong magnetic field in excess of the critical quantum electrodynamical (QED) limit (\(B=\frac{m_e^2c^3}{e\hbar } \simeq 4.4\times 10^{13}\) G) makes the electron cyclotron energy equal to the electron rest mass energy (\(m_ec^2=0.51\) MeV), some of the constituent particles in dense plasmas produced by the interaction of ultra-intense (\(\ge 10^{21}\) W/cm\(^2\)) laser pulses with matter may also acquire relativistic speed (Bonitz et al. 2014; Marklund and Shukla 2006). This necessitates the inclusion of relativistic corrections in addition to the quantum mechanical treatment in modeling the plasma dynamics. The Quark–Gluon plasmas (QGP) produced during the relativistic heavy-ion collision (RHIC) experiments (Arsene et al. 2005) is yet another example of relativistic quantum plasmas. The subject of relativistic quantum plasma (RQP) has, thus, been actively pursued by the astrophysical and plasma physics community (Melrose 2008; Asenjo et al. 2011; Mendonça 2011; Eliasson and Shukla 2011; Haas et al. 2012; Behery et al. 2016; Haas 2019; Islam et al. 2017; Singh et al. 2019; Jamil et al. 2019; Goshadze et al. 2019). Melrose (2008) has presented an excellent account of the various aspects of waves in unmagnetized relativistic-quantum plasmas using full QED formalism. This work has later been extended to include the magnetized cases (Melrose and Weise 2009, 2012).

With the help of fluid formalism, employing the Dirac equation for the spin-half RQP, a dispersion relation for an electromagnetic wave sustained by such a system is derived in Ref. (Asenjo et al. 2011), indicating higher transparency with the inclusion of the spin. Eliasson and Shukla (2011) have investigated the laser–plasma interactions in the relativistic quantum regime by employing a Kelin–Gordon equation for the relativistic degenerate electrons coupled with electromagnetic waves through Maxwell and Poisson equations. Recently, we have studied (Ikramullah et al. 2017) different properties of the relativistic quantum plasma, which comprises of relativistic degenerate electrons and positrons, and dynamic degenerate ions by extending the Eliasson–Shukla model (Eliasson and Shukla 2011). It was found that the presence of positrons has insignificant effect on the dispersion. However, enhancement in the plasma opacity was observed, and the growth rate of different parametric instabilities was shown to be affected by the inclusion of positrons in the system. We further extended the model by incorporating the Thomas–Fermi distribution of electrons in the background of relativistic quantum plasma composed of relativistic degenerate electrons and positrons and non-relativistic degenerate ions (Ikramullah et al. 2018). An electron-acoustic wave was observed in addition to the other two modes associated with positrons and ions, respectively. The spectrum and growth rates of different instabilities were also affected with the change in the quantum parameter and with the intensity of the circularly polarized electromagnetic (CPEM) wave.

In the present work, the Eliasson–Shukla model (Eliasson and Shukla 2011) is further extended to study different physical phenomena like dispersion of electrostatic waves, self-induced transparency and plasma opacity, the occurrence and growth rates of different parametric instabilities in 3-component plasma by including a beam of non-relativistic quantum electrons along with degenerate relativistic electrons and dynamic-degenerate ions. Ions are quantum-mechanically treated in Ref. (Shukla and Stenflo 2006) through the inclusion of Bohm potential, but in our case, the plasma is 3-component having two types of electrons (the relativistic degenerate electrons, and the beam of non-relativistic degenerate electrons) and the dynamic degenerate ions. The spin dynamics have not been included in the present study. We feel that the work presented in this article has relevance to both space and laboratory plasmas such as the high-density plasmas that can be produced by interacting ultrashort and ultra-intense laser pulses with solids.

This paper is organized in the following manner: in Sect. 2, a mathematical model based on the Klein–Gordon Equation (KGE) for relativistic degenerate electrons and Schrödinger Equations (SEs) for the dynamical degenerate ions and beam of non-relativistic degenerate electrons has been outlined. These equations are then coupled with the Maxwell’s equations in order to describe the nonlinear coupling between the relativistic quantum plasma and the CPEM waves. In Sect. 3, we derive the dispersion relations by using the Fourier analysis and have discussed the linear properties of electrostatic oscillations. The Sect. 4 deals with the phenomena of relativistic nonlinear propagation and opacity of plasma. In Sect. 5, we study the stimulated Raman scattering (SRS) and modulational instabilities (MI) in a relativistic 3-component quantum plasma. In Sect. 6, we have derived the dispersion relation by considering ion dynamics and numerically studied the stimulated Brillouin scattering (SBS) instability. We concluded our work in Sect. 7.

2 Mathematical Model

The mathematical model of the problem composed of the KGE for the degenerate relativistic electrons, SE for the degenerate ions (beam-electrons), and Maxwell’s and Poisson equations for the propagation and interaction of intense CPEM wave with the relativistic quantum plasma.

We use \(\mathcal {W}=i\hbar \frac{\partial }{\partial t}+e\phi\) and \(\textbf{P}=-i\hbar {\nabla }+e\textbf{A}\) in order to introduce electromagnetic interaction in KGE, given by

$$\begin{aligned}&\mathcal {W}^2 \psi _e-c^2\mathcal {P}^2\psi _e-m^2_e c^4\psi _e=0. \end{aligned}$$
(1)

Here, \(\psi _e\) represents an ensemble of degenerate relativistic electrons, \(m_e (e)\) is an electron mass (charge), and \(\phi (\textbf{A})\) is the electromagnetic scalar (vector)-potential, respectively. In this case, the charge and current densities have the following expressions, respectively:

$$\begin{aligned}&\rho _e=\frac{-e}{2 m_e c^2}\big (\psi ^{*}_e\mathcal {W}\psi _e+ \psi _e(\mathcal {W}\psi _e)^*\big ), \end{aligned}$$
(2)

and

$$\begin{aligned}&{} \textbf{j}_e=\frac{-e}{2 m_e }\big (\psi ^{*}_e\textbf{P}\psi _e+ \psi _e(\textbf{P}\psi _e)^*\big ). \end{aligned}$$
(3)

The coupling of an electromagnetic wave with the degenerate ions (non-relativistic beam electrons) is represented by

$$\begin{aligned} \left( i\hbar \frac{\partial }{\partial t}-q\phi \right) \psi _\nu =\frac{(-i\hbar {\nabla }-q\textbf{A})^2}{2m_\nu }\psi _\nu , \end{aligned}$$
(4)

where, the wavefunction \(\psi _\nu\) represents an ions ensemble (non-relativistic beam electrons), q is the charge of an ion (non-relativistic electron), and \(m_\nu\) is an ion (electron) mass, respectively. The electric charge and current densities of ions (non-relativistic beam-electrons) then take the following forms, respectively:

$$\begin{aligned}&\rho _\nu =q|\psi _\nu |^2, \end{aligned}$$
(5)

and

$$\begin{aligned}&\textbf{j}_\nu =\frac{iq\hbar }{2m_\nu }\big (\psi _\nu \mathbf{\nabla }\psi ^*_\nu -\psi ^*_\nu \mathbf{\nabla }\psi _\nu \big )-\frac{q^2}{m_\nu }|\psi _\nu |^{2}{} \textbf{A}. \end{aligned}$$
(6)

To close the model, the scalar and vector potential (\(\phi\), \(\textbf{A}\)) are obtained from the electromagnetic wave equation

$$\begin{aligned}&\frac{\partial ^2 \textbf{A}}{\partial t^2}+c^2{\nabla }\times \left( {{\nabla }\times \textbf{A}}\right) +{\nabla }\frac{\partial \phi }{\partial t}=\mu _0c^2\textbf{j}_T, \end{aligned}$$
(7)

and

$$\begin{aligned}&\nabla ^2\phi +{\nabla } \cdot \frac{\partial \textbf{A}}{\partial t}=-\frac{1}{\epsilon _0}\left( \rho _e+\sum \limits _{\nu =i,eb}\rho _\nu \right) , \end{aligned}$$
(8)

where \(\mu _0\) and \(\epsilon _0\) are the permeability and permittivity of vacuum, respectively, and \(\textbf{j}_T=\textbf{j}_e+\sum \limits _{\nu =i,eb}{} \textbf{j}_\nu\) is the total current density. The symbol eb represents the beam electrons.

By taking the divergence of Eq. (7) and then using \({\nabla }\cdot \textbf{A}=0\) (Coulomb gauge), we obtain from Eqs. (7) and (8), respectively,

$$\begin{aligned}&\nabla ^2\left( \frac{\partial ^2 \textbf{A}}{\partial t^2}-c^2\nabla ^2 \textbf{A}\right) =-c^2\mu _0\mathbf{\nabla }\times \left( {\nabla }\times \textbf{j}_T\right) , \end{aligned}$$
(9)

and

$$\begin{aligned} \nabla ^2\phi =-\frac{1}{\epsilon _0}\left( \rho _e+\sum \limits _{\nu =i,eb}\rho _\nu \right) . \end{aligned}$$
(10)

Equations (1), (9), and (10) constitute the complete model that describes the nonlinear coupling between the intense CPEM wave and the non-magnetized relativistic degenerate plasma.

3 Electrostatic Oscillations

For electrostatic waves, the electromagnetic vector potential (\(\textbf{A}\)) is assumed to be zero. The electrostatic oscillations arise due to the charge density fluctuations in the plasma. At wavelengths comparable to the interparticle distances, the quantum effects can cause dispersion of electrostatic waves. When the wavelength associated with an electron is of the order of the Compton length, the electron speed becomes relativistic that can change the dispersion relation for the electrostatic waves.

To derive a dispersion relation for the electrostatic waves, we transform the wavefunction \(\psi _e\) by using the following transformation:

$$\begin{aligned} \psi _e=\widetilde{\psi }_e\text {exp}\left( -ic^2m_et/\hbar \right) . \end{aligned}$$
(11)

The modified wavefunction \(\widetilde{\psi }_e\) then obeys the following KGE:

$$\begin{aligned}&\left( i\hbar \frac{\partial }{\partial t}+m_e c^2+e\phi \right) ^2 \widetilde{\psi }_e+\hbar ^2c^2\nabla ^2\widetilde{\psi }_e-m^2_e c^4\widetilde{\psi }_e=0, \end{aligned}$$
(12)

and the charge density of electron becomes

$$\begin{aligned}&\rho _e=\frac{-ie\hbar }{2 m_e c^2}\left( \widetilde{\psi }^{*}_e\frac{\partial \widetilde{\psi }_e}{\partial t}-\widetilde{\psi }_e\frac{\partial \widetilde{\psi }^{*}_e}{\partial t}\right) -\left( 1+\frac{e\phi }{m_e c^2}\right) e|\widetilde{\psi }_e|^2. \end{aligned}$$
(13)

The dynamics of ions (non-relativistic beam electrons) in the electrostatic case is governed by the SE:

$$\begin{aligned}&i\hbar \frac{\partial \psi _\nu }{\partial t}-q\phi \psi _\nu =-\frac{\hbar ^2\nabla ^2}{2m_\nu }\psi _\nu . \end{aligned}$$
(14)

The ion (beam electrons) charge density is given by Eq. (5):

We linearize the system of Eqs. (10), (12), and (14) by using \(\phi =\phi _1\), \(\widetilde{\psi }_e=\widetilde{\psi }_{0e}+\widetilde{\psi }_{1e}\), and \(\psi _\nu =\psi _{0\nu }+\psi _{1\nu }\). Here, \(|\widetilde{\psi }_{0e}|^2=n_{0e}\), and \(|\psi _{0\nu }|^2=n_{0\nu }\) are the unperturbed number densities of the relativistic-degenerate electrons and the degenerate ions (non-relativistic beam electrons), respectively. We Fourier decompose this by using \(\phi _1=\widehat{\phi }\exp \big (i\mathbf{K\cdot r}-i\Omega t\big )+c.c., \widetilde{\psi }_{1e}=\widehat{\psi }_{+e}\exp \big (i\mathbf{K\cdot r}-i\Omega t\big )+\widehat{\psi }_{-e}\exp \big (-i\mathbf{K\cdot r}+i\Omega t\big )\) , and \(\psi _{1\nu }=\psi _{+\nu }\exp \big (i\mathbf{K\cdot r}-i\Omega t \big )+\psi _{-\nu }\exp \big (-i\mathbf{K\cdot r}+i\Omega t \big )\). Separating Fourier modes, and then eliminating the different Fourier coefficients, we get a dispersion relation for the electrostatic waves as follow:

$$\begin{aligned} \varepsilon = 1+\chi _{e}+\sum \limits _{\nu =i,eb}\chi _{\nu } = 0. \end{aligned}$$
(15)

Here,

$$\begin{aligned}&\chi _{e}=\frac{\omega ^2_{pe}\Big (4m^2_e c^4-\hbar ^2\big (\Omega ^2-c^2K^2\big )\Big )}{\hbar ^2\big (\Omega ^2-c^2K^2\big )^2-4m^2_e c^4{\Omega ^2}}, \end{aligned}$$
(16)

and

$$\begin{aligned}&\chi _\nu =-\frac{4\omega ^2_{p\nu } m^2_\nu }{4m^2_\nu \Omega ^2-\hbar ^2K^4}, \end{aligned}$$
(17)

are the electric susceptibilities of the relativistic degenerate electrons and ions (beam electrons), respectively. Here, \(\omega _{pe}=\big (n_{0e}e^2/\epsilon _0m_e\big )^{1/2}\) and \(\omega _{p\nu }=\big (n_{0\nu }e^2/\epsilon _0m_\nu \big )^{1/2}\) are, respectively, the plasma oscillation frequencies of relativistic electrons and ions ( beam electrons ).

To study the electron-acoustic and ion-acoustic waves associated with the low-frequency fluctuations, we apply the low-frequency limits on the Eq. (15). Assuming \(\Omega<<cK\), and ignoring the high powers of \(\Omega\), we obtain the following dispersion relation:

$$\begin{aligned} 1+\acute{\chi _{e}}+\sum \limits _{\nu =i,eb}\chi _{\nu } =0. \end{aligned}$$
(18)

Here,

$$\begin{aligned} \acute{\chi _{e}}=\frac{\omega ^2_{pe}\big (4m^2_ec^2+\hbar ^2k^2\big )}{\hbar ^2c^2k^4-4m^2_ec^2\Omega ^2}, \end{aligned}$$
(19)

is the electric susceptibility of the low-frequency electrons.

The ratio of the densities of the non-relativistic degenerate beam electrons and the relativistic degenerate electrons is denoted by \(\beta\).

Fig. 1
figure 1

Dispersion curves, obtained by plotting the solution of Eq. (15), for a plasma consisting of relativistic degenerate electrons, dynamic degenerate ions, and non-relativistic electrons beam for \(H = 0.007\) and \(\beta =10^{-5}\)

Full size image
Fig. 2
figure 2

Figure showing the dispersion in the low-frequency limit, obtained by plotting the solution of Eq. (18), using \(H=0.007\) and \(\beta =10^{-5}\)

Full size image

In Fig. 1, the solution of Eq. (15) is plotted where four different frequency branches are observed. The dashed curve is associated to the relativistic electrons having initial oscillation at the electrons plasma frequency. The dashed-dotted curve is ascribed to the ion waves, and the dotted curve represents the acoustic waves associated with the non-relativistic beam of electrons. The solid curve with the largest frequency may be attributed to the so-called "pair branch" or "positronic" states. The value of the plasma density (hence the quantum parameter H) is chosen \(10^{34}\) \(m^{-3}\) (\(H=0.007\)) and \(\beta = 10^{-5}\). We see that the phase velocity of the acoustic waves associated with the non-relativistic degenerate beam electrons is initially higher than the ion-acoustic waves and increases with a uniform rate to a certain K values beyond which it starts to decrease with a uniform rate.

In Fig. 2, Eq. (18) is plotted showing the low-frequency limit (\(\Omega<<cK\)) for a 3-component plasma composed of the relativistic degenerate electrons, dynamic degenerate ions, and non-relativistic beam electrons by using \(H=0.007\) and \(\beta =10^{-5}\). The phase velocity of the electron-acoustic waves changes linearly in this low-frequency limit case.

We observe a behavior almost similar to what we saw in our previous studies (Ikramullah et al. 2017, 2018). The corresponding ion and the non-relativistic beam electrons wave frequencies increase as \(K \rightarrow 0\) by increasing the value of the quantum parameter. The beam and ion modes, both, behave in the same way. However, in this case, the low-frequency waves resulted from the beam of electrons are lower in frequency as compared to the low-frequency waves in the Thomas–Fermi distributed electrons (Ikramullah et al. 2018). Similarly, the frequency of ion-acoustic waves is also lower in the beam case than the Thomas–Fermi case.

4 Nonlinear Propagation of Intense Electromagnetic Waves Through Degenerate Plasma

We use the Klein–Gordon–Schrödinger–Maxwell model to study the propagation of intense CPEM wave through the 3-component plasma. We consider nonlinear effects produced from the coupling of a CPEM wave \(\textbf{A}= {\text{ A }}_0\big [\hat{\textbf{x}} \cos \big (k z-\omega t)\big )-\hat{\textbf{y}} \sin \big (kz-\omega t\big )\big ]\) with the 3-component relativistic degenerate plasma. Here, \(\omega\) and k are the angular frequency and wave number of the incident electromagnetic wave. We choose CPEM wave in a manner that the nonlinear term, which is proportional to \({\text{ A }}^2\) in the KGE and SEs, vanish. It is further assumed that the plasmas oscillate transversely to the propagation direction of electromagnetic wave and, therefore, we put \(\phi = 0\). Further, assuming that \(\psi _e\) and \(\psi _\nu\) are time dependent only, we get the following equations from the KGE. (1) and SE (4), respectively:

$$\begin{aligned} \hbar ^2\frac{\partial ^2\psi _{e}}{\partial t^2}+c^2\big (-i\hbar {\nabla }+e \textbf{A}\big )^2\psi _{e}+m^2_{e}c^4\psi _{e}=0, \end{aligned}$$
(20)

and

$$\begin{aligned} i\hbar \frac{\partial \psi _\nu }{\partial t}=\frac{q^2A^2}{2m_\nu }\psi _\nu . \end{aligned}$$
(21)

By putting the value of \(\textbf{A}\), and further simplifying the above equations Eqs. (20) and (23), we get

$$\begin{aligned} \hbar ^2\frac{\partial ^2\psi _e}{\partial t^2}+m^2_e c^4\gamma _A\psi _e=0, \end{aligned}$$
(22)

and

$$\begin{aligned} i\hbar \frac{\partial \psi _\nu }{\partial t}=\frac{q^2A^2_0}{2m_\nu }\psi _\nu . \end{aligned}$$
(23)

Here, \(\gamma _A =\Big (1+e^2{\text{ A }}^2_0/m^2_e c^2\Big )^{1/2}\) is the relativistic gamma factor signifying an increase in the mass of electron due to interaction with the intense CPEM waves. The solution of Eqs. (22) and (23) are:

$$\begin{aligned} \psi _e=&\psi _{0e} \text {exp}\big (-im_e c^2 \gamma _A t/\hbar \big ), \end{aligned}$$
(24)
$$\begin{aligned} \psi _\nu =&\psi _{0\nu } \text {exp}\big (-ie^2{A}^2_0 t/2m_\nu \hbar \big ). \end{aligned}$$
(25)

The electron number density in equilibrium can be determined by putting Eq. (24) in Eq. (2), and using \(\rho _{e}=-en_{0e}\) as,

$$\begin{aligned}&|\psi _{0e}|^{2}=n_{0e}/\gamma _A. \end{aligned}$$
(26)

Similarly, the unperturbed ion (non-relativistic beam electrons) number density is calculated by putting \(\rho _\nu =qn_{0\nu }\) and Eq. (25) in Eq. (5),

$$\begin{aligned}&|\psi _{0\nu }|^{2}=n_{0\nu }. \end{aligned}$$
(27)

The current densities are calculated by using Eq. (24) in Eq. (3) and Eq. (25) in Eq. (6) as

$$\begin{aligned}&\textbf{J}_{e}=-\frac{e^{2}|\psi _{0e}|^{2}}{m_e}\textbf{A}=-\frac{e^{2}n_{0e}}{\gamma _A m_e}{} \textbf{A}, \end{aligned}$$
(28)

and

$$\begin{aligned}&\textbf{J}_\nu =-\frac{q^2|\psi _{0\nu }|^{2}}{m_\nu }\textbf{A}=-\frac{q^2n_{0\nu }}{m_\nu }{} \textbf{A}. \end{aligned}$$
(29)

Using Eqs. (28) and (29), and the expression of total current density \(\textbf{J}_T\) in Eq. (9), we get the following relation:

$$\begin{aligned}&\frac{1\partial ^{2}{} \textbf{A}}{c^2\partial t^{2}} -\nabla ^{2}{} \textbf{A}=-\frac{\mu _0e^2n_{0e}}{\gamma _Am_e}\textbf{A}-\frac{\mu _0q^2n_{0\nu }}{m_\nu }{} \textbf{A}. \end{aligned}$$
(30)

By putting the value of \(\textbf{A}\) in Eq. (30), we get the nonlinear dispersion relation as in follow:

$$\begin{aligned} \omega ^2=k^2c^2+\frac{\omega ^2_{pe}}{\gamma _A} +\sum _{\nu =i,eb} \omega ^2_{p\nu }. \end{aligned}$$
(31)

If ions are considered to be static, the nonlinear dispersion relation changes to the following relation:

$$\begin{aligned} \omega ^2=k^2c^2+\frac{\omega ^2_{pe}}{\gamma _A}+\omega ^2_{peb}. \end{aligned}$$
(32)
Fig. 3
figure 3

Plots showing dispersion of incident waves for \((\beta = 0.00001, 0.001, 0.1)\) and \(a_0 = 01\)

Full size image

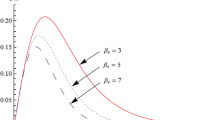
Figure 3 shows the dispersion of carrier waves for different \(\beta\) (non-relativistic quantum beam electrons concentration) at fixed wave amplitude. It is observed that the opacity of the plasma increases with the increase in \(\beta\).

5 Stimulated Raman Scattering and Modulational Instabilities

In the simulated Raman scattering (SRS), the decay of CPEM wave results in a scattered electromagnetic wave and an electron plasma wave. We assume the ions to be static, serving as a uniform neutralizing background. For simplicity, we introduce the transformation \(\psi _{e}=\widetilde{\psi }_e\text {exp}\big (-i m_e \gamma _A c^2 t/\hbar \big )\), where \(\gamma _A=\sqrt{1+e^2 {\text{ A }}^2_0/m^2_e c^2}\) is the gamma factor and \(\mathbf{\text{ A }}_0\) is the amplitude of the incident CPEM wave. The modified wave function \(\widetilde{\psi }_e\) then obeys the KGE in the following form:

$$\begin{aligned}&\left( i\hbar \frac{\partial }{\partial t}+\gamma _A m_e c^2+e\phi \right) ^2 \widetilde{\psi }_e-c^2\left( -i\hbar {\nabla }+e \textbf{A}\right) ^2\widetilde{\psi }_e-\nonumber \\&m^2_e c^4\widetilde{\psi }_e=0, \end{aligned}$$
(33)

The charge density then takes the following form:

$$\begin{aligned}&\rho _e=\frac{-ie\hbar }{2 m_e c^2}\left( \widetilde{\psi }^{*}_e\frac{\partial \widetilde{\psi }_e}{\partial t}-\widetilde{\psi }_e\frac{\partial \widetilde{\psi }^{*}_e}{\partial t}\right) -\left( \gamma _A+\frac{e\phi }{m_e c^2}\right) e|\widetilde{\psi }_e|^2. \end{aligned}$$
(34)

The system of Eqs. (4), (9), (10), (33), and (34) in the SRS case are linearized by using \(\widetilde{\psi }_{e}(\textbf{r},t)=\widetilde{\psi }_{0e}+\widetilde{\psi }_{1e}(\textbf{r},t)\), \({\psi }_{eb}(\textbf{r},t)={\psi }_{0eb}+{\psi }_{1eb}(\textbf{r},t)\), \(\textbf{A}(\textbf{r},t)=\textbf{A}_0(\textbf{r},t)+\textbf{A}_1(\textbf{r},t)\) and \(\phi (\textbf{r},t)=\phi _1(\textbf{r},t)\) to obtain the following linearized equations:

$$\begin{aligned}{} &{} \hbar ^2\left( -\frac{\partial ^2\widetilde{\psi }_{1e}}{\partial t^2}+c^2\nabla ^2\widetilde{\psi }_{1e}\right) +2i\hbar \gamma _Am_e c^2\frac{\partial \widetilde{\psi }_{1e}}{\partial t} \nonumber \\{} & {} \quad +2i\hbar c^2e \textbf{A}_0\cdot {\nabla }\widetilde{\psi }_{1e} +e\left( 2\gamma _Am_e c^2\phi _1+i\hbar \frac{\partial \phi _1}{\partial t}\right) \widetilde{\psi }_{0e}\nonumber \\{} & {} \quad -2c^2e^2\textbf{A}_0\cdot \textbf{A}_1\widetilde{\psi }_{0e}=0, \end{aligned}$$
(35)
$$\begin{aligned}{} & {} \nabla ^2\phi _1=\frac{ie\hbar }{2\epsilon _0m_e c^2}\Big (\widetilde{\psi }^{*}_{0e}\frac{\partial \widetilde{\psi }_{1e}}{\partial t}-\widetilde{\psi }_{0e}\frac{\partial \widetilde{\psi }^{*}_{1e}}{\partial t}\Big ) \nonumber \\{} & {} \quad +\frac{e\gamma _A}{\epsilon _0}\Big (\widetilde{\psi }^{*}_{0e}\widetilde{\psi }_{1e}+\widetilde{\psi }^{*}_{1e}\widetilde{\psi }_{0e}\Big )+\frac{\omega ^2_{pe}}{\gamma _A c^2}\phi _1\nonumber \\{} & {} \quad +\frac{e}{\epsilon _0}\Big ({\psi }^{*}_{0eb}{\psi }_{1eb}+{\psi }^{*}_{1eb}{\psi }_{0eb}\Big ), \end{aligned}$$
(36)
$$\begin{aligned}{} & {} i\hbar \frac{\partial \psi _{eb}}{\partial t}+e\psi _{0eb}\phi _1=\frac{1}{2m_e}\Big (-\hbar ^2{\nabla }^2+2e^2\psi _{0eb}\mathbf{A_0}\cdot \mathbf{A_1}\Big )\psi _{eb} \end{aligned}$$
(37)
$$\begin{aligned}{} & {} \nabla ^2\Big (\frac{\partial ^2 \textbf{A}_1}{\partial t^2}-c^2\nabla ^2\textbf{A}_1+\frac{\omega ^2_{pe}}{\gamma _A}{} \textbf{A}_1 +\omega _{peb}^2\mathbf{A_1}\Big )\nonumber \\{} & {} \quad =\frac{\omega ^2_{pe}}{n_{0e}}\nabla \times \big ({\nabla } \times \big ( \textbf{A}_0\big (\widetilde{\psi }^{*}_{0e}\widetilde{\psi }_{1e}+\widetilde{\psi }^{*}_{1e}\widetilde{\psi }_{0e}\big )\big )\big ) \nonumber \\{} & {} \quad +\frac{\omega ^2_{peb}}{n_{0eb}}\nabla \times \big ({\nabla } \times \big ( \textbf{A}_0\big (\psi ^{*}_{0eb}\psi _{1eb}+\psi ^{*}_{1eb}\psi _{0eb}\big )\big )\big ) \end{aligned}$$
(38)

The term \(\textbf{A}_0\cdot {\nabla }\widetilde{\psi }_{1e}\) in the Eq. (35) is associated with the two-plasmon decay, which will not be considered in this study. In what follows, we use the following Fourier representations: \(\widetilde{\psi }_{1e}=\widehat{\psi }_{+e} \exp \big [i\big (\textbf{K}\cdot \textbf{r}-\Omega t\big )\big ]+\widehat{\psi }_{-e} \exp \big [-i\big (\textbf{K}\cdot \textbf{r}-\Omega t\big )\big ],\) \(\psi _{1eb}=\widehat{\psi }_{+eb} \exp \big [i\big (\textbf{K}\cdot \textbf{r}-\Omega t\big )\big ]+\widehat{\psi }_{-eb} \exp \big [-i\big (\textbf{K}\cdot \textbf{r}-\Omega t\big )\big ],\) \(\phi _1=\widehat{\phi } \exp \big [i\big (\textbf{K}\cdot \textbf{r}-\Omega t\big )\big ]+c.c.,\) \(\textbf{A}_0=(1/2)\widehat{\textbf{A}}_0 \exp \big [i\big (\mathbf{k_0}\cdot \textbf{r}-\omega _0 t\big )\big ]+c.c.\) and \(\textbf{A}_1=\widehat{\textbf{A}}_{+} \exp \big [i\big (\textbf{k}_+\cdot \textbf{r}-\omega _+ t\big )\big ]+\widehat{\textbf{A}}_{-} \exp \big [-i\big (\textbf{k}_-\cdot \textbf{r}-\omega _- t\big )\big ]+c.c.\) where \(\omega _{\pm }=\omega _0\pm \Omega\) and \(\textbf{k}_{\pm }=\textbf{k}_0\pm \textbf{K}\).

Now Fourier decomposing Eqs. (35), (36), (37), and (38), and eliminating different Fourier coefficients, we get the dispersion relation as follows:

$$\begin{aligned}&1+\frac{\gamma _AB}{\omega ^2_{pe}}- \frac{4\gamma _A\omega ^2_{peb}m^2_eB}{\omega ^2_{pe}AC}= \Bigg [\frac{(-\Omega ^{'2}+\omega ^2_{pe}/\gamma _A)}{A}+\nonumber \\&\quad \frac{4\omega ^2_{peb}m^2_e\Omega ^{'2}}{A C}+ \frac{\omega ^2_{peb}K^2\hbar ^2\Omega ^{'2}}{c^2AC}- \frac{4\gamma ^2_Am_e^2c^2K^2\omega ^2_{peb}}{AC}+\nonumber \\&\quad \frac{8\gamma _A\omega ^2_{peb}c^2K^2m^2_e}{AC} - \frac{\gamma _A\omega ^2_{peb}K^2(\hbar ^2\Omega ^{'4}-4\gamma ^2_Am_e^2c^4\Omega ^2)}{c^2\omega ^2_{pe} AC}\Bigg ]\nonumber \\&\quad \times c^2e^2M^\prime , \end{aligned}$$
(39)

where

$$\begin{aligned} M^\prime =\,\,&\frac{{\mid \textbf{k}_+\times \widehat{\textbf{A}}_0\mid }^2}{\textbf{k}^2_+{D_A}(\omega _+,\textbf{k}_+)}+ \frac{{\mid \textbf{k}_-\times \widehat{\textbf{A}}_0\mid }^2}{\textbf{k}^2_-{D_A}(\omega _-,\textbf{k}_-)},\\ A=\,\,&(4\gamma ^2_Am_e^2c^4-\hbar ^2\Omega ^{'2}), \\ B=\,\,&(\hbar ^2\Omega ^{'4}-4\gamma ^2_Am^2_ec^4\Omega ^2),\\ C=\,\,&(4m^2_e\Omega ^2-\hbar ^2K^4),\\ \Omega ^{'2}=\,\,&(\Omega ^2-c^2K^2). \end{aligned}$$

Here, relation \(D_A(\omega _{\pm },k_{\pm })=c^2k^2_{\pm }-\omega ^2_{\pm }+\omega ^2_{pe}/\gamma _A+\omega ^2_{peb}\) governs the electromagnetic side-bands.

Fig. 4
figure 4

Plots displaying the SRS growth rate as function of the wavenumbers \({K_\parallel }\) and \({ K}_\perp\) for \(H=0.007\), for CPEM amplitudes \(a_0 = 1.0, 5.0, 20.0\), and for the beam electrons concentration, \(\beta =10^{-5}\)

Full size image
Fig. 5
figure 5

Plots depicting the growth rate of the MI as a function of the wave numbers \({K_\parallel }\) and \({ K}_\perp\) for CPEM amplitude of \(a_0=1.0,5.0,20\), quantum parameter \(H= 0.007,\), and beam electrons concentration, \(\beta =10^{-5}\)

Full size image
Fig. 6
figure 6

Figure depicting the growth rate of the SBS as a function of the wavenumbers \({K_\parallel }\) and \({ K}_\perp\) for the quantum parameter \(H=0.007\), CPEM amplitude \(a_0 = 1.0, 5.0, 20.0\) and beam concentration, \(\beta =10^{-5}\)

Full size image

To evaluate the nonlinear dispersion relation Eq. (39) numerically, we use a coordinate system such that \(\textbf{k}_0=k_0\widehat{\textbf{z}}\) and \(\widehat{\textbf{A}}_0={A}_0(\widehat{\textbf{x}}+i\widehat{\textbf{y}})\). We take \(\textbf{K} = K_\parallel \widehat{\textbf{z}}+K_\perp \widehat{\textbf{y}}\). Therefore, we have \(K^2=K^2_\perp +K^2_\parallel\), \(\gamma _A = \sqrt{(1+e^2|\widehat{A}_0|^2/m^2_{\mu }c^2)}\), \(|\textbf{k}_\pm \times \widehat{\textbf{A}}_0|^2=|{\widehat{A}}_0|^2[2(k_0\pm K_\parallel )^2+K^2_\perp ]\) and \(k^2_\pm =K^2_\perp +(k_0\pm K_\parallel )^2\). The incident wave \(\textbf{A}_0\) obeys the nonlinear dispersion relation given by: \(\omega _0=\sqrt{c^2k^2_0+\omega ^2_{peb}+\omega ^2_{pe}/\gamma _A}\).

Now, we assume that \(\Omega = \Omega _R +i\Omega _I\), where \(\Omega _R\) and \(\Omega _I\) are the real part of the frequency and the growth rate, respectively, and we solve the Eq. (39) numerically.

In Fig. 4, we have shown the growth rate of the SRS instability in the 3-component relativistic quantum plasma with quantum parameter H = 0.007 for different CPEM wave amplitudes. As was observed in Refs. (Eliasson and Shukla 2011; Ikramullah et al. 2017) for the 2- and 3-component plasma, we observe a spread in the spectrum with the increasing amplitude of the CPEM wave. The growth rate increases with an increase in the amplitude of the CPEM wave and has an optimum value at \(a_0=05\).

Figure 5 shows the growth rate of the MI at various wave amplitudes, and at quantum parameter \(H = 0.007\). As was noticed in the case of the Raman scattering, one can see that both the spectrum and the growth rate reaches to an optimum value at \(a_0 = 5.0\) and then drops as one moves to the higher CPEM wave amplitudes.

6 Stimulated Brillouin (SBS) Scattering

In the SBS instability, an incident electromagnetic wave changes to a low-frquency ion-acoustic wave associated with the ions density fluctuations and a high-frequency scattered electromagnetic wave. In the 3-component plasma undertaken here, the KGE describes the collective oscillatory motion of electrons in the plasma. The linearized KGE for electrons coupled with the CPEM waves is given by Eq. (35). The ions (non-relativistic beam electrons) dynamics is modeled by the Schrödinger equation coupled to the CPEM wave through Poisson and Maxwell equations. By using \(\widetilde{\psi }_\nu (\textbf{r}, t)=\widetilde{\psi }_{0\nu }+\widetilde{\psi }_{1\nu }(\textbf{r}, t)\), \(\phi (\textbf{r}, t)=\phi _1(\textbf{r}, t)\) and \(\textbf{A}(\textbf{r}, t)=\textbf{A}_0(\textbf{r}, t) +\textbf{A}_1(\textbf{r}, t)\), the linearized Schrödinger equation is rewritten here while neglecting the term proportional to the Two-Plasmon Decay.

$$\begin{aligned} i\hbar \frac{\partial }{\partial t}\psi _{1\nu }-q\psi _{0\nu }\phi _1=\,&\frac{1}{2m_\nu }\left( -\hbar ^2\nabla ^2\psi _{1\nu }+\right. \nonumber \\&\left. 2c^2\psi _{0\nu } \textbf{A}_0\cdot \textbf{A}_1\right) \end{aligned}$$
(40)

The linearized wave and Poisson equations given by Eqs. (9) and (10) in case of dynamical ions then take the following form:

$$\begin{aligned} \nabla ^2\phi _1=&\frac{ie\hbar }{2\epsilon _0m_e c^2}\left( \widetilde{\psi }^{*}_{0e}\frac{\partial \widetilde{\psi }_{1e}}{\partial t}-\widetilde{\psi }_{0e}\frac{\partial \widetilde{\psi }^{*}_{1e}}{\partial t}\right) \nonumber \\&+\frac{e\gamma _A}{\epsilon _0}\left( \widetilde{\psi }^{*}_{0e}\widetilde{\psi }_{1e}+\widetilde{\psi }^{*}_{1e} \widetilde{\psi }_{0e}\right) +\frac{\omega ^2_{pe}}{\gamma _A c^2}\phi _1\nonumber \\&-\sum _{\nu =i,eb}\frac{q}{\epsilon _0}\big (\psi _{0\nu }\psi ^{*}_{1\nu }+\psi ^{*}_{0\nu }\psi _{1\nu }\big ), \end{aligned}$$
(41)

and

$$\begin{aligned}&\nabla ^2\left( \frac{\partial ^2 A_1}{\partial t^2}-c^2\nabla ^2A_1+\frac{\omega ^2_{pe}}{\gamma _A}A_1+\sum _{\nu =i,eb}\omega ^2_{p\nu }A_1\right) \nonumber \\&\quad =\frac{\omega ^2_{pe}}{n_{0e}} \nabla \times \big (\nabla \times \big ( A_0\big (\widetilde{\psi }^{*}_{0e}\widetilde{\psi }_{1e}+ \widetilde{\psi }^{*}_{1e}\widetilde{\psi }_{0e}\big )\big )\big ) \nonumber \\&\quad\quad +\sum _{\nu =i,eb}\frac{\omega ^2_{p\nu }}{n_{0\nu }}\nabla \times \big (\nabla \times \big ( A_0\big ({\psi }^{*}_{0\nu }{\psi }_{1\nu }+{\psi }^{*}_{1\nu }{\psi }_{0\nu }\big )\big )\big ). \end{aligned}$$
(42)

Now Fourier decomposing the above equations by using \(\psi _{1\nu }=\widehat{\psi }_{+\nu }\exp \big [i\big (\textbf{K}\cdot \textbf{r}-\Omega t \big )\big ]+\widehat{\psi }_{-\nu }\exp \big [-i\big (K\cdot \textbf{r}-\Omega t \big )\big ],\) \(\phi _1=\widehat{\phi }\exp \big [i\big (\textbf{K}\cdot \textbf{r}-\Omega t\big )\big ]+c.c.,\) \(\widetilde{\psi }_{e}=\widehat{\psi }_{+e}\exp \big [i\big (i\textbf{K}\cdot \textbf{r}-i\Omega t\big )\big ]+\widehat{\psi }_{-e}\exp \big [-i\big (\textbf{K}\cdot \textbf{r}-i\Omega t\big )\big ],\) \(\textbf{A}_0=\frac{1}{2}\widehat{\textbf{A}}_0\exp \big [i\big (\mathbf{k_0}\cdot \textbf{r}-\omega _0 t\big )\big ]+c.c.,\) \(\textbf{A}_1=\widehat{\textbf{A}}_{+}\exp \big [i\big (\textbf{k}_+\cdot \textbf{r}-\omega _+ t\big )\big ]+\widehat{\textbf{A}}_{-}\exp \big [i\big (\textbf{k}_-\cdot \textbf{r}-\omega _- t\big )\big ]+c.c.,\) where \(\omega _{\pm }=\omega _0\pm \Omega\) and \(\textbf{k}_{\pm }=\textbf{k}_0\pm \textbf{K}\) and c.c. denotes the complex conjugate.

We now separate the Fourier modes by using the Fourier decomposition in Eqs. (35), (40), (41), and (42), and eliminating different Fourier coefficients, we get the nonlinear dispersion relation in the following form:

$$\begin{aligned}&1+\frac{\gamma _AB}{\omega ^2_{pe}A}- \frac{4\gamma _A\omega ^2_{pi}m^2_iB}{\omega ^2_{pe}AD}- \frac{4\gamma _A\omega ^2_{peb}m^2_eB}{\omega ^2_{pe}AC} =\nonumber \\&\quad \Bigg [\frac{(-\Omega ^{'2}+\omega ^2_{pe}/\gamma _A)}{A}+ \frac{4\omega ^2_{pi}m^2_i\Omega ^{'2}}{AD}+ \frac{\omega ^2_{pi}K^2\hbar ^2\Omega ^{'2}}{c^2A D}- \nonumber \\&\quad \frac{4\gamma ^2_Am_e^2c^2K^2\omega ^2_{pi}}{AD}- \frac{8\gamma _A\omega ^2_{pi}c^2K^2m_e m_i}{AD} - \frac{\gamma _A\omega ^2_{pi}K^2B}{c^2\omega ^2_{pe} AD}+ \nonumber \\&\quad \frac{4\omega ^2_{peb}m^2_e\Omega ^{'2}}{AC}+ \frac{\omega ^2_{peb}K^2\hbar ^2\Omega ^{'2}}{c^2AC}- \frac{4\gamma ^2_Am_e^2c^2K^2\omega ^2_{peb}}{AC}+ \nonumber \\&\quad \frac{8\gamma _A\omega ^2_{peb}c^2K^2m^2_e }{AC} - \frac{\gamma _A\omega ^2_{peb}K^2B}{c^2\omega ^2_{pe} AC}+ \nonumber \\&\quad \frac{4\gamma _A\omega _pi^2\omega ^2_{peb}K^2(m_e+m_i)^2B}{c^2\omega ^2_{pe} ACD}\Bigg ]\times c^2e^2M^\prime , \end{aligned}$$
(43)

where

$$\begin{aligned} M^\prime =\,\,&\frac{{\mid \textbf{k}_+\times \widehat{A}_0\mid }^2}{{ k}^2_+{D_A}(\omega _+,\textbf{k}_+)}+ \frac{{\mid \textbf{k}_-\times \widehat{A}_0\mid }^2}{{ k}^2_-{D_A}(\omega _-,\textbf{k}_-)},\\ D=\,\,&(4m^2_i\Omega ^2-\hbar ^2K^4). \end{aligned}$$

Here, \({D_A}(\omega _{\pm },\textbf{k}_{\pm })=c^2k^2_{\pm }-\omega ^2_{\pm }+\sum \limits _{\nu =i,eb}\omega ^2_{p\nu }+\omega ^2_{pe}/\gamma _A\) governs the electromagnetic sidebands.

In case of SBS, \(\Omega<<cK\), therefore, we neglect \(\Omega ^2\) and its higher powers. We, therefore, get the following expression from the nonlinear dispersion relation Eq. (43):

$$\begin{aligned}&1+\frac{\gamma _Ac^2E}{\omega ^2_{pe}F}- \frac{4\gamma _A\omega ^2_{pi}m^2_ic^2E}{\omega ^2_{pe}ED}- \frac{4\gamma _A\omega ^2_{peb}m^2_ec^2E}{\omega ^2_{pe}FC} \nonumber \\&\quad =\Bigg [\frac{(c^2K^2+\omega ^2_{pe}/\gamma _A)}{c^2F}- \frac{4\omega ^2_{pi}m^2_iK^2}{FD}-\frac{\omega ^2_{pi}K^4\hbar ^2}{c^2FD} \nonumber \\&\quad -\frac{4\gamma ^2_Am_e^2K^2\omega ^2_{pi}}{(FD}- \frac{8\gamma _A\omega ^2_{pi}K^2m_e m_i}{FD} - \frac{\gamma _A\omega ^2_{pi}K^2E}{c^2\omega ^2_{pe} FD}\nonumber \\&\quad -\frac{4\omega ^2_{peb}m^2_eK^2}{FC}-\frac{\omega ^2_{peb}K^4\hbar ^2}{c^2FC}- \frac{4\gamma ^2_Am_e^2K^2\omega ^2_{peb}}{FC} \nonumber \\&\quad +\frac{8\gamma _A\omega ^2_{pb}K^2m_e m_e}{(4\gamma ^2_Am_e^2c^2+\hbar ^2K^2)(4m^2_e\Omega ^2-\hbar ^2K^4)} -\frac{\gamma _A\omega ^2_{peb}K^2E}{c^2\omega ^2_{pe} FC} \nonumber \\&\quad +\frac{4\gamma _A\omega _pi^2\omega ^2_{peb}K^2(m_e+m_i)^2E}{\omega ^2_{pe} FDC}\Bigg ]\times c^2e^2M^{\prime \prime }, \end{aligned}$$
(44)

where

$$\begin{aligned} M^{\prime \prime }=&\frac{{\mid \textbf{k}_+\times {\widehat{\textbf{A}}_0}\mid }^2}{{ k^2}_+(c^2{ k}^2_+-(\omega ^2_0+2\omega _0\Omega )+\omega ^2_{pe}/\gamma _A+\sum \limits _{\nu =i,eb}\omega ^2_{p\nu })}+\\&\frac{{\mid \textbf{k}_-\times \widehat{\textbf{A}_0}\mid }^2}{{ k^2}_-(c^2{ k}^2_--(\omega ^2_0-2\omega _0\Omega )+\omega ^2_{pe}/\gamma _A+\sum \limits _{\nu =i,eb}\omega ^2_{p\nu })},\\ E=&(\hbar ^2K^4-4\gamma ^2_Am_e^2\Omega ^2), \\ F=&(4\gamma ^2_Am^2_ec^2+\hbar ^2K^2). \end{aligned}$$

To solve Eq. (44) numerically, we use the same coordinate system as was used in the case of SRS and we simplify various expressions in a fashion similar to what employed in the case of Eq. (39).

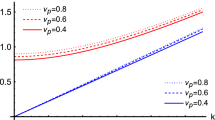
From Fig. 6, we observe that the spectrum spreads with the increasing values of the CPEM amplitude, and the growth rate is maximum at \(a_0 = 05\). We also note that the growth rate of the instability enhances and that the spectrum spreads with an increase in the beam electrons concentration.

Our study shows a signature of strong correlation between the growth rates of these instabilities and the relativistic quantum parameter H. This suggests a strong association between the particles collective motion at the quantum scale and the dispersive properties of the plasma, thus, affecting the growth rates of the parametric instabilities as was earlier observed by Shukla and Stenflo Ref. (Shukla and Stenflo 2006).

7 Conclusion

The extension of the models developed in Refs. (Eliasson and Shukla 2011; Ikramullah et al. 2017) is carried out for the 3-component relativistic quantum plasma comprising of relativistic degenerate electrons, dynamic degenerate ions, and non-relativistic quantum beam of electrons. The KGE is used for the relativistic degenerate electrons, while the dynamical degenerate ions and the non-relativistic beam of degenerate electrons are modeled through the SEs. Four modes have been observed in the dispersion. These modes are affected by a change in the quantum parameter (the density) of the plasma. The interaction of the intense CPEM waves with the 3-component quantum plasma shows that while an increase in the CPEM amplitude leads to self-induced transparency due to the relativistic mass increase, the addition of non-relativistic degenerate electron beam increases the plasma opacity. The growth rates of both the SRS and the SBS instabilities reduce with an increase in the quantum parameter H, and the scattering spectra get restricted to small wave-number regions. Whereas the spectra of these parametric instabilities remain largely insensitive to the changes in the beam concentration for small amplitude CPEM waves, the spectra change significantly with a change in the beam concentration when CPEM waves of large amplitude interact with the 3-component plasma. Furthermore, the growth rates increase with an increase in the non-relativistic electrons beam concentration. The width of the scattering spectra increases with an increase in the amplitudes of the CPEM wave. The growth-rate first enhances and then reduces with the increasing intensity of the CPEM wave. The growth rate of the MI also shows dependence on the quantum parameter as well as on the beam concentration.