1 Introduction

The significant part of contents in numerical analysis field is designing and analyzing of efficient algorithms to meet demands that have been appeared in other sciences. Among the available methods, the operational matrix methods (omm) have dedicated itself a lot of researches. These methods are based on expansion of all functions in the problem under investigation with various basic functions and using popular matrices which are named omi and operational matrix of differentiation (omd). Different functions and polynomials have been extensively utilized as basic functions by mathematicians to approximate the solution of underlying problem. For examples, Chebyshev polynomials have been employed by Heydari et al. to solve variable order fractional biharmonic equation and nonlinear Ginzburg–Landau equation in Heydari and Avazzadeh (2018) and Heydari et al. (2019), respectively. Abbasbandy et al. (2015) applied Legendre functions to estimate the solution of time fractional convection-diffusion equation. An applicable technique based on Bernoulli polynomials together with its accuracy analysis has been introduced by Singh et al. (2018). Euler polynomials have been used as basic functions in Balcı and Sezer (2016) to find the numerical solution of generalized linear Fredholm integro-differential difference equations. A numerical technique based on Bernstein polynomials has been improved by Chen et al. to estimate the solution of variable order linear cable equation in Chen et al. (2014). Finally, block-pulse functions have been proposed by Maleknejad et al. (2012), delta functions have been used by Roodaki and Almasieh (2012), triangular functions have been employed by Asgari and Khodabin (2017), hat functions have been suggested by Tripathi et al. (2013), to solve various and numerous problems of mathematics.

Fractional calculus has gained the attention of scholars as a mathematical modeling tool to describe occurred phenomena in many various disciplines. Fractional order models are more appropriate than integer order models to survey the behavior of processes with memory and hereditary features. The mathematical scientists have to focus on numerical schemes due to only a few number of such equations have analytical solution. The many efforts of researchers to estimate the solution of fractional problems have led to the development of various numerical techniques. The common methods are wavelet method (ur Rehman and Khan 2011), operational matrix methods (Mirzaee and Samadyar 2019; Rahimkhani et al. 2017), Galerkin method (Kamrani 2016), collocation method (Rahimkhani et al. 2019), finite difference method (Li et al. 2011), finite element method (Li et al. 2018), meshless method (Mirzaee and Samadyar 2019), spectral element method (Dehghan and Abbaszadeh 2018), the multistep Laplace optimized decomposition method (Maayah et al. 2022), etc.

Existence of various stochastic perturbation factors and production of powerful computing tools have led us that occurred phenomena in real life are modeled via different types of stochastic problems to reveal more accurate details in behavior description of such phenomena. In addition to no having the exact solution of such equations in many situations, it is also difficult obtaining their numerical solution. Thereby among introduced schemes in published papers, one method can play a more important role among other numerical methods if it produces more accurate results and can be extended to solve other problems. Finite difference method which has been utilized to solve linear stochastic integro-differential equations in Dareiotis and Leahy (2016) can be caused many difficulties in real life problems. For instance, discretization of domain and generating meshes is a time consuming and costly activity. Furthermore, some finite difference ideas are unconditionally stable. In the last decade, omm have been extremely used to obtain sufficiently high accuracy and alleviate accumulation of truncated error, complexity, computational operations and CPU times. For example, it has been greatly utilized to solve stochastic Volterra–Fredholm integral equations in Khodabin et al. (2012). Stochastic Volterra integral equations has been numerically solved by this method based on block-pulse and triangular functions in Maleknejad et al. (2012) and Khodabin et al. (2013), respectively. Samadyar et al. introduced orthonormal Bernoulli polynomials and applied them to approximate solution of stochastic Itô–Volterra integral equations of Abel type in Samadyar and Mirzaee (2020). In Heydari et al. (2016), omm based on second kind Chebyshev wavelets has been suggested by Heydari et al. to achieve an accurate numerical solution of stochastic heat equation. Shifted Legendre Spectral Collocation Algorithm has been applied to investigate the existence and uniqueness of the solution of fractional stochastic integro differential equations and obtain its numerical simulation in Badawi et al. (2022). The approximate solution of fractional stochastic integro differential equations using Legendre-shifted spectral approach and Legendre Gauss spectral collocation method has been presented by Badawi et al. in the papers Badawi et al. (2023a, b), respectively.

Sheng et al. (2011) introduced vofBm in the Riemann–Liouville sense as follows:

$$\begin{aligned} B^{H(t)}(t)=\frac{1}{\Gamma (H(t)+\frac{1}{2})}\int _0^t (t-s)^{H(t)-\frac{1}{2}}\rm{d}B(s), \end{aligned}$$
(1)

where \(H(t)\in (0,1)\). Notice that specific situations of this process are classical fBm and sBm that obtain by considering \(H(t)=H\) and \(H(t)=\frac{1}{2}\), respectively. Although solving stochastic problems driven by sBm and classical fBm is difficult, there have been more works on the numerical solution of such equations rather than the numerical solution of stochastic problems driven by vofBm. Providing a flexible method together with analyzing its convergence to solve stochastic evolution equations driven by fBm has been done in Kamrani and Jamshidi (2017). Nonlinear stochastic Itô–Volterra integral equations driven by fBm have been solved by omm based on hat functions and modification of hat functions in Hashemi et al. (2017) and Mirzaee and Samadyar (2018), respectively. It is essential that mentioned that classical fBm is appropriate only for modeling mono fractal phenomena which have similar global irregularity and fixed memory. On the other hand, global self-similarity is rarely appeared and fixed scaling is only satisfied for a series of certain finite intervals. Moreover, experimental data show that scaling exponent and order of similarity have multivalues and there exist phenomena in real life which have multifractal properties with variable space and time dependent memory. Thus, vofBm is a suitable way to overcome these limitations and it has been recently used for modeling events with variable irregularities or variable memory properties.

Suppose that \(B^{H(t)}(t), t\ge 0\), be a vofBm process which is defined in Eq. (1). An differential equation of the form Heydari et al. (2019)

$$\begin{aligned} {\left\{ \begin{array}{ll} \rm{d}U(t)=\mu \bigl (t,U(t)\bigl )\rm{d}t+\sigma \bigl (t,U(t)\bigl )\rm{d}B^{H(t)}(t), t\in [0,1],\\ U(0)=U_0, \end{array}\right. } \end{aligned}$$
(2)

where the functions \(\mu (u,t)\) and \(\sigma (u,t)\) are known smooth functions and U(t) is an unknown stochastic process defined on a certain probability space \((\Omega , {\mathcal {F}},{\mathcal {P}})\), is named nonlinear SDE driven by vofBm. The process B(t) denotes a sBm defined on same probability space and \(U_0\) is a given deterministic initial value. The functions \(\mu (u,t)\) and \(\sigma (u,t)\) are called the coefficients of this equation.

Equation of the form (2) is seen in modeling various problems such as signal processing (Sheng et al. 2012), geophysics (Echelard et al. 2010), financial time series (Corlay et al. 2014), but unfortunately its exact solution in many situations is not available. In the present time, it is very difficult to solve the nonlinear SDEs driven by vofBm either analytically or numerically. So, there are not many published literatures on this subject. In this paper, we introduced an efficient idea to find the numerical solution of nonlinear SDE expressed in Eq. (2). The structure of this method is such that it first transform the mentioned SDE into a corresponding SIE driven by vofBm and expand all functions in the obtained SIE with Bernoulli polynomials. In the sequel, stochastic omi driven by vofBm based on Bernoulli polynomials is derived, and then it together with ordinary omi are used to convert solving the mentioned problem into solving a set of nonlinear equations. That way, we try to find the numerical solution of this equation with higher accuracy and lower computational performance. The most important advantages of the presented method are as follows:

  • Using this method, equation under consideration is converted to a system of algebraic equations which can be easily solved. Therefore, the complexity of this equation, which is caused by fractional and stochastic terms, becomes very simple.

  • The unknown coefficients of the approximation of the function with these basis are easily calculated without any integration. Therefore, the computational cost of the proposed numerical method is low.

  • Because of the simplicity of Bernoulli polynomials, this method is a powerful mathematical tool to solve various kinds of equations with little additional works. In other words, Bernoulli polynomials are the simple basis functions, so the proposed method is easy to implement and it is a powerful mathematical tool to obtain the numerical solution of various kind of problems with little additional works.

  • The proposed scheme is convergent. Also, when the exact solution of the problem is a polynomial of degree n, we obtain the exact solution.

The outline of the rest of this paper is organized as follows. Simulation of vofBm by using block-pulse and hat functions has been done in Sect. 2. The definition of Bernoulli polynomials and some of their properties are presented in Sect. 3. In Sect. 4, a numerical method for solving the nonlinear SDEs driven by vofBm is proposed. The error analysis has been investigated in Sect. 5. The numerical results and application of under consideration problem in real world are carried out in Sect. 6 and Sect. 7, respectively. Finally, the conclusion is included in the Sect. 8.

2 Simulation of vofBm

.

2.1 Variable Order Fractional Integral Operator

Definition 1

Suppose that \(\alpha (t)\ge 0\) is a known continuous function. The Riemann–Liouville fractional integral of function f(t) of variable order \(\alpha (t)\) is defined as follows (Chen et al. 2014):

$$\begin{aligned} \bigl ({\mathcal {I}}^{\alpha (t)}f\bigl )(t)={\left\{ \begin{array}{ll} \frac{1}{\Gamma (\alpha (t))}\int _0^t (t-s)^{\alpha (t)-1}f(s)ds,&{}\alpha (t)>0,\\ f(t),&{} \alpha (t)=0. \end{array}\right. } \end{aligned}$$
(3)

2.2 The Block-Pulse Functions

Definition 2

(Maleknejad et al. 2012) Consider a vector of block-pulse functions with \(\hat{m}\) components over the interval \([0,{\textbf {T}})\) as follows:

$$\begin{aligned} \overrightarrow{\Phi _{\hat{m}}}(t)=[\phi _1(t),\phi _2(t),\ldots ,\phi _{\hat{m}}(t)]^T, \end{aligned}$$
(4)

where the ith components of this vector is defined by

$$\begin{aligned} \phi _i(t)={\left\{ \begin{array}{ll} 1,&{}(i-1)\frac{{\textbf {T}}}{\hat{m}}\le t<i\frac{{\textbf {T}}}{\hat{m}},\\ 0,&{}\text {otherwise}, \end{array}\right. }i=1,2,\ldots , \hat{m}. \end{aligned}$$
(5)

Any absolutely integrable function f(t), defined over the interval \([0,{\textbf {T}})\), can be expanded by \(\hat{m}\) terms of block-pulse functions as follows:

$$\begin{aligned} f(t)\simeq f_{\hat{m}}(t)=\sum _{i=1}^{\hat{m}} f_i\phi _i(t)=\overrightarrow{F_{\hat{m}}}^T\overrightarrow{\Phi _{\hat{m}}}(t), \end{aligned}$$
(6)

where \(\overrightarrow{\Phi _{\hat{m}}}(t)\) is defined in Eq. (4) and \(\overrightarrow{F_{\hat{m}}}=[f_1,f_2,\ldots ,f_{\hat{m}}]^T\). Furthermore, ith component of vector \(\overrightarrow{F_{\hat{m}}}\) is calculated by the following relation

$$\begin{aligned} f_i&=\frac{\hat{m}}{{\textbf {T}}}\int _{(i-1)\frac{{\textbf {T}}}{\hat{m}}}^{i\frac{{\textbf {T}}}{\hat{m}}}f(t)\phi _i(t)\rm{d}t=\frac{\hat{m}}{{\textbf {T}}}\int _{(i-1)\frac{{\textbf {T}}}{\hat{m}}}^{i\frac{{\textbf {T}}}{\hat{m}}}f(t)\rm{d}t\nonumber \\&\simeq f\Bigl (\frac{(2i-1){\textbf {T}}}{2\hat{m}}\Bigl ), \ i=1,2,\ldots , \hat{m}. \end{aligned}$$
(7)

Remark 1

(Kilicman and Al Zhour 2007) Integration and differentiation of block-pulse functions vector \(\overrightarrow{\Phi _{\hat{m}}}(t)\) for l-times is approximated as follows:

$$\begin{aligned}&\underbrace{\int _0^t \ldots \int _0^t}_{l\text {-times}}\overrightarrow{\Phi _{\hat{m}} }(s)ds\simeq {\textbf {I}}_{\hat{m}}^{(l)}\overrightarrow{\Phi _{\hat{m}}}(t),\ \frac{d^l\overrightarrow{\Phi _{\hat{m}}}(t)}{\rm{d}t^l}\simeq {\textbf {D}}_{\hat{m}}^{(l)}\overrightarrow{\Phi _{\hat{m}}}(t), \end{aligned}$$
(8)

where \({\textbf {I}}_{\hat{m}}^{(l)}\) and \({\textbf {D}}_{\hat{m}}^{(l)}\) are called block-pulse omi and omd of l-times, respectively, and are given by

$$\begin{aligned} {\textbf {I}}_{\hat{m}}^{(l)}=\Bigl (\frac{{\textbf {T}}}{\hat{m}}\Bigl )^l\frac{1}{(l+1)!}\begin{pmatrix} 1&{}\xi _1&{} \xi _2 &{}\ldots &{} \xi _{\hat{m}-1}\\ 0&{}1&{}\xi _1 &{}\ldots &{}\xi _{\hat{m}-2}\\ 0&{}0&{}1&{}\ldots &{}\xi _{\hat{m}-3}\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}\ldots &{}1 \end{pmatrix}_{\hat{m}\times \hat{m}}, \end{aligned}$$
(9)

and

$$\begin{aligned} {\textbf {D}}_{\hat{m}}^{(l)}=(l+1)!\Bigl (\frac{\hat{m}}{{\textbf {T}}}\Bigl )^l\begin{pmatrix} 1&{}\zeta _1&{} \zeta _2 &{}\ldots &{} \zeta _{\hat{m}-1}\\ 0&{}1&{}\zeta _1 &{}\ldots &{}\zeta _{\hat{m}-2}\\ 0&{}0&{}1&{}\ldots &{}\zeta _{\hat{m}-3}\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}\ldots &{}1 \end{pmatrix}_{\hat{m}\times \hat{m}}, \end{aligned}$$
(10)

where \(\xi _j=(j+1)^{l+1}-2j^{l+1}+(j-1)^{l+1}\) and \(\zeta _j=-\sum _{i=1}^j\xi _i \zeta _{j-i}\) and \(\zeta _0=1\).

2.3 The Hat Functions

Definition 3

(Hashemi et al. 2017) In a hat functions vector \(\overrightarrow{\Psi _{\hat{m}}}(t)=[\psi _0(t), \psi _1(t),\ldots , \psi _{\hat{m}-1}(t)]^T\) over the interval \([0,{\textbf {T}})\) with \(\hat{m}\) components, the first component is defined as follows:

$$\begin{aligned} \psi _0(t)={\left\{ \begin{array}{ll} \frac{h-t}{h},&{}0\le t<h,\\ 0,&{}\text {otherwise}. \end{array}\right. } \end{aligned}$$
(11)

The ith component is defined as follows:

$$\begin{aligned} \psi _i(t)={\left\{ \begin{array}{ll} \frac{t-(i-1)h}{h},&{} (i-1)h\le t<ih,\\ \frac{(i+1)h-t}{h},&{} ih\le t<(i+1)h,\\ 0,&{}\text {otherwise}, \end{array}\right. } \ i=1,2,\ldots , \hat{m}-2. \end{aligned}$$
(12)

Finally, the last component is defined as follows:

$$\begin{aligned} \psi _{\hat{m}-1}(t)={\left\{ \begin{array}{ll} \frac{t-({\textbf {T}}-h)}{h},&{} {\textbf {T}}-h\le t<{\textbf {T}},\\ 0,&{}\text {otherwise}, \end{array}\right. } \end{aligned}$$
(13)

where \(h=\frac{{\textbf {T}}}{\hat{m}-1}\).

Every continuous function g(t) can be approximated by using \(\hat{m}\) terms of hat functions as follows:

$$\begin{aligned} g(t)\simeq g_{\hat{m}}(t)= \sum _{i=0}^{\hat{m}-1} g_i\psi _i(t)= \overrightarrow{G_{\hat{m}}}^T\overrightarrow{\Psi _{\hat{m}}}(t), \end{aligned}$$
(14)

where \(\overrightarrow{G_{\hat{m}}}=[g_0,g_1,\ldots , g_{\hat{m}-1}]^T\), and \(g_i=g(ih)\) for \(i=0,1,\ldots , \hat{m}-1\).

Theorem 1

(Heydari et al. 2019) Consider positive continuous function \(\alpha (t): [0,{\textbf {T}})\rightarrow \mathbb {R}^+\) and hat functions vector \(\overrightarrow{\Psi _{\hat{m}}}(t)\). The Riemann–Liouville fractional integration \(\overrightarrow{\Psi _{\hat{m}}}(t)\) of variable order \(\alpha (t)\) is represented by \(\bigl ({\mathcal {I}}^{\alpha (t)}\overrightarrow{\Psi _{\hat{m}}}\bigl )(t)\), and is estimated as follows:

$$\begin{aligned} \bigl ({\mathcal {I}}^{\alpha (t)}\overrightarrow{\Psi _{\hat{m}}}\bigl )(t)\simeq {\textbf {L}}^{\alpha (t)}_{\hat{m}} \overrightarrow{\Psi _{\hat{m}}}(t), \end{aligned}$$
(15)

where \({\textbf {L}}^{\alpha (t)}_{\hat{m}}\) is called fractional omi of variable order \(\alpha (t)\) for hat functions and is computed as follows:

$$\begin{aligned} {\textbf {L}}^{\alpha (t)}_{\hat{m}}=\begin{pmatrix} 0&{} \rho _1 &{}\rho _2 &{} \ldots &{}\rho _{\hat{m}-2} &{}\rho _{\hat{m}-1}\\ 0 &{}\varrho _{1,1} &{}\varrho _{1,2} &{}\ldots &{}\varrho _{1,\hat{m}-2} &{}\varrho _{1,\hat{m}-1}\\ 0&{}0 &{}\varrho _{2,2} &{}\ldots &{}\varrho _{2,\hat{m}-2} &{}\varrho _{2,\hat{m}-1}\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}0&{}\ldots &{}\varrho _{\hat{m}-2,\hat{m}-2} &{}\varrho _{\hat{m}-2,\hat{m}-1}\\ 0&{}0&{}0&{} \ldots &{}0&{}\varrho _{\hat{m}-1,\hat{m}-1} \end{pmatrix}_{\hat{m}\times \hat{m}}, \end{aligned}$$
(16)

where

$$\begin{aligned} \rho _j=\frac{h^{\alpha (jh)}}{\Gamma (\alpha (jh)+2)}\Bigl ((j-1)^{\alpha (jh)+1}+j^{\alpha (jh)}\bigl (\alpha (jh)-j+1\bigl )\Bigl ),\ j=1,2,\ldots ,\hat{m}-1, \end{aligned}$$

and for \(i,j=1,\ldots ,\hat{m}-1\),

$$\begin{aligned} \varrho _{i,j}={\left\{ \begin{array}{ll} 0,&{} j<i,\\ \frac{h^{\alpha (jh)}}{\Gamma (\alpha (jh)+2)},&{} j=i,\\ \frac{h^{\alpha (jh)}}{\Gamma (\alpha (jh)+2)}\Bigl ((j-i+1)^{\alpha (jh)+1}-2(j-i)^{\alpha (jh)+1}+(j-i-1)^{\alpha (jh)+1}\Bigl ),&{} j>i, \end{array}\right. } \end{aligned}$$

Theorem 2

(Heydari et al. 2019) Assume that \(\overrightarrow{\Phi _{\hat{m}}}(t)\) and \(\overrightarrow{\Psi _{\hat{m}}}(t)\) denote the block-pulse and hat functions vectors, respectively. The vector \(\overrightarrow{\Phi _{\hat{m}}}(t)\) can be estimated as follows:

$$\begin{aligned} \overrightarrow{\Phi _{\hat{m}}}(t)\simeq {\textbf {R}}_{\hat{m}} \overrightarrow{\Psi _{\hat{m}}}(t), \end{aligned}$$
(17)

where \({\textbf {R}}_{\hat{m}}=({\textbf {r}}_{ij})\) is a matrix of order \(\hat{m}\times \hat{m}\) which its elements are computed from the following formula

$$\begin{aligned} {\textbf {r}}_{ij}=\phi _i\bigl ((j-1)h\bigl ),\ i,j=1,2,\ldots , \hat{m}. \end{aligned}$$
(18)

2.4 The vofBm Process Simulation

In this section, block-pulse and hat functions which are introduced in Subsects. 2.2 and 2.3 are employed to simulate the vofBm process. The strategy of constructing this stochastic process is divided into two parts. The sBm process is constructed in the first step by using the properties of this process and spline interpolation method. It is essential to mention that in this step other interpolation methods such as “linear”, “nearest”, “cubic” and “pchip” can be used instead of spline interpolation method. In the second step, first the simulated sBm process is estimated by block-pulse functions, and then, the relationship between block-pulse and hat functions is applied to obtain the vofBm process.

  1. Step 1.

    Simulation of sBm process: Let’s start by hinting the properties of sBm process. This process is denoted by \(B(t), t\in [0,{\textbf {T}}]\) and has the following properties (Mirzaee and Samadyar 2018):

    • \(B(0)=0\).

    • The increment \(B(t)-B(s)\) where \(0\le s<t\le {\textbf {T}}\) has normal distribution with mean 0 and variance \(t-s\), i.e., \(B(t)-B(s)\sim \sqrt{t-s}{\mathcal {N}}(0,1)\) such that \({\mathcal {N}}(0,1)\) denotes normal distribution with mean 0 and variance 1.

    • The increments \(B(t)-B(s)\) and \(B(v)-B(u)\), where \(0\le u<v<s<t\le {\textbf {T}}\) are independent.

    To construct sBm, first we choose a large positive integer number \(N\in \mathbb {Z}^+\) and let \(\delta t=\frac{{\textbf {T}}}{N}\). Then, we consider distinguished nodal points \(t_j=j\delta t\) for \(j=0,1,\ldots ,N\). The first condition of sBm tell us that \(B(0)=0\) with probability 1, and the second and third conditions ensure us that \(B(t_j)=B(t_{j-1})+\delta B(t_j)\) where \(j=1,2,\ldots ,N\), and \(\delta B(t_j) \sim \sqrt{\delta t}{\mathcal {N}}(0,1)\) is independent random variable. This procedure create a discretized sBm and then spline interpolation scheme is used to achieve a continuous function for sBm. The Matlab code for simulating sBm process over the interval [0, 1] with \(N=100\) has been presented in Algorithm 1. The command “randn” has been used to create a random number with normal distribution and mean 0 and variance 1.

  2. Step 2.

    Simulation of vofBm. As we mentioned in Sect. 2.2, every absolutely integrable function can be expanded in terms of block-pulse functions. So, the extension of sBm can be written as follows:

$$\begin{aligned} B(t)\simeq \overrightarrow{B_{\hat{m}}}^T\overrightarrow{\Phi _{\hat{m}}}(t), \end{aligned}$$
(19)

where \(\overrightarrow{B_{\hat{m}}}=[b_1,b_2,\ldots ,b_{\hat{m}}]^T\), \(b_i\simeq B\Bigl (\frac{(2i-1){\textbf {T}}}{2\hat{m}}\Bigl )\) for \(i=1,2,\ldots , \hat{m}\), and the block-pulse vector \(\overrightarrow{\Phi _{\hat{m}}}(t)\) has been introduced in Eq. (4). By substituting Eq. (19) into Eq. (1), we obtain

$$\begin{aligned} B^{H(t)}(t)\simeq \frac{1}{\Gamma (H(t)+\frac{1}{2})}\int _0^t (t-s)^{H(t)-\frac{1}{2}}d\bigl ( \overrightarrow{B_{\hat{m}}}^T\overrightarrow{\Phi _{\hat{m}}}(s)\bigl ). \end{aligned}$$
(20)

From Eqs. (8) and (17), we conclude

$$\begin{aligned} B^{H(t)}(t)&\simeq \frac{\overrightarrow{B_{\hat{m}}}^T{\textbf {D}}_{\hat{m}}^{(1)} {\textbf {R}}_{\hat{m}}}{\Gamma (H(t)+\frac{1}{2})}\int _0^t (t-s)^{H(t)-\frac{1}{2}}\overrightarrow{\Psi _{\hat{m}}}(s)ds\nonumber \\&=\overrightarrow{B_{\hat{m}}}^T{\textbf {D}}_{\hat{m}}^{(1)} {\textbf {R}}_{\hat{m}} \Bigl ({\mathcal {I}}^{H(t)+\frac{1}{2}}\overrightarrow{\Psi _{\hat{m}}}\Bigl )(t). \end{aligned}$$
(21)

Finally, Eq. (15) yields

$$\begin{aligned} B^{H(t)}(t) \simeq \overrightarrow{B_{\hat{m}}}^T{\textbf {D}}_{\hat{m}}^{(1)} {\textbf {R}}_{\hat{m}}{} {\textbf {L}}_{\hat{m}}^{H(t)+\frac{1}{2}}\overrightarrow{\Psi _{\hat{m}}}(t). \end{aligned}$$
(22)

The vofBm process simulation steps are summarized in Algorithm 2.

Algorithm 1.

Algorithm 2.

\(N=100\);

Input: \(\hat{m}, H(t)\).

\({\textbf {T}}=1\);

Output: \(B^{H(t)}(t)\).

\(\delta t\)=\(\frac{{\textbf {T}}}{N}\);

Step 1: Compute the value of \(h=\frac{{\textbf {T}}}{\hat{m}-1}\).

\({\textbf {for}}\) \(i=0:N\)

Step 2: Compute the vector \(\overrightarrow{B_{\hat{m}}}=[b_1,b_2,\ldots ,b_{\hat{m}}]^T\).

     \(t(i+1,1)=i\) \(\delta t\);

Step 3: Compute matrix \({\textbf {D}}_{\hat{m}}^{(l)}\) for \(l=1\) from Eq. (10).

\({\textbf {end}}\)

Step 4: Compute matrix \({\textbf {R}}_{\hat{m}}\) from Theorem 2.

\(B=\text {zeros}(N+1,1)\);

Step 4: Compute matrix \({\textbf {L}}_{\hat{m}}^{\alpha (t)}\) for \(\alpha (t)=H(t)+\frac{1}{2}\).

\({\textbf {for}}\) \(i=2:N+1\)

Step 5: Compute \(B^{H(t)}(t)\) from Eq. (22).

     \(B(i,1)=B(i-1,1)+\sqrt{\delta t}\) randn;

 

\({\textbf {end}}\)

 

sBm=plot(t, B);

 

3 Bernoulli Polynomials

Definition 4

(Bazm 2015) The Bernoulli polynomials satisfy in the following formula

$$\begin{aligned} \sum _{i=0}^j \left( {\begin{array}{c}j+1\\ i\end{array}}\right) {\mathfrak {B}}_i(t)=(j+1)t^j,\ j=0,1,2,\ldots . \end{aligned}$$
(23)

Equation (23) can be written in the following matrix form

$$\begin{aligned} {\textbf {G}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t)=\overrightarrow{X_{\hat{n}}}(t), \end{aligned}$$
(24)

where \(\overrightarrow{X_{\hat{n}}}(t)=[1,t,t^2,\ldots , t^{\hat{n}-1}]^T\), \(\overrightarrow{\Upsilon _{\hat{n}}}(t)=[{\mathfrak {B}}_0(t),{\mathfrak {B}}_1(t),\ldots , {\mathfrak {B}}_{\hat{n}-1}(t)]^T\) denotes Bernoulli basic vector, and \({\textbf {G}}_{\hat{n}}=({\textbf {g}}_{ij})\) is a lower triangular matrix of order \(\hat{n}\times \hat{n}\) and

$$\begin{aligned} {\textbf {g}}_{ij}={\left\{ \begin{array}{ll} \frac{1}{i}\left( {\begin{array}{l}i\\ j-1\end{array}}\right) ,&{}i\ge j,\\ 0,&{} i<j, \end{array}\right. } \ i,j=1,2,\ldots ,\hat{n}. \end{aligned}$$
(25)

Since all diagonal elements of matrix \({\textbf {G}}_{\hat{n}}\) are nonzero, then the matrix \({\textbf {G}}_{\hat{n}}\) is nonsingular and Bernoulli basic vector can be directly calculated from

$$\begin{aligned} \overrightarrow{\Upsilon _{\hat{n}}}(t)={\textbf {G}}_{\hat{n}} ^{-1}\overrightarrow{X_{\hat{n}}}(t). \end{aligned}$$
(26)

Every integrable function u(t) can be expanded by using \(\hat{n}\) terms of Bernoulli polynomials as follows:

$$\begin{aligned} u(t)\simeq u_{\hat{n}}(t)= \sum _{i=0}^{\hat{n}-1} u_i{\mathfrak {B}}_i(t)=\overrightarrow{U_{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t), \end{aligned}$$
(27)

where \(\overrightarrow{U_{\hat{n}}}=[u_0,u_1,\ldots ,u_{\hat{n}-1}]^T\), and the component \(u_i\) is computed from the following formula

$$\begin{aligned} u_i=\frac{1}{i!}\int _0^1 \frac{d^i u(t)}{\rm{d}t^i}\rm{d}t, i=0,1,\ldots , {\hat n}-1. \end{aligned}$$
(28)

Theorem 3

(Bazm 2015) The integral of Bernoulli vector \(\overrightarrow{\Upsilon _{\hat{n}}}(s)\) respect to variable s over the interval [0, t] can be estimated as follows:

$$\begin{aligned} \int _0^t \overrightarrow{\Upsilon _{\hat{n}}}(s)ds\simeq \overline{{\textbf {P}}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t), \end{aligned}$$
(29)

where the matrix \(\overline{{\textbf {P}}}_{\hat{n}}\) is named omi based on Bernoulli polynomials and is computed as follows:

$$\begin{aligned} \overline{{\textbf {P}}}_{\hat{n}}=\begin{pmatrix} -{\mathfrak {B}}_1(0)&{} 1&{}0&{} \ldots &{}0&{}0\\ -\frac{{\mathfrak {B}}_2(0)}{2}&{}0&{}\frac{1}{2}&{}\ldots &{}0&{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ -\frac{{\mathfrak {B}}_{\hat{n}-1}(0)}{\hat{n}-1} &{}0&{}0 &{}\ldots &{}0&{} \frac{1}{\hat{n}-1}\\ -\frac{{\mathfrak {B}}_{\hat{n}}(0)}{\hat{n}}&{}0&{}0&{}\ldots &{}0&{}0 \end{pmatrix}_{\hat{n}\times \hat{n}}. \end{aligned}$$
(30)

In the following, a theorem is stated for the first time in relation to stochastic omi driven by vofBm and then is proved by authors.

Theorem 4

The stochastic integral of Bernoulli polynomials vector \(\overrightarrow{\Upsilon _{\hat{n}}}(s)\) respect to vofBm \(B^{H(s)}(s)\) over the interval [0, t] can be approximated as follows:

$$\begin{aligned} \int _0^t \overrightarrow{\Upsilon _{\hat{n}}}(s)\rm{d}B^{H(s)}(s)\simeq \overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t), \end{aligned}$$
(31)

where \(\overline{{\textbf {P}}}_{\hat{n}}^s\) is a matrix of order \(\hat{n}\times \hat{n}\) and is called stochastic omi driven by vofBm. Also, we have \(\overline{{\textbf {P}}}_{\hat{n}}^s={\textbf {G}}^{-1}_{\hat{n}} {\textbf {A}}_{\hat{n}}{} {\textbf {G}}_{\hat{n}}\) where \({\textbf {A}}_{\hat{n}}=({\textbf {a}}_{ij})\) is a diagonal matrix with the following diagonal components

$$\begin{aligned} {\textbf {a}}_{ij}=\Bigl (1-\frac{i-1}{4}\Bigl )B^{H(0.5)}(0.5)-\Bigl (\frac{i-1}{2^{i-1}}\Bigl )B^{H(0.25)}(0.25), i=j=1,2,\ldots , \hat{n}. \end{aligned}$$
(32)

Proof

From Eq. (26), we have

$$\begin{aligned} \int _0^t \overrightarrow{\Upsilon _{\hat{n}}}(s)\rm{d}B^{H(s)}(s)={\textbf {G}}_{\hat{n}} ^{-1}\int _0^t \overrightarrow{X_{\hat{n}}}(s)\rm{d}B^{H(s)}(s). \end{aligned}$$
(33)

Using part by part integration idea, we conclude

$$\begin{aligned} \int _0^t \overrightarrow{X_{\hat{n}}}(s)\rm{d}B^{H(s)}(s)&=\begin{pmatrix} \int _0^t \rm{d} B^{H(s)}(s)\\ \int _0^t s \rm{d} B^{H(s)}(s) \\ \vdots \\ \int _0^t s^{\hat{n}-1}\rm{d} B^{H(s)}(s) \end{pmatrix}\nonumber \\&=\begin{pmatrix} B^{H(t)}(t)\\ tB^{H(t)}(t)-\int _0^t B^{H(s)}(s)ds \\ \vdots \\ t^{\hat{n}-1}B^{H(t)}(t)-\int _0^t (\hat{n}-1)s^{\hat{n}-2}B^{H(s)}(s)ds \end{pmatrix}\nonumber \\&=B^{H(t)}(t)\begin{pmatrix} 1\\ t\\ \vdots \\ t^{\hat{n}-1} \end{pmatrix}-\begin{pmatrix} 0\\ \int _0^t B^{H(s)}(s)ds \\ \vdots \\ \int _0^t (\hat{n}-1)s^{\hat{n}-2}B^{H(s)}(s)ds \end{pmatrix}. \end{aligned}$$

Let \(\overrightarrow{\Xi _{\hat{n}}}(t)=\int _0^t \overrightarrow{X_{\hat{n}}}(s)\rm{d}B^{H(s)}(s)\), where \(\overrightarrow{\Xi _{\hat{n}}}(t)=[\varpi _0(t), \varpi _1(t),\ldots , \varpi _{\hat{n}-1}(t)]^T\) and

$$\begin{aligned} \varpi _l(t)=t^lB^{H(t)}(t)-\int _0^t ls^{l-1}B^{H(s)}(s)ds, \ l=0,1,\ldots , \hat{n}-1. \end{aligned}$$
(34)

The existing integral in Eq. (34) is calculated via composite trapezoidal numerical integration rule. Thus, we obtain

$$\begin{aligned} \varpi _l(t)&\simeq t^lB^{H(t)}(t)-\frac{tl}{4}\Bigl (2\bigl (\frac{t}{2}\bigl )^{l-1}B^{H(\frac{t}{2})}\bigl (\frac{t}{2}\bigl )+t^{l-1}B^{H(t)}(t)\Bigl )\nonumber \\&=\Bigl (1-\frac{l}{4}\Bigl )t^lB^{H(t)}(t)-\Bigl (\frac{l}{2^l}\Bigl )t^lB^{H(\frac{t}{2})}\bigl (\frac{t}{2}\bigl )\nonumber \\&=\left( \Bigl (1-\frac{l}{4}\Bigl )B^{H(t)}(t)-\Bigl (\frac{l}{2^l}\Bigl )B^{H(\frac{t}{2})}\bigl (\frac{t}{2}\bigl )\right) t^l, \ l=0,1,\ldots , \hat{n}-1. \end{aligned}$$
(35)

The values of \(B^{H(t)}(t)\) and \(B^{H(\frac{t}{2})}\bigl (\frac{t}{2}\bigl )\) in Eq. (35) for \(0\le t\le 1\) can be approximated by \(\varpi :=B^{H(0.5)}(0.5)\) and \(\varrho :=B^{H(0.25)}(0.25)\), respectively. So, we can write

$$\begin{aligned} \overrightarrow{\Xi _{\hat{n}}}(t)&\simeq \underbrace{\begin{pmatrix} \varpi &{}0&{}\ldots &{}0\\ 0&{}\frac{3}{4}\varpi -\frac{1}{2}\varrho &{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{} \Bigl (1-\frac{\hat{n}-1}{4}\Bigl )\varpi -\Bigl (\frac{\hat{n}-1}{2^{\hat{n}-1}}\Bigl ) \varrho \end{pmatrix}}_{{\textbf {A}}_{\hat{n}}}\begin{pmatrix} 1\\ t\\ \vdots \\ t^{\hat{n}-1} \end{pmatrix}\nonumber \\&={\textbf {A}}_{\hat{n}}\overrightarrow{X_{\hat{n}}}(t). \end{aligned}$$
(36)

Using Eqs. (24), (33) and (36), we have

$$\begin{aligned} \int _0^t \overrightarrow{\Upsilon _{\hat{n}}}(s)\rm{d}B^{H(s)}(s)={\textbf {G}}_{\hat{n}} ^{-1}{} {\textbf {A}}_{\hat{n}}\overrightarrow{X_{\hat{n}}}(t)={\textbf {G}}_{\hat{n}} ^{-1}{} {\textbf {A}}_{\hat{n}}{} {\textbf {G}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t)=\overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t), \end{aligned}$$
(37)

where \(\overline{{\textbf {P}}}_{\hat{n}}^s ={\textbf {G}}_{\hat{n}} ^{-1}{} {\textbf {A}}_{\hat{n}}{} {\textbf {G}}_{\hat{n}}\). \(\square\)

4 Numerical Scheme

The nonlinear SDE (2) can be written in the following SIE form

$$\begin{aligned} U(t)=U_0+\int _0^t \mu \bigl (s,U(s)\bigl )ds+\int _0^t \sigma \bigl (s,U(s)\bigl )\rm{d}B^{H(s)}(s), \ t\in [0,1]. \end{aligned}$$
(38)

Let

$$\begin{aligned} \omega (t)=\mu \bigl (t,U(t)\bigl ), \ \theta (t)=\sigma \bigl (t,U(t)\bigl ). \end{aligned}$$
(39)

Thus, we should solve the following SIE driven by vofBm

$$\begin{aligned} U(t)=U_0+\int _0^t \omega (s)ds+\int _0^t \theta (s)\rm{d}B^{H(s)}(s), \ t\in [0,1]. \end{aligned}$$
(40)

From Eqs. (39) and (40), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \omega (t)=\mu \bigl (t,U_0+\int _0^t \omega (s)ds+\int _0^t \theta (s)\rm{d}B^{H(s)}(s)\bigl ),\\ \theta (t)=\sigma \bigl (t,U_0+\int _0^t \omega (s)ds+\int _0^t \theta (s)\rm{d}B^{H(s)}(s)\bigl ). \end{array}\right. } \end{aligned}$$
(41)

The unknown functions \(\omega (t)\) and \(\theta (t)\) can be expanded in terms of Bernoulli polynomials as follows:

$$\begin{aligned} \omega (t)\simeq \overrightarrow{\Omega _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t),\ \theta (t)\simeq \overrightarrow{\Theta _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t), \end{aligned}$$
(42)

where \(\overrightarrow{\Omega _{\hat{n}}}\) and \(\overrightarrow{\Theta _{\hat{n}}}\) are Bernoulli coefficient vectors of \(\omega (t)\) and \(\theta (t)\), respectively. By inserting the approximations (42) into Eq. (41), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \overrightarrow{\Omega _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t)=\mu \bigl ( t,U_0+\int _0^t \overrightarrow{\Omega _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(s)ds+\int _0^t \overrightarrow{\Theta _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(s)\rm{d}B^{H(s)}(s)\bigl ),\\ \\ \overrightarrow{\Theta _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t)=\sigma \bigl ( t,U_0+\int _0^t \overrightarrow{\Omega _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(s)ds+\int _0^t \overrightarrow{\Theta _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(s)\rm{d}B^{H(s)}(s)\bigl ). \end{array}\right. } \end{aligned}$$
(43)

Using operational matrices of integration defined in Eqs. (29) and (31), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \overrightarrow{\Omega _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t)=\mu \bigl ( t,U_0+ \overrightarrow{\Omega _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t) + \overrightarrow{\Theta _{\hat{n}}}^T \overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t)\bigl ),\\ \\ \overrightarrow{\Theta _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t)=\sigma \bigl ( t,U_0+ \overrightarrow{\Omega _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t) + \overrightarrow{\Theta _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t)\bigl ). \end{array}\right. } \end{aligned}$$
(44)

We consider \(\hat{n}\) Newton-Cotes collocation nodes which are calculated as follows:

$$\begin{aligned} t_l=\frac{2l+1}{2\hat{n}}, \ l=0,1,\ldots , \hat{n}-1. \end{aligned}$$
(45)

By inserting collocation points \(t_l\) into Eq. (44), we obtain the following nonlinear system of \(2\hat{n}\) algebraic equations and \(2\hat{n}\) unknowns

$$\begin{aligned} {\left\{ \begin{array}{ll} \overrightarrow{\Omega _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t_l)=\mu \bigl ( t_l,U_0+ \overrightarrow{\Omega _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t_l) + \overrightarrow{\Theta _{\hat{n}}}^T \overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t_l)\bigl ),\\ \\ \overrightarrow{\Theta _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t_l)=\sigma \bigl ( t_l,U_0+ \overrightarrow{\Omega _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t_l) + \overrightarrow{\Theta _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t_l)\bigl ). \end{array}\right. } \end{aligned}$$
(46)

The approximate solution of Eq. (2) is determined after solving system (46) and computing unknown vectors as follows:

$$\begin{aligned} U(t)\simeq U_{\hat{n}}(t)=U_0+\overrightarrow{\Omega _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t) + \overrightarrow{\Theta _{\hat{n}}}^T \overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t). \end{aligned}$$
(47)

The process of the proposed method is described in the step-by-step in Algorithm 3.

Algorithm 3.

Input: The number \(\hat{n}\), the vofBm \(B^{H(t)}(t)\), the initial value \(U_0\),

and the functions \(\mu , \sigma : [0,1]\times \mathbb {R} \rightarrow \mathbb {R}\).

Output:The numerical solution of \(U(t)\simeq U_0+\overrightarrow{\Omega _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t) + \overrightarrow{\Theta _{\hat{n}}}^T \overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t)\).

Step 1: Construct the vector \(\overrightarrow{\Upsilon _{\hat{n}}}(t)=[{\mathfrak {B}}_0(t),{\mathfrak {B}}_1(t),\ldots , {\mathfrak {B}}_{\hat{n}-1}(t)]^T\) which \({\mathfrak {B}}_i(t)\)

for \(i=0,1,\ldots , \hat{n}-1\) satisfied in Eq. (23).

Step 2: Let \(\omega (t)=\mu \bigl (t,U(t)\bigl )\) and \(\theta (t)=\sigma \bigl (t,U(t)\bigl )\).

Step 3: Define the Bernoulli coefficient vectors of \(\omega (t)\) and \(\theta (t)\) which are denoted by \(\overrightarrow{\Omega _{\hat{n}}}\) and \(\overrightarrow{\Theta _{\hat{n}}}\).

Step 4: Compute the matrix \(\overline{{\textbf {P}}}_{\hat{n}}\) using Eq. (30).

Step 5: Compute the matrix \({\textbf {G}}_{\hat{n}}=({\textbf {g}}_{ij})\), which \({\textbf {g}}_{ij}\) for \(i,j=1,2,\ldots , \hat{n}\) are computed

using Eq. (25).

Step 6: Compute the matrix \({\textbf {A}}_{\hat{n}}=({\textbf {a}}_{ij})\) , which \({\textbf {a}}_{ij}\) for \(i,j=1,2,\ldots , \hat{n}\) are computed

using Eq. (32).

Step 7: Calculate the matrix \(\overline{{\textbf {P}}}_{\hat{n}}^s ={\textbf {G}}_{\hat{n}} ^{-1}{} {\textbf {A}}_{\hat{n}}{} {\textbf {G}}_{\hat{n}}\).

Step 8: Consider \(\hat{n}\) Newton-Cotes collocation nodes \(t_l\) for \(l=0,1,\ldots , \hat{n}-1\) using Eq. (45).

Step 9: Put \({\left\{ \begin{array}{ll} \overrightarrow{\Omega _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t_l)=\mu \bigl ( t_l,U_0+ \overrightarrow{\Omega _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t_l) + \overrightarrow{\Theta _{\hat{n}}}^T \overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t_l)\bigl )\\ \overrightarrow{\Theta _{\hat{n}}}^T\overrightarrow{\Upsilon _{\hat{n}}}(t_l)=\sigma \bigl ( t_l,U_0+ \overrightarrow{\Omega _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}\overrightarrow{\Upsilon _{\hat{n}}}(t_l) + \overrightarrow{\Theta _{\hat{n}}}^T\overline{{\textbf {P}}}_{\hat{n}}^s \overrightarrow{\Upsilon _{\hat{n}}}(t_l)\bigl ) \end{array}\right. }\).

Step 10: Solve the nonlinear system in Step 9 and compute the unknown vectors \(\overrightarrow{\Omega _{\hat{n}}}\) and \(\overrightarrow{\Theta _{\hat{n}}}\).

5 Error Analysis

Theorem 5

(Tohidi et al. 2013) Suppose that f(t) is an infinity continuous function over the interval [0, 1] and \(f_{\hat{n}}(t)\) is the approximate function of f(t) via Bernoulli polynomials. The following upper error bound has been achieved

$$\left| {f(t) - f_{{\hat{n}}} (t)} \right| \le \frac{1}{{(\hat{n} - 1)!}}\mathop {\max }\limits_{{t \in [0,1]}} {{ }}{\mathfrak{B}}_{{\hat{n} - 1}} (t)\mathop {\max }\limits_{{t \in [0,1]}} \frac{{d^{{\hat{n} - 1}} f(t)}}{{dt^{{\hat{n} - 1}} }}.$$
(48)

Theorem 6

Assume that \(\omega (t)=\mu (t,U(t))\) and \(\theta (t)=\sigma (t,U(t))\) be the exact solutions of Eq. (41) such that satisfy in the Lipschitz condition, i.e.,

$$\begin{aligned} \vert \mu (t,U)-\mu (t,V) \vert +\vert \sigma (t,U)-\sigma (t,V)\vert \le {\mathcal {L}} \vert U-V\vert . \end{aligned}$$
(49)

Let

$$\begin{aligned} \omega _{\hat{n}}(t)=\mu \bigl (t,U_{\hat{n}}(t)\bigl ), \ \theta _{\hat{n}}(t)=\sigma \bigl ( t, U_{\hat{n}}(t)\bigl ), \end{aligned}$$
(50)

and consider

$$\begin{aligned} \omega _{\hat{n}}^{\hat{n}}(t)=\mu _{\hat{n}}\bigl (t,U_{\hat{n}}(t)\bigl ), \ \theta _{\hat{n}}^{\hat{n}}(t)=\sigma _{\hat{n}}\bigl ( t, U_{\hat{n}}(t)\bigl ), \end{aligned}$$
(51)

as the approximate solutions of the mentioned equation, where \(\omega _{\hat{n}}^{\hat{n}}(t)\) and \(\theta _{\hat{n}}^{\hat{n}}(t)\) are the estimation of \(\omega _{\hat{n}}(t)\) and \(\theta _{\hat{n}}(t)\) via Bernoulli polynomials. Also, suppose that the following assumption is satisfied

$$\begin{aligned} 1-{\mathcal {L}}-{\mathcal {H}}_{\hat{n}}{\mathcal {L}}>0. \end{aligned}$$
(52)

Then, the following upper error bound is obtained

$$\begin{aligned} \vert U(t)-U_{\hat{n}}(t)\vert \le \frac{{\mathcal {W}}_{\hat{n}}+{\mathcal {H}}_{\hat{n}}{\mathcal {T}}_{\hat{n}}}{1-{\mathcal {L}}-{\mathcal {H}}_{\hat{n}}{\mathcal {L}}}, \end{aligned}$$
(53)

where

$$\begin{aligned}&{\mathcal {H}}_{\hat{n}}=\max _{t\in [0,1]}B^{H(t)}(t),\nonumber \\&{\mathcal {W}}_{\hat{n}}=\max _{t\in [0,1]} \vert \omega _{\hat{n}}(t)-\omega _{\hat{n}}^{\hat{n}}(t)\vert =\frac{1}{(\hat{n}-1)!}\max _{t\in [0,1]}{\mathfrak {B}}_{\hat{n}-1}(t)\max _{t\in [0,1]}\frac{d^{\hat{n}-1}\omega _{\hat{n}}(t)}{\rm{d}t^{\hat{n}-1}},\\&{\mathcal {T}}_{\hat{n}}=\max _{t\in [0,1]}\vert \theta _{\hat{n}}(t)-\theta _{\hat{n}}^{\hat{n}}(t)\vert =\frac{1}{(\hat{n}-1)!}\max _{t\in [0,1]}{\mathfrak {B}}_{\hat{n}-1}(t)\max _{t\in [0,1]}\frac{d^{\hat{n}-1}\theta _{\hat{n}}(t)}{\rm{d}t^{\hat{n}-1}}.\nonumber \end{aligned}$$
(54)

Proof

According to Eq. (49) and Theorem 5, we have

$$\begin{aligned}&\vert \omega (t)-\omega _{\hat{n}}^{\hat{n}}(t)\vert \le \vert \omega (t)-\omega _{\hat{n}}(t)\vert +\vert \omega _{\hat{n}}(t)-\omega _{\hat{n}}^{\hat{n}}(t)\vert \le {\mathcal {L}}\vert U(t)-U_{\hat{n}}(t)\vert +{\mathcal {W}}_{\hat{n}},\nonumber \\&\vert \theta (t)-\theta _{\hat{n}}^{\hat{n}}(t)\vert \le \vert \theta (t)-\theta _{\hat{n}}(t)\vert +\vert \theta _{\hat{n}}(t)-\theta _{\hat{n}}^{\hat{n}}(t)\vert \le {\mathcal {L}}\vert U(t)-U_{\hat{n}}(t)\vert +{\mathcal {T}}_{\hat{n}}, \end{aligned}$$
(55)

where \({\mathcal {W}}_{\hat{n}}\) and \({\mathcal {T}}_{\hat{n}}\) have been defined in Eq. (54). On the other hand, the approximate solution of Eq. (40) is as follows:

$$\begin{aligned} U_{\hat{n}}(t)=U_0+\int _0^t \omega _{\hat{n}}^{\hat{n}}(s)ds+\int _0^t \theta _{\hat{n}}^{\hat{n}}(s)\rm{d}B^{H(s)}(s), \ t\in [0,1]. \end{aligned}$$
(56)

Equations (40) and (56) yield

$$\begin{aligned} \vert U(t)-U_{\hat{n}}(t)\vert \le \max _{t\in [0,1]}\vert \omega (t)-\omega _{\hat{n}}^{\hat{n}}(t)\vert +{\mathcal {H}}_{\hat{n}}\max _{t\in [0,1]}\vert \theta (t)-\theta _{\hat{n}}^{\hat{n}}(t)\vert , \end{aligned}$$
(57)

where \({\mathcal {H}}_{\hat{n}}=\max _{t\in [0,1]} B^{H(t)}(t)\). From Eqs. (55) and (57), we get

$$\begin{aligned} \vert U(t)-U_{\hat{n}}(t)\vert \le {\mathcal {L}} \vert U(t)-U_{\hat{n}}(t)\vert +{\mathcal {W}}_{\hat{n}}+{\mathcal {H}}_{\hat{n}}{\mathcal {L}}\vert U(t)-U_{\hat{n}}(t)\vert +{\mathcal {H}}_{\hat{n}}{\mathcal {T}}_{\hat{n}}. \end{aligned}$$
(58)

From Eqs. (58) and (52), we conclude

$$\begin{aligned} \vert U(t)-U_{\hat{n}}(t)\vert \le \frac{{\mathcal {W}}_{\hat{n}}+{\mathcal {H}}_{\hat{n}}{\mathcal {T}}_{\hat{n}}}{1-{\mathcal {L}}-{\mathcal {H}}_{\hat{n}}{\mathcal {L}}}. \end{aligned}$$
(59)

\(\square\)

Remark 2

Equation (53) tells us that if \(\hat{n}\rightarrow \infty\) then \({\mathcal {W}}_{\hat{n}},{\mathcal {T}}_{\hat{n}},{\mathcal {H}}_{\hat{n}}\rightarrow 0\), and therefore \(\frac{{\mathcal {W}}_{\hat{n}}+{\mathcal {H}}_{\hat{n}}{\mathcal {T}}_{\hat{n}}}{1-{\mathcal {L}}-{\mathcal {H}}_{\hat{n}}{\mathcal {L}}} \rightarrow 0\). It means that by increasing \(\hat{n}\), the approximate solution \(U_{\hat{n}}(t)\) tends to the exact solution U(t).

6 Numerical Results

Two numerical examples are solved in this section via proposed method to check applicability and computational efficiency of the suggested technique. In reporting the values of absolute errors (AEs) for some used Bernoulli polynomials \(\hat{n}\), we pursue two goals. The first goal is that the presented theoretical results in Sect. 5 are numerically investigated in this section, and the second goal is that presented numerical method is compared with Ccw method (Heydari et al. 2019).

Example 1

(Heydari et al. 2019) Consider the following SDE driven by vofBm

$$\begin{aligned} {\left\{ \begin{array}{ll} \rm{d}U(t)=\nu ^2 \cos \bigl (U(t)\bigl )\sin ^3 \bigl (U(t)\bigl )\rm{d}t-\nu \sin ^2\bigl (U(t)\bigl )\rm{d}B^{H(t)}(t),\\ U(0)=U_0, \end{array}\right. } \end{aligned}$$
(60)

such that its exact solution is given by

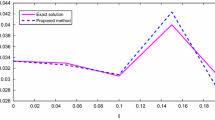
$$\begin{aligned} U(t)=\text {arccot}\bigl (\nu B^{H(t)}(t)+\cot (U_0)\bigl ). \end{aligned}$$
(61)

  • The presented method in the Sect. 4 has been employed to solve this example for three values \(\hat{n}=6,8,10\) and two functions \(H(t)=0.5+0.3\sin (\pi t)\) and \(H(t)=0.6-0.2\exp (-2t)\), and obtained AEs at some nodal points are reported in Tables 1 and 2, respectively. Other variable parameters are considered as \({\textbf {T}}=1, N=50, \hat{m}=100\), and \(U_0=\nu =\frac{1}{20}\). It is mentioned in Heydari et al. (2019) that the values of AEs obtained by considering \(M=3\) and \(k=3,4,5\). So, authors have applied Ccw vector with \(2^kM=24, 48, 96\) elements which this caused to generating larger matrices and more computations. The results of these tables reveal that our suggested method is more accurate and efficient than Ccw method, and indicate the effect of \(\hat{n}\) on the approximate solution. The value of \(\hat{n}\) have inverse relation with the values of AEs, and by increasing \(\hat{n}\) AEs decrease.

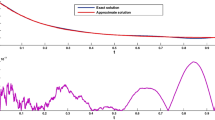
  • Also, the behavior of AEs by considering mentioned parameters is illustrated in Fig. 1. The truth of our claim that the values of AEs decrease by increasing Bernoulli vector’s size, can be more clearly seen from this diagram.

  • For investigating the effect of initial value and \(\nu\) on the values of AEs, we consider the rest of the parameters as \(N=100, \hat{m}=100, \hat{n}=6, {\textbf {T}}=1, H(t)=0.3+0.2\cos (-3t),\) and run the Matlab code for different values of \(U_0=\frac{1}{10}, \frac{1}{20}, \frac{1}{30}\) and \(\nu =\frac{1}{20}\). Once again, we consider the value of \(U_0=\frac{1}{20}\) fixed and run programming code for various values of \(\nu =\frac{1}{10}, \frac{1}{20}, \frac{1}{30}\). The obtained results are reported in Table 3 and are plotted in Fig. 2 which demonstrate that there is a direct relation between initial value and the values of AEs. Furthermore, the values of AEs are also related on \(\nu\) directly.

Table 1 Comparison of AEs of our method and Ccw method for Example 1 with \(H(t)=0.5+0.3\sin (\pi t)\)
Full size table
Table 2 Comparison of AEs of our method and Ccw method for Example 1 with \(H(t)=0.6-0.2\exp (-2t)\)
Full size table
Table 3 Investigating influence of the values \(U_0\) and \(\nu\) on the values of AEs
Full size table
Fig. 1
figure 1

The graph of AEs for Example 1 with two selected H(t)

Full size image
Fig. 2
figure 2

Investigating the effect of \(U_0\) (left) and parameter \(\nu\) (right) on the values of AEs

Full size image

Example 2

(Heydari et al. 2019) Consider the following SDE driven by vofBm

$$\begin{aligned} {\left\{ \begin{array}{ll} \rm{d}U(t)=\nu ^2 U(t)\bigl (U^2(t)-1\bigl )\rm{d}t+\nu \bigl (1-U^2(t)\bigl )\rm{d}B^{H(t)}(t),\\ U(0)=U_0, \end{array}\right. } \end{aligned}$$
(62)

such that its exact solution is given by

$$\begin{aligned} U(t)=\frac{(1+U_0)\exp (2\nu B^{H(t)}(t))+U_0-1}{(1+U_0)\exp (\nu B^{H(t)}(t))-U_0+1}. \end{aligned}$$
(63)

  • The presented method in the Sect. 4 has been employed to solve this example for three values \(\hat{n}=8,10,12\) and two functions \(H(t)=0.7+0.2\sin (\pi t)\) and \(H(t)=0.7-0.25\exp (-t)\), and obtained AEs at some nodal points are reported in Tables 4 and 5, respectively. Other variable parameters are considered as \({\textbf {T}}=1, N=50, \hat{m}=100\), \(U_0=0.01\), and \(\nu =\frac{1}{30}\). It is mentioned in Heydari et al. (2019) that the values of AEs obtained by considering \(M=2\) and \(k=4,5,6\). So, authors have applied Ccw vector with \(2^kM=32, 64, 128\) elements which this caused to generating larger matrices and more computations. The results of these tables reveal that our suggested method is more accurate and efficient than Ccw method, and indicate the effect of \(\hat{n}\) on the approximate solution. The value of \(\hat{n}\) have inverse relation with the values of AEs, and by increasing \(\hat{n}\) AEs decrease.

  • Also, the behavior of AEs by considering mentioned parameters is illustrated in Fig. 3. The truth of our claim that the values of AEs decrease by increasing Bernoulli vector’s size, can be more clearly seen from this diagram.

  • For investigating the effect of initial value and \(\nu\) on the values of AEs, we consider the rest of the parameters as \(N=100, \hat{m}=100, \hat{n}=8, {\textbf {T}}=1, H(t)=0.4+0.3t^2,\) and run the Matlab code for different values of \(U_0=0.01, 0.005, 0.001\) and \(\nu =\frac{1}{30}\). Once again, we consider the value of \(U_0=0.01\) fixed and run programming code for various values of \(\nu =\frac{1}{20}, \frac{1}{30}, \frac{1}{40}\). The obtained results are reported in Table 6 and are plotted in Fig. 4 which demonstrate that there is a direct relation between initial value and the values of AEs. Furthermore, the values of AEs are also related on \(\nu\) directly.

Table 4 Comparison of AEs of our method and Ccw method for Example 2 with \(H(t)=0.7+0.2\sin (\pi t)\)
Full size table
Table 5 Comparison of AEs of our method and Ccw method for Example 2 with \(H(t)=0.7-0.25\exp (-t)\)
Full size table
Table 6 Investigating influence of the values \(U_0\) and \(\nu\) on the values of AEs
Full size table
Fig. 3
figure 3

The graph of AEs for Example 2 with two selected H(t)

Full size image
Fig. 4
figure 4

Investigating the effect of \(U_0\) (left) and parameter \(\nu\) (right) on the values of AEs

Full size image

7 Application in Real World

One of the most well-known equation in the ecology science is logistic equation which has the following form

$$\begin{aligned} {\left\{ \begin{array}{ll} \rm{d}U(t)=rU(t)\bigl (1-\frac{U(t)}{\tau }\bigl )\rm{d}t,\\ U(0)=U_0. \end{array}\right. } \end{aligned}$$
(64)

In Eq. (64), \(U(t), \tau >0\) and r denote the population size at time t, carrying capacity of environment, and population growth rate, respectively. As we know, the rate of population growth is uncertain in real world and it can be perturbed by white noise process \(\xi (t)\) as \(r\rightarrow r+\nu \xi (t)\) where \(\xi (t)=\frac{\rm{d}B(t)}{\rm{d}t}\) and \(\nu\) is a constant number. So, the classical logistic equation (64) is transformed to the following stochastic logistic equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \rm{d}U(t)=rU(t)\bigl (1-\frac{U(t)}{\tau }\bigl )\rm{d}t+\nu U(t)\bigl (1-\frac{U(t)}{\tau }\bigl )\rm{d}B(t),\\ U(0)=U_0. \end{array}\right. } \end{aligned}$$
(65)

Since the rate of population growth depends on time t, it is better to study non-autonomous form of stochastic logistic equation which obtain from \(r\rightarrow r(t)+\nu (t)\xi (t)\). Furthermore, stochastic form of logistic equation driven by vofBm is introduced as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \rm{d}U(t)=r(t)U(t)\bigl (1-\frac{U(t)}{\tau }\bigl )\rm{d}t+\nu (t) U(t)\bigl (1-\frac{U(t)}{\tau }\bigl )\rm{d}B^{H(t)}(t),\\ U(0)=U_0. \end{array}\right. } \end{aligned}$$
(66)

The introduced method in Sect. 4 is applied to solve Eq. (66) for \(H(t)=0.5+0.3\cos (1000t)\) and \(H(t)=0.3+0.3\exp (-t)\) and obtained results are plotted in Fig. 5. Also, other parameters are considered as \(N=100, \hat{m}=100, \hat{n}=8, U_0=0.3, r(t)=0.2,\tau =1\) and three values \(\nu (t)=0, \nu (t)=0.8+0.2\cos (t)\) and \(\nu (t)= 0.7+0.2\sin (t)\).

Fig. 5
figure 5

Simulation of stochastic logistic equation behavior via suggested method

Full size image

8 Conclusion and Future Works

The studied model in this paper is a nonlinear SDE driven by vofBm that it has no analytical solution in many situations. On the other hand, the complexity of this model is so great that until now only one numerical method has been proposed to solve it. In order to solve this model, first we have derived stochastic omi driven by vofBm, then this operator together with ordinary omi based on Bernoulli polynomials are used to convert mentioned model to a nonlinear system of algebraic equations. The obtained system is solved via Newton’s numerical method and the approximate solution of this equation is achieved. In Sect. 5, we theoretically proved that by increasing the number of used Bernoulli polynomials \(\hat{n}\), the approximate solution tends to the exact solution. The effect of the number of used Bernoulli polynomials \(\hat{n}\), initial value \(U_0\), and constant coefficient \(\nu\), on the AEs values have been investigated in Sect. 6. Also, the presented method has been compared with Ccw method in the same section to confirm the superiority of our method respected to previous methods. The numerical results for different values of \(\hat{n}\) are reported in order to is established that by increasing \(\hat{n}\) the approximate solution converges to the exact solution. Reported numerical results in Sect. 6 confirm that one can obtain accurate approximate solution even by using small number of basic functions and performing few calculation efforts. Also, numerical results demonstrate that the values of \(U_0\) and \(\nu\) have an direct relationship with the values of AEs, i.e., by reducing the values of \(U_0\) and \(\nu\), the AEs values are also reduced. It seems that the values of N and \(\hat{m}\) are affected on the error values which investigation of this fact is recommended for future research works.