1 Introduction

At the beginning of the twentieth century, the general theory of relativity proposed by Albert Einstein changed the perception of the universe. This theory played a significant role in describing the geodesic nature of spacetime. Later, the general theory of relativity was successfully tested in the solar system tests, but it failed to describe all the gravity phenomena, including accelerated expansion, flatness issues, and fine-tuning problems. In the last few decades, the modern cosmological observations of the high redshift supernovae experiments confirmed that the expansion of the Universe is accelerating (Riess and Filippenko 1998; Perlmutter and Aldering 1999). Also, studies of the cosmic microwave background radiation (Spergel and Verde 2003; Bennett and Hill 2003; Spergel and Bean 2007) and large-scale structure (Tegmark and Strauss 2004; Tegmark and Blanton 2004) provide a shred of circumstantial support for the late time accelerated expansion of the universe. Modern research asserts that the expansion is instancing and examines the effect of a enigmatic Dark Energy, which has a critical pressure and positive energy density (Wetterich 1988; Amendola 2000; Caldwell 2002). However, no irrefutable evidence of the existence of Dark Energy has yet materialized. As a subsequence, many alternative theories have been proposed to explain this issue. It is suggested that the theory of general relativity can be modified to address the issue of cosmic expansion, potentially leading to a better understanding of the nature of gravity.

Mathematical modeling within the framework of the general theory of relativity has been used to explain the behavior and structure of massive objects such as neutron stars, quark stars, black holes, pulsars, and white dwarfs and requires finding the exact solutions of the Einstein-Maxwell system of field equations. Early attempts to seek solutions to the field equations were crude and for the most part unrealistic. A survey (Delgaty and Lake 1998) on exact solutions describing stellar objects revealed that only a limited subset of precise solutions pass the rigorous tests for physical viability, regularity, and stability of fluid spheres. Researchers had to link the observed macroscopic characteristics of stars to microphysics to find more accurate stellar models within general relativity. A new era of stellar modeling was begun, when the well-motivated techniques including assumptions on the metric potentials, density, pressure, electric field intensity, and even the matter content, were intrinsically connected to physics. General Relativity has been used successfully to anticipate various phenomena that Newtonian gravitation fails to explain. However, it failed to explain the accelerated expansion of the universe. Later, it is claimed that cosmic acceleration can be achieved by replacing or adding curvature invariants their corresponding generic functions in the geometric part of the Einstein-Hilbert action. Modified Gravity Theories have been suggested as a new paradigm for addressing the shortcomings of General theory of Relativity at the infrared and ultraviolet scales. By preserving the positive results of the General Theory of Relativity, the modified theory aims to address experimental and conceptual problems that have recently come to light in Cosmology, Astrophysics, and High Energy Physics.

Several modifications to general relativity have been made over the last decade to provide a natural gravitational alternative. Because of the cosmological significance of \(f(\mathcal {R})\) models, among the various modifications of gravity theory, \(f(\mathcal {R})\) theory of gravity is treated most suitable. Some viable \(f(\mathcal {R})\) models, which illustrate the unification of early time inflation and late time acceleration, can be found in Multamäki and Vilja (2006, 2007); Henttunen et al. (2008); Nojiri and Odintsov (2007); Shamir (2010). However, flaws in the solar system scale have been revealed, and it has been claimed that the \(f(\mathcal {R})\) theory does not appear to be adequate for the galactic scales (Rahaman et al. 2010).

In 2011, another extension of the general theory of relativity, the \(f(\mathcal {R},\mathcal {T})\) modified theory of gravity, was proposed by Harko and his accomplices (Harko et al. 2011). This was a generalization of \(f(\mathcal {R})\) gravity theory, where an arbitrary function of the trace of the stress-energy tensor \(\mathcal {T}\) and the Ricci scalar \(\mathcal {R}\) determine the gravitational Lagrangian. The authors claimed that these theories will provide better clarification of cosmic development. Using a Hilbert–Einstein-type variational principal, they have derived the system of field equations in the context of \(f(\mathcal {R},\mathcal {T})\) gravity and obtained the covariant divergence of the stress-energy tensor as well. The \(f(\mathcal {R},\mathcal {T})\) gravity model depends on a source term, which represents the variation of the matter stress-energy tensor for the metric. Because of the interaction between matter and geometry, the movement of test particles is non-geodesic and constantly accelerated. The \(f(\mathcal {R},\mathcal {T})\) theory portrays the regime of the solar system (Shabani and Farhoudi 2014) as well as the galactic impacts of dark matter (Zaregonbadi et al. 2016).

Soon after the inception of \(f(\mathcal {R},\mathcal {T})\) gravity, its cosmological and thermodynamic implications, such as the dynamical analysis and energy conditions, were extensively discussed. By taking several functional forms of f, numerous authors have investigated cosmological solutions in the framework of \(f(\mathcal {R},\mathcal {T})\) gravity (Shabani and Farhoudi 2014; Alvarenga et al. 2013; Sharif and Zubair 2012a, b; Jamil et al. 2012; Sharif and Zubair 2013; Xu et al. 2016). The feasibility of some \(f(\mathcal {R},\mathcal {T})\) models in the cosmological scenario has also been discussed (Velten and Caramês 2017; Godani 2019; Gamonal 2021). However, apart from the cosmological importance, \(f(\mathcal {R},\mathcal {T})\) theory of gravity can also be used as a test-bed for dealing with the strong-gravity regime such as compact stars. Based on the findings of cosmology and comparison with observational evidence, one cannot agree or disagree with such hypotheses (Maurya et al. 2020). To develop a satisfactory gravity theory, it is necessary to study gravity at the astrophysical level. The study of compact structures mainly concerns isotropic, anisotropic, and charged fluids. In the context of \(f(\mathcal {R},\mathcal {T})\) gravity, numerous works on the evolution of compact stars can be found in the literature. The matter inside compact stars is compressed at sufficiently high densities and the“escape velocity” near the surface approaches the speed of light. As a result, creating similar environments in a terrestrial laboratory is difficult, and we construct theoretical models to study the structural properties of these compact stars. Several theoretical compact star models have been developed by researchers, which provide required information about the features and evolution of these structures. Uncharged stellar models with isotropic pressure in \(f(\mathcal {R},\mathcal {T})\) gravity have been obtained in Hansraj (2018); Maurya et al. (2020); Kumar et al. (2021); Bhar et al. (2021, 2022). The stellar equilibrium configurations of compact stars have been investigated in the context of \(f(\mathcal {R},\mathcal {T})\) gravity (Deb et al. 2018; Pretel et al. 2021; Biswas et al. 2019; Lobato et al. 2020). For various charged and uncharged anisotropic models in \(f(\mathcal {R},\mathcal {T})\) gravity, one can see (Maurya and Tello-Ortiz 2020; Rahaman et al. 2020; Ilyas 2020; Bhar and Rej 2021; Rej and Bhar 2021; Bhar 2021).

Taking inspiration from the above literature survey, we study a new class of physical solutions of modified Einstein-Maxwell field equations for static and spherically symmetric charged isotropic fluid distribution within the framework of \(f(\mathcal {R},\mathcal {T})\) gravity. We choose the algebraic function \(f(\mathcal {R},\mathcal {T})\) to be a separable function, i.e., sum of two independent functions, of the form \(f(\mathcal {R},\mathcal {T}) = \mathcal {R}+ 2 f(\mathcal {T})\) (proposed by Harko et al. Bhar and Rej (2021)), where \(f(\mathcal {T})\) depend on the trace \(\mathcal {T}\). Due to the presence of nonlinear terms in the field equations, it is difficult to investigate exact the spherical solutions for relativistic compact objects. To overcome this problem, we used metric potentials as generating functions and went on to calculate energy density, electric field intensity, and pressure. We model an astrophysical compact configuration, namely ‘Hercules X-1’, and show that the obtained new exact solution is feasible.

This paper has the following flows:

Section 2: We introduce the Einstein-Maxwell system of field equations for a charged isotropic fluid sphere in \(f(\mathcal {R},\mathcal {T})\) gravity.

Section 3: We propose a model for charged isotropic compact stars by choosing Buchdahl ansatz (1959) and obtained expressions for modified energy density, modified pressure, etc.

Section 4: We discuss junction conditions for our model and determine the constants which have been used.

Section 5: We elaborate the physical requirements for acceptance of our model in \(f(\mathcal {R},\mathcal {T})\) gravity.

Section 6: We study the conditions for equilibrium and stability of our Model

Section 7: We analyze the physical features and stability of the presented compact stars model in \(f(\mathcal {R},\mathcal {T})\) gravity using graphs.

Section 8: We summarize our study on structural properties of compact star in \(f(\mathcal {R},\mathcal {T})\) gravity.

2 Einstein-Maxwell Field Equations in \(f(\mathcal {R},\mathcal {T})\) Gravity

The four-dimensional line element for static and spherically symmetric spacetime is given by,

$$\begin{aligned} {\rm d}s^2=-e^{\lambda (r)}\textrm{d}r^2+e^{\nu (r)}\textrm{d}t^2-r^2(\textrm{d}\theta ^2+{\rm sin}^2\theta \textrm{d}\phi ^2) \end{aligned}$$
(1)

where the metric potential functions \(e^\lambda\) and \(e^\nu\) are purely radial functions, with radial coordinate range \(0 \le r < \infty\), and they play a significant role in obtaining the mass function and the redshift function, respectively.

The \(f(\mathcal {R},\mathcal {T})\) action in a four-dimensional spacetime is given by

$$\begin{aligned} S=\frac{1}{2\kappa }\int {f(\mathcal {R},\mathcal {T})\sqrt{-g}d^4 x}+\int {\mathcal {L}_\mathcal {M} \sqrt{-g}d^4 x}+\int {\mathcal {L}_e \sqrt{-g}d^4 x} \end{aligned}$$
(2)

where, \({\kappa = \frac{8\pi G}{c^4}}\), with gravitational constant G and the speed of light c (in vacuum); \(f(\mathcal {R},\mathcal {T})\) is an arbitrary function of \(\mathcal {R}\) and \(\mathcal {T}\), \(\mathcal {R}\) is the Ricci scalar, and \(\mathcal {T}\) is the trace of the stress-energy tensor \(\mathcal {T}_{\xi \eta }\). Here, g is the determinant of the metric tensor \(g_{\xi \eta }\), \(\mathcal {L}_\mathcal {M}\) is the Lagrangian density of matter, and \(\mathcal {L}_e\) denote the Lagrangian for the electromagnetic field. The stress-energy tensor of matter can be defined as Landau (2013)

$$\begin{aligned} \mathcal {T}_{\xi \eta }=-\frac{2}{\sqrt{-g}} \frac{\delta (\sqrt{-g} \mathcal {L}_\mathcal {M})}{\delta \sqrt{g^{\xi \eta }}} \end{aligned}$$
(3)

and its trace is \(\mathcal {T}=g^{\xi \eta }\mathcal {T}_{\xi \eta }\). Now, we assume that the Lagrangian density \(\mathcal {L}_\mathcal {M}\) of matter is only dependent on the metric tensor components \(g_{\xi \eta }\) and not on its derivatives. As a result we obtain the following relation (Harko et al. 2011)

$$\begin{aligned} \mathcal {T}_{\xi \eta }=g_{\xi \eta }\mathcal {L}_\mathcal {M}-\frac{2\partial ( \mathcal {L}_\mathcal {M})}{\partial g^{\xi \eta }} \end{aligned}$$
(4)

Let \(E_{\xi \eta }\) be the electromagnetic energy-momentum tensor, defined as \(E_{\xi \eta }=\frac{2}{\kappa }\left( F^\alpha _\xi F_{\eta \alpha }-\frac{1}{4}F^{\alpha \beta } F_{\alpha \beta }g_{\xi \eta }\right)\). Let \(F_{\xi \eta }\) denote the anti-symmetric electromagnetic field strength tensor, defined by \(F_{\xi \eta } = \frac{\partial A_{\eta }}{\partial x_{\xi }}-\frac{\partial A_{\xi }}{\partial x_{\eta }}\) which satisfies Maxwells equations,

$$\begin{aligned} F_{\xi \chi ,\eta }+F_{\chi \eta ;\xi }+F_{\eta \xi ;\chi }=0 and F^{\xi \eta }_{;\eta }[\sqrt{-g} F^{\xi \eta }]=-\frac{\kappa }{2} J^{\xi } \end{aligned}$$

Here \(A_\eta = (\phi (r), 0, 0, 0)\) is the four-potential and \(J^{\xi }\) is the four electromagnetic current vector defined as \(J^\xi = \frac{\rho _e}{\sqrt{g_{00}}}\frac{dx^\xi }{dx^0}\), where \(\rho _e\) represents the proper charge density. For the static system, \(J^0\) is the only non-vanishing component of the four current. Thus, \(F^{01}\) and \(F_{10}\), the only two non-vanishing components of the electromagnetic field tensor, are related by \(F^{01}=F_{10}\). The expression for the electric field can be obtained as,

$$\begin{aligned} F^{01}=-e^{\frac{\lambda +\nu }{2}}\frac{q(r)}{r^2} \end{aligned}$$
(5)

where q(r), defined as

$$\begin{aligned} q(r)=\frac{\kappa }{2}\int _{0}^{r}\rho _e e^\frac{\lambda }{2}r^2\textrm{d}r \end{aligned}$$
(6)

represents the net charge inside a fluid sphere of radius r, which actually determines the electric field by

$$\begin{aligned} \mathcal {E}(r)=\frac{q(r)}{r^2} \end{aligned}$$
(7)

The field Eq. of \(f(\mathcal {R},\mathcal {T})\) gravity are obtained by varying the action S in Eq. 2 with respect to the metric tensor \(g_{\xi \eta }\) and given by

$$\begin{aligned} f_{{\mathcal{R}}} G_{{\xi \eta }} = \kappa ({\mathcal{T}}_{{\xi \eta }} + E_{{\xi \eta }} ) + {\triangledown }_{\xi } {\triangledown }_{\eta } f_{R} - g_{{\xi \eta }} \square f_{{\mathcal{R}}} \\ & + \frac{f}{2}g_{{\xi \eta }} - \frac{{\mathcal{R}}}{2}f_{{\mathcal{R}}} g_{{\xi \eta }} - f_{{\mathcal{T}}} ({\mathcal{T}}_{{\xi \eta }} + {\Psi }_{{\xi \eta }} ) \\ \end{aligned}$$
(8)

where \(f_\mathcal {R}=\frac{\partial f}{\partial \mathcal {R}}\) and \(f_T=\frac{\partial f}{\partial \mathcal {T}}\). The \(\bigtriangledown _{\xi }\) denotes covariant derivative, the operator \(\square\) is defined as \(\square =\frac{1}{\sqrt{-g}} \frac{\partial }{\partial x^{\xi }}(\sqrt{-g} g^{\xi \eta } \frac{\partial }{\partial x^{\eta }})\), and \(\varPsi _{\xi \eta }=g^{\alpha \beta }\frac{\delta \mathcal {T}_{\alpha \beta }}{\delta g^{\xi \eta }}\).

By performing the covariant derivative of Eq. (8), one can obtain the following expression (Barrientos and Rubilar 2014)

$${\triangledown }^{\xi } {\mathcal{T}}_{{\xi \eta }} = \frac{{f_{{\mathcal{T}}} }}{{\kappa - f_{{\mathcal{T}}} }}{\text{ }}\left[ {({\mathcal{T}}_{{\xi \eta }} + _{{\xi \eta }} ){\triangledown }^{\xi } \ln f_{{\mathcal{T}}} + {\triangledown }^{\xi } _{{\xi \eta }} \quad - \frac{1}{2}g_{{\xi \eta }} {\triangledown }^{\xi } {\mathcal{T}} - \frac{\kappa }{{f_{{\mathcal{T}}} }}{\triangledown }^{\xi } E_{{\xi \eta }} } \right].$$
(9)

We can verify from above equation that for \(F_\mathcal {T}(\mathcal {R},\mathcal {T})\ne 0\), \(\bigtriangledown ^{\xi } \mathcal {T}_{\xi \eta }\ne 0\). This implies that the stress-tensor \(T_{\xi \eta }\) in \(f(\mathcal {R},\mathcal {T})\) gravity does not obey the law of conservation as in Einstein general relativity. Using Eq. (4), we can obtain the tensor \(\varPsi _{\xi \eta }\) as

$$\begin{aligned} \varPsi _{\xi \eta }=-2\mathcal {T}_{\xi \eta }+g_{\xi \eta }\mathcal {L}_\mathcal {M} -2g^{\alpha \beta }\frac{\partial ^2 \mathcal {L}_\mathcal {M}}{\partial g^{\xi \eta }\partial g^{\alpha \beta }} \end{aligned}$$
(10)

Following (Bhar and Rej 2021), we consider the matter Lagrangian to be \(\mathcal {L}_\mathcal {M}=\rho\), where \(\rho (r)\) denote the matter density of the fluid configuration, and obtain Eq. (10) as

$$\begin{aligned} \varPsi _{\xi \eta }=-2\mathcal {T}_{\xi \eta }+\rho g_{\xi \eta } \end{aligned}$$
(11)

Further, to get the final form of the modified field equations, we need to know the functional \(f(\mathcal {R},\mathcal {T})\). Let us consider a separable functional form for \(f(\mathcal {R},\mathcal {T})\) given by, \(f(\mathcal {R},\mathcal {T})=\mathcal {R}+2\zeta \mathcal {T}\), where \(\zeta\) is a coupling constant. The assumed linear expression of \(f(\mathcal {R},\mathcal {T})\) has accepted physical advantages while addressing cosmological and astrophysical problems (Rahaman et al. 2020). The term \(2\zeta \mathcal {T}\) induces time-dependent interaction between matter and curvature. It also corresponds to \(\Lambda\) CDM model with a time-dependent cosmological constant (Bhar 2020). Using this definition of \(f(\mathcal {R},\mathcal {T})\), the field Eq. (8) takes the following form (Harko et al. 2011)

$$\begin{aligned} G_{\xi \eta }=\kappa \mathcal {T}_{\xi \eta }+\zeta \mathcal {T}g_{\xi \eta }+2\zeta \left( \mathcal {T}_{\xi \eta }-\rho g_{\xi \eta }\right) +\kappa E_{\xi \eta } \end{aligned}$$
(12)

It is clearly a simple nontrivial extrapolation of the Einstein to the \(f(\mathcal {R},\mathcal {T})\) paradigm. Note that, when \(\zeta =0\), i.e., \(f(\mathcal {R},\mathcal {T})\equiv \mathcal {R}\), the Einstein field Eqs in \(f(\mathcal {R},\mathcal {T})\) gravity get reduces to Einstein field equations in general relativity. The term \(\zeta T\) induces a interaction (coupling) between curvature and matter which is time-dependent.

By substituting \(f(\mathcal {R},\mathcal {T})=\mathcal {R}+2\zeta \mathcal {T}\) and utilizing Eq. (11), Eq. (9) yields

$$\begin{aligned} \bigtriangledown ^{\xi }\mathcal {T}_{\xi \eta }=-\frac{\zeta }{\kappa +2\zeta }\left[ g_{\xi \eta }\bigtriangledown ^{\xi }\mathcal {T}-2\bigtriangledown ^{\xi }\left( \rho g_{\xi \eta }\right) \right] \end{aligned}$$
(13)

As we want investigate the solutions of field equations for isotropic compact stars in \(f(\mathcal {R},\mathcal {T})\) gravity, let's consider the stress-energy tensor in the form

$$\begin{aligned} T_{\xi \eta } = (\rho +p)u_\xi u_\eta -pg_{\xi \eta }, \end{aligned}$$
(14)

where \(u_\xi\) is the fluid four-velocity satisfying \(u_\xi u^\xi =1\) and \(u_\eta \bigtriangledown ^{\xi } u_\eta =0\). Here p(r) denotes the pressure of the fluid configuration. For the line element (1) and stress-energy tensor (14), the Einstein-Maxwell field Eqs in \(f(\mathcal {R},\mathcal {T})\) gravity (12) provide the following relations (Bhar and Rej 2021)

$$\begin{aligned} \rho= & {} \frac{\kappa }{(\kappa +2\zeta )(\kappa +4\zeta )}\left[ c^2(\kappa +5\zeta )\rho _E+3\zeta p_E\right] \end{aligned}$$
(15)
$$\begin{aligned} p= & \frac{\kappa }{(\kappa +2\zeta )(\kappa +4\zeta )}\left[ -c^2\zeta \rho _E+(\kappa +\zeta )p_{E}\right] \end{aligned}$$
(16)

with, \(\zeta \ne \frac{-\kappa }{4}, \frac{-\kappa }{2}\). Here, \(\rho _E\) and are, respectively, density, pressure in general relativity and are defined by

$$\begin{aligned} c^2 \kappa \rho _E+\frac{q^2}{r^4}= & {} \Big (\lambda '-\frac{1-e^{\lambda }}{r}\Big )\frac{e^{-\lambda }}{r} \end{aligned}$$
(17)
$$\begin{aligned} 2\kappa p_{E}= & {} \Big (\nu ''-\frac{\lambda ' \nu '}{2}+\frac{\nu '^2}{2}+\frac{3\nu '-\lambda '}{r}+\frac{2}{r^2}\Big )\frac{e^{-\lambda }}{2}-\frac{1}{r^2} \end{aligned}$$
(18)
$$\begin{aligned} \text {with,} \ \ \frac{2q^2}{r^4}= & {} \Big (\frac{\nu ''}{2}-\frac{\lambda ' \nu '}{4}+\frac{\nu '^2}{4}-\frac{\nu '+\lambda '}{2r}-\frac{1}{r^2}\Big )e^{-\lambda }+\frac{1}{r^2} \end{aligned}$$
(19)

and the prime denotes the radial derivative. In the succeeding section, we will solve the system of modified field Eqs. (15, 16) to obtain a model for compact stars.

3 The Proposed Model

As Eqs. (15), (16) involve more unknown functions than the number of equations and that too with high nonlinearity, getting an exact solution is a difficult task. Several authors have used a variety of techniques to obtain the solution. In this paper, we will utilize the technique of considering some of the unknown functions as given one and generate the remainings from basic equations. We must make a previous decision for any two of the four unknowns because we have only two equations for them. We can choose it in \(^4C_2\) ways. But, we have only control over the function we chose and we completely lost over the functions resulting from the solution. Although we choose regular and positive prior functions, there may arise a situation where the resulting functions are not physically realistic.

To construct a feasible charged isotropic model, we chose the coefficients \(g_{rr}\) and \(g_{tt}\) as,

$$\begin{aligned} e^{\lambda }=\frac{\mathcal {K}(1+x)}{\mathcal {K}+x} \ \ \ \& \ \ \ e^{\nu /2}=\mathcal {Z} \end{aligned}$$
(20)

where \(x=\mathcal {C}r^2\), and \(\mathcal {Z}\) is a function of r. We consider \(\mathcal {C}\) (in \(km^{-2}\)) to be a positive constant and \(\mathcal {K}\) to be a dimensionless parameter having no values in [0, 1], so that, the metric coefficients \(e^{\lambda }\) be regular and increase from core to the surface, as suggested in Lake (2003). The fulfillment of the same required criteria for \(\nu\), on the other hand, is dependent on our choice for \(\mathcal {Z}\). This form of \(\lambda\), which depends on two parameters \(\mathcal {K}\) and \(\mathcal {C}\), was proposed by Buchdahl (1959) for finding a feasible spherically symmetric perfect fluid solution. It is non-singular at the center of a fluid configuration and possesses monotonically decreasing density toward the boundary (which may depend on the choice of suitable parameters in some cases), i.e., it satisfies the primary physical requirements of a relativistic compact star proposed by Lake (2003). This metric potential has been successfully used to construct many feasible models for charged and uncharged isotropic compact stars (see Sharma et al. (2021); Kumar and Bharti (2022b); Prasad and Kumar (2021); Kumar et al. (2022); Kumar and Bharti (2022a) and references therein). Furthermore, the contribution of this metric to the development of the compact stars model in the background of modified gravity theory can also be found in the literature (Kumar et al. 2021; Maurya et al. 2020).

With the help of Eq. (20), the expression of electric field given in Eq. (19) can be obtained as follows:

$$\begin{aligned} {\mathcal{E}}^{2} & = \frac{{{\mathcal{K}} + x}}{{2{\mathcal{K}}(1 + x)^{2} }}; \\ & \quad \left[ {\frac{{{\mathcal{Z}^{\prime\prime}}}}{{\mathcal{Z}}} - \sqrt {\frac{{\mathcal{C}}}{x}} \frac{{{\mathcal{Z}^{\prime}}}}{{\mathcal{Z}}} + \frac{{x({\mathcal{K}} - 1)}}{{({\mathcal{K}} + x)(1 + x)}}\left( {\sqrt {{\mathcal{C}}x} - \frac{{{\mathcal{Z}^{\prime}}}}{{\mathcal{Z}}}} \right)} \right] \end{aligned}$$
(21)

Our initial aim is to find a function for electric field \(\mathcal {E}\), which is zero at the center and monotonically increasing toward the surface of compact objects. Let’s consider the function \(\mathcal {Z}\) as:

$$\begin{aligned} \mathcal {Z}= {\mathcal {A}{\mid 1-\mathcal {Y}^2\mid }^{1/4}\frac{\alpha +\beta \mathcal {Y}}{\mathcal {Y}} \bigg [\frac{g(x)}{\beta ^3}+\frac{\mathcal {B}}{\mathcal {A}}\bigg ] } \end{aligned}$$
(22)

where \(\mathcal {Y}=\sqrt{\frac{\mathcal {K}+x}{\mathcal {K}-1}}\) and \(g(x)=\beta \mathcal {Y}-\frac{\alpha ^2}{\alpha +\beta \mathcal {Y}}-\alpha \ln {(\alpha +\beta \mathcal {Y})^2}\). Also, \(\alpha\), \(\beta\) are nonzero parameters; and \(\mathcal {A}\), \(\mathcal {B}\) are constants to be determined.

Plugging (20) and (22) into Eqs. (17 and 18), we obtain,

$$\begin{aligned} c^2\kappa \rho _E= & {} \frac{\mathcal {C}(\mathcal {K}-1)(3+x)}{\mathcal {K}(1+x)^2}- \frac{\mathcal {C}x\mathcal {G}(x)}{2\mathcal {K}(1+x)^2} \ \ \& \end{aligned}$$
(23)
$$\begin{aligned} \kappa p_E= & {} \frac{\mathcal {C}\left( 1-\mathcal {Y}^2\mathcal {F}(x)\right) }{\mathcal {K}(1-\mathcal {Y}^2)}+ \frac{\mathcal {C}x\mathcal {G}(x)}{2\mathcal {K}(1+x)^2} \end{aligned}$$
(24)

where \(\mathcal {F}(x)=\frac{2}{(\mathcal {K}-1)}\frac{f_{1} f_{2}+f_{3}}{(\alpha +\beta \mathcal {Y})f_{2}}\) with \(f_{1}=\Big (\frac{\alpha +\beta \mathcal {Y}}{2(\mathcal {Y}^2-1)}-\frac{\alpha }{\mathcal {Y}^2}\Big )\), \(f_{2}=\frac{g(x)}{\beta ^3}+\frac{B}{A}\), \(f_{3}=\frac{\mathcal {Y}}{\alpha +\beta \mathcal {Y}}\); and, \(\mathcal {G}(x)=\frac{5}{4(1-\mathcal {Y}^2)}-\frac{2\alpha (1-\mathcal {Y}^2)}{\mathcal {Y}^2(\alpha +\beta \mathcal {Y})}+\mathcal {K}-\frac{7}{4}\).

Now, Eqs. (15) (16) provide the following relationship:

$$\begin{aligned} \rho= & {} \frac{1}{(\kappa +2\zeta )(\kappa +4\zeta )}\nonumber \\{} & {} \quad \bigg [(\kappa +5\zeta )\left\{ \frac{\mathcal {C}(\mathcal {K}-1)(3+x)}{\mathcal {K}(1+x)^2}\right\} +3\zeta \frac{\mathcal {C}\left( 1-\mathcal {Y}^2\mathcal {F}(x)\right) }{\nonumber }\\{} & {} \quad {\mathcal {K}(1-\mathcal {Y}^2)}-(\kappa +2\zeta )\frac{\mathcal {C}x\mathcal {G}(x)}{2\mathcal {K}(1+x)^2}\bigg ] \end{aligned}$$
(25)
$$\begin{aligned} \ p= & {} \frac{1}{(\kappa +2\zeta )(\kappa +4\zeta )}\nonumber \\{} & {} \quad \bigg [-\zeta \frac{C(\mathcal {K}-1)(3+x)}{\mathcal {K}(1+x)^2}+(\kappa +\zeta ) \frac{\mathcal {C}\left( 1-\mathcal {Y}^2\mathcal {F}(x)\right) }{\nonumber }\\{} & {} \quad {\mathcal {K}(1-\mathcal {Y}^2)}+(\kappa +2\zeta )\frac{\mathcal {C}x\mathcal {G}(x)}{2\mathcal {K}(1+x)^2}\bigg ] \end{aligned}$$
(26)

Thus, the model parameters, like density, and pressure in the framework of \(f(\mathcal {R},\mathcal {T})\) gravity have been successfully obtained.

4 Junction Condition and Determination of the Constants \(\mathcal {A}\) and \(\mathcal {B}\)

All astrophysical objects are immersed in vacuum spacetime and the interior solution is matched with the appropriate exterior vacuum solution at a junction interface. As there is no matter in the vacuum spacetime, the exterior spacetime is zero. Therefore, the solution for the exterior spacetime metric in \(f(\mathcal {R},\mathcal {T})\) gravity will be same of the corresponding solution in the general relativity. As we are working with uncharged matter distributions, for \(Q=q(R)\), the exterior solution for spherically symmetric spacetimes with junction radius R is described by the Reissner-Nördstrom metric,

$$\begin{aligned} {\text{d}}s^{2} & = - \frac{{{\text{d}}r^{2} }}{{1 - \frac{{2M}}{r} + \frac{{Q^{2} }}{{R^{2} }}}} + (1 - \frac{{2M}}{r} + \frac{{Q^{2} }}{{R^{2} }}){\text{d}}t^{2} \\ & \quad - r^{2} ({\text{d}}\theta ^{2} + {\text{sin}}^{2} \theta {\text{d}}\phi ^{2} ) \end{aligned}$$
(27)

Here, M is the total gravitational mass, which determines the amount of force exerted on the object by a gravitational field.

The first fundamental form dictates that a well-behaved stellar interior has smooth geometry at its surface. The continuity of the metric coefficients between the interior and exterior regions of the star across the boundary surface yields the following:

$$\begin{aligned} e^{\nu (R)}=1- \frac{2M}{R}+\frac{Q^2}{R^2}= e^{-\lambda (R)} \end{aligned}$$
(28)

Also, the second fundamental form demands

$$\begin{aligned} p_r(R)=0. \end{aligned}$$
(29)

This condition conveys that an object cannot expand indefinitely. Consequently, this constraint determines the size (radius) of the compact object.

To find out the constants \(\mathcal {A}\) and \(\mathcal {B}\), we use the junction conditions (28) and (29), and calculated the values of these constants as,

$$\begin{aligned}{} \frac{\mathcal {B}}{\mathcal {A}} & = \frac{f_{3R}}{\alpha +\beta Y_R}\bigg [\frac{1}{2Y_R^2} \left\{ \frac{2\zeta (\mathcal {K}-1)(3+\mathcal {C}R^2)-\kappa \mathcal {C}R^2\mathcal {G}_R}{2(\kappa +\zeta )(1+\mathcal {C}R^2)}+\mathcal {K}-1\right\} \nonumber \\{} & {} \quad -\frac{f_{1R}}{\alpha +\beta Y_R}\bigg ]^{-1}-f_{2R}\nonumber \\{} \mathcal {A} & =\frac{Y_R\mid Y_R\mid }{\sqrt{K} \mid 1-{Y_R}^2\mid ^{3/4}(\alpha +\beta Y_R)(f_{2R}+\frac{\mathcal {B}}{\mathcal {A}})} \end{aligned}$$

where \(Y_R=\mathcal {Y}(R)\), \(f_{nR}=f_{n}(R)\) for \(n=1, \ 3 \ \& \ 4\); \(f_{2R}=f_{2}(R)-\frac{\mathcal {B}}{\mathcal {A}}\); and \(\mathcal {G}_R=\frac{5}{4}\frac{1}{(1-Y_R^2)}-\frac{2\alpha (1-Y_R^2)}{Y_R^2(\alpha +\beta Y_R)}+\mathcal {K}-\frac{7}{4}\).

5 Physical Requirements for Acceptance of the Model in \(f(\mathcal {R},\mathcal {T})\) gravity

5.1 Metric Potential

In this paper, we have chosen the metric potentials as follows: \(e^{\lambda }=\frac{\mathcal {K}(1+x)}{\mathcal {K}+x}\) and \(e^{\nu /2}=\mathcal {A}{\mid 1-\mathcal {Y}^2\mid }^{1/4}\frac{\alpha +\beta \mathcal {Y}}{\mathcal {Y}} \bigg [\frac{g(x)}{\beta ^3}+\frac{\mathcal {B}}{\mathcal {A}}\bigg ]\). We have, \(e^{\nu (0)}=\frac{\left( \alpha \sqrt{\mid \mathcal {K}-1 \mid }+\beta \sqrt{\mid \mathcal {K} \mid }\right) ^2}{\mid \mathcal {K}\mid \sqrt{ \mid \mathcal {K}-1\mid }} \left( \mathcal {A}\frac{f(0)}{\beta ^3}+\mathcal {B} \right) ^2\), \(e^{\lambda (0)} = 1\), and \(\lambda '(0)=0=\nu '(0)\). Lake (2003) has prescribed certain conditions on the metric coefficients to create a viable model. These conditions are: \(e^{\lambda }\) and \(e^{\nu }\) should increase in a regular and monotonic manner as r increases. Both should be positive, free of singularities at the center, with \(\lambda '(0)=0\) and \(\nu '(0) = 0\). Thus, a positive value of \(e^{\nu (0)}\) is required for the metric potential functions to behave well at the core of the configuration.

5.2 Density and Pressure

The main thermodynamic variables must fulfill certain specific requirements in this regard. From Eqs. (25), at the core of the compact configuration we have

$$\begin{aligned} \rho _c= & {} \frac{1}{(\kappa +2\zeta )(\kappa +4\zeta )}\bigg [(\kappa +2\zeta )\frac{3\mathcal {C}(\mathcal {K}-1)}{\mathcal {K}}+3\zeta \mathcal {F}_R\bigg ] \\ p_c= & {} \frac{1}{(\kappa +2\zeta )(\kappa +4\zeta )}\bigg [(\kappa +4\zeta )\frac{\mathcal {C}(1-\mathcal {K})}{\mathcal {K}}+(\kappa +\zeta )\mathcal {F}_R\bigg ] \end{aligned}$$

with, \(\mathcal {F}_R=\frac{2}{(\mathcal {K}-1)}\frac{f_{1R} f_{2R}+f_{3R}}{(\alpha +\beta \mathcal {Y})f_{2R}}\). Here \(\rho _c\) and \(p_c\) are, respectively, the central density and central pressure of the compact star in \(f(\mathcal {R},\mathcal {T})\) gravity.

By differentiating Eqs. (25) and (26) with respect to r, we get the density gradient and pressure gradient for the proposed model as follows:

$$\begin{aligned}{} & {} \frac{\textrm{d}\rho }{\textrm{d}r}=\frac{\mathcal {C}^{3/2}\sqrt{x}}{(\kappa +2\zeta )(\kappa +4\zeta )}\Bigg [(\kappa +5\zeta )\frac{2(1-\mathcal {K})(5+x)}{ \mathcal {K}(1+x)^3}+\nonumber \\{} & {} \quad \Bigg \{ \frac{2\mathcal {Y}^2 \mathcal {H}(x)}{(\mathcal {K}-1)^2f_2(x)(\alpha +\beta \mathcal {Y})} +\frac{2\left( 1-\mathcal {F}(x)\mathcal {Y}\right) }{(1+x)}\bigg \} \\ \nonumber{} & {} \quad \frac{3\zeta }{\mathcal {K}(\mathcal {Y}^2-1)}+\frac{(\kappa -2\zeta )}{(1+x)^2} \bigg \{\frac{(1-x)}{\mathcal {K}(1+x)}\mathcal {G}(x)+\frac{x}{4\mathcal {K}(1-\mathcal {K})}\nonumber \\{} & {} \quad \bigg (\frac{5}{(1-\mathcal {Y}^2)^2}-\frac{8\alpha }{\mathcal {Y}^2(\alpha +\beta \mathcal {Y})}-\\{} & {} \quad \frac{4\alpha (1-\mathcal {Y}^2)(2\alpha +3\beta \mathcal {Y})}{\mathcal {Y}^4(\alpha +\beta \mathcal {Y})^2}\bigg )\bigg \}\bigg ] \\{} & {} \frac{\textrm{d}p}{\textrm{d}r}=\frac{\mathcal {C}^{3/2}\sqrt{x}}{(\kappa +2\zeta )(\kappa +4\zeta )} \bigg [-2\zeta \frac{(1-\mathcal {K})(5+x)}{\mathcal {K}(1+x)^3}+\nonumber \\{} & {} \quad \bigg \{\frac{2\mathcal {Y}^2 \mathcal {H}(x)}{(\mathcal {K}-1)^2f_2(x)(\alpha +\beta \mathcal {Y})}+\frac{2\left( 1-\mathcal {F}(x)Y\right) }{(1+x)}\bigg \}\\{} & {} \quad \frac{(\kappa +\zeta )}{\mathcal {K}(\mathcal {Y}^2-1)}+\frac{\kappa +2\zeta }{(1+x)^2} \bigg \{\frac{(1-x)}{\mathcal {K}(1+x)}\mathcal {G}(x)+\frac{x}{4\mathcal {K}(1-\mathcal {K})}\nonumber \\{} & {} \quad \bigg (\frac{5}{(1-\mathcal {Y}^2)^2}-\frac{8\alpha }{\mathcal {Y}^2(\alpha +\beta \mathcal {Y})}-\\{} & {} \quad \frac{4\alpha (1-\mathcal {Y}^2)(2\alpha +3\beta \mathcal {Y})}{\mathcal {Y}^4(\alpha +\beta \mathcal {Y})^2}\bigg )\bigg \}\bigg ] \end{aligned}$$

where \(\mathcal {H}(x)= \frac{\mathcal {Y}^2f_1(x)+\alpha }{Y(\alpha +\beta \mathcal {Y})^2}-\left( \frac{Y(\alpha +\beta \mathcal {Y})+(\beta +\alpha \mathcal {Y})}{2\mathcal {Y}(\mathcal {Y}^2-1)}\right) f_2(x)-\left( \frac{(\mathcal {K}-1)\mathcal {Y}}{2(\alpha +\beta \mathcal {Y})}-\frac{\beta f_2}{2\mathcal {Y}}\right) \mathcal {F}(x)\).

We see that \(\rho '(0)=p'(0)=0\). Also, \(\rho ''(0)=\frac{C^2}{(\kappa +2\zeta )(\kappa +4\zeta )}\left[ 10(\kappa +5\zeta ) \frac{(1-\mathcal {K})}{\mathcal {K}}+\frac{3\zeta (\mathcal {K}-1)}{\mathcal {K}}n-(\kappa +2\zeta ) \frac{\mathcal {G}(0)}{\mathcal {K}}\right]\), and, \(p''(0)=\frac{C^2}{(\kappa -2\zeta )(\kappa +4\zeta )}\left[ -10\zeta \frac{(1-\mathcal {K})}{\mathcal {K}}+\frac{(\kappa +\zeta )(\mathcal {K}-1)}{\mathcal {K}}n+(\kappa +2\zeta ) \frac{\mathcal {G}(0)}{\mathcal {K}}\right]\), where \(n=\frac{2\left( \sqrt{\mid \mathcal {K}-1\mid }-\mathcal {F}(0)\sqrt{\mid \mathcal {K} \mid }\right) }{\sqrt{\mid \mathcal {K}-1\mid }}+\frac{2\mathcal {K} \mathcal {H}(0)}{|\mathcal {K}-1|^{5/2}f_2(0)(\alpha \sqrt{\mid \mathcal {K}-1\mid }+\beta \sqrt{\mid \mathcal {K} \mid })}\).

For an acceptable model, within the configuration of a stellar object, the matter density and pressure should have positive values, and therefore \(\rho _c, p_c >0\). Also, \(\rho _c\) should strictly dominate \(p_c\) (Zeldovich and Novikov 1971). The pressure should vanish at the configuration’s surface. Furthermore, for a compact star’s density and pressure to decrease monotonically from the core to the surface, the gradient of density and gradient of pressure must have negative values throughout the configuration, which suggests that at the center, \(\rho '\), and, \(p'\) must be zero and \(\rho ''\) and \(p''\) must have a negative value.

5.3 Causality Condition

The square of velocity of sound \(v^2\) is given by

$$\begin{aligned} \nonumber{} & {} v^2(r)=\frac{\textrm{d}p}{\textrm{d}\rho }=\\{} & {} \quad \frac{-2\zeta (1-\mathcal {K})(5+x)+(\kappa +\zeta )(\mathcal {K}-1)(1+x)^2\mathcal {J}_1+(\kappa +2\zeta ) \mathcal {K}(1+x)\mathcal {J}_2}{2(\kappa +5\zeta )(1-\mathcal {K})(5+x)+3\zeta (\mathcal {K}-1)(1+x)^2\mathcal {J}_1+ (\kappa -2\zeta ) \mathcal {K}(1+x)\mathcal {J}_2 } \end{aligned}$$

where \(\mathcal {J}_1=\frac{2\mathcal {Y}^2 \mathcal {H}(x)}{(\mathcal {K}-1)^2 f_2(x) (\alpha +\beta \mathcal {Y})}+\frac{2\left( 1-g(x)Y\right) }{(1+x)}\) and \(\mathcal {J}_2=\frac{x}{4\mathcal {K}(1-\mathcal {K})}\left( \frac{5}{(1-\mathcal {Y}^2)^2}-\frac{8\alpha }{\mathcal {Y}^2(\alpha +\beta \mathcal {Y})}-\frac{4\alpha (1-\mathcal {Y}^2)(2\alpha +3\beta \mathcal {Y})}{\mathcal {Y}^4(\alpha +\beta \mathcal {Y})^2}\right) +\frac{(1-x)}{\mathcal {K}(1+x)}\mathcal {G}(x)\).

To fulfill the physical requirements for realistic models, it is necessary to examine the causality condition of the present self gravitating system, which says that the velocity of sound must be less than the velocity of light throughout the interior of the stellar object. Along with this, it should decrease toward the surface.

5.4 Pressure–Density Relationship

The relationship between matter density and pressure can be described by a dimensionless quantity known as ’the equation of state (EoS) parameter, denoted by the symbol \(\omega\). Several works can be found in literature that suggest that the EoS, \(p= p(\rho )\), should be well approximated by a linear function of the energy density. Furthermore, a linear relationship between the energy density and the pressure ensures that the conservation of causality condition holds (Rahaman et al. 2020).

The equations of state parameter \(\omega\) for our model is obtained as,

$$\begin{aligned}{} & {} \omega =\frac{p}{\rho }=\nonumber \\{} & {} \quad \frac{-2\zeta (\mathcal {K}-1)\mathcal {C}(3+x) -2(\kappa +\zeta )(\mathcal {K}-1)\mathcal {C}(1+x)\left( 1-\mathcal {Y}^2\mathcal {F}(x)\right) +(\kappa +2\zeta )\mathcal {C}x\mathcal {G}(x)}{2(\kappa +5\zeta )(\mathcal {K}-1)\mathcal {C}(3+x)-6\zeta (\mathcal {K}-1)\mathcal {C}(1+x){\left( 1-\mathcal {Y}^2\mathcal {F}(x)\right) }-(\kappa +2\zeta ){\mathcal {C}x\mathcal {G}(x)} } \end{aligned}$$
(30)

The equations of state parameter should lie in the range \(0< \omega < 1\), which corresponds to the radiation era (Sharif and Waseem 2016). Fulfillment of this condition implies that, everywhere within the configuration, density is dominating over the corresponding pressures, which suggests that the underlying matter distribution is not exotic (Rahaman et al. 2010).

5.5 Electric Field Intensity

Electric field intensity produces considerable effects on the structure and the stability of compact stars. The expression of the electric field in \(f(\mathcal {R},\mathcal {T})\) gravity can be obtained as,

$$\begin{aligned}{} & {} \mathcal {E}^2(r)=\frac{q^2}{r^4}= \frac{\mathcal {C}x}{8\mathcal {K}(\mathcal {K}-1)^2}\nonumber \\{} & {} \quad \left[ \frac{-8\alpha +4\mathcal {K}\mathcal {Y}^2(1-\mathcal {Y}^2)(\alpha +\beta \mathcal {Y})+2\mathcal {Y}^2(7\alpha -\beta \mathcal {Y})+\mathcal {Y}^2(7\beta \mathcal {Y}-\alpha )}{\mathcal {Y}^2(1-\mathcal {Y}^2)^3(\alpha +\beta \mathcal {Y})}\right] \end{aligned}$$
(31)

For a physically viable model it is required that \(\mathcal {E}(0)=0\). The intensity of the electric field within a compact star configuration should increase toward the configuration’s surface.

5.6 Energy Conditions

Energy conditions in the cosmological model are crucial for understanding various features of the cosmos, especially its current accelerating expansion. These conditions are very helpful in constraining the constant parameters used in the solutions so that to get a viable model in the underlying framework.

The energy-momentum tensor \(T_{\xi \eta }\) describes the energy-momentum distribution and stress due to matter or any other non-gravitational field. A realistic matter source must meet certain requirements to be fulfilled by all states of matter and non-gravitational fields. There are different types of these conditions, including averaged energy conditions and point-wise energy conditions. The average stress-energy tensor along a desirable curve determines averaged energy conditions, whereas point-wise energy conditions are determined by the stress-energy tensor at a specific point in space. Null energy condition (NEC), dominant energy condition (DEC), weak energy condition (WEC), and strong energy condition (SEC) are the standard point-wise energy conditions. The “Raychaudhuri equation”, which describes the behavior of timelike, lightlike, or spacelike curves of congruence and attractiveness of the gravity, is used to formulate these conditions (Kar and Sengupta 2007; Carroll 2004).

  • The NEC is the consequence of \(T_{\xi \eta } k^\xi k^\eta \ge 0\), which leads to the well-known form \(\rho +p\ge 0\). The NEC implies that as the universe expands its density decreases; the violation of it could result in a Big Rip of the universe. NEC is a guarantee of the applicability of the second law of thermodynamics.

  • In addition to NEC, the WEC requires that energy density be positive for an observer at any point, i.e., \(\rho \ge 0\), \(\rho +p\ge 0\).

  • The SEC is produced by the positivity condition for the timelike vector \(u^\xi\), which in the effective field reduces to \(\rho +p\ge 0\), \(\rho +3p\ge 0\).

  • The constraint on energy that it cannot move faster than light yields one of the DEC inequality, the complete set of which is \(\rho \ge 0\), \(\rho \pm p\ge 0\).

Since the violation of NEC and WEC leads to the violation of other energy conditions, these two are the most important.

5.7 Mass Function and Compactness Factor

The gravitational mass m(r) within the radius r of the charged compact star in \(f(\mathcal {R},\mathcal {T})\) gravity is given by Murad and Fatema (2015)

$$\begin{aligned} m(r) = & \frac{\kappa }{2}\int_{0}^{r} \rho r^{2} {\text{d}}r + \frac{1}{2}\int_{0}^{r} {\frac{{q^{2} }}{{r^{2} }}} dr + \frac{{q^{2} }}{{2r}} \\ = & \frac{{\kappa ^{2} }}{{2(\kappa + 2\zeta )(\kappa + 4\zeta )}}\quad \left[ {(\kappa + 5\zeta )\int_{0}^{r} {c^{2} } \rho _{E} r^{2} {\text{d}}r + 3\zeta \int_{0}^{r} {p_{E} } r^{2} {\text{d}}r} \right]\quad + \frac{1}{2}\int_{0}^{r} {\frac{{q^{2} }}{{r^{2} }}} {\text{d}}r + \frac{{q^{2} }}{{2r}} \\ = & \frac{\kappa }{{2(\kappa + 2\zeta )(\kappa + 4\zeta )}}\quad \left[ {(\kappa + 5\zeta )\int_{0}^{r} {\frac{{({\mathcal{K}} - 1)x(3 + x)}}{{{\mathcal{K}}(1 + x)^{2} }}} {\text{d}}r\quad + 3\zeta \int_{0}^{r} {\frac{{x\left( {1 - {\mathcal{Y}}^{2} {\mathcal{F}}(x)} \right)}}{{{\mathcal{K}}(1 - {\mathcal{Y}}^{2} )}}} {\text{d}}r - \quad (\kappa + 2\zeta )\int_{0}^{r} {\frac{{x^{2} {\mathcal{G}}(x)}}{{2{\mathcal{K}}(1 + x)^{2} }}} dr} \right] \\ & + \frac{1}{2}\int_{0}^{r} {\frac{{x^{2} {\mathcal{G}}(x)}}{{2{\mathcal{K}}(1 + x)^{2} }}} {\text{d}}r + \frac{{x^{{\frac{5}{2}}} {\mathcal{G}}(x)}}{{4{\mathcal{K}}\sqrt {\mathcal{C}} (1 + x)^{2} }} \\ = & \frac{\kappa }{{2(\kappa + 2\zeta )(\kappa + 4\zeta )}}\left[ {(\kappa + 5\zeta )\int_{0}^{r} {\frac{{({\mathcal{K}} - 1)x(3 + x)}}{{{\mathcal{K}}(1 + x)^{2} }}} {\text{d}}r\quad + 3\zeta \int_{0}^{r} {\frac{{x\left( {1 - {\mathcal{Y}}^{2} {\mathcal{F}}(x)} \right)}}{{{\mathcal{K}}(1 - {\mathcal{Y}}^{2} )}}} {\text{d}}r - \quad (\kappa + 2\zeta )\int_{0}^{r} {\frac{{x^{2} {\mathcal{G}}(x)}}{{2{\mathcal{K}}(1 + x)^{2} }}} {\text{d}}r} \right] \\ & + \frac{1}{2}\int_{0}^{r} {\frac{{x^{2} {\mathcal{G}}(x)}}{{2{\mathcal{K}}(1 + x)^{2} }}} {\text{d}}r\quad + \frac{{x^{{\frac{5}{2}}} {\mathcal{G}}(x)}}{{4{\mathcal{K}}\sqrt {\mathcal{C}} (1 + x)^{2} }} \\ \end{aligned}$$
(32)

The mass for stellar structures should be zero in the core and maximum at the boundary surfaces. Along with this, the mass function should be an increasing function of r that is regular and monotonic.

The compactness of the relativistic compact structure can be found as \(\mathcal {U}=\frac{m(r)}{r}\). The compactness factor plays a significant role in the classification of compact objects. For normal stars \(\mathcal {U} \sim 10^{-5}\), for white dwarfs: \(\mathcal {U} \sim 10^{-3}\), for neutron star: \(10^{-1}<\mathcal {U}<\frac{1}{4}\), for ultra-compact star:\(\frac{1}{4}<\mathcal {U}<\frac{1}{2}\), and, for Black hole: \(\mathcal {U}=\frac{1}{2}\). Also, there is a lower bound and upper bound is defined on the compactness factor of a charged compact object as follows (Böhmer and Harko 2007; Andréasson 2009):

$$\begin{aligned} \frac{Q^2}{R^2}\left( \frac{Q^2+18R^2}{12R^2+Q^2}\right) \le 2 \mathcal {U} \le \frac{2}{R}\left[ \frac{\sqrt{R}}{3}+\sqrt{\frac{R^2+3Q^2}{9R}}\right] ^2. \end{aligned}$$
(33)

5.8 Redshifts

Gravitational redshift is the phrase used to describe the phenomena in which electromagnetic waves or photons appear to lose energy when they leave a gravitational well. As electromagnetic radiation travels out of a gravitational well, its wavelength lengthens and photons expand their energy to escape. Since the photons have to travel at the speed of light, it loses their energy through a change of frequency which corresponds to a decrease in the wave frequency and an increase in the wavelength of the photon, i.e., a shift to the red end of the electromagnetic spectrum, known as a redshift.

In comparison to when a photon emerges from near the surface when it emerges from the center, it has to travel a greater distance through a denser zone. As a result, there is more dispersion, which causes more energy loss in the first scenario. Hence, the surface and the center have the lowest and highest interior gravitational redshift, respectively.

It is the surface gravity (i.e., overall mass and radius) of stellar objects which determines the surface redshift. As an increase in mass and radius results in more surface gravity, in contrast with gravitational redshift, surface redshift increases toward the surface. However, both of these redshifts coincide at the surface of the compact star’s configuration.

The interior gravitational redshift \(z_g(r)\) and surface redshift \(z_s(r)\) for a the charged compact star in \(f(\mathcal {R},\mathcal {T})\) gravity is given by

$$\begin{aligned} z_g(r)= & {} \frac{1}{\sqrt{|e^{\nu (r)}|}}-1 \end{aligned}$$
(34)
$$\begin{aligned} z_s(r)= & {} \frac{1}{\sqrt{1-2\mathcal {U}+\frac{q^2}{r^2}}}-1 \end{aligned}$$
(35)

In General Relativity, surface redshift has a maximum limit \(z_s(R) \ (=z_g(R))\le 2\) for isotropic distributions.

6 Conditions for Stability and Equilibrium of the Model

Here our main interest is discussing the conditions for equilibrium as well as stability of the compact star model in \(f(\mathcal {R},\mathcal {T})\) gravity. For a non-collapsing compact object, the equilibrium position and stable state are most important situations. The stability of any stellar structure ensures that the system’s equilibrium is not disturbed.

6.1 Equilibrium Under Various Forces

It is important to examine whether the stellar system is in a stable equilibrium stage under hydrostatic force \(F_h\), gravitational force \(F_g\), electric force \(F_e\), and, force due to the modified (\(f(\mathcal {R}, \mathcal {T})\)) gravity \(F_m\). This can be analyzed using the generalized TOV equation in \(f(\mathcal {R},\mathcal {T})\) gravity, given as,

$$\begin{aligned} F_{g} + F_{h}+F_{e}+F_{m}=0 \end{aligned}$$
(36)

where \(F_{g}=-\frac{\nu '}{2}(\rho +p)\), \(F_{h}=-\frac{\textrm{d}p}{\textrm{d}r}\), \(F_{e}=\frac{1}{(\kappa +2\zeta ) r^4}\frac{dq^2}{\textrm{d}r}\), and, \(F_m=\frac{-\zeta }{\kappa +2\zeta }(\rho '+3p')\). For our model, these forces can be obtained as,

$$\begin{aligned}{} & {} F_{g}= -\frac{\mathcal {C}^{3/2}\sqrt{x}}{2(\kappa +2\zeta )} \mathcal {F}(x) \\{} & {} \quad \left[ \frac{2}{\mathcal {K}(\mathcal {K}-1)(\mathcal {Y}^2-1)^2} + \frac{\mathcal {Y}^2}{\mathcal {K}(\mathcal {Y}^2-1)} \mathcal {F}(x)\right] \\{} & {} \quad F_{h}=-\frac{\mathcal {C}^{3/2}\sqrt{x}}{(\kappa +2\zeta )(\kappa +4\zeta )} \bigg [-2\zeta \frac{(1-\mathcal {K})(5+x)}{\mathcal {K}(1+x)^3}+\\{} & {} \quad \bigg \{\frac{2\mathcal {Y}^2 \mathcal {H}(x)}{(\mathcal {K}-1)^2f_2(x)(\alpha +\beta \mathcal {Y})}+\frac{2\left( 1-\mathcal {F}(x)Y\right) }{(1+x)}\bigg \}\\{} & {} \quad \frac{(\kappa +\zeta )}{\mathcal {K}(\mathcal {Y}^2-1)}+\frac{\kappa +2\zeta }{(1+x)^2} \bigg \{\frac{x}{4\mathcal {K}(1-\mathcal {K})}\\{} & {} \quad \bigg (\frac{5}{(1-\mathcal {Y}^2)^2}-\frac{8\alpha }{\mathcal {Y}^2(\alpha +\beta \mathcal {Y})} -\frac{4\alpha (1-\mathcal {Y}^2)(2\alpha +3\beta \mathcal {Y})}{\mathcal {Y}^4(\alpha +\beta \mathcal {Y})^2}\bigg )\\{} & {} \quad +\frac{(1-x)}{\mathcal {K}(1+x)}\mathcal {G}(x)\bigg \}\bigg ] \\{} & {} \quad F_{e}=\frac{\mathcal {C}^{3/2}\sqrt{x}}{(\kappa +2\zeta )} \left[ \frac{3+x}{\mathcal {K}(1+x)^3}\mathcal {G}(x)+\frac{x}{4\mathcal {K}(1-\mathcal {K})}\right. \\{} & {} \quad \left. \left( \frac{5}{(1-\mathcal {Y}^2)^2}-\frac{8\alpha }{\mathcal {Y}^2(\alpha +\beta \mathcal {Y})} -\frac{4\alpha (1-\mathcal {Y}^2)(2\alpha +3\beta \mathcal {\mathcal {Y}})}{\mathcal {Y}^4 (\alpha +\beta \mathcal {Y})^2}\right) \right] \\{} & {} \quad F_{m}=\frac{\mathcal {C}^{3/2}\sqrt{x}\zeta }{(\kappa +2\zeta )^2(\kappa +4\zeta )} \bigg [\frac{2(\kappa -\zeta )(1-\mathcal {K})(5+x)}{ \mathcal {K}(1+x)^3}+\\{} & {} \quad \bigg \{\frac{2\mathcal {Y}^2 \mathcal {H}(x)}{(\mathcal {K}-1)^2f_2(x) (\alpha +\beta \mathcal {Y})}+\frac{2\left( 1-\mathcal {F}(x)\mathcal {Y}\right) }{(1+x)}\bigg \}\\{} & {} \frac{3(\kappa +2\zeta )}{\mathcal {K}(\mathcal {Y}^2-1)}+\frac{2\kappa }{(1+x)^2} \bigg \{\frac{x}{4\mathcal {K}(1-\mathcal {K})}\\{} & {} \quad \bigg (\frac{5}{(1-\mathcal {Y}^2)^2}-\frac{8\alpha }{\mathcal {Y}^2(\alpha +\beta \mathcal {Y})} -\frac{4\alpha (1-\mathcal {Y}^2)(2\alpha +3\beta \mathcal {Y})}{\mathcal {Y}^4(\alpha +\beta \mathcal {Y})^2}\bigg ) \\{} & {} +\frac{(1-x)}{\mathcal {K}(1+x)}\mathcal {G}(x)\bigg \} \bigg ] \end{aligned}$$

6.2 Adiabatic Index and Stability Condition

For a relativistic isotropic fluid configuration, the stability is related to the adiabatic index \(\Gamma\), the ratio of two specific heats, defined by Chandrasekhar (1964a, b),

$$\begin{aligned} \Gamma =\Big (\frac{\rho +p}{p} \Big )\Big (\frac{\textrm{d}p}{\textrm{d}\rho }\Big ) \end{aligned}$$
(37)

To be stable in Newtonian gravity, the adiabatic index \(\Gamma\) of an isotropic star must be strictly greater than \(\frac{4}{3}\) (Bondi 1964). For a relativistic isotropic compact star, this condition changes due to the regenerative effect of pressure. In the post-Newtonian approximation, the condition for stability of isotropic configuration takes the form Chan (1993):

$$\begin{aligned} \Gamma > \frac{4}{3}+\textrm{max}\bigg (\frac{\kappa }{3}\frac{r\rho p}{|p'|}\bigg ) \end{aligned}$$
(38)

However, relativistic correction to the adiabatic index may introduce some instabilities within the configuration. As a result, Moustakidis Moustakidis (2017) proposed a more stringent condition on the adiabatic index. He asserted that the critical value of the adiabatic index (\(\Gamma_{\rm {critcal}}\)) is determined by the amplitude of the Lagrangian displacement from equilibrium and compactness, which is calculated as

$$\begin{aligned} \Gamma_{\rm {critical}}=\frac{4}{3}+\frac{19}{21}\frac{M}{R}, \end{aligned}$$
(39)

and the condition for stability became \(\Gamma \ge \Gamma_{\rm {critical}}\).

6.3 Harrison–Zeldovich–Novikov Static Stability Criterion

Harrison et al. (1965) and Zeldovich and Novikov (1971) demonstrated that the adiabatic index of a pulsating star is the same as that of a slowly deformed matter. This results in a stable configuration only if the star’s mass increases with central density, i.e., \(\frac{\partial M}{\partial \rho _c}>0\) and an unstable configuration if \(\frac{\partial M}{\partial \rho _c}<0\).

7 Physical Features and Stability Analysis of the Presented Compact Stars Model in \(f(\mathcal {R},\mathcal {T})\) Gravity

We present a physical and stability analysis of our model in this section, with a focus on regularity and stability related to f(R, T) Gravity. Compact stars, the most fundamental objects in galaxies, have attracted the interest of researchers studying their ages, structures, and evolutions in Cosmology and Astrophysics. It is worthwhile to investigate the structure of astrophysical objects within the framework of a theory to test it. For this purpose, we have discussed the physical analysis of rotating neutron stars ‘Hercules X-1’, observed mass and radius of which are \(0.85\pm 0.15 M_\odot\) and \(8.1 \pm 0.41\) km, respectively (Gangopadhyay et al. 2013). Hercules X-1 (Her X-1) is a moderately strong X-ray binary source composed of neutron star accreting matter that was discovered by the Uhuru satellite. We choose some real values for the constants used in the solutions as \(\alpha =-2.87\), \(\beta =0.9499\), \(C=0.004344307\) and \(K=1.99\) and estimate the value of \(\frac{M}{R}\) for the model as 0.15478, which is consistent with Buchdahl limit. This value of \(\frac{M}{R}\) suggests that for studying the compatibility of the model, ‘Hercules X-1’ might be a suitable choice. The estimated mass and radius of ‘Hercules X-1’ through our model are \(M=0.85\) and \(R=8.1\), respectively, which are within the range of their corresponding observed values. To examine the effect of coupling constant \(\zeta\), we consider the range \(-\frac{\kappa }{8\pi } \le \zeta \le \frac{\kappa }{8\pi }\). For the different values of \(\zeta\), the calculated numerical values of electric field intensity at the surface, central density, surface density, central pressure, surface redshift, and central adiabatic index of Hercules X-1 are given in Table 1.

Table 1 Numerical values of electric field intensity at surface \(\mathcal {E}_s\), central density \(\rho _c\), surface density \(\rho _s\), central pressure \(p_c\), maximum value of surface redshift \(Z_s\), and adiabatic index at the core \(\Gamma _c\) of ‘Hercules X-1’
Full size table

In our model, the metric potential \(e^\lambda\) and the electric field is unaffected by the value of \(\zeta\). As a result, for all \(\zeta\) considered, the total mass of the configuration at the surface remains the same, resulting in the same value for gravitational redshift at the compact star’s surface. We use the graphical representation to describe the physical acceptability of the presented stellar model in \(f(\mathcal {R},\mathcal {T})\) Gravity.

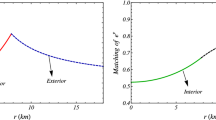
The profile of metric potentials \(e^\lambda\) and \(e^\nu\) is plotted in Fig.  1. The figure shows that the metric potentials are regular and finite within the Hercules X-1 configuration. Also, \(e^{-\lambda }\) and \(e^\nu\) coincides at the boundary of the compact star configuration, which confirms the fulfillment of matching condition (28). Hence, the chosen metric potentials are appropriate for generating the model for the neutron star ’Hercules X-1’.

Fig. 1
figure 1

Behavior of metric potentials of Hercules X-1 model for \(-\frac{\kappa }{8\pi } \le \zeta \le \frac{\kappa }{8\pi }\)

Full size image
Fig. 2
figure 2

Density (Left) and pressure (Right) profiles within the configuration of Hercules X-1 for \(-\frac{\kappa }{8\pi } \le \zeta \le \frac{\kappa }{8\pi }\)

Full size image

As can be seen in Fig.  2 (Left), the density profile is a decreasing function of the scaled radial coordinate (r/R). The behavior of pressure is depicted in Fig.  2 (Right). The calculated value of central density of ‘Hercules X-1’, using this model, is of order \(10^{14}\) (g/cc), which is consistent with its observed value. The pressure is found to be a monotonically decreasing function of the scaled radial coordinate. It vanishes for some finite radius denoting the boundary between the interior spacetime and the vacuum exterior described by the Reissner-Nördstrom solution.

Fig. 3
figure 3

Nature of the velocity of sound (Left) and equation of state parameter (Right) within the configuration of Hercules X-1 for \(-\frac{\kappa }{8\pi } \le \zeta \le \frac{\kappa }{8\pi }\)

Full size image

For geometrized units, \(G = c = 1\), the causality condition get reduced to \(0\le v<1\). It can be verified from Fig.  3 (Left) that our system is consistent with the causality condition. The EoS of dense matter has great significance in various physical objects, including compact astrophysical objects. The nature of the variation of pressure with respect to the density has been graphically shown in Fig.  3 (Right). Despite the complex relationship between radial pressure and energy density, the behavior of an object from its surface to its core is roughly linear. The figure shows that the EoS parameter \(\omega\) takes the maximum value at the center of the star and decreases toward the boundary. Furthermore, it is in the range \(0<\omega < 1\), which corresponds to the radiation era.

Fig. 4
figure 4

Graphical representation of electric field intensity (Left) and energy conditions (Right) for the neutron star Hercules X-1 with \(-\frac{\kappa }{8\pi } \le \zeta \le \frac{\kappa }{8\pi }\)

Full size image

The estimated electric charge, which has a significant impact on the structure of neutron stars, generates a surface electric field of the order of \(10^{20}\) (in V/m). Fig.  4 (Left) depicts the behavior of the electric field \(\mathcal {E}\) for various values of \(\zeta\). The electric field begins at zero in the center and increases toward the star’s surface. Fig.  4 (Right) depicts the expressions on the left-hand side of the inequalities in energy conditions. The figure clearly shows that all of the energy conditions have been satisfied. The fulfillment of all these conditions confirms the existence of ordinary matter in the configuration. SEC is satisfied in our study of the charged compact star, implying that gravity will be attractive and the matter-energy density will always be positive.

Fig. 5
figure 5

Redshift profile of the neutron star Hercules X-1 for \(-\frac{\kappa }{8\pi } \le \zeta \le \frac{\kappa }{8\pi }\)

Full size image

The variation in redshift of Hercules X-1 for each \(\zeta\) within the range is depicted graphically in Fig.  5. The figures confirm that the redshift evolution from the core to the surface is within the limit.

Fig. 6
figure 6

Behavior of different forces acting on the Hercules X-1 configuration (Left) and Adiabatic Indices of Hercules X-1 (Right) for \(-\frac{\kappa }{8\pi } \le \zeta \le \frac{\kappa }{8\pi }\)

Full size image

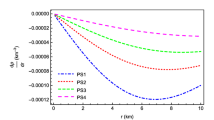
For different values of \(\zeta\), all the forces acting on the system are shown in Fig.  6 (Left). The figure shows that gravitational force is attractive as well as dominating in nature. The hydrostatic and electric forces are repellent in nature. Among all the forces, the effect of modified gravity is comparatively less. The figures show that the combined effect of all forces equals zero, and thus, the charge compact star’s equilibrium condition in \(f(\mathcal {R},\mathcal {T})\) gravity is obtained. Fig.  6 (Right) shows that our models satisfy the Chandrasekhar stability criterion. Also, the critical value of the adiabatic index (\(\Gamma_{{\rm critcal}}\)) for the neutron star ‘Hercules X-1’ is calculated as 1.473375. The adiabatic index \(\Gamma\) is increasing and more than 3 throughout the compact star configuration, which surpasses the \(\Gamma_{{\rm critcal}}\).

The figures also show the effect of varying the \(f(\mathcal {R}, \mathcal {T})\) coupling constant \(\zeta\). Fig.  1 shows that the \(e^\lambda\) profile is the same for all values of \(\zeta\), whereas a decrement in the \(e^\nu\) profile with an increase in \(\zeta\) value can be seen. Even though the basic nature of density and pressure within the configuration is not violated, a decrease in density and pressure is accompanied by an increase in \(\zeta\) (see Fig.  2). When we move in the negative direction from \(\zeta =0\), which represents the same in Einstein’s gravity, we see an increase in these profiles, and when we move in the positive direction, we see a decrease in these profiles. Similar behavior for the velocity of sound (v) and the equation of state parameter (\(\omega\)) can be seen in Fig.  3. Fig.  4 reveals that \(\zeta\) doesn’t have any impact on the electric field intensity. Gravitational redshift increases as the magnitude of the positive coupling constant increases, while it decreases with the increment in the magnitude of the negative coupling constant (see Fig.  5). With increase in magnitude with rise in \(\zeta\) from \(-\frac{\kappa }{8\pi }\) to \(\frac{\kappa }{8\pi }\) gravitational force remain attractive in nature for all values of \(\zeta\). With an increase in \(\zeta\), there is an increase in hydrostatic force and electric force, both of which are repulsive in nature for all \(\zeta\). But, as the magnitude of the force corresponding to modified gravity, \(F_m\), changes, the nature of the force changes as well. The nature of \(F_m\), however, is determined by the sign of \(\zeta\). Positive \(\zeta\) makes the \(F_m\) attractive, while negative \(\zeta\) makes it repulsive in nature (See Fig.  6 (Left)). In both cases, an increment in the magnitude of \(F_m\) is accompanied by an increment in the magnitude of \(\zeta\). It’s worth noting that with an increase in \(\zeta\) adiabatic indices decreases (See, Table 1 and Fig.  6 (Right)), i.e., increasing the coupling constant \(\zeta\) tends to make the configuration less stable. An interesting observation is that the positive decoupling constant reduces stability, while the negative decoupling constant increases it.

8 Conclusion

Modified theories of gravity provide a substantial possibility for resolving or avoiding certain issues that appear when general theory of relativity is considered. This fascinating theory has several significant advantages. The model based on the modified theory of gravity can describe both the inflationary and accelerated expansion periods. In this regard, we have worked in \(f(\mathcal {R},\mathcal {T})\) theory background. To depict the complete solution of field equations for the distribution filled of charged isotropic matter subject to \(f(\mathcal {R},\mathcal {T})\) gravity, we used the simplified linear and separable form for the arbitrary function \(f(\mathcal {R},\mathcal {T})\) as \(f(\mathcal {R},\mathcal {T})=\mathcal {R}+2\zeta \mathcal {T}\), with \(\zeta\) a coupling constant, and specific matter Lagrangian as \(\mathcal {L}_\mathcal {M}=\rho\). Our research is dedicated to generating a completely new class of generalized solutions for charged isotropic spherically symmetric relativistic neutron stars. We have obtained a singularity free spacetime in the background of \(f(\mathcal {R},\mathcal {T})\) gravity by employing the Buchdahl ansatz \(e^{\lambda (r)}=\frac{\mathcal {K}(1+x)}{(\mathcal {K}+x)}\) for the metric potential paired with \(e^\nu =\sqrt{{\mid 1-\mathcal {Y}^2\mid }}\frac{(\alpha +\beta \mathcal {Y})^2}{\mathcal {Y}^2} \Big (\mathcal {A}\frac{\alpha }{\beta ^3}g(x)+\mathcal {B}\Big )^2\), with \(g(x)=\beta \mathcal {Y}-\frac{\alpha ^2}{\alpha +\beta \mathcal {Y}}-\alpha \ln {(\alpha +\beta \mathcal {Y})^2}\), \(\mathcal {Y}=\sqrt{\frac{\mathcal {K}+x}{\mathcal {K}-1}}\) and \(x = \mathcal {C}r^2\). As testing candidates for our model, we have taken a rotating neutron star with charged isotropic configuration, namely ’Hercules X-1’. We present our results for various parametric values of \(\zeta\) in the range \(\frac{-\kappa }{8\pi }\le \zeta \le \frac{\kappa }{8\pi }\), to examine the effect of \(\zeta\) on physical properties of the studied compact stars. We have investigated the variation of structural variables of the considered compact stars to radial distance from the core to the surface of stars. Through graphical analysis, we have demonstrated that our model complies with the requirements for the acceptability of physical systems. A stability analysis using the Chandrasekhar adiabatic index revealed that our models are stable, and the negative coupling constants enhance the stability. Finally, we conclude that in the context of \(f(\mathcal {R},\mathcal {T})\) gravity; a viable model to describe relativistic charged isotropic compact stars, particularly neutron stars, has been obtained.