1 Introduction

Since, there exist connection between phenomena in the real world and partial differential equations (PDEs), so they have been extensively used to formulate a wide range of applied problems. In many practical situations such as advection-diffusion equation which is one of the most important PDEs and arising in ground water flows, such ideal information is rarely encountered. For example, our information about the permeability of the soil, magnitude of source term, inflow or outflow conditions, etc, are not accurate. Uncertainties in this problem can be modeled by stochastic advection-diffusion equation. Over a long period of time, these random factors were ignored due to lack of powerful computational tools and problems were modeled by deterministic advection-diffusion equation. In the last years, researchers published some papers on the development of numerical methods to solve various kinds of advection-diffusion equations. For example finite difference method (Sousa 2009; Singh et al. 2019), difference methods (Liu et al. 2007), explicit and implicit Euler approximations method (Zhuang et al. 2009), finite element method (Zheng et al. 2010; Badr et al. 2018), generalized finite difference method (Prieto et al. 2011), lattice Boltzmann method (Servan-Camas and Tsai 2008), implicit MLS meshless method (Zhuang et al. 2011), finite volume scheme (Ollivier-Gooch and Van Altena 2002), Ritz approximation (Firoozjaee et al. 2018), predictor-corrector method (Babaei et al. 2019), etc. In recent decade, by increasing the computational power, mathematicians imported some random factors into deterministic models and studied more accurate functional equation models to solve more demanding problems. Stochastic functional equations were created by inserting random factors into deterministic functional equations. Study of stochastic functional equations such as stochastic differential equations (SDEs), stochastic partial differential equations (SPDEs) and stochastic integral equations (SIEs) can be very useful in applications, since they arise in many real situations. Presenting an accurate and efficient scheme to approximate solution of stochastic functional equations is a essential requirement, due to the fact that most stochastic functional equations no have analytical solution or providing their analytic solution is very hard. These numerical techniques include wavelet method (Khodabin et al. 2015), meshless method based on radial basis functions (Mirzaee and Samadyar 2018; Ahmadi et al. 2017; Dehghan and Shirzadi 2015), spectral method (Taheri et al. 2017), operational matrix method (Heydari et al. 2014; Mirzaee and Samadyar 2017), implicit Euler approximation (Kamrani and Jamshidi 2017), wavelet Galerkin method (Heydari et al. 2016), etc.

Fractional calculus plays an important role in many branches of science, as it can fill the gap left for the correct discovery of real phenomena. Many control, biophysical, electromagnetic, biophysical, mechanical, signal and image processing, blood flow, HIV infection, etc. problems are modeled through fractional differential equations (Baleanu et al. 2012; Mirzaee and Samadyar 2018). In many cases, the exact solution of these equations is unknown and it is very difficult and even impossible to find the exact solution. On the other hand, it still remains a lot of improvements in the present numerical approaches due to the non-local property of the fractional derivative. Therefore, providing an accurate numerical scheme to solve fractional differential equations is one of the most important subject in numerical analysis which has attracted interest of many researchers. Recently, fractional differential equations and fractional integral equations have been extensively studied. For example, operator splitting for fractional reaction-diffusion equations (Baeumer et al. 2008), some numerical approaches based on piecewise interpolation for fractional calculus, and some new improved approaches based on the Simpson method for the fractional differential equations (Li et al. 2011), discussing on stability and convergence of the fractional Euler method, the fractional Adams method and the high order methods based on the convolution formula by using the generalized discrete Gronwall inequality (Li and Zeng 2013), using spline approximation for the Caputo derivative in the fractional diffusion and obtaining an implicit numerical method for solving it (Sousa 2011), finite difference method to solve the space-fractional convection-diffusion equation and discussion on stability, consistency and therefore convergence of this method (Su et al. 2011), numerical solution of a fractional partial differential equation with Riesz space fractional derivatives (Yang et al. 2010), finite element method to solve singularly perturbed fractional advection–dispersion equation with boundary layer (Roop 2008), using operational matrix method based on second kind Chebyshev polynomials for the fourth-order biharmonic equation (Heydari and Avazzadeh 2018), unconditionally stable weighted average finite difference method for fractional diffusion equation (Sousa and Li 2015), introducing operational matrix of fractional order based on Legendre functions and application of them to solve time fractional convection-diffusion equations (Abbasbandy et al. 2015).

In this paper, we are concerned with a fractional stochastic advection-diffusion equation with a time fractional derivative of order \(\alpha \) (\(0<\alpha \le 1\)). The general form of time fractional stochastic advection-diffusion type equation is given by

$$\begin{aligned}\frac{\partial ^\alpha u(x,t)}{\partial t^\alpha }&=\left( \beta +\gamma \frac{dB(t)}{dt}\right) \frac{\partial ^2 u(x,t)}{\partial x^2}\nonumber \\&\quad +\,\sigma \frac{\partial u(x,t)}{\partial x}, \quad (x,t)\in [0,1]\times [0,1], \end{aligned}$$
(1)

with the following initial and boundary conditions

$$\begin{aligned}&u(x,0)=f(x), \quad x\in [0,1],\nonumber \\&u(0,t)=g_0(t), \quad t\in [0,1]\nonumber \\&u(1,t)=g_1(t),\quad t\in [0,1], \end{aligned}$$
(2)

where \(\beta \), \(\gamma \) and \(\sigma \) are real constant, f(x), \(g_0(t)\) and \(g_1(t)\) are the stochastic processes defined on the probability space \((\Omega ,{\mathcal {F}},{\mathcal {P}})\), u(x, t) is an unknown stochastic process which should be approximated.\(\frac{\partial ^\alpha u(x,t)}{\partial t^\alpha }\) represents Caputo partial derivative of order \(\alpha \) which is defined as follows (Mirzaee and Samadyar 2017):

$$\begin{aligned}D^\alpha f(t)&=\frac{1}{\Gamma (n-\alpha )}\nonumber \\&\quad \int _0^t\frac{f^{(n)}(s)}{(t-s)^{1-n+\alpha }}ds, \quad n-1<\alpha \le n, t>0. \end{aligned}$$
(3)

Moreover, B(t) denotes one-dimensional Brownian motion process which satisfies in the following properties (Mirzaee and Samadyar 2019):

  1. (1)

    \(B(0)=0\) (with the probability 1).

  2. (2)

    For \(0\le s <t \le T\) the increment \(B(t)-B(s)\) is random variable with mean zero and variance \(t-s\). Consequently, \(B(t)-B(s)\sim \sqrt{t-s} {\mathcal {N}}(0,1)\) where \({\mathcal {N}}(0,1)\) denotes normal distribution with zero mean and unit variance.

  3. (3)

    For \(0\le s<t<u<v\le T\) the increments \(B(t)-B(s)\) and \(B(v)-B(u)\) are independent.

From Eq. (1), we can obtain the following popular PDEs:

\(\bullet \):

Deterministic time fractional advection-diffusion equation is obtained by letting \(\gamma =0\).

\(\bullet \):

Time fractional stochastic diffusion type equation (Heat equation) is obtained by letting \(\sigma =0\) and \(\gamma \ne 0\).

\(\bullet \):

Deterministic time fractional advection equation is obtained by letting \(\beta =\gamma =0\) and \(\sigma \ne 0\).

In the current paper, we employ finite difference method and spline approximation to provide approximate solution of time fractional stochastic advection-diffusion type equation (1) with the initial and boundary conditions (2).

The outline of this article is as follows: Sect. 2 is devoted to presenting a new method based on finite difference method and spline approximation to solve time fractional stochastic advection-diffusion type equation (1) with the initial and boundary conditions (2), numerically. Section 3 discussed on error analysis of the suggested method. Accuracy and efficiency of the proposed method are checked in Sect. 4 via some test problems. Finally, this paper end with some concluding remarks in Sect. 5.

2 Numerical Scheme

In this section, we develop an efficient numerical scheme to estimate the solution of time fractional stochastic advection-diffusion type equation (1) with initial and boundary conditions (2).

To present numerical method to solve Eq. (1), we consider an arbitrary positive integer number N and defined time step-size as \(\Delta t=\frac{1}{N}\). Also, we define mesh points as \(t_j=j\Delta t\) where \(j=0,1,\ldots ,N\) and insert \(t=t_j\ (j=1,2,\ldots ,N)\) into Eq. (1). So, we have

$$\begin{aligned} \frac{\partial ^\alpha u(x,t_j)}{\partial t^\alpha }=\left( \beta +\gamma \frac{dB(t_j)}{dt}\right) \frac{\partial ^2 u(x,t_j)}{\partial x^2}+\sigma \frac{\partial u(x,t_j)}{\partial x}. \end{aligned}$$
(4)

Let \(y_j(x)=u(x,t_j), j=0,1,\ldots ,N\). Thus from initial and boundary conditions (2), we have \(y_j(0)=g_0(t_j)\), \(y_j(1)=g_1(t_j)\), and \(y_0(x)=f(x)\).

Backward finite difference formula to approximate \(\frac{dB(t_j)}{dt}\) is given by

$$\begin{aligned}&\xi _j=\frac{dB(t_j)}{dt}\approx \frac{B(t_{j})-B(t_{j-1})}{\Delta t},\nonumber \\&\quad j=1,2,\ldots ,N. \end{aligned}$$
(5)

By substituting Eq. (5) into Eq. (4) and using notation \(y_j(x)=u(x,t_j)\), we have the following system of N boundary value problems

$$\begin{aligned}&\frac{\partial ^\alpha u(x,t_j)}{\partial t^\alpha }=(\beta +\gamma \xi _j)y_j''(x)+\sigma y_j'(x), \nonumber \\&\quad j=1,2,\ldots ,N, \end{aligned}$$
(6)

subject to the following boundary conditions

$$\begin{aligned}&y_j(0)=g_0(t_j),\quad j=1,2,\ldots ,N,\nonumber \\&y_j(1)=g_1(t_j),\quad j=1,2,\ldots ,N. \end{aligned}$$
(7)

Let \({\mathcal {I}}_j=\frac{\partial ^\alpha u(x,t_j)}{\partial t^\alpha } (j=1,2,\ldots ,N)\) and use Eq. (3). So, we get

$$\begin{aligned} {\mathcal {I}}_j&=\frac{1}{\Gamma (1-\alpha )}\int _ 0^{t_j} (t_j-s)^{-\alpha }\frac{\partial u(x,s)}{\partial s}ds\nonumber \\&=\frac{1}{\Gamma (1-\alpha )}\sum _{k=0}^{j-1}\int _ {t_k}^{t_{k+1}} (t_j-s)^{-\alpha }\frac{\partial u(x,s)}{\partial s}ds. \end{aligned}$$
(8)

Spline linear approximation of \(\frac{\partial u(x,s)}{\partial s}\) where \(t_k\le s\le t_{k+1}\) is given by

$$\begin{aligned} S _k(x,s)=\frac{s-t_k}{\Delta t}\frac{\partial u(x,t_{k+1})}{\partial t}+\frac{t_{k+1}-s}{\Delta t}\frac{\partial u(x,t_k)}{\partial t}+O(\Delta t^2). \end{aligned}$$
(9)

By inserting \(S _k(x,s)\) into Eq. (8) and doing some computations, we conclude

$$\begin{aligned} {\mathcal {I}}_j&=\frac{1}{\Gamma (1-\alpha )}\sum _{k=0}^{j-1}\int _ {t_k}^{t_{k+1}} (t_j-s)^{-\alpha } S_k(x,s) ds\nonumber \\&=\frac{\Delta t^{1-\alpha }}{\Gamma (3-\alpha )} \sum _{k=0}^j a_{kj}\frac{\partial u(x,t_k)}{\partial t}+\frac{t_j^{1-\alpha }}{\Gamma (2-\alpha )}O(\Delta t^2), \end{aligned}$$
(10)

where the coefficients \(a_{kj}\) are given by

$$\begin{aligned}&a_{kj}\\ &\quad ={\left\{ \begin{array}{ll} (j-1)^{2-\alpha }-j^{1-\alpha }(j+\alpha -2), &k=0,\\ (j-k+1)^{2-\alpha }-2(j-k)^{2-\alpha }+(j-k-1)^{2-\alpha }, &\le k\le j-1,\\ 1,& k=j. \end{array}\right. } \end{aligned}$$

Remark 1

From definitions of \(a_{kj}\), we can easily show that

$$\begin{aligned} \sum _{k=0}^j a_{kj}=(2-\alpha )j^{1-\alpha }. \end{aligned}$$
(11)

At this step, we should estimate \(\frac{\partial u(x,t_k)}{\partial t}\) for \(k=0,1,\ldots , N\). For \(k=0\), we use forward finite difference formula as follows

$$\begin{aligned} \delta _0(x)&=\frac{\partial u(x,t_0)}{\partial t}=\frac{-u(x,t_2)+4u(x,t_1)-3u(x,t_0)}{2\Delta t}\nonumber \\&=\frac{-y_2(x)+4y_1(x)-3y_0(x)}{2\Delta t}. \end{aligned}$$
(12)

The first order derivative \(\frac{\partial u(x,t_k)}{\partial t}\) for \(k=1,2,\ldots ,N-1\) can be approximated via central finite difference formula as

$$\begin{aligned} \delta _k(x)&=\frac{\partial u(x,t_k)}{\partial t}=\frac{u(x,t_{k+1})-u(x,t_{k-1})}{2\Delta t}\nonumber \\&=\frac{y_{k+1}(x)-y_{k-1}(x)}{2\Delta t}, \end{aligned}$$
(13)

and for \(k=N\), we apply backward finite difference formula as

$$\begin{aligned} \delta _N(x)&=\frac{\partial u(x,t_N)}{\partial t}=\frac{3u(x,t_N)-4u(x,t_{N-1})+u(x,t_{N-2})}{2\Delta t}\nonumber \\&=\frac{3y_N(x)-4y_{N-1}(x)+y_{N-2}(x)}{2\Delta t}. \end{aligned}$$
(14)

From Eqs. (12)–(14), we conclude

$$\begin{aligned} \frac{\partial u(x,t_k)}{\partial t}=\delta _k(x)+O(\Delta t^2),\quad k=0,1,\ldots ,N . \end{aligned}$$
(15)

Substituting Eq. (15) into Eq. (10) and using Remark 1, conclude

$$\begin{aligned} {\mathcal {I}}_j&= \frac{\Delta t^{1-\alpha }}{\Gamma (3-\alpha )} \sum _{k=0}^j a_{kj}\bigl ( \delta _k(x)+O(\Delta t^2)\bigl )\nonumber \\&\quad +\frac{t_j^{1-\alpha }}{\Gamma (2-\alpha )}O(\Delta t^2)\nonumber \\&=\frac{\Delta t^{1-\alpha }}{\Gamma (3-\alpha )} \sum _{k=0}^j a_{kj} \delta _k(x)+\frac{O(\Delta t^2)\Delta t^{1-\alpha }}{\Gamma (3-\alpha )} \sum _{k=0}^j a_{kj}\nonumber \\&\quad +\frac{t_j^{1-\alpha }}{\Gamma (2-\alpha )}O(\Delta t^2)\nonumber \\&=\frac{\Delta t^{1-\alpha }}{\Gamma (3-\alpha )} \sum _{k=0}^j a_{kj}\delta _k(x)+\frac{2t_j^{1-\alpha }}{\Gamma (2-\alpha )}O(\Delta t^2). \end{aligned}$$
(16)

Therefore, by using Eq. (16), the system of N boundary value problem (6) can be written as follows

$$\begin{aligned}&(\beta +\gamma \xi _j)y_j''(x)+\sigma y_j'(x)=\frac{\Delta t^{1-\alpha }}{\Gamma (3-\alpha )} \sum _{k=0}^j a_{kj}\delta _k(x)\nonumber \\&\quad +\frac{2t_j^{1-\alpha }}{\Gamma (2-\alpha )}O(\Delta t^2),\quad j=1,2,\ldots ,N, \end{aligned}$$
(17)

subject to the boundary conditions (7).

For \(j=1,2,\ldots ,N\), we let

$$\begin{aligned}&\zeta _j=\frac{2t_j^{1-\alpha }}{\Gamma (2-\alpha )}, \\&\theta_j =\beta +\gamma \xi _j,\quad \eta _j=-\frac{3}{2}a_{0j}-\frac{1}{2}a_{1j}, \end{aligned}$$

and put

$$\begin{aligned}&\Upsilon =\begin{pmatrix} \zeta _1 \\ \quad \zeta _2 \\ \vdots \\ \zeta _N \end{pmatrix}, \Theta =\begin{pmatrix} \theta _1 &{}\quad 0&{}\quad \ldots &{}\quad 0\\ 0&{}\quad \theta _2 &{}\quad \ldots &{}\quad 0\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad 0&{}\quad \ldots &{}\quad \theta _N \end{pmatrix},\\&\mathbf{y }(x)=\begin{pmatrix} y_1(x)\\ y_2(x)\\ \vdots \\ y_N(x) \end{pmatrix}, \quad \mathbf{v }(x)=\frac{\Delta t^{-\alpha }}{\Gamma (3-\alpha )}y_0(x)\begin{pmatrix} \theta _1 \\ \theta _2 \\ \vdots \\ \theta _N \end{pmatrix}. \end{aligned}$$

So, the system of N boundary value problem (17) can be written in the following matrix form

$$\begin{aligned} \Theta \mathbf{y }''(x)+\sigma \mathbf{y }'(x)=\mathbf{v }(x)+\Lambda \mathbf{y }(x)+\Upsilon O(\Delta t^2), \end{aligned}$$
(18)

where \(\Lambda =\frac{\Delta t^{-\alpha }}{\Gamma (3-\alpha )} [AX+B]\), and

$$\begin{aligned}&A=\begin{pmatrix} a_{11}&{}\quad 0&{}\quad 0&{}\quad \ldots &{}\quad 0\\ a_{12}&{}\quad a_{22}&{}\quad 0&{}\quad \ldots &{}\quad 0\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ a_{1N}&{} \quad a_{2N}&{}\quad a_{3N}&{}\quad \ldots &{}\quad a_{NN} \end{pmatrix},X=\begin{pmatrix} 0&{}\quad \frac{1}{2}&{}\quad &{}\quad &{}\quad \\ \frac{-1}{2}&{}\quad 0&{}\quad \frac{1}{2}&{}\quad &{}\quad \\ &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \\ &{}\quad &{}\quad \frac{-1}{2} &{}\quad 0&{}\quad \frac{1}{2}\\ &{}\quad &{}\quad &{}\quad \frac{-1}{2}&{}\quad 0 \end{pmatrix},\\&B=\begin{pmatrix} 2a_{01} &{}\quad \frac{-1}{2}a_{01}&{}\quad 0&{}\quad \ldots &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 2a_{02} &{}\quad \frac{-1}{2}a_{02}&{}\quad 0&{}\quad \ldots &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ 2a_{0 N-1} &{}\quad \frac{-1}{2}a_{0N-1}&{}\quad 0&{}\ldots &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 2a_{0N} &{}\quad \frac{-1}{2}a_{0N}&{}\quad 0&{}\quad \ldots &{}\quad 0&{}\quad \frac{1}{2}a_{NN}&{}\quad \frac{-3}{2}a_{NN}&{}\quad \frac{3}{2}a_{NN} \end{pmatrix}. \end{aligned}$$

The error term \(\Upsilon O(\Delta t^2)\) in the system of N boundary value problems is neglected and the following system is concluded

$$\begin{aligned} \Theta \tilde{\mathbf{y }}''(x)+\sigma \tilde{\mathbf{y }}'(x)=\mathbf{v }(x)+\Lambda \tilde{\mathbf{y }}(x). \end{aligned}$$
(19)

We solve the system (19) by backward differentiation formula which has been explained in Salehi et al. (2018).

3 Error Analysis

In this section to investigate the error analysis of the present method, we let \(\sigma =0\). Thus, the obtained exact and approximate system of N boundary value problem take the following form:

$$\begin{aligned}&\Theta \mathbf{y }''(x)=\mathbf{v }(x)+\Lambda \mathbf{y }(x)+\Upsilon O(\Delta t^2), \nonumber \\&\mathbf{y }(0)=G_0,\quad \mathbf{y }(1)=G_1, \end{aligned}$$
(20)

and

$$\begin{aligned}&\Theta \tilde{\mathbf{y }}''(x)=\mathbf{v }(x)+\Lambda \tilde{\mathbf{y }}(x), \nonumber \\&\tilde{\mathbf{y }}(0)=G_0,\quad \tilde{\mathbf{y }}(1)=G_1, \end{aligned}$$
(21)

where \(G_0=[g_0(t_1),g_0(t_2),\ldots ,g_0(t_N)]^T\) and \(G_1=[g_1(t_1),g_1(t_2),\ldots ,g_01(t_N)]^T\).

In the following, we intend show that how neglecting the error term can impact on the solution. Let \(\mathbf{e }(x)=\mathbf{y }(x)-\tilde{\mathbf{y }}(x)\), and then by using Eqs (20) and (21), we get

$$\begin{aligned}&\Theta \mathbf{e }''(x)=\Lambda \mathbf{e }(x)+\Upsilon O(\Delta t^2), \nonumber \\&\mathbf{e }(0)=0,\mathbf{e }(1)=0, \end{aligned}$$
(22)

Assume that \(\Theta \) is an invertible matrix. By multiplying Eq. (22) in \(\Theta ^{-1}\), we have the following system of N boundary value problems

$$\begin{aligned}&\mathbf{e }''(x)={\tilde{\Lambda }}\mathbf{e }(x)+{\tilde{\Upsilon }} O(\Delta t^2), \nonumber \\&\mathbf{e }(0)=0,\quad \mathbf{e }(1)=0, \end{aligned}$$
(23)

where \({\tilde{\Lambda }}=\Theta ^{-1}\Lambda \) and \({\tilde{\Upsilon }}=\Theta ^{-1} \Upsilon \). Let \(\lambda _1 ,\lambda _2,\ldots ,\lambda _N\) be the distinct eigenvalues of the matrix \({\tilde{\Lambda }}\) and \(v_1,v_2,\ldots ,v_N\) be the corresponding eigenvectors of them. It is easily to show that all eigenvalues \(\lambda _1 ,\lambda _2,\ldots ,\lambda _N\) are negative. Let \(\sqrt{\lambda _j}=\alpha _j+i\beta _j\) for \(j=1,2,\ldots ,N\). So, the exact solution of Eq. (23) is obtained as follows

$$\begin{aligned}\mathbf{e }(x)&=\sum _{j=1}^N\exp (\alpha _j x)\bigl (c_{1j}\cos (\beta _j x)+c_{2j}\sin (\beta _j x)\bigl )v_j\nonumber \\&\quad +\overrightarrow{a_1}+\overrightarrow{a_2}x, \end{aligned}$$
(24)

where the unknown constant values \(c_{1j}\) and \(c_{2j}\) for \(j=1,2,\ldots ,N\) are determined via boundary conditions and \(\overrightarrow{a_1}\) and \(\overrightarrow{a_2}\) are constant unknown vectors such that

$$\begin{aligned} \Lambda \overrightarrow{a_2}=0, \quad \Lambda \overrightarrow{a_1}=\Theta \bigl (a_2-\Theta ^{-1}\Upsilon O(\Delta t^2)\bigl ). \end{aligned}$$
(25)

Suppose that \(\Lambda \) is a non-singular matrix and use Eq. (6). Therefore, we conclude

$$\begin{aligned} \overrightarrow{a_2}=0, \quad \Lambda \overrightarrow{a_1}=-\Lambda ^{-1}\Upsilon O(\Delta t^2). \end{aligned}$$
(26)

By inserting the obtained values in Eq. (26) into Eq. (25), we have the following formula for error function

$$\begin{aligned}&\mathbf{e }(x)=\sum _{j=1}^N\exp (\alpha _j x)\bigl (c_{1j}\cos (\beta _j x)+c_{2j}\sin (\beta _j x)\bigl )v_j \nonumber \\&\quad -\Lambda ^{-1}\Upsilon O(\Delta t^2). \end{aligned}$$
(27)

Since the eigenvalues of the matrix \({\tilde{\Lambda }}\) have negative real parts, the sigma in vector function \(\mathbf{e }(x)\) exponentially converges to zero whenever x increases or \(\Delta t\rightarrow 0\). Therefore,

$$\begin{aligned} \Vert \mathbf{e }(x)\Vert _\infty \le \epsilon +\Vert \Lambda ^{-1}\Vert _\infty M_1 O(\Delta t^2), \end{aligned}$$
(28)

where \(M_1=\Vert \Upsilon \Vert _\infty =\frac{2}{\Gamma (2-\alpha )}\). We require provide an upper bound for \(\Vert \Lambda ^{-1}\Vert _\infty \) when \(\Delta t\) decreases. The values of \(\Vert \Lambda ^{-1}\Vert _\infty \) for different values of \(\alpha \) and \(\Delta t\) have been reported in Table 1. This table indicates that the values of \(\Vert \Lambda ^{-1}\Vert _\infty \) are independent of the variation of \(\Delta t\) and only dependent on \(\alpha \). Also, from this table we conclude that the values of \(\Vert \Lambda ^{-1}\Vert _\infty \) decrease when \(\alpha \) approaches to 2. Suppose that \(M_2\) be an upper bound for \(\Vert \Lambda ^{-1}\Vert _\infty \). The numerical computations insure that this value exists and is independent of \(\Delta t\). Therefore,

$$\begin{aligned} \Vert \mathbf{e }(x)\Vert _\infty \le \epsilon + M_1 M_2 O(\Delta t^2), \end{aligned}$$
(29)

or

$$\begin{aligned} \Vert \mathbf{e }(x)\Vert _\infty \le \epsilon + M O(\Delta t^2), \end{aligned}$$
(30)

where \(M=M_1M_2\).

In fact, we computationally proved the following theorem.

Theorem 1

Suppose that \(\mathbf{y }(x)\) and \(\tilde{\mathbf{y }}(x)\) denote the solution of system of boundary value problems (20) and (21), respectively. So, we have

$$\begin{aligned} \Vert \mathbf{y }(x)-\tilde{\mathbf{y }}(x)\Vert _\infty \le \epsilon + \frac{2M_2}{\Gamma (2-\alpha )} O(\Delta t^2), x\in [0,1], \end{aligned}$$
(31)

where \(\epsilon \) exponentially converges to zero as x increase or \(\Delta t\rightarrow 0\), \(M_2\) is an upper bound of \(\Vert \Lambda ^{-1}\Vert _\infty \) which is independent of \(\Delta (t)\). Thus, for sufficiently small \(\Delta t\), we have

$$\begin{aligned} \Vert \mathbf{y }(x)-\tilde{\mathbf{y }}(x)\Vert _\infty =O(\Delta t^2), x\in [0,1]. \end{aligned}$$
(32)
Table 1 Values of \(\Vert \Lambda ^{-1}\Vert _\infty \) for different choice of \(\Delta t\) and \(\alpha \)
Full size table

4 Numerical Example

In this section, numerical results of applying proposed method on three test problems are reported to verify the validity of theoretical discussion presented in the Sect. 2. The accuracy and efficiency of the mentioned method are checked via absolute error measure which is defined as follows:

$$\begin{aligned}&e(x_i,t)=\bigl |u_{exact}(x_i,t)-u_{approx}(x_i,t)\bigl |, \nonumber \\&\quad i=1,2,\ldots ,M-1, \end{aligned}$$
(33)

for a fixed certain time \(t\in (0,1]\) and nodal points \(x_i=i\Delta x\) where \(\Delta x\) denotes spatial step size which is calculated as \(\Delta x=\frac{1}{M}\). Furthermore, as we mentioned in the previous section, \(\Delta t\) denotes time step size which is computed as \(\Delta t=\frac{1}{N}\). Notice that in this section M and N denote the number of nodal points in x and t directions, respectively. It is noteworthy that the associated algorithms with the present approach have been written in the Matlab software and have been performed on a Laptop with Intel Core i3 CPU (2.40 GHz) and 4.00 GB RAM.

Example 1

Consider the following time fractional stochastic advection-diffusion type equation

$$\begin{aligned}&\frac{\partial ^\alpha u(x,t)}{\partial t^\alpha }=\Bigl ( \frac{1}{\pi ^2}+\frac{dB(t)}{dt}\Bigl )\frac{\partial ^2 u(x,t)}{\partial x^2}+\frac{\partial u(x,t)}{\partial x}\nonumber \\&\quad +f(x,t), \quad (x,t)\in [0,1]\times [0,1], \end{aligned}$$
(34)

together with the following initial and boundary conditions

$$\begin{aligned}&u(x,0)=0, \quad 0\le x\le 1,\nonumber \\&u(0,t)=0, \quad 0\le t\le 1,\nonumber \\&u(1,t)=0, \quad 0\le t\le 1, \end{aligned}$$
(35)

and

$$\begin{aligned}&f(x,t)=\frac{2t^{2-\alpha }\sin (\pi x)}{\Gamma (3-\alpha )}+\Bigl ( \frac{1}{\pi ^2}+\frac{dB(t)}{dt}\Bigl )\pi ^2t^2 \sin (\pi x)\\&\quad -\pi t^2 \cos (\pi x). \end{aligned}$$

The exact solution of Eq. (34) is \(u(x,t)=t^2\sin (\pi x)\).

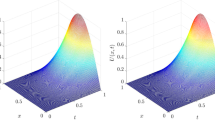
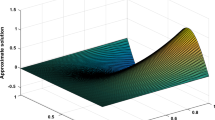
In this paper, finite difference method and spline approximation are employed to compute approximate solution of Eq. (34) with the initial and boundary conditions (35). The values of exact solution and approximate solution at time \(t=1\) for different values of \(\alpha =0.25,0.5,0.75,1\) for \(\Delta x=\Delta t=0.01\) and \(\Delta x=\Delta t=0.002\) are reported in Tables 2 and 3, respectively. These results confirm that there exist a good agreement between the numerical solution and exact solutions. Also, the graphs of absolute error for \(\Delta x=\Delta t=0.01\) and \(\Delta x=\Delta t=0.002\) at time \(t=1\) are plotted in Figs. 1 and 2, respectively. This figures show that our proposed method is reliable to obtain an accurate approximate solution.

Fig. 1
figure 1

Absolute errors of presented scheme for Example 1 with \(\Delta t=\Delta x=0.01\) at time \(t=1\)

Full size image
Table 2 Numerical results of Example 1 with \(\Delta t=\Delta x=0.01\) at time \(t=1\)
Full size table
Fig. 2
figure 2

Absolute errors of presented scheme for Example 1 with \(\Delta t=\Delta x=0.002\) at time \(t=1\)

Full size image
Table 3 Numerical results of Example 1 with \(\Delta t=\Delta x=0.002\) at time \(t=1\)
Full size table

Example 2

Consider the following stochastic advection-diffusion equation

$$\begin{aligned}&\frac{\partial u(x,t)}{\partial t}=\Bigl (1+\beta \frac{dB(t)}{dt}\Bigl )\frac{\partial ^2 u(x,t)}{\partial x^2}-3\frac{\partial u(x,t)}{\partial x}\nonumber \\&\quad +f(x,t), \quad (x,t)\in [0,1]\times [0,1], \end{aligned}$$
(36)

together with the following initial and boundary conditions

$$\begin{aligned}&u(x,0)=\exp (2x), \quad 0\le x\le 1,\nonumber \\&u(0,t)=\exp (-2t), \quad 0\le t\le 1,\nonumber \\&u(1,t)=\exp (2-2t), \quad 0\le t\le 1, \end{aligned}$$
(37)

and

$$\begin{aligned} f(x,t)=-2\exp (2x-2t)\Bigl [ 1+2\Bigl (1+\beta \frac{dB(t)}{dt}\Bigl )-3\Bigl ]. \end{aligned}$$

The exact solution of Eq. (36) is \(u(x,t)=\exp (2x-2t)\).

In this paper, finite difference method and spline approximation are employed to compute approximate solution of Eq. (36) with \(\beta =1\) and the initial and boundary conditions (37). The values of exact solution and approximate solution at time \(t=1\) for different values of \(\alpha =0.25,0.5,0.75,1\) for \(\Delta x=\Delta t=0.01\) and \(\Delta x=\Delta t=0.002\) are reported in Tables 4 and 5, respectively. These results confirm that there exist a good agreement between the numerical solution and exact solutions. Also, the graphs of absolute error for \(\Delta x=\Delta t=0.01\) and \(\Delta x=\Delta t=0.002\) at time \(t=1\) are plotted in Figs. 3 and 4, respectively. This figures show that our proposed method is reliable to obtain an accurate approximate solution. Also, we consider wavelet Galerkin method (Heydari et al. 2016) to compare this method with the previous method for solving stochastic advection-diffusion equation. Wavelet Galerkin method has been used to solve stochastic advection-diffusion equation (36) with \(\beta =0\), numerically. Notic that, by considering \(\beta =0\), Eq. (36) is transformed into the following ordinary advection-diffusion equation

$$\begin{aligned} \frac{\partial u(x,t)}{\partial t}=\frac{\partial ^2 u(x,t)}{\partial x^2}-3\frac{\partial u(x,t)}{\partial x}, \quad (x,t)\in [0,1]\times [0,1]. \end{aligned}$$
(38)

It is necessary to mention that solving Eq. (36) due to randomness is more difficult than Eq. (38). However, the values of absolute error obtained via presented method for \(\Delta x=\Delta t=0.002\) are compared with the values of absolute error achieved by wavelet Galerkin method in Table 6. From this table, we conclude that our method is more accurate than wavelet Galerkin method.

Fig. 3
figure 3

Absolute errors of presented scheme for Example 2 with \(\Delta t=\Delta x=0.01\) at time \(t=1\)

Full size image
Table 4 Numerical results of Example 2 with \(\Delta t=\Delta x=0.01\) at time \(t=1\)
Full size table
Fig. 4
figure 4

Absolute errors of presented scheme for Example 2 with \(\Delta t=\Delta x=0.002\) at time \(t=1\)

Full size image
Table 5 Numerical results of Example 2 with \(\Delta t=\Delta x=0.002\) at time \(t=1\)
Full size table
Table 6 Comparison of absolute errors of Example 2 obtained by two different methods
Full size table

Example 3

Consider the following time fractional stochastic advection-diffusion type equation

$$\begin{aligned} \frac{\partial ^\alpha u(x,t)}{\partial t^\alpha }=\Bigl (1+ \frac{dB(t)}{dt}\Bigl )\frac{\partial ^2 u(x,t)}{\partial x^2}+\sigma \frac{\partial u(x,t)}{\partial x}+f(x,t), \quad (x,t)\in [0,1]\times [0,1], \end{aligned}$$
(39)

together with the following initial and boundary conditions

$$\begin{aligned}&u(x,0)=0, \quad 0\le x\le 1,\nonumber \\&u(0,t)=\int _0^t B(s)ds, \quad 0\le t\le 1,\nonumber \\&u(1,t)=t^2+\int _0^t B(s)ds, \quad 0\le t\le 1, \end{aligned}$$
(40)

and

$$\begin{aligned}&f(x,t)=\frac{2xt^{2-\alpha }}{\Gamma (3-\alpha )}+\frac{1}{\Gamma (1-\alpha )}\int _ 0^t (t-s)^{-\alpha }B(s)ds\\&\quad -\sigma t^2-\sigma \int _0^t B(s)ds. \end{aligned}$$

The exact solution of Eq. (39) is \(u(x,t)=xt^2+\int _0^t B(s)ds\).

In this paper, finite difference method and spline approximation are employed to compute approximate solution of Eq. (39) with \(\sigma =1\) and the initial and boundary conditions (40). The values of exact solution and approximate solution at time \(t=1\) for different values of \(\alpha =0.25,0.5,0.75,1\) for \(\Delta x=\Delta t=0.01\) and \(\Delta x=\Delta t=0.002\) are reported in Tables 7 and 8, respectively. These results confirm that there exist a good agreement between the numerical solution and exact solutions. Also, the graphs of absolute error for \(\Delta x=\Delta t=0.01\) and \(\Delta x=\Delta t=0.002\) at time \(t=1\) are plotted in Figs. 5 and 6, respectively. This figures show that our proposed method is reliable to obtain an accurate approximate solution. Also, we consider wavelet Galerkin method (Heydari et al. 2016) to compare this method with the previous method for solving stochastic advection-diffusion equation. Wavelet Galerkin method has been used to solve stochastic advection-diffusion equation (39) with \(\sigma =0\), numerically. Notic that, by considering \(\sigma =0\), Eq. (39) is transformed to stochastic heat equation. By comparing absolute error graphs in this paper with absolute error graph in the paper (Heydari et al. 2016), we conclude that our method is more accurate than wavelet Galerkin method.

Fig. 5
figure 5

Absolute errors of presented scheme for Example 3 with \(\Delta t=\Delta x=0.01\) at time \(t=1\)

Full size image
Table 7 Numerical results of Example 3 with \(\Delta t=\Delta x=0.01\) at time \(t=1\)
Full size table
Fig. 6
figure 6

Absolute errors of presented scheme for Example 3 with \(\Delta t=\Delta x=0.002\) at time \(t=1\)

Full size image
Table 8 Numerical results of Example 3 with \(\Delta t=\Delta x=0.002\) at time \(t=1\)
Full size table

5 Conclusion

In this paper, a new efficient technique is developed for solving time fractional stochastic advection-diffusion type equation. In this method, first we discrete the time direction and substitute nodal points \(t_j\) in the consideration equation. Moreover, the existent first derivative in the definition of Caputo time fractional derivative is approximated via linear spline approximation. After some computations, the solution of time fractional stochastic advection-diffusion type equation is transformed into the system of boundary value problems. Also, we prove that neglecting error terms in the system of boundary value problems will give a truncation error \(O(\Delta t^2)\). Finally, we have applied present method to solve three test problems and obtained numerical results have been reported in tables. Numerical results demonstrate that the present scheme is accurate, efficient, very fast and can produce acceptable results.