Confidence Intervals for Quantiles in Ranked Set Sampling

Abstract

This article concerns the problem of interval estimation for the population quantiles in ranked set sampling. Some intervals are developed using asymptotic normality of nonparametric quantile estimator and/or resampling methods. The proposed procedures are evaluated in terms of coverage rate and average length. Some comparisons with analogous intervals in simple random sampling are also made. Finally, a medical data set is used to illustrate application of the intervals.

1 Introduction

Ranked set sampling (RSS) is a sampling method that can be used when there is a mechanism to rank potential sample units inexpensively and fairly accurately, without actually measuring them. It was first employed by McIntyre (1952) for estimating average yields in agriculture. In this specific problem, an expert may provide a reliable ranking of the yields for a few adjacent plots based on visual inspection. The aforesaid informal ranking process is known as “judgment ranking” in RSS literature. It is often implemented visually, but using one or more concomitant variables could be a viable alternative. If the rankings are free of errors, it is called perfect ranking. In practical situations, the ranking errors are inevitable, which is referred to as imperfect ranking.

An unbalanced ranked set sample is drawn as follows. One first specifies a set size k and values $m_1,\ldots ,m_k$. For $r=1,\ldots ,k$, one then draws $m_r$ independent simple random samples of size k and ranks the units within each sample from smallest to largest using the judgment ranking. Finally, the unit with rank r is selected for measurement from each sample. The resulting sample is denoted by $\{X_{[r]i}: r=1,\ldots ,k\,;i=1,\ldots ,m_r \}$, where $X_{[r]i}$ is the rth judgment order statistic from the ith cycle. Balanced RSS corresponds to special case that $m_1=\cdots =m_k=m$. The set size k is typically chosen to be small so that units in sets of size k can be ranked accurately.

A ranked set sample is more informative than a simple random sample of comparable size. This is so because the judgment ranking process serves as a guide to select the units. This may be interpreted as a kind of stratification performed at the sample level. It is formally shown that many RSS-based methods outperform their SRS versions as long as the ranking quality is better than random. Wolfe (2012) provides a good review of RSS and its applications. Some applications of RSS include agriculture (Murray et al. 2000), environmental monitoring (Kvam 2003), reliability (Mahdizadeh and Zamanzade 2018a, c), and medicine (Mahdizadeh and Zamanzade 2019a).

Nonparametric estimation based on RSS has drawn much attention in the literature. Several variations of RSS have been introduced for estimating the population mean (Mahdizadeh and Zamanzade 2018d, 2019b). Many statistical methods have been proposed based on RSS and its modifications. Stokes and Sager (1988) considered estimation of the population distribution function in RSS. Al-Omari (2015, 2016) dealt with this problem in L RSS and quartile RSS. Zamanzade and Mahdizadeh (2018, 2019) explored the proportion estimation under some variations of RSS. Chen (2000) developed quantile estimator in balanced RSS and showed that it is asymptotically more efficient than its SRS counterpart if the perfect ranking is assumed. Mahdizadeh and Arghami (2012) addressed quantile estimation in RSS from a population with known mean. Balakrishnan and Li (2006) studied confidence intervals (CIs) for quantiles and tolerance intervals based on ordered ranked set samples. Mahdizadeh and Zamanzade (2018b) proposed some CIs for the reliability parameter in RSS. This article deals with the problem of interval estimation for the population quantiles in balanced RSS.

In Sect. 2, quantile estimator in RSS and its asymptotic normality are reviewed. Next, estimating the asymptotic variance is discussed. Based on asymptotic normality of the quantile estimator and/or resampling methods, some CIs for quantiles are constructed in Sect. 3. In Sect. 4, coverage rates and average lengths of the proposed intervals are judged by means of Monte Carlo simulation. Application of the developed procedures is illustrated using a medical data set in Sect. 5. A summary of the findings appears in Sect. 6.

2 Quantile Estimation

Let $\{X_{[r]i}: r=1,\ldots ,k\,;i=1,\ldots ,m \}$ be a balanced ranked set sample from a population with probability density function (PDF) f(x) and cumulative distribution function (CDF) F(x). The empirical CDF in RSS is given by:

$$\begin{aligned} \tilde{F}_n(x)=\frac{1}{n} \sum _{r=1}^k \sum _{i=1}^m I\left( X_{[r]i} \le x \right) , \end{aligned}$$

(1)

where $n=mk$, and $I\left( .\right)$ is the indicator function. Stokes and Sager (1988) showed that the above estimator is unbiased for F(x) and has smaller variance than its SRS competitor, given a total sample size.

The problem of estimating pth population quantile, denoted by $\xi _p$, is closely related to that of CDF estimation. Chen (2000) proposed the pth quantile estimator in RSS as:

$$\begin{aligned} \tilde{\xi }_p=\inf \{x: \tilde{F}_n(x) \ge p \}, \quad p \in (0,1), \end{aligned}$$

where $\tilde{F}_n(x)$ is defined in (1). Suppose B(a, b; t) is the CDF of beta distribution with parameters a and b evaluated at t, i.e.,

$$\begin{aligned} B(a,b;t)=\int _0^t \frac{\Gamma (a+b)}{\Gamma (a) \Gamma (b)}\, x^{a-1} (1-x)^{b-1} \text {d}x, \end{aligned}$$

where $\Gamma (.)$ is the gamma function. The asymptotic normality of $\tilde{\xi }_p$ is stated in the following result due to Chen (2000). It should be mentioned that in asymptotic theory of RSS design, the number of cycles goes to infinity, while the set size is fixed.

Proposition 1

Suppose that f(x) is positive in a neighborhood of$\xi _p$and is continuous at$\xi _p$. If the judgment ranking is perfect, then

$$\begin{aligned} \sqrt{n} \left( \tilde{\xi }_p-\xi _p \right)\, {\mathop {\rightarrow }\limits ^{d}}\, N\left( 0, \frac{\sigma ^2_{k,p}}{f^2(\xi _p)} \right) , \end{aligned}$$

(2)

where

$$\begin{aligned} \sigma ^2_{k,p}=\frac{1}{k} \sum _{r=1}^k B(r,k-r+1;p) \left[ 1-B(r,k-r+1;p) \right] . \end{aligned}$$

If the perfect ranking is assumed, then it can be shown that the asymptotic variance of $\tilde{\xi }_p$ is smaller than its SRS analog. The proof simply follows from Lemma 1 in Chen (2000). It is worth noting that the asymptotic normality still holds in the imperfect ranking setup, but the expression of $\sigma ^2_{k,p}$ needs some adjustment. Naturally, one would expect some improvement in interval estimation for $\xi _p$ based on RSS as compared with that in SRS. In the following, we discuss two approaches for estimating the asymptotic variance of $\tilde{\xi }_p$. These methods will be used in the next section to construct CIs.

The variance expression for $\tilde{\xi }_p$ involves the unknown quantity $f(\xi _p)$, which needs to be replaced with a consistent estimate. Chen (1999) considered the density estimation by the kernel method in RSS. The estimator is given by:

$$\begin{aligned} \widehat{f}_{\mathrm{RSS}}(x)=\frac{1}{n h} \sum _{r=1}^k \sum _{i=1}^m K\left( \frac{x-X_{[r]i}}{h} \right) , \end{aligned}$$

where the kernel K(.) is a symmetric PDF, and the smoothing parameter h is known as the bandwidth. It is shown that the bias (variance) of $\widehat{f}_{\mathrm{RSS}}(x)$ is equal to (no larger than) its SRS counterpart.

The bandwidth selection in SRS is a well-treated topic in the literature. Based on a partial simulation study (whose result is not reported here), we only consider two methods which will be described shortly. Minimizing asymptotic mean integrated squared error (AMISE) of the kernel density estimator is a basic scheme. Silverman (1986) recommended the normal reference (NR) bandwidth given by $1.06\, s\, n^{-0.2}$, where s is the sample standard deviation. To choose the bandwidth in the RSS, we may treat data as if collected by SRS. Finally, $f(\xi _p)$ can be estimated by $\widehat{f}_{\mathrm{RSS}}(\tilde{\xi }_p)$, where the required bandwidth is determined by the above two methods. The estimates obtained by using AMISE and NR bandwidth selection methods will be denoted by $\widehat{f}_{\mathrm{RSS},1}(\tilde{\xi }_p)$ and $\widehat{f}_{\mathrm{RSS},2}(\tilde{\xi }_p)$, respectively.

The asymptotic results are only valid if the total sample size n is large enough. On the other hand, RSS is applicable when it is difficult and/or expensive to measure too many sample units. Thus, it is interesting to have some procedures for estimating the variance of $\tilde{\xi }_p$ from small data sets. Jackknife and bootstrap are helpful tools that can be utilized in this setup.

The jackknife methodology has been applied in reducing a possible bias of an estimator, and in approximating its variance [see Quenouille (1956) and Tukey (1958)]. Let $\hat{\theta }(X_1,\ldots ,X_n)$ be a statistic of interest, where $X_ i$’s are iid random variables, and $\hat{\theta }$ is invariant under permutation of the arguments. Suppose $\hat{\theta }^{(i)}$ denotes the value of $\hat{\theta }$ based on $X_1,\ldots ,X_{i-1},X_{i+1},\ldots ,X_n$. The jackknife estimate of $Var(\hat{\theta })$ is computed as:

$$\begin{aligned} \widehat{Var}(\hat{\theta })=\frac{n-1}{n}\sum _{i=1}^n \left( \hat{\theta }^{(i)}-\hat{\theta }^{(0)}\right) ^2, \end{aligned}$$

where $\hat{\theta }^{(0)}=\sum _{i=1}^n \hat{\theta }^{(i)}/n$.

A ranked set sample consists of independent but not identically distributed random variables. More precisely, for any fixed r, $X_{[r]1},\ldots ,X_{[r]m}$ have a common distribution. The data, however, can be considered as m iid random vectors $\mathbf {X}_1,\ldots ,\mathbf {X}_m$, where $\mathbf {X}_i=(X_{[1]i},\ldots ,X_{[k]i})$ ($i=1,\ldots ,m$) contains elements of the sample in the ith cycle. Now, the jackknife technique may be used to estimate $Var(\tilde{\xi }_p)$. If $\tilde{\xi }_p^{(i)}$ is the value of pth sample quantile with $\mathbf {X}_i$ omitted from the data, then the jackknife estimate of the variance is given by:

$$\begin{aligned} {\widehat{Var}}_{\mathrm{jack}}(\tilde{\xi }_p)=\frac{m-1}{m} \sum _{i=1}^m \left( \tilde{\xi }_p^{(i)}-\tilde{\xi }^{(0)}\right) ^2, \end{aligned}$$

(3)

where $\tilde{\xi }^{(0)}=\sum _{i=1}^m \tilde{\xi }_p^{(i)}/m$.

Efron (1979) introduced the bootstrap as a method for estimating the standard error of a statistic. In the past four decades, a large body of the literature has developed around applied and theoretical research on the bootstrap technique (see Good (2006), for example). Bootstrap method in RSS has drawn some attention as well. The bootstrap ranked set sampling (BRSS) algorithm, due to Modarres et al. (2006), is an efficient one which is described here. Let $\tilde{F}_n$ be defined as in (1). According to the BRSS algorithm, a bootstrap sample is drawn as follows:

• 1. Assign a probability of $n^{-1}$ to each element of the ranked set sample.

• 2. Randomly draw k elements $\mathcal {X}_1,\ldots ,\mathcal {X}_k {\mathop {\sim }\limits ^{iid}} \tilde{F}_n$, sort them in ascending order $\mathcal {X}_{(1)},\ldots ,\mathcal {X}_{(k)}$, and retain $X_{[r]1}^*=\mathcal {X}_{(r)}$.

• 3. Perform step 2 for $r=1,\ldots ,k$.

• 4. Repeat steps 2 and 3 m times to obtain {$X_{[r]i}^*$}.

Suppose B bootstrap ranked set samples are generated, and $\tilde{\xi }_p^b$ is the value of the pth sample quantile based on data in the bth ($b=1,\ldots ,B$) replication. Then, bootstrap variance estimator is given by:

$$\begin{aligned} {\widehat{Var}}_{\mathrm{boot}}(\tilde{\xi }_p)=\frac{1}{B-1}\sum _{b=1}^B \left( \tilde{\xi }_p^b-\bar{\xi }^* \right) ^2, \end{aligned}$$

(4)

where $\bar{\xi }^*=\sum _{b=1}^B \tilde{\xi }_p^b/B$.

3 Interval Estimation

In this section, we develop different types of CIs for $\xi _p$. Ozturk and Deshpande (2006) proposed an exact quantile interval in RSS, but asymptotic and resampling methods are the center of interest here. Using pivotal quantity is a common method for constructing CI. In view of Proposition 1, the asymptotic distribution of

$$\begin{aligned} \frac{\tilde{\xi }_p-\xi _p}{\sqrt{\mathbb {VAR}(\tilde{\xi }_p)}} \end{aligned}$$

(5)

is approximately standard normal if $\mathbb {VAR}(\tilde{\xi }_p)$ is a suitable estimator for the variance of $\tilde{\xi }_p$ given in (2). The corresponding approximate ($1-\alpha$)-CI has the form of

$$\begin{aligned} \left( \tilde{\xi }_p- z_{\alpha /2} \sqrt{\mathbb {VAR}(\tilde{\xi }_p)}, \tilde{\xi }_p+ z_{\alpha /2} \sqrt{\mathbb {VAR}(\tilde{\xi }_p)} \right) , \end{aligned}$$

where $z_{\alpha /2}$ is the ($1-\alpha /2$) quantile of the standard normal distribution. Now, we may plug in any variance estimator introduced in the previous section into the above formula to arrive at a CI for $\xi _p$.

If the kernel-based estimator is employed, then one can use intervals

$$\begin{aligned} \left( \tilde{\xi }_p- z_{\alpha /2} \frac{\sigma _{k,p}}{\sqrt{n}\, \widehat{f}_{\mathrm{RSS},1}(\tilde{\xi }_p)}, \tilde{\xi }_p+ z_{\alpha /2} \frac{\sigma _{k,p}}{\sqrt{n}\, \widehat{f}_{\mathrm{RSS},1}(\tilde{\xi }_p)} \right) , \end{aligned}$$

(6)

and

$$\begin{aligned} \left( \tilde{\xi }_p- z_{\alpha /2} \frac{\sigma _{k,p}}{\sqrt{n}\, \widehat{f}_{\mathrm{RSS},2}(\tilde{\xi }_p)}, \tilde{\xi }_p+ z_{\alpha /2} \frac{\sigma _{k,p}}{\sqrt{n}\, \widehat{f}_{\mathrm{RSS},2}(\tilde{\xi }_p)} \right) , \end{aligned}$$

(7)

where $\widehat{f}_{\mathrm{RSS},1}(\tilde{\xi }_p)$ and $\widehat{f}_{\mathrm{RSS},2}(\tilde{\xi }_p)$ are introduced in Sect. 2.

Similarly, incorporating estimators (3) and (4) in the denominator of the pivotal quantity (5) yields intervals

$$\begin{aligned} \left( \tilde{\xi }_p-z_{\alpha /2}\sqrt{{\widehat{Var}}_{\mathrm{jack}}(\tilde{\xi }_p)},\tilde{\xi }_p+z_{\alpha /2}\sqrt{{\widehat{Var}}_{\mathrm{jack}}(\tilde{\xi }_p)} \right) , \end{aligned}$$

(8)

and

$$\begin{aligned} \left( \tilde{\xi }_p-z_{\alpha /2}\sqrt{{\widehat{Var}}_{\mathrm{boot}}(\tilde{\xi }_p)},\tilde{\xi }_p+z_{\alpha /2}\sqrt{{\widehat{Var}}_{\mathrm{boot}}(\tilde{\xi }_p)} \right) . \end{aligned}$$

(9)

Percentile bootstrap is an intuitive approach for constructing CI that uses quantiles of bootstrap distribution of $\tilde{\xi }_p$. If $\tilde{\xi }_p^{\beta }$ is the $\beta$ quantile of $\tilde{\xi }_p^1,\ldots ,\tilde{\xi }_p^B$, then the ($1-\alpha$) percentile bootstrap CI is defined as:

$$\begin{aligned} \left( \tilde{\xi }_p^{\alpha /2}, \tilde{\xi }_p^{1-\alpha /2} \right) . \end{aligned}$$

The above type interval is clearly simple to form and easy to understand, but fails to provide good coverage in small samples. To overcome this problem, expanded percentile bootstrap interval can be used. It is a variant of percentile bootstrap CI, which is obtained by adjusting quantiles of the bootstrap distribution. Let $\Phi (.)$ be the distribution function of standard normal random variable and $t_{n-1,\alpha /2}$ be the ($1-\alpha /2$) quantile of Student’s t distribution with $n-1$ degrees of freedom. The ($1-\alpha$) expanded percentile bootstrap CI is given by:

$$\begin{aligned} \left( \tilde{\xi }_p^{\alpha '/2}, \tilde{\xi }_p^{1-\alpha '/2} \right) , \end{aligned}$$

(10)

where $\alpha '/2=\Phi \left( -\sqrt{n/(n-1)}\, t_{n-1,\alpha /2} \right)$.

The procedure of the bootstrap-t interval is as follows. For each bootstrap sample, compute

$$\begin{aligned} T_b=\frac{\tilde{\xi }_p^b-\tilde{\xi }_p}{\sqrt{\mathbb {VAR}(\tilde{\xi }_p^b)}} \quad (b=1,\ldots ,B), \end{aligned}$$

where $\tilde{\xi }_p^b$ and $\mathbb {VAR}(\tilde{\xi }_p^b)$ are obtained from the bth bootstrap sample. If $t_{\beta }$ is the $\beta$ quantile of $T_1,\ldots ,T_B$, then the ($1-\alpha$) bootstrap-t interval is given by:

$$\begin{aligned} \left( \tilde{\xi }_p- t_{1-\alpha /2} \sqrt{\mathbb {VAR}(\tilde{\xi }_p)}, \tilde{\xi }_p- t_{\alpha /2} \sqrt{\mathbb {VAR}(\tilde{\xi }_p)} \right) . \end{aligned}$$

Again, using the kernel-based variance estimators in $T_b$ and in the above results in intervals

$$\begin{aligned} \left( \tilde{\xi }_p- t_{1-\alpha /2} \frac{\sigma _{k,p}}{\sqrt{n}\, \widehat{f}_{\mathrm{RSS},1}(\tilde{\xi }_p)}, \tilde{\xi }_p- t_{\alpha /2} \frac{\sigma _{k,p}}{\sqrt{n}\, \widehat{f}_{\mathrm{RSS},1}(\tilde{\xi }_p)} \right) , \end{aligned}$$

(11)

and

$$\begin{aligned} \left( \tilde{\xi }_p- t_{1-\alpha /2} \frac{\sigma _{k,p}}{\sqrt{n}\, \widehat{f}_{\mathrm{RSS},2}(\tilde{\xi }_p)}, \tilde{\xi }_p- t_{\alpha /2} \frac{\sigma _{k,p}}{\sqrt{n}\, \widehat{f}_{\mathrm{RSS},2}(\tilde{\xi }_p)} \right) . \end{aligned}$$

(12)

For brevity, the intervals (6), (7), (8), (9), (10), (11), and (12) will be referred to as Norm1, Norm2, Norm-J, Norm-B, Boot-p, Boot-t1, and Boot-t2, respectively.

4 Numerical Results

To assess performances of the proposed intervals, a comprehensive simulation study was carried out. In doing so, we assumed that the parent distribution is standard normal, standard exponential, or standard uniform. Also, the total sample sizes $n=10,20,30$ and the sizes $k=2,5$ were chosen. Under each distribution, 10,000 ranked set samples were generated for any combination of n and k. Next, 0.95 CIs for $\xi _p$, $p \in (0,1)$, were constructed from each sample. The number of bootstrap replications was set to $B=500$. Finally, coverage rate and average length of any interval were estimated based on the corresponding 10,000 intervals observed. In the following, the perfect ranking is assumed, unless otherwise stated. Also, output figures for $n=10,30$ are not reported here to save space, but they are available on request from the first author.

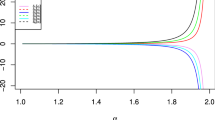
Figures 1, 2, and 3 display the results for the different distributions when $n=20$. For convenience, the nominal confidence coefficient is marked with a gray line in the corresponding plots. As expected, trends of coverage rate and length of the CIs are symmetric around the mean for symmetric distributions. An interval with good coverage probability is likely to be long. A property shared by different CIs is that coverage rate generally decreases for extreme quantiles. This is more evident in the case of some intervals other than Boot-t1 and Boot-t2. On the other hand, there is a sharp increase in length of Boot-t1 and Boot-t2 CIs for extreme quantiles.

Fig. 1

Estimated coverage rates and average lengths of 95% intervals for $n=20$ in the perfect ranking setup when the parent distribution is normal. Black/solid, blue/dashed, red/dotted, green/dotdash, orange/longdash, pink/twodash and skyblue/solid curves relate to Norm1, Norm2, Norm-J, Norm-B, Boot-p, Boot-t1, and Boot-t2 intervals, respectively

Fig. 2

Estimated coverage rates and average lengths of 95% intervals for $n=20$ in the perfect ranking setup when the parent distribution is exponential. Black/solid, blue/dashed, red/dotted, green/dotdash, orange/longdash, pink/twodash and skyblue/solid curves relate to Norm1, Norm2, Norm-J, Norm-B, Boot-p, Boot-t1, and Boot-t2 intervals, respectively

Fig. 3

Estimated coverage rates and average lengths of 95% intervals for $n=20$ in the perfect ranking setup when the parent distribution is uniform. Black/solid, blue/dashed, red/dotted, green/dotdash, orange/longdash, pink/twodash and skyblue/solid curves relate to Norm1, Norm2, Norm-J, Norm-B, Boot-p, Boot-t1, and Boot-t2 intervals, respectively

It is observed that Boot-t1 and Boot-t2 CIs show the best coverage rates for most of the quantiles, usually higher than the nominal level. This is achieved at the expense of extra length. In addition, Boot-t1 is always outperformed by Boot-t2 with respect to coverage rate, while the situation is reversed when comparing length. Also, it appears that if we are interested in estimating an extreme quantile, then Boot-t1 is a reliable CI in that it can attain good coverage rate with smaller length as compared with Boot-t2. This is highly important in the case of interval estimation for an extreme right tail quantile of exponential distribution, because other types of intervals have poor coverage rates.

One can see that Norm1 is the second best CI in terms of coverage rate in many situations, and much shorter than the two bootstrap-t intervals. It works satisfactorily, in view of both aspects of optimality, in estimating intermediate quantiles, especially when the parent distribution is symmetric.

The rest of the intervals, i.e., Norm2, Norm-J, Norm-B, and Boot-p, have comparable length, nearly similar to Norm1 interval. As to coverage rate, Norm2 and Boot-p CIs behave good for a smaller set of quantiles, as compared with Boot-t1, Boot-t2, and Norm1 intervals. Coverage probabilities of Norm-J and Norm-B CIs are always smaller than 0.95, where this is true in the former case often by a wide margin. Thus, these two intervals are not suggested for use in practice, although their lengths are in an acceptable range.

As mentioned in Sect. 1, RSS-based procedures are usually more efficient than their SRS competitors. We conducted a simulation study to investigate this property in the context of quantile estimation. In the following, we focus on Norm1 and Boot-p CIs as the general trends are more or less similar for other CIs. Although the details for constructing SRS versions of intervals (6)–(12) are not reported here, they are straightforward to derive. For example, by setting $k=1$ in Proposition 1, the asymptotic normality of the quantile estimator in SRS is established. This result can be used to develop CIs for quantiles from simple random samples. Obviously, some modifications for the jackknife and bootstrap methods in SRS are required. Figures 4 and 5 depict estimated coverage rates and average lengths of 95% intervals for $n=20$. It is observed that in both methods, RSS-based CIs are shorter than their SRS counterparts, regardless of the parent distribution. Moreover, increasing the set size leads to further reduction in length. As to coverage rate, RSS-based CI shows a very slight edge over their SRS rivals. Also, there is a minor improvement by increasing the set size.

Fig. 4

Estimated coverage rates and average lengths of 95% Norm1 interval for $n=20$ in the perfect ranking setup when the parent distribution is normal (a), exponential (b), or uniform (c). Blue/dashed and red/dotted curves relate to $k=2$ and $k=5$, respectively. Black/solid curve shows the analogous results in SRS

Fig. 5

Estimated coverage rates and average lengths of 95% Boot-p interval for $n=20$ in the perfect ranking setup when the parent distribution is normal (a), exponential (b), or uniform (c). Blue/dashed and red/dotted curves relate to $k=2$ and $k=5$, respectively. Black/solid curve shows the analogous results in SRS

Up to now, the perfect ranking was assumed. This is the ideal situation for any RSS-based method, but it is unlikely to happen in practice. Thus, it is vital to evaluate performance of the proposed CIs in the presence of judgment ranking errors. Toward this end, we consider an imperfect ranking model in which ranking the variable of interest X is done based on a concomitant variable Y. If $\mu _x$ and $\sigma _x$ are the mean and standard deviation of X, then the two variables are related as:

$$\begin{aligned} Y=\rho \left( \frac{X-\mu _x}{\sigma _x} \right) + \sqrt{1-\rho ^2}\, Z, \quad \rho \in [0,1], \end{aligned}$$

where Z is a standard normal random variable independent from X. Here, parameter $\rho$ is the correlation coefficient between X and Y and thus controls the ranking quality. The random ranking and the perfect ranking correspond to $\rho =0$ and $\rho =1$, respectively.

By selecting $\rho =0.7$ (fairly accurate ranking), coverage rates and average lengths of 95% Norm1 and Boot-p intervals were again estimated for $n=20$. The results appear in Figs. 6 and 7. The trends of interval length parallel those in Figs. 4 and 5. However, coverage rates of RSS-based CIs are no longer higher than their SRS analogs. The situation even deteriorates as the set size becomes larger, given a total sample size. This property is somewhat supported by findings of Terpstra and Miller (2006) in the context of exact inference for a population proportion based on the RSS. They observed that RSS-based CI is uniformly (as a function of the true population proportion) shorter than SRS-based CI. However, superiority for coverage probability is not uniform.

Fig. 6

Estimated coverage rates and average lengths of 95% Norm1 interval for $n=20$ in the imperfect ranking setup when the parent distribution is normal (a), exponential (b), or uniform (c). Blue/dashed and red/dotted curves relate to $k=2$ and $k=5$, respectively. Black/solid curve shows the analogous results in SRS

Fig. 7

Estimated coverage rates and average lengths of 95% Boot-p interval for $n=20$ in the imperfect ranking setup when the parent distribution is normal (a), exponential (b), or uniform (c). Blue/dashed and red/dotted curves relate to $k=2$ and $k=5$, respectively. Black/solid curve shows the analogous results in SRS

5 Application to Real Data

Obesity is no longer just a problem for the industrial nations. There is a growing number of overweight and obese people in other countries. Obese individuals are vulnerable to a great number of diseases and bodily malfunctions which root in the accumulation of excess body fat. For example, heart-related diseases and disorders are widespread among such people. Also, majority of the people having type 2 diabetes suffer from obesity. Body fat is an important index of health and fitness for the general population. There are several approaches for assessment of this measure. Dual energy X-ray absorptiometry (DXA) is one of the body fat testing methods that has been validated and thus is considered as the “gold standard,” but it is too costly to implement.

In this section, we illustrate the suggested procedures by using a real data in the context of body fat estimation. The data set has been used by Mahdizadeh and Zamanzade (2017) and includes 15 measured variables on 252 men.¹ The two variables considered are body fat percentage and abdomen circumference for each man which are denoted by X and Y, respectively. Suppose the set of 252 men is a hypothetical population, and we want to construct a CI for different quantiles of X. As mentioned before, accurate measurement of the variable of interest based on DXA technique is expensive. Thus, RSS method can be efficiently utilized in this setup. In particular, the judgment ranking process can be done using Y as a concomitant variable. The abdomen circumference is an obesity measure which is obtained readily. The correlation coefficient between X and Y is 0.81, ensuring that the judgment ranking can be implemented fairly accurately.

Coverage rates and average lengths of 95% Norm1 and Boot-p intervals and their SRS versions were estimated when $n=20$. These two CIs are selected because of the same reason mentioned in Sect. 4. Again, estimation is based on 10,000 samples, and 500 bootstrap resamples. In generating ranked set samples, set sizes $k=2, 5$ were used. The results are given in Fig. 8. One can see that the general trends are similar to those observed in Figs. 6 and 7, where the imperfect ranking is assumed. In particular, superiority of RSS-based intervals in terms of length is preserved, and it is improved by increasing the set size. A similar property does not hold for coverage rate, and larger set size leads to worse performance.

Fig. 8

Estimated coverage rates and average lengths of 95% Norm1 and Boot-p intervals for $n=20$ based on the body fat data. Blue/dashed and red/dotted curves relate to $k=2$ and $k=5$, respectively. Black/solid curve shows the analogous results in SRS

6 Conclusion

This article deals with constructing several CIs for quantiles from ranked set samples. Toward this end, we build on asymptotic normality of nonparametric quantile estimator and/or resampling methods. Seven types of CIs were developed: Norm1, Norm2, Norm-J, Norm-B, Boot-p, Boot-t1, and Boot-t2. A comprehensive simulation study was performed to shed light on finite sample properties of the proposed intervals. In particular, coverage rate and average length are the two criteria we focused on.

It turns out that Boot-t1 and Boot-t2 CIs often show the best coverage rates, mostly higher than the nominal level. As expected, these intervals are longer as compared to their competitors. Also, Norm1 is the second best CI in terms of coverage rate in many situations, and much shorter than the two bootstrap-t intervals. Norm2 and Boot-p CIs possess good coverage rate for a smaller set of quantiles, as compared with Boot-t1, Boot-t2, and Norm1 intervals. Using Norm-J and Norm-B CIs is not recommended as their coverage probabilities are always smaller than the nominal level. The main findings can be summarized as follows. If we are interested in estimating intermediate quantiles, then Norm1 interval is a good choice. As to the extreme quantiles, especially in the case of asymmetric distributions, bootstrap-t CIs should be employed because other types of intervals do not enjoy satisfactory coverage rates.

We also compared Norm1 and Boot-p CIs with their SRS counterparts. If the perfect ranking is assumed, RSS-based intervals are superior from both aspects, although improvement in coverage rate is not noticeable. In the presence of the judgment ranking errors, RSS-based intervals are still shorter, while their coverage rates are no longer higher.

In this article, we have developed some CIs for quantiles based on balanced RSS. In some situations, an unbalanced ranked set sample may further improve statistical efficiency. It would be interesting to propose similar intervals for use in the latter case. In doing so, resampling methods due to Amiri et al. (2014) may be employed. This will be considered in a follow-up article.