On the Extended Birnbaum–Saunders Distribution Based on the Skew-t-Normal Distribution

Abstract

In this article, a generalized version of the univariate Birnbaum–Saunders distribution based on the skew-t-normal distribution is introduced and its characterizations, properties are studied. Maximum likelihood estimation of the parameters via the ECM algorithm evaluated by Monte Carlo simulations is also discussed. Finally, two real datasets are analyzed for illustrative purposes.

1 Introduction

The two-parameter Birnbaum–Saunders (BS) distribution as a life distribution was originally introduced by Birnbaum and Saunders (1969) as a failure model due to cracks. A random variable U is said to have the BS distribution with shape and scale parameters $\alpha>0,\beta >0,$ respectively, if its cumulative distribution function (cdf) and probability density function (pdf) are given by

$$\begin{aligned} F_{\mathrm{BS}}(u; \alpha, \beta )& = \Phi (a(u;\alpha ,\beta )),\quad u>0, \\ f_{\mathrm{BS}}\left( u; \alpha, \beta \right)& = \phi (a(u;\alpha ,\beta ))A\left( u; \alpha, \beta \right), \quad u>0, \end{aligned}$$

respectively, where $\Phi (.)$ and $\phi (.)$ denote the cdf and pdf of the standard normal distribution, respectively, and $a(u;\alpha ,\beta )= \frac{1}{\alpha }\left( \sqrt{\frac{u}{\beta }}-\sqrt{\frac{\beta }{u}}\right)$ and $A(u;\alpha ,\beta )=\frac{{\text{ d }}a(u;\alpha ,\beta )}{{\text{ d }}u}=\frac{u+\beta }{2\alpha \sqrt{\beta }\sqrt{u^{3}}}.$ The stochastic representation of U is given by

$$\begin{aligned} U\overset{d}{=}\frac{\beta }{4}\left[ \alpha Z+\sqrt{(\alpha Z)^{2}+4}\right] ^{2}, \end{aligned}$$

(1)

where $\overset{d}{=}$ means equal in distribution, $Z\,\thicksim N(0,1)$ and consequently $Z\overset{d} = \frac{1}{\alpha }\left( \sqrt{\frac{U}{\beta }}-\sqrt{ \frac{\beta }{U}}\right)$.

The BS distribution as a skew distribution has been frequently applied in the last few years to biological model by Desmond (1985), to the medical field by Leiva et al. (2007) and Barros et al. (2008) and to the forestry and environmental sciences by Podaski (2008), Leiva et al. (2010) and Vilca et al. (2011).

For more flexibility, several extensions of the BS distribution have been considered in the literature. For example, one can refer to Diaz-Garcia and Leiva-Sanchez (2005), Sanhueza et al. (2008), Leiva et al. (2008) and Gomez et al. (2009).

The well-known skew-normal (SN) distribution introduced by Azzalini (1985, 1986) could be used instead of the usual normal distribution, whenever the data present skewness. In this case, percentiles concentrated on the left-tail or right-tail of the distribution should be predicted in a better way.

A random variable Y is said to have the standard SN distribution with shape parameter $\lambda \in R$, denoted by $Y\thicksim {\mathrm{SN}}(\lambda ),$ if its pdf is given by

$$\begin{aligned} f_{\mathrm{SN}}(y\,;\lambda )=2\phi (y)\Phi (\lambda y),\, \quad y\in R. \end{aligned}$$

Vilca et al. (2011) considered the ${\mathrm{SN}}(\lambda )$ for the random variable Z in (1) and obtained the skew-normal Birnbaum–Saunders (SN-BS) distribution with the pdf

$$\begin{aligned} f_{\mathrm{{SN-BS}}}(u;\alpha ,\beta ,\lambda )&= f_{\mathrm{SN}}(a(u;\alpha ,\beta );\lambda )A(u;\alpha ,\beta ) \\ &= 2\phi (a(u;\alpha ,\beta ))\Phi (\lambda a(u;\alpha ,\beta ))A(u;\alpha ,\beta ),\quad u,\alpha ,\beta >0,\lambda \in R. \end{aligned}$$

The maximum likelihood estimations of the SN-BS distribution parameters are usually obtained by ECM algorithm. Vilca et al. (2011) have shown that the extreme percentiles can be predicted with high accuracy by using their proposed model.

Also Hashmi et al. (2015) considered SNT distribution [see Nadarajah and Kotz (2003)] for the random variable Z in (1) and obtained some better results. The proposed pdf is

$$\begin{aligned} f_{\mathrm{{SNT-BS}}}(u;\alpha ,\beta ,\lambda ,\upsilon )=2\phi (a(u;\alpha ,\beta ))T(\lambda a(u;\alpha ,\beta );,\upsilon )A(u;\alpha ,\beta ),\quad u,\alpha ,\beta ,\upsilon >0,\lambda \in R, \end{aligned}$$

where $T(.;\upsilon )$ denotes the cdf of the Student's t-distribution.

Gomez et al. (2007) introduced the class of distributions, called skew symmetric distribution including the skew-t-normal (STN) distribution and showed that it fits well to model data with heavy tail and strong asymmetry. A Bayesian approach to the study of the scale mixtures log-Birnbaum–Saunders regression models with censored data is also proposed by Lachos et al. (2017).

In this paper, we extend the BS distribution based on the skew-t-normal distribution, called skew-t-normal Birnbaum–Saunders distribution (STN-BS), and show that extreme percentiles can be better predicted rather than some other extensions of the Birnbaum Saunders distribution.

The rest of this paper is organized as follows. Section 2 defines a new version of the BS distribution and presents a useful stochastic representation, where several properties for the proposed distribution are also given. Section 3 concerns with the estimation of the parameters by maximum likelihood method via the ECM algorithm, where the Fisher information matrix is also calculated. Finally in Sect. 4, we illustrate the proposed methodology by analyzing two real datasets.

2 The STN-BS model and some characterizations

In this section, we consider the STN distribution to define the BS distribution based on STN distribution and derive some of its properties. Following Gomez et al. (2007), recall that a random variable Y is said to have the STN distribution with skewness parameter $\lambda \in R$ and degree of freedom $\upsilon \in (0,\infty )$, denoted by $Y\thicksim {\mathrm{STN}}$$(\lambda ,\upsilon ),$ if its pdf is given by

$$\begin{aligned} f_{\mathrm{STN}}(y; \lambda , \upsilon )=2t(y; \upsilon )\Phi (\lambda y),\quad y\in R, \end{aligned}$$

(2)

where $t(y; \upsilon )$ denotes the pdf of the Student's t-distribution with degree of freedom $\upsilon$. The density (2) reduces to the $t(y; \upsilon )$ distribution when $\lambda =0,$ to the truncated Student's t-distribution, when$\mid \lambda \mid \longrightarrow \infty$, and to the SN distribution, when $\upsilon \longrightarrow \infty .$ Now, a BS distribution based on STN distribution is easily defined, as given in the following definition.

Definition 2.1

A random variable U is said to have the STN-BS distribution with parameter $(\alpha , \beta , \lambda , \upsilon )$ and is denoted by ${U}\sim$ STN-BS $(\alpha ,\beta ,\lambda ,\upsilon )$, if it has the following stochastic representation

$$\begin{aligned} {U}\overset{d} = \frac{\beta }{4}\left[ \alpha Y+\sqrt{(\alpha Y)^{2}+4}\right] ^{2}, \end{aligned}$$

where $Y\thicksim {\mathrm{STN}}(\lambda , \upsilon )$. Then, the pdf of U can be easily obtained as

$$\begin{aligned} f_{\mathrm{STN-BS}}({u}; \alpha , \beta , \lambda , \upsilon ) &= f_{\mathrm{STN}}(a(u; \alpha , \beta ); \lambda , \upsilon )A(u; \alpha , \beta ) \nonumber \\ &= 2t(a(u; \alpha , \beta ); \upsilon )\Phi (\lambda a(u; \alpha , \beta ))A(u; \alpha , \beta ),\quad u, \alpha , \beta , \upsilon >0,\lambda \in R. \end{aligned}$$

(3)

2.1 Simple properties and moments

In this section, we present some simple properties and expressions for the moments of STN-BS distributions.

• 1. For $\lambda =0$, the pdf in (3) reduces to the pdf of the T-BS distribution which is an extension of BS distribution obtained by replacing the random variable Z in (1) with the Student's t random variable with degree of freedom $\upsilon$. In this case, the pdf is given by

  $$\begin{aligned} f_{\text{T-BS}}(u; \upsilon )=t(a(u; \alpha , \beta ); \upsilon )A(u; \alpha , \beta )). \end{aligned}$$

• 2. The pdf in (3) tends to the pdf of the SN-BS distribution, as $\upsilon \longrightarrow +\infty$

• 3. If $U\sim {\text{STN-BS}}(\alpha , \beta , \lambda , \upsilon )$, then $U^{-1}\sim {\text{STN-BS}}(\alpha, \beta ^{-1}, -\lambda, \upsilon )$ and $cU\sim {\text{STN-BS}}(\alpha , c\beta , \lambda , \upsilon )$, for $c>0$.

• 4. If $U\sim {\text{STN-BS}}(\alpha , \beta , \lambda , \upsilon )$, then $V\overset{d}{= }\left| \frac{1}{\alpha }(\sqrt{\frac{U}{\beta }}-\sqrt{\frac{\beta }{U}} )\right| \thicksim \mathrm{HT}\left( \upsilon \right)$, where ${\mathrm{HT}}\left( \upsilon \right)$ denotes the Student's half-t-distribution with degree of freedom $\upsilon$.

• 5. If $U_{T^{*}}\sim {\text{T-BS}}(\alpha , \beta , \upsilon )$ and $T^{*}\sim t(.; \upsilon )$, then the mean, variance, coefficient of variation (CV), skewness (CS) and kurtosis (CK) of $U_{T^{*}}$ denoted by $E[U_{T^{*}}],$$V[U_{T^{*}}],$$\gamma [U_{T^{*}}],$$\alpha _{3}[U_{T^{*}}]$ and $\alpha _{4}[U_{T^{*}}]$ are given by

  $$\begin{aligned} E[U_{T^{*}}] &= \frac{\beta }{2}\left[ \alpha ^{2}ET^{*^{2}}+2\right] , \\ V[U_{T^{*}}] &= \frac{\beta ^{2}\alpha ^{2}}{4}\left[ \alpha ^{2}(2ET^{*^{4}}-E^{2}T^{*^{2}})+4ET^{*^{2}}\right] , \\ \gamma [U_{T^{*}}] &= \frac{\alpha \sqrt{\alpha ^{2}(2ET^{*^{4}}-E^{2}T^{*^{2}})+4ET^{*^{2}}}}{\left[ \alpha ^{2}ET^{*^{2}}+2\right] }, \\ \alpha _{3}[U_{T^{*}}] &= \frac{1}{\left[ V[U_{T^{*}}]\right] ^{ \frac{3}{2}}}\frac{\beta ^{3}\alpha ^{4}}{8}\left[ \alpha ^{2}(4ET^{*^{6}}-6ET^{*^{4}}ET^{*^{2}}+2E^{3}T^{*^{2}})+12ET^{*^{4}}-12E^{2}T^{*^{2}}\right] , \\ \alpha _{4}[U_{T^{*}}]&= \frac{1}{\left[ V[U_{T^{*}}]\right] ^{2}} \frac{\beta ^{4}\alpha ^{4}}{8}[\alpha ^{4}(8ET^{*^{8}}-16ET^{*2}ET^{*^{6}}+12ET^{*^{4}}E^{2}T^{*2}-3E^{4}T^{*2}) \\&+\alpha ^{2}(32ET^{*^{6}}-48ET^{*^{4}}ET^{*2}+24E^{3}T^{*^{3}})+16ET^{*^{4}}]. \end{aligned}$$

  respectively, where

  $$\begin{aligned} ET^{*2}&= \frac{\upsilon }{\upsilon -2},\text{ }\upsilon>2, \\ ET^{*4} &= \frac{3\upsilon ^{2}}{(\upsilon -2)(\upsilon -4)},\ \upsilon>4, \\ ET^{*6} &= \frac{15\upsilon ^{3}}{(\upsilon -2)(\upsilon -4)(\upsilon -6)},\ \upsilon>6, \\ ET^{*8} &= \frac{105\upsilon ^{4}}{(\upsilon -2)(\upsilon -4)(\upsilon -6)(\upsilon -8)},\ \upsilon >8. \end{aligned}$$

The moments of the STN-BS distribution can be expressed in terms of the moments of T-BS distribution. In the following proposition, we present the relationships between the means, variances, coefficients of variation, skewness and kurtosis of the STN-BS and T-BS distributions.

Proposition 2.1

Let$U\sim {\text{STN-BS}}$$(\alpha ,\beta ,\lambda ,\upsilon )$and$U_{T^{*}}\sim {\text{T-BS}}$$(\alpha ,\beta ,\upsilon ).$Then, the mean, variance, coefficient of variation, coefficient of skewness and the coefficient of kurtosis denoted byE[U], V[U],  $\gamma [U],$$\alpha _{3}[U],$and$\alpha _{4}[U],$ofUin terms of$U_{T^{*}}$are given by

$$\begin{aligned} E[U] &= E[U_{T^{*}}]+\frac{\alpha \beta }{2}\omega _{1}, \\ V[U] &= V[U_{T^{*}}]+\left[ \frac{\alpha \beta }{2}\right] ^{2}\alpha _{\omega }, \\ \gamma [U] &= \gamma [U_{T^{*}}]\frac{\sqrt{1+\frac{\alpha ^{2}\beta ^{2}\alpha _{\omega }}{V(2U_{T^{*}})}}}{1+\frac{\alpha \beta \omega _{1}}{E[2U_{T^{*}}]}}, \\ \alpha _{3}[U] &= \alpha _{3}[U_{T^{*}}]\left[ \frac{\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}}{\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}+\alpha \omega }\right] ^{\frac{3}{ 2}}+\frac{2[a_{0}+a_{1}\alpha +a_{2}\alpha ^{2}]}{[\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}+\alpha _{\omega }]^{\frac{3}{2}}}, \\ \alpha _{4}[U] &= \left[ \alpha _{4}[U_{T^{*}}]+\frac{ b_{0}+b_{1}\alpha +b_{2}\alpha ^{2}+b_{3}\alpha ^{3}}{(\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2})^{2}}\right] \frac{[\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}]^{2}}{[\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}+\alpha _{\omega }]^{2}}, \end{aligned}$$

respectively, where

$$\begin{aligned} \alpha _{\omega } &= 2\alpha (\omega _{3}-\omega _{1}ET^{*2})-\omega _{1}^{2}, \\ a_{0} & = \omega _{1}^{3}-6\omega _{1}ET^{*2}+2\omega _{3}, \\ a_{1}& = 3\omega _{1}^{2}ET^{*2}-3\omega _{1}\omega _{3}, \\ a_{2}& = 2\omega _{5}-3\omega _{3}ET^{*2}-3\omega _{1}ET^{*4}+3\omega _{1}E^{2}T^{*2}, \\ b_{0}& = -3\omega _{1}^{4}-16\omega _{1}\omega _{3}+24\omega _{1}^{2}ET^{*2}, \\ b_{1}& = 16\omega _{5}-16\omega _{3}ET^{*2}-48\omega _{1}ET^{*2}+48\omega _{1}E^{2}T^{*2}+12\omega _{1}^{2}\omega _{3}-12\omega _{1}^{3}ET^{*2}, \\ b_{2}& = -16\omega _{1}\omega _{5}+12\omega _{1}^{2}ET^{*4}-18\omega _{1}^{2}E^{2}T^{*2}+24\omega _{1}\omega _{3}ET^{*2}, \\ b_{3}& = 8\omega _{7}-16\omega _{1}ET^{*6}-16\omega _{5}ET^{*2}+12\omega _{3}E^{2}T^{*2}+24\omega _{1}ET^{*2}ET^{*4}-12\omega _{1}E^{3}T^{*2}, \\ \omega _{k}& = E[Y^{k}\sqrt{\alpha ^{2}Y^{2}+4}], k=1, 3, 5, 7, \end{aligned}$$

and$Y\sim {\mathrm{STN}}(\lambda , \upsilon ), T^{*}\sim t(\upsilon ).$For calculating the values for$\omega _{k},$the involved integrals must be solved by using some numerical methods. We have applied theintegratefunction in the statistical software R.

Table 1 provides values for the mean $(\mu )$, standard deviation (SD), CS and CK of the ${\text{STN-BS}}(\alpha , 1, \lambda , 9)$ for different values of $\alpha$ and $\lambda .$

Table 1 The values for the mean $(\mu )$, standard deviation (SD), CS and CK of the ${\text{STN-BS}}(\alpha , 1, \lambda , 9)$

We observe that, for both positive values of $\lambda$ and large values of $\alpha ,$ the distribution has very large kurtosis.

Fig. 1

The graph of the densities; BS, SN-BS, T-BS, SNT-BS and STN-BS for selected values of parameters

Figure 1 displays the graph of the densities, BS, SN-BS, SNT-BS, T-BS and STN-BS, for some of the selected values of parameters.

2.2 Some useful results

Here, we provide some useful results which will be used in the estimation methods. Following Cabral et al. (2008) and Ho et al. (2011), the following convenient stochastic representation holds for $Y\thicksim {\mathrm{STN}}(\lambda , \upsilon ),$

$$\begin{aligned} Y\overset{d}{=}\left[ \frac{\lambda \mid Z_{1}\mid }{\sqrt{\tau (\tau +\lambda ^{2})}}+\frac{Z_{2}}{\sqrt{\tau +\lambda ^{2}}}\right] , \end{aligned}$$

(4)

where $Z_{1}$, $Z_{2}$ are two independent N(0, 1) and $\tau$$\thicksim \Gamma (\frac{\upsilon }{2}, \frac{\upsilon }{2})$ (the gamma distribution with shape parameter $\frac{\upsilon }{2}$ and scale parameter $\frac{ \upsilon }{2})$ is independent of $Z_{1}$ and $Z_{2}.$ Set $\gamma =\sqrt{ \frac{\tau +\lambda ^{2}}{\tau }}{|}Z_{1}{|},$ then (4) becomes

$$\begin{aligned} Y\overset{d}{=}\left[ \frac{\lambda \gamma }{(\tau +\lambda ^{2})}+\frac{ Z_{2}}{\sqrt{\tau +\lambda ^{2}}}\right] . \end{aligned}$$

(5)

So the following representation for STN-BS random variable U holds,

$$\begin{aligned} U\overset{d} = \frac{\beta }{4}\left[ \alpha \left\{ \frac{ \lambda \gamma }{(\tau +\lambda ^{2})}+\frac{Z_{2}}{\sqrt{\tau +\lambda ^{2}} }\right\} +\sqrt{\left\{ \alpha \left( \frac{\lambda \gamma }{(\tau +\lambda ^{2})}+\frac{Z_{2}}{\sqrt{\tau +\lambda ^{2}}}\right) \right\} ^{2}+\,4}\right] ^{2}. \end{aligned}$$

The following two propositions are useful for the ML estimation of the STN-BS distribution parameters via ECM algorithm discussed in the next section. The proofs are collected in “Appendix.”

Proposition 2.2

Let$U\sim {\text{STN-BS}}$and$\gamma =\sqrt{\frac{\tau +\lambda ^{2}}{\tau }}|Z_{1}{|}$and$\tau$$\thicksim \Gamma (\frac{\upsilon }{2},\frac{\upsilon }{2})$, then the distributions of$U{|}(\gamma , \tau )$and$\gamma | \tau$are given by

$$\begin{aligned} U\mid \left( \gamma , \tau \right) \sim {\mathrm{EBS}}\left( \frac{\alpha }{ \sqrt{\tau +\lambda ^{2}}}, \beta, 2, \frac{-\lambda \gamma }{\sqrt{\tau +\lambda ^{2}}}\right), \end{aligned}$$

and

$$\begin{aligned} \gamma \mid \tau \sim {\mathrm{TN}}\left( 0, \frac{\tau +\lambda ^{2}}{\tau } , (0,+\infty )\right) , \end{aligned}$$

respectively, where${\textit{EBS}}(\alpha , \beta , \sigma , \lambda )$denotes the extended BSdistribution discussed by Leiva et al. (2010) and${\textit{TN}}(\mu, \sigma ^{2}; (a, b))$denotes the truncated normal distribution for$N(\mu , \sigma ^{2})$lying within the truncated interval (a, b).

Proposition 2.3

(a) The conditional expectation of $\tau$ given $U=u$ is

$$\begin{aligned} E(\tau \mid U=u)=\frac{\upsilon +1}{\upsilon +a^{2}(u; \alpha , \beta )}. \end{aligned}$$

(b) The conditional expectation of $\log \tau$ given $U=u$ is

$$\begin{aligned} E(\log \tau \mid U=u)=DG\left( \frac{\upsilon +1}{2}\right) -\log \left( \frac{\upsilon +a^{2}(u; \alpha , \beta )}{2}\right) , \end{aligned}$$

where $DG(x)=\frac{\text{ d }}{{\text{ d }}x}\log \Gamma (x)$ is the digamma function.

(c) The conditional expectation of $\gamma$ given $U=u$ is

$$\begin{aligned} E(\gamma \mid U=u)=\lambda a(u; \alpha, \beta )+\frac{\phi (\lambda a(u; \alpha , \beta ))}{\Phi (\lambda a(u; \alpha, \beta ))}. \end{aligned}$$

3 Maximum likelihood estimation

The EM-based algorithms are a multi-step optimization method to build a sequence of easier maximization problems whose limit is the answer to the original problem. Each iteration of the EM-algorithm contains two steps: the Expectation step or the E-step and the Maximization step or the M-step. The literature on EM-based algorithms and their applications is quite rich. For a comprehensive listing of the important references, details and more information, we refer the readers to Dempster et al. (1977), Meng and Rubin (1993) and McLachlan and Krishnan (2008) and references therein. In this part, we derive the ML estimation of the STN-BS distribution parameters via modification of the EM-algorithm [Expectation/Conditional Maximization (ECM) algorithm].

3.1 Estimation via ECM algorithm

Let $\mathbf{U}=[U_{1}, \ldots , U_{n}]^{\top }$ be a random sample of size n from STN-BS$(\alpha , \beta , \lambda , \upsilon ).$ From Proposition 2.2, we set the observed data by $\mathbf{u}=[u_{1}, \ldots, u_{n}]^{ \top }$, the missing data by ${\varvec{\tau }}=[\tau _{1}, \ldots, \tau _{n}]^{ \top }$ and ${\varvec{\gamma }}=[\gamma _{1},\ldots,\gamma _{n}]^{ \top },$ and the complete data by $\mathbf{u}^{(c)}=[\mathbf{u}^{ \top }, {\varvec{\tau }}^{\top }, {\varvec{\gamma }}^{\top }]^{\top }$.

Then, we construct the complete data log-likelihood function of ${\varvec{\theta }}=(\alpha , \beta , \lambda , \upsilon )$ given $\mathbf{u}^{(c)},$ ignoring additive constant terms, as follows:

$$\begin{aligned} \ell ^{(c)}({\varvec{\theta }}|\mathbf{u} ^{(c)})& = \sum _{i=1}^{n}\ell _{i}^{(c)}({\varvec{\theta }} |(u_{i},\tau _{i},\gamma _{i})) \\& = \frac{\lambda }{\alpha }\sum _{i=1}^{n}\gamma _{i}\varepsilon (u_{i}; \beta )-\frac{1}{2}\frac{\lambda ^{2}}{\alpha ^{2}}\sum _{i=1}^{n}\varepsilon ^{2}(u_{i}; \beta )-\frac{1}{2\alpha ^{2}}\sum _{i=1}^{n}\tau _{i}\varepsilon ^{2}(u_{i}; \beta )-\frac{\upsilon }{2}\sum _{i=1}^{n}\tau _{i} \\&+\sum _{i=1}^{n}\log \frac{u_{i}+\beta }{\sqrt{\beta }}-n\log (\alpha )+ \frac{n\upsilon }{2}\log \left( \frac{\upsilon }{2}\right) -n\log \Gamma \left( \frac{\upsilon }{2}\right) +\frac{\upsilon -1}{2}\sum _{i=1}^{n}\log \tau _{i}. \end{aligned}$$

Suppose $\widehat{{\varvec{\theta }}}^{(r)}=(\widehat{\alpha }^{(r)}, \widehat{\beta }^{(r)},\widehat{\lambda }^{(r)},\widehat{\upsilon }^{(r)})$ is the current estimate (in the rth iteration) of ${\varvec{\theta }}$. Based on the ECM algorithm principle, in the E-step, we should first form the following conditional expectation

$$\begin{aligned} \mathbf{Q}({\varvec{\theta }}|\widehat{{\varvec{\theta }}}^{(r)}) = & E(\ell ^{(c)}({\varvec{\theta }}| u^{(c)})) \nonumber \\& = \frac{\lambda }{\alpha }\sum _{i=1}^{n}\widehat{S}_{3i}^{(r)}\varepsilon (u_{i}; \beta )-\frac{1}{2}\frac{\lambda ^{2}}{\alpha ^{2}} \sum _{i=1}^{n}\varepsilon ^{2}(u_{i}; \beta )-\frac{1}{2\alpha ^{2}}\ \sum _{i=1}^{n}\widehat{S}_{1i}^{(r)}\varepsilon ^{2}(u_{i}; \beta )-\frac{ \upsilon }{2}\sum _{i=1}^{n}\widehat{S}_{1i}^{(r)} \nonumber \\&+\sum _{i=1}^{n}\log \frac{u_{i}+\beta }{\sqrt{\beta }}-n\log (\alpha )+ \frac{n\upsilon }{2}\log \left( \frac{\upsilon }{2}\right) -n\log \Gamma \left( \frac{\upsilon }{2}\right) +\frac{\upsilon -1}{2}\sum _{i=1}^{n}\widehat{S}_{2i}^{(r)}, \end{aligned}$$

(6)

where

$$\begin{aligned} \widehat{S}_{1i}^{(r)}& = E(\tau _{i}\mid u_{i}, \widehat{{\theta }} ^{(r)})=\frac{\widehat{\upsilon }^{(r)}+1}{\widehat{\upsilon } ^{(r)}+a^{2}(u_{i}; \widehat{\alpha }^{(r)}, \widehat{\beta }^{(r)})}, \end{aligned}$$

(7)

$$\begin{aligned} \widehat{S}_{2i}^{(r)}& = E(\log \tau _{i}\mid u_{i}, \widehat{{\theta }} ^{(r)})=DG\left( \frac{\widehat{\upsilon }^{(r)}+1}{2}\right) -\log \frac{\widehat{\upsilon }^{(r)}+a^{2}(u_{i}; \widehat{\alpha } ^{(r)}, \widehat{\beta }^{(r)})}{2}, \end{aligned}$$

(8)

$$\begin{aligned} \widehat{S}_{3i}^{(r)}& = E(\gamma _{i}\mid u_{i}, \widehat{{\theta }} ^{(r)})=\widehat{\lambda }^{(r)}a(u_{i}; \widehat{\alpha }^{(r)}, \widehat{ \beta }^{(r)})+\frac{\phi (\widehat{\lambda }^{(r)}a(u_{i}; \widehat{\alpha } ^{(r)}, \widehat{\beta }^{(r)}))}{\Phi (\widehat{\lambda }^{(r)}a(u_{i}; \widehat{\alpha }^{(r)}, \widehat{\beta }^{(r)}))}. \end{aligned}$$

(9)

Then, the corresponding ECM algorithm is done as follows:

E-step Given ${\varvec{\theta }}=\widehat{{\varvec{\theta }}}^{(r)}$, compute $\widehat{S}_{1i}^{(r)}, \widehat{S}_{2i}^{(r)},\widehat{S}_{3i}^{(r)}$, using Eqs. (7), (8) and (9) for $i=1, \ldots, n.$

CM-step1 Fix $\beta =\widehat{\beta }^{(r)}$ and update $\widehat{ \alpha }^{(r)},\widehat{\lambda }^{(r)}$ by maximizing (6) over $\alpha$ and $\lambda$, which leads to

$$\begin{aligned} \widehat{\lambda }^{(r+1)}& = \frac{\widehat{\alpha }^{(r+1)}\sum _{i=1}^{n} \varepsilon (u_{i};\widehat{\beta }^{(r)})\widehat{S}_{3i}^{(r)}}{\sum \varepsilon ^{2}(u_{i};\beta )}, \\ \widehat{\alpha }^{2(r+1)}& = \frac{1}{n}\sum _{i=1}^{n}\varepsilon ^{2}(u_{i};\widehat{\beta }^{(r)})\widehat{S}_{1i}^{(r)}. \end{aligned}$$

CM-step 2 Fix $\alpha =\widehat{\alpha }^{(r+1)}, \lambda = \widehat{\lambda }^{(r+1)}, \beta =\widehat{\beta }^{(r)}$ and update $\widehat{\upsilon }^{(r)}$ by maximizing (6) over $\upsilon$, which leads to solve the root of the following equation

$$\begin{aligned} \frac{n}{2}\left( \log \frac{\upsilon }{2}+1-DG\left( \frac{\upsilon }{2}\right) +\frac{1}{n}\sum _{i=1}^{n}(\widehat{S}_{2i}^{(r)}-\widehat{S} _{1i}^{(r)})\right) =0. \end{aligned}$$

CM-step 3 Fix $\alpha =\widehat{\alpha }^{(r+1)}, \lambda = \widehat{\lambda }^{(r+1)}, \upsilon =\widehat{\upsilon }^{(r+1)}$ and update $\widehat{\beta }^{(r)}$ using

$$\begin{aligned} \widehat{\beta }^{(r+1)}=\arg \max Q(\widehat{\alpha }^{(r+1)},\beta , \widehat{\lambda }^{(r+1)}, \widehat{\upsilon }^{(r+1)}\mid \widehat{{ \theta }}^{(r)}). \end{aligned}$$

Note that the CM-steps 2 and 3 require a one-dimensional search for the root of $\upsilon$ and optimization with respect to $\beta ,$ which can be easily obtained by using the uniroot and the optimize functions in the R statistical language package version 3.3.1 (R Development Core Team 2016).

Remark 3.1

(i) In the representation (4), when $\tau =1$, random variable T reduces to a random variable with SN-BS distribution. See Vilca et al. (2011).

(ii) For ensuring that the true ML estimates are obtained, we recommend running the ECM algorithm using a range of different starting values and checking whether all of them result in the same estimates. Also, the initial estimates are obtained using numerical methods, such as procedure DEoptim in the statistical software R for maximizing the corresponding likelihood function.

3.2 The information matrix

Under some regularity conditions, the covariance matrix of ML estimates $\widehat{{\varvec{\theta }}},$ can be approximated by the inverse of the observed information matrix, i.e., $I_{0}(\widehat{{\varvec{\theta }}}|\mathbf{u}) =\frac{-\partial ^{2}\ell ({\varvec{\theta }}|u)}{\partial {{\varvec{\theta }}}\partial {{\varvec{\theta }}}^{\top }} |_{{{\varvec{\theta }}}=\widehat{{\varvec{\theta }}}}$,

$$\begin{aligned} \ell ({\varvec{\theta }} | u)=\sum _{i=1}^{n}{\ell }_{i} ({\varvec{\theta }} | u_{i})=n\log 2+\sum _{i=1}^{n}\log t(a(u_{i},\alpha ,\beta );\upsilon )+\sum _{i=1}^{n}\log \Phi (\lambda a(u_{i},\alpha ,\beta ))+\log (A(u_{i},\alpha ,\beta )). \end{aligned}$$

Now we use Basford et al. (1997) to obtain

$$\begin{aligned} I_{0}(\widehat{{\varvec{\theta }}}| \mathbf{u})=\sum _{i=1}^{n} \widehat{\mathbf{S}}_{i}\widehat{\mathbf{S}}_{i}^\top , \end{aligned}$$

where

$$\begin{aligned} \widehat{\mathbf{S}}_{i}=\frac{\partial {\ell }_{i} ({\varvec{\theta }} | u_{i})}{\partial {\theta }}|_{{{\varvec{\theta }}} =\widehat{{\varvec{\theta }}}} =(\widehat{\mathbf{S}}_{i,\alpha },\widehat{\mathbf{S}}_{i,\beta },\widehat{\mathbf{S}}_{i,\lambda },\widehat{\mathbf{S}}_{i,\upsilon })^\top . \end{aligned}$$

The elements of $\widehat{\mathbf{S}}_{i}$ are obtained by

$$\begin{aligned} \widehat{\mathbf{S}}_{i,\alpha }& = -\left( \frac{\widehat{ \upsilon }+1}{\widehat{\upsilon }}\right) \left( 1+ \frac{a^{2}(u_{i}; \widehat{\alpha }, \widehat{\beta })}{\widehat{\upsilon }} \right) ^{-1}a(u_{i}; \widehat{\alpha }, \widehat{\beta })\frac{ \partial }{\partial \alpha }a(u_{i}; \widehat{\alpha },\widehat{\beta }) \\&+\frac{{\widehat{\lambda }}\phi (\widehat{\lambda }a(u_{i}; \widehat{\alpha }, \widehat{\beta }))}{\Phi (\widehat{\lambda } ^{(r)}a(u_{i}; \widehat{\alpha }^{(r)}, \widehat{\beta }^{(r)}))}\frac{ \partial }{\partial \alpha }a(u_{i}; \widehat{\alpha }, \widehat{\beta })+ \frac{\frac{\partial }{\partial \alpha }A(u_{i}, \widehat{\alpha }, \widehat{ \beta })}{A(u_{i},\widehat{\alpha },\widehat{\beta })},\\ \widehat{\mathbf{S}}_{i,\beta }& = -\left( \frac{\widehat{ \upsilon }+1}{\widehat{\upsilon }}\right) \left( 1+ \frac{a^{2}(u_{i}; \widehat{\alpha }, \widehat{\beta })}{\widehat{\upsilon }} \right) ^{-1}a(u_{i}; \widehat{\alpha }, \widehat{\beta })\frac{ \partial }{\partial \beta }a(u_{i}; \widehat{\alpha }, \widehat{\beta }) \\&+\frac{{\widehat{\lambda }}\phi (\widehat{\lambda }a(u_{i};, \widehat{\alpha },\widehat{\beta }))}{\Phi (\widehat{\lambda }a(u_{i}; \widehat{\alpha }, \widehat{\beta }))}\frac{\partial }{\partial \beta } a(u_{i}; \widehat{\alpha },\widehat{\beta })+\frac{\frac{\partial }{\partial \beta }A(u_{i}, \widehat{\alpha }, \widehat{\beta })}{A(u_{i}, \widehat{ \alpha }, \widehat{\beta })},\\ \widehat{\mathbf{S}}_{i,\lambda }& = \frac{\phi (\widehat{\lambda }a(u{i}; \widehat{\alpha }, \widehat{\beta }))}{\Phi (\widehat{\lambda }a(u_{i}; \widehat{\alpha }, \widehat{\beta }))}a(u_{i}; \widehat{\alpha }, \widehat{\beta }), \\ \widehat{\mathbf{S}}_{i,\upsilon }& = \frac{\frac{\partial }{\partial \upsilon }t(a(u_{i}; \widehat{\alpha },\widehat{\beta }); \widehat{\upsilon } )}{t(a(u_{i}; \widehat{\alpha }, \widehat{\beta }); \widehat{\upsilon })}. \end{aligned}$$

The covariance matrix can be useful for studying the asymptotic behavior of $\widehat{{\varvec{\theta }}}=(\widehat{\alpha }, \widehat{\beta },\widehat{\lambda }, \widehat{\upsilon })$ by the asymptotic normality of this ML estimator. Thus, we can form hypothesis tests and confidence regions for $\alpha , \beta , \lambda , \upsilon$ by using the multivariate normality of $\widehat{{\varvec{\theta }}}.$

4 Simulation study and illustrative examples

4.1 Simulation study

We use simulations to evaluate the finite-sample performance of the ML estimates of STN-BS distribution parameters from the ECM algorithm described in Sect. 3. The sample sizes and true values of the parameters are $n=50,100$ and 500,  $\alpha =.1,.5,.75,1.0$, $\lambda =.1,.2,.5$ and $\upsilon =2$. The scale parameter is also taken as $\beta =1.$ In order to examine the performance of the ML estimates, for each sample size and for each estimate $\widehat{{\theta }}_{i}$, we compute the mean $E[\widehat{{\theta }}_{i}]$, the relative bias (RB) in absolute value given by $\mathrm{RB}_{i}=\mid \{E[\widehat{{\theta }}_{i}]- {\theta }_{i}\}/{\theta }_{i}\mid$ and the root mean square error$\left( \sqrt{\text{MSE}}\right)$ given by $\sqrt{E[\widehat{{\theta }} _{i}-{\theta }_{i}]^{2}},$ for $i=1,2,3,4.$ The results for the ML estimates of the parameters $\alpha ,\beta ,\lambda$ and $\upsilon$ are given in Tables 2, 3 and 4.

Table 2 Parameter estimates when $\lambda =.1$ and $\beta =1.0$, $\upsilon =2$

Table 3 Parameter estimates when $\lambda =.2$ and $\beta =1.0$, $\upsilon =2$

Table 4 Parameter estimates when $\lambda =.5$ and $\beta =1.0$, $\upsilon =2$

It is observed that, as we expect, the values of RB and RMSE of the ML estimators of the parameters decrease as the sample size increases.

4.2 Real data

In this section, two real datasets are applied in order to illustrate the applicability of the STN-BS model. For each dataset, we first obtain the ML estimations of the parameters via ECM algorithm described in Sect. 3. Then to compare competitions models, we use the maximized log-likelihood $\ell ({\widehat{\theta }})$, and model selection criteria based on loss of information, such as the Akaike information criteria (AIC) and the Bayesian information criteria (BIC). Following Kass and Raftery (1995), we also use the Bayes factor (BF) to show more differences between the BIC values. Assuming that the data D have arisen from one of two hypothetical models, thus $H_{1}$ (model with a smaller BIC value) is contrasted to $H_{2}$ (model compared to $H_{1}),$ according to $P(D\mid H_{1})$ and $P(D\mid H_{2}).$ This factor can be obtained by using the following approximation proposed by Raftery (1995),

$$\begin{aligned} 2\log (B_{12})\approx 2\left[ \log (P(D\mid \widehat{{\theta }} _{1},H_{1}))-\log (P(D\mid \widehat{{\theta }}_{2},H_{2}))\right] - \left[ d_{1}-d_{2}\right] \log (n), \end{aligned}$$

where $P(D\mid \widehat{{\theta }}_{1},H_{1})=P(D\mid H_{1}),$ with $\widehat{{\theta }}_{r}$ being the ML estimate of ${\theta } _{r}$ under the model in $H_{r},$$d_{r}$ is the dimension of ${\theta }_{r}$, for $r=1,2,$ and n is the sample size; see Vilca et al. (2011). An interpretation of the BF is given in Table 5.

Table 5 Interpretation of the Bayes factor ($B_{12}$)

4.2.1 Ozone data

Table 6 presents a descriptive summary of Ozone data studied by Vilca et al. (2011), which are assumed to be uncorrelated and independent, including sample median, mean, standard deviation (SD), CV, CS and CK. As it is observed, the data come from a positively skewed distribution with a kurtosis greater than three. Thus, the STN-BS model can be suitable for these data.

Table 6 Descriptive statistics for ozone data

Vilca et al. (2011) showed that the SN-BS distribution provides a better fit than the usual BS distribution. Now, we show that the proposed STN-BS distribution performs better than some other extensions of the Birnbaum Saunders distribution to fit on this dataset.

Estimation and model checking are provided in Table 7, which consists of the ML estimates and value of $\ell (\widehat{\theta }),$ AIC and BIC. Considering these values, we find that the STN-BS model provides a better fit than the other models. For these data, we also use the BF (approximated by the BIC) to contrast two following hypothesis testing:

• (i) $H_{0}^{(1)}:{\text{STN-BS}}$ model versus $H_{1}^{(1)}:{\text{BS}}$ model, which gives the value $2\log B_{12}^{(1)}=7.491.$

• (ii) $H_{0}^{(2)}:{\text{STN-BS}}$ model versus $H_{1}^{(2)}:{\text{SN-BS}}$ model which gives the value $2\log B_{12}^{(2)}=5.262.$

• (iii) $H_{0}^{(3)}:{\text{STN-BS}}$ model versus $H_{1}^{(3)}:{\text{SNT-BS}}$ model which gives the value $2\log B_{12}^{(3)}=1.1564.$

• (iv) $H_{0}^{(4)}:{\text{STN-BS}}$ model versus $H_{1}^{(3)}:{\text{T-BS}}$ model which gives the value $2\log B_{12}^{(4)}=.838.$

According to Table 5, the above values of $2\log B_{12}$ indicate “strong,” “positive,” “weak” and “weak” evidence in favor of $H_{0}^{(1)}$ , $H_{0}^{(2)},$$H_{0}^{(3)}$and $H_{0}^{(4)}$.

Table 7 The ML estimates and information criteria based on the BS, SN-BS, SNT-BS, T-BS and STN-BS distributions for the ozone data

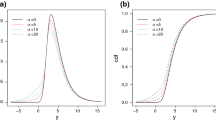
The estimated density functions of the ozone data including the respected histograms, plotted in Fig. 2, and the PP plots and empirical and theoretical cdf plots given in Figs. 3, 4, 5, 6 and 7 confirm again the appropriateness of the STN-BS distribution.

Fig. 2

Histograms with density estimates for ozone data

Fig. 3

PP plot (left) and empirical versus theoretical cdf (right) for the BS model of ozone data

Fig. 4

PP plot (left) and empirical versus theoretical cdf (right) for the SN-BS model of ozone data

Fig. 5

PP plot (left) and empirical versus theoretical cdf (right) for the SNT-BS model of ozone data

Fig. 6

PP plot (left) and empirical versus theoretical cdf (right) for the T-BS model of ozone data

Fig. 7

PP plot (left) and empirical versus theoretical cdf (right) for the STN-BS model of ozone data

4.2.2 Fatigue data

These data correspond to the fatigue life of 6061-T6 aluminum coupons cut parallel to the direction of rolling and oscillated at 18 cycles per second, were provided by Birnbaum and Saunders (1969). Table 8 presents a descriptive summary of fatigue data, which indicate that STN-BS model can be suitable in modeling this dataset.

Table 8 Descriptive statistics for fatigue data

We fit the STN-BS distribution to fatigue data and compare it to BS, SN-BS, SNT-BS and T-BS distributions. Estimation and model checking are provided in Table 9, which has the same configuration as given in Table 7. Considering the values of the $\ell (\widehat{\theta }),$ AIC and BIC given in this table, we find that the STN-BS model, once again provides a better fit than other models. Similarly to ozone data, we use the BF to highlight the differences between the values of the criteria presented in Table 9. We obtain values of $2\log B_{12}^{(1)}=2.206$, $2\log B_{12}^{(2)}=6.471$, $2\log B_{12}^{(3)}=1.584$ and $2\log B_{12}^{(4)}=2.432$ according to contrast hypothesis testing (i), (ii), (iii) and (iv) given above, indicating “positive,” “strong,” “weak” and “positive” evidence in accepted STN-BS distribution hypothesis; see Table 5.

Table 9 The ML estimates and information criteria based on the BS, SN-BS, SNT-BS, $\mathrm{T}\_\mathrm{BS},$${\text{STN-BS}}$ distribution for the fatigue data

Similar to ozone data, the estimated density functions of the fatigue data including the respected histograms, plotted in Fig. 8, and the PP plots and empirical and theoretical cdf plots given in Figs. 9, 10, 11, 12 and 13 confirm again the appropriateness of the STN-BS distribution.

Fig. 8

Histograms with density estimates for fatigue data

Fig. 9

PP plot (left) and empirical versus theoretical cdf (right) for the BS model of fatigue data

Fig. 10

PP plot (left) and empirical versus theoretical cdf (right) for the SN-BS model of fatigue data

Fig. 11

PP plot (left) and empirical versus theoretical cdf (right) for the SNT-BS model of fatigue data

Fig. 12

PP plot (left) and empirical versus theoretical cdf (right) for the T-BS model of fatigue data

Fig. 13

PP plot (left) and empirical versus theoretical cdf (right) for the STN-BS model of fatigue data

5 Concluding remarks

In this paper, a flexible class of distributions, called the skew-t-normal Birnbaum–Saunders distributions, based on the Birnbaum–Saunders models is introduced and its several properties are obtained. This skewed distribution extends the skew-normal Birnbaum–Saunders distribution, allowing a better prediction of the extreme percentiles. The parameters estimation via ECM algorithm is proposed, and their performances are evaluated by the Monte Carlo method. The simulation study shows the good performance of these estimators. The utility of this class is illustrated by means of two real data sets, allowing a better prediction of the extreme percentiles rather than another extensions of the Birnbaum Saunders distribution.

Appendix

This appendix presents the proof of Propositions 2.2 and 2.3.

Proof of Proposition 2.2

By using Eq.(5) the cdf of $T \mid \left( \gamma ,\tau \right)$ is

$$\begin{aligned} F(T\le t\mid \gamma ,\tau )=P(Y\le a(t; \alpha ,\beta )\mid \gamma ,\tau )=P\left( Z_{2}\le \sqrt{\tau +\lambda ^{2}}a(t; \alpha ,\beta )-\frac{\lambda \gamma }{\sqrt{\tau +\lambda ^{2}}}\mid \gamma, \tau \right), \end{aligned}$$

then the pdf of T$\mid \gamma ,\tau$ is

$$\begin{aligned} f(t\mid \gamma ,\tau )=\phi \left( \sqrt{\tau +\lambda ^{2}} a(t;\alpha ,\beta )-\frac{\lambda \gamma }{\sqrt{\tau +\lambda ^{2}}}\right) \sqrt{\tau +\lambda ^{2}}A(t;\alpha ,\beta ). \end{aligned}$$

The conditional distribution of $\gamma \mid \tau$ can be easily obtained from the definitions. $\square$

Proof of Proposition 2.2

From Proposition 2.2, the joint pdf of $T,\gamma$ and $\tau$ is given by

$$\begin{aligned} f(t,\gamma ,\tau )=\frac{1}{\pi }\exp \left\{ -\frac{1}{2}\left( \left( \gamma -\frac{\lambda }{\alpha }\varepsilon (t;\beta )\right) ^{2}+\frac{\tau }{\alpha ^{2} }\varepsilon ^{2}(t;\beta )+\upsilon \tau \right) \right\} A(t;\alpha ,\beta )\frac{\left( \frac{\upsilon }{2} \right) ^{\frac{\upsilon }{2}}}{\Gamma \left( \frac{ \upsilon }{2}\right) }\tau ^{\frac{\upsilon -1}{2}}. \end{aligned}$$

(6)

where $\varepsilon (t;\beta )=\sqrt{\frac{t}{\beta }}-\sqrt{\frac{\beta }{t}} .$

By integrating on $\gamma$ in (6), we get

$$\begin{aligned} f(t,\tau )=\sqrt{\frac{2}{\pi }}\frac{\left( \frac{\upsilon }{2}\right) ^{\frac{\upsilon }{2}}}{\Gamma \left( \frac{\upsilon }{2}\right) }\tau ^{\frac{\upsilon -1}{2}}A(t;\alpha ,\beta )\exp \left\{ \left( -\frac{\upsilon +\frac{\varepsilon ^{2}(t;\beta )}{\alpha ^{2}}}{2}\right) \tau \right\} \Phi \left( \lambda \frac{\varepsilon (t,\beta )}{\alpha }\right) . \end{aligned}$$

(7)

Dividing (7) by (3) gives

$$\begin{aligned} f(\tau \mid t)=\frac{\left( \frac{\upsilon +a^{2}(t;\alpha ,\beta )}{2}\right) ^{\frac{ \upsilon +1}{2}}}{\Gamma \left( \frac{\upsilon +1}{2}\right) }\tau ^{\frac{\upsilon +1}{2} -1}\exp \left( -\frac{\upsilon +a^{2}(t;\alpha ,\beta )}{2}\right) \tau , \end{aligned}$$

so

$$\begin{aligned} \tau \mid \left( T=t\right) \sim \Gamma \left( \frac{\upsilon +1}{ 2},\frac{\upsilon +a^{2}(t;\alpha ,\beta )}{2}\right) , \end{aligned}$$

which concludes parts (a) and (b),  and dividing (6) by (7), gives

$$\begin{aligned} f(\gamma \mid t,\tau )=\frac{1}{\Phi \left( \lambda \frac{\varepsilon (t; \beta )}{ \alpha }\right) }\frac{1}{\sqrt{2\pi }}\exp \left\{ -\frac{1}{2}\left( \gamma - \frac{\lambda }{\alpha }\varepsilon (t; \beta )\right) ^{2}\right\} I(0,+\infty )=f(\gamma \mid t), \end{aligned}$$

so $\gamma$ and $\tau$ are conditionally independent given $T=t$ and the conditional distribution of $\gamma$ given t is

$$\begin{aligned} \gamma \mid \left( T=t\right) \sim TN(\lambda a(t; \alpha , \beta ), 1, (0, \infty )), \end{aligned}$$

which concludes the part (c). $\square$