1 Introduction

Nanocomposites are materials where one of the phases has dimensions of less than 100 nm. On the other hand, these materials can also be made of nanoscale-repeated structures that form the material (Ajayan et al. 2003). There are considerable differences between the nanocomposites and composites owing to their high aspect ratio and high surface to volume ratio of the reinforcing phase. The reinforcing phase is the most important part of a nanocomposite which might be of different materials including particles, sheets (clay platelets) or fibers (carbon nanotubes) and may have substantial effects on the mechanical properties of the nanocomposite. Therefore, choosing a proper reinforcement is of great significance and this choice has to be made such that the required need is met. One of the reinforcements that have recently found many applications in different industries is carbon nanotube.

Carbon nanotubes (CNTs) were first discovered by (Ijima 1991) and since then, they have received a lot of attention owing to their superb mechanical properties. However, assessing the mechanical properties of the CNTs might be difficult and for this reason a lot of theoretical studies have been developed to estimate the mechanical properties of the CNTs whether single-walled carbon nanotube (SWCNT) or multi-walled carbon nanotube (MWCNT). These studies can be either based on molecular dynamics (MD) or continuum mechanics but few studies have been conducted in regard to MD (Iijima et al. 1996; Han and Elliott 2007; Yakobson et al. 1996; Franklanda et al. 2003; Griebel and Hamaekers 2004; Prylutskyy et al. 2000) which might be because of the computational cost of this method and also the restriction of time and length scale. Continuum mechanics based methods can be either based on finite element (FE) (Li and Chou 2003; Giannopoulos et al. 2008) or boundary element (BE) (Liu and Chen 2003; Liu et al. 2005; Ingber and Papathanasiou 1997; Liu et al. 2005) methods. Continuum mechanics based methods have drawn more attention in comparison with MD method which the reason was mentioned earlier. It should be noted that among all of these methods, finite element simulation seems to be more effective. The reason is that in this method one can simulate the matrix as a continuum medium and consequently the computational costs decrease and besides, some other methods such as BE cannot consider the atomistic features of the reinforcement. Therefore, considering these explanations, finite element method was applied in this paper to simulate the carbon nanotube and its surrounding. It has to be mentioned that the CNT type considered here was double-walled carbon nanotube (DWCNT).

In the theory of composite materials, the representative volume element (RVE) or the unit cell is the smallest volume in a material comprised of nanoparticles so that this unit cell can represent the whole material and the estimated property can extend to the whole specimen (Hill 1963). This property can be elastic modulus, electromagnetic properties, thermal properties or any other mechanical properties. The elastic modulus of an epoxy resin reinforced with DWCNT is the property of interest in this paper and the simulation of the RVE includes two types of materials, namely DWCNT and epoxy resin. It should be noted that the simulation of the RVE can be either based on the continuum mechanics or MD but as was mentioned in the preceding paragraph, the MD method has not drawn much attention because of its computational cost. There are two approaches as to the simulation of RVEs based on the continuum mechanics. One approach presumes a perfect bond between carbon nanotubes and resin matrix (Liu and Chen 2003) and the other assumes another region apart from resin and carbon nanotube which is the interphase region (Shokrieh and Rafiee 2010; Giannopoulos et al. 2010; Shokrieh and Rafiee 2010). In other words, the connection of resin and carbon nanotubes is made through this region which has different properties than the other two.

In this study, a RVE containing three phases, namely resin (matrix), carbon nanotube (reinforcement) and interphase region is simulated. The interphase region is simulated using linear spring elements which is the same procedure (Giannopoulos et al. 2010) utilized in their work. Then the RVE is subjected to a tensile loading and the elastic modulus of the RVE is computed. Afterwards, the obtained elastic modulus is compared with rule of mixtures, experimental analysis and other theoretical works. Finally some parametric studies such as the effect of the volume fraction of the DWCNT, elastic modulus of the resin, and the effect of the interfacial region stiffness on the Young’s modulus of DWCNT-reinforced composite will be conducted.

2 Finite Element Modeling of Representative Volume Element (RVE)

In this study, a RVE is simulated using ANSYS 11 commercial package and comprised three different regions, namely double-walled carbon nanotube (DWCNT), interphase and resin. DWCNT is embedded in the resin and the coupling between these two phases is simulated by an interphase region. There follows a detailed description of the procedure.

2.1 Double-Walled Carbon Nanotube

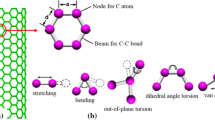
To simulate a CNT at nanoscale it is necessary to correlate between the mechanical properties and continuum mechanics. Li and Chou (2003) were pioneers in developing a continuum mechanics model regarding the correlation of the mechanical properties of nanotubes to molecular mechanics constants. They could set up a relation between sectional stiffness parameters in structural mechanics and the force-field constants in molecular mechanics to determine the elastic moduli of beam elements. Equation 1 shows these relations:

$$\frac{EA}{L} = k_{r} , \frac{EI}{L} = k_{\theta } , \frac{GJ}{L} = k_{\tau }$$
(1)

In this equation, E, A, I, G and J denote Young’s modulus, cross section area, moment of inertia, shear modulus and polar moment of inertia of the beam element, respectively.

The same strategy was utilized in this study to model the isolated CNT. Exploiting the analogy of (Li and Chou 2003) and presuming a circular cross section, the mechanical properties of carbon bonds can be obtained as follows (Tserpes and Papanikos 2005):

$$d = 4\sqrt {\frac{{k_{\theta } }}{{k_{r } }}} , E = \frac{{k_{r}^{2} L}}{{4\pi k_{\theta } }}, G = \frac{{k_{r}^{2} k_{\tau } L}}{{8\pi k_{\theta }^{2} }}$$
(2)

In this equation, the parameter L is the length of the C–C bond and is often taken as 0.142 nm. Having the parameters k θ , k r and k τ , the Young’s modulus, shear modulus and the diameter of the bonds can be found. In this analysis, the aforementioned parameters are given like the data in Table 1.

Table 1 The given parameters in Eq. (2) (Shokrieh and Rafiee 2010)
Full size table

To model the DWCNT using ANSYS software, nodes were considered as atoms and the bonds between these atoms were simulated using beam4 element. For the automatic generation of the FE models, a macro was created using the ANSYS macro-language. This code requires the Cartesian coordinates of carbon atoms as input. The FE model uses the coordinates of the carbon atoms for creating the nodes and then appropriate connection of the nodes generates the beam elements. Using Eq. (3) and utilizing the given parameters in Table 1, the corresponding values to model the beam elements are presented in Table 2:

Table 2 Properties for beam element
Full size table

Two different types of DWCNT namely, armchair and zigzag were investigated here which are shown in Fig. 1. Using a macro and the coordinates of the atoms, the CNTS were created. The coupling between the atoms of DWCNT is simulated by linear spring elements, which is the same procedure used by (Giannopoulos et al. 2010). It is worth mentioning that (Giannopoulos et al. 2010) created join elements that connected the atoms/nodes radially with corresponding nodes which belonged to the inner cylindrical surface of the matrix. However, a slightly different procedure was taken in this paper. According to Lennard-Jones “6–12” potential, van der Walls forces no longer exist at a distance more than 0.85 nm. For this reason, the linear spring elements between the atoms were created between the atoms whose distances are lower than 0.85 nm and to achieve this, a macro was written to create the elements. Besides, as is known, the van der Walls forces are highly nonlinear and this requires a lot of time for the simulation and solution of problem. In fact, instead of considering these nonlinear forces, linear springs are applied and their stiffness on the elastic modulus is a parameter to study. On the other hand, it should be mentioned that to save the computational cost, the spring elements were only created between: (1) the atoms of DWCNT and (2) the atoms of the inner surface of resin and each SWCNT of the DWCNT.

Fig. 1
figure 1

a An armchair MWCNT with the index of (8, 8) and (11, 11). b A zigzag MWCNT with the index of (8, 0) and (11, 0)

Full size image

To verify the Young’s modulus of the DWCNT some comparisons were performed with the data in literature which are presented in Table 3.

Table 3 Verification of the Young’s modulus of DWCNT with the data in literature
Full size table

2.2 Simulation of Resin

The volume fraction of CNT in composites can be up to 1% and this implies that the simulation of resin at molecular scale would be time taking and laborious. For this reason, the resin medium is simulated as a solid medium, while DWCNT is simulated at molecular scale. This procedure is called multi-scale modeling which is the same procedure that (Li and Chou 2003) utilized in their work. It is worth mentioning that some researchers (Odegard et al. 2003) simulated the resin using molecular dynamics (MD) method. In this study, the element used for the simulation of resin was SOLID45 which is a 3-D element and serves to model the solid structures. This element is defined by eight nodes having three degrees of freedom at each node. Further details can be found in ref (ANSYS). The resin was simulated as an isotropic material with the elastic modulus and Poisson’s ratio of 10 GPa and 0.3, respectively. The CNT considered here was long and the length of both CNT and resin were taken the same and considered 10 times larger than the radius of the CNT.

2.3 Interphase Region

Load transfer between CNT and resin has always been a controversial matter and to simulate this region, different procedures have been applied so far. Some researchers like (Shokrieh and Rafiee 2010) simulated this region using van der Waals (vdw) forces by applying Lennard-Jones “6–12” potential which is a nonlinear force–distance relation and some other researchers (Chen and Liu 2004; Joshi and Upadhyay 2013) considered a perfect bond between CNT and the resin and presented their data. In this study, the bond between DWCNT and resin is simulated using linear spring elements which is the same strategy applied by (Giannopoulos et al. 2010). Figure 2 depicts the front and isometric view of the RVE in which the three phases namely matrix, DWCNT and interphase can be observed. In Fig. 2b the front view with spring bonds are shown and it should be mentioned that the spring bonds were created between the atoms of the DWCNT, as well as the atoms of the DWCNT and inner surface of the resin. Besides, these bonds were created between the atoms whose distances are lower than 0.85 nm. It has to be mentioned that the in the isometric view (Fig. 2a) the spring bonds are not plotted.

Fig. 2
figure 2

A sample DWCNT-reinforced nanocomposite in which the index of the DWCNT is (8, 8) and (11, 11). a Isometric view. b Front view

Full size image

2.4 Evaluation of Young’s Modulus

To obtain the Young’s modulus of the nanocomposite, one end is totally constrained and the other is subjected to a uniform displacement as shown in Fig. 3.

Fig. 3
figure 3

Schematic view of the boundary conditions and loading

Full size image

After applying the boundary conditions and uniform displacement, the Young’s modulus of the RVE can be obtained using the following equation:

$$E = \frac{\sigma }{\varepsilon } = \frac{F/A}{\delta /L}$$
(3)

In this equation, F is the sum of reaction forces at the constrained edge and A denotes the cross section area which was considered as follows:

$$A = \pi \left( {r_{m}^{2} - \left( {r_{{ni}} + \frac{{t_{n} }}{2}} \right)^{2} } \right)$$
(4)

where r m denotes the outer radius of the matrix and r ni denotes the inner radius of SWCNT and t n is the wall thickness of graphene sheet which was taken 0.34 nm.

δ and L are displacement and initial length, respectively. In this study, the uniform displacement was given such that the total strain equaled 0.05.

The Young’s modulus of the nanocomposite can also be obtained by the following equation:

$$E_{c} = E_{n} V_{n} + (1 - V_{n} )E_{m}$$
(5)

This equation is the conventional rule of mixture (ROM) used for assessing the Young’s modulus of a composite. In this equation E n , E m are elastic modulus of DWCNT and matrix, respectively, and V n denotes the volume fraction of CNT.

3 Results and Discussion

In this section, the results of the simulation are presented and the effect of some parameters is investigated.

Figure 4a depicts the elastic modulus graph versus the volume fraction of a RVE containing DWCNT with the index of (8, 0) and (11, 0) at different stiffness for the linear springs. The range of the k i /k r ratio was taken as 0.001 ≤ k i /k r  ≤ 1 in which the lower interval (0.001) was obtained through a procedure discussed in the following. As is known from experimental data (Krishnan et al. 1998), the elastic modulus of a CNT is about 1.33 TPa and it is also notable the parameter k r is relevant to the interatomic interaction. Therefore, if the Young’s modulus of the epoxy is E m  = 0.010 TPa then one can write (Giannopoulos et al. 2010):

$$\frac{{k_{i} }}{{k_{r} }} = \frac{{E_{\text{epoxy}} }}{{E_{n} }} = \frac{0.010}{1.33} = 0.00751$$
(6)

Therefore, according to the equation above, a minimum limiting value of 0.001 was chosen as the lower interval.

Fig. 4
figure 4

Elastic modulus of a RVE at various stiffnesses. a A RVE containing a zigzag DWCNT with the index of (8, 0) and (11, 0). b A RVE containing an armchair DWCNT with the index of (8, 8) and (11, 11)

Full size image

As can be seen from Fig. 4, for k i /k r  = 1, the elastic modulus of the RVE is overestimated. The reason for this is that this case assumes that the carbon atoms are held tight together and thus neglects the interphase region. However, for k i /k r  = 7 × 10−3 a good correlation is observed with the experimental results (Andrews et al. 2002) which might be owing to taking the interphase region into consideration. It is worth mentioning that for the values smaller than 7 × 10−3 no noticeable change was observed and the data were roughly the same.

It can also be observed from Fig. 4a and b that the index of the DWCNT has no noticeable effect on the graph at small values of k i /k r .

The effect of different types of armchair DWCNTs on the elastic modulus of the RVE are presented in Fig. 5. It can be observed that different types of armchair DWCNTs have no noticeable effect on the elastic modulus of the RVE. However, for a specific type of DWCNT, increase in volume fraction leads to increase in elastic modulus of the RVE.

Fig. 5
figure 5

Effect of different armchair DWCNTS on elastic modulus

Full size image

Figure 6 depicts the effect of different types of zigzag DWCNTs on the elastic modulus of the RVE. Like the previous graph, one can follow that different types of zigzag DWCNTs have also no noticeable effect on the elastic modulus of the RVE. In general, it can be concluded that different types of DWCNTs, whether armchair or zigzag, have no dramatic effect on the elastic modulus. The reason for this is related to this fact that different types of carbon nanotubes—whether armchair or zigzag—have roughly the same elastic modulus which can be found in literature (Tserpes and Papanikos 2005; Li and Chou 2003). Therefore, since the elastic modulus of the CNT does not change noticeably, the elastic modulus of the nanocomposite does not change as well.

Fig. 6
figure 6

Effect of different zigzag DWCNTS on elastic modulus

Full size image

The effect of different matrix materials on the elastic modulus of the RVE is described in Fig. 7. As shown in this figure, the more the Young’s modulus of the resin increases, the less the effect of the DWCNT is observed. It can also be seen that after a certain value of the Young’s modulus of matrix, different volume fractions of DWCNT into the resin play no noticeable role in increasing the elastic modulus.

Fig. 7
figure 7

Variation of the Young’s modulus of nanocomposite versus different matrix materials

Full size image

4 Conclusion

In this study, a finite element approach was performed to obtain the elastic modulus of a RVE. To model the RVE three phases were considered: resin, DWCNT and Interphase region. As a matter of fact, a multi-scale modeling was conducted in this study in which the CNT was modeled at molecular scale, while the resin was modeled at macro scale. The Interphase region was simulated by linear spring elements and the effect of this stiffness on the elastic modulus were investigated. It was shown that the stiffness of the spring elements had noticeable effects on the elastic modulus of the RVE so that at greater values of stiffness, the elastic modulus is overestimated and in some specific values, adequate data are obtained. It was also shown that the different types of CNTs, whether armchair or zigzag, has no dramatic effect on the elastic modulus of the RVE. Finally, the effect of matrix material on the elastic modulus of the RVE was taken into consideration and was shown that as the Young’s modulus of the matrix increases, the effect of CNT into the resin is less noticeable.