Abstract
Effective properties of a heterogeneous material have been successfully predicted by using the homogenization scheme. The aim of the homogenization scheme is to get an equivalent homogeneous material resembling the same heterogeneous material. In this work, a 3D multi-scale computational model has been implemented to characterize mechanical properties of a heterogeneous composite system. At first, a micro-mechanical approach has been utilized to determine effective properties of the carbon-nanotube (CNT)–polymer composite using finite element modelling of representative volume element (RVE). The two material constituent phases, i.e. fillers (CNTs) and matrix [High-density polyethylene (HDPE)] are modelled as elastic and elasto-plastic material. The fillers are considered to be randomly distributed with various aspect ratios in the matrix. Further, macro-computational analysis is carried to predict mechanical strength and fracture toughness of CNT–polymer composite.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The inherent favourable characteristics of CNTs like low weight, high aspect ratio, extraordinary electrical, mechanical, optical and thermal properties have made them a vital candidate to tailor the properties of polymer-based nanocomposites [1,2,3,4,5]. CNTs have shown a tremendous increase in elastic moduli of nanocomposites. The effect of aligned CNTs reinforced in a polymer have been extensively studied [6,7,8,9]. The literature lacks in defining the nature of randomly distributed CNTs in the polymer matrix. Although the effect of randomly dispersed CNTs have been studied by some researchers, a micromechanical approach to study the variation of aspect ratio on strength and fracture toughness is very limited.
Alian et al. [10] studied the agglomeration effect of CNTs on epoxy nanocomposites using a multi-scale approach. Rai et al. [11] investigated the damage mechanism in CNT nanocomposite using molecular dynamics simulations. Savvas et al. [12] proposed a computational procedure to understand the effect of waviness and orientation of CNTs on the different properties of nanocomposites. Su et al. [13] prepared a multi-scale composite to investigate flexural and shear properties considering the random distribution of CNTs. Shajari et al. [14] developed a multi-scale model using time-dependent homogenizations to study viscoelastic properties of nanocomposites.
All these methods or models have used a micromechanical approach for 2D or 3D RVE analyses for CNT-reinforced–polymer composites. The use of molecular dynamics simulations to predict the effective properties has also gained popularity. But, a need to study the fracture behaviour of an equivalent homogeneous system for nanocomposites is still lacking. Thus, in the present study, 3D RVE composed of both matrix and nanofiller have been investigated. The effective properties of the heterogeneous composite system are predicted using mean-field homogenization method. A second-order Mori–Tanaka method has been employed with linear incremental for the homogenization of multiple phases. The equivalent properties are further being used in ABAQUS to analyse mechanical strength and fracture behaviour of carbon-nanotube–polymer composite. The effect of plasticity has been included in determining the stress–strain curve. Fracture response is analysed by considering the 3-point bending test.
2 Computational Method
A computational model is defined in this section. The basic of the model is a micromechanical theory with the use of RVEs. The CNTs are modelled in microscale, randomly distributed in the structure, following an elastic constitutive law. The matrix, i.e. HDPE is modelled in microscale, reinforced with CNTs, following an elasto-plastic constitutive law with isotropic hardening. The applied homogenization scheme and computational package are discussed in the following section.
2.1 Homogenization Scheme
An RVE is selected considering the microscopic heterogeneous and macroscopic homogenous materials. The boundary conditions are framed in terms of linear displacement vectors or macro-field traction vector. The RVE is assumed to be deformable and in an equilibrium state. Inertial and body forces are neglected. Thus, the equivalent properties of the system are represented as
All the information related to microstructure is carried by the unknown parameters which are defined by the strain concentration tensor A. In other terms, the \( C^{\text{eff}} \) and \( {\mathbf{A}} \) are related as
where \( c^{0} \) and \( c^{X} \) represent the uniform stiffness tensor of matrix and phase, \( {\mathbf{\rm A}}^{X} \) represents the global strain concentration tensor and \( v_{X} \) is the volume fraction of phase \( X \).
with \( {\mathbf{a}}^{X} \) representing local strain concentration tensor, \( \Delta c^{X} = c^{J} - C^{\text{rh}} \) and \( C^{\text{rh}} \) are termed as uniform stiffness tensor of reference homogenous medium. \( {\mathbf{T}}^{IJ} \) is the tensor representing the interaction between the inclusions in the RVE. It is represented as
where \( {\varvec{\Gamma}}(r - r^{{\prime }} ) \) is the modified Green tensor. The medium used as reference is replaced by matrix when the Mori–Tanaka scheme is selected for homogenization. Inside the matrix, the average strain field approximation is calculated by the strain in the reference medium. Therefore, on the following assumptions, the equivalent Mori–Tanaka properties (MTP) are represented as
where \( {\mathbf{A}}^{0} \) denotes the global strain concentration tensor of the matrix. The expression for \( {\mathbf{A}}^{0} \) is expanded as
2.2 Digimat-MF Modelling
Digimat-MF is the mean field homogenization (MFH) software to predict the non-linear constitutive behaviour of composite materials. Macro-material properties of the individual material are the inputs for the constitutive laws. The shape and volume fraction of the filler are the critical requirements to be inserted during the analysis. The type of loading or selection of study depends on the type of effective properties to be evaluated. The generalized constitutive equation for an RVE at any arbitrary point inside it is defined as [2]
where \( \left\{ {\sigma_{rs} } \right\}(r,s = x,y,z) \) are the stress components, \( \left\{ {\varepsilon_{tu} } \right\}(t,u = x,y,z) \) are the strain components and \( \left[ {C_{vw} } \right] \) (v, w = 1–6) are the elements of the stiffness matrix. The values of stiffness matrix for a composite could be calculated by MFH technique using Digimat-MF. The Mori–Tanaka homogenization method in Digimat-MF calculates the equivalent or effective properties either in terms of stiffness matrix or compliance matrix or directly provides the moduli.
3 Hierarchical Modelling
3.1 Modelling of the 2-Phase Composite
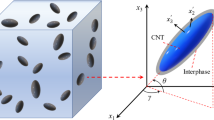
The 2-phase composite modelling consists of randomly distributed CNTs reinforced in the HDPE matrix. The CNTs are modelled using Digimat-MF tool. The CNTs with different aspect ratios and volume fraction within an RVE distributed spatially is shown in Fig. 1.
The matrix has been considered as elasto-plastic. Therefore, it is necessary to define the hardening model for the matrix. The properties of the HDPE matrix and the CNTs are presented in Tables 1 and 2, respectively. Hardening of HDPE is defined by the exponential and linear law as [1]
where R(p) is equivalent stress, p is accumulated plastic strain, k1 is linear hardening modulus, k2 is hardening modulus, m is hardening exponent.
Mechanical characterizations as shown in Fig. 2 have been performed on the composite material. These characterizations help in the prediction of failure situations of engineering components. The application of these nanocomposites is mainly in the aerospace field, thus mechanical characterizations are necessary to be done.
4 Numerical Results and Discussions
4.1 Application of MFH Technique
As an application of the MFH technique, an estimation of material properties of the homogenized composite is presented in this section. Mori–Tanaka homogenization scheme presented in Digimat-MF is implemented to estimate the average properties of the composite. Composite considered in the study mainly consists of randomly distributed CNTs in HDPE polymer. The individual properties are already mentioned in Tables 1 and 2, respectively. HDPE polymer is modelled as elasto-plastic matrix material; whereas CNTs are modelled as linear elastic cylindrical nanofillers.
Several mean-field simulations with the different volume fraction of CNTs were carried out. Figure 3 shows the tensile responses of the CNT, composite and HDPE in the form of stress–strain curves evaluated after MF simulation within the elastic limit.
4.2 Macro-scale FE Simulation of the Composite
As an example of multi-scale modelling, the two cases are presented in this section. The first would be the FE characterization of a rectangular composite subjected to tensile stress. The second would be the fracture toughness estimation of a composite. These two cases would be taking effective material properties (as given in Table 3) obtained from MF simulations as input to the material step. ABAQUS 6.14 has been used to accomplish the FE characterizations.
Tensile testing of the composite. A rectangular specimen is subjected to tensile stress as shown in Fig. 4. The length and width of the specimen are 80 and 18 mm, respectively. The specimen is stressed by a 10 kN force. The non-linear response for the tensile specimen is shown in Fig. 5. The maximum stress and strain for the various volume fractions can be seen from the figure and could be used for an engineering application.
The tensile stress–strain curve for 20% volume fraction tested experimentally is also shown in Fig. 5. The experimental and simulated curve is in good agreement up to 5% strain. The deviation in the curve after that could be due to the defects, voids or stress concentration at the tail/head of the CNTs. The tensile-tested specimen was fabricated using a microwave oven. Power mode of the oven was used to develop the pellets of the composites into laminae.
Fracture toughness estimation of the composite. It is always important to estimate the fracture toughness of a composite. In this subsection, a specimen of the same dimensions as that of the tensile test is taken into consideration as shown in Fig. 6. A crack of half the width is introduced in the body. The top edge of the cracked domain is subjected to the mechanical traction of 1 kN load. The bottom edge of the domain is constrained to move in any direction. Mode-I SIFs (KI) have been predicted for CNT–polymer composite at different volume fractions as shown in Fig. 7. A decreasing trend has been observed with increase in Vf of CNTs. The reason behind it is the strengthening of composites due to addition of CNTs.
5 Conclusions
The present paper shows the capabilities and advantages of the homogenization technique in the assessment of the effective properties of the composite. Macro-computational analysis has been presented to predict mechanical strength and fracture toughness of the CNT–polymer composite. The following conclusions have been observed from the present work:
-
Axial Young’s modulus has been increased with the volume fraction of CNTs in composites.
-
A non-linear behaviour in the stress–strain curve of the composite could be considered as the resistance of CNTs to failure during testing.
-
Furthermore, the fracture toughness has shown a decreasing trend when the CNT volume fraction is increased.
-
As an outlook, the study for randomly distributed CNTs needs to be extended to examine the behaviour of composite practically. These simulated estimates could be helpful while investigating the other properties of the composite.
References
Alian, A.R., Kundalwal, S.I., Meguid, S.A.: Multiscale modeling of carbon nanotube epoxy composites. Polym. (Guildf). 70, 149–160 (2015)
Backes, E.H., Passador, F.R., Leopold, C., Fiedler, B., Pessan, L.A.: Electrical, thermal and thermo-mechanical properties of epoxy/multi-wall carbon nanotubes/mineral fillers nanocomposites. J. Compos. Mater. 23, 1–9 (2018)
Doghri, I., Brassart, L., Adam, L., Gérard, J.S.: A second-moment incremental formulation for the mean-field homogenization of elasto-plastic composites. Int. J. Plast 27(3), 352–371 (2011)
Drathi, M.R., Ghosh, A.: Multiscale modeling of polymer-matrix composites. Comput. Mater. Sci. 99, 62–66 (2015)
Kundalwal, S.I., Kumar, S.: Multiscale modeling of stress transfer in continuous microscale fiber reinforced composites with nano-engineered interphase. Mech. Mater. 102, 117–131 (2016)
Kundalwal, S.I., Meguid, S.A.: Multiscale modeling of regularly staggered carbon fibers embedded in nano-reinforced composites. Eur. J. Mech. A/Solids. 64, 69–84 (2017)
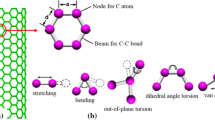
Li, C., Chou, T.-W.: A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 40(10), 2487–2499 (2003)
Li, K., Gao, X.L., Roy, A.K.: Micromechanical modeling of viscoelastic properties of carbon nanotube-reinforced polymer composites. Mech. Adv. Mater. Struct. 13(4), 317–328 (2006)
Punetha, V.D., Rana, S., Yoo, H.J., Chaurasia, A., McLeskey, J.T., Ramasamy, M.S., Sahoo, N.G., Cho, J.W.: Functionalization of carbon nanomaterials for advanced polymer nanocomposites: a comparison study between CNT and graphene. Prog. Polym. Sci. 67, 1–47 (2017)
Rai, A., Subramanian, N., Chattopadhyay, A.: Investigation of damage mechanisms in CNT nanocomposites using multiscale analysis. Int. J. Solids Struct. 120, 115–124 (2017)
Savvas, D., Stefanou, G., Papadopoulos, V., Papadrakakis, M.: Effect of waviness and orientation of carbon nanotubes on random apparent material properties and RVE size of CNT reinforced composites. Compos. Struct. 152, 870–882 (2016)
Shajari, A.R., Ghajar, R., Shokrieh, M.M.: Multiscale modeling of the viscoelastic properties of CNT/polymer nanocomposites, using complex and time-dependent homogenizations. Comput. Mater. Sci. 142, 395–409 (2018)
Su, Y., Zhang, S., Zhang, X., Zhao, Z., Jing, D.: Preparation and properties of carbon nanotubes/carbon fiber/poly (ether ether ketone) multiscale composites. Compos. Part A Appl. Sci. Manuf. 108, 89–98 (2018)
Takeda, T.: Micromechanics model for three-dimensional effective elastic properties of composite laminates with ply wrinkles. Compos. Struct. 189, 419–427 (2018)
Acknowledgements
The authors are grateful for the support received from the Indian Institute of Technology Mandi (IIT Mandi) through grant file no. IITM/SG/HP/54.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Arora, G., Pathak, H. (2020). Multi-scale Computational Analysis of Carbon-Nanotube–Polymer Composite. In: Biswal, B., Sarkar, B., Mahanta, P. (eds) Advances in Mechanical Engineering. Lecture Notes in Mechanical Engineering. Springer, Singapore. https://doi.org/10.1007/978-981-15-0124-1_19
Download citation
DOI: https://doi.org/10.1007/978-981-15-0124-1_19
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-15-0123-4
Online ISBN: 978-981-15-0124-1
eBook Packages: EngineeringEngineering (R0)