Multiscale Agricultural Commodities Forecasting Using Wavelet-SARIMA Process

Abstract

Forecasts of spot or future prices for agricultural commodities make it possible to anticipate the favorable or above all unfavorable development of future profits from the exploitation of agricultural farms or agri-food enterprises. Previous research has shown that cyclical behavior is a dominant feature of the time series of prices of certain agricultural commodities, which may be affected by a seasonal component. Wavelet analysis makes it possible to capture this cyclicity by decomposing a time series into its frequency and time domains. This paper proposes a time-frequency decomposition based approach to choose a seasonal auto-regressive aggregate (SARIMA) model for forecasting the monthly prices of certain agricultural futures prices. The originality of the proposed approach is due to the identification of the optimal combination of the wavelet transformation type, the wavelet function and the number of decomposition levels used in the multi-resolution approach (MRA), that significantly increase the accuracy of the forecast. Our SARIMA hybrid approach contributes to take into account the cyclicity and of the seasonality when predicting commodity prices. As a relevant result, our study allows an economic agent, according to his forecasting horizon, to choose according to the available data, a specific SARIMA process for forecasting.

Introduction

Time series forecasting can be important for business and market decision support. It has been widely used, in particular for forecasting sales or for analyzing price variations from financial markets. Well-established forecasting methods are already adopted by firms or market players, such as linear extrapolation and SARIMA. However, their performance remains limited since the time series studied are very volatile with some particular stylized facts. For instance, agricultural commodity prices sometimes present some specific stylized facts.

International institutions such as the World Bank and the International Monetary Fund, individual countries as well as companies involved in importing or exporting activities wish to forecasts prices of agricultural commodities or metals. Moreover, the World Bank expects a significant recovery in industrial commodities such as energy and metals in 2017, due to tighter supply and increased demand. With regard to certain energy or agricultural commodities, under certain assumptions, market forecasting publications are made in "Commodity Markets Outlook". These price forecasts allow the economic agent to identify the confrontation between supply and demand on a commodity market at a given future date. Predicting agricultural prices is difficult because other price series such as, the price of crude oil, the price of shares, or the prices of other financial assets, and the series of prices of agricultural commodities are influenced by several other uncertain abiotic factors (extreme weather variables, natural disasters, etc.) and biotic variables (pests, diseases, etc.) in addition to other invisible market forces and administrative measures (Wang et al. 2019). These explanatory factors taken together add more complexity to the analysis of the time series of prices agricultural products, which makes them difficult, an efficient forecast of agricultural prices. In recent literature (Xiong et al. 2018; Li et al. 2021) it’s been shown that some vegetable price series are much more volatile and complex than the price series of other agricultural products due to their short duration and their seasonality. In addition, the perishable nature of vegetables further complicates obtaining effective vegetable price forecasts. The literature (Wang et al. 2019 and some references therin) highlights the complexities of price series, with as a corollary the difficulty of analyzing them in order to obtain a better forecast. Statistical models often used for forecasting agricultural prices include models like ARIMA (Box et al. 2015; Jadhav et al. 2018) and its constituent models (Hayat and Bhatti 2013). However, the use of the previous models does not take into account the heterogeneity of the agents involved in these agricultural markets. In this article, we propose a hybrid forecasting scheme that combines the classical SARIMA method and the wavelet transform (SARIMA-Wavelet). We believe that the proposed hybrid method is highly applicable for forecasting time series with specific stylized facts in the firm or the markets.

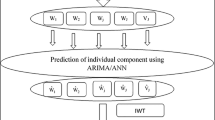
Also, the actors (arbitrageurs, hedgers or speculators) in the agricultural markets, do not have the same investment horizon. Thus, we opt in our paper to find the optimal SARIMA model, for each class of investors in the agricultural market, according to its investment horizon. To do this, in addition to the analysis of the complete series of available data, we carry out analyzes of the sub-series obtained from the available series, by means of a time-frequency decomposition of the available series, via recourse to wavelet theory. Intuitively, we know that the investment horizon is the reverse of the frequency. Thus, a frequency band is considered to be a band of investment horizons. We can therefore consider on each frequency band a time sub-series of the initial series. Thus, on this frequency band and therefore for this category of investors having investment horizons associated with the frequency band considered, it suffices to analyze the sub-series corresponding to this frequency band, to determine the optimal SARIMA process that will be used by the investors with a specific investment horizon. The procedure to build a SARIMA model on each sub-series consists of data preprocessing, model identification, parameter estimation, model diagnosis and finally application. For different sub-series, the optimal SARIMA model and it’s parameters for the prices sub-series of both markets are shown.

Indeed, we define the best hybrid Wavelet-SARIMA approach for agricultural commodities price forecasting, which reflects quite clearly the fundamental concept of analysis in signal processing, where we decompose a complex and transitory signal into several sub-series. We highlight the pedagogical connection between the theory of wavelet transform and classical time series analysis SARIMA used in econometrics. A transitory signal is associated with a variable signal not periodic, which changes state suddenly. According to Yves Meyer¹, a wavelet is “ the simplest transitory signal imaginable ”. M. Misiti, Y. Misiti, G. Oppenheim, J-M. Poggi, in “ Wavelets and its applications ” (2003), define wavelets as “ a signal processing tool for the analysis on several time scales, the local properties of complex signals can present areas of unsteadiness ”. Therefore, analysis by wavelets help in the use of a well localized window fully scalable and along the signal to characterize the various components time-frequencies at any point. By the way, it is essential to use this method to identify the best statistical model able to describe each sub-series generated by the decomposition and give the best visibility of future values. For instance, the time-frequency Analysis of the Relationship Between EUA and CER Carbon Markets Sadefo Kamdem et al. (2016).

The wavelet transform is carried out in an amount of temporal subsets associated with frequency bands at the same sensitivity. In financial markets, each of the frequency bands represents a category of investors. Indeed, these agents adopt, according to the information they hold, a very heterogeneous behaviour. A combination of their actions produces very random changes in commodity prices. Thus, with the aim to support the regular decision making and monitor these markets through the introduction of prudent rules, the strategic conclusions of this document can help governments and economic authorities in the diagnosis and the detection of different speculative behaviour in the agricultural market.

In contrast to traditional Fourier analysis based on the frequency space, the wavelets analyse a signal in several horizons and frequencies by using the multi-resolution analysis. These specificities are repeatedly solicited in many economic studies. For example: to identify the cyclical phenomenal changes in the market of stock indices, to study the co-movements and the effects of contagion between markets or within the same market. For that purpose, we base on the econometrics of stochastic processes in the time domain, but especially in that of frequencies using this theory. Indeed, it is interesting to understand the gaps between all investor behaviours as highlighted by their investment choices. However, in economic times series with a lot of high frequencies, values are not in the same time interval, and thus it is not possible to apply the usual econometrics technical. Because, the applications of the appropriate methods are modelled for the database with the same interval, (cf. Engel and Russell, 1997– 1998). Hence we use the wavelet transform of random series where a signal projection is applied on analytical functions without any change in fundamentals properties. This allows us to highlight some characteristics of price and their variations: the hidden bumps and jumps detected during the evolution of a stock. They are usually caused by the impact of the few exogenous events not covered by the contract. In addition, there are seasonal features and extra-seasonal usually seen in a serial type namely the seasonal pattern that occurs permanently and regularly, the stochastic trend and / or seasonal phenomena that are cyclic. Finally, the volatility involved non-stationarity, the presence of any unit roots or phenomena long memories, non-linearity, etc. These points are important because they emphasize the essential information processed by wavelets.

The aim of this paper is to study the intriguing facts of combining the SARIMA model with wavelet transform to measure and anticipate the prices or returns time series. To achieve this, the descriptive analysis of Table 2 data, help to subtly explore the time series data of each product by studying its probability distribution.Some specificities detected thanks to the indicators of variability, asymmetry and fat tails of returns. This, to produce fair and reliable future values of monthly price indices. Three main points are given as follows:

• to test the best configuration of multi-resolution analysis by choosing one type of wavelet transform between (Cwt, Dwt and Modwt), the appropriate wavelet function and the number of decomposition on the robustness forecast of hybrid model Wavelet-SARIMA

• to calibrate the Wavelet-SARIMA model such that the combination selected in Mra (Mallat 1989) can realize good forecasts of price indices for cereals and oleaginous.

• to estimate the quality of forecast by the indicators like RMSE or MAE and compare it to classical SARIMA models and to White noise models on the basis of performance on series of price indices without any wavelet decomposition.

This is the best way to test significantly the effect of Mra configuration on economics times series forecasting using wavelet transform. Indeed, a large number of forecasts is simulated for having the smallest modelling error by solid tests.

The economic aspect of this paper is to contribute to the lighting of policy-makers and serve to aid decision-making tools of public policy or investment in the development control rules, sanctions and market security. These rules, once in place will serve as disincentives to speculative behaviour being adopted generally investors and therefore regulate and supervise the market for transactions of those raw materials (Fig. 1).

Fig. 1

Process modelling

Wavelet transform

The wavelet transform is a smart method capable of detecting all frequencies, and to consolidate those with the same sensitivity. Therefore, it separates all details or highs values from the trend in original times series.

The theoretical frame: Signal processing has greatly focused on the study of invariant operators in time or in space that modify properties of stationary signal. This has led to the reign of the Fourier transform, but leaving aside the essential of the information processing. To avoid losses, representations of time-frequency, have been developed to analyze any non-stationary process $(f(t))_{t \in T}$ indexed by t in any time space T using the transformation $W_f(u,s)$ (W as Wavelet) configured by two variables: the position u and the scale s. We consider f(t) taking these values in E $\forall \ t \in T$:

$$\begin{aligned} T = \left\{ \begin{array}{rcll} N,Z,R &{} et &{} E = R &{} \text{ for } \text{ univariate } \text{ times } \text{ series } \\ &{} \\ N,Z,R &{} et &{} E = R^d \ (d \ge 2) &{} \text{ for } \text{ multivariate } \text{ times } \text{ series } \\ \end{array} \right. \end{aligned}$$

A time-frequency representation is a transformation associating to f(t) a real function of variables $W_f(u,s)$. It consist in a projection of signal on analysing functions $\psi _{u,s}$:

$$\begin{aligned} W_f(u,s) = \left\langle f, \psi _{u,s} \right\rangle = \int _{-\infty }^{+\infty } f(t)\overline{\psi _{u,s}(t)}dt \end{aligned}$$

(1)

with :

• u the parameter of position, s the parameter of scale

• f the signal to analyze , $\psi _{u,s}$ the wavelet function chosen $\in$ $L^2(R)$² and $\overline{\psi _{u,s}(t)}$ his conjugate. A wavelet $\psi$, defined in $L^2(R)$ presents at least the conditions below:

  $$\begin{aligned} T = \left\{ \begin{array}{rl} \int _{-\infty }^{+\infty } \left| \psi (t)\right| dt = 0 \ {} &{} \text{ vanishing } \text{ moments } \\ \ {} &{} \\ \left\| \psi \right\| = \sqrt{\int _{-\infty }^{+\infty } \left| \psi (t)\right| ^2dt} = 1 &{} \text{ the } \text{ energy } \text{ of } \text{ analysing } \text{ functions } \text{ is } \text{ constant } \\ \end{array} \right. \end{aligned}$$

The wavelets are regrouped by family. And, the most used in economics is the Daubechies family thanks to their excellent properties. From the single function $\psi$, we construct by translation (u) and by dilatation/contraction (s) a wavelets family representing the analysing functions.

$$\begin{aligned} \psi _{u,s}(t) = \frac{1}{\sqrt{s}}\psi (\frac{t-u}{s}), \psi \ with \ s \in R^+, u \in R \end{aligned}$$

(2)

The inverse wavelet transform helps to return an exactly reconstitution of the initial signal based on their coefficients of position and scale without any loss of information.

$$\begin{aligned} f(t) = \frac{1}{W_f(u,s)} \int _{-\infty }^{+\infty } \int _{-\infty }^{+\infty } W_f(u,s) \frac{1}{\sqrt{s}}\psi (\frac{t-u}{s}) \frac{dt ds}{s^2} \end{aligned}$$

(3)

The multi-resolution analysis: The fast algorithm of decomposition and reconstitution is applied to any process to view the representation of signals in different layers in order to have better visibility of local fluctuations at every stage of its resolution (Mallat 1989). The reconstitution is realized from the wavelets coefficients and scales via the inverse wavelet transform (equation 3). And, for more study, it will be possible to analyze and explain each frequency bands by spectral moments in a superior order, or doing forecast according to each sub-series generated by this algorithm. This type of analysis is important in financial markets, because it helps to decompose the evolution of their actions into several others signals. In the same vein, to identify potential flow accelerators per time horizon. However, it is more convenient to consider that it is the heterogeneous behaviour of agents that influences significantly the volatility of price indexes.

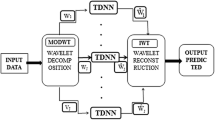
Doing the Mra need at first to choose a type of transform to do. With the discrete sample times series, we both apply a discrete wavelet transform (Dwt), a maximum overlap discrete wavelet transform (Modwt). The Dwt form determines a optimal number of wavelet coefficients and scales to decompose and reconstruct the signal. The Modwt form, uses all wavelet coefficients without any rebound possible. The contrary is the object of continuous wavelets transform (Cwt). It is very rebound and difficult to compute and to compile in practice. With these agricultural prices indices, we apply the additive decomposition based on the Modwt. Then, a list of wavelets is chosen, specially the Daubechies family. According to the signal to explore and it analysis, there are nowadays 25 wavelets functions with their properties. In economic and finance, the family of Daubechies is currently used. At the end, the number of decomposition is defined by $J \ \forall \ 2^{J} \le N$ where N represent the number of data or sample.

$$\begin{aligned} f(t) = \sum _{j=1}^J {D_{J,t}} + A_{J,t} \end{aligned}$$

(4)

The equation 4 is the result of the algorithm of decomposition-reconstitution at different scale j and calibrated on the Mra configuration. It separates the initial time series in a smooth series $A_J$ into many other detail series $\left\{ D_j \ \forall j = 1 \ldots J\right\}$. The smooth image represents the general shape of signal in the half of its resolution. The details are all the high frequencies when we move from resolution j to $j+1$ ($[2^j - 2^{j+1}[$). During this period, the approximation is bigger. It grows bigger and bigger until all information is lost. But, by adding each detail $D_j$ to $A_J$, the precision is increasingly brought in order to rebuild the original series. The table below defines N / J / $D_j$ / $A_J$ / $[2^j - 2^{j+1}]$.

Table 1 MRA in different level of scale

Numerical data

Graphical representation

The Figs. 2 and 3 below represent respectively the changes of price indices of high agricultural products $I^{'}_t$ and their returns $\delta I^{'}_t = \frac{I^{'}_t - I^{'}_{t-1}}{I^{'}_{t-1}}$ between dates $t-1$ and t. It is about wheat, corn, sorghum, rice and oleaginous like soy, olive, palm and colza. Each chronicle has got 444 observations defined from January 1980 to December 2016³. To reduce the flexibility for modelling, a logarithmic transformation is applied on initial data $I^{'}_t = \log (I_t)$. Theoretically, the normalisation depend on the distribution of frequency values. The usual methodology developed by Box and Cox (1964) can help to give a better transformation by choosing the best $\gamma$ parameter:

$$\begin{aligned} I^{'}_t = \left\{ \begin{array}{rl} \frac{I^{\gamma }_t - 1}{\gamma } &{} \hbox { if }\ \ \gamma \ne 0 \\ &{} \\ \log (I_t) &{} \hbox { if }\ \ \gamma = 0 \\ \end{array} \right. \end{aligned}$$

Fig. 2

Indices and returns cereals prices

Fig. 3

Indices and returns oils prices

Before the year 2000, changes seem to have sometimes the same behaviour. But, in 2007 and 2008, the price indices increase significantly. Indeed, strong spikes and troughs appeared in these years. According to an OCDE’s report (2008) on the causes and consequences of agricultural commodities prices, these gaps are explained by a lot of combined factors. We notice the result of stationary production or inferior to the trend, a high increase of the demand and the investments on the derived agricultural product market. The exogenous factors are so complex. They are the periods of drought which affect the major grain areas, the weakness of the reserve of cereals and oleaginous, the development of use of agricultural commodities for biofuel production, the fast increase of crud oil prices. Finally, there is the continued devaluation of Us dollar, currency in which are generally expressed indicative prices of raw materials. All the changes intervened in a unstable context in the world economy, particularly the financial crisis of 2007/2008. This crisis effect on the speculative behaviour of producers or financial agents. Moreover, the rate of increase represented in parallel give more visibility on the flexibility of price indices. Because, a surge is often offset by a smaller increase in the following month, hence the appearance of those many “ peaks and troughs ”.

In the Figs. 2 and 3 it is complex to identify clearly at first, a seasonal and a trend in any data series. As an alternative, we aggregate annually (Fig. 11 in Appendix) and monthly (Fig. 12 in Appendix) in order to highlight these general characteristics or other cyclical effects. On these graphics, there are “ peaks and troughs ” particularly with corn data in different periods. For the soy and the sorghum, “ peaks ” are in November and December and the “ troughs ” from June to August. The corn increase more and more until it “ peaks ” (June), then decreases to its poor levels in September to leave relatively well until the end of the year. The rice has the same changes but at different extremes: peaks ” on April and “ troughs ” on the last trimester. The series of soy and olive changes almost together but with a noticeable difference in the second half. So, their maximum are achieved respectively in November and August. As to palm and colza series, we notice the same trajectory: a strong start and a fall from May and June. But we detect no seasonality. However, at the annual average prices, a periodic behaviour and a trend seems to be emerging over time (Table 1).

Descriptive statistics

The Table 2 present a descriptive statistics summary on data. It highlights some stylized facts of these data. According to the coefficients of variation ($\frac{\sigma }{mean}$), we can see a high variability in the price times series.

Table 2 Basics descriptive statistics for times series data

High volatility reflects a lot of information hidden: the high irregularity of price indices, their non stationary, an unstable market, the impacts of exogenous factors or random phenomena. They are impossible to explore by a simple econometric model. The skewness $\beta _1^{1/2} = \frac{\mu _3}{\mu _2^{3/2}}$ and kurtosis $\beta _2 = \frac{\mu _4}{\mu _2^2}$ coefficients are indicators of asymmetry and fat tails of price returns. So, if they follow a normal distribution then $\beta _1^{1/2} = 0$ and $\beta _2 = 3$⁴, but that is not the case. Indeed, the positive skewness demonstrates an asymmetric distribution to the right due to the impact of extremes values. The kurtosis are bigger than 3 ($\beta _2 > 3$), so more concentrated in opposite to the normal distribution.

Processing and data analysis

We try to find the best SARIMA model for explaining the increase rates of agricultural price indices and make forecast. So, the data are decomposed in two periods: from January 1980 to December 2016 (37 years / 444 observations) and the 2017 period. The first part is a framework of calibration of econometric models. We built the SARIMA model by studying the fundamental characteristics (seasonality, stationary, cyclical phenomenal, unit root, trend). Indeed, we propose a model, estimate the parameters, test its suitability and analyse the residuals. Several models can intervene or agree. But thanks to the selection criterion AIC or Bic and especially with sparingly, simple models are preferred. Then, the model chosen is used to re-estimate the 2017 values. The indicators below are used to measure the accuracy of the forecast:

• mean absolute error $MAE = \frac{1}{n}\sum _1^n\left| x_t - {\hat{x}}_t\right|$

• root mean error $RMSE = \sqrt{\frac{1}{n}\sum _1^n\left( x_t - {\hat{x}}_t\right) ^2}$

Diagnostics: Based on the returns data series $\delta I^{'}_t$, we find the number of lags that are able to denoise the residuals. Indeed, we start with a general modelling with a linear trend (Trend) and respectively with a drift (Drift) and none (None) model. On each case, we apply the unit root test for stationarity according to Dickey-Fuller (1979). But, Given the annual seasonality observed in the qualitative analysis (Fig. 11 in Appendix) and empirical (Table 4), we choose a lag 11. After estimation, the maximum lag is 0 instead of 11. In addition, we use other tests of Philips-Perron (1987) and Kpss (1992) in Table 3.

Table 3 Stationary

The $p_{values}$ of three models are all inferior to 5% (Table 3). It means there is stationarity in returns data series. It is slightly visible on Fig. 2 and 3 in “Numerical data”) even if there are some spikes and troughs. Indeed, the calculations of returns removes any trend in these series to focus mainly on seasonal effects and the rest we hope to be white noise or modelling a stationary process. So, it is not necessary to make them stationary. In addition, the graphics of lags (Fig. 4) present no linear relationship. It opposes the returns series by themselves shifted some lag ($\forall \ h = 1 \ldots 12$). If the point clouds along the right equation $y = x$, then there is a strong autocorrelation else a dispersion around the means. No graphics supports the presence of trend.

Fig. 4

Lagplot of returns times series

The empirical test has been implemented to determine the number of differentiation required for having stationarity. There are for example the test of Ocsb: (Osborn et al. (1988) and that of Hyndman and Khandakar (2008). The result “ 1 ” means that there exists a seasonal unit root contrary to “ 0 ” (Table 4). Moreover, the methodology highlights the auto.arima function in R and by using their package forecast helps us to verify the seasonality. It is inspired by precursors like Hannan and Rissanen (1982), Liu (1989), Gomez and Maravall (1998), Melard and Pasteels (2000). It starts from the general model (Arima(p, d, q)(P, D, Q)s to recover the degree of differentiation (the parameter I of Arima) providing seasonality.

The seasonal adjustment of returns times series $\delta I^{'}_t$ is done thanks to a linear filter F at lag 12 like: $F = 1 - B^{12}$. We obtain a new time series $S_t = \delta I^{'}_t (1 - B^{12})$.

Table 4 Seasonality

Framework of calibration: Arima is a generalization of an Auto-Regressive Integrated Moving Average model that represents an important example of the Box and Jenkins (1976) approach. In particular, the Sarima model contains a seasonal component and it is the famous linear model for time-series analysis and forecasting. With its success, it occupies an essential place in academic research and in fields such as economics, finance and agro-industry. A time series ${X_t \ \forall \ t = 1, 2, \ldots , k}$ is generated by a $Sarima(p,d,q)(P,D,Q)_s$ process if:

$$\begin{aligned} \phi _p(B)\Phi _p(B^s)(1-B)^d(1-B^s)^D X_t = \theta _q(B)\Theta _Q(B^s)\epsilon _t \end{aligned}$$

(5)

where N is the number of observations; p, d, q, P, D and Q are positives integers; B is the lag operator; s is the seasonal period length.

• d reflects the initial differentiation obtained with the calculation of increases in rates in the times series between the dates $t-1$ and t by $\delta I^{'}_t = \frac{I^{'}_t - I^{'}_{t-1}}{I^{'}_{t-1}}$. It means the number of regular differences is ($d<=2$) (Shumway and Stoffer 2006): so $d=1$.

• s represents the annual seasonal adjustment observed and determined above respectively at Fig. 12 in Appendix: so we have $s=12$ and $D=1$. D is the number of seasonal differences. If there is seasonality effect, $D=1$ in the most cases. Else, if there is no seasonality effect, $D=0$.

• $\epsilon _t$ is the estimated residual at time t that is identically and independently distributed as a normal random variable with an average value equal to zero $\mu _{\epsilon } = 0$ and a variance $\sigma _{\epsilon }$.

• The orders p and P are the parameters of the regulars seasonal and autoregressive operator ( Ar and Sar). They are determined by using the partial auto-correlogramme function Fap.

• The orders q and Q are those of the regulars seasonal and moving average functions (Ma and Sma), they are determined by using the simple auto-correlogram function Fac.

$$\begin{aligned} Sarima \left\{ \begin{array}{ll} \phi (B) = 1 - \phi _1 B - \phi _2 B^2 - \ldots - \phi _p B^p &{} \text{ is } \text{ the } \text{ Ar(p) } \\ \Phi (B^s) = 1 - \Phi _1 B^s - \Phi _2 B^{2s} - \ldots - \Phi _p B^{ps} &{} \text{ is } \text{ the } \text{ Sar(p) } \\ \theta (B) = 1 - \theta _1 B - \theta _2 B^2 - \ldots - \theta _p B^q &{} \text{ is } \text{ the } \text{ Ma(q) } \\ \Theta (B^s) = 1 - \Theta _1 B^s - \Theta _2 B^{2s} - \ldots - \Theta _p B^{ps} &{} \text{ is } \text{ the } \text{ Sma(Q) } \\ \end{array} \right. \end{aligned}$$

Autoarima model

At first, we use the Autoarima model developed and implemented by Hyndman et al. (2008) before using the equation 5. It built a better model with the best AIC or BIC criterion. The terms of errors $\epsilon _i$ are estimated by the residuals $r_i = y - {\hat{y}}$. We suppose they are a white noise signal following a normal distribution $N(0,\sigma ^2)$. So: $E(\epsilon _i) = 0 \ \forall \ i$ and $V(\epsilon _i) = \sigma ^2 \ \forall \ i$). The variance of the residuals from the model is not homogeneous, but depend on the position of observation i. Thus, we check for stationary behaviour by plotting the residuals $r_i$ on times t. The independence between $\epsilon _i$ is managed by $\frac{{\hat{cov}}(r_i,r_j)}{\sqrt{s^2(r_i)}\sqrt{s^2(r_j)}} = 0$ for any point (i, j). For verification, the Durbin-Watson or Ljung-Box test is use.

The graphics of validation model⁵ help to test the efficiency of each model via its residuals. The residuals graphics $r_i$ in term of times is generally the first diagnostic. Indeed, thanks to its logical order in having data, these representations support the missing or not of serial positive correlations between $\epsilon _i$. The auto-correlations functions and its probabilities of Ljung-Box test support that the residuals are all auto-correlated. Indeed, on the graphics, some points are out of the reject area of missing auto-correlation of $\epsilon _i$. The double differentiation at the orders 1 and 12 on original data series probably did not completely rule out the dependence between observations. An empirical test confirm the presence of auto-correlations between the $r_i$ according to their weak $P_{value}$ ($P_{value}<0,05$). But, a focus on the simple autocorrelation, show the lags superiors to 12 are slightly higher and thus reveal a slight long-term dependency.

Table 5 Times series analysis with Autoarima model

Seasonal Arima model

The White noise model is the simplest modelling because, it takes no auto-regressive and no moving average component.

Table 6 Times series analysis with White noise model

The first autocorrelation coefficients are higher and always support a short-term dependency. Following the modelling, we add in the moving average and auto-regressive components respectively on the Sma et Sar parts from the white noise model. This methodology built the best Sarima model. At first, we start by Sma a model like $Sarima(0,1,q)(0,1,Q)_{12}$. The orders q and Q are determined by using the simple autocorrelation function Fac on stationary time series. For the order q, we look for the last lag which leaves the band at the same time inferior to 12. For the order Q, the selection is done on all the lag multiples to 12 which also leave the same band. So after analysis, we are:

q orders::

$q_{Wheat}=10$, $q_{Corn}=2$, $q_{Sorghum}=10$, $q_{Rice}=8$, $q_{Soy}=10$, $q_{Olive}=3$, $q_{Palm}=11$ and $q_{Colza}=10$.

Q orders::

$Q_{Wheat}=1$, $Q_{Corn}=2$, $Q_{Sorghum}=1$, $Q_{Rice}=2$, $Q_{Soy}=1$, $Q_{Olive}=1$, $Q_{Palm}=2$ and $Q_{Colza}=1$.

Table 7 Times series analysis with Sma model

Now, the modelling is about Sar model like $Sarima(p,1,0)(P,1,0)_{12}$. From the White noise model, we complete by adding the news components on the seasonal and auto-regressive part. Based on the partial autocorrelation function of stationary time series, we applied the rule above to choose the orders p and P.

p orders::

$p_{Wheat}=10$, $p_{Corn}=1$, $p_{Sorghum}=11$, $p_{Rice}=9$, $p_{Soy}=11$, $p_{Olive}=10$, $p_{Palm}=11$ and $p_{Colza}=11$.

P orders::

$P_{Wheat}=2$, $P_{Corn}=2$, $P_{Sorghum}=2$, $P_{Rice} = 2$, $P_{Soy}=2$, $P_{Olive}=2$, $P_{Palm}=2$ and $P_{Colza}=2$.

Table 8 Times series analysis with Sma model

In this part, we combine the MA and SARI components calculated above in order to find a better SARIMA model like $Sarima(p,1,q)(P,1,Q)_{12}$ for all agricultural data. In the precede modelling, there could be some complexity because of their very high orders p, P, q and Q, even if their AIC criterion have improved significantly compared to previous models. By parsimony, we have shown and set to 0 insignificant coefficient to simplify. We calculated the $p_{value}$ of estimated parameters and analyze the models and remove those whose probabilities are superior than 0.05. This process is thus repeated until we obtain the best models where all coefficients are significantly non-zero.

On the graphics of Ljung-Box (Figs. 13 and 14 in Appendix) some points are out of the band to reject with autocorrelation missing. In contrast, the graphics of simple autocorrelation function show almost no significant lag. The residuals $r_i$ are stationary. Besides, on the representations of standardized residuals, the graphics reflect an average behaviour of the evolution of the mean and variance over time.

Table 9 Times series analysis with Sma model

These models are more precise for econometric analysis and they take into account the singular and regular parts of $S_t$. Furthermore, they represent the best AIC, MAE and RMSE for forecast and oppose to the hybrid Wavelet-Sarima model.

Hybrid forecasting based on wavelet transform and Sarima

The processing Wavelet-Sarima model requires at first, an optimal Mra setting. Then, we define a type of transform, the wavelet function and the number of decomposition to use on those data series.

$$\begin{aligned} Mra = \left\{ \begin{array}{lllll} Dwt &{} / &{} Wavelet &{} / &{} J \\ Modwt &{} / &{} Wavelet &{} / &{} J \\ Cwt &{} / &{} Wavelet &{} / &{} J \\ \end{array} \right. \end{aligned}$$

The data analysis are applied on each sub-series in order to identify the best model able to describe the speculative behaviour adopted by people in order to monetize its kitty. At the end, the global forecast is obtained by adding the forecast of new sub-series. The application of this hybrid methodology is used only in two data series: wheat and soy data series. We hope that it can improve the accuracy in the forecast better than the Sarima model (Tables 5, 6, 7, 8, 9).

Configuration of multiresolution analysis

The wheat data sub-series and it variation represented in Figs. 5 and 6 are the result of the multi-resolution analysis. These data sub-series are separated into a first component smooth (the general appearance) and a set of details base on their resolution $[2^{j} ; 2^{j+1}[$. Each frequency band is specific because it describe the change of wheat’s price indices in any horizon. So, there are the high, middle and low frequencies. In the agricultural market, each class of agents or producers acts according to their investment horizons. The same multi-resolution analysis is done with soy data series and his variation (cf. Figs. 15 and 16 in Appendix). In both case, working with the variation data series by using this kind of resolution is more interesting in multi-scale analysis. For this way, we analyse to find the best modelling for any agricultural commodities. The Table 10 uses the same indicators like in Table 2. It specifies information by time horizon. The differences between the measurements indicate that the first frequency bands have more memory than the others. In addition, they decrease when the space-time become larger. The kurtosis being slightly superior than 3 supports the presence of a low leptokurticity compared to normal Gauss distribution. The skewness are positives or negatives according to sub-series. The KPSS’s test determine the missing of unit root in bands of wheat and soy data series. The probabilities of this test are inferior than $5\%$ in D(7), D(8) and A(8) band. But, for the other sub-series: D(1), D(2), D(3), D(4), D(5) and D(6), the $P_{value} = 10\%$. It means that there is no unit root. So they are stationary in opposite to those with a low frequency unless we use a double differentiation in modelling.

Table 10 Basic descriptives statistics for times sub-series

Fig. 5

MRA on Wheat times series

Fig. 6

MRA on LogWheat times series

Framework of calibration and validation

Each sub-series is modelled by using directly information obtained with the simple and partial autocorrelation function (Fac and Fap). But before modelling, an empirical test for unit root on the bands denote the low probabilities test ($\le 0;05$) for D7, D8 and A8, so no stationary and we must make them stationary. They must be neutralized by a filter $F = (1 - B)^2$. In contrast, the bands D1 to D6 are stationary. Regular process requiring the knowledge of an infinite number of parameters to specify them fully. We choose the SARIMA process which represent a huge class of stationary processes and needs some parameters. The Fac’s and Fap’s graphics are used to define the orders q, Q, p, P.

Simple and Partial autocorrelation function: The Fac’s Figs. 7a and b for wheat and 9a and b for soy are many lags out of the critical area and they are different. If one considers the high frequencies of the signals $D1, \ldots D6$, we identify the orders q and Q in modelling. For the bands D7, D8 and A8, a differentiation is necessary. Indeed, some bands of each data prices highlight all characteristics omitted and allow the detection of high values, seasonal, cyclical and trend effect. The Fap’s Figs. 8a and b for wheat and 10a and b for soy, are important lags depending on the time horizon. The orders p and P of auto-regressive and their seasonal version parts are important in high frequencies and decrease at low frequencies. When, they are no information in D7, D8 and A8, the move is similar to an auto-regressive process at order 1 (Ar(1)).

Diagnostic and validation: The normality test have probabilities inferior to 0.05. So the normal of residuals hypothesis is to reject. The stationarity test and the missing of auto-correlation between the terms of errors. We use the test of KPSS and Ljung-Box. The $P_{value}$ are higher than 0.05 on all frequencies. The residuals are therefore stationary and no auto-correlated. The Table 11 represented all informations detected in the residuals diagnostic and the quality of forecast.

Fig. 7

Wavelet Simple autocorrelation function - LogWheat

Fig. 8

Wavelet Partial autocorrelation function - LogWheat

Fig. 9

Wavelet Simple autocorrelation function - LogSoy

Fig. 10

Wavelet Partial autocorrelation function - LogSoy

Table 11 Diagnostic of residuals on originals data series models

Table 12 Diagnostic of residuals on transforms data series models

Discussions and conclusion

According to the difference modelling, the complete Seasonal ARIMA model $Sarima(p,d,q)(P,D,Q)_{12}$ is better in the forecast of agricultural data series. Thus, it’ll be used for forecasting the futures values. However, the tool of multi-resolution analysis of wavelet theory is more specific because it carries a segmented analysis of chronic resting on exploration temp and scale. t identifies that these time series are further broken down into components although the trend and seasonality. Moreover, the same results prove that the Wavelet-Sarima model give the better accuracy with the root mean square error RMSE both its calibration as its validation. The decomposition of these series in itself is already a first resolution of the complexity hidden information. Thanks to the strength of wavelets, the modelling improved greatly the usual models. This precision and technical ability provided by this model combinations $Wavelet-Sarima \ / \ Wavelet-Arima$ are demonstrated by Conejo et al. (2005) for the study of electricity prices, by Rivas et al. (2013) in the detection of cyclical behaviour of metal indices prices. But the gain in this quest for precision with this methodology is to achieve the best configuration that is in the multiple resolution analysis. The hardest part was choosing the wavelet name. So why, in the multi-resolution analysis, we choose other wavelet function in another wavelet family.

These families differ on four main criteria. The length of the support or the compact nature of their support. They have the faculty to represent effectively signals that possess disruptions, discontinuities or abrupt escalations. These characteristics are essential precisely in the share prices of raw materials. In addition, there’s the symmetry of forms of wavelets and their number of vanishing moments. Because, the more null moments in the wavelet function the more the transition between the space is smooth. Finally, there is the regularity. It is strongly related to the number of null moments (Tables 12, 13). The Daubechies wavelets are the most completely family. But, the choice of the function depend on the characteristics of times series analysed (Gencay et al., 2001).

Table 13 Forecast and Comparison

This study demonstrates that the combination between the wavelet transform and the seasonal auto-regressive and moving average is of technical interest in the forecast of data series with seasonal components. The commodity price indices like cereals and oleaginous product help to prove how to obtain the best accuracy in forecast. But, it is necessary to have the optimal setting in multi-resolution analysis. In this configuration the main parameter is the choice of wavelet function. By referring to the previous research done in economic and financial data series, the Daubechies’s wavelet is the most used. So, the same support has been used in these multi-scales applications with agricultural commodities. But, according to the type of data analysis and the object of the study, this resolution can be made by using another type of wavelet.

Appendix

See Figs. 11, 12, 13, 14, 15, 16, 17, 18, 19, 20.

Fig. 11

Annual average data series

Fig. 12

Monthly average indices prices

Fig. 13

Residuals diagnostics by Seasonal Arima model for cereals data series

Fig. 14

Residuals diagnostics by Seasonal Arima model for oleaginous data series

Fig. 15

MRA on Soy times series

Fig. 16

MRA on LogSoy times series

Fig. 17

Wavelet Simple autocorrelation function - Wheat

Fig. 18

Wavelet Partial autocorrelation function - Wheat

Fig. 19

Wavelet Simple autocorrelation function - Soy

Fig. 20

Wavelet Partial autocorrelation function - Soy