Introduction

An important step in designing modern predictive models is to cope with high-dimensional data, presenting large numbers of (cor)related variables and complex properties. “Big data” is both an increase in the number of samples collected over time, and an increase in the number of potential explanatory variables and predictors. When dimension grows, the specificities of high-dimensional spaces and data must then be taken into account in the design of predictive models. While this is valid in general, its importance is heightened when using nonlinear tools such as artificial neural networks. Most nonlinear models involve more parameters than the dimension of the data space which may result in a lack of identifiability, lead to instability, and overfitting (Huber 2011; Cherkassky et al. 1994; Moody 1991). Selection of significant predictors, and model complexity are the key tasks of designing accurate predictive models in data-rich environments.

Feature extraction and feature selection are broadly the two main approaches to dimensionality reduction. Extraction transforms the original features into a lower dimensional space preserving all its fundamentals. Feature selection methods select a small subset of the original features without a transformation. Extraction methods include principal component analysis (Pearson 1901; Eckart and Young 1936), factor analysis (Spearman 1904), canonical correlations analysis (Hotelling 1936), and several others.Footnote 1 Feature selection is accomplished by such methods as Ridge (Hoerl and Kennard 1970), LASSO (Tibshirani 1996) and Elastic Net (Zou and Hastie 2005).

In this work, our main focus is on feature selection techniques. We apply shrinkage approaches (usually referred to as regularization in machine learning literature). We embed feature selection in the backpropagation algorithm as part of its overall operation. Accordingly, we extend our loss function to include \(L_1\) norm for the weights of the dense network, and \(L_2\) norm for the weights in the skip-layer. The dense network corresponds to a multilayer neural network, whereas the skip-layer denotes the direct connection from each of the input variables to each of the output variables, which is similar to a linear regression model.

Shrinkage is an implicitly embedded feature selection. It is an example of model selection since only a subset of variables contributes to the final predictor. It has frequently been observed that \(L_1\) shrinkage produces many zero parameters, leading to some features being dropped and a sparse model. Only those parameters whose impact on the empirical risk is considerable appear in the fitted model (Ng 2004). Shrinkage is a proper means of controlling complexity in the nonlinear component. From an optimization point of view we have a neural network learned/estimated by LASSO. This prevents hidden units from getting stuck near zero and/or exploding weights.

Simultaneously, we employ the \(L_2\) shrinkage on the skip-layer connections (linear part of the model), in order to penalize groups of parameters, and encourage the sum of the squares of the parameters to be small. Therefore we will not drop specific features from linear component, making it possible to interpret the marginal impact of predictors on the target variable. It is worth mentioning that the linear part of the model can be interpreted as a Ridge regression.

There are other benefits to shrinkage/regularization. Empirically, penalizing the magnitude of network parameters is also a way to reduce overfitting and to increase prediction accuracy (Ng 2004; Chui and Li 1992). This is especially true in the state-of-art models, such as deep learning models with large number of parameters. Our proposed algorithm combines the neural network’s advantage of describing the nonlinear process with the superior accuracy of feature selection that is provided by a penalized loss function that combines \(L_1\) and \(L_2\) norms.

There is increasing interest in merging neural networks with more traditional statistical techniques, like shrinkage methods. For instance, in LassoNet (Lemhadri et al. 2021) a neural network is combined with global feature selection. This framework uses an input to output skip connection and allows a feature to have non-zero weight in a hidden unit only if its linear connection is active. The main drawback of this approach is that the model ignores the possibility of nonlinear relationships between features and target variables at the beginning of the process, the main reason for using a nonlinear neural network. However, in the dense layer the model captures the nonlinear relationship between the remaining features and the target variable. In contrast to LassoNet, in our AAShNet feature selection and sparsity have been tackled by the nonlinear layer allowing for all nonlinear relationships to be captured. There are also recent attempt to select features for neural networks using group lasso regularization [see: Ho and Dinh (2020)]. It is established that this feature selection method is consistent for single-output feed-forward neural networks with one hidden layer and hyperbolic tangent activation function.

Many studies have suggested neural networks as a promising alternative to linear regression models. Empirical evidence on out-of-sample forecasting performance is, however, mixed. It is challenging to determine linear and nonlinear components. Linearity tests do often suggest that real world series are rarely purely linear or nonlinear.

We consider the possibility that the series \((y_t)\) contain both a linear component, \((\mathcal {L}_t)\), and a nonlinear component \((\mathcal {N}_t)\).

$$\begin{aligned} y_t= \mathcal {L}_t + \mathcal {N}_t \end{aligned}$$
(1)

Neural network alone is not best suited to handle both linear and nonlinear components, especially when the linear component is superior to the nonlinear component [see Habibnia (2016) for a detailed discussion of testing linearity and nonlinear time series models].

Two different approaches to model and forecast series with both linear and nonlinear patterns are available. The first approach is a two step methodology to combine linear time series models and neural network models. In this approach, the first step residuals are obtained from the fitted linear model \(\hat{e_t}= y_t - \hat{\mathcal {L}_t}\). In the second step a nonlinear model (e.g., GARCH, neural nets) is trained on the residuals of the first step. In principle, this “hybrid” two step approach can provide superior predictions when both the linear and neural network model are well specified. In practice, however, two types of model specification errors are introduced without an ability to assess their mutual impact.

The alternative approach that we are proposing in this paper models both linear and nonlinear components adoptively. It is based on a neural network with skip-layer connections including both linear and nonlinear structures.

The rest of the paper is organized as follows. Section “The Model” provides the basic framework of the proposed model. In Section “Gradient-Based Hyperparameter Optimization” we investigate proper estimation of shrinkage hyperparameters and introduce gradient-based techniques based on reverse-mode automatic differentiation (RMAD) to accomplish this. Section “Case Study: Return Prediction” presents an application to US financial returns. Section “Concluding Remarks” contains some concluding remarks.

The Model

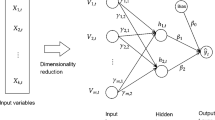
In this study, we examine a feedforward neural network with one hidden layer, known as a dense network. Neural network models can be seen as generalizations of linear models, when one allows direct connections from the input variables to the output layer with a linear transfer function,Footnote 2 that we refer to as the skip-layer. The model is expressed as

$$\begin{aligned} y_t= \Phi ({\varvec{x}};{\varvec{w}}) = \sum _{i\rightarrow k} x_{it}w_{ik} +\sum _{j\rightarrow k} \phi _j \left( \sum _{i\rightarrow j} x_{it} w_{ij} \right) w_{jk}+\varepsilon _t, \end{aligned}$$
(2)

where \(\Phi \) describes the network by a vector function. We associate subscript i with the input layer, subscript j with the hidden layer, and subscript k with the output layer. \(x_{it} = (x_{1t},x_{2t},...,x_{mn})\) is the value of the ith input node, which can be a constant input representing biases, a matrix of lagged values of \(y_t\) and some exogenous variables. \(\phi _j(.)\) are the activation functions used at the hidden layer. A single-hidden-layer neural network with skip-layer connections is shown in Fig. 1. A network with only one hidden layer and skip-layer connections has three sets of weights: those for direct connections between the inputs and the output (\(w_{ik}\)), those connecting the inputs to the hidden layer (\(w_{ij}\)), and those connecting the output of the hidden layer to the final output layer(\(w_{jk}\)).

First term in Eq. (2) represents a linear regression term. Understanding the theoretical advantage of skip connections and residual connections has recently attracted much attention in the realm of deep learning. Training very deep neural nets are generally more difficult but skip connections is widely used to alleviate numerical issues in deep neural nets, with additional benefits in optimization efficiency and statistical accuracy. The benefits of skip connections are likely due to multiple factors, including better generalization ability (or feature learning ability), better signal propagation and better optimization landscape. For instance, Orhan (2017) shows that skip connections eliminate the singularity and suggests that these direct connections improve the landscape by breaking symmetry. Skip connections have an uninterrupted gradient flow by creating short paths from the first layer to the last layer, which tackles the vanishing gradient problem. The model is easy to train because skip connections improve the flow of information and gradient. As a side note, skip connections can be used flexibly. They are not restricted to the form presented in this work which we only have direct connections from the input layer to the model output and can be used between any pair of hidden layers similar to the residual neural network (ResNet) architecture and its variants [see: He et al. (2015)]. As a final note, it has been experimentally validated (Li et al. 2017) the loss landscape changes significantly when introducing skip connections.

The second term in Eq. (2) denotes the dense network of the two layers, hidden and output, is usually referred to as a multi-layer perceptron in the literature. It has been shown to be able to perform well with nonlinear complex data. A greater capacity of the dense network, compared to the skip-layer, is realized by stacking two layers, enabling it to model more complex data. A differentiable nonlinear activation function \(\phi \) is used in the hidden units. \(\varepsilon _t\) is a random disturbance term which captures all other factors influencing y than the x. A linear component term moves the model in the linear direction. This aids statistical interpretation and unravels the structure behind the network, otherwise left to a black box. This simultaneous approach has the advantage, when we apply shrinkage techniques to estimate network parameters for an essentially linear process, of pruning the hidden neurons.

Fig. 1
figure 1

A single-hidden-layer neural network with skip-layer connections

Full size image

Estimation of network elementary parameters based on prediction error minimisation is known as training/learning. The most common cost/risk function is the mean squared prediction error (MSE), \(E = \frac{1}{n}\sum _{t=1}^n (y_t - \hat{y}_t)^2\). Given target values \(y_t\) and network estimated outputs \(\hat{y}_t\) error functions are obtained for each parameter set, followed by tuning of the parameters.

The error surface becomes increasingly complicated with the number of input variables and network parameters. It is common to employ the conventional feed-forward neural network, trained with the popular and revolutionary gradient-descent-type algorithm known as backpropagation. The backpropagation algorithm was first introduced by Bryson et al. (1979) and popularized in the field of artificial neural network research by Werbos (1988) and Rumelhart et al. (1986). Error function’s sensitivity to network parameters is assessed via Gradient Descent optimization. Gradient is normally defined as the first order derivative of the error function with respect to each of the model parameters. Working out the gradients can be performed in a completely mechanical way known as Automatic Differentiation (Baydin et al. 2017). AD employs the Jacobian matrix of gradients for each parameter \(w_i\) to identify directions that decrease the height of the error surface (see “Appendix”). In fact backpropagation is only a specific case of reverse-mode AD that is applied to an objective function errors as functions of model parameters.

The weight adjustment is given by

$$\begin{aligned} w^{new} = w^{old} - \eta ~ \frac{\partial E(\varvec{w})}{\partial w} \end{aligned}$$
(3)

where the constant \(\eta \) is the learning rate (step size) for updating elementary parameters, its value falls between zero and one. By iteratively repeating this mechanism, the network can be trained in a way that converges to the optima. The set of new elementary parameters are repeatedly presented to the network until the error value is minimized. Around the optimum point, all the elements of the gradient would be very small, leading to tiny changes in new parameters.

We add the \(L_1\) and \(L_2\) penalties in training our model to the loss function \(\widetilde{E}(.)\), the original MSE. The following optimization problem is used for training:

$$\begin{aligned} \begin{aligned} {\varvec{w}}^*&= \underset{\varvec{w}}{\arg \!\min }~ \widetilde{E}(\varvec{w}|\lambda , X) = \underset{\varvec{w}}{\arg \!\min }~ E(\varvec{w}|\lambda , X) ~+~ ~\Omega (\varvec{w,\lambda })\\ \end{aligned} \end{aligned}$$
(4)

where the regularization term \(\Omega (\varvec{w, \lambda })\) is a combination of the L1 norm and the L2 norm of the parameter vector. \(\lambda \) sets the impact of shrinkage on the loss, with larger values resulting in more penalization. Using the regularized objective causes the training procedure to be inclined to smaller parameter values; unless larger parameters considerably improve the original error value (MSE). Assuming a fixed \(\lambda \), to learn \(w^*\), we only need to include the derivative of \(\Omega (\varvec{w, \lambda })\) in our derivatives:

$$\begin{aligned} \left\{ \begin{array}{lr} \Delta = \frac{\partial E({\varvec{w}})}{\partial w} + \frac{\partial \Omega ({\varvec{w}, \lambda })}{\partial w} \\ w^{new} = w^{old} ~ - ~ \eta \Delta \end{array} \right. \end{aligned}$$
(5)

where \(\Delta \) is the gradient of the regularized loss function. \(\lambda > 0\) is proportional to complexity of the model but is not a parameter that appears in the model. It is a hyperparameter. In the next section, we explain the impact of hyperparameters and elaborate on our procedure for tuning them.

We employ \(L_1\) and \(L_2\) shrinkage on the parameters of the dense network and skip-layer, respectively; as is depicted by following optimization problem:

$$\begin{aligned} {\varvec{w}}^* = \underset{\varvec{w}}{\arg \!\min }~ E(\varvec{w}|\lambda , X) ~+~ \frac{\lambda _2}{2}\sum _{i\rightarrow k} w^2_{ik}~+~\lambda _1\left( \sum _{i\rightarrow j} |w_{ij}|+\sum _{j\rightarrow k}|w_{jk}|\right) \end{aligned}$$
(6)

which can be realized by iteratively adjusting the parameters using the updating rules below

$$\begin{aligned} \left\{ \begin{array}{lr} w_{ik}^{new} = w_{ik}^{old} - \eta ~ \left( \frac{\partial E\left( {w|\lambda , X}\right) }{\partial w_{ik}} + \lambda _2w_{ik}^{old}\right) \\ w_{ij}^{new} = w_{ij}^{old} - \eta ~ \left( \frac{\partial E\left( {w|\lambda , X}\right) }{\partial w_{ij}} + \lambda _1sgn\left( w_{ij}^{old}\right) \right) \\ w_{jk}^{new} = w_{jk}^{old} - \eta ~ \left( \frac{\partial E\left( {w|\lambda , X}\right) }{\partial w_{jk}} + \lambda _1sgn\left( w_{jk}^{old}\right) \right) \\ \end{array} \right. \end{aligned}$$
(7)

where \(\lambda _1\) and \(\lambda _2\) are non-negative values known as shrinkage hyperparameters. \(L_1\) sparsity norm and \(L_2\) smoothing norm are two closely related regularizers that can be used to impose a penalty on the complexity of the model that is to be learned. Shrinkage estimation of the model can be seen as an implementation of Occam’s razor, introducing a controllable trade-off between fitting data and model complexity, enabling us to have models of less complexity with adequate generalization capability. Regularization in neural networks limits the magnitude of network parameters by adding a penalty for weights to the model error function. In this study, \(L_2\) shrinkage penalizes parameters in skip-layer connections by adding sum of their squared values to the error term. \(L_1\) shrinkage penalizes parameters in the dense network to encourage the topology of the learned network to be sparse. The relative importance of the compromise between finding small weights and minimizing the original risk function depends on the size of \(\lambda \).

To use \(L_2\) shrinkage, we add a \(\lambda _2 w\) term to the gradient as the derivative of \(w^2\) is 2w. \(L_2\) shrinkage works with all forms of learning algorithms, but does not provide implicit feature selection. The derivative of the absolute value of w is w/|w|, however \(L_1\) norm is not differentiable at zero and hence poses a problem for gradient-based methods.

The problem can be solved using the exact gradient, which is discontinuous at zero. We can also solve the problem by the smooth approximation approach which will allow us to use gradient descent. To smooth out the \(L_1\) norm using an approximation, we use \(\sqrt{w^2 +\epsilon }\) in place of |w| , where \(\epsilon \) is a smoothing parameter which can also be interpreted as a sort of sparsity parameter. When \(\epsilon \) is large compared to w, the expression \(w + \epsilon \) is dominated by \(\epsilon \) and taking the squared root yields approximately \(\sqrt{\epsilon }\) (Lee et al. 2006).

Gradient-Based Hyperparameter Optimization

The major drawback of shrinkage is that it introduces additional hyperparameters. In practice we have two set of parameters: model elementary parameters (network weights and biases), and learning algorithm hyperparameters (magnitude of \(L_1\) and \(L_2\) penalties, and learning rate). We would ideally like to determine these hyperparameters to get optimal generalization.Footnote 3 As opposed to elementary parameters, these hyperparamters cannot be directly trained by the data. Whereas the elementary parameters specify how to transform the input data into the desired output, the hyperparameters define how our model and algorithm are actually structured.

The performance and robustness of neural networks relies to a large extent on hyperparameters. Tuning these hyperparameters not only makes the investigation of methods difficult, but also hinders reproducibility (Bergstra et al. 2011). Transparent tuning of hyperparameters can be part of an Hyperparameter Optimization (HPO), as an outer loop in training procedures.

The de-facto naïve approach of searching through combinations of potential values of hypergradients and choosing the one that performed the best (a.k.a. grid search) is very time-consuming and becomes quickly infeasible as the dimension of hyperparameter space grows. In many practical applications manually searching the space of hyperparameter settings is tedious and tends to lead to unsatisfactory outcomes. Bergstra and Bengio (2012) show empirically and theoretically that random search more efficient than grid search. Statistical techniques such as cross-validation (Wahba 1990; Larson 1931), bootstrapping (Efron and Tibshirani 1994), and Bayesian methods (MacKay 1992) can also assist in determining hyperparameters.

HPO must be guided by some performance metric, typically measured by cross-validation (CV) on the training set, or evaluation on a held-out validation set. The rationale behind CV is to split the data into the training samples used for learning the algorithm, and the validation samples (one or several folds) for estimating the risk of each algorithm and for evaluation of its performance. CV consists of averaging several hold-out estimators (folds) of the risk corresponding to different splits of the data, and selecting the algorithm with the smallest estimated risk. Within each fold, hyperparameters are fixed and we only estimate model elementary parameters. The validation samples play the role of new unseen data as long as the data are i.i.d.Footnote 4 For a general description of the CV see Geisser (1975), Chen and Hagan (1999), and Arlot and Celisse (2010) for a comprehensive review on cross-validation procedures and their applications in different algorithms and frameworks. Several studies such as Rivals and Personnaz (1999) show cases in which CV performance is less than satisfactory.

Recently, automated approaches for estimation of hyperparameters have been proposed which can provide substantial improvements and transparency. Although one may also “hyperparameterize” certain discrete choices in design of the model (e.g. number of hidden units), we focus only on the continuous hyperparameters in this work. There are a number of gradient-free automated optimization methods (Hutter et al. 2011; Bergstra et al. 2011, 2013; Snoek et al. 2012), all of which rely on multiple complete training runs with varied fixed hyperparameters. Hyperparameters are chosen to optimize the validation loss after complete training of the model parameters.

Gradient-based HPO approaches, proposed by Larsen et al. (1996) and Andersen et al. (1997), emerged in the 1990s.

We can distinguish two main approaches of gradient-based optimization: Implicit differentiation and iterative differentiation.

Implicit differentiation, first proposed by Larsen et al. (1996), computes the derivative of the cost \(L_{valid}\) with respect to \(\lambda \) based on the observation that, under some regularity conditions, the implicit function theorem can be applied in order to calculate the gradients of the loss function. In particular, the cost function is assumed to smooth and converge to local minima. The inner optimization \(w(\lambda ) \in argmin _{w}L_{train}\) can be characterized by the implicit equation \(\nabla _w L_{train} = 0\). Bengio (2000) derived the gradients for unconstrained cost function and applied the algorithm to L2 shrinkage for linear regression. The method has also been used to find kernel parameters of Support Vector Machines (Keerthi et al. 2007). Pedregosa (2016) proposes HOAG which uses inexact gradients, allowing the gradient with respect to hyperparameters to be computed approximately.

In iterative differentiation, first proposed by Domke (2012), Larsen et al. (2012), the gradient for hyperparameters are calculated by differentiating each iteration of the inner optimization loop and using the chain rule to aggregate the results. However, the problem with this reverse-mode approach is that one must retain the entire history of elementary parameter updates, making a naïve implementation impractical due to memory constraints. Reverse-mode differentiation requires intermediate variables to be maintained in the memory for the reverse pass and evaluation of validation loss needs hundreds or thousands of inner optimization iterations. Maclaurin et al. (2015), Franceschi et al. (2017) later extended this for setting of stochastic gradient descent via reverse mode automatic differentiation of validation loss. The burden of storing the entire training trajectory \(w_1,\ldots ,w_T\) is avoided by an algorithm that exactly reverses SGD with momentum to compute gradients with respect to all training parameters, only using a relatively small memory footprint, making a solution feasible for large-scale big data machine learning problems.

We defined the updating rule for elementary parameters as \(w_{t+1} = w_t - \eta \nabla L_{train}\) where \(L_{train} = \widetilde{E}(w_t|\lambda , X_{train})\) is the regularized loss value on train data. To calculate hypergradients we rely on the unregularized loss function, that is \(L_{valid} = E(w_t|\lambda , X_{valid})\), as the actual generalization performance of the model, on unseen data points, does not directly depend on regularizers; otherwise the model with no regularization would be always selected:

$$\begin{aligned} \begin{aligned} \lambda ^{*} \;&= argmin _{\lambda }L_{valid}\\ s.t.\;\; w(\lambda )&\in argmin _{w}L_{train} \end{aligned} \end{aligned}$$
(8)

There are cases where SGD can become very slow. The method of momentum is designed to accelerate learning, especially in the face of high curvature, small but consistent gradients, or noisy gradients (Goodfellow et al. 2016). We modify our training (Algorithm 1) to include a velocity variable v storing the momentum by calculating exponentially decaying moving average of past gradients.

figure a

where \(\gamma _t\) is the momentum decay rate. The training procedure starts with elementary parameters velocity \(v_1=0\) and \(\varvec{w_1}\) and ends with \(v_T\) and \(\varvec{w_T} = \varvec{w_{T-1}} + \eta _{T-1}v_{T-1}\). Algorithm 2 is then used to calculate the gradients of validation loss with regard to the hyperparameters.

figure b

The velocity \(v_t\) is needed to reverse the path, otherwise without momentum, \(g_t\) and \(\eta _t\) alone would not be able to recover \(\varvec{w_{t-1}}\). Notice that the loss of information caused by finite precision arithmetic in computers leads to failure of this algorithm. For this reason, we need to store the bits lost in \(v_t\) when multiplied by \(\gamma _{t}\).

Given this powerful gradient-based mechanism for finding hyperparameters, a natural extension to our model is to introduce a hyperparameter \(\alpha \) denoting the contribution of skip-layer and dense-network in producing predictions with higher generalization. That is to say, our model can be reformulated as:

$$\begin{aligned} y_t= \Phi ({\varvec{x}};{\varvec{w}}) = \alpha \sum _{i\rightarrow k} x_{it}w_{ik} +(1-\alpha )\sum _{j\rightarrow k} \phi _j \bigg (\sum _{i\rightarrow j} x_{it} w_{ij} \bigg )w_{jk}+\varepsilon _t, \end{aligned}$$
(9)

where \(\alpha \) assumes a value between zero and one. Appreciating that the skip-layer and the dense network have unbalanced effects on the outcome, one can see how this may result in faster convergence of training procedure. More importantly, \(\alpha \) can be interpreted as the activation of skip-layer and dense network and can point to linearity or nonlinearity components.

There is some similarity to averaging estimators. In lower dimensions, a nonparametric model may replace the Neural component. See, for example, Wooldridge (1992), Rahman et al. (1997), Fan and Ullah (1999), Kotlyarova and Zinde-Walsh (2006) and Hansen (2007). Fan and Ullah (1999) considers a combined estimator of the regression mean in the i.i.d framework. Their combined estimator is a linear combination of a parametric estimator and a nonparametric estimator with the weights automatically determined by data. They established favorable convergence properties for their estimator under different asymptotic conditions on the global discrepancy between the parametric model and the true regression function. Mostly, the use of combined estimators in the literature is restricted to convex combinations where a convex combination of a parametric and a non-parametric regression estimator is employed to offer robustness to misspecification of the regression functions. Here we do not impose such restrictions and shrinkage estimation of the coefficients is allowing for the best bias-variance trade-off point for the learning algorithm. Semi nonparametric methods (series models) lie in between our method and the just mentioned nonparametric methods, but with greater ability to handle larger dimensions as in our setting.

Case Study: Return Prediction

Research into modelling and forecasting financial returns has a long history. Several models are described in Tsay (2005) and Campbell et al. (1996) that attempt to explain return time series using linear combinations of one or more financial market factors. The most widely studied single factor model is the capital asset pricing model (CAPM) of Sharpe (1964) and Lintner (1965) that relates the expected return of equities to the expected rate of return on a market index (such as the Standard and Poor’s 500 Index). The empirical performance of CAPM is poor as it cannot explain the behaviour of asset returns, see Fama and French (2004). This failure is perhaps due to the absence of multiple factors. Arbitrage pricing theory (APT) is a general model proposed by Ross (1976) to account for these deficiencies. APT presents a linear approximate model of expected asset returns based on an unknown number of macroeconomic “factors” or market indices. The relationship between the factors and historical returns is routinely determined linearly.

Return time series present characteristics such as comovement, nonlinearity, non-Gausianity (skewness and heavy tails), volatility clustering and leverage effect. This makes the modelling task very challenging, see Hsieh (1991), Bollerslev et al. (1994), Brooks (1996), Cont (2001).

The data are daily returns of \( m =\) 418 equities on the S&P 500 index from 03.01.2006 through 28.09.2018, for a total of 3208 observations. The initial sample 03.01.2006–28.09.2017 is used for estimation (training), with \(T =\) 2957 in-sample size. The holdout sample period 01.10.2017–28.09.2018 (251 observations) is employed to examine the models’ out-of-sample forecasting performance. 1-step (here one day) ahead forecasts of targets (\( {\hat{y}}_{it+1|t} \)) are based on a rolling estimation window. Parameter estimates are updated every five steps.

We believe accounting for comovements between financial returns is important in forecasting returns. Consequently, the lags of other equities are included as predictors for any return series. We examine the nonlinear high-dimensional forecasting model described in the prior sections (AAShNet model) as well as several competing models and benchmarks.

We compare our proposed model with a benchmark, the sample mean of \({\varvec{y}}_t\) over the in-sample window, as the 1-step ahead forecast. This corresponds to assuming the log daily price follows a random walk (RW) with drift. It is almost equivalent to the “zero forecast” when the in-sample window is large enough. Furthermore, a buy-and-hold (B&H) strategy in the market portfolio (S&P 500 Index) has been considered as another benchmark. To understand whether allowing nonlinearity improves portfolio performance we examine the AAShNet algorithm (with Ridge and Lasso) optimized by cross-validation.

Since predictability of financial returns has major consequences for financial decision making, the model with minimal forecast error is deemed optimal. However, the model with minimum forecast error does not necessarily guarantee profit maximization, the primary objective of financial decision makers. Armstrong and Collopy (1992), Pesaran and Timmermann (1995, 2000), Granger and Pesaran (2000) and Engle and Colacito (2006) argue that a forecast evaluation criterion should be related to decision making and judge predictability of financial returns in terms of portfolio simulation. More specifically, a trading (portfolio) simulation approach assumes that all competing models are applied with stock market virtual investment decisions, and out-of-sample portfolio performances are used to evaluate the predictability of alternative models.

Consequently, this paper examines both statistical and portfolio performance measures (the out-of-sample RMSE and the portfolio performance during the out-of-sample period). Figure 2 illustrates portfolio excess returns for the out-of-sample period for the proposed model (ASShNet) against competing approaches. We randomly selected 50 stocks out of 418 stocks to construct the portfolio. However, the forecast of each selected stock is based on the lags of all 418 equities.

Fig. 2
figure 2

Comparison of AAShNet, and the competing models based on the portfolio excess returns in the out-of-sample period

Full size image

Consider a passive, equally weighted (1/M) portfolios with short selling. This portfolio is known to be a very stringent benchmark that many optimization models fail to outperform [see DeMiguel et al. (2009)]. We compute the portfolio’s out-of-sample excess returns and volatility as well as the Sharpe ratio. Sharpe ratio measures risk-adjusted returns, a portfolio with a greater Sharpe ratio offers greater returns for the same risk. If a portfolio with lower Sharpe ratio has returned better over a time period than another portfolio with a higher ratio, the risk of losing by investing in the former fund will be higher.

Table 1 Average RMSEs and performance of investment portfolios for competing forecasting models
Full size table

The proposed penalized neural net behaves noticeably better in this empirical analysis. Table 1 provides evidence for out-of-sample forecasting ability of this model vis-à-vis competing approaches in terms of the Sharp ratio. AAShNet also offers an appreciable improvement over linear shrinkage models and benchmarks based on RMSE and actual portfolio performance. In the Ridge and Lasso regressions, the best model is selected by cross-validation. We perform generalized cross-validation, which is an efficient leave-one-out cross-validation.

AAShNet produces higher returns (10.24%) at the end of the out-of-sample period, with a Sharpe ratio of (1.143) that is superior to alternative models. This indicates that significantly improved forecast is obtained by modelling nonlinear dynamics among variables. One should note that Random Walk with drift and AR(1) are special cases of shrinkage models and AAShNet when there is no dependence on other equities.

Concluding Remarks

Forecasting with many predictors has received a good deal of attention in recent years. Shrinkage methods are one of the most common approaches for forecasting with many predictors. Such methods have generally ignored nonlinear dynamic relations among predictors and the target variable.

In this study, we suggested an Adaptable and Automated Shrinkage Estimation of Neural Networks (AAShNet). We explained how skip-layer connections move the model in the right direction when the data contains both linear and nonlinear components. To overcome the curse of dimensionality and to manage model complexity, we penalized the model loss function with \(L_1\) and \(L_2\) norms. Setting the size of shrinkage is still an open question. Recent studies have proposed automated approaches for estimation of algorithm hyperparameters. We employed the gradient-based automated approaches which treat shrinkage hyperparameters in the same manner as the network weights during training, and simultaneously optimize both sets of parameters.

The empirical application to forecasting daily returns of equities in the S&P 500 index from 2006 to 2018 provides support for the out-of-sample forecasting ability of AAShNet algorithm vis-à-vis some competing approaches, both in terms of statistical criteria and trading simulation performance. Our empirical results encourage further research toward other possible applications of the proposed model.

Appendix: Automatic Differentiation

There are three main approaches that computer can work out the derivatives: Numerical, Symbolic and Automatic differentiation.

Automatic differentiation refers to a family of procedures to automatically calculate exact derivatives of any function, including program subroutines, with time complexity at most a small constant factor of the time complexity of the original function. It is not inherently ill-conditioned and unstable similar to the numerical method and has much less computational complexity. It also does not suffer from expression swell problem of symbolic differentiation.

AD augments the standard computation with calculation of derivatives whose combination through chain rule gives the derivative for overall composition. AD can be applied on evaluation trace of arbitrary program subroutines which can be more than closed-form functions and are in fact capable of incorporating complex control flows which do not directly alter values. An automatic differentiator takes a code subroutine that computes a function of several independent variables as input and gives as output a code that computes the original function along the gradient of the function with respect to the independent variables. As most of the functions are piece-wise differentiable and control flows not directly interfering with calculations, chain rule can be used repeatedly in such a way that gradients are calculated along intermediate values being computed.

Based on modus operandi of automatic differentiation there can be two implementations of this technique; the forward mode and the reverse mode. We investigate each method, by applying them on the same trivial function \(y = f(x_1, x_2) = x_1x_2-cos(x_1)\) at \((x_1, x_2) = (6, 3)\).

$$\begin{aligned} \begin{aligned} v_1&= x_1&= 6\\ v_2&= x_2&= 3\\ v_3&= v_1v_2&= 6\times 3\\ v_4&= cos(v_1)&= cos(6)\\ v_5&= v_3-v_4&= 18-0.96\\ y&= v_5&= 17.04 \end{aligned} \end{aligned}$$
(10)

In forward mode, we build a Forward Primal Trace of the values propagating through the function and a corresponding Forward Tangent Trace. Equation 10 shows the forward evaluation of primals. Forward primal trace depicts the natural flow of composition. Equation 11 is the corresponding tangent trace for \(\dot{y} = \frac{\partial f}{\partial x_1}\), that is the rate of change of the function f with respect to the input \(x_1\). Notice that both traces are evaluated as written, top to bottom. To calculate the derivative with respect to n different parameters, n forward mode differentiations would be needed. This makes the forward-mode very inefficient for deep learning models where the number of parameters may amount to millions.

$$\begin{aligned} \begin{aligned} \dot{v_1}&= \dot{x_1}&= 1\\ \dot{v_2}&= \dot{x_2}&= 0\\ \dot{v_3}&= \dot{v_1}v_2+\dot{v_2}v_1&= 1 \times 3+0 \times 6\\ \dot{v_4}&= \dot{v_1}\times -sin(v_1)&= 1 \times -sin(6)\\ \dot{v_5}&= \dot{v_3}-\dot{v_4}&= 3 - 0.279\\ \dot{y}&= \dot{v_5}&= 2.72 \end{aligned} \end{aligned}$$
(11)

The reverse mode works by complementing each intermediate variable \(v_i\) with an adjoint \(\bar{v_i}\) representing the sensitivity of output y to changes in \(v_i\). In reverse mode the code is executed and the trace is stored in memory at first stage. At second stage, the adjoints are calculated in opposite direction of the execution of the original function. The reverse adjoint trace corresponding to Eq. 11 is depicted in 12.

$$\begin{aligned} \begin{aligned} \bar{v_5}&= \bar{y}&= 1 \\ \bar{v_4}&= \bar{v_5}\frac{\partial v_5}{\partial v_4}&= \bar{v_5}\times -1&= -1 \\ \bar{v_3}&= \bar{v_5}\frac{\partial v_5}{\partial v_3}&= \bar{v_5}\times 1&= 1 \\ \bar{v_1}&= \bar{v_4}\frac{\partial v_4}{\partial v_1}&= \bar{v_4}\times -sin(v_2)&= -0.27 \\ \bar{v_2}&= \bar{v_3}\frac{\partial v_3}{\partial v_2}&= \bar{v_3}\times v_1&= 6\\ \bar{v_1}&= \bar{v_1} + \bar{v_3}\frac{\partial v_3}{\partial v_1}&= \bar{v_1} + \bar{v_3} \times v_2&= 2.72 \\ \bar{x_1}&= \bar{v_1}&= 2.72\\ \bar{x_2}&= \bar{v_2}&= 6\\ \end{aligned} \end{aligned}$$
(12)

For a function \(f:\mathbb {R}^n \rightarrow \mathbb {R}^m\) whose number of operations to be evaluated is denoted by \(ops (f)\), the complexity of calculating the Jacobian by forward and reverse modes are \(n \times c \times ops (f)\) and \(m \times c \times ops (f)\), respectively, where it is guaranteed that \(c < 6\) (Griewank and Walther 2008). That is if \(n\gg m\), backward-mode is preferable, although it would have increased memory requirements. And forward mode should be used when the number of dependent variables is greater than the number of independent variables.