Introduction

Geotechnical engineering, a specialized discipline, deals with the complexities of earth materials behaviors, the aspects of water–soil interactions, and soil–structures interactions. Yet, modeling the behavior of soil with inclusions remains a challenge when using conventional techniques. Soft computing (SC) are advanced modeling techniques, including machine learning, artificial neural networks (ANN), and fuzzy logic, which deal with approximation and uncertainty to solve complex problems [1]. Using soft computing (SC) techniques has recently become popular in modeling complex behavior in geotechnical applications due to its predictive capabilities when compared to conventional techniques and methods [2]. In the context of shallow foundations, two predominant factors drive their design: the ultimate bearing capacity and settlement, often referred to as serviceability [3].

Previous studies have successfully applied SC techniques for solving geotechnical engineering problems, specifically predictions of reinforced foundations behavior [4,5,6,7,8,9,10,11,12,13,14,15,16,17]. For reinforced sands, in particular, and given the complexity and often uncertainty in their bearing capacity and settlement analysis, SC techniques have attracted broad interest as an effective alternative to normal regression [18]. Related previous attempts to model the reinforced soil behavior are summarized in Table 1.

Table 1 Previous studies attempt to model reinforced soil behavior using soft computing techniques and their limitations
Full size table

Soleimanbeigi and Hataf [5] investigated the possibility of using backpropagation and feedforward ANNs to predict reinforced sands’ ultimate bearing capacity of shallow foundations. However, the developed ANN model ignored several practical parameters such as the effect of the geogrid’s aperture size and soil gradation parameters. Sahu et al. [7, 8] implemented neuro-fuzzy and ANN modeling techniques to estimate the bearing capacity of inclined loading on shallow strip footing on reinforced sands with specific type of geogrid reinforcement. The authors reported an R2 of 0.997 and 0.994 for neuro-fuzzy and ANN modeling, respectively. Raja and Shukla [18] used ANN to model the settlement of reinforced foundations using numerical simulation results; therefore, the effect of geogrid geometry and soil gradation was not included in the study. The authors reported an R2 of 0.962 with best-performed ANN. More recently, Kumar et al. [19] utilized advanced predictive models such as extreme learning machine (ELM) and multivariate adaptive regression splines (MARS) to model the bearing capacity; the R2 of ELM and MARS regression was 0.976 and 0.995, respectively. However, the authors did not include the effect of reinforcement in their analysis.

Previous studies relied heavily on well-established SC techniques, innovative models such as support vector machines (SVM) [20] and Gaussian process regression (GPR) [21], despite their increasing usage, have not attracted substantial interest in the geotechnical community as The emergence of advanced models inspired by natural systems [22] provides a chance for evaluating more intricately coupled systems, like reinforced soils. Yet, existing literature deals with soil and reinforcement reinforcing inclusions as independent entities, and less focus as a grand integrated system, where the overall behavior of the system is a result of interaction between soil particles and geogrid. In addition, the SC techniques adopted by previous studies yield models that are perceived complex and impractical for field engineers. These models, often considered ‘black boxes,’ offer limited accessibility for practitioners due to their lack of explicit equations for practical implementation.

In the same context, the pursuit of analytical solutions for the bearing capacity of reinforced soils continues to be of interest to researchers. Existing analytical solutions, such as those detailed by Sharma et al. [23], have largely been limited to square footing. Although Chen and Abu-Farsakh [24] addressed this limitation in their work, these analytical solutions are typically based on Terzaghi’s and Meyerhof’s approach with bearing capacity factors and coefficients [24]. Therefore, these analytical solutions fail to integrate the effect of individual and interrelated impacts of soil particle and reinforcement sizes.

In this research, a large database of physical testing of footings with different sizes on reinforced soil was collected from several peer-reviewed studies. The collected dataset encompasses diverse properties of soil, reinforcements, and foundations. The collected dataset was investigated using several SC techniques, namely support vectors machines (SVM), ensemble tree (ET), Gaussian's process regressions (GPR), regression trees (RT) and artificial neural network (ANN). These models were chosen due to their widespread adoption in geotechnical engineering, particularly in examining the behavior of shallow foundations [25]. Beyond traditional SC models, user-friendly nomograph, leveraging results from the top-performing SC model was developed. The upshot is a powerful tool that equips both on-site engineers and researchers to leverage the insights of advanced AI models within seconds, using nothing more than a piece of paper. This simplified nomograph is believed to enable site engineers and researchers to use the developed comprehensive artificial intelligent models within seconds using only a piece of paper. This combination of sophisticated modeling with practical design is a significant leap forward, fostering greater precision, speed, and efficiency in geotechnical engineering.

Data Collection and Preprocessing

For this study, comprehensive dataset was collected from various peer-reviewed articles. These papers explored the ultimate bearing capacities of reinforced dry compacted sands through experimental studies. Specifically, Table 2 summarizes the sources that were incorporated in the dataset.

Table 2 Sources of the dataset collected
Full size table

The collected dataset covered a wide range of laboratory models and sizes. A total of 261 bearing capacity test results were collected and employed in the dataset. For each of experiments, 15 variables were collected and recorded, in addition to the ultimate bearing capacity. Table 3 shows the variables in the collected dataset, with an explanation of each symbol and the units of measurements. Figure 1 shows a schematic of experimental bearing capacity test setup and the 15 variables defined in the collected dataset. The collected variables aimed to cover both physical and mechanical aspects of the geogrid-reinforced soil; the collected physical variables were (B, L, N, Aw, AL, b/B, h/B, D10, D30, D50, D60, and u/B) and mechanical variables were (Dr, ϕ, and T). It should be mentioned that the dataset for reinforced sand beds analysis with under hydrostatic groundwater conditions are scarce in the literature; therefore, tests with dry sands with hygroscopic water content 1–3% were only included. In addition, data used here are limited to experiments conducted on surface footings as data associated with footings placed at an impediment depth is extremely limited.

Table 3 The collected variables and units in the current dataset
Full size table
Fig. 1
figure 1

General schematic diagram for physical testing model

Full size image

While various other variables could have been considered for this investigation, we chose to exclude them. This decision was influenced by the fact that many studies did not report specific results, including those related to soil geochemistry, particle shape, and others.

Several variables were not readily available from the original dataset, and it is believed to improve the predictions of the response [41]. Especially those variables that combine the effects of multiple parameters. For instance, D50 may be considered as an important parameter that may incorporate the effects of other particle size percentages. The particle sizes (D10, D30, D50, and D60) were normalized by reinforcement aperture width, Aw. In addition, the width and spacing of the reinforcement layers and the depth of the first reinforcement layer were normalized by the footing width. Overall, the dataset included 15 variables, as well as the response variable, i.e., bearing capacity.

Statistical Analysis of Collected Dataset

Before using the dataset for SC modeling, a statistical analysis was conducted to determine the statistical indices of analysis input parameters in the collected dataset. Table 4 summarizes the statistical features of the parameters adopted in this study. The mean and standard deviation of the ultimate bearing capacity were 375.64 and 309.18 kPa, respectively. Moreover, a matrix plot between all parameters is shown in Fig. 2, with correlation coefficient values following linear fittings. The matrix shows the highest correlation for the UBC with ϕ and Dr with coefficients of 0.69 and 0.56, respectively.

Table 4 Statistical analysis of collected variables
Full size table
Fig. 2
figure 2

Matrix plot showing distribution and correlation coefficients values assuming linear correlations for all input parameters used in the current study

Full size image

It is worth noting that the footings dimensions covered in this study vary from 50 to 610 mm. This range covers the scale effect between all parameters, as discussed by Ahmad et al. [42] and Mehjardi and Khazaei [43].

Ahmad et al. [42] conducted several experimental tests on geogrid-reinforced soils response to investigate the scale effects. Their results have shown that the scale effect vanishes for footings with a width of more than 600 mm (strip footing). Moreover, Mehjardi and Khazaei [43] studied the scale effect on the behavior of geogrid-reinforced soils under the circular footing. They stated that the scale effect vanishes for footings with diameter more than 120 mm.

Modeling Approaches

SC are computational methods that can “learn” from input datasets to develop predictive abilities. The idea behind SC is finding common similarities between previous dataset input and their consequent output. This is attained by modifying pairs of input and output from the dataset to the model and then tweaking the connection biases and weights of the model to minimize the errors between the model-predicted available outputs (i.e., training). The issue under deliberation in this research requires a supervised regression SC approach (provided output). From various available existing supervised regression techniques, those selected were Gaussian process regression (GPR), support vector machine (SVM), regression trees (RT), ensemble trees (ET), and artificial neural networks (ANN).

Gaussian Process Regression (GPR)

Gaussian process regressions take inspiration from the concept of Gaussian distributions in statistics, which are often observed in natural phenomena. GPR models capture the uncertainty in data by representing it as a distribution over possible functions, allowing for more robust predictions and accounting for natural variations and noise. GPR models are powerful tools used for solving difficult ML problems. Their importance is owed to the fact that they are flexible non-parametric models. Another key advantage of GPR models is their ability to mimic the smoothness and noise parameters from the training dataset [44]. A GPR is a stochastic process in which random variables are assumed to follow a Gaussian distribution. There are four main types of Gaussian processes: squared exponential (SE), exponential (EX), matern (MN), and rational quadratic (RQ). The kernel functions in GPR mainly determine how the response at one input point (\(x\)) is affected by responses at other point (x′), which is also called input distance (x − x′). The difference between these processes is the utilized kernel function (K) as illustrated in Eqs. (1)–(4)

$${K}_{SE}\left(x,x^{\prime}\right)={\sigma }_{f}^{2}\mathrm{ exp}\left(-\frac{{\left|x-x^{\prime}\right|}^{2}}{2{l}^{2}}\right),$$
(1)

where \(x\) and x′ are input vectors that are either in training or testing datasets, parameter \(l\) defines the characteristic length-scale that depends on input distance, and \({\sigma }_{f}^{2}\) is the single standard deviation. Parameter \(l\) briefly defines how far the input values \(x,\) can be for the response values to become uncorrelated.

$${K}_{EX}\left(x,x^{\prime}\right)={\sigma }_{f}^{2}\mathrm{ exp}\left({\left(-\frac{\left|x-x^{\prime}\right|}{l}\right)}^{Q}\right)\, \mathrm{for }\,0<Q\le 2,$$
(2)

\(Q\) s vector parameter ~ \(N(\mathrm{0,1})\), it should be noted here that having γ = 2 turns the EX kernel to squared exponential as shown in Eq. (3).

$${K}_{MN}\left(x,x^{\prime}\right)=\frac{{\sigma }_{f}^{2} }{{2}^{v-1}\Gamma (v)}{\left(\frac{\sqrt{2v}}{l}|(x-x^{\prime})|\right)}^{v}{k}_{v}\left(\frac{\sqrt{2v}}{l}|(x-x^{\prime})|\right),$$
(3)

where \({k}_{v}\) is the Bessel function [45], Γ is the gamma function, and ν is the gamma distribution shape parameter. It is worth noting that Matern 5/2 or 3/2 models are obtained by replacing the ν by 5/2 and 3/2 values, respectively.

$${K}_{RQ}\left(x,x^{\prime}\right)={{\sigma }_{f}^{2} \left(1+\frac{{\left|x-{x}^{\prime}\right|}^{2}}{2\alpha {l}^{2}}\right)}^{-\alpha }\,\mathrm{ for }\,\alpha > 0,$$
(4)

where α is a scale-mixture parameter.

Support Vector Machine (SVM)

The design of support vector machines (SVM) is inspired by the way biological systems separate different classes of data. SVMs aim to find an optimal hyperplane that maximally separates data points from different classes, mimicking the concept of decision boundaries in nature. SVM is a machine learning technique that employs kernel functions to transform data into a high-dimensional feature space. In this space, a linear model is used to accommodate any complex nonlinear relationships [46]. The main idea behind SVM modeling is the computation of a linear regression function in a high-dimensional feature space, where the input data are mapped via a nonlinear function. This technique has been garnering more attention recently and has been used by several researchers. There are several types of SVM, such as linear, quadratic, and cubic. Equation (5) illustrates the mathematical kernel function of these models.

$$k\left(x,y\right)={\left(1+\left(x,y\right)\right)}^{p},$$
(5)

where \(p\) is a parameter that is specified by the user to express weather the kernel is linear, quadratic, or cubic. Furthermore, SVM can be further divided into coarse, medium, and fine Gaussian by setting kernel scale to \(\sqrt{p \times 4}\), \(\sqrt{p}\) and \(\sqrt{p/4}\), respectively, where \(p\) is the number of predictors.

Regression Trees (RT)

Regression trees (RT) mimic the branching structure of natural decision-making processes. Inspired by the hierarchical organization of natural systems, regression trees recursively split data into subsets based on feature values, creating a tree-like structure that represents the decision process and captures complex relationships in the data. RT are a type of empirical tree representation used for segmenting data by applying a sequence of simple rules. Decision-tree modeling involves generating a set of rules that can be used for prediction through the repetitive process of splitting. One of the most common tree methods is the regression decision tree. A major advantage of the decision tree is that the resulting model provides a clear picture of the importance of the significant factors affecting the accuracy of the prediction model. The tree is composed of roots, leaves, and branches [47]. Usually, numeric records are sorted according to the tree, starting from the root at the topmost node. At every internal node, a conditional test is conducted to decide the corresponding path among the tree branches. There are various criteria to judge the conditional testing at each node, for instance summation of square error. The eventual prediction of the tree model is obtained from the leaf at the end of the path. In essence, partitioning the data is done by lessening the deviance from the mean of the output features, which is mathematically summarized in Eq. (6).

$${D}_{\mathrm{total}}=\sum {\left({Y}_{i}-\overline{Y }\right)}^{2},$$
(6)

where \(\overline{Y }\) and \({Y}_{i}\) are the mean of the output and target features. Given that the cut point splits the data into two mutually exclusive subsets, right and left, the deviance reduction (\({\Delta }_{j \mathrm{Total}}\)) is redefined as shown in Eq. (7):

$${\Delta }_{j \mathrm{Total}}={D}_{\mathrm{Total}}-\left({D}_{\mathrm{Right}}-{D}_{\mathrm{Left}}\right),$$
(7)

where \({D}_{\mathrm{Left}}\) and \({D}_{\mathrm{Right}}\) are the deviances of left and subsets, respectively.

Furthermore, various types of regression trees can be obtained by varying required minimum leaf sizes, such as complex, medium, and fine trees. The fine, medium, and coarse tree has a minimum of 4, 12, and 36 leaves, respectively.

Ensemble Trees (ET)

Ensemble trees (ET) draw inspiration from the collective behavior and cooperation seen in natural systems. By combining multiple decision trees into an ensemble, they leverage the wisdom of the crowd to make more accurate predictions. Each tree in the ensemble learns from different subsets of the data, mimicking the diversity and collaboration found in ecosystems. An ET technique is a set of separate weak models (number of learners) that, when combined (number of predictors), provide a reliable mathematical prediction. There are two types of ensemble decision trees: boosted and bagged trees [48]. Bagged trees (parallel) consist of combining different ensembled bootstraps into separated decision trees, all tresses are then combined into one decision tree, where the final decision is computed by averaging the trees results. Boosted trees (sequential), on the other hand, are also an ensemble of regression trees but have a cost function that combines the final models. Ensemble trees use subsets of the original data to produce a series of sequential averagely performing models. Whereafter, the models are improved by combining them using a certain cost function, such as Eq. (8).

$${\widehat{y}}_{\mathrm{bag}}\left(x\right)=\frac{1}{U}\sum_{w=1}^{u}\widehat{Y} w\left(x\right),$$
(8)

where \({\widehat{y}}_{\mathrm{bag}}\) is a target value resulted from average results, \(\widehat{Y}w(x)\) is the detected target value for observation \(x\) in bootstrap sample \(u\), and \(U\) is the number of bootstrap samples.

Artificial Neural Networks (ANN)

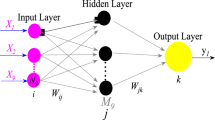
Artificial neural networks draw inspiration from the structure and functionality of biological neural networks in the brain. With interconnected nodes (neurons) organized in layers, ANNs process information and learn from data in a way that resembles the adaptability and parallel processing capabilities of the human brain, enabling them to model complex patterns and make predictions. Numerous numbers of studies in geotechnical engineering have utilized the ANNs for assessing the collected data due to their familiarity and robustness [17]. The basic structure of an ANN models consists of nodes, connection (weights), transfer function, and bias forming the input, hidden and output layers. The ANN model used in this study is a typical ANN with one hidden layer feedforward ANN, linear output neurons, sigmoid activation function and Levenberg–Marquardt backpropagation training algorithm. A total of 10 artificial neural network models were tested in the current study. The neurons were varied from 10 to 50 neurons with 10-step intervals, to come up with the best, least complex model. The equation of single neuron can be written as in Eq. (9).

$$N = f\left(c+\sum_{i=1}^{n}{I}_{i}{W}_{i}\right),$$
(9)

where \(N\) is the neuron numerical value, \(f\) is the activation function, \(c\) is the bias, \(W\) is weight matrix (dimension 1 × n), \(I\) is the input matrix (dimension 1 × n), and \(n\) is the number of variables.

Optimization of SC Models’ Hypermeters

This study aims to investigate the best-performing model to predict the bearing capacity of shallow foundations. To obtain the best-performing hypermeters for each SC technique described earlier, Hyperparameter Optimization option in Machine learning toolbox was utilized. The use of optimized hypermeter will ensure the highest accuracy possible for a certain SC technique.

This option navigates through possible hypermeters using Bayesian optimization with the goal of reducing prediction error [49]. Additional information on the comprehensive and computations for optimization of hypermeters can be found in statistics and machine learning toolbox [49].

Independent Variable Importance

Independent variable importance was executed for best-performing model following Nowruzi and Ghassemi [50] importance method; variables with relative importance of 40% or less were excluded and the best-performed model was retrained. This procedure was designed to produce the highest possible accurate results with the least number of variables, which would significantly reduce the computation time and model complexity.

Results and Discussion

Before the implementation of SC models, the collected dataset was randomly divided into three sets: training, cross-validation, and testing with percentages of 70, 15, and 15%, respectively, with similar dataset ranges. The training set (70%) was used to calibrate the SC models by reducing prediction errors, whereas the cross-validation set (15%) was utilized to avoid overfitting the collected data. The accuracy and performance of the trained SC models were assessed using the testing dataset (15%).

The performance and accuracy measures considered in this study were: (1) coefficients of determination (R2), mean absolute error (MAE) in kPa, and (3) root mean square error (RMSE) in kPa. The SC techniques in this study were accessed using the Machine Learning and Statistics Toolbox in MATLAB R2022a. The accuracy of the used SC techniques is summarized graphically in Fig. 3 and numerically in Table 5 for testing and validation datasets. It should be mentioned that all models had validation results that are close to testing dataset results, as shown in Table 5, which confirms that none of the models has observed overfitting.

Fig. 3
figure 3

Graphical representation of performance measures for all used SC models

Full size image
Table 5 Performance measures of SC models
Full size table

Modeling Results

The optimized hypermeter values for all models are summarized in Table 6, following the optimization methodology using Bayesian optimization in statistics and machine learning toolbox [49]. The accuracies of the models varied depending on models used, complex and medium RT models have shown the highest R2 (0.99), while fine RT model had the lowest R2 value of 0.73. The complex RT model had the lowest RMSE and MAE of 168.42 and 98.8 kPa, respectively, among RT modeling techniques. Furthermore, fine, coarse, and quadratic SVM models had relatively low R2 results as shown in Table 5 and Fig. 3, while linear and medium Gaussian SVM models had R2 of 0.98 and 0.96, respectively. Regarding ET modeling, Boosted ET model had better performance compared to bagged ET with R2, MAE and RMSE values of 0.99, 107.69, and 184.68 kPa, respectively.

Table 6 Optimized hypermeter values for each trained model
Full size table

The RMSE and MAE value differences for GPR models were not significant. RMSE values of all GPR models ranged between 119.26 and 132.59 kPa for Matern 5/2 and Exponential GPR, respectively. Finally, ANN detailed optimization results are summarized in Fig. 3 for the 10 ANN models used in the current study. Initially, all 14 variables were considered as inputs for the ANN models. ANN modeling began with 10 neurons and increased up to 50 neurons by 10 neurons each step, resulting in five ANN models shown in Fig. 3 as dashed lines. The highest R2 and lowest RMSE were achieved with the more complex neural network model (50 neurons), with values of 0.989 and 45.71 kPa, respectively, which reveal that ANN model at 50 neurons has the best performance with lowest RMSE and MAE and highest R2.

Best Performing Model

The results in Table 5 for testing and validation of SC techniques reveal that ANN outperformed all other SC techniques with R2, MAE, and RMSE values of 0.99, 27.36, and 45.71 kPa, respectively. The performance of SC techniques is dependent on several concepts including the dataset itself. For the methodology and datasets used in this study, ANN outperformed other SC technique, which in line with previous studies [51,52,53] (Fig. 4).

Fig. 4
figure 4

RMSE and R-squared of the ANN model with and without low importance variables

Full size image

Normalized Variables Importance

Normalized variable importance was calculated for the best-performing SC technique (i.e., ANN model). Results of variable importance are summarized in Fig. 5. It was shown that the highest normalized variable importance scores were for D50/Aw, friction angle (ϕ), depth to footing ratio (u/B), and relative density (Dr), all of which related to soil properties and referred internally to the interaction of the soil-geogrid matrix. This observation suggests that practitioners should prioritize the soil gradation (D50) and geogrid aperture size (Aw) when compared to enhancing soil properties such as ϕ and Dr. ϕ and Dr are considered important parameters as well relative to other parameters. The particle size has the highest effect on bearing capacity of reinforced sands, as the geogrid efficiency depends mainly on its applicability of confining the soil particles within geogrid cells. After assuring the occurring of soil confinement, soil friction angle is then to be considered. It would then be pointless and gratuitous to have soil with a high friction angle or density without proper confinement. Thus, this logical flow of soil-geogrid matrix behavior sounds logical from the flow of obtained importance results.

Fig. 5
figure 5

Variable importance of best-performed ANN model

Full size image

On the other hand, the least variable importance was observed for footing length (L), number of reinforcement layers (N) and the normalized width of reinforcement layers (b/B). This refers to the fact that those variables were interrelated in the neural network model by other parameters. For example, the number of layers were impeded in spacing between geogrid layers (h/B) if more than one layer exists.

To investigate the least important parameters impact on predicting the ultimate bearing capacities of reinforced soil, all variables with relative importance of 40% or less were eliminated (from length of footing L to (D60/Aw)). Then, the preceding ANN procedure was repeated using only the remaining important parameters (from normalized depth of first layer (u/B) to D50/Aw), resulting in five new artificial neural network models. Figure 4 summarizes the results of the five new ANN models excluding the least important variables.

Overall, no significant changes in performance measures were spotted in ANN models without the least important parameters. The results obtained at 10 neurons without least important had an R2 and RMSE values of 0.969 and 76.3 kPa, respectively, compared to 0.975 and 72.03 kPa in the model including all variables. However, the new ANN model excluding the least important variable had very low improvement with an increasing number of neurons. However, sacrificing minor values of accuracy may be more practical to reduce the model complexity by using a smaller number of input variables.

Developing the ‘Neuro-nomograph’

Among all SC techniques, the ANN models have shown the lowest RSME and MAE. Researchers and geotechnical engineers require simpler and practical tools for obtaining accurate results from the trained SC models rather than computations that requires specialized computational software such as MATLAB or SPSS, which may not always be available. Thus, some researchers demonstrated simplified computational methods to obtain the response of given dataset using the artificial neural network model developed. For example, Soleimanbeigi and Hataf [5] explained how to utilize the weights from their ANN model to obtain the settlement results of reinforced sand from given inputs. An additional example is found in Shahin et al. [54], where the authors developed a two-neurons ANN-based equation for predicting sand elastic settlement. To make this method practical for engineers and researchers, the authors reduced the number of neurons to obtain a simpler ANN that can be modeled using an equation.

In this article, a relatively more user-friendly graphical method was adopted known as the nomograph. Nomographs, which were first used in 1795 by the French government, introduced a powerful tool for performing simple and complex calculations in a variety of applications with a relatively low time and effort [55]. The nomograph (also known as nomogram) is a diagram that mimics a numerical formula, where each variable is represented by a graduated line, and the solution can be obtained by connecting the required variables’ values by straight lines ending with the solution value. The numerical formula is mimicked by changing the graduated lines (variables) scales, orientation, and distances from each other [56].

As a result, applications of nomographs are considered useful in several fields: compaction properties of soils [57], earth dams safety factors [58], bearing capacity and elastic settlement [59], probabilistic seismic hazard [60], hazard distances from a blast wave [61], punching shear capacity of slabs [62], tunnels’ safety factors in cohesive soils [63], and many others.

Previous researchers have developed nomographs derived from regression equations between variables. In this research, the trained model weights of the best-performed ANN model were used to develop the nomographic diagram. This approach is rarely used in literature, which gives a remarkable add-on value to the trained ANN model. The Python 3.9 language and PyNomo library were used to develop an adapted neuro-nomograph shown in Fig. 6. PyNomo is a nomograph-generating program based on the Python text developed by Glasser and Doerfler [64]. Additional information on the origins and development of PyNomo programming code can be found in [64].

Fig. 6
figure 6

Neuro-nomograph for predicting bearing capacity of reinforced soil

Full size image

To obtain a precise graphical solution for a traditional regression formula, PyNomo software calibrates the variable scales, distances, and orientations to mimic the regression equation. On the other hand, in this research, the traditional formula was substituted with the ANN formula that was exported from Machine Learning Toolbox in MATLAB. The exported formula from MATLAB can be summarized using Eq. (10):

$${\mathrm{BC}}_{\mathrm{Pred}}={[w}_{\mathrm{I}}]*\left(\left(\frac{2}{1 +\mathrm{exp}\left(-2\left(\left[{w}_{\mathrm{H}}\right]*\left[I\right]+\left[b\right]\right)\right)}\right)- 1\right) + k,$$
(10)

where \({w}_{\mathrm{I}}\) is the weights matrix for input layer; \({w}_{\mathrm{H}}\) is the weights matrix for hidden layer; \(I\) is the input matrix; b is the matrix of biases and \(k\) is a single-value bias value. \({w}_{\mathrm{I}}\), \({w}_{\mathrm{H}}\), b, and \(k\) are constants that were obtained from Machine Learning Toolbox in MATLAB after ANN model training.

The adopted nomograph (Fig. 6) can be utilized to predict the ANN-ultimate bearing capacity of reinforced sands. Parameters used in developing the adapted neuro-nomograph were the most important in terms of soil (friction angle), geogrid (tensile strength), and the interrelated parameters between both of them (depth and width of the geosynthetic, in addition to D50/Aw). An example shown as a dashed line with procedure explained is found in Fig. 7.

Fig. 7
figure 7

Example of how to use the neuro-nomograph for reinforced soil bearing capacity prediction

Full size image

Neuro-nomograph Validation

The easiness of neuro-nomograph found in this study is attractive. Yet, it must be ensured that these graphs can yield accurate predictions. Therefore, 20 random ultimate bearing capacity results that were not used in the training of ANN model (testing dataset) are used to check the accurateness of the neuro-nomographs. Figure 8 shows measured UBC values versus predicted UBC values using the neuro-nomograph. The close proximity of the points to the 1:1-line attests to the model validity. Furthermore, the predicted values are positioned within a ± 0.5 standard deviation and confidence intervals of ± 5% of measured values and with an R2 of 0.98. Such results agree with the previously obtained ANN model for the most significant parameters using MATLAB (Fig. 5). Additionally, the ratio of measured ultimate bearing capacity to those predicted from the developed neuro-nomograph (UBCtest/UBCpred) have shown variation coefficient (COV) of 0.13 and mean of 1.11, respectively, verifying the validity of the adapted neuro-nomograph.

Fig. 8
figure 8

Validation of adapted neuro-nomograph using 20 random test results

Full size image

Practical Applications

The developed ‘neuro nomograph’ is believed to be a helpful design aid tool for practitioners in designing reinforced shallow foundations as quick estimations harnessing the power of SC models. Moreover, the outcomes of this study suggest that although ϕ and Dr are considered important parameters for reinforced foundation design, designers and practitioners should prioritize the soil gradation (D50) and geogrid aperture size (Aw) when compared to enhancing mechanical soil properties.

Limitations of Models and Nomographs

The nomographs and models obtained are governed by the collected dataset used. Results of this study are not expected to have accurate estimations of bearing capacities when extrapolated to values above the maximum or below the minimum values for the different input parameters used in the current study shown in Table 4.

Conclusions

Ultimate bearing capacity (UBC) of reinforced sands is one of the key parameters in designing geotechnical engineering structures. In this article, several soft computing (SC) approaches were applied to estimate the bearing capacity of reinforced dry sands using results from a total of 261 tests collected from the literature. The following conclusions can be drawn:

  1. 1.

    Artificial neural network (ANN) outperformed all SC techniques, including regression trees, ensembled trees, support vector machine, gaussian process regression, in terms of accuracy measures such as R2, MAE, and RMSE. ANN achieved an R2 value of 0.99, MAE of 27.36 kPa, and RMSE of 45.71 kPa, indicating its superior performance in predicting the ultimate bearing capacities of reinforced soil.

  2. 2.

    The performance of the SC techniques varied depending on the specific models used. Complex and medium regression trees models showed the highest R2 value of 0.99, while fine regression trees model had the lowest R2 value of 0.73. Boosted ensembled trees model performed better than bagged ensembled trees model for RT modeling techniques. Linear and medium Gaussian SVM) models had relatively high R2 values of 0.98 and 0.96, respectively, while quadratic SVM models had lower R2 results.

  3. 3.

    GPR models showed relatively low differences in RMSE values, ranging between 119.26 and 132.59 kPa for different GPR models. ANN models achieved the lowest RMSE of 45.71 kPa, indicating its superior predictive performance compared to GPR models.

  4. 4.

    The variable importance analysis revealed that the most significant variables for predicting the ultimate bearing capacities of reinforced soil were D50/Aw (soil gradation and geogrid aperture size), friction angle (ϕ), depth to footing ratio (u/B), and relative density (Dr). These variables were related to soil properties and the interaction of the soil-geogrid matrix. Footing length (L), number of reinforcement layers (N), and normalized width of reinforcement layers (b/B) were found to be least important among input parameters used in the neural network model.

  5. 5.

    A neuro-nomograph, a graphical tool based on the trained ANN model, was developed to provide a simplified and practical method for obtaining accurate results without the need for specialized computational software. The neuro-nomograph showed good accuracy in predicting the ultimate bearing capacities of reinforced sands, with predicted values positioned within a ± 0.5 standard deviation and confidence intervals of ± 5% of measured values.

The “neuro-nomograph” is a useful design aid tool for practitioners in designing reinforced shallow foundations, providing quick estimations harnessing advanced computation models. The study emphasizes prioritizing soil gradation and geogrid aperture size over mechanical soil properties in reinforced foundation design.