Laboratory experiments can pre-design to address power and selection issues

Abstract

In this paper, motivated by aspects of preregistration plans we discuss issues that we believe have important implications for how experiments are designed. To make possible valid inferences about the effects of a treatment in question, we first illustrate how economic theories can help allocate subjects across treatments in a manner that boosts statistical power. Using data from two laboratory experiments where subject behavior deviated sharply from theory, we show that the ex-post subject allocation to maximize statistical power is closer to these ex-ante calculations relative to traditional designs that balances the number of subjects across treatments. Finally, we call for increased attention to (i) the appropriate levels of the type I and type II errors for power calculations, and (ii) how experimenters consider balance in part by properly handling over-subscription to sessions.

1 Introduction

To help improve research transparency a number of initiatives including pre-analysis plans, hypothesis registries, and replications have recently sprung into operation across multiple disciplines including political science, neuroscience and economics. These initiatives have been announced by specific academic journals, professional associations and funding agencies to deal with concerns ranging from specification search and failure to replicate.¹ Coffman and Niederle (2015) recently summarize the pros and cons of these initiatives and claims that the benefits of preanalysis plans are likely limited for experimental economists, since there is a strong opportunity for replication by recruiting new subjects.² Our paper will make a case that the reverse is true even for lab experimenters by showing the statistical benefits from aspects involved in pre-designing the study. After all, a central component of a pre-specified analysis plan is that it can allow researchers to take advantage of all the statistical power of well-designed statistical tests and to reduce concerns related to robustness to specifications.

To make this case we consider laboratory experiments that adopt a between subject design to inform on economic theories.³ The general design of such an experiment is to create a controlled environment in the lab where a single specific theoretical parameter varies between sessions, thereby providing a direct test of some comparative static prediction(s) of a theory.⁴ Similar to randomized controlled experiments in medicine and other fields within economics, using a between-session design is intuitive and easy to explain. Researchers generally focus their interpretation of findings from their experiments through the lens of the outcome of hypothesis tests that compare subject behavior between treatments.

In this paper, we show that thoughtful design of a laboratory experiment may present a host of potential benefits to lab experimenters by improving the overall experimental design prior to its implementation. These benefits are not related to concerns such as “p-hacking” or specification searching, which could be handled by carrying out additional sessions, nor motivated by multiple testing issues.⁵

This paper complements List et al. (2011) and Czibor et al. (2019), who each provide concrete guidance on how to improve lab studies. We extend their guidance in three distinct ways. First, we show how ex-ante statistical power calculations can utilize economic theories to inform on optimal research designs. Second, we discuss the challenge presented by oversubscription of subjects into a session, an issue that has received little attention in the experimental literature. This final contribution extends Slonim et al. (2013) by making an additional recommendation on how to reduce potential sources of selection bias that could arise during the implementation of the experiment itself.

The rest of the paper is organized as follows. In the next section, we review how statistical power is calculated and discuss how lab experimenters interested in testing economic theories can use knowledge of these models to help their experimental design. We illustrate this approach with data from two experimental studies in which subject behavior deviated greatly from the quantitative predictions of the underlying theory. We find that the ex-post subject allocation to maximize statistical power is closer to these proposed by ex-ante calculations based on the underlying economic theories as compared to traditional designs that simply balance the number of subjects across treatments.⁶ Section 3 examines how pre-analysis plans can further help determine how many sessions to undertake, in which sessions specific treatments should be carried out, and why having a plan to handle over-subscription of subjects to an individual session can be valuable. The final section concludes and suggests a direction for future research.

2 Power analysis for laboratory experiments

2.1 Setting the stage

For expository purposes, we consider a laboratory experiment that compares subject’s decision-making across two conditions. We define treatment status for subject i in session s, by an indicator variable $D_{is},$ where $D_{is}=1$ denotes random assignment to treatment 1 and $D_{is}=0$ reflects the status-quo condition (or control). To estimate the effect of the treatment on a continuous outcome $y_{ist}$ measured for subject i at experimental period t in session s, researchers estimate either

$$\begin{aligned} y_{ist}=\gamma _{0}+\gamma _{1}D_{is}+e_{1ist} \end{aligned}$$

(1)

or

$$\begin{aligned} y_{ist}=\beta _{0}+\beta _{1}D_{is}+\beta _{2}X_{ist}+e_{2ist}, \end{aligned}$$

(2)

where covariates $X_{ist}$ are included in Eq. (2). These covariates may include demographic information as well as those variables suggested by theory. Both $e_{1ist}$ and $e_{2ist}$ are random error terms. Since $D_{is}$ is randomly assigned, the inclusion of $X_{ist}$ should not affect the expected value of an OLS estimator of the coefficient on treatment between Eqs. (1) and (2), that is $E[ \widehat{\gamma }_{1}]=E[\widehat{\beta }_{1}],$ but can influence the size of the standard error on $\widehat{\beta }_{1}$ by reducing the variance of the residual.⁷

Often guided by an underlying theoretical model, experimenters want to test the effect of the treatment $D_{is}$ on a subject outcome of interest. This involves testing some hypothesis about our parameter of interest $\gamma _{1}$ in Eq. (1), or $\beta _{1}$ in Eq. (2). The probability of a Type I error is the probability of rejecting the null hypothesis when it is correct and the probability of a Type II error is the probability of failing to reject the null hypothesis when it is false.

Power analysis is used to optimize hypothesis tests and experimental designs. Since asymptotic normal approximations are valid for tests on $\widehat{\gamma }_{1}$ in a wide variety of applications, we will focus our discussion on the Wald test. The Wald test uses the test statistic $\frac{ \widehat{\theta }-\theta _{o}}{\widehat{SE}},$ where $\widehat{\theta }$ and $\widehat{SE}$ are the sample estimated statistic and standard error while $\theta _{o}$ is the parameter value under the Null hypothesis. For example, in the commonly used test of statistical significance $\theta _{o}=0$ and statistical software would report a t-statistic for Eq. (1) of $\frac{\widehat{\gamma _{1}}\text { }-\text { }0}{\sigma _{ \widehat{\gamma _{1}}}}.$

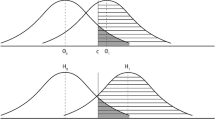
The power of a statistical test is the probability that the test correctly rejects the null hypothesis and is equal to 1-Pr[type II error]. Holding all other factors constant, the most powerful test is always preferred. The power of the test depends on (i) sample size through the estimated standard error, (ii) probability of a Type I error, and (iii) the effect size $\widehat{ \gamma }_{1}$. To show how these variables are related under simple random sampling we present a series of visualizations in Fig. 1.⁸ The first panel illustrates the distribution of our estimator $\widehat{\gamma }_{1}$ under the Null hypothesis ($\gamma _{1}=0$ ) for a two sided test which defines the rejection region as the shaded area that captures the probability of making a Type 1 error. We refer to this as the Null distribution and the standard deviation of the distribution is given by the estimated standard error $\sigma _{\widehat{\gamma }_{1}}$. The conventional experimental design first fixes the probability of a Type I error at 5%. The effect size presented in the second panel is assumed to be 2.5 standard deviations away from the Null value. The third panel presents the alternative distribution, which is distributed Normal with the mean taking the value of the effect size and the standard deviation identical to that of the Null distribution $\sigma _{\widehat{\gamma }_{1}}$. Prior to conducting a study, the researcher is unaware of the effect size and can be faced with a difficult choice on choosing a value. However, for many laboratory experiments one could use a prediction from a comparative static exercise of the underlying theory to make a meaningful and plausible choice for the effect size.

Fig. 1

Illustrating how statistical power is calculated for a two-sided test of statistical significance. The panels in this illustrate how statistical power is calculated for a test of the Null of no difference at the 5% level when the effect is 2.5σ away from the Null value. The rejection region of the test is shown in panel 1, panel 2 shows the effect lands in the rejection region and panel 3 illustrates that the alternative distribution is centered at the effect size. The final panel shows that statistical power is the probability the Null is rejected at the 5% when the effect is 2.5σ away from the Null value

The fourth panel shows how to calculate statistical power, the chance a researcher will be able to detect an effect of the size introduced in the second panel, if there really is one. We place a vertical line at the “significance” cutoff of 1.96 from the Null distribution. The unshaded area under the alternative distribution to the left of this line provide us with the probability that we would fail to reject the null if we had an effect of 2.5. The shaded area under the alternative distribution to the right of the line is our statistical power; thus the greater the shaded area, the greater the statistical power. Lastly, sample size plays a role since it affects the size of the estimated standard error and hence variation in both the Null and alternative distributions. Larger samples often increase statistical power.

To undertake power analysis for a research project involving testing a hypothesis about the parameter, $\gamma _{1}$, first requires determining what a “Minimal Detectable Effect” is. The minimal detectable effect $(\gamma _{1}^{\rm{MDE}})$ is the smallest possible value for $\widehat{\gamma _{1}}$ at which the Null hypothesis is rejected for a given significance level. For example, undertaking a two-sided test at a significance level of $\alpha =0.05,$ if a researcher wishes to achieve power at the level of $\kappa =0.8,$ where the effect estimator has a limiting normal distribution,⁹ then $\gamma _{1}^{\rm{MDE}}=(t_{\alpha /2}+$ $t_{(1-\kappa )})\sigma _{\widehat{\gamma _{1}}}$. For a large sample size,¹⁰ plugging in $t_{(1-\kappa )}$ and $t_{\alpha /2}$ as obtained from a standard t-distribution yields $\gamma _{1}^{\rm{MDE}}=(1.96+0.84)\sigma _{\widehat{\gamma _{1}}}=2.8\sigma _{\widehat{ \gamma _{1}}}$.¹¹ Once a minimal detectable effect is chosen, researchers can rearrange the expressions above to solve for an expression for $\sigma _{\widehat{\gamma _{1}}}$ and achieve such an effect at a specified type 1 error and power level. The expression of $\sigma _{\widehat{\gamma _{1}}}$ depends on two design parameters that the researcher can adjust: sample size and optimal treatment allocation as we demonstrate shortly. Finally, since adding explanatory variables to an estimating equation tends to decrease the residual standard deviation, the required sample size for any specified level of precision or power is thus reduced if estimating Eq. (2) in place of Eq. (1); only if their coefficients are truly non-zero.

2.2 The appropriate choice of $\alpha$ and $\kappa$ may depend on the audience for the study

In the above example, the values for $\alpha =0.05$ and $\kappa =0.8$ were chosen since they reflect the standards commonly used in other branches of social science research. Whether these values should also be the benchmark for studies in experimental economic settings may depend on the goal of the laboratory study. A possible rationale for this default setting that allows for low occurrence of Type 1 error at 5%, but tolerates much greater chance of Type II error at 20%, is to ensure that any discovered new treatment is really effective. After all, switching from the status quo to the new treatment may be costly in many policy areas such as education, health care or social policies. Thus, this design is biased against the new treatment by setting a narrow margin for it to pass, but a much wider margin of falsely concluding that it fails when it did not.

Since one of the primary motivations for undertaking experimental research is to inform theory, not policy with a status quo bias, the rationale for selection of these conventional error probabilities no longer applies.¹² There is no apparent reason to tolerate a substantially greater probability of Type II error than Type I error in a laboratory setting. Further, many economic researchers themselves would not anticipate that a model would hold exactly and would likely be willing to accept a lower probability of a Type I error.¹³ We next show how the economic theory being tested can inform research design through the estimated standard error in the laboratory.

2.3 Economic theories are quite useful in power calculations

Recall, the between subject design introduced earlier in lab, our sample of subjects, indexed by $i=1,...,n$ to a session that offered either the $D=1$ or $D=0$ protocol. For $p=Pr[D=1]$ such that $1<pn<n-1$, we randomly select pn individuals to receive $D=1$ and the remaining $(1-p)n$ subjects to receive $D=0$. Without control variables, the experimental treatment effect for some outcome Y is calculated as $\widehat{\gamma _{1}}=\frac{1}{pn} \underset{i\in D=1}{\sum }Y_{i}-\frac{1}{(1-p)n}\underset{i\in D=0}{\sum } Y_{i}.$ It is well known that when D is binary, $Var(\widehat{\gamma _{1}})= \frac{1}{n}(\frac{s_{1}^{2}}{p}+\frac{s_{0}^{2}}{(1-p)}),$ where $s_{1}^{2}$ and $s_{0}^{2}$ are sample variances of the outcomes in the $D=1$ and $D=0$ groups respectively. Plugging this expression into the minimal detectable effect equation $\gamma _{1}^{\rm{MDE}}=(t_{\alpha /2}+$ $t_{(1-\kappa )})\sigma _{\widehat{\gamma _{1}}},$ permits the calculation of the minimum required sample size

$$\begin{aligned} n^{*}=\frac{(t_{\alpha /2}+t_{(1-\kappa )})^{2}(\frac{s_{1}^{2}}{p}+ \frac{s_{0}^{2}}{(1-p)})}{(\gamma _{1}^{\rm{MDE}})^{2}}. \end{aligned}$$

(3)

If the sample variances are identical between the groups ($s_{1}^{2}=s_{0}^{2}$) we can express, $\sigma _{\widehat{\gamma _{1}}}=\sqrt{ \frac{\sigma ^{2}}{p*(1-p)*n}},$ where $\sigma ^{2}$ is the variance of the residual from Eq. (1). Holding $\sigma ^{2}$ and n constant, $\sigma _{\widehat{\gamma _{1}}}$ is minimized when $p=0.5,$ which is when the number of subjects is balanced between the treatment and control groups. Thus, a design that equally splits the sample to $D=1$ and $D=0$ ceteris paribus, maximizes statistical power since one could detect a smaller $\gamma _{1}$ for a given level of power $(\kappa )$ and significance level $(\alpha )$. The variability in the Null and alternative distribution is represented by the standard error that is minimized when $p=0.5,$ and this may explain why the tradition in experimental economics is to assign 50% of subjects to $D=1$ and the remainder to $D=0$.

The above calculations ignore the fact that financial cost varies between the two treatments. Cochran (1977) (and subsequently Duflo et al. 2007) shows that if the cost per subject vary across treatments, researchers can optimally choose p to minimize the minimal detectable effect (and hence maximize statistical power) subject to their budget constraint. Solving the Lagrangean indicates that the optimal allocation of subjects between the treatment and control arms is given by the ratio $\frac{p}{1-p}=\sqrt{\frac{ c_{D=0}}{c_{D=1}},}$ where $c_{D=0}$ and $c_{D=1}$ is respectively the unit cost per comparison and treated subject. In other word, the optimal allocation ratio is inversely related to the square root of the relative total costs of each treatment.¹⁴

In many field experiments, the experimenter is ex-ante fully aware of the per subject costs of the different treatments. In lab experiments, the per subject treatment cost depends in large part on the decisions made by the subjects themselves as well as others within the session. However, ex-ante, experimenters set participation fees and often calculate expected earnings in the lab based on the underlying theory. Yet, this information is not used to determine the design of the study and generally an equal number of each treatment is carried out. In the next section, we illustrate how the optimal subject allocation could be calculated using in part these predictions on expected earnings from economic theory in two experimental studies.

2.4 Illustration of statistical power calculation in two experimental studies

We consider two examples: the first price affiliated private value auction of Ham et al. (2005) and the legislative bargaining experiment of Fréchette et al. (2003). In both studies, the subject first received a participation fee of $5. Otherwise individual compensation differed sharply as one involved subject payment based on cumulative earnings throughout the session, while the other study randomly selected a few periods to determine subject payment.

Ham et al. (2005) conducted sessions with 4-bidders ($D=1)$ and sessions with 6-bidders $(D=0)$ that involved 30 periods. The subjects were paid the total earnings from the auction including a $7 starting balance as well as earnings from a per-period lottery. The lottery generates an expected earnings of 25 cents per period. Subjects in the 4 bidder sessions are more likely to win more auctions than subjects in the 6 bidder sessions. Moreover, under the symmetric risk-neutral Nash equilibrium bid function (SRNNE), the expected profit to the highest bidder is greater in the 4-bidder sessions relative to the 6-bidder sessions.¹⁵ The ratio of expected costs across treatments per subject is given by

$$\begin{aligned} \frac{c_{D=1}}{c_{D=0}}=\frac{4\text {-bidder}}{6\text {-bidder}}=\frac{ \$5+(30*\$.25)+(\$7+(\frac{1}{4}*30*\$6))}{\$5+(30*\$.25)+(\$7+(\frac{1}{6}*30*\$4))}= 1.\, 632\,9 \end{aligned}$$

(4)

Ex ante, the optimal design to maximize statistical power where expected costs are calculated using economic theory is to set $\frac{p}{1-p}=\sqrt{ \frac{1}{1+1.6329}}=$ 0.616. In other words, there should be in total 1.63 more subjects in 6-bidder sessions $(D=0)$ relative to 4-bidder sessions $(D=1)$ to detect the smallest treatment effect for a given budget. In Ham et al. (2005), there were a total of 96 subjects. The research interest in Ham et al. (2005) was to estimate the effect of cash balances on bidding behavior. However, if the research interest was in detecting the effect of number of bidders on outcomes and budget constraints are binding, they could have allocated 36 subjects to 4-bidder sessions and 60 subjects to 6-bidder sessions to maximize statistical power.

Similarly, (Fréchette et al. 2003) provide a test of the Baron and Ferejohn (1989) legislative bargaining model on the effect of a closed amendment rule $(D=1)$ versus an open amendment rule $(D=0)$. Subjects took part in sessions in which 15 elections were conducted, at the end of the session 4 elections were randomly selected for payment. Under the parameters selected by Fréchette et al. (2003) any undivided pie would shrink by 20% in the next round of voting. The underlying theory predicts that $5 expected earnings in each election in the $D=1$ sessions and $\$4.1667$ in the $D=0$ sessions.¹⁶ The ratio of expected costs across treatments per subject is given by

$$\begin{aligned} \frac{c_{D=1}}{c_{D=0}}=\frac{Closed Rule}{Open Rule}=\frac{\$5+(4*\$5)}{\$5+(4*\$4.1667)}= 1.\, 1538. \end{aligned}$$

(5)

Using these expected earnings from theory in conjunction with the ratio that chooses the optimal p to maximize statistical power, one would assign subjects to closed versus open rule treatment by setting $\frac{p}{1-p}= \sqrt{\frac{1}{1+1.1538}}=0.681\,.$ This is an approximate 3:2 ratio for $D=0$ relative to $D=1.$ That is, to maximize statistical power if we were to recruit 50 subjects, 20 subjects should be assigned to a closed rule session and the remaining 30 subjects should be assigned to an open rule session.

Note, it is common in experiments to observe important quantitative differences between data and the tested theories. For example, in Fréchette et al. (2003) delays were less frequent than theory predicts under the open rule treatment. Similarly, bidders were more aggressive than theory predicts in Ham et al. (2005). If we were to recalculate the optimal ratio based on ex-post experimental earnings, we find in Ham et al. (2005), $\frac{ p}{1-p}=\sqrt{\frac{1}{1+1.359}}=0.651\,$ (compared to 0.616 calculation from theory) and in Fréchette et al. (2003) $\frac{p}{1-p}= \sqrt{\frac{1}{1+1.056}}=0.697$ (compared to 0.681 by theoretical prediction). In both cases, we observe that the ratio of subjects across treatment arms remain unbalanced ($\ne$ 0.5) and the ex-post ratios both exceed and deviate less from the ex-ante design ratio informed by theory than a even split.

2.5 Power for testing qualitative outcomes

In many experiments, the outcome of interest might be a limited dependent variable. For example, in many bargaining experiments, there is interest in whether a delay in reaching an agreement occurred. For such an outcome, a logit regression model could be deployed to estimate Eqs. (1) and (2), in place of the OLS estimator. Since the logit estimator is nonlinear and involves maximizing a likelihood function, formulas to compute statistical power depend on whether a Wald test, a likelihood ratio test, or score test is used to determine statistical significance.¹⁷ For space considerations here we do not repeat the previous exercise calculating minimum sample size required as well as optimal allocation of subjects into treatment and control. The interested reader can examine Bush (2015)’s Monte Carlo study, which concludes that Shieh’s (2000) likelihood ratio test most accurately and consistently achieves the desired level of statistical power.

3 Preanalysis plans can further inform the design of sessions

3.1 Allocating subjects to sessions and possible selection bias

The statistical power calculations presented in the preceding section are used to solve for minimum sample size in total and optimal subject allocation across treatment arms. In this section, we outline how lab experiments could use a pre-analysis plan that contains details on how the experiment is implemented to anticipate potential selection bias issues and remedies. Currently, the implementation of laboratory experiments are often sequential. Lab experimenters frequently send a mass e-mail to their subject pool enlisting sign up and participation in sessions held at specific days or time slots. However, participants in an experimental session on a particular day at a specific time slot can differ based on many factors including those related to course selection, and subjects rarely are allowed to participate in the same experiment twice. Further, the experimenter also could decide immediately prior to the start of the session whether to offer $D=1$ or $D=0$, and this decision could potentially be based on which type of subjects have shown up in the session.

Coffman and Niederle (2015) consider sequentiality an advantage since it provides an opportunity to examine the replicability of any finding. We suggest that a form of experimenter session and subject selection bias could arise, if following the arrival of subjects to the lab, the experimenter has the discretion on which treatment to offer in that particular session,¹⁸ and as discussed in the next subsection who can participate if the session is oversubscribed. If lab experiments are implemented in the manner described above, there is no inherent guarantee that unobserved characteristics of potential on-site participants across treatment arms are balanced.

How subjects are allocated across treatment arms in laboratory experiments contrasts sharply with how it is done in many field experiments in applied economics. In those studies, participating subjects are randomized whether to receive the intervention only after signing up to participate in the study. Randomization is conducted at that point of time in a bid to ensure observed and unobserved characteristics of the participants are balanced across treatment arms.

Lab experiments could use a pre-analysis plan to randomize treatments into specific sessions. This could minimize the threat of selection bias from the experimenter’s side by reducing their discretion on what treatment to offer in which session. Further improvement can arise from using block randomization that randomizes sessions within blocks defined by day and time to carry out the session.¹⁹

Alternatively, a lab experimenter could pre-commit to randomize their subject pool into two groups at the beginning of their study. Only members of one group would receive invitations to the $D=1$ sessions, and the people assigned to the other group would only be eligible to receive invitations to participate in $D=0$ sessions. This would balance the characteristics of potential subjects prior to signing up to participate in the study.²⁰ Unfortunately, if there are different rates of attendance across sessions, there is no guarantee that one will have random assignment among those that show up (see e. g.  Ham and LaLonde 1996).

These two alternatives of allocating subjects to sessions differ from the status quo method by using randomization to remove an experimenter’s discretion on which treatment to carry out in a specific session, increasing the chance that both observed and unobserved covariates are balanced across treatment arms. With the experimenter selection biases minimized, the bias from the subjects’ self-selective participation remains. Preanalysis plans could ensure appropriate data is collected from either the subject pool or the participating subjects themselves, to both undertake statistical tests of subject selection based on when a session was carried out (e.g. afternoon sessions may disproportionately attract lazier subjects) as well as consider any necessary statistical adjustments to overcome bias arising from the subject’s participation decision.²¹ This bias would threaten the validity of the estimated treatment effect if there is a lack of balance in the observed and unobserved characteristics of participating subjects in the treatment and control arms.

3.2 Oversubscribed sessions

In practice, it is common to recruit more subjects than needed for each individual session since some subjects that have subscribed fail to show up in person. When a laboratory session is oversubscribed researchers would either offer a financial incentive for some volunteers to leave the study, or use a first-come first-served protocol asking the later arrivals to accept a participation fee and exit the experiment.²²

These usual strategies to handle oversubscription generate selection bias; they also differ from how field experimenters handle this challenge. In the field if a study is oversubscribed, a lottery is often carried out to determine who will receive a treatment.²³ If oversubscription is handled via a voluntary departure induced by a financial incentive, subjects could very well self-select into or out of a study. If first come first served and the late arrivals are students from a class that ended late, the characteristics of the stayers may no longer look like the exiters. Moreover, if the rates of oversubscription differ across the treatments (and sessions), it may no longer be the case that the unobserved characteristics of subjects are balanced across sessions (and treatments). A lottery would give all subjects in an oversubscribed session an equal chance of participating further and can solve this selection problem unless those who show up constitute a random sample.

4 Conclusion

This paper raises three issues that, to the best of our knowledge, have not been discussed in the experimental economics literature. First, what is the appropriate level of the type I and type II errors that a researcher should choose to provide evidence that best informs their intended audience? Second, how many subjects should be allocated to each treatment arm in a study? Third, how should researchers determine which subjects stay in the laboratory when a session is oversubscribed. We suggest that a simple lottery be carried out.

We further argue that there are indeed other benefits from formulating a pre-analysis plan to design the experiment and determine the minimum required sample size, how subjects should be allocated to the control and treatment sessions. We strongly suggest researchers consider utilizing economic theory to predict the relative cost across the treatment arms when trying to maximize statistical power. We illustrate these strategies and show with data from two laboratory experiments where subject behavior deviated sharply from theory that the use of even split designs as the default design often leads to less statistical power. Finally, we encourage experimenters to adopt new sampling schemes that assign subjects to sessions. These schemes would increase the likelihood that subject characteristics are balanced across the treatment and control arms.