Abstract
A W-algebra action is constructed via Hecke transformations on the equivariant Borel–Moore homology of the Hilbert scheme of points on a nonreduced plane in three-dimensional affine space. The resulting W-module is then identified to the vacuum module. The construction is based on a generalization of the ADHM construction as well as the W-action on the equivariant Borel–Moore homology of the moduli space of instantons constructed by Schiffmann and Vasserot.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The AGT conjecture [1] leads to conjectural geometric constructions of W-algebra actions on the equivariant Borel–Moore homology of moduli spaces of sheaves on surfaces. Independent proofs of this conjecture for moduli spaces of rank \(r\geqslant 1\) framed sheaves on the complex projective plane were given by Schiffmann, Vasserot [33] and Maulik, Okounkov [18]. In both cases one first constructs an action of the affine Yangian of \(\mathfrak {gl}_1\) on the equivariant Borel–Moore homology of the corresponding moduli space, while the W-algebra action is obtained through a free field realization. A generalization to moduli spaces of framed G-instantons on \({\mathbb {C}}^2\) for more general reductive group G using Donaldson–Uhlenbeck compactifications was proven by Braverman, Finkelberg and Nakajima in [5].
An alternative geometric construction of the W-algebra action was carried out by Negut [23] using the shuffle algebra realization of the affine Yangian. Using the Ext operators of [7, 8], this yields a proof of the AGT conjecture for rank two quiver gauge theories on \({\mathbb {C}}^2\) as well as a proof [25] of the five-dimensional analog of the AGT conjecture for any quiver gauge theory with gauge group \(\mathrm{SU}(r)\), \(r\geqslant 1\). The latter involves a q-deformed W-algebra action on the equivariant K-theory of moduli spaces. This construction has been further generalized to moduli spaces of stable sheaves on smooth projective surfaces in [24].
Finally, motivated by work of Gaiotto and Rapcak [13], Nekrasov [26], and Nekrasov and Prabhakar [27], an action of a more general class of vertex algebras on the dual of the compactly supported equivariant vanishing cycle cohomology of certain quiver moduli spaces was constructed by Rapcak, Soibelman, Yang and Zhao in [30].
A central element in the constructions of [30, 33] is the action of certain cohomological Hall algebras on the cohomology of moduli spaces. Cohomological Hall algebra (3d COHA for short) was introduced by Kontsevich and Soibelman [16] for categories of modules associated to Quillen-smooth algebras with potential e.g. path algebras of quivers with potential. Those are the hearts of t-structures of Calabi–Yau categories of dimension three. An independent construction of a certain cohomological Hall algebra (2d COHA for short) for categories of modules over preprojective algebras, which are hearts of t-structures of two-dimensional Calabi–Yau categories, was developed by Schiffmann and Vasserot [33,34,35], and also Yang and Zhao [38]. A comparison between the two approaches was carried out in [31] where it was shown that the 2d COHA can be obtained by dimensional reduction of a special case of 3d COHA. Further developments on 3d COHAs and their representations include [10, 11, 36] while geometric constructions of 2d COHAs for various categories of coherent sheaves on surfaces have been developed in [15, 19, 29, 32]. It should be also noted that the proof of the AGT conjecture given in [33] uses the two-dimensional variant, while the generalization proven in [30] employs three-dimensional cohomological Hall algebras.
From this perspective, the geometric framework of the present paper consists of torsion sheaves on a Calabi–Yau threefold with set theoretic support on a given divisor. Such a generalization of the AGT framework was first proposed in [30].
In more detail, let \(D_r\subset {{\mathbb {A}}}^3{:=}\mathrm{Spec}\, {\mathbb {C}}[x_1, x_2, x_3]\) be the divisor \(x_3^r=0\). Let also \(\mathrm{Hilb}(r,n)\) be the Hilbert scheme of zero-dimensional coherent quotients \({{\mathscr {O}}}_{D_r}\!\twoheadrightarrow Q\) with \(\chi (Q)=n\) and let

be the generating function of Euler numbers. Then [13, Section 9.3.2] shows that \(Z_r(q)\) is equal to the vacuum character of the W-algebra \(W_{\kappa }(\mathfrak {gl}_r)\) up to a prefactor. More precisely, for any level k, one has

with
Motivated by this observation, the main goal of the present work is to provide an explicit geometric construction of a W-algebra action on the localized equivariant Borel–Moore homology of the Hilbert scheme

and prove that the resulting W-module is isomorphic to the vacuum module. The equivariant structure is induced by the torus action  ,
,

Let  , let \(R_0\simeq {\mathbb {C}}[x,y]\) be the cohomology ring of the classifying space \(B\mathbf{T}_0\) and let \(K_0\simeq {\mathbb {C}}(x,y)\) be its fraction field. For further reference let
, let \(R_0\simeq {\mathbb {C}}[x,y]\) be the cohomology ring of the classifying space \(B\mathbf{T}_0\) and let \(K_0\simeq {\mathbb {C}}(x,y)\) be its fraction field. For further reference let

denote the localized equivariant Borel–Moore homology of the Hilbert scheme. As in [18, 33] one first constructs a degenerate DAHA, or, equivalently, Yangian action via Hecke transformations.
1.1 The degenerate DAHA action
The degenerate DAHA is an infinite dimensional associative algebra \(\mathbf{SH}^c\) constructed by Schiffmann and Vasserot [33] as a degeneration of Cherednik’s \(\mathrm{GL}_n\) double affine Hecke algebra. As briefly reviewed in Sect. 6.1, this algebra is generated by the elements \(D_{1,l}, D_{0, l}, D_{-1,l}\), \(l\geqslant 0\), over a polynomial ring \({\mathbb {C}}(\kappa )[\mathbf{c}_0, \mathbf{c}_1, \ldots ]\) where \(\kappa \) is a formal parameter and \(\mathbf{c}_l\), \(l\geqslant 0\), are central elements. The defining relations are written explicitly in equations (6.2)–(6.6). As shown in [4] it is in fact related by specialization to the Yangian algebra of affine \(\mathfrak {gl}_1\). A specialization \({\mathbb {C}}(\kappa )[\mathbf{c}_0, \mathbf{c}_1, \ldots ]\rightarrow K\) of this algebra has been shown in [33, Theorem 3.2] to act on the localized equivariant Borel–Moore homology
of the moduli space of rank r framed torsion free sheaves on the projective plane. Here \(\mathbf{T}_{r+2} = ({\mathbb {C}}^{\times })^{r+2}\) denotes the natural torus which acts on these moduli spaces and \(K_{r+2}\) is the field of fractions of the cohomology ring of the classifying space, \(H(B\mathbf{T}_{r+2})\). More details are provided in Sects. 4.1 and 6.3.
In the Hilbert scheme context the direct construction of Hecke transformations encounters significant technical problems. The natural Hecke correspondence in this case is the nested Hilbert scheme \(\mathrm{Hilb} (r,n,n+1)\) parametrizing flags of ideal sheaves \({{\mathscr {I}}}_1\subset {{\mathscr {I}}}_2\) on \(D_r\) with \(\chi ({{\mathscr {O}}}_{D_r}/{{\mathscr {I}}}_2)=n\) and \(\chi ({{\mathscr {O}}}_{D_r}/{{\mathscr {I}}}_1) = n+1\). By construction there are natural projections  and
and  , and \(\rho _2\) and \(\rho _2\) can be shown to be proper. The main technical difficulty resides in the fact that \(\rho _1\) is not a locally complete intersection morphism, hence one cannot construct a refined Gysin pull-back \(\rho _1^!\). This problem has been encountered in a similar context in [15, 24, 29, 34, 39] where it was solved using various techniques. The construction of [34] uses a factorization of \(\rho _1\) into simpler morphisms which is specific to moduli spaces of Nakajima quiver varieties. The constructions of [15, 24, 29, 39] use virtual pull-backs, as constructed in [17] or some derived variant. A common feature of all these cases is that their constructions take place in an abelian category of homological dimension two, which is an essential condition. Such an approach does not apply to the present case since the relative obstruction theory of \(\rho _1\) is not perfect of amplitude \([-1, 0]\). This reflects the fact that the present construction takes place in a category of homological dimension three rather than two as in loc. cit.
, and \(\rho _2\) and \(\rho _2\) can be shown to be proper. The main technical difficulty resides in the fact that \(\rho _1\) is not a locally complete intersection morphism, hence one cannot construct a refined Gysin pull-back \(\rho _1^!\). This problem has been encountered in a similar context in [15, 24, 29, 34, 39] where it was solved using various techniques. The construction of [34] uses a factorization of \(\rho _1\) into simpler morphisms which is specific to moduli spaces of Nakajima quiver varieties. The constructions of [15, 24, 29, 39] use virtual pull-backs, as constructed in [17] or some derived variant. A common feature of all these cases is that their constructions take place in an abelian category of homological dimension two, which is an essential condition. Such an approach does not apply to the present case since the relative obstruction theory of \(\rho _1\) is not perfect of amplitude \([-1, 0]\). This reflects the fact that the present construction takes place in a category of homological dimension three rather than two as in loc. cit.
In order to circumvent this obstacle, the strategy used in this paper employs an equivariant embedding of the Hilbert scheme \(\mathrm{Hilb}(r,n)\) in a smooth ambient space which yields an injection for localized Borel–Moore homology. This is obtained in Propositions 3.8 and 2.2 which construct a closed embedding  , in the moduli space of rank r framed sheaves on the projective plane with second Chern class n. Moreover, as shown in Sect. 4.2, there is an injective group homomorphism \(\mathbf{T}_0\hookrightarrow \mathbf{T}_{r+2}\),
, in the moduli space of rank r framed sheaves on the projective plane with second Chern class n. Moreover, as shown in Sect. 4.2, there is an injective group homomorphism \(\mathbf{T}_0\hookrightarrow \mathbf{T}_{r+2}\),
such that f is equivariant. Then an important technical result in the current approach states that any connected component of the \(\mathbf{T}_0\)-fixed locus in \({{\mathscr {M}}}(r,n)\) which intersects \(\mathrm{Hilb} (r,n)\) nontrivially must be:
-
(a)
contained in \(\mathrm{Hilb} (r,n)\), and
-
(b)
zero-dimensional, i.e., a single closed point.
This is proven in Sect. 4.2, Corollary 4.7 and Lemma 4.8. Then the push-forward map for localized equivariant Borel–Moore homology is injective and yields an identification

For future reference let
Using these results, Hecke transformations for the Hilbert scheme are constructed in Sect. 5.3 by analogy to [33, Section 3.2]. Let  , \(1\leqslant i \leqslant 2\), denote the canonical projections and let \(\tau _{n,n+1}\) denote the universal line bundle on the correspondence variety \({{\mathscr {A}}}(r,n,n+1)\). Let
, \(1\leqslant i \leqslant 2\), denote the canonical projections and let \(\tau _{n,n+1}\) denote the universal line bundle on the correspondence variety \({{\mathscr {A}}}(r,n,n+1)\). Let  denote the canonical closed embedding. Then Lemmas 5.6 and 5.6 show that the transformations
denote the canonical closed embedding. Then Lemmas 5.6 and 5.6 show that the transformations

are well defined for any \(l\geqslant 0\) and factor through  . Therefore, by a slight abuse of notation, one obtains linear transformations \(h^{\pm }_l\in \mathrm{End}_{K_0}(\mathbf{V}^{(r)}_{K_0})\). In addition, one defines the diagonal transformations \(h^0_l\in \mathrm{End}_{K_0}(\mathbf{V}^{(r)}_{K_0})\) using the plethystic powers of the universal vector bundle \({{\mathscr {V}}}_{r,n}\) on \({{\mathscr {M}}}(r,n)\). Namely, denoting by \({{\mathscr {L}}}_k\), \(1\leqslant k\leqslant n\), the virtual equivariant Chern roots of \({{\mathscr {V}}}_{r,n}\), let
. Therefore, by a slight abuse of notation, one obtains linear transformations \(h^{\pm }_l\in \mathrm{End}_{K_0}(\mathbf{V}^{(r)}_{K_0})\). In addition, one defines the diagonal transformations \(h^0_l\in \mathrm{End}_{K_0}(\mathbf{V}^{(r)}_{K_0})\) using the plethystic powers of the universal vector bundle \({{\mathscr {V}}}_{r,n}\) on \({{\mathscr {M}}}(r,n)\). Namely, denoting by \({{\mathscr {L}}}_k\), \(1\leqslant k\leqslant n\), the virtual equivariant Chern roots of \({{\mathscr {V}}}_{r,n}\), let
Finally, in order to state the first main result of the present paper let \(\mathbf{SH}^{(r)}_{K_0}\) be the specialization of the degenerate DAHA induced by the injective group homomorphism \(\mathbf{T}_0\subset \mathbf{T}_{r+2}\). By construction, this is an algebra over \(K_0={\mathbb {C}}(x,y)\). Then one has:
Theorem 1.1
The map \(\{D_{-1,l}, D_{0,l}, D_{1,l}\,{|}\, l \in {\mathbb {Z}}, l\geqslant 0\}\rightarrow \mathrm{End}_{K_0}(\mathbf{V}^{(r)}_{K_0})\) given by
extends uniquely to an algebra homomorphism
Theorem 1.1 is proven in Lemma 6.3 using Lemmas 5.4, 5.6, 5.7 and 6.2. The main strategy is to derive the above result from [33, Theorem 3.2] by a detailed equivariant fixed point analysis.
1.2 The W-algebra action
The next goal is to convert the \(\mathbf{SH}^{(r)}_{K_0}\)-action in Theorem 1.1 into a W-algebra action. Let \(W_\kappa (\mathfrak {gl}_r)\) be the W-algebra for \(\mathfrak {gl}_r\) at level \(\kappa = -x^{-1}y\) considered as an algebra over the ground field \(F={\mathbb {C}}(\kappa )\). A rigorous mathematical theory of W-algebras and their representations has been developed in [2]. A brief introduction is provided for completeness in Sect. 7.1. In particular there is a canonical vacuum module \(\pi _0\) which admits a free field realization.
In the present context the relation between the degenerate DAHA and the W-algebra is obtained by a careful specialization of [33, Theorem 8.21], including the main steps in the proof. This is carried out in detail in Appendix A. In particular, Lemma A.3 shows that there is a surjective homomorphism of algebras
where the domain is the current algebra of the degenerate DAHA and the target is the image of the current algebra \({\mathfrak U}(W_\kappa (\mathfrak { gl}_r))\) in \(\mathrm{End}(\pi _0)\). Corollary A.4 states that the restriction
yields a categorical equivalence of admissible modules.
As in [33, Definition 8.10], admissible modules are \({\mathbb {Z}}\)-graded modules with respect to a natural \({\mathbb {Z}}\)-grading on the degenerate DAHA whose graded summands are trivial for sufficiently high degree. Moreover, by construction, the underlying \(K_0\)-vector space of any admissible \(\mathbf{SH}_{K_0}^{(r)}\)-module is canonically identified with the underlying \(K_0\)-vector space of the corresponding \({{\mathscr {U}}}_0(W_\kappa (\mathfrak {gl}_r))\)-module. This is briefly reviewed in Sect. A.3.
In conclusion, one obtains a representation
Then the second main result of this paper is:
Theorem 1.2
For any \(r\geqslant 1\) the representation \(\pi _0^{(r)}\) is isomorphic to the vacuum representation of the W-algebra.
The proof of Theorem 1.2 is analogous to the proof of [33, Theorem 8.21]. The required structure results are proven in the present context in Lemmas 6.5 and 6.7.
1.3 Further remarks and open directions
In order to conclude this section, it may be helpful to add a few comments on the relation of the present work to [30], as well as mention a few possible open directions.
One of the main results of [30], is a construction of a certain vertex algebra action on the dual to equivariant vanishing cycle cohomology of the moduli spaces of spiked instantons constructed in [26, 27]. Spiked instantons admit a presentation in terms of framed quiver representations of a triply framed generalization of the ADHM quiver labelled by framing vectors \((r_1,r_2,r_3)\in ({\mathbb {Z}}_{\geqslant 0})^{\times 3}\). It was shown in [30] that the dual of the compactly supported equivariant vanishing cycle cohomology of moduli spaces of stable framed representations with fixed \((r_1,r_2,r_3)\) carries an action of the vertex algebra \(V_{r_1,r_2,r_3}\) introduced in [13]. Moreover, the resulting module is identified with a Verma module with the highest weight depending on the equivariant parameters. In particular for \((r_1,r_2,r_3) = (r,0,0)\) the moduli space reduces to the standard moduli space of stable ADHM data, and the action reduces to the W-action constructed in [18, 33].
The present paper generalizes the results of [18, 33] in a different direction, using framed quiver representations associated to geometric objects as explained above. In particular, as shown in Sect. 3, spectral correspondence leads to the new framed quiver with potential shown in diagram (3.1). The Hilbert scheme \(\mathrm{Hilb}_n(D_r)\) is then isomorphic to a closed subscheme \({{\mathscr {Q}}}_0(r,n)\) of the moduli space \({{\mathscr {Q}}}(r,n)\) of framed quiver representations constructed in Proposition 4.1. Moreover, this closed embedding yields an isomorphism in localized equivariant Borel–Moore homology and Theorem 1.2 identifies the latter with a vacuum W-module.
From the point of view of the underlying Calabi–Yau geometry, the moduli space \({{\mathscr {Q}}}(r,n)\) is in fact more natural than the Hilbert scheme, since it admits a global presentation as the critical locus of a polynomial potential. As such, it is endowed with an equivariant sheaf of vanishing cycles. Then one is naturally led to the following conjecture:
Conjecture 1.3
Let \(H_{\mathbf{T}_0}^{{\mathrm{van}}}({{\mathscr {Q}}}(r,n))\) denote the dual to the compactly supported equivariant vanishing cycle cohomology of the framed quiver moduli space \({{\mathscr {Q}}}(r,n)\). Let \(H_{\mathbf{T}_0}^{{\mathrm{van}}}({{\mathscr {Q}}}(r,n))_{K_0}\) denote its localization at (0). Then there is an explicit \(\mathbf{SH}_{K_0}^{(r)}\) action on \(H_{\mathbf{T}_0}^{{\mathrm{van}}}({{\mathscr {Q}}}(r,n))_{K_0}\) constructed via Hecke correspondences for vanishing cycle cohomology by analogy to [30].
The main difficulty in proving Conjecture 1.3 resides in the technical difficulties involved in working with sheaves of vanishing cycles.
As was pointed out in [30], a natural question for further study is whether similar algebraic structures can be associated to more general configurations of divisors in Calabi–Yau threefolds. It was explicitly conjectured in loc. cit. that this should be possible at least for divisors of the form  in \({{\mathbb {A}}}^3\). At the current stage, the construction of a quiver with potential associated to such configurations is an open problem. At the same time the results of [24] point to another possible generalization associated to compact nonreduced divisors in Calabi–Yau threefolds.
in \({{\mathbb {A}}}^3\). At the current stage, the construction of a quiver with potential associated to such configurations is an open problem. At the same time the results of [24] point to another possible generalization associated to compact nonreduced divisors in Calabi–Yau threefolds.
2 Hilbert schemes and framed Higgs sheaves
Let S be a smooth complex projective surface, let L be a line bundle on S and let X be the total space of the line bundle L. Let \(\pi :X\rightarrow S\) denote the canonical projection and \(\zeta \in H^0(X, \pi ^*L)\) denote the tautological section. The zero locus of \(\zeta \) is the image of the zero section \(S \rightarrow L\), which will be denoted by \(S_1\). More generally, for any positive integer \(r\geqslant 1\) let \(S_r\) denote the nonreduced divisor \(\zeta ^r\! =0\), and let \(\iota _r:S_r \hookrightarrow X\) denote the canonical closed embedding into X. Note also that the projection \(\pi :X\rightarrow S\) yields by restriction a projection map \(\pi _r:S_r \rightarrow S\). Moreover, the zero section \(\sigma :S \hookrightarrow X\) factors through a closed embedding \(\sigma _r:S \rightarrow S_r\).
As proven in [37, Proposition 2.2], the abelian category \(\mathrm{Coh}_{\mathrm{c}}(X)\) of coherent \({{\mathscr {O}}}_X\)-modules with compact support is equivalent to the category of Higgs sheaves on S with coefficients in L. A Higgs sheaf on S with coefficients in L is defined as a pair \((E, \Phi )\) where E is a coherent \({{\mathscr {O}}}_S\)-module and  is a morphism of \({{\mathscr {O}}}_S\)-modules. Such pairs form naturally an abelian category \(\mathrm{Higgs}(S,L)\), where the morphisms are defined as morphisms \(f:E\rightarrow E'\) of \( {{\mathscr {O}}}_S\) modules such that \(\Phi '{\circ } f = (f {\otimes }\, \mathbf{1}_L)\,{\circ }\, \Phi \). Then Proposition 2.2 of loc. cit. proves that there is an equivalence of abelian categories
is a morphism of \({{\mathscr {O}}}_S\)-modules. Such pairs form naturally an abelian category \(\mathrm{Higgs}(S,L)\), where the morphisms are defined as morphisms \(f:E\rightarrow E'\) of \( {{\mathscr {O}}}_S\) modules such that \(\Phi '{\circ } f = (f {\otimes }\, \mathbf{1}_L)\,{\circ }\, \Phi \). Then Proposition 2.2 of loc. cit. proves that there is an equivalence of abelian categories

where \(\mathrm{Coh}_{\mathrm{c}}(X)\) denotes the abelian category of coherent \({{\mathscr {O}}}_X\)-modules with compact support. This equivalence associates to any such sheaf F its direct image \(E=\pi _*F\), while the Higgs field  is the direct image, \(\Phi =\pi _*(\zeta _F)\) of the canonical morphism
is the direct image, \(\Phi =\pi _*(\zeta _F)\) of the canonical morphism  .
.
Now let \(\Delta \subset S\) be a smooth connected effective divisor on S, and let \(\Delta _r = \pi _r^{-1}(\Delta )\subset S_r\) be its inverse image in \(S_r\). For any positive integer \(r\geqslant 1\) let \(D_r\) be the complement of \(\Delta _r\) in \(S_r\) and let \(\mathrm{Hilb}_n(D_r)\) be the Hilbert scheme of zero dimensional quotients
with \(\chi (Q)=n\) such that the support of Q is contained in \(D_r\). For each such quotient let  . Clearly the extension of \({{\mathscr {I}}}_{S_r}\) by zero to X is a pure dimension two torsion sheaf with compact support. Using the equivalence (2.1), the goal of this section is to prove that the Hilbert scheme \(\mathrm{Hilb}_n(D_r)\) is isomorphic to a moduli space of framed Higgs sheaf quotients on S.
. Clearly the extension of \({{\mathscr {I}}}_{S_r}\) by zero to X is a pure dimension two torsion sheaf with compact support. Using the equivalence (2.1), the goal of this section is to prove that the Hilbert scheme \(\mathrm{Hilb}_n(D_r)\) is isomorphic to a moduli space of framed Higgs sheaf quotients on S.
2.1 Framed sheaves
This section summarizes the main results on framed sheaves needed in this paper following [6]. Let F be a fixed locally free \({{\mathscr {O}}}_\Delta \)-module. A framed torsion free sheaf on S with respect to \((\Delta ,F)\) is a pair \((E, \xi )\) where E is a torsion free sheaf on S, and  is an isomorphism of \({{\mathscr {O}}}_\Delta \)-modules. For any such a pair \((E,\xi )\), let \(f_\xi :E \rightarrow F\) denote the morphism of \({{\mathscr {O}}}_S\)-modules obtained by composing
is an isomorphism of \({{\mathscr {O}}}_\Delta \)-modules. For any such a pair \((E,\xi )\), let \(f_\xi :E \rightarrow F\) denote the morphism of \({{\mathscr {O}}}_S\)-modules obtained by composing  with the natural projection
with the natural projection  . An isomorphism of framed sheaves \((E_1, \xi _1)\), \((E_2, \xi _2)\) is an isomorphism of sheaves \(\phi :E_1\rightarrow E_2\) such that
. An isomorphism of framed sheaves \((E_1, \xi _1)\), \((E_2, \xi _2)\) is an isomorphism of sheaves \(\phi :E_1\rightarrow E_2\) such that

Moreover, given a parameter scheme T over \({\mathbb {C}}\), let \(F_T\) denote the pull-back of F to  . Then a flat family of rank \(r\geqslant 1\) torsion free sheaves on S is a coherent \({{\mathscr {O}}}_{S\times T}\)-module \(E_T\), flat over T, and an isomorphism
. Then a flat family of rank \(r\geqslant 1\) torsion free sheaves on S is a coherent \({{\mathscr {O}}}_{S\times T}\)-module \(E_T\), flat over T, and an isomorphism  .
.
Next suppose the following additional conditions are satisfied:
-
(1)
\(\Delta \) is nef and \(\Delta ^2\geqslant 0\) in the intersection ring of S, and
-
(2)
F is a good framing sheaf as defined in [6, Definition 2.4] satisfying in addition the vanishing condition
 for all \(k\in {\mathbb {Z}}\), \(k\geqslant 1\).
for all \(k\in {\mathbb {Z}}\), \(k\geqslant 1\).
Then [6, Theorem 3.1] proves that there is a smooth quasi-projective fine moduli space \({{\mathscr {M}}}(r,\beta , n)\) of framed torsion free sheaves with topological invariants

In particular, under the above conditions, any framed sheaf \((E,\xi )\) has trivial automorphism group.
2.2 Framed Higgs sheaves
In the above framework, a framed Higgs sheaf will be a triple \((E,\xi ,\Phi )\) where \((E,\xi )\) is a framed torsion free sheaf and  a Higgs field satisfying a certain framing condition along \(\Delta \). The framing condition is naturally inferred from the following special case.
a Higgs field satisfying a certain framing condition along \(\Delta \). The framing condition is naturally inferred from the following special case.
Lemma 2.1
Let \((O_r,\Lambda _r)\) be the Higgs sheaf associated to the torsion \({{\mathscr {O}}}_X\)-module \({{\mathscr {O}}}_{S_r}\) via correspondence (2.1). Then there is a direct sum decomposition
identifying the off-diagonal components of the Higgs field to the canonical isomorphisms

Moreover, all other components of \(\Lambda _r\) are identically zero.
Proof
By construction, \(O_r=\pi _{*}{{\mathscr {O}}}_{S_r}\). Equation (2.2) will be proven below by induction on \(r \geqslant 1\). The case \(r=1\) is obvious. Suppose equation (2.2) holds for \((O_r, \Lambda _r)\) and note the canonical exact sequence
Note also the canonical isomorphism \({{\mathscr {O}}}_X(S_1) \simeq \pi ^*L\) determined by the tautological section \(\zeta :{{\mathscr {O}}}_X \rightarrow \pi ^*L\). Then applying \(\pi _*\) to the exact sequence (2.4), one obtains the exact sequences of \({{\mathscr {O}}}_S\)-modules

Let \({{\overline{X}}}\) be the total space of the projective bundle  , which contains X as an open subscheme. Let \({{\overline{\pi }}}:{{\overline{X}}} \rightarrow S\) denote the canonical projection. Then there is a commutative diagram of morphisms of \({{\mathscr {O}}}_{{\overline{X}}}\)-modules
, which contains X as an open subscheme. Let \({{\overline{\pi }}}:{{\overline{X}}} \rightarrow S\) denote the canonical projection. Then there is a commutative diagram of morphisms of \({{\mathscr {O}}}_{{\overline{X}}}\)-modules

where all arrows are canonical projections. Applying \({{\overline{\pi }}}_*\) yields a commutative diagram of morphisms of \({{\mathscr {O}}}_S\)-modules

where \({{\overline{\pi }}}_*p= \mathbf{1}_{{{\mathscr {O}}}_S}\). Therefore \({\overline{\pi }}_*q\) determines a splitting of the exact sequence (2.5). This proves the inductive step.
The Higgs field \(\Lambda _r\) is the direct image of the canonical map

As observed above, the the tautological section \(\zeta :{{\mathscr {O}}}_X \rightarrow \pi ^*L\) determines a canonical isomorphism \({{\mathscr {O}}}_X(S_1) \simeq \pi ^*L\). Therefore, equation (2.3) follows immediately. \(\square \)
The framing data for Higgs sheaves on S will be specified by the Higgs sheaf \((F_r,\Psi _r)\) obtained by restricting \((O_r, \Lambda _r)\) to \(\Delta \subset S\). Therefore, a framed Higgs sheaf of rank r on S will be a framed rank r torsion sheaf \((E, \xi )\) and a Higgs field  such that the following diagram is commutative:
such that the following diagram is commutative:

For completeness, recall that the morphism \(f_\xi \) in the above diagram is the composition of  with the natural projection
with the natural projection  . Similarly
. Similarly  is the natural projection. Naturally, an isomorphism of framed Higgs sheaves
is the natural projection. Naturally, an isomorphism of framed Higgs sheaves  is an isomorphism
is an isomorphism  of framed sheaves which is at the same time an isomorphism
of framed sheaves which is at the same time an isomorphism  of Higgs sheaves. The definition of flat families is also natural, hence the details will be omitted.
of Higgs sheaves. The definition of flat families is also natural, hence the details will be omitted.
The next result will show that the Hilbert scheme \(\mathrm{Hilb}_n(D_r)\) is isomorphic to a moduli space of Higgs sheaf quotients. Let

be an exact sequence of \({{\mathscr {O}}}_{S_r}\) modules, where Q is zero-dimensional, supported in the complement  . By extension by zero, this yields an exact sequence of \({{\mathscr {O}}}_X\)-modules. Let \((E, \Phi )\) be the associated Higgs sheaf via correspondence (2.1). Taking the direct image of the exact sequence (2.7) via \(\pi :X\rightarrow S\) yields an exact sequence
. By extension by zero, this yields an exact sequence of \({{\mathscr {O}}}_X\)-modules. Let \((E, \Phi )\) be the associated Higgs sheaf via correspondence (2.1). Taking the direct image of the exact sequence (2.7) via \(\pi :X\rightarrow S\) yields an exact sequence
in the abelian category  . Here \((G, \Upsilon )\) is a zero-dimensional Higgs sheaf on S supported in the complement
. Here \((G, \Upsilon )\) is a zero-dimensional Higgs sheaf on S supported in the complement  such that \(\chi (G) = \chi (Q)=n\).
such that \(\chi (G) = \chi (Q)=n\).
For any \(r,n \in {\mathbb {Z}}\), \(r\geqslant 1\) let  be the Quot-scheme parametrizing quotients
be the Quot-scheme parametrizing quotients
in the abelian category \({{\mathscr {H}}}(S,L)\), where \((G, \Upsilon )\) is a zero-dimensional Higgs sheaf on S supported in  such that \(\chi (G) = \chi (Q)=n\). Then the equivalence (2.1) yields
such that \(\chi (G) = \chi (Q)=n\). Then the equivalence (2.1) yields
Proposition 2.2
There is an isomorphism  mapping a quotient \({{\mathscr {O}}}_{S_r}\!\twoheadrightarrow Q\) to the corresponding quotient \((O_r, \Lambda _r) \twoheadrightarrow (G,\Upsilon )\).
mapping a quotient \({{\mathscr {O}}}_{S_r}\!\twoheadrightarrow Q\) to the corresponding quotient \((O_r, \Lambda _r) \twoheadrightarrow (G,\Upsilon )\).
Proof
This follows by a routine verification for flat families. \(\square \)
Remark 2.3
Note that the kernel of the epimorphism (2.9) is naturally a framed Higgs sheaf \((E,\Phi )\) on S with topological invariants

Let \({{\mathscr {H}}}(r,n)\) denote the moduli stack of all such framed Higgs sheaves. Then Proposition 2.2 yields a stack morphism
In the next section it will be shown that this is in fact a closed embedding of schemes in the case where S is the complex projective space, \(L = {{\mathscr {O}}}_S\) and \(\Delta \subset S\) is a projective line.
3 Framed Higgs sheaves on the projective plane
In this section \(S={\mathbb {P}}^2\) with homogeneous coordinates \([z_0, z_1, z_2]\), the line bundle L is trivial, \(L={{\mathscr {O}}}_S\), and \(\Delta \subset S\) is the projective line \(z_0=0\). Then the Higgs bundle \((O_r, \Lambda _r)\) obtained in Lemma 2.1 has underlying vector bundle  . The Higgs field \(\Lambda _r:O_r\rightarrow O_r\) is given by
. The Higgs field \(\Lambda _r:O_r\rightarrow O_r\) is given by

where \(A_r\in M_r({\mathbb {C}})\) is the lower triangular  regular nilpotent Jordan block. As in the previous section, \({{\mathscr {H}}}(r,n)\) denotes the resulting moduli stack of framed Higgs sheaves on S with rank \(r\geqslant 1\) and second Chern number n. The framing condition implies that the first Chern class must vanish. Let \({{\mathscr {M}}}(r,n)\) denote the moduli space of framed sheaves on S, which is smooth and quasi-projective. Then note that there is a natural forgetful morphism \(\jmath :{{\mathscr {H}}}(r,n)\rightarrow {{\mathscr {M}}}(r,n)\) forgetting the Higgs field. In this section we will prove that the moduli stack \({{\mathscr {H}}}(r,n)\) in fact is isomorphic to a moduli scheme of framed quiver representations and the morphism \(\jmath \) is a closed embedding.
regular nilpotent Jordan block. As in the previous section, \({{\mathscr {H}}}(r,n)\) denotes the resulting moduli stack of framed Higgs sheaves on S with rank \(r\geqslant 1\) and second Chern number n. The framing condition implies that the first Chern class must vanish. Let \({{\mathscr {M}}}(r,n)\) denote the moduli space of framed sheaves on S, which is smooth and quasi-projective. Then note that there is a natural forgetful morphism \(\jmath :{{\mathscr {H}}}(r,n)\rightarrow {{\mathscr {M}}}(r,n)\) forgetting the Higgs field. In this section we will prove that the moduli stack \({{\mathscr {H}}}(r,n)\) in fact is isomorphic to a moduli scheme of framed quiver representations and the morphism \(\jmath \) is a closed embedding.
3.1 ADHM data for framed Higgs sheaves
Consider the following quiver \({{\mathscr {Q}}}\):

with potential

As usual, a representation of the above quiver with potential is defined as a pair of vector spaces \((V,V_\infty )\) and linear maps
satisfying the relations derived from the potential function
The dimension vector of such a representation is the pair of integers (r, n), where

An isomorphism between two such representations \(\varrho , \varrho '\) is a pair of vector space isomorphisms  ,
,  intertwining between the linear maps belonging to the two representations.
intertwining between the linear maps belonging to the two representations.
Definition 3.1
A representation of dimension vector (r, n) will be called framed if the following conditions are satisfied:
-
(Fr.1)
The vector space \(V_{\infty }\) is a fixed vector space of dimension r, equipped with a fixed basis \(\mathbf{e}_{a}\), \(1\leqslant a\leqslant r\).
-
(Fr.2)
The map \(A:V_{\infty }\rightarrow V_{\infty }\) is fixed and given by the regular nilpotent endomorhism
$$\begin{aligned} A_r (\mathbf{e}_a) = \mathbf{e}_{a+1}, \quad 1\leqslant a \leqslant r, \end{aligned}$$where \(\mathbf{e}_{r+1}=0\). In particular if \(0\leqslant r \leqslant 1\), the map A is identically zero.
-
(Fr.3)
The representation satisfies the relations derived from the potential function
$$\begin{aligned} W^{\mathrm{fr}} = \mathrm{Tr}_V ( B_3[B_1,B_2] + B_3IJ -I A_r J ), \end{aligned}$$where the map \(A_r\) is fixed as in (Fr.1), (Fr.2) above. The resulting relations are:
$$\begin{aligned} \begin{aligned}&[B_1,B_2]+IJ =0,&\quad JB_3-A_rJ=0, \quad B_3I-IA_r=0,\\&[B_3,B_1]=0,&\quad [B_3, B_2]=0. \end{aligned} \end{aligned}$$(3.2)
Furthermore, a framed representation as defined above will be called cyclic if it satisfies the following additional condition:
-
(Fr.4)
There is no proper nonzero linear subspace
 preserved by \(B_1,B_2, B_3\) and at the same time containing the image of \(I:V_{\infty }\rightarrow V\).
preserved by \(B_1,B_2, B_3\) and at the same time containing the image of \(I:V_{\infty }\rightarrow V\).
Finally, in the formulation of the moduli problem, two framed representations \(\varrho , \varrho '\) will be said to be isomorphic if and only if they are related by an isomorphism of the form \((\phi , \mathbf{1}_{V_{\infty }})\). It is clear that such isomorphisms preserve the fixed framing data.
At this point it is helpful to note the relation between the quiver (3.1) and the standard ADHM quiver. The latter is defined by the following diagram:

subject to the quadratic relation

By analogy with (Fr.1)–(Fr.4) above, a fixed isomorphism \(V_\infty \simeq {\mathbb {C}}^r\) will be fixed by choosing a basis, where \(V_\infty \) is the vector space assigned to the node \(\Box \). Then framed representations of the ADHM quiver are defined by data \(\alpha =(V, V_\infty , B_1, B_2,I,J)\) where  , \(1\leqslant i\leqslant 2\),
, \(1\leqslant i\leqslant 2\),  and
and  are linear maps corresponding to \(\beta _i, \eta , \sigma \) respectively. Hence they satisfy the quadratic relation \([B_1,B_2]+IJ=0\). Isomorphisms of framed representations are required to preserve the identification \(V_\infty \simeq {\mathbb {C}}^r\). Moreover, recall that \(\alpha \) is cyclic, or stable, if and only if there is no proper nontrivial linear subspace
are linear maps corresponding to \(\beta _i, \eta , \sigma \) respectively. Hence they satisfy the quadratic relation \([B_1,B_2]+IJ=0\). Isomorphisms of framed representations are required to preserve the identification \(V_\infty \simeq {\mathbb {C}}^r\). Moreover, recall that \(\alpha \) is cyclic, or stable, if and only if there is no proper nontrivial linear subspace  preserved by \(B_1, B_2\) and at the same time containing the image of I. As shown for example in [20, Section 3.1], there is a smooth quasi-projective fine moduli space \({{\mathscr {A}}}(r,n)\) of stable framed ADHM representations of fixed dimension vector (n, r).
preserved by \(B_1, B_2\) and at the same time containing the image of I. As shown for example in [20, Section 3.1], there is a smooth quasi-projective fine moduli space \({{\mathscr {A}}}(r,n)\) of stable framed ADHM representations of fixed dimension vector (n, r).
Now note that for each framed representation \(\varrho =(V,V_\infty ,B_1,B_2, B_3, I,J)\) defined in (Fr.1)–(Fr.4) above, the data \(\alpha =(V, V_\infty , B_1, B_2,I,J)\) is a framed representation of the ADHM quiver. A priori \(\alpha \) need not be cyclic even if \(\varrho \) is. The next result will show that in fact the two cyclicity conditions are compatible.
Lemma 3.2
Let \(\varrho \) be a framed representation of \(({{\mathscr {Q}}},{{\mathscr {W}}})\) satisfying conditions (Fr.1)–(Fr.3). Let \(\alpha \) be the underlying ADHM representation. Then \(\varrho \) is cyclic as defined in (Fr.4) if and only if \(\alpha \) is cyclic as an ADHM representation.
Proof
The inverse implication is clear. In order to prove the direct implication, suppose \(\varrho \) is cyclic, and suppose  is a proper nonzero linear subspace preserved by \(B_1, B_2\) and at the same time containing the image of I. Let \(v_a = I(\mathbf{e}_a)\), \(1\leqslant a \leqslant r\). Since \(\varrho \) is cyclic, V is generated by elements of the form
is a proper nonzero linear subspace preserved by \(B_1, B_2\) and at the same time containing the image of I. Let \(v_a = I(\mathbf{e}_a)\), \(1\leqslant a \leqslant r\). Since \(\varrho \) is cyclic, V is generated by elements of the form

where \(m(B_1,B_2,B_3)\) are monomials in  . Hence \(V'\) will be generated by certain linear combinations of such elements. Then relations (3.2) imply that \(V'\) is also preserved by \(B_3\). \(\square \)
. Hence \(V'\) will be generated by certain linear combinations of such elements. Then relations (3.2) imply that \(V'\) is also preserved by \(B_3\). \(\square \)
The construction of the moduli space of framed cyclic representations  with fixed dimension vector is very similar to the GIT construction of the moduli space of ADHM quiver representations presented in [20, Section 3.1]. In particular, proceeding by analogy with loc. cit., the cyclicity condition (Fr.4) is equivalent to a GIT stability condition, and the following holds.
with fixed dimension vector is very similar to the GIT construction of the moduli space of ADHM quiver representations presented in [20, Section 3.1]. In particular, proceeding by analogy with loc. cit., the cyclicity condition (Fr.4) is equivalent to a GIT stability condition, and the following holds.
Proposition 3.3
For any \(n, r \in {\mathbb {Z}}\), \(n,r \geqslant 1\), there is a quasi-projective fine moduli space \({{\mathscr {Q}}}(r,n)\) of framed cyclic representations \((V,B_1,B_2,B_3,I,J)\) of dimension vector (r, n). In particular any such representation has trivial automorphism group. Furthermore there is a natural forgetful morphism \(\imath :{{\mathscr {Q}}}(r,n)\rightarrow {{\mathscr {A}}}(r,n)\) to the moduli space of stable framed ADHM representations obtained by omitting the map \(B_3:V\rightarrow V\).
The connection to framed Higgs sheaves is provided by:
Proposition 3.4
There is a commutative diagram of morphisms of moduli stacks

where the vertical arrows are isomorphisms.
Proof
This follows from the construction of the left vertical isomorphism in diagram (3.3) given in [20, Theorem 2.1], which is based on the Beilinson spectral sequence. Then note that the latter is functorial with respect to morphisms of sheaves, and all the steps carried out in Section 2.1 of loc. cit. are naturally compatible with morphisms of framed sheaves. \(\square \)
3.2 Embedding in the ADHM moduli space
The main technical result of this section states that the forgetful morphism \(\imath :{{\mathscr {Q}}}(r,n)\rightarrow {{\mathscr {A}}}(r,n)\) is a closed embedding. This will be shown in several steps using the criterion proved in [28, Lemma 4]. In order to formulate the required conditions, note that the map \(\imath \) naturally preserves residual fields. That is, if \(\varrho _K\) is a point of \({{\mathscr {N}}}(r,n)\) with residual field K, then the residual field of the point \(\alpha _K=\imath (\varrho _K)\) is canonically isomorphic to K. This implies that there exists an induced map on Zariski tangent spaces
Then, as shown in [28, Lemma 4], it suffices to prove that:
-
(1)
\(\imath \) is universally injective, i.e., for any point \(\alpha _K\) of \({{\mathscr {A}}}(r,n)\) with residual field K there is at most one point \(\varrho _K\) of \({{\mathscr {N}}}(r,n)\), also with residual field K, such that \(\imath (\varrho _K)=\alpha _K\).
-
(2)
\(\imath \) is proper.
-
(3)
For any point \(\varrho _K\) of \({{\mathscr {Q}}}(r,n)\) the induced map on Zariski tangent spaces (3.4) is injective.
This will be carried out in three separate lemmas. Since \(\imath \) is the identity map for \(r=1\), it will be assumed \(r\geqslant 2\) below.
Lemma 3.5
\(\imath \) is universally injective.
Proof
This follows easily from the cyclicity condition (Fr.4). Let \(\varrho _K\) be an arbitrary framed cyclic representation defined over a \({\mathbb {C}}\)-field K of characteristic zero. Then its underlying vector space \(V_K\) is the K-linear span of
where \(m(B_{1,K}, B_{2,K})\) is an arbitrary monomial in the endomorphism ring \(\mathrm{End}_K(V_K)\). This uniquely determines \(B_{3,K}\) via the relations

This completes the proof. \(\square \)
Lemma 3.6
\(\imath \) is proper.
Proof
This will be proven using the valuative criterion for properness. Let R be a discrete valuation ring over \({\mathbb {C}}\), let \({\mathfrak m}\subset R\) denote the unique maximal ideal, and K its field of fractions. Using the categorical equivalence between R-modules and sheaves on  , flat families of stable representations of the ADHM quiver parametrized by
, flat families of stable representations of the ADHM quiver parametrized by  are in one-to-one correspondence to representations \(\alpha _R=(V_R, B_{1,R}, B_{2,R}, I_R, J_R)\) the ADHM quiver over R satisfying the following conditions:
are in one-to-one correspondence to representations \(\alpha _R=(V_R, B_{1,R}, B_{2,R}, I_R, J_R)\) the ADHM quiver over R satisfying the following conditions:
-
\(V_R\) is a free R-module, and \(B_{1,R}, B_{2,R} \in \mathrm{End}_R(V_R)\), \(I_R \in \mathrm{Hom}_R(R^{\oplus r}\!, V_R)\), \(J_R\in \mathrm{Hom}_R(V_R, R^{\oplus r})\) are morphisms of R modules such that
$$\begin{aligned}{}[B_{1,R}, B_{2,R}]+I_RJ_R=0. \end{aligned}$$ -
For any prime ideal \({{\mathfrak {p}}}\subset R\) the induced ADHM representation
 over the residual field \(k({{\mathfrak {p}}})\) is stable.
over the residual field \(k({{\mathfrak {p}}})\) is stable.
For simplicity let \(\alpha = (V, B_1, B_2, I,J)\) denote \(\alpha _{k({{\mathfrak {m}}})}\), which is a complex ADHM representation. Let also \(I_{R,a}:R \rightarrow V_R\), \(1\leqslant a\leqslant r\), denote the components of \(I_{R}\). Analogous notation will be used for the induced representations \(\alpha _K, \alpha \).
Since V is a finite dimensional complex vector space, it admits a finite set of generators
for some positive integers \(N_a\geqslant 1\). Therefore there is an exact sequence of \({\mathbb {C}}\)-vector spaces
where p is the canonical projection. By Nakayama’s lemma the elements

generate \(V_R\) as an R-module. In particular, the elements

generate \(V_K\) as a K-vector space. Moreover there is an exact sequence of finitely generated R-modules
as well as an exact sequence of K-vector spaces
where \(p_R,p_K\) are again the canonical projections. Since \(V_R\) is free, it follows that \(Y_R\) is isomorphic to a free module as well.
Suppose \(B_{3,K}:V_K \rightarrow V_K\) is a K-linear map satisfying relations (3.5). In detail, this is equivalent to
for all \(1\leqslant a\leqslant r-1\), \(1\leqslant i \leqslant N_a\) and
for all \(1\leqslant i \leqslant N_r\). Let
be the linear map determined on basis elements by
for all \(1\leqslant a\leqslant r-1\), \(1\leqslant i \leqslant N_a\) and
for all \(1\leqslant i \leqslant N_r\). By construction there is a commutative diagram

In particular,

Clearly, \({\overline{B}}_{3,K}\) extends to an R-module morphism
such that
for all \(1\leqslant a\leqslant r-1\), \(1\leqslant i \leqslant N_a\) and
for all \(1\leqslant i \leqslant N_r\). Furthermore, relation (3.6) implies

Hence  yields a morphism of R-modules \(B_{3,R} :V_R \rightarrow V_R\). By construction, this also satisfies the relations
yields a morphism of R-modules \(B_{3,R} :V_R \rightarrow V_R\). By construction, this also satisfies the relations
for all \(1\leqslant a\leqslant r-1\), \(1\leqslant i \leqslant N_a\) and
for all \(1\leqslant i \leqslant N_r\). Therefore this is the required extension. It is also unique by Lemma 3.5. \(\square \)
Finally, the third part of the proof consists of:
Lemma 3.7
For any point \(\varrho _K\) of \(\,{{\mathscr {Q}}}(r,n)\) the induced map on Zariski tangent spaces \(\imath _*:T_{\varrho _K}{{\mathscr {Q}}}(r,n) \rightarrow T_{\imath (\varrho _K)}{{\mathscr {A}}}(r,n)\) is injective.
Proof
The Zariski tangent spaces for moduli of quiver representations are canonically determined by linearizing the specified relations. In the present case, \(T_{\varrho _K}{{\mathscr {Q}}}(r,n)\) is isomorphic to the middle cohomology of the following complex of amplitude [0, 2):

where
for \(1\leqslant i\leqslant 3\). For simplicity, the subscript K in the notation used for the data of the representation \(\varrho _K\) has been suppressed. This convention will be employed only in the proof of the current lemma.
At the same time \(T_{\imath (\varrho )}{{\mathscr {A}}}(r,n)\) is isomorphic to the middle cohomology of the following complex of amplitude [0, 2):

where
for \(1\leqslant i \leqslant 2\). Note that there is a natural degree zero map of complexes determined by the obvious term-by-term canonical injections. Moreover, the cyclicity condition implies that \(f_0, g_0\) are injective by a straightforward argument.
Next note that the induced map on degree 1 cochains is also injective. Suppose a degree 1 cochain \((\epsilon _i, \epsilon , \delta )\) of the first complex maps to 0 in the second complex. This implies \(\epsilon =0\) and \(\eta =0\). Therefore the condition \(g_1(\epsilon _i, \epsilon , \delta ) = 0\) yields
Then the cyclicity condition implies that \(\epsilon _3\) must be identically zero. Since \(f_0, g_0\) are injective, this implies that the induced map in degree 1 cohomology is also injective. \(\square \)
In conclusion, using [28, Lemma 4], Lemmas 3.5, 3.6, 3.7 prove:
Proposition 3.8
The morphism \(\imath :{{\mathscr {Q}}}(r,n) \rightarrow {{\mathscr {A}}}(r,n)\) is a closed embedding.
3.3 The Hilbert scheme as a quiver moduli space
In order to simplify the notation, let  since \(D_r\) will always be a nonreduced plane in the following. The main goal of this section is to show that the natural forgetful morphism
since \(D_r\) will always be a nonreduced plane in the following. The main goal of this section is to show that the natural forgetful morphism  obtained from Proposition 2.2 is also a closed embedding. More precisely using the isomorphism
obtained from Proposition 2.2 is also a closed embedding. More precisely using the isomorphism  constructed in Proposition 3.4, it will be shown that h yields an isomorphism onto the closed subscheme of \({{\mathscr {Q}}}_0(r,n)\subset {{\mathscr {Q}}}(r,n)\) parametrizing representations \(\varrho \) with \(J=0\). The main idea of the proof is to show that the framed Higgs sheaf corresponding to a framed cyclic representation \(\varrho =(V,B_1,B_2,B_3, I, J)\) is a Higgs sheaf quotient as in Proposition 2.2 if and only if \(J=0\). This will require some intermediate steps. In the next two lemmas the ground field will be an arbitrary \({\mathbb {C}}\)-field K, although the index K will be suppressed in order to simplify the notation.
constructed in Proposition 3.4, it will be shown that h yields an isomorphism onto the closed subscheme of \({{\mathscr {Q}}}_0(r,n)\subset {{\mathscr {Q}}}(r,n)\) parametrizing representations \(\varrho \) with \(J=0\). The main idea of the proof is to show that the framed Higgs sheaf corresponding to a framed cyclic representation \(\varrho =(V,B_1,B_2,B_3, I, J)\) is a Higgs sheaf quotient as in Proposition 2.2 if and only if \(J=0\). This will require some intermediate steps. In the next two lemmas the ground field will be an arbitrary \({\mathbb {C}}\)-field K, although the index K will be suppressed in order to simplify the notation.
Let \(\alpha = (V,B_1,B_2, I,J)\) be the underlying ADHM representation of \(\varrho \). As shown in [20, Section 2.1], the framed sheaf corresponding to \(\alpha \) is the middle cohomology sheaf of the monad complex

where the terms have degrees \(-1,0,1\) and the differentials are given by
This complex will be denoted by \({{\mathscr {C}}}_\alpha \) in the following. As proven in [20, Lemma 2.7], it has trivial cohomology in degrees \(-1,1\). These statements are proven in loc. cit for ground field \({\mathbb {C}}\), but the generalization to an arbitrary ground field K is straightforward.
Now let \({{\mathscr {B}}}_\alpha \) denote the complex

where, again, the terms have degrees \(-1,0,1\) and the differentials are given by
If \(J=0\) there is an exact sequence of complexes

where the map \({{\mathscr {B}}}_\alpha \rightarrow {{\mathscr {C}}}_\alpha \) is the natural injection in each degree. It will be shown next that \({{\mathscr {B}}}_\alpha \) has trivial cohomology in degrees \(-1,0\).
Lemma 3.9
Suppose \(\alpha =(V,B_1,B_2,I,J)\) is a stable ADHM representation. Then the complex \({{\mathscr {B}}}_\alpha \) has trivial cohomology in degrees \(-1,0\) while its degree 1 cohomology sheaf has zero-dimensional support contained in  .
.
Proof
First note that the restriction of \({{\mathscr {B}}}_\alpha \) to \(\Delta \) is exact since \(z_1|_\Delta , z_2|_\Delta \) do not have any common zeroes. This implies that
is zero, hence \(H^1({{\mathscr {B}}}_\alpha )\) must be a torsion sheaf on S supported in the complement  . Since
. Since  , this implies that \(H^1({{\mathscr {B}}}_\alpha )\) must be a zero-dimensional sheaf, which further implies that
, this implies that \(H^1({{\mathscr {B}}}_\alpha )\) must be a zero-dimensional sheaf, which further implies that
Next note that \(g_{-1}\) is injective by the same argument as in [20, Lemma 2.7 (1)]. Namely, suppose \(g_{-1}\) is not injective. Then its kernel must be a nonzero torsion free sheaf and there is an exact sequence of \({{\mathscr {O}}}_S\)-modules

Moreover,  is a nonzero subsheaf since \(g_{-1}\) is not identically zero. Therefore
is a nonzero subsheaf since \(g_{-1}\) is not identically zero. Therefore  is a also a nonzero torsion free sheaf, hence locally free on the complement of a zero-dimensional subscheme \(Y\subset S\). This implies that
is a also a nonzero torsion free sheaf, hence locally free on the complement of a zero-dimensional subscheme \(Y\subset S\). This implies that  is locally free at any K-point
is locally free at any K-point  and the fiber
and the fiber  is the kernel of the restriction \(g_{-1}|_p\). As in [20, Lemma 2.7 (1)], this further implies that
is the kernel of the restriction \(g_{-1}|_p\). As in [20, Lemma 2.7 (1)], this further implies that  is a simultaneous eigenspace of \(B_1,B_2\) with eigenvalues \(\lambda _1, \lambda _2\) determined by
is a simultaneous eigenspace of \(B_1,B_2\) with eigenvalues \(\lambda _1, \lambda _2\) determined by
Since \(B_1, B_2\) are fixed, this condition can only hold for finitely many K-points p, leading to a contradiction. In conclusion \(g_{-1}\) is injective.
In order to prove exactness in the degree zero, suppose the middle cohomology sheaf \(H^0({{\mathscr {B}}}_\alpha )\) is not zero. Then the snake lemma yields an exact sequence

At the same time, since \(g_{-1}\) is injective,  has a two term locally free resolution, which implies that it is torsion free. Hence \(H^0({{\mathscr {B}}}_\alpha )\) must be a nonzero torsion free sheaf. However, since \(H^{-1}({{\mathscr {B}}}_\alpha )=0\), equation (3.7) implies that \(\mathrm{rk}\, H^0({{\mathscr {B}}}_\alpha )=0\), leading to a contradiction. In conclusion, \(H^0({{\mathscr {B}}}_\alpha )\) is also zero. \(\square \)
has a two term locally free resolution, which implies that it is torsion free. Hence \(H^0({{\mathscr {B}}}_\alpha )\) must be a nonzero torsion free sheaf. However, since \(H^{-1}({{\mathscr {B}}}_\alpha )=0\), equation (3.7) implies that \(\mathrm{rk}\, H^0({{\mathscr {B}}}_\alpha )=0\), leading to a contradiction. In conclusion, \(H^0({{\mathscr {B}}}_\alpha )\) is also zero. \(\square \)
Lemma 3.10
Let \(\varrho =(V,B_{1},B_{2},B_{3}, I,J)\) be a cyclic framed representation of \(({{\mathscr {Q}}},{{\mathscr {W}}})\). Then the framed Higgs sheaf corresponding to \(\varrho \) via Proposition 3.8 is a Higgs sheaf quotient as in Proposition 2.2 if and only if \(J=0\).
Proof
\((\Rightarrow )\). Suppose \(J=0\). As above, the framed sheaf \(E_\alpha \) corresponding to the ADHM representation \(\alpha =(V,B_1,B_2,I,J)\) is the middle cohomology sheaf of the monad complex \({{\mathscr {C}}}_\alpha \). Since \(J=0\), there is an exact sequence of complexes

where the last term from the left is regarded as a complex supported in degree 0. Using Lemma 3.9, this yields an exact sequence

where \(G_\alpha =H^1({{\mathscr {B}}}_\alpha )\) is a zero-dimensional \({{\mathscr {O}}}_S\)-module. Using the monad construction, the map \(B_3:V\rightarrow V\) yields morphisms \(\Phi :E_\alpha \rightarrow E_\alpha \), respectively \(\Upsilon :G_\alpha \rightarrow G_\alpha \) which are naturally compatible with the differentials of the above complex. Moreover, by construction, \(\Phi \) also satisfies the framing condition (2.6). Therefore one obtains indeed an exact sequence of framed Higgs sheaves
\((\Leftarrow )\). The above steps are reversible using the functoriality of the Beilinson spectral sequence. \(\square \)
To conclude, let \({{\mathscr {Q}}}_0(r,n)\) denote the closed subscheme of the moduli scheme \({{\mathscr {Q}}}(r,n)\) parameterizing cyclic framed representations \(\varrho \) with \(J=0\). Let \({{\mathscr {H}}}_0(r,n)\) denote the corresponding closed subscheme of the framed Higgs moduli space \({{\mathscr {H}}}(r,n)\) under the isomorphism \({{\mathscr {Q}}}(r,n) \simeq {{\mathscr {H}}}(r,n)\). Proposition 2.2 and Lemma 3.10 show that h yields a bijection between the set of K-points of the Hilbert scheme and the set of K-points of \({{\mathscr {H}}}_0(r,n)\) for any field K over \({\mathbb {C}}\). In fact, a stronger statement holds:
Proposition 3.11
The morphism  constructed below Proposition 2.2 factors through an isomorphism
constructed below Proposition 2.2 factors through an isomorphism  . In particular, h is a closed embedding.
. In particular, h is a closed embedding.
Proof
It suffices to generalize Lemma 3.10 to flat families. This is straightforward since the monad construction works in the relative setting. The details are very similar to those in [12, Sections 7.1 and 7.2], hence will be omitted. \(\square \)
4 Torus actions and fixed loci
Summarizing the previous results, there is a commutative diagram of scheme morphisms

where all horizontal arrows are closed embeddings. The top row consists of geometric moduli spaces, while the bottom row consists of the framed quiver moduli spaces obtained from the Beilinson spectral sequence. The goal of this section is to construct certain torus actions on all moduli spaces in the above diagram such that all arrows are equivariant, and prove certain properties of the fixed loci.
4.1 Generic torus action
First recall the natural action on the moduli space of framed sheaves of the \((r\,{+}\,2)\)-dimensional torus, namely,  with
with  . Namely, for any \((t_1,t_2, u_1, \dots , u_r)\in \mathbf{T}_{r+2}\) let \(\eta (t_1, t_2):{\mathbb {P}}^2 \rightarrow {\mathbb {P}}^2\) be the morphism induced by
. Namely, for any \((t_1,t_2, u_1, \dots , u_r)\in \mathbf{T}_{r+2}\) let \(\eta (t_1, t_2):{\mathbb {P}}^2 \rightarrow {\mathbb {P}}^2\) be the morphism induced by

and let u denote the diagonal \(r\times r\) matrix with diagonal elements \(u_1, \ldots , u_r\). Then the \(\mathbf{T}_{r+2}\)-action on \({{\mathscr {M}}}(r,n)\) is given by

This action does not preserve the moduli space of framed Higgs sheaves.
Let \(\mathbf{T}:=\mathbf{T}_3\) denote the torus  with coordinates \((t_1,t_2,t_3)\). The threefold X in Sect. 2 is canonically isomorphic to
with coordinates \((t_1,t_2,t_3)\). The threefold X in Sect. 2 is canonically isomorphic to  . Hence there is a three-dimensional torus action on the Hilbert scheme determined by the geometric action
. Hence there is a three-dimensional torus action on the Hilbert scheme determined by the geometric action  ,
,

There is also a natural \(\mathbf{T}\)-action on framed sheaf moduli, as well as framed Higgs sheaf moduli, making all the morphisms in the above diagram equivariant. This is obtained by restricting the \(\mathbf{T}_{r+2}\)-action on \({{\mathscr {M}}}(r,n)\) to a \(\mathbf{T}\)-action via the injective group morphism \(\mathbf{T} \hookrightarrow \mathbf{T}_{r+2}\),
It is straightforward to check that the resulting \(\mathbf{T}\)-action on \({{\mathscr {M}}}(r,n)\) preserves the closed subscheme \({{\mathscr {H}}}(r,n)\).
The corresponding \(\mathbf{T}\)-actions on the framed quiver moduli spaces \({{\mathscr {N}}}(r,n)\) and \({{\mathscr {A}}}(r,n)\) are then easily obtained from the monad construction. As in the previous section, the components of I, J with respect to the fixed basis of \(V_\infty \) will be denoted by \(I_a:{\mathbb {C}}\rightarrow V\), \(J_a:V \rightarrow {\mathbb {C}}\), \(1\leqslant a \leqslant r\). Then the potential function is rewritten as
where by convention \(J_{0}=0\). The \(\mathbf{T}\)-action on \({{\mathscr {N}}}(r,n)\) will be given by

while the \(\mathbf{T}\)-action on \({{\mathscr {A}}}(r,n)\) will be given by the same expression with \(B_3\) omitted.
The next goal is to determine the T-fixed points in the framed quiver moduli space \({{\mathscr {Q}}}(r,n)\) up to  gauge transformations. The fixed locus \({{\mathscr {A}}}(r,n)^{\mathbf{T}_{r+2}}\) is finite and in one-to-one correspondence to r-partitions \(\mu =(\mu _1, \ldots , \mu _r)\) of n, as shown for example in [22, Proposition 2.9]. Geometrically, the fixed points in the moduli space of framed sheaves \({{\mathscr {M}}}(r,n)\) parametrize framed sheaves of the form
gauge transformations. The fixed locus \({{\mathscr {A}}}(r,n)^{\mathbf{T}_{r+2}}\) is finite and in one-to-one correspondence to r-partitions \(\mu =(\mu _1, \ldots , \mu _r)\) of n, as shown for example in [22, Proposition 2.9]. Geometrically, the fixed points in the moduli space of framed sheaves \({{\mathscr {M}}}(r,n)\) parametrize framed sheaves of the form
where \(I_{Z_a}\) is the ideal sheaf of the \(\mathbf{T}_{r+2}\)-invariant zero-dimensional subscheme \(Z_{\mu _a}\) parameterized by the partition \(\mu _a\). The framing \(\xi _\mu \) is the natural framing determined by the injections  , \(1\leqslant a\leqslant r\).
, \(1\leqslant a\leqslant r\).
Partitions will be identified to Young diagrams using the conventions in [33, Section 0.1]. A partition \(\nu =(\nu ^1\geqslant \cdots \geqslant \nu ^{l})\) will be identified with the set of integral points

consisting of l columns of heights \(\nu ^i\), \(1\leqslant i \leqslant l\). As usual, such a set is also canonically identified with a collection of boxes. Then note:
Proposition 4.1
-
(i)
The \(\mathbf{T}\)-fixed locus \({{\mathscr {A}}}(r,n)^\mathbf{T}\) coincides with \({{\mathscr {A}}}(r,n)^{\mathbf{T}_{r+2}}\).
-
(ii)
A T-fixed point \(\alpha _\mu \in {{\mathscr {A}}}(r,n)^\mathbf{T}\) belongs to \({{\mathscr {Q}}}(r,n)^\mathbf{T}\) if and only if the r-partition \(\mu \) is nested, i.e.,
$$\begin{aligned} \mu _r\subseteq \mu _{r-1} \subseteq \cdots \subseteq \mu _1 \end{aligned}$$(4.1)as Young diagrams. Hence the T-fixed locus \({{\mathscr {Q}}}(r,n)^\mathbf{T}\) is finite and in one-to-one correspondence to nested r-partitions.
-
(iii)
The natural closed embedding \(\eta :{{\mathscr {Q}}}_0(r,n) \hookrightarrow {{\mathscr {Q}}}(r,n)\) yields an isomorphism of \(\mathbf{T}\)-fixed loci. Hence the T-fixed locus \({{\mathscr {Q}}}_0(r,n)^\mathbf{T}\) is also finite and in one-to-one correspondence to nested r-partitions.
Proof
Statement (i) follows from the observation that \(\mathbf{T}\subset \mathbf{T}_{r+2}\) is sufficiently generic. In particular, since \((t_1, t_2, t_3)\) are independent parameters, any \(\mathbf{T}\)-fixed framed sheaf still has to split as a direct sum of equivariant ideal sheaves.
(ii) Suppose \((E,\xi , \Phi )\) is a \(\mathbf{T}\)-fixed framed Higgs sheaf. Then \((E,\xi )\) is a T-fixed framed Higgs sheaf, hence it is isomorphic to a framed sheaf of the form \((E_\mu , \xi _\mu )\). Moreover, the T-fixed condition implies that the only nonzero components of the Higgs field are injections  , \(1\leqslant a \leqslant r\), where \(Z_{r+1}\) is the empty subscheme. Using the snake lemma, each such injection is equivalent to an equivariant surjective morphism
, \(1\leqslant a \leqslant r\), where \(Z_{r+1}\) is the empty subscheme. Using the snake lemma, each such injection is equivalent to an equivariant surjective morphism  , which yields the nesting condition (4.1). Clearly, the converse, also holds, since the equivariant projections
, which yields the nesting condition (4.1). Clearly, the converse, also holds, since the equivariant projections  are uniquely determined by the inclusions \(\mu _{a+1} \subseteq \mu _a\).
are uniquely determined by the inclusions \(\mu _{a+1} \subseteq \mu _a\).
Using Proposition 3.11, it suffices to note that all \(\mathbf{T}\)-fixed ADHM data have \(J=0\). \(\square \)
Note that nested ideal sheaves on surfaces occur through localization in a similar context [14, 37].
4.2 Calabi–Yau specialization
The Calabi–Yau torus is by definition the two-dimensional subtorus \(\mathbf{T}_0\hookrightarrow \mathbf{T}\) defined by
Geometrically this is the subtorus of \(\mathbf{T}\) which preserves the natural holomorphic three-form on  , where \({{\mathbb {A}}}^2 \subset {\mathbb {P}}^2\) is the complement of \(\Delta = \{z_0=0\}\). The goal of this section is to analyze the behavior of the fixed loci under this specialization.
, where \({{\mathbb {A}}}^2 \subset {\mathbb {P}}^2\) is the complement of \(\Delta = \{z_0=0\}\). The goal of this section is to analyze the behavior of the fixed loci under this specialization.
First note the following:
Remark 4.2
-
(i)
For rank \(r=1\) the \(\mathbf{T}_0\)-action on the moduli space \({{\mathscr {A}}}(1,n)\), \(n\geqslant 1\), coincides with the standard two-dimensional torus action induced by the scaling action on \({{\mathbb {A}}}^2\). In particular the \(\mathbf{T}_0\)-fixed locus in \({{\mathscr {A}}}(1,n)\) is a finite set of closed points in one-to-one correspondence with partitions \(\mu \) of n.
-
(ii)
For \(r\geqslant 2\) there is a natural action of the quotient torus \(\mathbf{S}=\mathbf{T}/\mathbf{T}_0\simeq {\mathbb {C}}^\times \) on the fixed locus \({{\mathscr {A}}}(r,n)^\mathbf{T}\) given by
 (4.2)
(4.2)Clearly, the fixed locus of the S-action on \({{\mathscr {A}}}(r,n)^{\mathbf{T}_0}\) coincides with the fixed locus \({{\mathscr {A}}}(r,n)^\mathbf{T}\). The \(\mathbf{S}\)-action on the \(\mathbf{T}_0\)-fixed locus will be called residual torus action.
The main goal of this section is a detailed analysis of \(\mathbf{T}_0\)-fixed locus in \({{\mathscr {A}}}(r,n)\). In order to fix ideas, note the following basic facts on flat families of \(\mathbf{T}_0\)-fixed loci.
Let Z be an arbitrary parameter scheme over \({\mathbb {C}}\). A flat family of stable framed ADHM quiver representations parametrized by Z is defined by a pair \((\alpha , \zeta )\) where
-
\(\alpha =(V, V_\Box , B_1, B_2, I, J)\) is a locally free ADHM quiver sheaf on Z with
 ,
, -
 is an isomorphism of \({{\mathscr {O}}}_Z\)-modules, and
is an isomorphism of \({{\mathscr {O}}}_Z\)-modules, and -
the restriction of the pair \((\alpha , \zeta )\) to any point in Z is a stable framed representation of the ADHM quiver over the corresponding residual field.
For each \(1\leqslant a \leqslant r\) let \(I_a, J_a\) denote the components of the morphisms  and
and  respectively. Let also
respectively. Let also  denote the principal
denote the principal  -bundle associated to V on Z.
-bundle associated to V on Z.
A flat family of \(\mathbf{T}_0\)-fixed framed stable ADHM quiver representations is defined by the data \((\alpha , \zeta , \eta )\) where \((\alpha , \zeta )\) are as above, and  is a morphism of groups over Z such that
is a morphism of groups over Z such that
for any morphisms \(t_1, t_2:Z \rightarrow \mathbf{T}_0\). In particular, \(\eta \) determines a \(\mathbf{T}_0\)-equivariant structure on the underlying locally free \({{\mathscr {O}}}_Z\)-module V. Let

denote the resulting character decomposition. Then conditions (4.3) imply that

for all \(1\leqslant a \leqslant r\). Moreover, only the following components:
of \(B_1, B_2\) are allowed to be nonzero. All other components must vanish identically. Hence the ADHM relation reduces to
for all \(1\leqslant a\leqslant r\).
The first structure result is the following.
Lemma 4.3
Let Y be a connected component of the fixed locus \({{\mathscr {A}}}(r,n)^{\mathbf{T}_0}\). Let \(y\in Y\) be an arbitrary closed point and let  be the \(\mathbf{S}\)-orbit through y. Then \(f_y\) extends uniquely to a morphism \({{\overline{f}}}_y :{{\mathbb {A}}}^1\rightarrow Y\). In particular the \(\mathbf{S}\)-fixed locus \(Y^\mathbf{S}\) contains at least one point.
be the \(\mathbf{S}\)-orbit through y. Then \(f_y\) extends uniquely to a morphism \({{\overline{f}}}_y :{{\mathbb {A}}}^1\rightarrow Y\). In particular the \(\mathbf{S}\)-fixed locus \(Y^\mathbf{S}\) contains at least one point.
Proof
If the \(\mathbf{S}\)-action on Y is trivial, Y is a connected component of the fixed locus \({{\mathscr {A}}}(r,n)^\mathbf{T}\), which is finite. Hence the claim is obvious.
Suppose the \(\mathbf{S}\)-action on Y is not trivial. If \(y \in Y^\mathbf{S}\), which is again finite, the claim follows. Therefore it suffices to consider the case where y is not \(\mathbf{S}\)-fixed. Then the given orbit is nontrivial and the claim is proven by analogy to [21, Theorem 3.7]. The moduli space \({{\mathscr {A}}}(r, n)\) is a GIT quotient  where
where

is the zero locus \([B_1,B_2]+IJ=0\). By construction, there is a projective morphism \(\pi :{{\mathscr {A}}}(r,n)\rightarrow {{\mathscr {A}}}_{0}(r,n)\) to the affine algebro-geometric quotient, which is the spectrum of the ring of  -invariant polynomials on \({{\mathscr {R}}}(r,n)\). As in the proof of [21, Theorem 3.7], the latter is generated by the following types of functions:
-invariant polynomials on \({{\mathscr {R}}}(r,n)\). As in the proof of [21, Theorem 3.7], the latter is generated by the following types of functions:
where \(m(B_1,B_2)\) denotes an arbitrary monomial in  . The functions of the first type have weights
. The functions of the first type have weights
under the action of \(\mathbf{T}=({\mathbb {C}}^{\times })^{\times 3}\). The functions of the second type have weights
If all the above invariant functions have trivial restriction to Y, it follows that Y is a closed subscheme of \(\pi ^{-1}(0)\), hence it is projective. Then the claim follows.
Suppose this is not the case. Then note that the fixed locus conditions (4.4) and (4.5) imply that \(f_y^*\pi ^*\mathrm{Tr}_{\,{\mathbb {C}}^n}(m(B_1,B_2))=0\). Therefore the exists a pair (a, b), \(1\leqslant a,b\leqslant r\), such that \(f_y^*\pi ^*(J_b\,m(B_1,B_2)I_a)\) is nonzero. Then the fixed locus conditions imply that
and the \(\mathbf{S}\)-weight of \(f_y^*\pi ^*(J_b\, m(B_1,B_2)I_a)=0\) is \(a-b \geqslant 1\). This further implies that the morphism  extends uniquely to \({{\mathbb {A}}}^1\). Since \(\pi \) is projective, \(f_y\) can be also extended to a morphism \({{\mathbb {A}}}^1 \rightarrow {{\mathscr {A}}}(r,n)\). Since Y is a closed subscheme of \({{\mathscr {A}}}(r,n)\), the claim follows. \(\square \)
extends uniquely to \({{\mathbb {A}}}^1\). Since \(\pi \) is projective, \(f_y\) can be also extended to a morphism \({{\mathbb {A}}}^1 \rightarrow {{\mathscr {A}}}(r,n)\). Since Y is a closed subscheme of \({{\mathscr {A}}}(r,n)\), the claim follows. \(\square \)
In order to formulate the next result note that, omitting the rigidifying isomorphism \(\zeta :V_\Box \rightarrow {{\mathscr {O}}}_Z^{\oplus r}\), coherent ADHM quiver sheaves on Z form an abelian category \({{\mathscr {A}}}_Z\). Let also \(\mathbf{e}_a\), \(1\leqslant a \leqslant r\), be the standard basis vectors in \({\mathbb {C}}^r\) and let
be the filtration defined by

all inclusions being canonical. Then one has:
Lemma 4.4
Let \(\alpha \) be a flat family of \(\,\mathbf{T}_0\)-fixed stable framed ADHM quiver representations with dimension vector (r, n) parametrized by a connected scheme Z. Suppose furthermore that J is identically zero. Let

be the filtration induced by (4.6). Then there exist an unique r-partition \(\mu \) of n and a filtration \(\alpha _\bullet \)
in the abelian category \({{\mathscr {A}}}_Z\) such that
-
(i)
the restriction of \(\alpha _\bullet \) to the node \(\Box \) coincides with the filtration (4.7), and
-
(ii)
each successive quotient \({{\overline{\alpha }}}_a\), \(1\leqslant a\leqslant r\), is isomorphic to the stable framed ADHM representation corresponding to \(\mathbf{T}_0\)-fixed point \(\alpha _{\mu _a}\!\in {{\mathscr {A}}}(1, |\mu _a|)^{\mathbf{T}_0}\).
Proof
As observed above, V has a \(\mathbf{T}_0\)-character decomposition
such that the ADHM data satisfy conditions (4.4) and (4.5). Moreover, stability implies that V(i, j) is identically zero if \(i\geqslant r\) or \(j\geqslant r\). Let
be the filtration defined by

where all the inclusions are canonical. Then conditions (4.4), (4.5) imply that
In addition, since J is assumed identically zero, the ADHM relation restricts to
Let \({{\overline{V}}}_a= V^{(a)}/V^{(a-1)}\), respectively \({\overline{V}}_{\Box ,a}= V^{(a)}_\Box /V^{(a-1)}_\Box \simeq {\mathbb {C}}\langle \mathbf{e}_a\rangle \), \(1\leqslant a\leqslant r\), where \(V^{(0)}=0\) and \(V_\Box ^{(0)}=0\). Equations (4.9) imply that there are naturally induced maps
such that \([{{\overline{B}}}_{1,a}, {{\overline{B}}}_{2,a}]=0\). At the same time, the ADHM stability condition on \(\alpha \) implies that the data \({{\overline{\alpha }}}_a = ({{\overline{V}}}_a, {{\overline{B}}}_{i,a}, {{\overline{I}}}_a)\) is a framed stable rank one ADHM representation over Z for each \(1\leqslant a \leqslant r\). Finally, by construction, each \({{\overline{\alpha }}}_a\) is a \(\mathbf{T}_0\)-fixed point in the moduli space of rank one ADHM representations \({{\mathscr {A}}}(1,n_a)^{\mathbf{T}_0}\) where  . Since Z is connected and \({{\mathscr {A}}}(1,n_a)^{\mathbf{T}_0}\) is a finite set of closed points indexed by partitions of \(n_a\), the claim follows. \(\square \)
. Since Z is connected and \({{\mathscr {A}}}(1,n_a)^{\mathbf{T}_0}\) is a finite set of closed points indexed by partitions of \(n_a\), the claim follows. \(\square \)
In order to formulate a useful consequence of Lemmas 4.3 and 4.4 recall the projective morphism to the affine geometric quotient, \(\pi :{{\mathscr {A}}}(r,n)\rightarrow {{\mathscr {A}}}_0(r,n)\), used in the proof of Lemma 4.3. Then one has:
Corollary 4.5
Let \(Y\subset {{\mathscr {A}}}(r,n)^{\mathbf{T}_0}\) be a connected component of the \(\mathbf{T}_0\)-fixed locus such that \(\mathbf{S}\)-action on Y is nontrivial. Then Y is not projective over \({\mathbb {C}}\).
Proof
A priori Y is smooth quasi-projective. Suppose Y is projective. Then the fixed locus \(Y^\mathbf{S}\) is nonempty and consists of finitely many points in \({{\mathscr {A}}}(r,n)^\mathbf{T}\). Moreover, all T-fixed points are mapped to 0 by \(\pi \). Since \({{\mathscr {A}}}_0(r,n)\) is affine and Y is connected, it follows that Y must be contained as a closed subscheme in the fiber \(\pi ^{-1}(0)\).
Let \(\alpha _Y\) denote the restriction of the universal family of stable framed ADHM data to Y. Since \(\pi (Y)=\{0\}\) all the generators of polynomial ring \(\varGamma ({{\mathscr {A}}}_0(r,n))\), in particular
have trivial pull-back to Y. Then the ADHM stability condition implies that the family \(\alpha _Y\) has \(J=0\). Therefore, as shown in Lemma 4.4, there is a filtration of the form (4.8). However, given the action (4.2) of \(\mathbf{S}\), a point \(y\in Y\) is fixed by S if and only if the induced filtration on \(\alpha _Y|_y\) is split. Therefore \(Y^\mathbf{S}\) consists of the unique closed point \(\alpha _\mu \in {{\mathscr {A}}}(r,n)^\mathbf{T}\), where \(\mu \) is the r-partition determined by \(\alpha _Y\) as in Lemma 4.4. This contradicts the assumption that Y is smooth projective and the \(\mathbf{S}\)-action on Y is nontrivial. \(\square \)
Next, a \(\mathbf{T}\)-fixed point \(\alpha _\mu \in {{\mathscr {A}}}(r,n)^\mathbf{T}\) will be called \(\mathbf{T}_0\)-isolated if and only if \(\{\alpha _\mu \}\) is a zero-dimensional connected component of the fixed locus \({{\mathscr {A}}}(r,n)^{\mathbf{T}_0}\). Then it will be shown below that \(\alpha _\mu \) is \(\mathbf{T}_0\)-isolated for all nested partitions \(\mu \). The proof will use the \(\mathbf{T}_{r+2}\)-character decomposition of the tangent space to the fixed point \({\alpha _\mu }\in {{\mathscr {A}}}(r,n)^{\mathbf{T}_{r+2}}\). As in [33, Section 3.2], let \(q,t,\chi _a:\mathbf{T}_{r+2}\rightarrow {\mathbb {C}}\) be the characters defined by

Given a partition \(\nu \subset {\mathbb {Z}}^2\), for any box \(s= (i(s), j(s))\in {\mathbb {Z}}^2\) one defines
-
\(\ell _\nu (s) = \nu _{i(s)} - j(s)-1\),
-
\(a_\nu (s) = \nu ^{t}_{j(s)} -i(s) -1\)
where \(\nu _{i}\) denotes the number of boxes on the i-th column of \(\nu \) and \(\nu ^t_j\) denotes the number of boxes on the j-th column of \(\nu ^t\), which is the same as the number of boxes on the j-th row of \(\nu \). Note that the above numbers are negative if \(s\notin \nu \).
Then, as shown in [22, Theorem 2.11], the explicit formula for the character decomposition of \(T_\mu \) is

Abusing notation, below let q, t denote the restrictions of the characters q, t to \(\mathbf{T}\). Let also \(\sigma :\mathbf{T}\rightarrow {\mathbb {C}}\) denote the character \(\sigma (t_1,t_2,t_3) = t_1t_2t_3\). For any r-partition \(\mu \) of n, let

be the \(\mathbf{T}\)-character decomposition of \(T_\mu \). Moreover, let \(\mathsf{S}_1(\mu )\) denote the set of triples (b, c, s) defined by the following conditions:

Let also \(\mathsf{S}_2({\mu })\) denote the set of triples (b, c, s) defined by:

Then the following holds:
Lemma 4.6
Let \(\mu \) be an r-partition of n. Then, using the notation in (4.12), there is an identity

in the character ring of \(\,\mathbf{T}\).
Proof
Specializing (4.11) to \(\mathbf{T}\subset \mathbf{T}_{r+2}\), one obtains

Therefore such eigenvectors are in one-to-one correspondence to triples (b, c, s), \(1\leqslant b,c \leqslant r\), satisfying one of the following two conditions:
For any triple (b, c, s) as in (4.16) one has \(a_{\mu _b}(s) \geqslant 0\) since \(s\in \mu _b\). Hence \(b-c \geqslant 1\) from the second equation in (4.16), and \(\ell _{\mu _c}(s) = c-b \leqslant -1\) from the first equation in (4.16). In particular,  , which must be necessarily nonempty. This yields conditions (4.13).
, which must be necessarily nonempty. This yields conditions (4.13).
For any triple (b, c, s) as in (4.17), one has \(a_{\mu _c}(s) \geqslant 0\) since \(s\in \mu _c\). Hence \(b-c\leqslant 0\) from the second equation in (4.17). If \(b-c=0\), then \(\mu _b=\mu _c\) and \(\ell _{\mu _b}(s) \geqslant 0\). This contradicts the first equation in (4.17). Therefore \( b-c\leqslant -1\), and the first equation in (4.17) implies \(\ell _{\mu _b}(s) = b-c-1\leqslant -2\). Hence  must be nonempty and
must be nonempty and  .
.
In conclusion, equation (4.14) follows from (4.15). \(\square \)
In order to formulate the next result, note that an r-partition \(\mu \) of n will be said to be contained, \(\mu \subset \lambda \), into an r-partition of \(n+1\) if there exists \(1\leqslant a \leqslant r\) such that \(\mu _b = \lambda _b\) for all \(1\leqslant b\leqslant r\), \(b\ne a\), while \(\mu _a\subset \lambda _a\) as Young diagrams. In particular,  consists of a single box. Then one has the following consequence of Lemma 4.6.
consists of a single box. Then one has the following consequence of Lemma 4.6.
Corollary 4.7
-
(i)
Let \(\mu \) be a nested r-partition of n, i.e.,
$$\begin{aligned} \mu _r \subseteq \mu _{r-1} \subseteq \cdots \subseteq \mu _1. \end{aligned}$$Then identity (4.14) reduces to
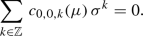
-
(ii)
Let \(\lambda \) be a nested r-partition of n and let \(\mu \supset \lambda \) be an r-partition of \(n+1\) such that \(\mu \) is not nested. Then identity (4.14) reduces to

-
(iii)
Let \(\lambda \) be a nested r-partition of \(n+1\) and let \(\mu \subset \lambda \) be an r-partition of n such that \(\mu \) is not nested. Then identity (4.14) reduces to

Furthermore, in each case suppose Y is the unique connected component of the \(\mathbf{T}_0\)-fixed locus containing the T-fixed point \(\alpha _\mu \). Then \(Y=\{\alpha _\mu \}\) in case (i), while in cases (ii) and (iii) one has an isomorphism \(Y\simeq {{\mathbb {A}}}^1\) mapping \(\alpha _\mu \) to \(0\in {{\mathbb {A}}}^1\).
Proof
(i) Since \(\mu \) is nested, one has \(\mathsf{S}_1(\mu ) = \mathsf{S}_2(\mu ) =\varnothing \).
(ii) Under the stated assumptions, there exists exactly one index \(2\leqslant b \leqslant r\) such that \(\lambda _c=\mu _c\) for all \(1\leqslant c \leqslant r\), \(c\ne b\), while  consists of a single box s. Since \(\mu \) is nested one has \(\mathsf{S}_1(\lambda )=\{(b,b-1,s)\}\). At the same time note that for all triples in \(\mathsf{S}_2(\mu )\) one has \(\ell _{\mu _b}\leqslant -2\). Since \(\mu \) is nested, this implies \(\mathsf{S}_2(\mu )=\varnothing \).
consists of a single box s. Since \(\mu \) is nested one has \(\mathsf{S}_1(\lambda )=\{(b,b-1,s)\}\). At the same time note that for all triples in \(\mathsf{S}_2(\mu )\) one has \(\ell _{\mu _b}\leqslant -2\). Since \(\mu \) is nested, this implies \(\mathsf{S}_2(\mu )=\varnothing \).
The proof of (iii) is analogous to that of (ii).
The last statement then follows from Corollary 4.5. \(\square \)
Finally, note the following.
Lemma 4.8
The \(\mathbf{T}_0\)-fixed locus  coincides with the \(\mathbf{T}\)-fixed locus
coincides with the \(\mathbf{T}\)-fixed locus  . Moreover, any \(\mathbf{T}_0\)-connected component Y intersecting \(\mathrm{Hilb}(r,n)\) nontrivially must be a single \(\mathbf{T}_0\)-isolated point belonging to
. Moreover, any \(\mathbf{T}_0\)-connected component Y intersecting \(\mathrm{Hilb}(r,n)\) nontrivially must be a single \(\mathbf{T}_0\)-isolated point belonging to  .
.
Proof
Clearly, there is a closed embedding  . Let Z be a nonempty connected component of
. Let Z be a nonempty connected component of  . Since \(\mathrm{Hilb}(r,n)\) is a closed subscheme of \({{\mathscr {A}}}(r,n)\), there exists a unique connected component Y of \({{\mathscr {A}}}(r,n)^{\mathbf{T}_0}\) such that Z is the scheme theoretic intersection
. Since \(\mathrm{Hilb}(r,n)\) is a closed subscheme of \({{\mathscr {A}}}(r,n)\), there exists a unique connected component Y of \({{\mathscr {A}}}(r,n)^{\mathbf{T}_0}\) such that Z is the scheme theoretic intersection  . In particular Z is a closed subscheme of Y. Moreover, Z is also naturally preserved by the residual S-action.
. In particular Z is a closed subscheme of Y. Moreover, Z is also naturally preserved by the residual S-action.
If the \(\mathbf{S}\)-action on Z is trivial, then Z is a finite set of \(\mathbf{T}\)-fixed closed points in \({{\mathscr {A}}}(r,n)\) which also belong to \(\mathrm{Hilb}(r,n)\). Then Corollary 4.7 shows that each such point is \(\mathbf{T}_0\)-isolated. Hence Z coincides with Y, which is assumed connected. Hence Y must reduce to a single T-fixed point belonging to \(\mathrm{Hilb}(r,n)\).
Suppose the \(\mathbf{S}\)-action on Z in not trivial. Since Z is closed in Y, Lemma 4.3 implies that Z contains at least one S-fixed point. Then the same argument as in the previous paragraph shows that Y must be a single \(\mathbf{T}\)-fixed point belonging to \(\mathrm{Hilb}(r,n)\). \(\square \)
5 Hecke transformations
The goal of this section is to review the construction of Hecke transformations used in [33], at the same time proving certain properties of fixed points in the correspondence variety.
5.1 The ADHM correspondence variety
As in [33, Section 3.3], let \({{\mathscr {A}}}(r,n,n+1)\subset {{\mathscr {A}}}(r,n) \times {{\mathscr {A}}}(r,n+1)\) denote the Hecke correspondence parameterizing elementary modifications of framed torsion sheaves on \({\mathbb {P}}^2\) supported at a single closed point \(p\in {{\mathbb {A}}}^2\). Let \({{\mathscr {A}}}_{\mathrm{c}}(r,n,n+1)\subset {{\mathscr {A}}}(r,n,n+1)\) denote the closed subvariety where \(p=0\). According to [33, Proposition 3.1], the following holds.
Proposition 5.1
-
(1)
The correspondence variety \({{\mathscr {A}}}(r,n,n+1)\) is a smooth quasi-projective variety of dimension \(2rn+r+1\).
-
(2)
The natural morphism
 is a closed embedding, and the restriction of the projection
is a closed embedding, and the restriction of the projection  to \({{\mathscr {A}}}(r,n,n+1)\) is proper.
to \({{\mathscr {A}}}(r,n,n+1)\) is proper. -
(3)
The restriction of the projection
 to \({{\mathscr {A}}}_{\mathrm{c}}(r,n,n+1)\) is also proper.
to \({{\mathscr {A}}}_{\mathrm{c}}(r,n,n+1)\) is also proper. -
(4)
The correspondence variety is preserved by the \(\mathbf{T}_{r+2}\)-action on the product and the fixed locus \({{\mathscr {A}}}(r, n, n+1)^{\mathbf{T}_{r+2}}\) is a finite set of closed points in one-to-one correspondence with pairs of r-partitions \((\mu , \lambda )\) such that
$$\begin{aligned} |\mu |=n, \quad |\lambda | = n+1, \quad \mu \subset \lambda . \end{aligned}$$(5.1)Written more explicitly, the last condition in (5.1) states that there exists \(1\leqslant b \leqslant r\) such that \(\mu _a=\lambda _a\) for all \(1\leqslant a\leqslant r\), \(a\ne b\), while \(\mu _b \subset \lambda _b\) and
 consists of a single box s.
consists of a single box s.
Remark 5.2
Note that Proposition 4.1 (i) implies that the fixed locus \({{\mathscr {A}}}(r,n,n+1)^\mathbf{T}\) coincides with the \(\mathbf{T}_{r+2}\) fixed locus. Therefore T-equivariant Hecke transformations are defined in complete analogy to [33]. This is briefly reviewed below.
Let  denote the natural closed embedding, which is clearly \(\mathbf{T}\)-equivariant. As in [33, Section 2.2], any equivariant Borel–Moore homology class \(z\in H^{\mathbf{T}}({{\mathscr {A}}}(r,n,n+1))\) determines a Hecke transformation,
denote the natural closed embedding, which is clearly \(\mathbf{T}\)-equivariant. As in [33, Section 2.2], any equivariant Borel–Moore homology class \(z\in H^{\mathbf{T}}({{\mathscr {A}}}(r,n,n+1))\) determines a Hecke transformation,

The pull-back and push-forward maps in equivariant Borel–Moore homology are well defined since \(\gamma \) is a closed embedding and the restriction of \(\pi _2\) to \({{\mathscr {A}}}(r,n,n+1)\) is proper. Although \(\pi _1\) is not proper, its restriction to the \(\mathbf{T}\)-fixed locus is. Therefore, using the localization theorem one can define downward Hecke transformations on equivariant Borel–Moore homology

Moreover, the following explicit formulas hold by a straightforward application of the localization theorem for the correspondence variety. These formulas have been used for example in [33, Appendix C], hence the proof will be omitted.
Lemma 5.3
-
(i)
For any r-partition \(\mu \),
 (5.4)
(5.4)where \(z_{\nu , \lambda }\) denotes the restriction of z to the fixed point \((\alpha _\nu , \alpha _\lambda )\).
-
(ii)
In the opposite direction,
 (5.5)
(5.5)
In order to construct analogous transformations for the Hilbert scheme  one needs first some structure results for the fixed locus \({{\mathscr {A}}}(r,n)^{\mathbf{T}_0}\), which are proven in the next section.
one needs first some structure results for the fixed locus \({{\mathscr {A}}}(r,n)^{\mathbf{T}_0}\), which are proven in the next section.
5.2 The fixed locus of the Calabi–Yau torus action
For any fixed point \(\alpha _\mu \in {{\mathscr {A}}}(r,n)^{\mathbf{T}_{r+2}}\) let \(V_\mu \) denote the underlying vector space, which carries a linear \(\mathbf{T}_{r+2}\)-action such that
As in (4.10), the characters \(q,t, \chi _a\), \(1\leqslant a \leqslant r\), are defined by
Using the notation in [33, Section 3.4], set \(\tau _\mu = {\mathrm{ch}}_{\,\mathbf{T}_{r+2}}\, V_\mu \) and \(w= \sum _{b=1}^r \chi _b^{-1}\) and let \(T_{\mu }\) denote the tangent space to \({{\mathscr {A}}}(r,n)\) at the fixed point \(\alpha _\mu \). As shown in [22, Theorem 2.11], the character of the equivariant tangent space \(T_{\mu }\) is given by

For any pair \((\mu ,\lambda )\) with \(|\mu |=n\), \(|\lambda |=n+1\) and \(\mu \subset \lambda \) let \(N_{\mu , \lambda }\) denote the fiber of the equivariant normal bundle to \({{\mathscr {A}}}(r,n,n+1)\) in the product  at the fixed point \((\alpha _\mu , \alpha _\lambda )\). Then the character of the \(\mathbf{T}_{r+2}\)-action on \(N_{\mu , \lambda }\) is given by [33, Equation (3.11)], which reads
at the fixed point \((\alpha _\mu , \alpha _\lambda )\). Then the character of the \(\mathbf{T}_{r+2}\)-action on \(N_{\mu , \lambda }\) is given by [33, Equation (3.11)], which reads

As observed in Remark 5.2, the fixed locus in the correspondence variety remains unchanged under specialization to \(\mathbf{T}\subset \mathbf{T}_{r+2}\). Moreover, the character decomposition of the tangent space to a fixed point \((\alpha _\mu , \alpha _\lambda )\) is obtained by straightforward specialization. As in Lemma 4.6, let \(\sigma :\mathbf{T}\rightarrow {\mathbb {C}}^\times \) denote the character \(\sigma (t_1,t_2, t_3) = t_1t_2t_3\). Then
Let \(T_{\mu ,\lambda }\) denote the \(\mathbf{T}\)-equivariant tangent space to the fixed point  . Let
. Let

be the \(\mathbf{T}\)-character decomposition of \(T_{\mu , \lambda }\). As in Sect. 4.2, a fixed point \((\alpha _\mu , \alpha _\lambda )\in {{\mathscr {A}}}(r,n,n+1)^\mathbf{T}\) will be called \(\mathbf{T}_0\)-isolated if and only if it is a connected component of the \(\mathbf{T}_0\)-fixed locus. Then one has:
Lemma 5.4
-
(i)
Suppose at least one r-partition of the pair \((\mu , \lambda )\) is nested. Then \(c_{0,0,k}=0\) for all \(k \geqslant 0\). In particular the fixed point \((\alpha _\mu , \alpha _\nu )\) is \(\mathbf{T}_0\)-isolated.
-
(ii)
Suppose \(\mu \) and \(\lambda \) are not nested, \(n\geqslant 1\), and there is a nested r-partition \(\nu \) of \(n-1\) such that \(\nu \subset \mu \). Then \(c_{0,0,1}=1\) and \(c_{0,0,k}=0\) for all \(k\in {\mathbb {Z}}\), \(k\ne 1\).
Proof
Note that
Using equations (5.6) and (5.7) one has

By assumption \(\tau _\lambda - \tau _\mu \) is a one dimensional representation of \(\mathbf{T}_{r+2}\) since \(\mu \subset \lambda \), and  consists of a single box. Hence the right-hand side of (5.8) reduces to
consists of a single box. Hence the right-hand side of (5.8) reduces to

Let

By analogy with [22, Theorem 2.11] this expression is given by
The \(\mathbf{T}\)-specialization of \(E_{\mu , \lambda }\) is
Let \(1\leqslant d\leqslant r\) be such that  while \(\lambda _b = \mu _b\) for \(b\ne d\). The terms with \(b=d\) and \(s=u\) in the right-hand side of the above equation are
while \(\lambda _b = \mu _b\) for \(b\ne d\). The terms with \(b=d\) and \(s=u\) in the right-hand side of the above equation are
where \(a_{\mu _d}(u) =-1\). Therefore the only term that specializes to 1 when \(\sigma =1\) corresponds to \(c=d\). This implies that all terms in (5.9) specializing to 1 as \(\sigma =1\) are obtained as follows.
Let \(\mathsf{S}_1(\mu , \lambda )\) denote the set of triples (b, c, s) with \(1\leqslant b, c \leqslant r\) and \(s\in \lambda _b\), \(s\ne u\) if \(b=d\), such that
Let \(\mathsf{S}_2(\mu , \lambda )\) denote the set of triples (b, c, s) with \(1\leqslant b, c \leqslant r\) and \(s\in \mu _c\) such that
Then the terms in (5.9) which specialize to 1 as \(\sigma =1\) are given by

Now consider a triple \((b,c,s)\in \mathsf{S}_1(\mu , \lambda )\). Since \(s\ne u\) for \(b=d\), it follows that \(s\in \mu _b\). This implies \(a_{\mu _b}(s)\geqslant 0\), hence \(b\geqslant c+1\). At the same time, \(\ell _{\lambda _c}(s) = c-b \leqslant -1\), hence \(s\notin \lambda _c\). In conclusion, \(b\geqslant c+1\) and  for any triple
for any triple  . Since \(\mu _b\subseteq \lambda _b\) and \(\mu _c \subseteq \lambda _c\), if \(\mu \) or \(\lambda \) is nested, this leads to a contradiction. Hence in that case \(\mathsf{S}_1(\mu , \lambda )=\varnothing \).
. Since \(\mu _b\subseteq \lambda _b\) and \(\mu _c \subseteq \lambda _c\), if \(\mu \) or \(\lambda \) is nested, this leads to a contradiction. Hence in that case \(\mathsf{S}_1(\mu , \lambda )=\varnothing \).
Suppose \(\mu , \lambda \) are not nested, and the conditions of Lemma 5.4 (ii) are satisfied. Since \(\nu \) is nested and \(\nu \subset \mu \) there is a unique index \(1\leqslant e \leqslant r-1\) and a unique box  such that \(v \notin \mu _e\). For all other indices \(1\leqslant b \leqslant r-1\), \(b \ne e\) one has \(\mu _{b+1}\subseteq \mu _b\). Then the argument in the previous paragraph implies that
such that \(v \notin \mu _e\). For all other indices \(1\leqslant b \leqslant r-1\), \(b \ne e\) one has \(\mu _{b+1}\subseteq \mu _b\). Then the argument in the previous paragraph implies that
A similar analysis applies to the set \(\mathsf{S}_2(\mu , \lambda )\). Let \((b,c,s) \in \mathsf{S}_2(\mu , \lambda )\). Since \(\mu _c \subseteq \lambda _c\) and \(s\in \mu _c\), it follows that \(a_{\lambda _c}(s)\geqslant 0\), hence \(c\geqslant b\). If \(c=b\), in order for \(s\in \mathsf{S}_2(\mu , \lambda )\) one must have
This leads to a contradiction since \(\mu _b \subseteq \lambda _b\) by assumption. Therefore one must have \(c\geqslant b+1\). This implies that \(a_{\lambda _c}(s)\geqslant 1\) and \(\ell _{\mu _b}(s) \leqslant -2\). The second condition implies that \(s\notin \mu _b\). If \(\mu \) or \(\lambda \) is nested this leads to a contradiction. Hence \(\mathsf{S}_2(\mu , \lambda )=\varnothing \).
In order to finish the proof, suppose \(\mu ,\lambda \) are not nested and the conditions of Lemma 5.4 (ii) are satisfied. Hence \(\mu = \nu \cup \{v\}\) with \(\nu \) nested. Since  with \(b \leqslant c-1\) one must have \((b,c,s) = (e,e+1,v)\). However in that case \(\ell _{\mu _b}(v) =-1\), which leads again to a contradiction. In conclusion \(\mathsf{S}_2(\mu , \lambda )=\varnothing \). \(\square \)
with \(b \leqslant c-1\) one must have \((b,c,s) = (e,e+1,v)\). However in that case \(\ell _{\mu _b}(v) =-1\), which leads again to a contradiction. In conclusion \(\mathsf{S}_2(\mu , \lambda )=\varnothing \). \(\square \)
To conclude, note the following consequence of Lemma 5.4.
Corollary 5.5
-
(i)
Let \(\mu \) be a nested r-partition of n. Suppose a connected component Z of \({{\mathscr {A}}}(r,n,n+1)^{\mathbf{T}_0}\) has nontrivial set theoretic intersection with the closed subvariety

Then Z must be a closed point \((\alpha _\mu , \alpha _\lambda )\) for some r-partition \(\lambda \) of \(n+1\) such that \(\lambda \supset \mu \).
-
(ii)
Let \(\lambda \) be a nested r-partition of \(n+1\). Suppose a connected component Z of \({{\mathscr {A}}}(r,n,n+1)^{\mathbf{T}_0}\) has nontrivial set theoretic intersection with the closed subvariety

Then Z must be a closed point \((\alpha _\mu , \alpha _\lambda )\) for some r-partition \(\mu \) of n such that \(\mu \subset \lambda \).
Proof
(i) Corollary 4.7 (i) shows that \(\alpha _\mu \) is an isolated point of the fixed locus \({{\mathscr {A}}}(r,n)^{\mathbf{T}_0}\). Therefore, Z must be contained as a closed subvariety in the fiber \(\pi _1^{-1}(\alpha _\mu )\). Moreover, since the fixed locus  , any connected component of \({{\mathscr {A}}}(r,n,n+1)^{\mathbf{T}_0}\) is a closed subvariety of \({{\mathscr {A}}}_{\mathrm{c}}(r,n,n+1)\). Since \({{\mathscr {A}}}_{\mathrm{c}}(r,n,n+1)\) is proper over \({{\mathscr {A}}}(r,n)\) by Proposition 5.1 (3), this implies that Z is proper over \({\mathbb {C}}\), hence projective. Therefore the induced residual \(\mathbf{S}\)-action on Z has at least one fixed point \((\alpha _\mu , \alpha _\lambda )\) with \(\mu \subset \lambda \). Since \(\mu \) is nested by assumption, Lemma 5.4 (i) shows that this fixed point is \(\mathbf{T}_0\)-isolated. Then the claim follows since Z is assumed connected.
, any connected component of \({{\mathscr {A}}}(r,n,n+1)^{\mathbf{T}_0}\) is a closed subvariety of \({{\mathscr {A}}}_{\mathrm{c}}(r,n,n+1)\). Since \({{\mathscr {A}}}_{\mathrm{c}}(r,n,n+1)\) is proper over \({{\mathscr {A}}}(r,n)\) by Proposition 5.1 (3), this implies that Z is proper over \({\mathbb {C}}\), hence projective. Therefore the induced residual \(\mathbf{S}\)-action on Z has at least one fixed point \((\alpha _\mu , \alpha _\lambda )\) with \(\mu \subset \lambda \). Since \(\mu \) is nested by assumption, Lemma 5.4 (i) shows that this fixed point is \(\mathbf{T}_0\)-isolated. Then the claim follows since Z is assumed connected.
The proof of (ii) is analogous. Z must be again projective since \({{\mathscr {A}}}(r,n,n+1)\) is proper over \({{\mathscr {A}}}(r,n,n+1)\). \(\square \)
5.3 Hecke transformations for the Hilbert scheme
The goal of this section is to construct analogues of the Hecke transformations (5.2) and (5.3) for the \(\mathbf{T}_0\)-equivariant Borel–Moore homology of the moduli space \(\mathrm{Hilb}(r,n)\) of framed cyclic representations of the quiver (3.1). As shown in Proposition 3.8, for each pair (r, n) there is a closed embedding  . Let
. Let  denote the scheme theoretic intersection of
denote the scheme theoretic intersection of  and
and  in
in  . Hence one has a Cartesian square
. Hence one has a Cartesian square

Let  and
and  . The second is proper by base change since the projection
. The second is proper by base change since the projection  is proper. However 1.1, one cannot define a refined Gysin pull-back \(\rho _1^!\) because \(\rho _1\) is not l.c.i. Furthermore, the construction of a virtual pull-back as in [17] also fails because the relative obstruction theory of \(\rho _1\) is not perfect of amplitude \([-1, 0]\). This precludes a straightfoward generalization of the Hecke transformations (5.2) and (5.3).
is proper. However 1.1, one cannot define a refined Gysin pull-back \(\rho _1^!\) because \(\rho _1\) is not l.c.i. Furthermore, the construction of a virtual pull-back as in [17] also fails because the relative obstruction theory of \(\rho _1\) is not perfect of amplitude \([-1, 0]\). This precludes a straightfoward generalization of the Hecke transformations (5.2) and (5.3).
One can use instead the embedding into the smooth ambient space \({{\mathscr {A}}}(r,n)\). Lemma 4.8 proves that the fixed locus  is finite and in one-to-one correspondence to nested r-partitions \(\mu \) of n. Moreover, each fixed \(\mathbf{T}_0\)-fixed point \(\alpha _\mu \) is isolated as a \(\mathbf{T}_0\)-fixed point in \({{\mathscr {A}}}(r,n)\). Therefore the push-forward map for localized homology is injective and yields an identification
is finite and in one-to-one correspondence to nested r-partitions \(\mu \) of n. Moreover, each fixed \(\mathbf{T}_0\)-fixed point \(\alpha _\mu \) is isolated as a \(\mathbf{T}_0\)-fixed point in \({{\mathscr {A}}}(r,n)\). Therefore the push-forward map for localized homology is injective and yields an identification

Here \(K_0\) denotes the fraction field of the cohomology ring \(H(B\mathbf{T}_0)\) and \([\alpha _\mu ]=i_{\mu *}(1)\) for any nested r-partition \(\mu \). Let also  denote the natural closed embedding, which is clearly \(\mathbf{T}_0\)-equivariant. As in [33, Section 2.2], any equivariant Borel–Moore homology class \(z\in H^{\mathbf{T}_0}({{\mathscr {A}}}(r,n,n+1))\) determines a Hecke transformation,
denote the natural closed embedding, which is clearly \(\mathbf{T}_0\)-equivariant. As in [33, Section 2.2], any equivariant Borel–Moore homology class \(z\in H^{\mathbf{T}_0}({{\mathscr {A}}}(r,n,n+1))\) determines a Hecke transformation,

The pull-back and push-forward maps in equivariant Borel–Moore homology are well defined since \(\gamma \) is a closed embedding and the restriction of \(\pi _2\) to \({{\mathscr {A}}}(r,n,n+1)\) is proper.
As shown in Lemma 5.4 (i), for any pair of r-partitions \((\nu , \lambda )\) with \(\nu \) nested, the closed point \((\alpha _\nu , \alpha _\lambda ) \in {{\mathscr {A}}}(r,n,n+1)\) is an isolated \(\mathbf{T}_0\)-fixed point. Let \(T_{\nu , \lambda }\) denote the tangent space to \({{\mathscr {A}}}(r,n,n+1)\) at \((\alpha _\nu , \alpha _\lambda )\). For any pair (r, n) let \({{\mathscr {P}}}(r,n)\) denote the set of r-partitions of n.
Lemma 5.6
For any nested r-partition \(\nu \),

where \(z_{\nu , \lambda }\) denotes the restriction of z to the fixed point \((\alpha _\nu , \alpha _\lambda )\). In particular, the Hecke transformation (5.10) maps  to
to  .
.
Proof
Note the Cartesian diagram

where the horizontal maps are closed embeddings. As observed below equation (2.8) in [33, Section 2.1], this yields the base-change identity
Since \(k_\nu \) is a closed embedding of smooth varieties, there is an identity

in the intersection ring of \({{\mathscr {A}}}(r,n){\times }\, {{\mathscr {A}}}(r,n+1)\). See for example [9, Section 2.6.21]. For each connected component Z of the fixed locus \({{\mathscr {A}}}(r,n,n+1)^{\mathbf{T}_0}\) let \(q_Z:Z\hookrightarrow {{\mathscr {A}}}(r,n,n+1)\) denote the natural closed embedding. Since the correspondence variety is smooth, the localization theorem yields
where \({{\mathscr {V}}}_Z\) is the normal bundle to Z in \({{\mathscr {A}}}(r,n,n+1)\). Then
Clearly, if the set theoretic intersection of Z with  in
in  is empty, the corresponding term in the right-hand side of (5.11) vanishes. On the other hand, Corollary 5.5 shows that the connected components intersecting
is empty, the corresponding term in the right-hand side of (5.11) vanishes. On the other hand, Corollary 5.5 shows that the connected components intersecting  nontrivially coincide with the finite set of isolated fixed points \((\alpha _\nu , \alpha _\lambda )\) where \(\lambda \supset \nu \). For each such fixed point, let \(q_{\nu , \lambda }:(\alpha _\nu , \alpha _\lambda )\hookrightarrow {{\mathscr {A}}}(r,n+1,n)\) denote the natural closed embedding and let
nontrivially coincide with the finite set of isolated fixed points \((\alpha _\nu , \alpha _\lambda )\) where \(\lambda \supset \nu \). For each such fixed point, let \(q_{\nu , \lambda }:(\alpha _\nu , \alpha _\lambda )\hookrightarrow {{\mathscr {A}}}(r,n+1,n)\) denote the natural closed embedding and let

Then

where \(T_{\nu , \lambda }\) is the tangent space to \({{\mathscr {A}}}(r,n,n+1)\) at \((\alpha _\nu , \alpha _\lambda )\), and \(z_{\nu ,\lambda }=q_{\nu ,\lambda }^*z\) denotes the restriction of z to \((\alpha _\nu , \alpha _\lambda )\).
Now let \(i_Y :Y\hookrightarrow {{\mathscr {A}}}(r, n+1)\) denote a connected component of the fixed locus \({{\mathscr {A}}}(r,n+1)^{\mathbf{T}_0}\) and let  denote the corresponding closed embedding. Let also \(N_Y\) denote the normal bundle to Y in \({{\mathscr {A}}}(r, n+1)\). The localization theorem yields
denote the corresponding closed embedding. Let also \(N_Y\) denote the normal bundle to Y in \({{\mathscr {A}}}(r, n+1)\). The localization theorem yields
where \(k_\nu ^* \gamma _{*} z\) is given by the right-hand side of equation (5.12). Clearly, one has

unless the component Y contains the point \(\alpha _\lambda \). If this is the case, Corollary 4.7 shows that

Moreover, in each case \(\alpha _\lambda \) is the unique \(\mathbf{S}\)-fixed point in Y. For ease of exposition, such a component will be denoted below by \(Y_\lambda \) while their equivariant normal bundles in \({{\mathscr {A}}}(r,n+1)\) will be denoted by \(N_\lambda \).
In conclusion, using equations (5.12) and (5.13) reduces to

Now let \(f_\lambda :\{\alpha _\lambda \}\hookrightarrow Y_\lambda \) denote the natural closed embedding. Note that  is a connected component of the \(\mathbf{T}_0\) action on
is a connected component of the \(\mathbf{T}_0\) action on  and its equivariant normal bundle in the product is naturally isomorphic to
and its equivariant normal bundle in the product is naturally isomorphic to

Moreover,

hence

Here \(f_{\lambda *}\) is the push-forward map

If \(\lambda \supset \nu \) is not nested, \(Y_\lambda \simeq {{\mathbb {A}}}^1\), hence the degree zero Borel–Moore homology vanishes, \(H_0(Y_\lambda ) =0\). Therefore if this is the case,

If \(\lambda \supset \nu \) is nested, \(Y_\lambda \) coincides with \(\alpha _\lambda \), hence

Therefore equation (5.14) reduces to

This yields equation (5.10). \(\square \)
In the opposite direction, let  be a basis element, where \(\lambda \) is a nested r-partition of \(n+1\). Let
be a basis element, where \(\lambda \) is a nested r-partition of \(n+1\). Let  be the natural closed embedding. Then
be the natural closed embedding. Then

and

The composition  is the identity, hence clearly,
is the identity, hence clearly,  is well defined. This defines a Hecke transformation in the opposite direction,
is well defined. This defines a Hecke transformation in the opposite direction,

Lemma 5.7
For any nested r-partition \(\lambda \),

In particular, the Hecke transformation (5.15) maps  to
to  .
.
Proof
Completely analogous to the proof of Lemma 5.6. \(\square \)
In conclusion, Lemmas 5.6 and 5.7 yield upward and downward Hecke transformations on the equivariant homology space

Abusing notation, they will be denoted by the same symbols, \(h^+_{z,n}\), \(h_{z,n+1}^-\), the distinction being clear from the context.
6 Degenerate DAHA action
The goal of this section is to prove that the transformations (5.10) and (5.15) yield a degenerate DAHA action on \(\mathbf{V}^{(r)}_{K_0}\).
6.1 The degenerate DAHA of Schiffmann and Vasserot
This section is a brief review the construction of the family algebras \(\mathbf{{SH}^\mathbf{c}}\) introduced in [33, Section 1], and further studied in [4]. The construction employs a formal parameter \(\kappa \) as well as an infinite set of formal parameters \(\mathbf{c}=(\mathbf{c}_l)_{l\geqslant 0}\). Using the notation of [33, Section 1.5], for any \(l\geqslant 0\) one defines

where s is yet another formal parameter. The right-hand sides of the last two equations should be regarded as formal Laurent power series of s by formally expanding the log functions. Then \(\mathbf{SH}^\mathbf{c}\) is generated by \(D_{-1,l}\), \(D_{0,l}\), \(D_{1,l}\), \(l\in {\mathbb {Z}}\), \(l\geqslant 0\), satisfying the relations:
The elements \(E_l\) are expressed in terms of the generators via the power series identity

The parameters \(\mathbf{c}_l\), \(l\geqslant 0\), are central. Note that relations (6.3) and (6.4) were derived in [4]. Moreover, the following structure results were proven in [33, Propositions (1.34) and (1.36)] respectively.
Lemma 6.1
-
(i)
The algebra \(\mathbf{SH}^\mathbf{c}\) is generated by the elements \(\mathbf{c}_l, D_{1,0}, D_{-1,0}, D_{0,2}\).
-
(ii)
Any element of \(\,\mathbf{SH}^\mathbf{c}\) can be written as a linear combination of monomials in the generators \(D_{k,l}\) such that \(D_{1,l}\), \(D_{0,l}\), \(D_{-1,l}\), \(l\geqslant 0\), appear exactly in this order from left to right.
6.2 Calabi–Yau DAHA
In order to simplify the formulas let \(K_{r+2} = K_{\mathbf{T}_{r+2}}\) denote the fraction field of the cohomology ring \(H(B\mathbf{T}_{r+2})\). Then note that [33, Theorem 3.2] proves that a certain specialization of \(\mathbf{SH}^\mathbf{c}\) acts on the localized equivariant Borel–Moore homology
via Hecke correspondences. The specialization relates the formal parameters \(\kappa , \mathbf{c}\) to the canonical generators \((x, y, e_1, \ldots , e_r)\) of the cohomology ring of the classifying space \(B\mathbf{T}_{r+2}\) as shown below. Let \({\mathbb {C}}(\kappa )[\mathbf{c}] = {\mathbb {C}}(\kappa )[\mathbf{c}_0, \mathbf{c}_1, \ldots ]\) and let
be the algebra homomorphism mapping
where \(\epsilon _a= x^{-1}e_a\), \(1\leqslant a\leqslant r\), and \(p_l\), \(l\geqslant 0\), are the symmetric power functions in r variables. Using the \({\mathbb {C}}(\kappa )[\mathbf{c}]\)-module structure on \(K_{\mathbf{T}_{r+2}}\) obtained from (6.7), let

Let (x, y, z) be the canonical generators of the cohomology ring of \(B\mathbf{T}\). Then \(\mathbf{T}\)-specialization is defined by setting

Finally, the specialization to \(\mathbf{T}_0\subset \mathbf{T}\) is obtained by further setting \(z= -(x+y)\), which yields

where \(\xi = 1-\kappa \) as in (6.1).
Note that both specializations are well defined since the right-hand side of equation (6.3) is a formal power series of \(\mathbf{c}_l\), \(l\geqslant 0\). In particular the \(\mathbf{T}_0\)-specialization of \(\mathbf{SH}^{\mathbf{c}}\) will be denoted by \(\mathbf{SH}^{(r)}_{K_0}\).
6.3 \(\mathbf{SH}^{(r)}_{K_0}\)-module structure
This section will prove that the specialization \(\mathbf{SH}^{(r)}_{K_0}\) acts on \(\mathbf{V}_{K_0}^{(r)}\) using the Hecke transformations (5.10) and (5.15). First recall the subalgebra \(\mathbf{U}^{(r)}_{K_{r+2}}\) of the convolution algebra constructed in [33, Section 3.5]. As in Section 3.4 of loc. cit., let \(\tau _{n+1,n}\) denote the universal line bundle on the correspondence variety \({{\mathscr {A}}}(r,n,n+1)\). Using the notation of Sect. 5.1, the algebra \(\mathbf{U}_{K_{r+2}}^{(r)}\) is generated by the Hecke transformations

where \(E_n\) is the universal rank n vector bundle over \({{\mathscr {A}}}(r,n)\). The Chern classes \(c_l\), \(l\geqslant 0\), in the above formulas are \(\mathbf{T}_{r+2}\)-equivariant. In addition one defines the diagonal operators

which can be written as polynomial functions of the \(e_{0,l}\), \(l\in {\mathbb {Z}}\).
Then [33, Theorem 3.2] proves that there is a unique isomorphism of algebras
mapping
As observed in Remark 5.2 the above construction admits a straightforward specialization to \(\mathbf{T}\subset \mathbf{T}_{r+2}\). This results in an isomorphism
Abusing notation, the \(\mathbf{T}\)-equivariant counterparts of the above Hecke transformations will be denoted by the same symbols. The distinction will be clear from the context. Note also that explicit formulas for the matrix elements of the generators in the above representation follow immediately from Lemma 5.3.
Next note the direct sum decomposition

where

Suppose A is one of the K-linear transformations \(f_{1,l,n}\), \(f_{-1,l,n}\), \(f_{0,l,n}\) which generate the convolution algebra. Let
be the block form decomposition of A with respect to the direct sum (6.10). Then define the K-linear transformations

as
Recall that K is the field of rational functions \({\mathbb {C}}(x,y,z)\), where (x, y, z) are the canonical generators of the cohomology ring of \(B\mathbf{T}\). Let \(s= c_1(\sigma )\) where  is the character used in Lemma 5.4, and note that \(s= -(x+y+z)\). At the same time, \({K}_0={\mathbb {C}}(x,y)\) and there is a canonical isomorphism of K-vector spaces
is the character used in Lemma 5.4, and note that \(s= -(x+y+z)\). At the same time, \({K}_0={\mathbb {C}}(x,y)\) and there is a canonical isomorphism of K-vector spaces

mapping

for any nested r-partition \(\mu \). Let
Finally, recall that each T-fixed point \(\alpha _\mu \in {{\mathscr {A}}}(r,n)^\mathbf{T}\), with \(\mu \) nested, is \(\mathbf{T}_0\)-isolated and the equivariant Euler class
is nonzero. Similarly, as shown in Lemma 5.4 (i), for any nested partitions \(\mu \subset \lambda \) the fixed point \((\alpha _\mu , \alpha _\lambda )\in {{\mathscr {A}}}(r,n,n+1)^\mathbf{T}\) is \(\mathbf{T}_0\)-isolated and
is nonzero. Moreover, for any box \(s\in \mu \) set

where \(1\leqslant a \leqslant r\) indicates that \(s\in \mu _a\), and for any pair \(\mu \subset \lambda \) with  set
set

where  . Then the following holds
. Then the following holds
Lemma 6.2
The matrix elements of the K-linear transformations \(g_{i,l} \in \mathrm{End}_{K}(\mathbf{V}_{K})\), \(i\in \{-1,0,1\}\), \(l\in {\mathbb {Z}}\), with respect to the fixed point basis \(\{[\alpha _\mu ]\}\), with \(\mu \) a nested r-partition, have well defined specializations \(g_{i,l}|_{s=0}\) at \(s=0\). In particular there exist unique \(K_0\)-linear transformations \(g_{i,l}^0\in \mathrm{End}_{K_0}(\mathbf{V}_{K_0})\) such that  . Moreover, the explicit expressions of \(g_{i,l}^0\) in the fixed point basis are given by
. Moreover, the explicit expressions of \(g_{i,l}^0\) in the fixed point basis are given by

Proof
Let A be an element of \(\{f_{0,l,n}, f_{1,l,n}, f_{-1,l,n}\}\). Consider the following cases:
(1) Suppose A is one of the \(f_{0,l,n}\). Then the above block decomposition is diagonal and the claim is obvious.
(2) Suppose A is one of the \(f_{1,l,n}\). Then Lemma 4.6 (i) shows that for any nested r-partition \(\mu \) of n the equivariant Euler class \(e_{\mathbf{T}}(\alpha _\mu )\in {\mathbb {C}}(x,y,z)\) has well defined specialization at \(s=0\), which is furthermore equal to \(e_{\mathbf{T}_0}([\alpha _\mu ])\). Moreover, for any pair of nested r-partitions \(\mu , \lambda \) of \(n,n+1\) respectively, with \(\mu \subset \lambda \), Lemma 5.4 (i) shows that the equivariant Euler class \(e_{\mathbf{T}}(T_{\mu ,\lambda })\in {\mathbb {C}}(x,y,z)\) has well defined specialization at \(s=0\), which is furthermore equal to \(e_{\mathbf{T}_0}(T_{\mu , \lambda })\). Then the claim follows from equations (5.10).
(3) Suppose A is one of the \(f_{-1,l,n}\). This case is completely analogous to (2).
Equations (6.12) follow immediately by specialization from (5.4) and (5.5). \(\square \)
Lemma 6.3
The map
extends uniquely to a homomorphism of \(K_0\)-algebras
Proof
The proof will proceed by truncating the relations satisfied by the generators (6.9) to their (1, 1) blocks and specializing to \(s=0\). Again, suppose A is one of the transformations \(f_{i,l,n}\), \(i \in \{-1,0,1\}\), \(l\in {\mathbb {Z}}\), \(n \in {\mathbb {Z}}_{\geqslant 0}\), and consider the following cases.
(1) Suppose A is one of the \(f_{0,l,n}\). Then, clearly, \(A_{12}=0\) and \(A_{21}=0\).
(2) Suppose A is one of the \(f_{1,l,n}\). Then note that the matrix elements of
are given by

where \(\mu , \nu \) are nested r-partitions,
and
Moreover, \(\mu , \nu \) are nested while \(\lambda , \rho \) are not. Then Lemma 4.6 (ii) shows that
where \({{\tilde{e}}}(T_\lambda )\) has well defined specialization at \(s=0\). At the same time Lemma 5.4 (i) shows that \(e_\mathbf{T}(T_{\mu , \lambda })^{-1}\) has well defined specialization at \(s=0\). In conclusion,
where \({{\widetilde{A}}}_{12}\) has well defined specialization at \(s=0\). Similarly, Lemmas 4.6 (i) and 5.4 (i) imply that \(A_{21}\) has well defined specialization at \(s=0\).
(3) Suppose A is one of the \(f_{-1,l,n}\). In complete analogy to (2), Lemmas 4.6 and 5.4 imply that, again,
where \({{\tilde{A}}}_{12}\) has well defined specialization at \(s=0\). At the same time \(A_{21}\) has well defined specialization at \(s=0\).
The above observations imply that the claim holds for the quadratic relations (6.2)–(6.4). Suppose A, B are two linear transformations among the \(f_{i,l,n}\), \(i \in \{-1,0,1\}\), \(l\in {\mathbb {Z}}\), \(n \in {\mathbb {Z}}_{\geqslant 0}\), such that the target of B coincides with the domain of A. Using the block form decomposition (6.11), the product AB is written as
Note that the product \(A_{11}B_{11}\) has well defined specialization at \(s=0\) by Lemma 6.2. Then, using (1), (2) and (3) above it follows that the same holds for the component \((AB)_{11}\), and
This proves that the transformations \(g_{i,l}^0\) satisfy the quadratic relations (6.2)–(6.4).
In order to prove the cubic relations (6.5), suppose A, B, C are transformations of the form \(f_{1,l,n+1}\), \(f_{1,l,n}\), \(f_{1,l,n-1}\) respectively, where \(n\geqslant 1\). The (1, 1) block of the triple product ABC reads
Again, remarks (1), (2), (3) above imply that
have well defined specializations at \(s=0\), and
Using Lemma 5.4 (ii), it will be shown below that the product \({{\widetilde{A}}}_{12}B_{22}C_{21}\) also has well defined specialization at \(s=0\). The matrix elements of the triple product \({A}_{12}B_{22}C_{21}\) are given by
where \(\nu , \rho \) are nested r-partitions of \(n-1, n+2\) respectively and the sum is over all sequences of r-partitions \(\nu \subset \mu \subset \lambda \subset \rho \) with \(|\mu |=n\), \(|\lambda |=n+1\), and \(\mu , \lambda \) not nested. Lemmas 4.6 (i) and 5.4 (i) imply that
has well defined specialization at \(s=0\). Moreover, Lemmas 4.6 (ii) and 5.4 (ii) imply that

where \({{\tilde{e}}}(T_\mu )\), \({{\tilde{e}}}(T_{\mu , \lambda })^{-1}\) have well defined specializations at \(s=0\). Therefore the same holds for

Similarly, Lemmas 4.6 (ii) and 5.4 (i) imply that

where \({{\tilde{e}}}(T_{\lambda }), e_\mathbf{T}(T_{\lambda ,\rho })^{-1}\) also have well defined specialization at \(s=0\). Since \({A}_{12}B_{22}C_{21}=s{{\tilde{A}}}_{12}B_{22}C_{21}\), it follows that, indeed, \({{\widetilde{A}}}_{12}B_{22}C_{21}\) has well defined specialization at \(s=0\) as claimed above. Then, using relation (6.14) this implies that the transformations \(g_{1,l}^0\) also satisfy the cubic relations (6.5). \(\square \)
Proof of Theorem 1.1
For any \(l\geqslant 0\) set \(z=e_{\mathbf{T}_0}(\tau _{n,n+1})^l\) in Lemmas 5.6 and 5.7. Let \(h^+_{l}, h^-_{l}\) denote the resulting linear transformations in  . Then equations (5.10), (5.15) and (6.12) show that
. Then equations (5.10), (5.15) and (6.12) show that
for all \(l\geqslant 0\). Moreover \(h^0_l = g^0_{0,l}\) holds by construction for all \(l\geqslant 0\). Therefore Theorem 1.1 follows from Lemma 6.3. \(\square \)
6.4 Some structure results
The next goal is to prove some structure results for the action (6.13) which are needed in the proof of Theorem 1.2.
Lemma 6.4
For \(r=1\) the representation (6.13) is faithful.
Proof
This follows from [33, Proposition 6.7] since for \(r=1\) the representations \(\rho _0^{(r)}\) and \(\rho ^{(r)}\) are isomorphic. \(\square \)
Next, one has to prove the analogues of [33, Lemmas 8.33 and 8.34.a]. Let \([\alpha _{\varnothing ^r}]\in \mathbf{V}^{(r)}_{K_0}\) denote the element corresponding to the empty r-partition.
Lemma 6.5
\([\alpha _{\varnothing ^r}]\) is annihilated by all endomorphisms of the form \(\rho _0^{(r)}(D_{0,l})\), \(\rho _0^{(r)}(D_{-l,0})\), \(l\geqslant 1\).
Proof
This is analogous to [33, Lemma 8.34.a]. The claim follows from equations (5.15). \(\square \)
Lemma 8.33 in [33] shows that
The proof of loc. cit. is based on the following observation. Recall that \({{\mathscr {P}}}_{r,n}\) denotes the set of r-partitions of n. Let  be the map defined by
be the map defined by
where in the right-hand side \(s\in \mu _a\) and \(\mathbf{e}_a\) are the canonical generators of \({\mathbb {Z}}^r\) for \(1\leqslant a\leqslant r\). Then \(\phi \) is injective.
In order to prove the analogue of Lemma 8.33 under Calabi–Yau specialization, one has to first prove the following analogous result.
Lemma 6.6
Let \({{\mathscr {P}}}_{r,n}^{\subset } \subset {{\mathscr {P}}}_{r,n}\) be the subset of nested r-partitions of n. Let
be the map defined by
where in the right-hand side \(1\leqslant a \leqslant r\) and \(s\in \mu _a\). Then \(\phi _0\) is injective.
Proof
Suppose \(\mu =(\mu _a)\) and \(\lambda =(\lambda _a)\), \(1\leqslant a\leqslant r\), are two nested r-partitions of n such that \(\phi _0(\mu )=\phi _0(\lambda )\). For each \(1\leqslant a \leqslant r\) the partition \(\mu _a\subset {\mathbb {Z}}^2\) can be written as a union of L-shaped sets in the plane
Clearly, \(\mu _{a,k}=\varnothing \) for \(k\leqslant 0\) and \(\mu _{a,k}\cap \mu _{a,l}=\varnothing \) for \(k \ne l\). The translation of each set \(\mu _{a,k}\) by \((-a,-a)\) will be denoted by \(\mu _{a,k}-(a,a)\). Then note that
for any \(l \geqslant 0\) since \(\mu _a\) is a Young diagram. Moreover, for any \(1\leqslant a, b\leqslant r\), and any \(k,l\in {\mathbb {Z}}\) the subsets \(\mu _{a,k}-(a,a)\) and \(\mu _{b,l}-(b,b)\) of \({\mathbb {Z}}^2\) are disjoint unless \(k-a = l-b\). For any \(n \in {\mathbb {Z}}\) let \(\mathsf{S}_n(\mu )\) be the disjoint union

and let

denote the set theoretic union as subsets of \({\mathbb {Z}}^2\). As observed above, \(|\mathsf{S}_n(\mu )|\cap |\mathsf{S}_m(\mu )|=\varnothing \) for \(n\ne m\). Hence
Since \(\mu \) is nested, inclusion (6.15) implies that there are inclusions
where by convention \(\mu _{r+1,k+1}=\varnothing \). Therefore the following statement holds for each set \(\mathsf{S}_{k-a}(\mu )\):
(i) Each point

occurs with multiplicity exactly a in \(\mathsf{S}_{k-a}(\mu )\).
In complete analogy, one also has
where the subsets \(\mathsf{S}_m(\lambda )\) satisfy analogous properties. In particular, one has:
(ii) Each point

occurs with multiplicity a in \(\mathsf{S}_{k-a}(\lambda )\).
In order to finish the proof note that \(|\mathsf{S}_n(\mu )|\cap |\mathsf{S}_m(\lambda )|=\varnothing \) for \(n\ne m\). Therefore \(\phi _0(\mu )=\phi _0(\lambda )\) if and only if \(\mathsf{S}_n(\mu )=\mathsf{S}_n(\lambda )\) for all \(n \in {\mathbb {Z}}\). If that is the case, properties (i) and (ii) above imply that

for all \(1\leqslant a\leqslant r\) and all \(k \in {\mathbb {Z}}\). This implies that \(\mu =\lambda \). \(\square \)
Now one has:
Lemma 6.7
\(\mathbf{V}^{(r)}_{K_0} = \rho _0^{(r)}(\mathbf{SH}^{(r)}_{K_0})([\alpha _{\varnothing ^r}])\).
Proof
This is analogous to [33, Lemma 8.33]. The proof proceeds by induction on n, i.e., suppose \([\alpha ]_\mu \in \rho _0^{(r)}(\mathbf{SH}^{(r)}_{K_0})(|0\rangle )\) for all r-partitions \(\mu \) of \(n-1\). Recall the formula for \(g_{1,l}^0\) in equation (5.15):

As in loc. cit., this implies that for any r-partition \(\lambda \) with \(|\lambda |=n\) one can find a nested partition \(\mu \), \(|\mu |=n-1\) such that the coefficient of \([\alpha _\lambda ]\) in \(\rho _0^{(r)}(D_{1,l})([\alpha _\mu ])\) is nonzero for some \(l\geqslant 0\). Next note that

from (5.15). By analogy with Lemma 8.33, there is a map
mapping

Lemma 6.6 shows that this map is injective. Hence, as in loc. cit., the Hilbert nullstellensatz implies that there there is a polynomial f in the generators \(D_{0,l}\) such that \(f([\alpha _\lambda ])=1\) and \(f([\alpha _\rho ])=0\) for any r-partition \(\rho \ne \lambda \) of n. \(\square \)
7 W-module structure
This section provides a brief overview of W-algebras and concludes the proof of Theorem 1.2.
7.1 W-algebras
A succinct definition of the W-algebra \(W_\kappa (\mathfrak {gl}_r)\) and its free field realization via quantum Miura transform is presented in [33, Section 8.4]. The main points will be briefly summarized below.
In this section the ground field is \(F={\mathbb {C}}(\kappa )\). Let \(b_a\), \(1\leqslant a \leqslant r\), be a basis of the standard Cartan algebra \({{\mathfrak {h}}}\subset \mathfrak {gl}_r\) and let \(b^{(a)}\), \(1\leqslant a \leqslant r\), be the dual basis. Let \(b^{(a)}(z)\), \(1\leqslant a\leqslant r\), be free boson fields such that the zero modes \(b^{(a)}_0\) coincide with \(b^{(a)}\) for all \(1\leqslant a \leqslant r\) and their OPEs are given by

For any \(h \in {{\mathfrak {h}}}^\vee \) let

where the angular brackets denote the canonical pairing  . Let \(\pi _0\) be the Fock space of \(b^{(a)}(z)\), \(1\leqslant a\leqslant r\).
. Let \(\pi _0\) be the Fock space of \(b^{(a)}(z)\), \(1\leqslant a\leqslant r\).
Now let \(h^{(a)}\) be the fundamental weights of \(\mathfrak {sl}_r\). The W-fields  are defined by
are defined by

where  indicates normal ordering and
indicates normal ordering and
This yields \(W_0(z)=1\), \(W_1(z)=0\), and some more complicated expressions for \(W_d(z)\), \(d\geqslant 2\). Abusing notation, for \(d=1\) one sets
as opposed to \(W_1(z)=0\). Then the W-algebra \(W_\kappa (\mathfrak {gl}_r)\) is the vertex subalgebra of \(\pi _0\) generated by the Fourier modes of \(W_d(z)\), \(1\leqslant d \leqslant r\).
Next note that any \(\beta \in {{\mathfrak {h}}}\) determines a Verma module for the Heisenberg algebra \({{\mathscr {H}}}^{(r)}\) generated by the highest weight vector \(|\beta \rangle \) satisfying

Then there is a representation of \(W_\kappa (\mathfrak {gl}_r)\) on \(\pi _\beta \) such that

where

In particular, for \(\beta =0\) one obtains the vacuum W-module \(\pi _0\).
7.2 Module structure
Let \({{\mathfrak {U}}}(W_{\kappa }(\mathfrak {gl}_r))\) denote the current algebra of the W-algebra, and let \({\mathscr {U}}_0(W_{\kappa }(\mathfrak {gl}_r))\) denote its image in  As shown in Corollary A.3, which is analogous to [33, Lemmas 8.22 and 8.24], there is an embedding of degreewise topological \(K_0\)-algebras
As shown in Corollary A.3, which is analogous to [33, Lemmas 8.22 and 8.24], there is an embedding of degreewise topological \(K_0\)-algebras
which lifts to a surjective morphism of degreewise topological \(K_0\)-algebras
In particular, as observed in Corollary A.4, this yields a representation

As in [33], the morphism (7.1) is obtained from a comparison the free field realizations of \(\mathbf{SH}^{(r)}_{K_0}\) and respectively the W-algebra. The proof consists of a step-by-step \(\mathbf{T}_0\)-specialization of the proof given in [33]. This is a straightforward, if somewhat tedious process, the details being provided in Appendix A.
Now one can conclude the proof of Theorem 1.2 which states that \(\pi _0^{(r)}\) is isomorphic to the vacuum representation of the W-algebra.
Proof of Theorem 1.2
Having proven the \(\mathbf{T}_0\) variants of [33, Lemmas 8.33 and 8.34.a], namely Lemmas 6.7 and 6.5, the proof is now completely analogous to the proof of the first part of Theorem 8.32 in loc. cit. Using Corollary A.4, the above lemmas imply that \(\mathbf{V}^{(r)}_{K_0}\) is Verma module for \({{\mathfrak {U}}}_0(W_\kappa (\mathfrak {gl}_r))\) with highest weight vector \([\alpha _{\varnothing ^r}]\). Using the epimorhism (7.2), for each element \(W_{d,0}\) of \({\mathfrak U}(W_\kappa (\mathfrak {gl}_r))\) there exists an element \(W'_{d,0}\) in \({{\mathfrak {U}}}(\mathbf{SH}^{(r)}_{K_0})\) mapped to \(W_{d,0}\) in \({{\mathfrak {U}}}(W_\kappa (\mathfrak {gl}_r))\). Lemma A.2 and Corollary A.5 imply that \(W'_{d,0}\) acts in the same way on the vacua \([\alpha _{\varnothing ^r}]\) and \([\alpha _{\varnothing }]^{\,{\otimes }\, r}\). This concludes the proof. \(\square \)
8 Appendix: From degenerate DAHA to W
The main goal of this section is to show that the relation between degenerate DAHA modules and W-modules proven in [33] also holds for their Calabi–Yau specializations. This includes the construction of the free field representation of \(\mathbf{SH}^{(r)}_{K_{r+2}}\) carried out in [33, Section 8.5], the algebra morphism obtained in Theorem 8.21 of loc. cit. as well as the resulting categorical equivalence of admissible modules. The proof consists of a straightforward step-by-step verification that all intermediate steps in loc. cit. admit correct specialization under the inclusion \(\mathbf{T}_0\subset \mathbf{T}_{r+2}\). The details are included here for completeness.
8.1 Grading and order filtration
This is brief summary of [33, Section 1.9]. Using the notation of Sect. 6.1, let \(D_{l,0}\), \(l\geqslant {\mathbb {Z}}\), be the elements of \(\mathbf{SH}^{\mathbf{c}}\) defined recursively by
Moreover, for \(l,k\geqslant 1\) set
As shown in [33, Section 1.9], by construction there is an order filtration
where \(l\geqslant 0\). Proposition 1.38 in loc. cit shows that this filtration is completely determined by assigning the elements \(D_{k,l}\), \(\mathbf{c}_l\) order degrees l and 0 respectively. Moreover, one has
hence the associated graded inherits an algebra structure.
In addition there is also a \({\mathbb {Z}}\)-grading such that \(D_{l,0}\) has degree l while \(D_{0,l}\) has degree zero. This \({\mathbb {Z}}\)-grading is compatible with the above filtration.
8.2 Coproduct
The topological tensor product  is defined as
is defined as

Then [33, Theorem 7.9] proves that there exists a coproduct  which is uniquely determined by the formulas
which is uniquely determined by the formulas

Here \(\delta \) is the standard diagonal map.
The main application of the coproduct resides in the construction of the free field representation

in [33, Section 8.5]. As shown in loc. cit., Proposition 8.5, the coproduct determines naturally an injective algebra homomorphism

Moreover the case \(r=1\) of Theorem 3.2 in loc. cit shows that there is a faithful representation

As observed in Corollary 8.7 of loc. cit, this yields a faithful representation (A.2).
The important point for the present purposes is the following:
Lemma A.1
There is a faithful representation

Proof
Clearly, using formulas (A.1) the construction of the injective algebra homomorphism (A.3) specializes immediately to \(\mathbf{SH}^{(r)}_{K_0}\). Moreover, fact for \(r=1\), the factor \(({{\mathbb {C}}}^{\times })^{\times r}\) acts trivially on \({{\mathscr {A}}}(1,n)\) and the quotient \(\mathbf{T}_{r+2}/ ({{\mathbb {C}}}^{\times })^{\times r}\) is isomorphic to \(\mathbf{T}_0\). Therefore the specialization of the rank \(r=1\) case of Theorem 3.2 to \(\mathbf{SH}^{(r)}_{K_0}\) is also immediate. This implies that the analogue of Corollary 8.7 in loc. cit also holds for the \(\mathbf{T}_0\)-specialization. Therefore Lemma A.1 holds. \(\square \)
To conclude this section, by analogy to [33, Lemma 8.34.b], one has:
Lemma A.2
Let \([\alpha _{\varnothing }]^{\otimes r}\!\in (\mathbf{V}^{(1)}_{K_0})^{\otimes r}\) denote the vacuum vector. Then \([\alpha _{\varnothing }]^{\otimes r}\) is annihilated by all endomorphisms of the form \(\rho ^{(1^r)}_0(D_{0,l})\), \(\rho _0^{(1^r)}(D_{-l,0})\), \(l\geqslant 1\).
Proof
This follows from the \(r=1\) case of Lemma 6.5 using [33, Lemma 7.11]. \(\square \)
8.3 Degreewise completion
As explained for example in [2, Appendix A], any \({\mathbb {Z}}\)-graded algebra as above has a natural degreewise linear topology defined by the decreasing sequence

This means that for any degree s element \(v\in \mathbf{SH}^{(r)}_{K_{r+2}}[s]\) the subsets \(\{ v \,{+}\, {\mathscr {J}}_N[s]\}\) form a fundamental system of open neighborhoods of v.
The standard degreewise completion of \(\mathbf{SH}^{(r)}_{K_{r+2}}\) is defined by
Clearly the grading, order filtration and degreewise completion remain well defined under \(\mathbf{T}_0\) specialization.
Now, [33, Section 8.6, Definition 8.10] introduces the notion of admissible \(\mathbf{SH}^{(r)}_{K_{r+2}}\)-module. This is a \({\mathbb {Z}}\)-graded module \(M = \bigoplus _{s\in {\mathbb {Z}}} M[s]\) such that \(M[s]=0\) for sufficiently large s. This definition readily extends to modules over the degreewise completion (A.4). Then Proposition 8.11 in loc. cit. proves that
(1) The faithful representation (A.2) extends to a faithful representation of \({{\mathfrak {U}}}{} \mathbf{SH}^{(r)}_{K_{r+2}}\) on \((\mathbf{L}^{(1)}_{K_0}){}^{\otimes r}\).
(2) The canonical map \(\mathbf{SH}^{(r)}_{K_{r+2}}\!\rightarrow {{\mathfrak {U}}}{} \mathbf{SH}^{(r)}_{K_{r+2}}\) is an embedding of degreewise topological algebras.
Both statements are consequences on Corollary 8.7 in loc. cit, hence, in the view of Lemma A.1, they remain valid under \(\mathbf{T}_0\)-specialization.
8.4 From \(\mathbf{SH}^{\mathbf{c}}\) to W
Now let \({\mathfrak {U}}(W_{\kappa }(\mathfrak {gl}_r))\) be the current algebra associated to the W-algebra. It was shown in [2] that this is a graded degreewise complete topological F-algebra as defined in Sect. A.3. The grading is defined by the conformal degree.
Let \({{\mathscr {U}}}(W_\kappa (\mathfrak {gl}_r))\) be the image of \({{\mathfrak {U}}}(W_\kappa (\mathfrak {gl}_r))\) in  where \(\beta \) is determined by the relations
where \(\beta \) is determined by the relations

One of the main technical results in [33, Theorem 8.21], states that there is an embedding
of degreewise topological \(K_{r+2}\)-algebras with a degreewise dense image. Furthermore, Lemma 8.24 in loc. cit. proves that \(\Theta ^{(r)}\) extends to a surjective morphism of degreewise topological \(K_{r+2}\)-algebras
Finally, Corollary 8.27 proves that the pull-back via \(\Theta ^{(r)}\) yields an equivalence from the category of admissible \({\mathscr {U}}(W_\kappa (\mathfrak {gl}_r))\)-modules to the category of admissible \(\mathbf{SH}^{(r)}_{K_{\mathbf{T}_{r+2}}}\)-modules. This equivalence intertwines between the free field realizations \(\rho ^{(1^r)}\) and \(\pi _\beta \).
The analogous statement for the \(\mathbf{T}_0\)-specialization is proven below. First note that the Calabi–Yau specialization sets

in equation (A.5). Therefore \(\pi _\beta \) specializes to the Fock vacuum module \(\pi _0\) of the Heisenberg algebra \({{\mathscr {H}}}^{(r)}\). As above, let \({\mathscr {U}}_0(W_\kappa (\mathfrak {gl}_r))\) denote the image of the W-algebra in  .
.
Lemma A.3
-
(i)
There is an embedding
$$\begin{aligned} \Theta _0^{(r)}:\mathbf{SH}^{(r)}_{K_{0}} \rightarrow {\mathscr {U}}_0(W_\kappa (\mathfrak {gl}_r)) \end{aligned}$$of degreewise topological \(K_{0}\)-algebras with a degreewise dense image.
-
(ii)
\(\Theta _0^{(r)}\) extends to a surjective morphism of degreewise topological \(K_{0}\)-algebras
$$\begin{aligned} {{\mathfrak {U}}}\bigl (\mathbf{SH}^{(r)}_{K_{0}}\bigr ) \rightarrow {\mathscr {U}}_0(W_\kappa (\mathfrak {gl}_r)). \end{aligned}$$(A.6)
Proof
First recall the construction of the map map \(\Theta ^{(r)}\), which is based on the free field realization

Using the coproduct structure in Sect. A.2, the morphism \(\Theta ^{(r)}\) is determined by \(\Theta ^{(1)}\) and \(\Theta ^{(2)}\). In order to summarize the explicit formulas for these maps, it will be helpful to recall that the algebra \(\mathbf{SH}^{(\mathbf{c})}\) is generated by the elements \(\mathbf{c}_l, D_{1,0}, D_{-1,0}, D_{0,2}\), as shown in [33, Proposition 1.34], Moreover, it shown in Section 1.11 of loc. cit that the elements
with \(l\geqslant 1\), and \(\mathbf{c}_0\) define a Heisenberg subalgebra of \(\mathbf{SH}^{\mathbf{c}}\). That is
The analogous statements will hold for the \(\mathbf{T}_{r+2}\) and \(\mathbf{T}_0\) specializations. Then the construction of \(\Theta ^{(r)}\) proceeds as follows.
For \(r=1\) there is a single W-field
and \(\pi _\beta \) is a Verma module of the Heisenberg algebra \({{\mathscr {H}}}^{(1)}\) with height weight
By [33, Proposition 1.40] there exists a unique isomorphism of \(K_{{r+2}}\)-vector spaces
mapping \([\alpha _\varnothing ]\) to \(|\beta \rangle \) which intertwines naturally between the action of Heisenberg subalgebra of \(\mathbf{SH}^{(1)}_{K_{{r+2}}}\) on \(\mathbf{L}_K^{(1)}\) and the action of \({{\mathscr {H}}}^{(1)}\) on \(\pi _\beta \). As shown in Propositions 8.15 and 8.16 of loc. cit. this extends to an embedding \(\Theta ^{(1)}\) where
The \(\mathbf{T}_0\) specialization sets \(\epsilon _1=0\), hence in this case \(\pi _\beta = \pi _0\) is the Fock vacuum module of the Heisenberg algebra. Clearly, the all the above formulas have well defined specialization. In particular,
and
define again an embedding of degreewise topological algebras.
An analogous computation holds for \(r=2\). In this case one identifies

Note also that the \(K_{{r+2}}\)-vector space \(\pi _\beta \) is canonically isomorphic to \((\mathbf{L}^{(1)}_{K_{{r+2}}})^{\otimes 2}\). Then \(\Theta ^{(2)}\) is determined in this case by the formulas

where

The \(\mathbf{T}_0\) specialization sets
and \(\pi _\beta \) is again the Fock module \(\pi _0\). Again, the above formulas well defined specializations. In fact the only \(\epsilon \)-dependence is through the constant c which is polynomial in \(\epsilon _1, \epsilon _2\). Therefore \(\Theta ^{(2)}_0\) is again well defined and yields an embedding of topological algebras.
For \(r\geqslant 2\), the map \(\Theta ^{(r)}\) is determined naturally by \(\Theta ^{(1)}\) and \(\Theta ^{(2)}\) using the coproduct (A.1) as shown in [33, Theorem 8.21]. Since formulas (A.1) are independent of \(\epsilon \), it follows that the \(\mathbf{T}_0\)-specialization of \(\Theta ^{(r)}\) is well defined and determines an embedding of topological algebras by analogy with [33, Theorem 8.21]. Note here that Theorem 8.23 used in loc. cit. also holds for \(\pi ^{\beta }=\pi _0\), as proven in [3, Proposition 5.5].
The \(\mathbf{T}_0\) specialization of [33, Lemma 8.24] also holds since the formulas proven in Claims 8.25 and 8.26 of loc. cit. are independent of \(\epsilon \). Therefore the map \(\Theta ^{(r)}_0\) extends to a surjective morphism of degreewise topological algebras (A.6). \(\square \)
Finally, note that the \(\mathbf{T}_0\)-specialization of [33, Corollary 8.27] also holds since the proof given in loc. cit. is completely independent of parameters. In conclusion one has:
Corollary A.4
The pull-back via \(\Theta ^{(r)}_0\) yields an equivalence from the category of admissible \({\mathscr {U}}_0(W_\kappa (\mathfrak {gl}_r))\)-modules to the category of admissible \(\mathbf{SH}^{(r)}_{K_0}\)-modules. This equivalence intertwines between the free field realizations \(\rho _0^{(1^r)}\) and \(\pi _0\). In particular, the vacuum vector \(|0\rangle \) of \(\pi _0\) is identified with the element  .
.
A second consequence of the proof of Lemma A.3 is recorded below.
Corollary A.5
For any \(d\geqslant 1\) let \(W'_{d,0}\) in \({{\mathfrak {U}}}(\mathbf{SH}^{(r)}_{K_0})\) be the element mapped by \(\Theta _0\) to \(W_{d,0}\) in \({{\mathfrak {U}}}(W_\kappa (\mathfrak {gl}_r))\). Then \(W'_{d,0}\) is a linear combination of monomials
where \(D_{1,l}\), \(D_{0,l}\), \(D_{-1,l}\), \(l\geqslant 0\), appear exactly in this order from left to right.
Proof
This is analogous to [33, Equation (8.123)]. It follows from the construction of the map \(\Theta _0^{(r)}\) in Lemma A.3 using [33, Proposition 8.3] and Lemma 6.1 (ii). \(\square \)
References
Alday, L.F., Gaiotto, D., Tachikawa, Y.: Liouville correlation functions from four-dimensional gauge theories. Lett. Math. Phys. 91(2), 167–197 (2010)
Arakawa, T.: Representation theory of \(W\)-algebras. Invent. Math. 169(2), 219–320 (2007)
Arakawa, T., Creutzig, T., Linshaw, A.R.: \(W\)-algebras as coset vertex algebras. Invent. Math. 218(1), 145–195 (2019). arXiv:1801.03822
Arbesfeld, N., Schiffmann, O.: A presentation of the deformed \(W_{1+\infty }\) algebra. In: Iohara, K., et al. (eds.) Symmetries, Integrable Systems and Representations. Springer Proceedings in Mathematics & Statistics, vol. 40, pp. 1–13. Springer, Heidelberg (2013)
Braverman, A., Finkelberg, M., Nakajima, H.: Instanton Moduli Spaces and \(W\)-Algebras. Astérisque, vol. 385. Société Mathématique de France, Paris (2016)
Bruzzo, U., Markushevich, D.: Moduli of framed sheaves on projective surfaces. Doc. Math. 16, 399–410 (2011)
Carlsson, E., Nekrasov, N., Okounkov, A.: Five dimensional gauge theories and vertex operators. Mosc. Math. J. 14(1), 39–61 (2014)
Carlsson, E., Okounkov, A.: Exts and vertex operators. Duke Math. J. 161(9), 1797–1815 (2012)
Chriss, N., Ginzburg, V.: Representation Theory and Complex Geometry. Modern Birkhäuser Classics. Birkhäuser, Boston (2010)
Davison, B.: The critical CoHA of a quiver with potential. Q. J. Math. 68(2), 635–703 (2017). arXiv:1311.7172
Davison, B., Meinhardt, S.: Cohomological Donaldson–Thomas theory of a quiver with potential and quantum enveloping algebras. Invent. Math. 221(3), 777–871 (2020). arXiv:1601.02479
Diaconescu, D.-E.: Moduli of ADHM sheaves and local Donaldson–Thomas theory. J. Geom. Phys. 62(4), 763–799 (2012). arXiv:0801.0820
Gaiotto, D., Rapčák, M.: Vertex algebras at the corner. J. High Energy Phys. 2019(1), # 160 (2019). arXiv:1703.00982
Gholampour, A., Sheshmani, A., Yau, S.-T.: Localized Donaldson–Thomas theory of surfaces. Amer. J. Math. 142(2), 405–442 (2020). arXiv:1701.08902
Kapranov, M., Vasserot, E.: The cohomological Hall algebra of a surface and factorization cohomology (2019). arXiv:1901.07641
Kontsevich, M., Soibelman, Y.: Cohomological Hall algebra, exponential Hodge structures and motivic Donaldson-Thomas invariants. Commun. Number Theory Phys. 5(2), 231–352 (2011)
Manolache, C.: Virtual pull-backs. J. Algebraic Geom. 21(2), 201–245 (2012). arXiv:0805.2065
Maulik, D., Okounkov, A.: Quantum Groups and Quantum Cohomology. Astérisque, vol. 408. Société Mathématique de France, Paris (2019). arXiv:1211.1287
Minets, A.: Cohomological Hall algebras for Higgs torsion sheaves, moduli of triples and sheaves on surfaces. Selecta Math. (N.S.) 26(2), # 30 (2020). arXiv:1801.01429
Nakajima, H.: Lectures on Hilbert Schemes of Points on Surfaces. University Lecture Series, vol. 18. American Mathematical Society, Providence (1999)
Nakajima, H., Yoshioka, K.: Lectures on instanton counting. In: Hurtubise, J., Markman, E. (eds.) Algebraic Structures and Moduli Spaces. CRM Proceedings & Lecture Notes, vol. 38, pp. 31–101. American Mathematical Society, Providence (2004)
Nakajima, H., Yoshioka, K.: Instanton counting on blowup. I. 4-dimensional pure gauge theory. Invent. Math. 162(2), 313–355 (2005)
Neguţ, A.: Exts and the AGT relations. Lett. Math. Phys. 106(9), 1265–1316 (2016)
Neguţ, A.: AGT relations for sheaves on surfaces (2017). arXiv:1711.00390
Neguţ, A.: The \(q\)-AGT-W relations via shuffle algebras. Comm. Math. Phys. 358(1), 101–170 (2018)
Nekrasov, N.: BPS/CFT correspondence II: Instantons at crossroads, moduli and compactness theorem. Adv. Theor. Math. Phys. 21(2), 503–583 (2017). arXiv:1608.07272
Nekrasov, N., Prabhakar, N.S.: Spiked instantons from intersecting D-branes. Nucl. Phys. B 914, 257–300 (2017). arXiv:1611.03478
Nitsure, N.: Schematic Harder-Narasimhan stratification. Internat. J. Math. 22(10), 1365–1373 (2011)
Porta, M., Sala, F.: Two-dimensional categorified Hall algebras (2019). arXiv:1903.07253
Rapčák, M., Soibelman, Y., Yang, Y., Zhao, G.: Cohomological Hall algebras, vertex algebras and instantons. Comm. Math. Phys. 376(3), 1803–1873 (2020). arXiv:1810.10402
Ren, J., Soibelman, Y.: Cohomological Hall algebras, semicanonical bases and Donaldson–Thomas invariants for $2$-dimensional Calabi–Yau categories (with an appendix by Ben Davison). In: Auroux, D. et al. (eds.) Algebra, Geometry, and Physics in the 21st Century. Progress in Mathematics, vol. 324. Birkhäuser, Cham (2017). arXiv:1508.06068
Sala, F., Schiffmann, O.: Cohomological Hall algebra of Higgs sheaves on a curve. Algebr. Geom. 7(3), 346–376 (2020). arXiv:1801.03482
Schiffmann, O., Vasserot, E.: Cherednik algebras, W-algebras and the equivariant cohomology of the moduli space of instantons on \({\mathbf{A}}^2\). Publ. Math. Inst. Hautes Études Sci. 118, 213–342 (2013)
Schiffmann, O., Vasserot, E.: On cohomological Hall algebras of quivers: generators. J. Reine Angew. Math. 760, 59–132 (2020). arXiv:1705.07488
Schiffmann, O., Vasserot, E.: On cohomological Hall algebras of quivers: Yangians (2017). arXiv:1705.07491
Soibelman, Y.: Remarks on cohomological Hall algebras and their representations. In: Ballmann, W. et al. (eds.) Arbeitstagung Bonn 2013. Progress in Mathematics, vol. 319, pp. 355–385. Birkhäuser, Cham (2016). arXiv:1404.1606
Tanaka, Y., Thomas, R.P.: Vafa–Witten invariants for projective surfaces I: stable case. J. Algebraic Geom. 29(4), 603–668 (2020). arXiv:1702.08487
Yang, Y., Zhao, G.: The cohomological Hall algebra of a preprojective algebra. Proc. London Math. Soc. 116(5), 1029–1074 (2018)
Zhao, Y.: On the \(K\)-theoretic Hall algebra of a surface. IMRN, rnaa123 (2020). arXiv:1901.00831
Acknowledgements
We would like to thank Davide Gaiotto, Nikita Nekrasov, Andrei Okounkov, Miroslav Rapcak, Francesco Sala, Olivier Schiffmann, Yaping Yang, Gufang Zhao and Yu Zhao for very helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work of W.-Y.C. was partly supported by MOST grant 107-2115-M-002-009-MY2. T.C. is supported by NSERC \(\#\) RES0020460. The work of D.-E.D was partially supported by NSF grants DMS-1501612 and DMS-1802410. The work of Y.S. was partially supported by an NSF grant and Munson-Simu award of KSU.
Rights and permissions
About this article
Cite this article
Chuang, WY., Creutzig, T., Diaconescu, DE. et al. Hilbert schemes of nonreduced divisors in Calabi–Yau threefolds and W-algebras. European Journal of Mathematics 7, 807–868 (2021). https://doi.org/10.1007/s40879-021-00464-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-021-00464-x


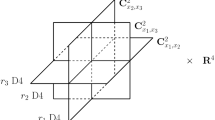

 for all
for all  preserved by
preserved by  over the residual field
over the residual field 
 ,
, is an isomorphism of
is an isomorphism of 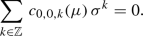


 is a closed embedding, and the restriction of the projection
is a closed embedding, and the restriction of the projection  to
to  to
to  consists of a single box s.
consists of a single box s.


