Abstract
We explore finitely generated groups by studying the nilpotent towers and the various Lie algebras attached to such groups. Our main goal is to relate an isomorphism extension problem in the Postnikov tower to the existence of certain commuting diagrams. This recasts a result of Grigory Rybnikov in a more general framework and leads to an application to hyperplane arrangements, whereby we show that all the nilpotent quotients of a decomposable arrangement group are combinatorially determined.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Motivation
The motivation for this paper comes from an effort to understand Rybnikov’s invariant used in [36,37,38] to distinguish between the fundamental groups of complements of two hyperplane arrangements with the same incidence structure. Work of Arnol’d, Brieskorn, and Orlik–Solomon insures that an arrangement complement,  , is rationally formal, and that the cohomology ring
, is rationally formal, and that the cohomology ring  is determined solely by the intersection lattice,
is determined solely by the intersection lattice,  . Thus, the complements of the Rybnikov pair of arrangements share the same rational homotopy type; in particular, the respective fundamental groups share the same rational associated graded Lie algebras and second nilpotent quotients. Nevertheless, the third nilpotent quotients of those two groups are not isomorphic, for reasons that are to this date somewhat mysterious, despite repeated attempts to elucidate this phenomenon, see e.g. [1, 2, 26, 27].
. Thus, the complements of the Rybnikov pair of arrangements share the same rational homotopy type; in particular, the respective fundamental groups share the same rational associated graded Lie algebras and second nilpotent quotients. Nevertheless, the third nilpotent quotients of those two groups are not isomorphic, for reasons that are to this date somewhat mysterious, despite repeated attempts to elucidate this phenomenon, see e.g. [1, 2, 26, 27].
We take here a different approach, closely modeled on Rybnikov’s original approach from [36, 37], yet from a more general point of view. In the process, we develop a machinery for determining when a given isomorphism between the n-th nilpotent quotients of two groups satisfying certain mild finiteness and homological assumptions extends to an isomorphism between the \((n+1)\)-st stages of the respective nilpotent towers.
1.2 The holonomy map
Let X be a connected CW-complex. We will assume throughout that the first homology group \(H_1(X)\) is finitely generated and torsion-free. Let \(G=\pi _1(X)\) be the fundamental group of X, and let \(\Gamma _n(G)\) denote its lower central series subgroups. Finally, let \(X\rightarrow K(G_{\mathrm{ab}},1)\) be a classifying map corresponding to the abelianization homomorphism \(G\rightarrow G_{\mathrm{ab}}\). The induced homomorphism of second homology groups, \(h:H_2(X)\rightarrow H_2(G_{\mathrm{ab}})\), is called the holonomy map of X.
Particularly interesting is the situation when the holonomy map is injective; this happens, for instance, when X is the complement of a complex hyperplane arrangement, or of a ‘rigid’ link, or of an arrangement of transverse planes in \({\mathbb {R}}^4\), [27]. Under this injectivity assumption, we show in Theorem 3.1 that there is a split exact sequence

Many properties of a finitely generated group G are reflected in the Lie algebras associated to it. One of those is the associated graded Lie algebra, \(\mathrm{gr}(G)\), whose graded pieces are defined as \(\mathrm{gr}_n(G)=\Gamma _n(G)/\Gamma _{n+1}(G)\), and whose Lie bracket is induced from the group commutator. The study of the associated graded Lie algebra was initiated in work of Magnus [21], Witt [47], Hall [18], and Lazard [20]. Much of the power of this approach comes from the various connections between the lower central series, nilpotent quotients, and group homology, as evidenced in the work of Stallings [42], Quillen [34], Dwyer [13], and many others.
Another Lie algebra associated to a group G is the holonomy Lie algebra, \(\mathfrak {h}(G)\), which was introduced in work of Chen [8], Kohno [19], and Markl–Papadima [24], and studied more recently by Papadima–Suciu [30] and Suciu–Wang [44, 45]. This Lie algebra depends only on data extracted from the cohomology of G in low degrees. In more detail, assuming \(G_{\mathrm{ab}}\) is torsion-free, \(\mathfrak {h}(G)\) is defined as the quotient of the free Lie algebra on \(G_{\mathrm{ab}}\) modulo the ideal generated by the image of the holonomy map, \(H_2(G)\rightarrow H_2(G_{\mathrm{ab}})\).
The holonomy Lie algebra \(\mathfrak {h}(G)\) may be viewed as a quadratic approximation of the associated graded Lie algebra \(\mathrm{gr}(G)\). More precisely, there is a canonical epimorphism of graded Lie algebras, \(\mathfrak {h}(G)\twoheadrightarrow \mathrm{gr}(G)\), which is an isomorphism in degrees \(n\leqslant 2\), but is not necessarily injective in higher degrees (see, for instance, the examples in [45] of groups that are not graded-formal). Nevertheless, we show in Theorem 4.3 that the map \(\mathfrak {h}_3(G)\rightarrow \mathrm{gr}_3(G)\) is an isomorphism under the aforementioned injectivity assumption for the holonomy map.
1.3 The main result
Let \(X_a\) and \(X_b\) be two path-connected spaces as above. From [42] it follows that if a map \(f:X_a \rightarrow X_b\) induces an isomorphism of first homology groups and an epimorphism of second homology groups, then f induces an isomorphism  for \(n \geqslant 2\), where \(G_a\) and \(G_b\) denote the fundamental groups of \(X_a\) and \(X_b\); respectively.
for \(n \geqslant 2\), where \(G_a\) and \(G_b\) denote the fundamental groups of \(X_a\) and \(X_b\); respectively.
The main result in this paper gives a necessary and sufficient condition for a given map of coalgebras,

with \(\overline{g}_1\) an isomorphism and \(\overline{g}_2\) an epimorphism, to extend to an isomorphism of nilpotent quotients for a given value of n; more precisely, that there be an isomorphism \(f_n:{G_a}/\Gamma _{n}({G_a})\rightarrow {G_b}/\Gamma _{n}({G_b})\) such that the diagram

commutes. To state the result, let N be a nilpotent group with \(N \cong {N}/\Gamma _{n}({N})\). Assume that the holonomy maps of \(X_a\) and \(X_b\) are injective, and there is a map \(\ell _b :X_b \rightarrow K(N,1)\) inducing an isomorphism  . We then show in Theorems 6.1 and 6.2 that there is an isomorphism
. We then show in Theorems 6.1 and 6.2 that there is an isomorphism
extending \(\overline{g}_2\) if and only if there is a map \(\ell _a :X_a \rightarrow K(N,1)\) inducing an isomorphism  , and a splitting \(\sigma \) of the exact sequence (1.1) such that the following diagram commutes:
, and a splitting \(\sigma \) of the exact sequence (1.1) such that the following diagram commutes:

Analogous results in characteristic p are proved in Theorems 6.4 and 6.5. In the case \(n=3\) the obstruction to extending the map \(\overline{g}_2\) to an isomorphism  is computed by generalized Massey triple products. This result along with further results and applications will be given in a subsequent paper.
is computed by generalized Massey triple products. This result along with further results and applications will be given in a subsequent paper.
1.4 Hyperplane arrangements
Returning now to the setting of hyperplane arrangements, let  be a finite set of hyperplanes in some finite-dimensional complex vector space. The complement
be a finite set of hyperplanes in some finite-dimensional complex vector space. The complement  , then, has the homotopy type of a connected, finite CW-complex. Moreover, the cohomology ring
, then, has the homotopy type of a connected, finite CW-complex. Moreover, the cohomology ring  is torsion-free and generated in degree 1, and so the holonomy map of
is torsion-free and generated in degree 1, and so the holonomy map of  is injective. Consequently, if
is injective. Consequently, if  is the fundamental group of the complement, then \(\mathrm{gr}_3(G)\cong \mathfrak {h}_3(G)\).
is the fundamental group of the complement, then \(\mathrm{gr}_3(G)\cong \mathfrak {h}_3(G)\).
The second nilpotent quotient of an arrangement group is combinatorially determined; that is, if  and
and  are two arrangements such that
are two arrangements such that  , then
, then  . On the other hand, as previously mentioned, Rybnikov showed that the next nilpotent quotient,
. On the other hand, as previously mentioned, Rybnikov showed that the next nilpotent quotient,  is not always determined by
is not always determined by  .
.
The invariant that Rybnikov defined in [36,37,38] to prove this result comes from the case \(n=3\) of the main result in this paper, as follows. In [36, 37] it is further assumed that \(\mathfrak {h}_3(G)\) is torsion-free. Replacing then the modules and maps in Theorem 6.1 with their \(\mathrm{Hom}\) duals gives the result corresponding to [36, Theorem 2.2]. These replacements in Theorem 6.2 yield [37, item 2 of Theorem 12].
Particularly interesting is the class of “decomposable" hyperplane arrangements. Building on work of Papadima and Suciu [31] and applying Theorem 6.2, we prove in Theorem 8.8 that, for such an arrangement  , the tower of nilpotent quotients of
, the tower of nilpotent quotients of  is fully determined by the truncated intersection lattice
is fully determined by the truncated intersection lattice  . Our result leaves open the question whether the group
. Our result leaves open the question whether the group  itself is combinatorially determined when
itself is combinatorially determined when  is decomposable.
is decomposable.
1.5 Organization of the paper
The paper is divided into three parts, of roughly equal length.
The first part deals with the nilpotent quotients and Lie algebras associated to a finitely generated group G. In Sect. 2 we describe the tower of nilpotent quotients \(\{G/\Gamma _n(G)\}_{n\geqslant 1}\), while in Sect. 3 we review the associated graded Lie algebra \(\mathrm{gr}(G)\) and the Malcev Lie algebra \(\mathfrak {m}(G)\). Finally, in Sect. 4 we discuss the holonomy Lie algebra \(\mathfrak {h}(G)\) and relate it to \(\mathrm{gr}(G)\).
In the second part we reprove and extend Rybnikov’s theorem. We start in Sect. 5 with some preparatory material on group extensions, splittings, and k-invariants. The main results, including an extension in characteristic p, are stated and proved in Sect. 6.
In the third part we apply our machinery to the theory of hyperplane arrangements. We start in Sect. 7 with a review of the relevant material on the topology and combinatorics of arrangements, and give a quick application to Lie algebras associated to arrangement groups. Finally, in Sect. 8 we show that the nilpotent quotients of decomposable arrangement groups are combinatorially determined.
2 Lower central series and Postnikov towers
In this section we discuss the lower central series and the tower of nilpotent quotients of a group. General references include the works of Hall [18], Magnus [22], Stallings [42], and Dwyer [13].
2.1 Lower central series
Let G be a group. The lower central series (LCS) is the sequence of subgroups \(\{\Gamma _n(G)\}_{n\geqslant 1}\) defined inductively by \(\Gamma _1(G) = G\) and
for \(n \geqslant 1\). Here, if H and K are subgroups of G, then [H, K] denotes the subgroup of G generated by all elements of the form \([a,b]=aba^{-1}b^{-1}\) for \(a \in H\) and \(b \in K\). If both H and K are normal subgroups, then their commutator [H, K] is again a normal subgroup.
In our situation, the subgroups \(\Gamma _n(G)\) are, in fact, characteristic subgroups of G. Moreover, the LCS filtration is multiplicative, in the sense that, for all m, n,
Note that \(\Gamma _2(G)=[G,G]\) is the derived subgroup of G, and so \(G/\Gamma _2(G)=G_{\mathrm{ab}}\), the abelianization of G. Furthermore, each term \(\Gamma _{n+1}(G)\) contains \([ \Gamma _n(G),\Gamma _n(G)]\), and thus the quotient group

is abelian.
Now let \(G=F/R\) be a presentation for our group, with F a free group and R a normal subgroup. Then \(\Gamma _n(G)=\Gamma _n(F)/\Gamma _n(F)\cap R\). Moreover, if G is finitely generated, then so are the LCS quotients from (2.1). We will write \(\phi _n(G)=\mathrm{rank}\,\mathrm{gr}_n(G)\) for the ranks of these groups.
For instance, if \(F_k\) is the free group on k generators, then all its LCS quotients are torsion-free, with ranks \(\phi _n=\phi _n(F_k)\) given by  , or, equivalently,
, or, equivalently,  , where \(\mu \) denotes the Möbius function.
, where \(\mu \) denotes the Möbius function.
2.2 Nilpotent quotients
It is readily seen that \(G/\Gamma _{n+1}(G)\) is a nilpotent group, and in fact, the maximal n-step nilpotent quotient of G. Letting  be the projection map, we obtain a tower of nilpotent groups,
be the projection map, we obtain a tower of nilpotent groups,

For each \(n\geqslant 1\), we have a central extension,

Passing to classifying spaces, we obtain a commutative diagram

where \(\psi _n\) corresponds to the projection \(G\rightarrow G/\Gamma _{n}(G)\) and \(\pi _n\) corresponds to the projection \(q_n\). Note that \(\pi _{n}\) may be viewed as the fibration with fiber \(K(\mathrm{gr}_n(G),1)\) obtained as the pullback of the pathspace fibration with base \(K(\mathrm{gr}_n(G),2)\) via a k-invariant
2.3 Postnikov tower and the holonomy map
Now let X be a connected CW-complex, and let \(G = \pi _1(X)\) be its fundamental group. An Eilenberg–MacLane space K(G, 1) can be constructed by adding to X cells of dimension three or more; let \(\iota :X\rightarrow K(G,1)\) be the inclusion map. For each \(n\geqslant 1\), let \(h_n:X\rightarrow K(G/\Gamma _{n}(G),1)\) be the composite  . This gives the following Postnikov tower of fibrations:
. This gives the following Postnikov tower of fibrations:

We take now homology with coefficients in \({\mathbb {Z}}\). From the above discussion, we deduce the well-known fact that the map \(\iota :X\rightarrow K(G,1)\) induces an isomorphism  and an epimorphism \(\iota _*:H_2(X)\twoheadrightarrow H_2(G)\).
and an epimorphism \(\iota _*:H_2(X)\twoheadrightarrow H_2(G)\).
Consider now the Lyndon–Hochschild–Serre spectral sequence defined in [4],
where G is a group, N is a normal subgroup of G, and M is a G-module. For the central central extension (2.2), the 5-term exact sequence arising from the terms of low degree (see e.g. [42, Theorem 2.1]) reduces to a short exact sequence

where the map \(\chi _n\) corresponds to the k-invariant from (2.4) via the Universal Coefficient Theorem. Using now the surjectivity of the map \(\iota _*:H_2(X)\rightarrow H_2(G)\) we obtain an exact sequence

In general, the sequence in (2.7) is natural but not split exact. We call the homomorphism

the holonomy map of X. The following lemma easily follows from the definitions and the Universal Coefficient Theorem.
Lemma 2.1
Suppose \(H_1(X)\) is finitely generated and torsion-free. Then the holonomy map of X is dual to the cup-product map

Consequently, if the cup-product map from (2.9) is surjective, the holonomy map from (2.8) is injective.
As the next example shows, the converse of the last statement does not hold.
Example 2.2
Let X be the connected, 2-dimensional CW-complex associated to the group G with presentation \(G=\langle x,y\,{|}\, x^2yx^{-2}y^{-1}=1\rangle \). Clearly, \(H_1(X)={\mathbb {Z}}^2\) and \(H_2(X)={\mathbb {Z}}\). With these identifications, the holonomy map \((h_2)_*:{\mathbb {Z}}\rightarrow {\mathbb {Z}}\) is multiplication by 2, and thus injective, while the cup-product map \(\cup :{\mathbb {Z}}\rightarrow {\mathbb {Z}}\) is also multiplication by 2, and thus not surjective.
3 Associated graded Lie algebras and Malcev Lie algebras
3.1 The associated graded Lie algebra of a group
Given a group G, we let \(\mathrm{gr}(G)\) be the direct sum of the successive quotients of the lower central series of G; that is,
The map  induces homomorphisms
induces homomorphisms  . It is readily seen that the following “Witt–Hall identities" hold in G:
. It is readily seen that the following “Witt–Hall identities" hold in G:

where \({}^a b= aba^{-1}\). It follows that \(\mathrm{gr}(G)\), endowed with the aforementioned bracket, has the structure of a graded Lie algebra, see for instance [22, 41]. The construction is functorial: every group homomorphism \(f:G\rightarrow H\) induces a morphism of graded Lie algebras, \(\mathrm{gr}(f):\mathrm{gr}(G)\rightarrow \mathrm{gr}(H)\).
If F is a free group, then, as shown by Magnus and Witt, \(\mathrm{gr}(F)\) is the free Lie algebra on the same set of generators as F; in particular, if \(F=F_\ell \), then \(\mathrm{gr}(F)=\mathrm{Lie}({\mathbb {Z}}^\ell )\), the free Lie algebra of rank \(\ell \).
3.2 Injective holonomy map and an exact sequence
Once again, let X be a path-connected space, with fundamental group \(G=\pi _1(X)\).
Theorem 3.1
Assume that the group \(H_1(X)\) is finitely generated, torsion-free, and the holonomy map  from (2.8) is injective. For each \(n \geqslant 2\), there is then a natural, split exact sequence
from (2.8) is injective. For each \(n \geqslant 2\), there is then a natural, split exact sequence

Proof
Recall that given a fibration of CW-complexes with base B, fiber F, and total space E, the filtration of \(C_*(E)\) by the inverse images of the skeleta of B gives a homology Serre spectral sequence with differentials
Furthermore, if the fundamental group of the base acts trivially on the fibers, then

For the fibration (2.3), the kernel of the differential \(d^2:H_2(B) \rightarrow H_1(F)\) is by equation (2.6) the image of \(H_2(X)\) in \(H_2(G/\Gamma _{n}(G))\). In turn, this image can be identified with \(H_2(X)\), since by assumption the holonomy map is a monomorphism. This gives an exact sequence

where \(F^1\) denotes the image in \(H_2(G/\Gamma _{n+1}(G))\) of the inverse image of the 1-skeleton in \(K(G/\Gamma _{n}(G),1)\). It follows that a map \((h_{n+1})_*\) gives a right splitting of the exact sequence (3.2). The result now follows from (2.7). \(\square \)
In particular, under the above hypothesis there is a natural exact sequence

Furthermore, this sequence is split exact. We do not claim that there is a natural splitting of the exact sequence (3.3), or of the other exact sequences from (3.1).
3.3 Malcev completion and the Malcev Lie algebra
In [23], Malcev established a one-to-one correspondence between certain nilpotent Lie algebras over \({\mathbb {Q}}\), and nilpotent groups over \({\mathbb {Q}}\), leading to the Malcev Lie algebra of a group. This was extended by Lazard [20] to groups with enough divisibility in central series subgroups to establish a one-to-one correspondence between a wider class of nilpotent groups and Lie algebras. An important next step was taken by Quillen, who established in [35] an equivalence between rational homotopy theory and the homotopy theory of reduced differential graded Lie algebras over \({\mathbb {Q}}\) with Malcev Lie algebras as the equivalent of the rational fundamental group. This was extended by Dwyer in [14] to an equivalence between the tame homotopy theory of 2-connected spaces and differential graded Lazard Lie algebras.
In more detail, assume that G is a finitely generated group. It is then possible to replace each nilpotent quotient \(N_n=G/\Gamma _{n}(G)\) by  , the (rationally defined) nilpotent Lie group associated to the discrete, torsion-free nilpotent group \(N_n/\mathrm{tors}(N_n)\). The corresponding inverse limit,
, the (rationally defined) nilpotent Lie group associated to the discrete, torsion-free nilpotent group \(N_n/\mathrm{tors}(N_n)\). The corresponding inverse limit,

is a prounipotent, filtered Lie group over \({\mathbb {Q}}\), which is called the prounipotent completion, or Malcev completion of G.
Let us denote by  the Lie algebra of a Lie group K. The pronilpotent Lie algebra
the Lie algebra of a Lie group K. The pronilpotent Lie algebra

endowed with the inverse limit filtration, is called the Malcev Lie algebra of G. By construction,  is a functor from the category of finitely generated groups to the category of complete, separated, filtered Lie algebras over \({\mathbb {Q}}\).
is a functor from the category of finitely generated groups to the category of complete, separated, filtered Lie algebras over \({\mathbb {Q}}\).
In [34, 35], Quillen showed that \(\mathfrak {m}(G)\) is the set of all primitive elements in \(\widehat{{\mathbb {Q}}{G}}\), the completion of the group algebra of G with respect to the filtration by powers of the augmentation ideal, and that the associated graded Lie algebra of \(\mathfrak {m}(G)\) with respect to the inverse limit filtration is isomorphic to \(\mathrm{gr}(G;{\mathbb {Q}})\). Furthermore, the set of all group-like elements in \( \widehat{{\mathbb {Q}}{G}}\), with multiplication and filtration inherited from \(\widehat{{\mathbb {Q}}{G}}\), forms a complete, filtered group isomorphic to \({\mathfrak {M}}(G)\).
3.4 The Sullivan minimal model
In a seminal paper [46], Sullivan showed that commutative differential graded algebras (cdgas) of differential forms over \({\mathbb {Q}}\) can be used to model rational homotopy theory. From this perspective the commutative differential graded algebra corresponding to the Malcev Lie algebra of a group is obtained by taking the free commutative differential graded algebra \(\mathrm{Hom}\) dual to nilpotent quotients of the Lie algebra and passing to the limit.
More precisely, Sullivan associated to each space X a cdga over the rationals, denoted \(A_{\scriptscriptstyle \mathrm{PL}}^{*}(X)\), for which there is an isomorphism \(H^{*}(A_{\scriptscriptstyle \mathrm{PL}}(X)) \cong H^{*}(X,{\mathbb {Q}})\) under which induced homomorphisms in cohomology correspond. A space X is said to be formal if \(A_{\scriptscriptstyle \mathrm{PL}}^{*}(X)\cong (H^{*}(X;{\mathbb {Q}}),d=0)\), i.e., Sullivan’s algebra can be connected by a zig–zag of quasi-isomorphisms to the rational cohomology ring of X, endowed with the zero differential.
A Hirsch extension (of degree i) is a cdga inclusion  , where V is a \({\mathbb {Q}}\)-vector space concentrated in degree i, while
, where V is a \({\mathbb {Q}}\)-vector space concentrated in degree i, while  is the free graded-commutative algebra generated by V, and d sends V into \(A^{i+1}\). A cdga (A, d) is called minimal if A is connected (i.e.,
is the free graded-commutative algebra generated by V, and d sends V into \(A^{i+1}\). A cdga (A, d) is called minimal if A is connected (i.e.,  ), and the following two conditions are satisfied: (1)
), and the following two conditions are satisfied: (1)  , where \(A_0={\mathbb {Q}}\) and each
, where \(A_0={\mathbb {Q}}\) and each  is a Hirsch extension of
is a Hirsch extension of  ; (2) the differential is decomposable, i.e.,
; (2) the differential is decomposable, i.e.,  , where
, where  . A basic result of Sullivan [46] and Morgan [28] asserts the following: Each connected cdga (A, d) has a minimal model
. A basic result of Sullivan [46] and Morgan [28] asserts the following: Each connected cdga (A, d) has a minimal model  , unique up to isomorphism.
, unique up to isomorphism.
Suppose now that X is a connected CW-complex with finitely many 1-cells. Then the Lie algebra dual to the first stage of the minimal model associated to \(A_{\scriptscriptstyle \mathrm{PL}}^{*}(X)\) is isomorphic to the Malcev Lie algebra \(\mathfrak {m}(\pi _1(X))\). A finitely generated group G is said to be 1-formal (over \({\mathbb {Q}}\)) if it has a classifying space K(G, 1) which is 1-formal, or, equivalently, if the Malcev Lie algebra \(\mathfrak {m}(G)\) is the completion of a quadratic Lie algebra. For a comprehensive discussion of all these notions and more we refer to the monographs [16, 17] and to the papers [32, 45].
The next step is to look for invariants beyond rational homotopy theory. Chen, Fox, and Lyndon [9] gave examples using Fox derivatives to find groups whose successive quotients in the lower central series have torsion. Stallings [42] related homological properties of a group to successive quotients in the lower central series and also to successive quotients in a mod p descending series. Building on this work, Dwyer [13] related Massey products in the cohomology of a group to properties of the quotients in the lower central series and also to a mod p central series different than the one used by Stallings. In [5,6,7], Cenkl and Porter used a commutative algebra of differential forms to model tame homotopy theory and the Lazard Lie algebra completion of the fundamental group.
Massey products were defined in [25] and applied to prove the Jacobi identity for Whitehead products. Porter [33] gave a general formula for Massey products in a commutator relators group in terms of coefficients in the Magnus expansions of the relators and provided applications to links. In [26], Matei gave examples of complements of hyperplane arrangements with nonzero mod p Massey products. This shows that while arrangement complements are formal over the rationals—and hence all Massey products with rational coefficients contain zero—they are not necessarily formal over the integers. Recently, Salvatore [39] gave examples of configuration spaces that are not formal over the integers.
4 Holonomy Lie algebras
Among all the Lie algebras one can associate to a group, the simplest is the holonomy Lie algebra, which only depends on data extracted from cohomology in low degrees. In this section we shed new light on the relationship between the holonomy Lie algebra and the associated graded Lie algebra of a group.
4.1 The holonomy Lie algebra of a group
Let G be a group, and fix a coefficient ring \(\mathbb {k}\), which we will take to be either a field or the integers. We will assume throughout that \(H=H_1(G,\mathbb {k})\) is a finitely generated \(\mathbb {k}\)-module; moreover, when \(\mathbb {k}={\mathbb {Z}}\), we will assume for simplicity that H is torsion-free. We let \(\mathrm{Lie}(H)\) denote the free Lie algebra on the free \(\mathbb {k}\)-module H; note that \(\mathrm{Lie}_1(H)=H\) and  .
.
Following [8, 19, 24, 30, 44, 45], we define \(\mathfrak {h}(G,\mathbb {k})\), the holonomy Lie algebra of G, as the quotient of the free Lie algebra on \(H_1(G,\mathbb {k})\) by the Lie ideal generated by the image of the holonomy map,  :
:

The holonomy Lie algebra of G is a quadratic Lie algebra: it is generated in degree 1 by \(\mathfrak {h}_1(G,\mathbb {k})=H_1(G,\mathbb {k})\), and all the relations are in degree 2. For \(\mathbb {k}={\mathbb {Z}}\), we simply write \(\mathfrak {h}(G)=\mathfrak {h}(G,{\mathbb {Z}})\). Clearly, the construction is functorial: every group homomorphism \(f:G\rightarrow H\) induces a morphism of graded Lie algebras, \(\mathfrak {h}(f):\mathfrak {h}(G,\mathbb {k})\rightarrow \mathfrak {h}(H,\mathbb {k})\).
As noted in [44], the projection map \(\psi _n:G\twoheadrightarrow G/\Gamma _n(G)\) induces an isomorphism  for all \(n\geqslant 3\). In particular, the holonomy Lie algebra of G depends only on its second nilpotent quotient, \(G/\Gamma _3 (G)\).
for all \(n\geqslant 3\). In particular, the holonomy Lie algebra of G depends only on its second nilpotent quotient, \(G/\Gamma _3 (G)\).
In a completely analogous fashion, one may define the holonomy Lie algebra \(\mathfrak {h}(A)\) of a graded, graded-commutative \(\mathbb {k}\)-algebra A, provided that \(A^0=\mathbb {k}\) and \(A^1\) is finite-dimensional (and torsion-free if \(\mathbb {k}={\mathbb {Z}}\)). It is readily seen that \(\mathfrak {h}(A)=\mathfrak {h}(A^{\leqslant 2})\). Moreover, if G is a group as above, \(\mathfrak {h}(G)=\mathfrak {h}(H^*(G;\mathbb {k}))\). In fact, if X is any path-connected space with \(G=\pi _1(X)\), then we may define  , after which it is easily verified that \(\mathfrak {h}(X)\cong \mathfrak {h}(G)\).
, after which it is easily verified that \(\mathfrak {h}(X)\cong \mathfrak {h}(G)\).
On a historical note, the holonomy Lie algebra of a group G was first defined (over \(\mathbb {k}={\mathbb {Q}}\)) by Chen in [8], and later considered by Kohno in [19] in the case when G is the fundamental group of the complement of a complex projective hypersurface. In [24], Markl and Papadima extended the definition of the holonomy Lie algebra to integral coefficients. Further in-depth studies were done by Papadima–Suciu [30] and Suciu–Wang [44, 45]; in particular, the more general case when the group \(H=H_1(G,{\mathbb {Z}})\) is allowed to have torsion is treated in [44].
4.2 A comparison map
Now set  , and let \(\mathrm{gr}(G,\mathbb {k}) = \bigoplus _{n\geqslant 1} \mathrm{gr}_n(G,\mathbb {k})\) be the associated graded Lie algebra of G over \(\mathbb {k}\). As shown in [24, 30, 44, 45], there is a (functorially defined) surjective morphism of graded Lie algebras,
, and let \(\mathrm{gr}(G,\mathbb {k}) = \bigoplus _{n\geqslant 1} \mathrm{gr}_n(G,\mathbb {k})\) be the associated graded Lie algebra of G over \(\mathbb {k}\). As shown in [24, 30, 44, 45], there is a (functorially defined) surjective morphism of graded Lie algebras,
which restricts to isomorphisms \(\mathfrak {h}_n(G,\mathbb {k}) \rightarrow \mathrm{gr}_n(G;\mathbb {k})\) for \(n\leqslant 2\).
The above map is an isomorphism if the group G is 1-formal over a field \(\mathbb {k}\) of characteristic 0, but in general it fails to be injective in degrees \(n\geqslant 3\). Nevertheless, for a large class of (not necessarily 1-formal) groups, the map \(\mathfrak {h}_3(G,\mathbb {k}) \rightarrow \mathrm{gr}_3(G;\mathbb {k})\) is an isomorphism, even for \(\mathbb {k}={\mathbb {Z}}\). This will be made more precise in Theorem 4.3 below.
4.3 Another exact sequence
As before, let \(h_2:X \rightarrow K(G/\Gamma _{2}(G),1)\) be the continuous map induced by the projection of G to \(G/\Gamma _{2}(G)\), and let \((h_2)_*:H_2(X) \rightarrow H_2(G/\Gamma _{2}(G))\) be the corresponding holonomy map.
Theorem 4.1
If \(H_1(X)\) is finitely generated and torsion-free, then there is an exact sequence

Proof
We shall make use of the homology Serre spectral sequence associated to the extension

The \(E^2\) page of this spectral sequence is depicted in diagram (4.3) below.

Assume first that \(\mathfrak {h}_2\) is torsion-free, where \(\mathfrak {h}=\mathfrak {h}(G)\). Our hypotheses on the abelian groups \(G/\Gamma _{2}(G)=\mathfrak {h}_1=H_1(X)\) and \(\mathrm{gr}_2(G)=\mathfrak {h}_2\) imply that all the terms \(E^2_{p,q}=H_p(G/\Gamma _{2}(G),H_q(\mathfrak {h}_2))\) are finitely generated and torsion-free, and hence, Hom dual to the \(E_2\) terms and differentials \(d_2\) in the cohomology spectral sequence associated to extension (4.2). Since the \(E_2\) terms and differentials form a commutative differential graded algebra, the differentials \(d_2\) are determined by the differential \(d_2^{\,0,1}\) dual to \(d^{\,2}_{2,0}:H_2(G/\Gamma _{2}(G)) \rightarrow H_1 (\mathfrak {h}_2)\), which is given by

where  denotes the bracket map from
denotes the bracket map from  to \(\mathfrak {h}_2\). Computing the differential \(d^{1,1}_2\) and \(d^{0,2}_2\) and then taking the dual maps gives the following:
to \(\mathfrak {h}_2\). Computing the differential \(d^{1,1}_2\) and \(d^{0,2}_2\) and then taking the dual maps gives the following:

for \(x_a, x_b, x_c \in \mathfrak {h}_1\) and

for \(x_a, x_b \in \mathfrak {h}_1\) and \(x_d \in \mathfrak {h}_2\).
From (4.4) and (4.6) it follows that \(E^3_{0,2} = 0\), while from (4.5) it follows that \(E^3_{1,1} = \mathfrak {h}_3\). Now note that \(E^3_{2,0}\) is the kernel of the map \(d^{\,2}_{2,0}\) in equation (4.4). From the formula for \(d^{\,2}_{2,0}\) in (4.4) and the exact sequence (2.6), it follows that \(E^3_{2,0}\) is the image of \(H_2(X)\) in \(H_2(G/\Gamma _{2}(G))\), which is  .
.
Looking at the domains and ranges of the higher-order differentials in the spectral sequence, we see that since \(E^3_{0,2} = 0\), it follows that \(E^3_{p,q} = E^\infty _{p,q}\) for \(p+q \leqslant 2\). We conclude that

Equation (4.1) now follows, and the proof of the lemma is complete in the case where \(\mathfrak {h}_2(G)\) is torsion-free.
In the case where \(\mathfrak {h}_2\) has torsion, let \(x_1, \ldots , x_\ell \) be elements in G that project to a basis for \(G/\Gamma _{2}(G)\). Set \(\mathscr {F}\) equal to the free group on the generators \(x_i\), and note that \(\mathfrak {h}_1(\mathscr {F})=\mathfrak {h}_1\) and  . The identity map of generators gives a map of central extensions
. The identity map of generators gives a map of central extensions

and hence a map of the respective homology spectral sequences. By the argument above, equations (4.4), (4.5), and (4.6) hold in the spectral sequence for \(\mathscr {F}\) and hence in the spectral sequence for G. Moreover, each of the maps of the \(E^2\) terms involved in these equations is onto, so it follows that the equations in (4.7) hold for G as well. This completes the proof. \(\square \)
Remark 4.2
If the group \(\mathfrak {h}_2=\mathfrak {h}_2(G)\) is torsion-free, then the commutative differential graded algebra \((E_2,d_2)\) is the Chevalley–Eilenberg cochain complex [4] of the Lie algebra \(\mathfrak {h}/\Gamma _3(\mathfrak {h})\). Since \(E^3_{p,q} = E^\infty _{p,q}\) for \(p+q = 2\), it follows that the Lie algebra homology group \(H_2({\mathfrak {h}}/\Gamma _{3}({\mathfrak {h}}))\) is isomorphic to \(H_2(G/\Gamma _{3}(G))\).
4.4 Identifying \(\mathfrak {h}_3(G)\) with \(\mathrm{gr}_3(G)\)
We are now ready to state and prove the main result of this section. A proof of this theorem was first sketched by Rybnikov in [37, Section 3]; we provide here an alternate proof, with full details.
Theorem 4.3
Suppose \(H=H_1(G;{\mathbb {Z}})\) is a finitely-generated, free abelian group, and the holonomy map  is injective. Then the canonical projection \(\mathfrak {h}_3(G)\rightarrow \mathrm{gr}_3(G)\) is an isomorphism.
is injective. Then the canonical projection \(\mathfrak {h}_3(G)\rightarrow \mathrm{gr}_3(G)\) is an isomorphism.
Proof
Consider the homology spectral sequence of the exact sequence from (4.2), whose \(E^2\) page is pictured in diagram (4.3). As in the proof of Theorem 3.1, let \(F^1\) denote the image in \(H_2(G/\Gamma _{3}(G))\) of the inverse image of the 1-skeleton of \(K(G/\Gamma _{2}(G),1)\).
The proof of Theorem 4.1 shows that if H is torsion-free, then  .
.
The proof of Theorem 3.1 shows that if H is torsion-free and the holonomy map \((h_2)_{*}\) is injective, then  , and the result follows. \(\square \)
, and the result follows. \(\square \)
5 Second cohomology of nilpotent groups and associated k-invariants
The purpose of this section is to use the exact sequence in equation (3.1) to relate homomorphisms from \(H_2(X)\) to \(\mathrm{gr}_n(G)\) to the possible k-invariants of the central extension of \(G/\Gamma _{n}(G)\) to \(G/\Gamma _{n+1}(G)\) from (2.2). Throughout this section, homology will be taken with coefficients in \({\mathbb {Z}}\).
In general, given an exact sequence of abelian groups

a map \(\sigma :B \rightarrow A\) with  is called a left splitting and a map \(h:C \rightarrow B\) with
is called a left splitting and a map \(h:C \rightarrow B\) with  is called a right splitting. Recall the following well-known fact: The exact sequence in (5.1) splits (either on the left or the right) if and only if
is called a right splitting. Recall the following well-known fact: The exact sequence in (5.1) splits (either on the left or the right) if and only if  . Furthermore, the direct sum decompositions of this sort are in one-to-one correspondence with splitting maps \(B \rightarrow A\) (or \(C \rightarrow B\)). Moreover, as shown in the proof of Lemma 5.1 below, a splitting yields a bijection between all splittings and the set of homomorphisms from C to A.
. Furthermore, the direct sum decompositions of this sort are in one-to-one correspondence with splitting maps \(B \rightarrow A\) (or \(C \rightarrow B\)). Moreover, as shown in the proof of Lemma 5.1 below, a splitting yields a bijection between all splittings and the set of homomorphisms from C to A.
Once again, let X be a path-connected space such that \(H_1(X)\) is finitely generated and torsion-free, and such that the holonomy map  is injective. Set \(G=\pi _1(X)\). Recall from Theorem 3.1 that for \(n \geqslant 3\) there is a split exact sequence
is injective. Set \(G=\pi _1(X)\). Recall from Theorem 3.1 that for \(n \geqslant 3\) there is a split exact sequence

and from (2.6), the k-invariant \(\chi _n\) gives a splitting; that is, in the diagram

the map  is the identity on \(\mathrm{gr}_n(G)\), while
is the identity on \(\mathrm{gr}_n(G)\), while  is the identity on \(H_2(X)\) and
is the identity on \(H_2(X)\) and  .
.
Lemma 5.1
For \(n \geqslant 3\), any homomorphism \(\sigma :H_2(G/\Gamma _{n}(G)) \rightarrow \mathrm{gr}_n(G)\) with  equal to the identity on \(\mathrm{gr}_n(G)\) yields a bijection between splittings of the exact sequence (5.2) and elements in \(\mathrm{Hom}(H_2(X), \mathrm{gr}_n(G))\).
equal to the identity on \(\mathrm{gr}_n(G)\) yields a bijection between splittings of the exact sequence (5.2) and elements in \(\mathrm{Hom}(H_2(X), \mathrm{gr}_n(G))\).
Proof
The map \(\sigma \) gives an isomorphism between \(H_2(G/\Gamma _{n}(G))\) and  . Without loss of generality, we can assume that via this isomorphism the inclusion i and the projection \(\pi \) in (5.3) correspond to the maps \({\widetilde{i}}\) and \({\widetilde{\pi }}\) in the diagram below
. Without loss of generality, we can assume that via this isomorphism the inclusion i and the projection \(\pi \) in (5.3) correspond to the maps \({\widetilde{i}}\) and \({\widetilde{\pi }}\) in the diagram below

where \({\widetilde{i}}\) is the inclusion into the first coordinate and \({\widetilde{\pi }}\) is the projection onto the second coordinate.
An element \(\lambda \in \mathrm{Hom}(H_2(X), \mathrm{gr}_n(G))\) determines a splitting of (5.4) as follows. Given \(\lambda \), define a map  by \(h(c) = (\lambda (c), c)\), and define
by \(h(c) = (\lambda (c), c)\), and define  by \(\chi (x, c) = x - \lambda (c)\).
by \(\chi (x, c) = x - \lambda (c)\).
It is straightforward to check that in the diagram

the map  is the identity on \(\mathrm{gr}_n(G)\), while
is the identity on \(\mathrm{gr}_n(G)\), while  is the identity on \(H_2(X)\) and
is the identity on \(H_2(X)\) and  . Every homomorphism
. Every homomorphism  with
with  equal to the identity on \(H_2(X)\) has the form \(h(c) = (\lambda (c), c)\) and the lemma follows. \(\square \)
equal to the identity on \(H_2(X)\) has the form \(h(c) = (\lambda (c), c)\) and the lemma follows. \(\square \)
In the context of the Postnikov tower (2.5) and the exact sequence in (5.2), this leads to a formula for the k-invariant of the extension (2.2) from \(G/\Gamma _{n}(G)\) to \(G/\Gamma _{n+1}(G)\) for a fixed \(n \geqslant 3\), in terms of a splitting map \(\sigma :H_2(G/\Gamma _{n}(G)) \rightarrow \mathrm{gr}_n(G)\) and a map \(h_n :X \rightarrow K(G/\Gamma _{n}(G),1)\) corresponding to the projection of G to \(G/\Gamma _{n}(G)\).
Corollary 5.2
With assumptions and notation as above, the k-invariant of the extension \(0\rightarrow \mathrm{gr}_{2}(G) \rightarrow G/\Gamma _{3}(G) \rightarrow G/\Gamma _2(G) \rightarrow 0\) with respect to the direct sum decomposition given by the splitting \(\sigma :H_2(G/\Gamma _{n}(G)) \rightarrow \mathrm{gr}_n(G)\) is the element
given by the homomorphism \(\chi _n (x,c) = x - \lambda (c)\), where  .
.
Proof
The claim follows from Lemma 5.1 and the observation that for the map h in (5.5), we have that  . \(\square \)
. \(\square \)
Example 5.3
We illustrate the above corollary with a simple example (for a more general context, see Proposition 7.2 below). Let X be a wedge of \(\ell \) circles, so that \(G=\pi _1(X)\) is isomorphic to \(F_\ell \), the free group of rank \(\ell \). Identifying \(G/\Gamma _{2}(G)={\mathbb {Z}}^\ell \) and  , the second nilpotent quotient \(N=G/\Gamma _{3}(G)\) fits into a central extension
, the second nilpotent quotient \(N=G/\Gamma _{3}(G)\) fits into a central extension

Note that \(H_2(X)=0\), and so the homomorphism \(\lambda :H_2(X)\rightarrow {\mathbb {Z}}^\ell \) is the zero map. Hence, by Corollary 5.2, the extension (5.6) is classified by the k-invariant  .
.
6 Generalizations of Rybnikov’s theorem
6.1 The setup
Let X be a connected CW-complex. We will assume throughout that the homology group \(H_1(X)\) is finitely generated and torsion-free, and that the holonomy map  is injective.
is injective.
Let \(G = \pi _1(X)\), and fix an integer \(n\geqslant 2\). Recall from (2.7) the exact sequence

where the map \(h_n:X \rightarrow K(G/\Gamma _n(G),1)\) is induced by the projection of \(G\twoheadrightarrow G/\Gamma _n(G)\). If N is a nilpotent group with \(N \cong N/\Gamma _n(N) \cong G/\Gamma _n(G)\), then Theorem 3.1 gives a split exact sequence

Now let \(X_a\) and \(X_b\) be two spaces as above and let \(G_a\), and \(G_b\) be the respective fundamental groups. Suppose there is a map \(g:H^{\leqslant 2}(X_b) \rightarrow H^{\leqslant 2}(X_a)\) which is an isomorphism of graded rings. Set \(\overline{g}:H_{\leqslant 2}(X_a) \rightarrow H_{\leqslant 2}(X_b)\) equal to the dual to g. Then
-
There is an isomorphism
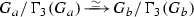 .
. -
The isomorphism \(\overline{g}_1:H_1(X_a) \rightarrow H_1(X_b)\) induces an isomorphism \(\overline{g}_{\#}:\mathfrak {h}_3(G_a) \rightarrow \mathfrak {h}_3(G_b)\).
If \(f:G_a\rightarrow G_b\) is a group homomorphism, we will denote by \(f_n:G_a/\Gamma _n(G_a) \rightarrow G_b/\Gamma _n(G_b)\) the induced homomorphisms between the respective nilpotent quotients.
6.2 Statement and proof of the theorem
We are ready now to state and proof our generalization of [37, Theorem 12].
Theorem 6.1
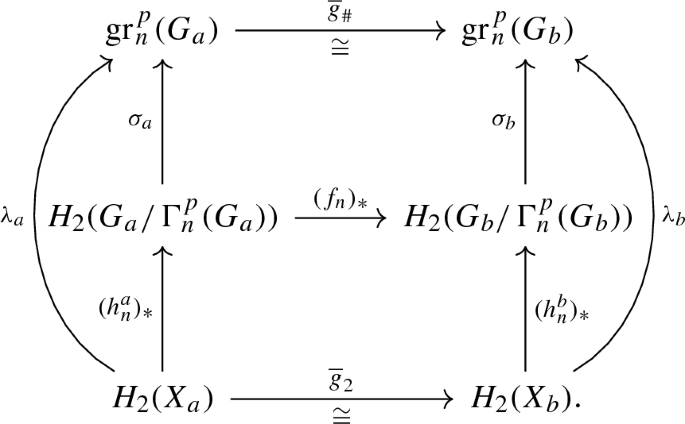
With the assumptions above, fix \(n\geqslant 3\), let \(\sigma _{a}:H_2(G_a/\Gamma _n(G_a)) \rightarrow \mathrm{gr}_n(G_a)\) be any left splitting of the exact sequence (6.1), and let \(f_n:G_a/\Gamma _n(G_a) \rightarrow G_b/\Gamma _n(G_b)\) be any isomorphism that extends the map \(\overline{g}_1:G_a/\Gamma _2(G_a) \rightarrow G_b/\Gamma _2(G_b)\). The following conditions are then equivalent:
-
1.
The map \(\overline{g}_1\) extends to an isomorphism
 .
. -
2.
There are liftings \(h_n^{c}:X_c \rightarrow K(G_c/\Gamma _{n}(G_c),1)\) for \(c = a\) and b such that the following diagram commutes:

In the above diagram, the map \({\overline{g}}_{\#}\) is the restriction of the map \((f_n)_{*}\) between the respective extensions of type (6.1).
Proof
First we show that if there is a commutative diagram such as the one above, then the isomorphism  extends to an isomorphism
extends to an isomorphism  .
.
From the commutativity of diagram (6.2), it follows that \(\sigma _b\) is a left splitting. Using the direct sum decompositions given by the left splittings, we may define maps

for \(c=a\) or b by
Consider now the homology spectral sequences associated to the extensions (2.2) for \(G=G_a\) and \(G=G_b\), respectively. From the naturality of the Serre spectral sequence and the commutativity of the aforementioned diagram, it follows that, with respect to the direct sum decompositions, the map \((f_n)_*\) corresponds to the map \((x,y) \rightarrow (g_\#(y), {\overline{g}}_2(y))\). Thus, the following diagram is commutative:

Let \(E(\kappa _a)\) and \(E(\kappa _b)\) be the central extensions with k-invariants \(\kappa _a\) and \(\kappa _b\), respectively. Then from the commutativity of the diagram in (6.3) it follows that \(f_n\) lifts to an isomorphism \({\widetilde{f}}_n:E(\kappa _a) \rightarrow E(\kappa _b)\). On the other hand, Corollary 5.2 implies that \(E(\kappa _a) = K(G_a/\Gamma _{n+1}(G_a),1)\) and \(E(\kappa _b) = K(G_b/\Gamma _{n+1}(G_b),1)\), and this completes the proof of the first part of the theorem.
To prove the reverse implication, assume that a left splitting \(\sigma _a:H_2(G_a/\Gamma _n(G_a)\rightarrow \mathfrak {h}_n(G_a)\) and an isomorphism \(f_n:G_a/\Gamma _n(G_a)\rightarrow G_b/\Gamma _n(G_b)\) are given; we will then show that there is a commutative diagram of the form (6.2).
Let \(e_{n+1}:G_a/\Gamma _{n+1}(G_a) \rightarrow G_b/\Gamma _{n+1}(G_b)\) be an isomorphism. The first step is to prove that there is a commutative diagram

Let \(e_n\) be the isomorphism from \(G_a/\Gamma _n(G_a)\) to \(G_b/\Gamma _n(G_b)\) induced by \(e_{n+1}\). Then \(e_n\) gives rise to the following commutative diagram in the tower of nilpotent quotients:

Since \(e_n\) and \(f_n\) are both extensions of \({\overline{g}}\), it follows that the automorphism 
 is an extension of the identity map. This gives the following commutative diagram:
is an extension of the identity map. This gives the following commutative diagram:

Putting diagrams (6.5) and (6.6) together and passing to homology gives the commutative diagram (6.4). Then the left splitting \(\sigma _a\) determines a left splitting \(\sigma _b\) such that the upper rectangle in the diagram (6.2) commutes, and the proof of the theorem is complete. \(\square \)
6.3 Further refinements
The above proof shows the following: if the map \(h_2^b:X_b\rightarrow K({G_b}/\Gamma _{2}({G_b}),1)\) is given, and if  is an isomorphism, then there is an extension of \(f_n\) to an isomorphism
is an isomorphism, then there is an extension of \(f_n\) to an isomorphism  if and only if there is a lifting \(h_n^a :X\rightarrow K({G_a}/\Gamma _{n}({G_a}),1)\) such that diagram (6.2) commutes. The next theorem recasts this result in a more compact fashion.
if and only if there is a lifting \(h_n^a :X\rightarrow K({G_a}/\Gamma _{n}({G_a}),1)\) such that diagram (6.2) commutes. The next theorem recasts this result in a more compact fashion.
Theorem 6.2
With notation and assumptions as above, suppose N is a nilpotent group with \(N \cong N/\Gamma _n (N)\) and that the map \(\ell _b:X_b \rightarrow K(N,1)\) induces an isomorphism  . Let \(\sigma :H_2(N)\rightarrow \mathrm{gr}_n(N)\) be a splitting of the exact sequence (6.1) and \(f_n :{G_a}/\Gamma _{n}({G_a}) \rightarrow {G_b}/\Gamma _{n}({G_b})\) an isomorphism. Then there is an isomorphism
. Let \(\sigma :H_2(N)\rightarrow \mathrm{gr}_n(N)\) be a splitting of the exact sequence (6.1) and \(f_n :{G_a}/\Gamma _{n}({G_a}) \rightarrow {G_b}/\Gamma _{n}({G_b})\) an isomorphism. Then there is an isomorphism
extending \(f_n\) if and only if there is a map \(\ell _a :X_a \rightarrow K(N,1)\) inducing an isomorphism  such that the following diagram commutes:
such that the following diagram commutes:

Proof
Let \(e_n^b\) be a isomorphism from \(K({G_b}/\Gamma _{n}({G_b}),1)\) to K(N, 1) and consider the following diagram:

where  and \(q_a\) is determined by the condition that on the first homology groups
and \(q_a\) is determined by the condition that on the first homology groups  . The corresponding diagram of homology groups and maps is
. The corresponding diagram of homology groups and maps is

Since the maps \(e_n^a\) and \(e_n^b\) in (6.8) are isomorphisms, it follows that there is a bijection between liftings \(\ell _a\) and \(h_n^a\) in (6.8), and also a bijection between liftings \(\ell _b\) and \(h_n^b\). Moreover, in (6.9)

Consider now the diagram

where the maps \((e_n^a)_\#\) and \((e_n^b)_\#\) are induced by the corresponding isomorphisms of groups \(e_n^a\) and \(e_n^b\), and the splittings \(\sigma _a\) and \(\sigma _b\) are defined by requiring that the top two rows in (6.11) form a commutative diagram.
From (6.10) and a diagram chase, it follows that (6.11) commutes if and only if the corresponding diagram (6.2) commutes, and also that (6.11) commutes if and only if diagram (6.7) commutes with  and
and  . The desired conclusion follows. \(\square \)
. The desired conclusion follows. \(\square \)
Remark 6.3
In the work of Rybnikov [36, 37], it is assumed that the groups \(\mathfrak {h}_2\) and \(\mathfrak {h}_3\) are torsion-free. Then replacing the modules and maps in Theorem 6.1 for \(n=3\) with their Hom duals yields [37, item 2 of Theorem 12]. The result in Theorem 6.2 for \(n=3\) corresponds to [36, Theorem 2.2].
6.4 The Stallings mod p lower central series
Let G be a group, and let \(p = 0\) or a prime. Following Stallings [42], define subgroups \(\Gamma _n^p(G)<G\) as follows:

where \(\langle U \rangle \) denotes the subgroup generated by a subset \(U\subset G\). Then \(\{ \Gamma _n^p(G)\}_{n\geqslant 1}\) is a descending central series of normal subgroups. For \(p=0\) it is the lower central series; for \(p\ne 0\) it is the most rapidly descending central series whose successive quotients are vector spaces over the field of p elements. If we set \(\mathrm{gr}_n^p(G) = \Gamma _n^p(G)/\Gamma _{n+1}^p(G)\), then  is a graded Lie algebra over \({\mathbb {Z}}_p\) in a natural way.
is a graded Lie algebra over \({\mathbb {Z}}_p\) in a natural way.
Now let X be a path-connected space, and \(G=\pi _1(X)\). For the remainder of this section all homology groups are with \({\mathbb {Z}}_p\) coefficients, where \({\mathbb {Z}}_0\) denotes the integers. As shown in [42], there is an exact sequence

where the map \(h_n:X \rightarrow G/\Gamma _n^p(G)\) is induced by the projection of \(G=\pi _1(X)\) to \(G/\Gamma _n^p(G)\). The proof of Theorem 3.1 extends to show that if \((h_2)_*\) is a monomorphism and N is a nilpotent group with \(N \cong N/\Gamma _n^p(N) \cong G/\Gamma _n^p(G)\), then there is a split exact sequence

for all \(n \geqslant 3\).
6.5 An extension of Rybnikov’s theorem in characteristic p
Let \(X_a\) and \(X_b\) be path-connected spaces with \(G_a = \pi _1(X_a)\) and \(G_b = \pi _1(X_b)\). Assume \(p=0\) or p a prime has been chosen; all homology groups in the following theorem are with \({\mathbb {Z}}_p\) coefficients. Assume also that \(H_1(X_a)\) and \(H_1 (X_b)\) are finitely generated, and the respective maps \((h_2)_*\) are monomorphisms.
Suppose we are given an isomorphism \(g:H^{\leqslant 2}(X_b) \rightarrow H^{\leqslant 2}(X_a)\) of graded algebras. Set \(\overline{g}:H_{\leqslant 2}(X_a) \rightarrow H_{\leqslant 2}(X_b)\) equal to the dual to g. Then given the exact sequences from (6.12) and (6.13), the steps in the proof of Theorem 6.1 apply to prove the following.
Theorem 6.4
With the assumptions above, fix \(n\geqslant 3\), let \(\sigma _{a}:H_2(G_a/\Gamma _n^p(G)) \rightarrow \mathrm{gr}_n^p(G_a)\) be any left splitting of the exact sequence (6.13), and let \(f_n:G_a/\Gamma _n^p(G_a) \rightarrow G_b/\Gamma _n^p(G_b)\) be any isomorphism that extends the map \(\overline{g}_1:G_a/\Gamma _2^p(G_a) \rightarrow G_b/\Gamma _2^p(G_b)\). The following conditions are then equivalent:
-
1.
The map \(\overline{g}_1\) extends to an isomorphism
 .
. -
2.
There are liftings \(h_n^{c}:X_c \rightarrow K(G_c/\Gamma _{n}^p(G_c),1)\) for \(c = a\) and b such that the following diagram commutes:
In the above diagram, the map \({\overline{g}}_{\#}\) is the restriction of the map \((f_n)_{*}\) between the respective extensions of type (6.13). The reasoning from Theorem 6.2 generalizes to show that Theorem 6.4 implies the following result.
Theorem 6.5
With the assumptions as in Theorem 6.4, assume N is a nilpotent group with \(N \cong N/\Gamma _n^p (N)\) and that \(\ell _b:X_b \rightarrow K(N,1)\) induces an isomorphism  . Let \(\sigma \) be a splitting of the exact sequence (6.13). Then there is an isomorphism
. Let \(\sigma \) be a splitting of the exact sequence (6.13). Then there is an isomorphism
extending \(\overline{g}_2\) if and only if there is a map \(\ell _a :X_a \rightarrow K(N,1)\) inducing an isomorphism of \(G_a/\Gamma _n^p(G_a) \rightarrow N\) such that the following diagram commutes:

7 Hyperplane arrangements
We now apply the tools developed in the previous sections to a class of spaces that arise in a combinatorial context. These spaces—complements of complex hyperplane arrangements—have motivated to a large extent the approach taken here, and provide a blueprint for further applications.
7.1 Complement and intersection lattice
We start with a brief review of arrangement theory; for details and references, we refer to the monograph of Orlik and Terao [29].
An arrangement of hyperplanes is a finite set  of codimension-1 linear subspaces in a finite-dimensional, complex vector space \({\mathbb {C}}^{n}\). The combinatorics of the arrangement is encoded in its intersection lattice,
of codimension-1 linear subspaces in a finite-dimensional, complex vector space \({\mathbb {C}}^{n}\). The combinatorics of the arrangement is encoded in its intersection lattice,  , that is, the poset of all intersections of hyperplanes in
, that is, the poset of all intersections of hyperplanes in  (also known as flats), ordered by reverse inclusion, and ranked by codimension. For a flat
(also known as flats), ordered by reverse inclusion, and ranked by codimension. For a flat  defined by a sub-arrangement
defined by a sub-arrangement  , we let \(\mathrm{rank}\,Y=\mathrm{codim}\,Y\); we also write
, we let \(\mathrm{rank}\,Y=\mathrm{codim}\,Y\); we also write  .
.
The main topological invariant associated to such an arrangement  is its complement,
is its complement,  . This is a connected, smooth complex quasi-projective variety. Moreover,
. This is a connected, smooth complex quasi-projective variety. Moreover,  is a Stein manifold, and thus has the homotopy type of a finite CW-complex of dimension at most n.
is a Stein manifold, and thus has the homotopy type of a finite CW-complex of dimension at most n.
Probably the best-known example is the braid arrangement  , consisting of the diagonal hyperplanes in \({\mathbb {C}}^{n}\). It is readily seen that
, consisting of the diagonal hyperplanes in \({\mathbb {C}}^{n}\). It is readily seen that  is the lattice of partitions of
is the lattice of partitions of  , ordered by refinement, while
, ordered by refinement, while  is the configuration space \(F({\mathbb {C}},n)\) of n ordered points in \({\mathbb {C}}\). In the early 1960s, Fox, Neuwirth, and Fadell showed that
is the configuration space \(F({\mathbb {C}},n)\) of n ordered points in \({\mathbb {C}}\). In the early 1960s, Fox, Neuwirth, and Fadell showed that  is a classifying space for \(P_{n}\), the pure braid group on n strings.
is a classifying space for \(P_{n}\), the pure braid group on n strings.
For a general arrangement  , the cohomology ring
, the cohomology ring  was computed by Brieskorn in the early 1970s, building on pioneering work of Arnol’d on the cohomology ring of the braid arrangement. It follows from Brieskorn’s work that the space
was computed by Brieskorn in the early 1970s, building on pioneering work of Arnol’d on the cohomology ring of the braid arrangement. It follows from Brieskorn’s work that the space  is formal over \({\mathbb {Q}}\). Consequently, the fundamental group of the complement,
is formal over \({\mathbb {Q}}\). Consequently, the fundamental group of the complement,  , is 1-formal over \({\mathbb {Q}}\).
, is 1-formal over \({\mathbb {Q}}\).
In 1980, Orlik and Solomon gave a simple combinatorial description of the ring  : it is the quotient
: it is the quotient  of the exterior algebra
of the exterior algebra  on classes dual to the meridians around the hyperplanes, modulo a certain ideal
on classes dual to the meridians around the hyperplanes, modulo a certain ideal  defined in terms of the intersection lattice of
defined in terms of the intersection lattice of  . In particular, the cohomology ring of the complement is combinatorially determined; that is to say, if
. In particular, the cohomology ring of the complement is combinatorially determined; that is to say, if  and
and  are arrangements with
are arrangements with  , then
, then  .
.
7.2 Localized sub-arrangements
The localization of an arrangement  at a flat
at a flat  is defined as the sub-arrangement
is defined as the sub-arrangement

The inclusion  gives rise to an inclusion of complements,
gives rise to an inclusion of complements,  . Choosing a point \(x_0\) sufficiently close to \(0\in {\mathbb {C}}^{n}\), we can make it a common basepoint for both
. Choosing a point \(x_0\) sufficiently close to \(0\in {\mathbb {C}}^{n}\), we can make it a common basepoint for both  and all local complements
and all local complements  .
.
Lemma 7.1
[12] There exist basepoint-preserving maps  such that
such that  relative to \(x_0\). Moreover, if
relative to \(x_0\). Moreover, if  and \(H\not \supset Y\), then the composite
and \(H\not \supset Y\), then the composite  is null-homotopic.
is null-homotopic.
In particular, if we set  , then the induced homomorphisms
, then the induced homomorphisms  are all injective.
are all injective.
The inclusions  assemble into a map
assemble into a map

The classical Brieskorn Lemma insures that the induced homomorphism in cohomology is an isomorphism in each degree \(k\geqslant 1\). By the Künneth formula, then, we have that

for all \(k\geqslant 1\). Likewise, the Orlik–Solomon ideal decomposes in each degree as

It follows that the homology groups of the complement of  are torsion-free, with ranks given by
are torsion-free, with ranks given by

where  is the Möbius function of the intersection lattice, defined inductively by \(\mu ({\mathbb {C}}^{n})=1\) and \(\mu (Y)=-\sum _{Z\supsetneq Y} \mu (Z)\). In particular,
is the Möbius function of the intersection lattice, defined inductively by \(\mu ({\mathbb {C}}^{n})=1\) and \(\mu (Y)=-\sum _{Z\supsetneq Y} \mu (Z)\). In particular,  is free abelian of rank equal to the cardinality of the arrangement,
is free abelian of rank equal to the cardinality of the arrangement,  .
.
Of particular interest to us is what happens in degree \(k=2\). For a 2-flat Y, the localized sub-arrangement  is a pencil of \(\left| Y \right| =\mu (Y)+1\) hyperplanes. Consequently,
is a pencil of \(\left| Y \right| =\mu (Y)+1\) hyperplanes. Consequently,  is homeomorphic to
is homeomorphic to  , and so
, and so  is a classifying space for the group
is a classifying space for the group  .
.
7.3 The second nilpotent quotient of an arrangement group
Let  be an arrangement group. Then G admits a commutator-relators presentation of the form \(G=F/R\), where F is the free group on generators
be an arrangement group. Then G admits a commutator-relators presentation of the form \(G=F/R\), where F is the free group on generators  corresponding to meridians about the hyperplanes, and \(R\subset [F,F]\) (see for instance [10] as well as [43] and references therein).
corresponding to meridians about the hyperplanes, and \(R\subset [F,F]\) (see for instance [10] as well as [43] and references therein).
Plainly, the abelianization  is the free abelian group on
is the free abelian group on  . On the other hand, as noted for instance in [27], the abelian group \(\mathrm{gr}_2(G)\) is the \({\mathbb {Z}}\)-dual of
. On the other hand, as noted for instance in [27], the abelian group \(\mathrm{gr}_2(G)\) is the \({\mathbb {Z}}\)-dual of  ; in particular, \(\mathrm{gr}_2(G)\) is also torsion-free. The central extension (2.2) with \(n=2\) takes a very explicit form, detailed in the next result.
; in particular, \(\mathrm{gr}_2(G)\) is also torsion-free. The central extension (2.2) with \(n=2\) takes a very explicit form, detailed in the next result.
Proposition 7.2
([27]) For any arrangement  , the second nilpotent quotient of
, the second nilpotent quotient of  fits into a central extension of the form
fits into a central extension of the form

Furthermore, the k-invariant of this extension, \(\chi _2 :H_2( G_{\mathrm{ab}} )\rightarrow \mathrm{gr}_2(G)\), is the dual of the inclusion map  .
.
It follows that \(G/\Gamma _3(G)\) is the quotient of the free, 2-step nilpotent group \(F/\Gamma _3(F)\) by all commutation relations of the form

indexed by pairs of hyperplanes  and flats
and flats  such that \(H\supset Y\) (see [27, 36]). From this description it is apparent that the second nilpotent quotient of an arrangement group is combinatorially determined. More precisely, if
such that \(H\supset Y\) (see [27, 36]). From this description it is apparent that the second nilpotent quotient of an arrangement group is combinatorially determined. More precisely, if  and
and  are two arrangements such that
are two arrangements such that  , there is then an induced isomorphism,
, there is then an induced isomorphism,  .
.
7.4 Holonomy Lie algebra
The holonomy Lie algebra of an arrangement  is defined as
is defined as  . Using the Orlik–Solomon description of the cohomology ring of
. Using the Orlik–Solomon description of the cohomology ring of  , it is readily seen that
, it is readily seen that  is the quotient of \(\mathbf{L }({\mathscr {A}})\), the free Lie algebra on variables
is the quotient of \(\mathbf{L }({\mathscr {A}})\), the free Lie algebra on variables  , modulo the ideal generated by relations arising from the rank 2 flats:
, modulo the ideal generated by relations arising from the rank 2 flats:

By construction, this is a quadratic Lie algebra which depends solely on the ranked poset  . More precisely, if
. More precisely, if  and
and  are two arrangements such that
are two arrangements such that  , there is then an induced isomorphism
, there is then an induced isomorphism  .
.
As shown by Kohno [19] (based on foundational work by Sullivan [46] and Morgan [28]), the associated graded Lie algebra  and the holonomy Lie algebra
and the holonomy Lie algebra  are rationally isomorphic:
are rationally isomorphic:

In [15], Falk sketched the construction of a 1-minimal model for  and used this to show that the rank of
and used this to show that the rank of  —now sometimes known as the “Falk invariant" of the arrangement—is equal to the nullity of the multiplication map
—now sometimes known as the “Falk invariant" of the arrangement—is equal to the nullity of the multiplication map  over \({\mathbb {Q}}\). Further information on the ranks of the LCS quotients
over \({\mathbb {Q}}\). Further information on the ranks of the LCS quotients  can be found in [40].
can be found in [40].
At the integral level, there is a surjective Lie algebra map,  , such that
, such that  is an isomorphism. In general, there exist arrangements for which the map \(\varPsi \) is not injective. Nevertheless, as a consequence of Theorem 4.3 and the preceding discussion, we have the following result.
is an isomorphism. In general, there exist arrangements for which the map \(\varPsi \) is not injective. Nevertheless, as a consequence of Theorem 4.3 and the preceding discussion, we have the following result.
Theorem 7.3
For any arrangement  , the map
, the map  is an isomorphism.
is an isomorphism.
Consequently, the group  is combinatorially determined; that is, if
is combinatorially determined; that is, if  and
and  are two arrangements such that
are two arrangements such that  , then
, then  .
.
On the other hand, as first noted in [43], there exist arrangements  for which
for which  has non-zero torsion for some \(k>3\). This naturally raised the question whether such torsion in the LCS quotients of arrangement groups is combinatorially determined. The question was recently answered by Artal Bartolo, Guerville-Ballé, and Viu-Sos [3], who produced a pair of arrangements
has non-zero torsion for some \(k>3\). This naturally raised the question whether such torsion in the LCS quotients of arrangement groups is combinatorially determined. The question was recently answered by Artal Bartolo, Guerville-Ballé, and Viu-Sos [3], who produced a pair of arrangements  and
and  with
with  , yet
, yet  ; the difference (detected by computer-aided computation) lies in the 2-torsion of the respective groups.
; the difference (detected by computer-aided computation) lies in the 2-torsion of the respective groups.
8 Decomposable arrangements and nilpotent quotients
We conclude with an in-depth study of a particularly nice class of hyperplane arrangements. Building on work of Papadima and Suciu [31], we show that the tower of nilpotent quotients of the fundamental group of the complement of a decomposable arrangement is fully determined by the intersection lattice.
8.1 Decomposable arrangements
Let  be an arrangement. As we saw in Sect. 7.2, for each 2-flat
be an arrangement. As we saw in Sect. 7.2, for each 2-flat  , the group
, the group  is isomorphic to
is isomorphic to  ; hence,
; hence,  . Furthermore, from the defining relations (7.2), we infer that
. Furthermore, from the defining relations (7.2), we infer that  .
.
Let j be the map from (7.1). Projecting onto the factors corresponding to rank 2 flats we obtain a map

The induced homomorphism on fundamental groups

defines a morphism of graded Lie algebras

Proposition 8.1
([31]) For any arrangement  , the homomorphism
, the homomorphism

is a surjection for \(n\geqslant 3\) and an isomorphism for \(n=2\).
Following [31], we say that the arrangement  is decomposable if the map \(\mathfrak {h}_3(j_{\#}) \) is an isomorphism (for related notions of decomposability, see also [11, 40]). The following theorem completely describes the structure of the associated graded and holonomy Lie algebras of a decomposable arrangement.
is decomposable if the map \(\mathfrak {h}_3(j_{\#}) \) is an isomorphism (for related notions of decomposability, see also [11, 40]). The following theorem completely describes the structure of the associated graded and holonomy Lie algebras of a decomposable arrangement.
Theorem 8.2
([31]) If  is a decomposable arrangement, then the following hold:
is a decomposable arrangement, then the following hold:
-
1.
The map
 is an isomorphism of graded Lie algebras.
is an isomorphism of graded Lie algebras. -
2.
The map
 is an isomorphism.
is an isomorphism.
It follows from this theorem that the groups  are torsion-free, with ranks
are torsion-free, with ranks  given by
given by

Moreover, since the holonomy Lie algebra of any arrangement is combinatorially determined, we have the following immediate corollary.
Corollary 8.3
If  and
and  are decomposable arrangements with
are decomposable arrangements with  , then
, then  .
.
8.2 Nilpotent quotients and localized arrangements
Our goal now is to strengthen Corollary 8.3 from the level of the LCS quotients  to the level of the nilpotent quotients
to the level of the nilpotent quotients  . We start with some preparatory results on the second homology of these nilpotent groups.
. We start with some preparatory results on the second homology of these nilpotent groups.
Lemma 8.4
Let  be an arrangement and set
be an arrangement and set  . There is then a natural, split exact sequence
. There is then a natural, split exact sequence

Moreover, if  is decomposable, then for every \(n\geqslant 3\) there is a natural, split exact sequence
is decomposable, then for every \(n\geqslant 3\) there is a natural, split exact sequence

Proof
The first assertion follows from Theorems 3.1 and 7.3, while the second assertion follows from Theorems 3.1 and 8.2. \(\square \)
For an arbitrary arrangement  and for a 2-flat
and for a 2-flat  , we let
, we let  be the corresponding localized arrangement, and write
be the corresponding localized arrangement, and write  . The inclusion map
. The inclusion map  induces a homomorphism \((j_Y)_{\#}:G\rightarrow G_Y\) on fundamental groups, which in turn induces homomorphisms
induces a homomorphism \((j_Y)_{\#}:G\rightarrow G_Y\) on fundamental groups, which in turn induces homomorphisms
on the respective nilpotent quotients. Assembling these maps, we obtain a homomorphism

Proposition 8.5
For any arrangement  , and for each \(n\geqslant 3\), the map \(N_n(j)\) induces a surjection in second homology,
, and for each \(n\geqslant 3\), the map \(N_n(j)\) induces a surjection in second homology,

Moreover, if  is decomposable, then the maps \(N_n(j)_*\) are isomorphisms, for all \(n\geqslant 3\).
is decomposable, then the maps \(N_n(j)_*\) are isomorphisms, for all \(n\geqslant 3\).
Proof
Fix \(n\geqslant 3\), and set  and
and  . Consider the following diagram:
. Consider the following diagram:

It follows from Lemma 8.4 that the top and bottom rows are (split) exact. Furthermore, the naturality of the exact sequence (8.1) implies that the diagram commutes. By Brieskorn’s Lemma, the map \(j_*\) is an isomorphism. Furthermore, by Proposition 8.1, the map \(\mathfrak {h}_n(j_{\#})\) is a surjection. The first claim follows at once.
If the arrangement is decomposable, then by Theorem 8.2 the map \(\mathfrak {h}_n(j_{\#})\) is an isomorphism, whence \(N_n(j)_*\) is also an isomorphism. \(\square \)
8.3 Lifting maps to nilpotent quotients
Let  be an arrangement and set
be an arrangement and set  . Composing a classifying map
. Composing a classifying map  with the map \(K(G,1)\rightarrow K(G_{\mathrm{ab}},1)\) induced by the abelianization homomorphism \(G\rightarrow G_{\mathrm{ab}}\), we obtain a map of spaces,
with the map \(K(G,1)\rightarrow K(G_{\mathrm{ab}},1)\) induced by the abelianization homomorphism \(G\rightarrow G_{\mathrm{ab}}\), we obtain a map of spaces,  , uniquely defined up to homotopy. Fix an integer \(n\geqslant 3\), and write \(N=G/\Gamma _n(G)\) and \(N_Y=G_Y/\Gamma _n(G_Y)\) for
, uniquely defined up to homotopy. Fix an integer \(n\geqslant 3\), and write \(N=G/\Gamma _n(G)\) and \(N_Y=G_Y/\Gamma _n(G_Y)\) for  .
.
Lemma 8.6
Suppose  is a (homotopy) lifting of h. For each 2-flat
is a (homotopy) lifting of h. For each 2-flat  , there is then a map
, there is then a map  which lifts the map
which lifts the map  and fits in the commuting diagram
and fits in the commuting diagram

Proof
We define the map \(\ell _Y\) by forming the composite

where the first map is the one from Lemma 7.1, while the last map is induced by the homomorphism \(N_n(j_Y):N\rightarrow N_Y\). The two claims follow at once. \(\square \)
We now prove a converse to Lemma 8.6: given “local lifts" \(\ell _Y\), there is a way to assemble them into a “global lift," which we will denote by \({{\widetilde{\ell }}}\). To state the result more precisely, start by recalling that the map  induces an isomorphism
induces an isomorphism  .
.
Lemma 8.7
Let  be an arrangement. Suppose that, for each 2-flat
be an arrangement. Suppose that, for each 2-flat  , we are given a lift
, we are given a lift  of the map
of the map  . There is then a map
. There is then a map  which lifts the map
which lifts the map  , and such that the following diagram commutes:
, and such that the following diagram commutes:

Proof
Recall that we have a central extension

Recall also that the group G is generated by meridians \(x_H\) about the hyperplanes  , and likewise for \(G_{\mathrm{ab}}\). Thus, if
, and likewise for \(G_{\mathrm{ab}}\). Thus, if  is any map which lifts
is any map which lifts  , the homomorphism \(\ell _{\#}:G \rightarrow N\) is given on generators by
, the homomorphism \(\ell _{\#}:G \rightarrow N\) is given on generators by
for some \(a_i(H) \in \mathrm{gr}_i(G)\). What we need to do is pick these elements \(a_i(H)\) in such a way so that diagram (8.2) commutes.
First note the following consequence of Lemma 7.1: If Z and Y are different 2-flats and \(H \supset Z\), then  is the identity element in \(N_Y\).
is the identity element in \(N_Y\).
The next step is to see that if Z and Y are distinct 2-flats and if \(a \in \mathrm{gr}_{i}(G_Z)\), for \(2 \leqslant i \leqslant n-1\), then \((j_Y)_\#(a)\) is the identity element in \(N_Y\). The group \(\mathrm{gr}_{i}(G_Z)\) is generated by iterated brackets of the generators \(x_H\) for  . If any one or more of these generators is replaced by the identity, then the resulting bracket equals the identity. Let a be an iterated bracket in \(\mathrm{gr}_i(G_Z)\). Since a involves at least one generator \(x_{H^\prime }\) with
. If any one or more of these generators is replaced by the identity, then the resulting bracket equals the identity. Let a be an iterated bracket in \(\mathrm{gr}_i(G_Z)\). Since a involves at least one generator \(x_{H^\prime }\) with  , and since
, and since  is the identity in \(N_Y\), it follows that
is the identity in \(N_Y\), it follows that  is also the identity in \(N_Y\).
is also the identity in \(N_Y\).
By (8.3), the homomorphism \((\ell _Y)_\#:G_Y\rightarrow N_Y\) is given on generators by
for some \(a_i(H,Y) \in \mathfrak {h}_i(G_Y)\), where \(H \supset Y\). Define a map  by requiring that
by requiring that

Now let X and Y be different 2-flats in  and consider the composition
and consider the composition

From the result above, it follows that \((\xi _{XY})_{\#}(x_H)\) is the identity in \(N_Y\) for all hyperplanes  such that \(H \supset X\) but \(H \not \supset Y\). Since there is a unique hyperplane K with \(K \supset X\) and \(K \supset Y\), the image of the homomorphism \((\xi _{XY})_{\#}:G_X\rightarrow N_Y\) is the (infinite cyclic) subgroup generated by the single element \((\xi _{XY})_{\#}(x_K)\). Hence, the map \(\xi _{XY}\) factors through \(K({\mathbb {Z}},1)\). Since \(H_2({\mathbb {Z}}) = 0\), it follows that the induced homomorphism
such that \(H \supset X\) but \(H \not \supset Y\). Since there is a unique hyperplane K with \(K \supset X\) and \(K \supset Y\), the image of the homomorphism \((\xi _{XY})_{\#}:G_X\rightarrow N_Y\) is the (infinite cyclic) subgroup generated by the single element \((\xi _{XY})_{\#}(x_K)\). Hence, the map \(\xi _{XY}\) factors through \(K({\mathbb {Z}},1)\). Since \(H_2({\mathbb {Z}}) = 0\), it follows that the induced homomorphism  is the zero map. The lemma now follows by a diagram chase. \(\square \)
is the zero map. The lemma now follows by a diagram chase. \(\square \)
8.4 The nilpotent quotients of a decomposable arrangement group
In [36, 37], Rybnikov showed that, in general, the third nilpotent quotient of an arrangement group is not determined by the intersection lattice. Specifically, he produced a pair of arrangements  and
and  of 13 hyperplanes in \({\mathbb {C}}^3\) such that
of 13 hyperplanes in \({\mathbb {C}}^3\) such that  , yet
, yet  . By contrast, we can use our approach to show that the phenomenon detected by Rybnikov cannot happen among decomposable arrangements. Here, then, is the main result of this section.
. By contrast, we can use our approach to show that the phenomenon detected by Rybnikov cannot happen among decomposable arrangements. Here, then, is the main result of this section.
Theorem 8.8
If  and
and  are decomposable arrangements with
are decomposable arrangements with  , then, for each \(n\geqslant 2\), there is an isomorphism
, then, for each \(n\geqslant 2\), there is an isomorphism

Proof
Let  and set \(N=G/\Gamma _n(G)\). We start by picking a lifting
and set \(N=G/\Gamma _n(G)\). We start by picking a lifting  of the map
of the map  . For each 2-flat
. For each 2-flat  , we obtain a map
, we obtain a map  , defined as in Lemma 8.6.
, defined as in Lemma 8.6.
Having an isomorphism of posets  means we have a bijection
means we have a bijection  which induces a compatible bijection
which induces a compatible bijection  . Let
. Let  and
and  be a pair of 2-flats which correspond under the aforementioned bijection. Using the description of localized arrangement complements from (7.2), we obtain a homeomorphism
be a pair of 2-flats which correspond under the aforementioned bijection. Using the description of localized arrangement complements from (7.2), we obtain a homeomorphism  between the respective complements.
between the respective complements.
By the forward implication of Theorem 6.2, there is a map  and a splitting \(\sigma _Y:H_2(N_Y)\rightarrow \mathfrak {h}_n(N_Y)\) such that the following diagram commutes:
and a splitting \(\sigma _Y:H_2(N_Y)\rightarrow \mathfrak {h}_n(N_Y)\) such that the following diagram commutes:

Using the bijection  , the maps \(f^{YZ}_*\) assemble to give an isomorphism
, the maps \(f^{YZ}_*\) assemble to give an isomorphism  . The decomposability assumption together with Theorem 8.2 insure that
. The decomposability assumption together with Theorem 8.2 insure that

Furthermore, by Proposition 8.5, we have that

Consequently, the homomorphisms \(\sigma _Z:H_2(N_Y)\rightarrow \mathfrak {h}_n(N_Y)\) may be assembled into a homomorphism \(\sigma :H_2(N)\rightarrow \mathfrak {h}_n(N)\).
Next, using the maps  , we define a lifting
, we define a lifting  by the procedure outlined in Lemma 8.7. It is then readily verified that the diagram
by the procedure outlined in Lemma 8.7. It is then readily verified that the diagram

commutes. The result follows from the backwards implication of Theorem 6.2. \(\square \)
References
Artal Bartolo, E., Carmona Ruber, J., Cogolludo-Agustín, J.I., Marco Buzunáriz, M.: Topology and combinatorics of real line arrangements. Compositio Math. 141(6), 1578–1588 (2005)
Artal Bartolo, E., Carmona Ruber, J., Cogolludo-Agustín, J.I., Marco Buzunáriz, M.Á.: Invariants of combinatorial line arrangements and Rybnikov’s example. In: Izumiya, S., et al. (eds.) Singularity Theory and Its Applications. Advanced Studies in Pure Mathematics, vol. 43, pp. 1–34. Mathematical Society of Japan, Tokyo (2007)
Artal Bartolo, E., Guerville-Ballé, B., Viu-Sos, J.: Fundamental groups of real arrangements and torsion in the lower central series quotients. Exp. Math. https://doi.org/10.1080/10586458.2018.1428131
Cartan, H., Eilenberg, S.: Homological Algebra. Princeton University Press, Princeton (1956)
Cenkl, B., Porter, R.: Tame homotopy. Colecao Atas (Sociedade Brasileira de Mathematica Segundo Encontro Brasileior de Topologia) 13, 1–32 (1980)
Cenkl, B., Porter, R.: Differential forms and torsion in the fundamental group. Adv. Math. 48(2), 189–204 (1983)
Cenkl, B., Porter, R.: Lazard completion of a group and free differential graded algebra models over subrings of the rationals. Topology 23(4), 445–464 (1984)
Chen, K.: Iterated integrals of differential forms and loop space homology. Ann. Math. 97(2), 217–246 (1973)
Chen, K.-T., Fox, R.H., Lyndon, R.C.: Free differential calculus. IV. The quotient groups of the lower central series. Ann. Math. 68(1), 81–95 (1958)
Cohen, D.C., Suciu, A.I.: The braid monodromy of plane algebraic curves and hyperplane arrangements. Comment. Math. Helv. 72(2), 285–315 (1997)
Cohen, D.C., Suciu, A.I.: Alexander invariants of complex hyperplane arrangements. Trans. Amer. Math. Soc. 351(10), 4043–4067 (1999)
Denham, G., Suciu, A.I., Yuzvinsky, S.: Combinatorial covers and vanishing of cohomology. Selecta Math. (N.S.) 22(2), 561–594 (2016)
Dwyer, W.G.: Homology, Massey products and maps between groups. J. Pure Appl. Algebra 6(2), 177–190 (1975)
Dwyer, W.G.: Tame homotopy theory. Topology 18(4), 321–338 (1979)
Falk, M.: The minimal model of the complement of an arrangement of hyperplanes. Trans. Amer. Math. Soc. 309(2), 543–556 (1988)
Félix, Y., Halperin, S., Thomas, J.-C.: Rational Homotopy Theory. Graduate Texts in Mathematics, vol. 205. Springer, New York (2001)
Félix, Y., Halperin, S., Thomas, J.-C.: Rational Homotopy Theory, vol. II. World Scientific, Hackensack (2015)
Hall, P.: A contribution to the theory of groups of prime-power order. Proc. London Math. Soc. 36, 29–95 (1933)
Kohno, T.: On the holonomy Lie algebra and the nilpotent completion of the fundamental group of the complement of hypersurfaces. Nagoya Math. J. 92, 21–37 (1983)
Lazard, M.: Sur les groupes nilpotents et les anneaux de Lie. Ann. Sci. Ecole Norm. Sup. 71, 101–190 (1954)
Magnus, W.: Über Beziehungen zwischen höheren Kommutatoren. J. Reine Angew. Math. 177, 105–115 (1937)
Magnus, W., Karrass, A., Solitar, D.: Combinatorial Group Theory. Presentations of Groups in Terms of Generators and Relations, 2nd revised edn. Dover, New York (1976)
Malcev, A.I.: Nilpotent torsion-free groups. Izv. Akad. Nauk. SSSR Ser. Mat. 13(3), 201–212 (1949) (in Russian)
Markl, M., Papadima, Ş.: Homotopy Lie algebras and fundamental groups via deformation theory. Ann. Inst. Fourier (Grenoble) 42(4), 905–935 (1992)
Massey, W.S.: Some higher order cohomology operations. In: International Symposium on Algebraic Topology, pp. 145–154. Universidad Nacional Autónoma de México and UNESCO, Mexico City (1958)
Matei, D.: Massey products of complex hypersurface complements. In: Izumiya, S., et al. (eds.) Singularity Theory and Its Applications. Advanced Studies in Pure Mathematics, vol. 43, pp. 205–219. Mathematical Society of Japan, Tokyo (2006)
Matei, D., Suciu, A.I.: Cohomology rings and nilpotent quotients of real and complex arrangements. In: Falk, M., Terao, H. (eds.) Arrangements-Tokyo 1998. Advanced Studies in Pure Mathematics, vol. 27, pp. 185–215. Kinokuniya, Tokyo (2000)
Morgan, J.W.: The algebraic topology of smooth algebraic varieties. Inst. Hautes Études Sci. Publ. Math. 48, 137–204 (1978)
Orlik, P., Terao, H.: Arrangements of Hyperplanes. Grundlehren der Mathematischen Wissenschaften, vol. 300. Springer, Berlin (1992)
Papadima, S., Suciu, A.I.: Chen Lie algebras. Int. Math. Res. Not. IMRN 2004(21), 1057–1086 (2004)
Papadima, S., Suciu, A.I.: When does the associated graded Lie algebra of an arrangement group decompose? Comment. Math. Helv. 81(4), 859–875 (2006)
Papadima, S., Suciu, A.: Geometric and algebraic aspects of 1-formality. Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 52(100), 355–375 (2009)
Porter, R.: Milnor’s \({\overline{\mu }}\)-invariants and Massey products. Trans. Amer. Math. Soc. 257(1), 39–71 (1980)
Quillen, D.G.: On the associated graded ring of a group ring. J. Algebra 10, 411–418 (1968)
Quillen, D.G.: Rational homotopy theory. Ann. Math. 90, 205–295 (1969)
Rybnikov, G.L.: On the fundamental group of the complement of a complex hyperplane arrangement. Funct. Anal. Appl. 45(2), 137–148 (2011)
Rybnikov, G.: On the fundamental group and triple Massey’s product (1998). arXiv:math.AG/9805061v1
Rybnikov, G.: The category of \(E_\infty \)-coalgebras, the \(E_\infty \)-coalgebra structure on the homology, and the dimension completion of the fundamental group (2014). arXiv:1402.6272v1
Salvatore, P.: Non-formality of planar configuration spaces in characteristic two. Int. Math. Res. Not. IMRN. https://doi.org/10.1093/imrn/rny091
Schenck, H.K., Suciu, A.I.: Lower central series and free resolutions of hyperplane arrangements. Trans. Amer. Math. Soc. 354(9), 3409–3433 (2002)
Serre, J.-P.: Lie Algebras and Lie Groups. 1964 Lectures Given at Harvard University, Lecture Notes in Mathematics, 2nd edn, vol. 1500. Springer, Berlin (1992)
Stallings, J.: Homology and central series of groups. J. Algebra 2(2), 170–181 (1965)
Suciu, A.I.: Fundamental groups of line arrangements: Enumerative aspects. In: Previato, E. (ed.) Advances in Algebraic Geometry Motivated by Physics. Contemporary Mathematics, vol. 276, pp. 43–79. American Mathematical Society, Providence (2001)
Suciu, A.I., Wang, H.: Cup products, lower central series, and holonomy Lie algebras. J. Pure Appl. Algebra 223(8), 3359–3385 (2019)
Suciu, A.I., Wang, H.: Formality properties of finitely generated groups and Lie algebras. Forum Math. 31(4), 867–905 (2019)
Sullivan, D.: Infinitesimal computations in topology. Inst. Hautes Études Sci. Publ. Math. 47, 269–331 (1977)
Witt, E.: Treue Darstellung Liescher Ringe. J. Reine Angew. Math. 177, 152–160 (1937)
Author information
Authors and Affiliations
Corresponding author
Additional information
To the memory of Ştefan Papadima, 1953–2018
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A.I. Suciu partially supported by the Simons Foundation Collaboration Grant for Mathematicians # 354156.
Rights and permissions
About this article
Cite this article
Porter, R.D., Suciu, A.I. Homology, lower central series, and hyperplane arrangements. European Journal of Mathematics 6, 1039–1072 (2020). https://doi.org/10.1007/s40879-019-00392-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-019-00392-x
Keywords
- Lower central series
- Tower of nilpotent quotients
- Cohomology ring
- Associated graded Lie algebra
- Holonomy Lie algebra
- Malcev Lie algebra
- Hyperplane arrangement
- Decomposable arrangement





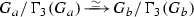 .
. .
.
 .
.
 is an isomorphism of graded Lie algebras.
is an isomorphism of graded Lie algebras. is an isomorphism.
is an isomorphism.