Abstract
We consider various classes of iterated function systems, such as those comprised of similarities and those satisfying the open set condition, and weakly contractive systems. Necessary properties are developed for a compact set to be an attractor for the various classes of iterated function systems. Since the Hausdorff metric space is complete, we are able to develop several results concerning typical compact sets and their invariance with respect to iterated function systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(X = (X,d)\) be a complete metric space, with \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\) a finite set of contraction maps \(S_{i}:X \rightarrow X\). We call a set E an attractor (non-empty invariant set) of the iterated function system (IFS) \({\mathscr {S}}\) if  ; that is, E is invariant with respect to \({\mathscr {S}}\). For any given finite set of contraction maps \({\mathscr {S}}\), there is a unique non-empty compact set E in X such that \(E= {\mathscr {S}}(E)\). In what follows, we frequently take \(\vert {\mathscr {S}} \vert \) to represent the necessarily unique attractor of the IFS \({\mathscr {S}}\). This and other results in [10] are recorded below.
; that is, E is invariant with respect to \({\mathscr {S}}\). For any given finite set of contraction maps \({\mathscr {S}}\), there is a unique non-empty compact set E in X such that \(E= {\mathscr {S}}(E)\). In what follows, we frequently take \(\vert {\mathscr {S}} \vert \) to represent the necessarily unique attractor of the IFS \({\mathscr {S}}\). This and other results in [10] are recorded below.
Theorem 1.1
Let X be a complete metric space with \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\) a finite set of contraction maps \(S_{i}:X \rightarrow X\).
-
(1)
There exists a unique non-empty compact set \(E \subseteq X\) such that \(E = {\mathscr {S}}(E)\).
-
(2)
The set E is the closure of the set of fixed points of the finite compositions
 of elements of \({\mathscr {S}}\).
of elements of \({\mathscr {S}}\). -
(3)
If A is any non-empty compact set in X, then \(\lim _{p \rightarrow \infty } {\mathscr {S}}^{p}(A)= E\) in the Hausdorff metric.
Now, suppose that the contraction maps found in \({\mathscr {S}}\) are similarities. That is, \(d(S_{i}(x), S_{i}(y)) = r_{i} d(x, y)\) for all x, y in X, and \(0< r_{i} < 1\). Each \(S_{i}\) takes subsets of X and sends them into geometrically similar sets. This produces attractors that are self-similar. Should the images of the sets \(S_{i}(F)\) not overlap “too much”, the self-similar attractor  has Hausdorff dimension equal to the value of s satisfying
has Hausdorff dimension equal to the value of s satisfying  .
.
The notion of insignificant overlap comes from the open set condition (OSC). Suppose \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\) is a finite set of contraction maps \(S_{i}:X \rightarrow X\). The contractive system \({\mathscr {S}}\) satisfies the OSC if there exists a non-empty open set V for which  and
and  whenever \(i \not = j\) [10, 15].
whenever \(i \not = j\) [10, 15].
If each of the \(S_{i}\) is a similarity, and \(d(S_{i}(x), S_{i}(y)) = r_{i} d(x, y)\) for all x, y in X, where \(0< r_{i} < 1\), then the Hausdorff dimension, \(\dim _{\mathscr {H}} (E)\), is equal to s, and \(0< {\mathscr {H}}^{s}(E) < \infty \), where \(E = {\mathscr {S}}(E)\) is the attractor for \({\mathscr {S}}\), and  .
.
As proved as an exercise in [8], if the unique non-empty invariant set E satisfies  whenever \(i \not = j\), then the system \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\) of contraction maps \(S_{i}:X \rightarrow X\) satisfies the OSC.
whenever \(i \not = j\), then the system \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\) of contraction maps \(S_{i}:X \rightarrow X\) satisfies the OSC.
The purpose of this paper is to study the attractors of the IFS that are comprised of similarities, that satisfy the OSC, or both. Let X be a complete metric space, take \({\mathscr {K}}(X)\) to be the collection of non-empty compact subsets of X, with \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\) a finite set of contraction maps \(S_{i}:X \rightarrow X\). We set

Finally, let  be the set of all attractors in \({\mathscr {K}}(X)\) generated by some \({\mathscr {S}}= \{S_{1}, \ldots , S_{m}\}\), a finite collection of contraction maps \(S_{i} :X \rightarrow X\). We call a finite collection of contraction maps a contractive system and a finite collection of weak contractions a weakly contractive system.
be the set of all attractors in \({\mathscr {K}}(X)\) generated by some \({\mathscr {S}}= \{S_{1}, \ldots , S_{m}\}\), a finite collection of contraction maps \(S_{i} :X \rightarrow X\). We call a finite collection of contraction maps a contractive system and a finite collection of weak contractions a weakly contractive system.
We proceed through several sections. Definitions, notation and some previously known results are presented in Sect. 2. There, we also record some observations concerning the sets \({\mathscr {I}}_{1}\) and \({\mathscr {I}}_{2}\). Section 3 is dedicated to the study of countable attractors. If  is homeomorphic to an element of \({\mathscr {I}}_{1}\) or \({\mathscr {I}}_{2}\), then E must be a singleton, or a Cantor set, or the closure of the union of countably many disjoint non-trivial closed intervals. Any nowhere dense element
is homeomorphic to an element of \({\mathscr {I}}_{1}\) or \({\mathscr {I}}_{2}\), then E must be a singleton, or a Cantor set, or the closure of the union of countably many disjoint non-trivial closed intervals. Any nowhere dense element  of \({\mathscr {I}}\) has a homeomorphic copy \(E'\) in \({\mathscr {I}}_{3}\). If E is a countable attractor, then it has a homeomorphic copy F such that \(F = {\mathscr {S}}(F)\) for some \({\mathscr {S}} = \{S_{1}, S_{2}\}\).
of \({\mathscr {I}}\) has a homeomorphic copy \(E'\) in \({\mathscr {I}}_{3}\). If E is a countable attractor, then it has a homeomorphic copy F such that \(F = {\mathscr {S}}(F)\) for some \({\mathscr {S}} = \{S_{1}, S_{2}\}\).
In Sect. 4, one studies weakly contractive systems. From [4], we know that the set of attractors in  generated by contractive systems is a first category \(F_{\sigma }\). This is also true for IFS composed of weak contractions. One also sees that the set of attractors generated by IFS of the form
generated by contractive systems is a first category \(F_{\sigma }\). This is also true for IFS composed of weak contractions. One also sees that the set of attractors generated by IFS of the form  is nowhere dense in
is nowhere dense in  . Since the set of attractors is dense in
. Since the set of attractors is dense in  , one concludes that most attractors can only be generated by IFS \({\mathscr {S}} = \{S_{1}, \ldots , S_{L}\}\), where \(L > M\).
, one concludes that most attractors can only be generated by IFS \({\mathscr {S}} = \{S_{1}, \ldots , S_{L}\}\), where \(L > M\).
Not only is the typical element of  not an attractor for any IFS, but one also can take that dense \(G_{\delta }\) subset of
not an attractor for any IFS, but one also can take that dense \(G_{\delta }\) subset of  so that \({\mathscr {H}}^{\phi }(E)= 0\) for each of its elements E, where \(\phi \) is some fixed gauge function. In Sect. 5, one sees that attractors with “large” measure—that is, \({\mathscr {H}}_{m}^{\phi }(E) \geqslant c\)—are also exceptional.
so that \({\mathscr {H}}^{\phi }(E)= 0\) for each of its elements E, where \(\phi \) is some fixed gauge function. In Sect. 5, one sees that attractors with “large” measure—that is, \({\mathscr {H}}_{m}^{\phi }(E) \geqslant c\)—are also exceptional.
Section 6 is dedicated to attractors with non-empty interior. There, we develop a necessary condition for a compact set with non-empty interior to be an attractor. This is similar to that developed by Nowak for countable sets [1, 12].
2 Preliminaries
We take (X, d) to be a compact metric space. For A subset of X, we denote by \(\vert A \vert \) its diameter, by \(\overline{A}\) its closure, by  its interior, by
its interior, by  its convex closure (meaning the closure of its convex hull), and by
its convex closure (meaning the closure of its convex hull), and by  its cardinality when A is finite.
its cardinality when A is finite.
Much of the analysis takes place in the Hausdorff metric space \({\mathscr {K}}(X) = ({\mathscr {K}}(X), {\mathscr {H}})\). Take \({\mathscr {K}}(X)\) to be the collection of non-empty compact subsets of X. Endow \({\mathscr {K}}(X)\) with the Hausdorff metric \({\mathscr {H}}\) given by

where the \(\delta \)-neighbourhood or \(\delta \)-parallel body, \(B_{\delta }(A)\), of a set A is the set of points within distance \(\delta \) of A. Thus,  , where
, where  is the open ball in X centered at x of radius \(\delta \). The Hausdorff metric space \(({\mathscr {K}}(X), {\mathscr {H}})\) is also compact.
is the open ball in X centered at x of radius \(\delta \). The Hausdorff metric space \(({\mathscr {K}}(X), {\mathscr {H}})\) is also compact.
Since \(({\mathscr {K}}(X), {\mathscr {H}})\) is complete, one can make good use of the Baire category theorem. A set is of the first category in the complete space (X, d) whenever it can be written as a countable union of nowhere dense sets; otherwise, the set is of the second category. A set is residual if it is the complement of a first category set, and an element of a residual set is called either typical or generic.
Theorem 2.1
(Baire category theorem) Let (X, d) be a complete metric space with B a first category subset of X. Then  is dense in X.
is dense in X.
Let \(\Phi \) denote the set of functions \(\phi \) that are continuous and increasing on  , with \(\phi (0) = 0\). For \(\phi \in \Phi \) and \(s \in {\mathbb N}\), set
, with \(\phi (0) = 0\). For \(\phi \in \Phi \) and \(s \in {\mathbb N}\), set

Then  defines a measure on the Borel sets in
defines a measure on the Borel sets in  . In what follows, our concern will be primarily with closed sets. In the case that \(\phi (x) = x^{s}\), one gets the usual s-dimensional Hausdorff measure [2, 4, 8, 9]. Define the Hausdorff dimension of a set E such that
. In what follows, our concern will be primarily with closed sets. In the case that \(\phi (x) = x^{s}\), one gets the usual s-dimensional Hausdorff measure [2, 4, 8, 9]. Define the Hausdorff dimension of a set E such that

In Sect. 3, we use \({\lambda }^{n}\) to refer to the Lebesgue n-dimensional measure.
Since our interest lies with contractions and weak contractions, the functions considered are all continuous. Let C(X, X) to be the set of continuous functions \(f :X \rightarrow X\). Within C(X, X) we use the uniform metric:  . Since X is compact,
. Since X is compact,  .
.
We recall that a topological space is a Cantor space if it is non-empty, perfect, compact, totally disconnected, and metrizable. In particular, a topological space is a Cantor space if it is homeomorphic to the Cantor ternary set.
A topological space X is said to be scattered if every non-empty subspace M has an isolated point in M. Every compact scattered Hausdorff space has a base consisting of clopen sets (is zero-dimensional), and a compact metric space is scattered if and only if it is countable. Let X be a compact scattered space. We let

be the Cantor–Bendixon derived set of X, and define inductively
The height of X is

By the Mazurkiewicz–Sierpiński Theorem [11], every countable compact scattered space X is homeomorphic to the space  , where
, where  and n is the number of elements of \(X^{(\beta )}\).
and n is the number of elements of \(X^{(\beta )}\).
Next we present some simple conclusions concerning elements in \({\mathscr {I}}_{1}\) and \({\mathscr {I}}_{2}\).
Proposition 2.2
Let \({\mathscr {S}}= \{S_{1}, \ldots , S_{N}\}\) be a finite set of similarities from \({\mathbb R}^{n}\) to \({\mathbb R}^{n}\) satisfying the OSC. Then the following are equivalent:
-
(1)
\(F = {\mathscr {S}}(F)\) is nowhere dense and perfect,
-
(2)
\(N \geqslant 2\) and
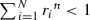 .
.
Proof
(1)\(\Rightarrow \)(2): Suppose \(F = {\mathscr {S}}(F)\) is nowhere dense and perfect. Then, \(N \geqslant 2\). Suppose \({\mathscr {S}}\) satisfies the OSC with V open. Since F is nowhere dense, V must contain some G, an open ball contained in the complement of F. Since  whenever \(i \not = j\), it follows that \(S_{{i_{1}} \ldots {i_{k}}}(V) \cap S_{{j_{1}} \ldots {j_{k}}}(V) = \varnothing \) whenever
whenever \(i \not = j\), it follows that \(S_{{i_{1}} \ldots {i_{k}}}(V) \cap S_{{j_{1}} \ldots {j_{k}}}(V) = \varnothing \) whenever  . Let \(x \in F\). For each \(k \in {\mathbb N}\), there exists a string of length k, say
. Let \(x \in F\). For each \(k \in {\mathbb N}\), there exists a string of length k, say  such that \(x \in S_{i_{1} i_{2} \ldots i_{k}}(F)\). As \(G \subseteq V\), \(S_{i_{1} i_{2} \ldots i_{k}}(G) \subseteq S_{i_{1} i_{2} \ldots i_{k}}(V)\), \(S_{i_{1} i_{2} \ldots i_{k}}(G)\) is complementary to F [10, p. 736], and the porosity
such that \(x \in S_{i_{1} i_{2} \ldots i_{k}}(F)\). As \(G \subseteq V\), \(S_{i_{1} i_{2} \ldots i_{k}}(G) \subseteq S_{i_{1} i_{2} \ldots i_{k}}(V)\), \(S_{i_{1} i_{2} \ldots i_{k}}(G)\) is complementary to F [10, p. 736], and the porosity

Thus, \(\dim _{\mathscr {H}} (F) <n\), and  ([9, Theorem 9.3], [17, Section 4F]).
([9, Theorem 9.3], [17, Section 4F]).
(2)\(\Rightarrow \)(1): Suppose \(F = {\mathscr {S}}(F)\) with \(N \geqslant 2\) and  . We show that it has no isolated point. Let \(x \in F\) with \(\epsilon >0\). Take \({i'_{1}}, \ldots ,{i'_{k}}\) so that \(S_{{i'_{1}} \ldots {i'_{k}}}(F) \subseteq B_{\epsilon }(x)\). Since F is not a singleton, there exists \(y \in S_{{i'_{1}} \ldots {i'_{k}}}(F)\) distinct from x. In particular, x is a limit point of F. So, F is perfect. Since \(\dim _{\mathscr {H}}(\vert {\mathscr {S}} \vert ) <n\), F contains no ball. \(\square \)
. We show that it has no isolated point. Let \(x \in F\) with \(\epsilon >0\). Take \({i'_{1}}, \ldots ,{i'_{k}}\) so that \(S_{{i'_{1}} \ldots {i'_{k}}}(F) \subseteq B_{\epsilon }(x)\). Since F is not a singleton, there exists \(y \in S_{{i'_{1}} \ldots {i'_{k}}}(F)\) distinct from x. In particular, x is a limit point of F. So, F is perfect. Since \(\dim _{\mathscr {H}}(\vert {\mathscr {S}} \vert ) <n\), F contains no ball. \(\square \)
Proposition 2.3
Let \({\mathscr {S}}= \{S_{1}, \ldots , S_{N}\}\) be a finite set of similarities from \({\mathbb R}^{n}\) to \({\mathbb R}^{n}\) satisfying the OSC. If \(F = {\mathscr {S}}(F)\), then the following are equivalent:
-
(1)
F contains a ball in \({\mathbb R}^{n}\).
-
(2)
F is the closure of a countable union of non-degenerate closed balls in \({\mathbb R}^{n}\).
-
(3)
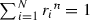 and \(N \geqslant 2\).
and \(N \geqslant 2\).
Proof
(1)\(\Rightarrow \)(2): Let \(x \in F\). It suffices to show that there is a sequence of balls converging to x. Let \(\epsilon >0\), and take \(i_{1} i_{2} \ldots i_{k}\) so that \(S_{i_{1} \ldots i_{k}}(F) \subseteq B_{\epsilon }(x)\). Since F contains a ball and \(S_{i_{1} \ldots i_{k}}\) is a composition of similarities, \(S_{i_{1} \ldots i_{k}}(F)\) also contains a ball.
(2)\(\Rightarrow \)(3): Since F has non-empty interior, \(N \geqslant 2\). Moreover, F is not nowhere dense, so  by Proposition 2.2.
by Proposition 2.2.
(3)\(\Rightarrow \)(1): Since  , F is not nowhere dense by Proposition 2.2, so it must necessarily contain a ball in \({\mathbb R}^{n}\). \(\square \)
, F is not nowhere dense by Proposition 2.2, so it must necessarily contain a ball in \({\mathbb R}^{n}\). \(\square \)
Proposition 2.4
Let \({\mathscr {S}} = \{S_{1}, S_{2}\}\) where each \(S_{i}:{\mathbb R} \rightarrow {\mathbb R}\) is a similarity. If \(r_{1} + r_{2} \leqslant 1\), and  , then \({\mathscr {S}}\) satisfies the OSC with
, then \({\mathscr {S}}\) satisfies the OSC with  .
.
This allows us to characterize, up to homeomorphism, those elements of \({\mathscr {I}}\) generated by a pair of similarities.
Proposition 2.5
Let \({\mathscr {S}} = \{S_{1}, S_{2}\}\) where each \(S_{i}:{\mathbb R} \rightarrow {\mathbb R}\) is a similarity. Necessarily, \({\mathscr {S}}\) satisfies the OSC so long as  and \(r_{1} + r_{2} \leqslant 1\). Set
and \(r_{1} + r_{2} \leqslant 1\). Set

Then  is homeomorphic to an element of \({\mathscr {T}}\) if and only if one of the following occurs:
is homeomorphic to an element of \({\mathscr {T}}\) if and only if one of the following occurs:
-
(1)
E is a singleton,
-
(2)
E is a Cantor set, or
-
(3)
E is an interval.
3 Countable attractors
In [12], Nowak completely characterizes, up to homeomorphism, countable attractors for iterated function systems. Nowak shows that every countable compact set of successor Cantor–Bendixon height with a single point of maximal rank has a homeomorphic copy in  that is an attractor of an IFS consisting of two contractions. This IFS satisfies the OSC, and the Lipschitz constants of its two components can be chosen to be as small as one wishes. Moreover, Nowak shows that if a countable compact metric space is an IFS-attractor, then its Cantor–Bendixson height cannot be a limit ordinal.
that is an attractor of an IFS consisting of two contractions. This IFS satisfies the OSC, and the Lipschitz constants of its two components can be chosen to be as small as one wishes. Moreover, Nowak shows that if a countable compact metric space is an IFS-attractor, then its Cantor–Bendixson height cannot be a limit ordinal.
Theorem 3.1
([12, Theorem 3]) A compact scattered metric space of limit Cantor–Bendixson height is not homeomorphic to any IFS-attractor consisting of weak contractions.
Theorem 3.2
([12, Theorem 4]) For every \(\epsilon >0\) and every countable ordinal \(\delta \) the scattered space  is homeomorphic to the attractor of an iterated function system consisting of two contractions
is homeomorphic to the attractor of an iterated function system consisting of two contractions  in the unit interval
in the unit interval  , such that
, such that

The main result of this section is the following theorem.
Theorem 3.3
Let  be countable and compact. Then E is homeomorphic to an attractor \(E{'}\) for some \({\mathscr {S}} = \{S_{1}, S_{2}\}\) which satisfies the OSC if and only if the height of E is a successor ordinal.
be countable and compact. Then E is homeomorphic to an attractor \(E{'}\) for some \({\mathscr {S}} = \{S_{1}, S_{2}\}\) which satisfies the OSC if and only if the height of E is a successor ordinal.
Theorem 3.3 is an immediate consequence of Theorem 3.2, and the following proposition. Frequently, we make use of the convex closure of a set E, and write  . We use this notation even in the case that E is closed, in an effort to somewhat limit the various notations used.
. We use this notation even in the case that E is closed, in an effort to somewhat limit the various notations used.
Proposition 3.4
Suppose \(E \in {\mathscr {I}}\), and \(E = {\mathscr {S}}(E)\) where \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\). Then, for any \(n \geqslant m\), there exists  and
and  which satisfies the OSC such that
which satisfies the OSC such that
-
(1)
\(F = {\mathscr {S}}'(F)\),
-
(2)
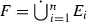 , where each \(E_{i}\) is similar to E (\(\dot{\bigcup }\) means disjoint union), and
, where each \(E_{i}\) is similar to E (\(\dot{\bigcup }\) means disjoint union), and -
(3)
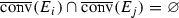 whenever \(i \not =j\).
whenever \(i \not =j\).
Proof
We give a proof in the case that \(m=2\). The general case then follows easily. Suppose \(E \in {\mathscr {I}}\), and for convenience and without loss of generality,  , and \(E = {\mathscr {S}}(E)\) for some \({\mathscr {S}} = \{S_{1}, S_{2}\}\). Take \(E_{1},E_{2},\ldots ,E_{n}\) such that
, and \(E = {\mathscr {S}}(E)\) for some \({\mathscr {S}} = \{S_{1}, S_{2}\}\). Take \(E_{1},E_{2},\ldots ,E_{n}\) such that
-
(i)
each is similar to E,
-
(ii)
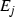 lies to the right of \(E_{l}\) whenever \(j < l\),
lies to the right of \(E_{l}\) whenever \(j < l\), -
(iii)
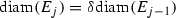 , where
, where 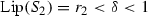 , for any \(1 < j \leqslant n\), and
, for any \(1 < j \leqslant n\), and -
(iv)
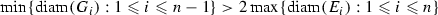 , where \(G_{i}\) is the open interval lying between \(E_{i}\) and \(E_{i+1}\), that is \(G_{i} = (\max E_{i+1}, \min E_{i})\).
, where \(G_{i}\) is the open interval lying between \(E_{i}\) and \(E_{i+1}\), that is \(G_{i} = (\max E_{i+1}, \min E_{i})\).
Moreover, take  . Define \(T_{1}\) so that it is linear on each of the intervals
. Define \(T_{1}\) so that it is linear on each of the intervals  and \(G_{i}\). In particular, take \(T_{1}\) so that
and \(G_{i}\). In particular, take \(T_{1}\) so that
-
(v)
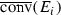 is mapped onto
is mapped onto 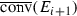 with \(T_{1}(E_{i}) = E_{i+1}\) for \(i=1,2,\ldots , {n-1}\),
with \(T_{1}(E_{i}) = E_{i+1}\) for \(i=1,2,\ldots , {n-1}\), -
(vi)
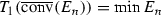 ,
, -
(vii)
\(G_{i}\) is mapped onto \(G_{i+1}\) for \(i=1,2, \ldots , n-2\), and
-
(viii)
\(T_{1}(G_{n-1}) = \min E_{n}\), too.
Then  is a contraction given the diameters of the sets \(E_{i}\) and \(G_{i}\), and
is a contraction given the diameters of the sets \(E_{i}\) and \(G_{i}\), and  .
.
Let us now define \(T_{2}\). Recall that \(E_{1}\) and \(E_{2}\) are both similar to E and  . Set
. Set  and take \({\phi }_{i}:E \rightarrow E_{i}\) to be the line such that \({\phi }_{i}(0) = \min E_{i}\) and \({\phi }_{i}(1) = \max E_{i}\). Define \(T_{2}\) on
and take \({\phi }_{i}:E \rightarrow E_{i}\) to be the line such that \({\phi }_{i}(0) = \min E_{i}\) and \({\phi }_{i}(1) = \max E_{i}\). Define \(T_{2}\) on  so that
so that  , and on
, and on  , define \(T_{2}\) so that
, define \(T_{2}\) so that  . Set \(T_{2}(x) = T_{2}(a_{2})\) for all \(x \leqslant a_{2}\), and extend \(T_{2}\) linearly on \(G_{1}\). Then
. Set \(T_{2}(x) = T_{2}(a_{2})\) for all \(x \leqslant a_{2}\), and extend \(T_{2}\) linearly on \(G_{1}\). Then

and

It follows, then, that  is a contraction map, and
is a contraction map, and

\(\square \)
Remark 3.5
From [6, Theorem 5.4] and the construction found in its proof, if  is nowhere dense and uncountable, then there exist \(F'\), a homeomorphic copy of F, and an IFS \({\mathscr {S}}\) satisfying the OSC such that
is nowhere dense and uncountable, then there exist \(F'\), a homeomorphic copy of F, and an IFS \({\mathscr {S}}\) satisfying the OSC such that  . This observation, coupled with Theorem 3.3, allows one to conclude that any nowhere dense attractor is homeomorphic to an element of \({\mathscr {I}}_{3}\).
. This observation, coupled with Theorem 3.3, allows one to conclude that any nowhere dense attractor is homeomorphic to an element of \({\mathscr {I}}_{3}\).
4 Systems of weak contractions
In this section we investigate IFS consisting of weak contractions. First, we observe that the typical element of  is not an attractor for any system of weak contractions. Then, we consider the function
is not an attractor for any system of weak contractions. Then, we consider the function  given by \({\mathscr {S}} \mapsto \vert {\mathscr {S}} \vert \), and investigate the images of
given by \({\mathscr {S}} \mapsto \vert {\mathscr {S}} \vert \), and investigate the images of  ,
,  , and of
, and of  . There, we focus on the case when
. There, we focus on the case when  .
.
In [4], we construct a residual subset \({\mathscr {K}}_{2}\) of  with the property that if \(E \in {\mathscr {K}}_{2}\), then \(E \not = {\mathscr {S}}(E)\) for any finite set of contraction maps \({\mathscr {S}}\) defined on
with the property that if \(E \in {\mathscr {K}}_{2}\), then \(E \not = {\mathscr {S}}(E)\) for any finite set of contraction maps \({\mathscr {S}}\) defined on  . The analysis developed for contractions is valid for weak contractions. This is recorded in the next result.
. The analysis developed for contractions is valid for weak contractions. This is recorded in the next result.
Theorem 4.1
There is a residual subset \({\mathscr {K}}_{2}\) of  such that \(E \not = {\mathscr {S}}(E)\) for any finite set of weak contraction maps \({\mathscr {S}}\) defined on
such that \(E \not = {\mathscr {S}}(E)\) for any finite set of weak contraction maps \({\mathscr {S}}\) defined on  , for any \(E \in {\mathscr {K}}_{2}\).
, for any \(E \in {\mathscr {K}}_{2}\).
For \(s >0\), set

and, for \(m \in {\mathbb N}\), set

As the following result in [6] shows, should we limit the number of contractions in our IFS to no more than N, and uniformly bound the Lipschitz constants of the contractions, then the set of attractors generated by such systems is closed.
Lemma 4.2
([6, Lemma 4.3]) Let (X, d) be a compact metric space. Let \(N \in {\mathbb N}\) and \(0< m < 1\). The set

is closed.
The following straightforward lemma shows not only that \({\mathscr {I}}_{1}\) is dense in the Hausdorff metric space  , but also that the attractors for iterated function systems generated by contractions with arbitrarily small Lipschitz constants are dense in
, but also that the attractors for iterated function systems generated by contractions with arbitrarily small Lipschitz constants are dense in  .
.
Lemma 4.3
The set of attractors \({\mathscr {I}}_{1}\) is dense in  .
.
Proof
Let  , and take \(\epsilon >0\). We use the Euclidean metric within
, and take \(\epsilon >0\). We use the Euclidean metric within  . Let \(F \subseteq E\) be a finite set so that \({\mathscr {H}}(E,F) < {\epsilon }/{2}\); say
. Let \(F \subseteq E\) be a finite set so that \({\mathscr {H}}(E,F) < {\epsilon }/{2}\); say  . To each \(x_{i}\) associate a non-degenerate closed ball \(I_{i}\) and a similarity \(S_{i}\) so that \(x_{i} \in I_{i}\),
. To each \(x_{i}\) associate a non-degenerate closed ball \(I_{i}\) and a similarity \(S_{i}\) so that \(x_{i} \in I_{i}\),  whenever \(i \not = j\),
whenever \(i \not = j\),  ,
,  and
and  . It follows that \(F \subseteq \vert \{S_{1}, S_{2}, \ldots , S_{n}\} \vert \subset B_{{\epsilon }/{2}}(F)\), and \({\mathscr {H}}(F, \vert \{S_{1}, S_{2}, \ldots , S_{n}\}\vert ) < {\epsilon }/{2}\). Now
. It follows that \(F \subseteq \vert \{S_{1}, S_{2}, \ldots , S_{n}\} \vert \subset B_{{\epsilon }/{2}}(F)\), and \({\mathscr {H}}(F, \vert \{S_{1}, S_{2}, \ldots , S_{n}\}\vert ) < {\epsilon }/{2}\). Now
The conclusion follows. \(\square \)
Set

and, for \(m \in {\mathbb N}\), set

Call  a weak contraction. We recall some simple observations.
a weak contraction. We recall some simple observations.
Remark 4.4
Let  .
.
-
(1)
The set
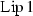 is closed.
is closed. -
(2)
The set
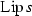 is a closed and nowhere dense subset of
is a closed and nowhere dense subset of 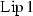 , for all \(s \in (0,1)\).
, for all \(s \in (0,1)\). -
(3)
Let
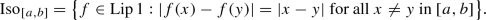
Then
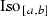 is closed in \(\mathrm{Lip}\,1\).
is closed in \(\mathrm{Lip}\,1\).
See also [7] for (2) in the case of maps on closed, convex and bounded subsets of a Hilbert space.
Should \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\) and \({\mathscr {T}} = \{T_{1}, \ldots , T_{m}\}\) be elements of  , set
, set  , where
, where  . Take a and b in \({\mathbb R}\). By
. Take a and b in \({\mathbb R}\). By  we denote the closed interval with endpoints a and b. That is, either
we denote the closed interval with endpoints a and b. That is, either  or
or  , should \(a<b\) or \(b <a\).
, should \(a<b\) or \(b <a\).
The next lemma shows that, while  is a very small subset of
is a very small subset of  for every \(s \in (0,1)\),
for every \(s \in (0,1)\),  is considerably larger. This is similar to a result found in [13] for maps defined on closed, convex and bounded subsets of a Banach space.
is considerably larger. This is similar to a result found in [13] for maps defined on closed, convex and bounded subsets of a Banach space.
Lemma 4.5
Let  . The set of weak contractions
. The set of weak contractions  , defined on X, is a dense \(G_{\delta }\) subset of
, defined on X, is a dense \(G_{\delta }\) subset of  .
.
Proof
Let \(\epsilon >0\). Suppose that  . Then there exist points \(x \not =y\) in
. Then there exist points \(x \not =y\) in  such that \(\vert f(x) - f(y) \vert = \vert x - y \vert \). Should \(\vert f(x) - f(y) \vert = \vert x - y \vert \), then it follows that \(\vert f(a) - f(b) \vert = \vert a -b \vert \) for all points a and b in
such that \(\vert f(x) - f(y) \vert = \vert x - y \vert \). Should \(\vert f(x) - f(y) \vert = \vert x - y \vert \), then it follows that \(\vert f(a) - f(b) \vert = \vert a -b \vert \) for all points a and b in  , as
, as  . Let
. Let  be an enumeration of
be an enumeration of  and set
and set  . From Remark 4.4 it follows that \(G_{n,m}\) is open in
. From Remark 4.4 it follows that \(G_{n,m}\) is open in  . Take
. Take  such that \(f(b) - f(a) = b-a\). Consider
such that \(f(b) - f(a) = b-a\). Consider  such that
such that

and g is extended linearly on (a, b). Then \(\Vert f - g \Vert < \epsilon \), and  . The construction of g is similar, should \(f(b) - f(a) = a - b\). We conclude that
. The construction of g is similar, should \(f(b) - f(a) = a - b\). We conclude that  is dense. Since \(G_{n,m}\) is both dense and open, one concludes that
is dense. Since \(G_{n,m}\) is both dense and open, one concludes that  is a dense \(G_{\delta }\) subset of
is a dense \(G_{\delta }\) subset of  . \(\square \)
. \(\square \)
Let us now turn our attention to attractors generated by sets of m-many weak contractions.
Lemma 4.6
Let X be a compact metric space. The function

given by \({\mathscr {S}} \mapsto \vert {\mathscr {S}} \vert \), is continuous.
Proof
Let  be such that
be such that  , or equivalently, \({\Vert {\mathscr {S}}_{k} - {\mathscr {S}} \Vert } \rightarrow 0\). Say \({\mathscr {S}}_{k}(E_{k}) = E_{k}\). Since \(({\mathscr {K}}(X), {\mathscr {H}})\) is compact, we may assume that
, or equivalently, \({\Vert {\mathscr {S}}_{k} - {\mathscr {S}} \Vert } \rightarrow 0\). Say \({\mathscr {S}}_{k}(E_{k}) = E_{k}\). Since \(({\mathscr {K}}(X), {\mathscr {H}})\) is compact, we may assume that  in the Hausdorff metric.
in the Hausdorff metric.
Say  and \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\). Since
and \({\mathscr {S}} = \{S_{1}, \ldots , S_{m}\}\). Since  , it follows that
, it follows that  uniformly for each \(1 \leqslant i \leqslant m\). Moreover,
uniformly for each \(1 \leqslant i \leqslant m\). Moreover,  and
and  , so that
, so that  . Thus, if
. Thus, if  , then
, then  , and our conclusion follows. \(\square \)
, and our conclusion follows. \(\square \)
Lemma 4.7
For any \(s \in (0, 1)\), the set  is closed and nowhere dense in
is closed and nowhere dense in  .
.
Proof
Let \(s \in (0,1)\). Since  is compact, and \({\mathscr {T}}\) is continuous, it follows that
is compact, and \({\mathscr {T}}\) is continuous, it follows that  is closed. Since
is closed. Since  ,
,  is nowhere dense. \(\square \)
is nowhere dense. \(\square \)
It is easy to determine the size of  since
since  is compact in
is compact in  . The proof of the following is considerably more involved, as
. The proof of the following is considerably more involved, as  is a \(G_{\delta }\) set.
is a \(G_{\delta }\) set.
The following observations are fundamental to the construction found in the proof of Theorem 4.8.
-
(1)
Let
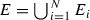 . If for any i, j and k in
. If for any i, j and k in  with \(i \not =j\), one has
with \(i \not =j\), one has 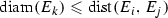 , then for every weak contraction \(f:E \rightarrow E\) and \(1 \leqslant k \leqslant N\), it follows that \(f(E_{k}) \subseteq E_{l}\), \(1 \leqslant l \leqslant N\).
, then for every weak contraction \(f:E \rightarrow E\) and \(1 \leqslant k \leqslant N\), it follows that \(f(E_{k}) \subseteq E_{l}\), \(1 \leqslant l \leqslant N\). -
(2)
Let
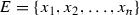 and
and 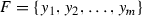 . Suppose that
. Suppose that 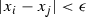 for all \(i \not = j\) in
for all \(i \not = j\) in 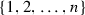 , and \(\vert y_{l} - y_{k} \vert > \epsilon \) for all \(l \not = k\) in \(\{1, 2, \ldots , m\}\). If \(f:E \rightarrow F\) is a weak contraction, then \(f(E) = y_{i}\), for some \(1 \leqslant i \leqslant m\).
, and \(\vert y_{l} - y_{k} \vert > \epsilon \) for all \(l \not = k\) in \(\{1, 2, \ldots , m\}\). If \(f:E \rightarrow F\) is a weak contraction, then \(f(E) = y_{i}\), for some \(1 \leqslant i \leqslant m\).
Theorem 4.8
The set  is nowhere dense in
is nowhere dense in  .
.
Proof
We can assume \(m >1\) since the result is clear for \(m=1\). Fix \(\delta >0\). We begin by developing a set E.
-
(1)
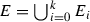 , with
, with 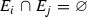 for each \(i \not = j\).
for each \(i \not = j\). -
(2)
Each \(E_{i}\) contains \(2^{2^{i}}\) points that are distributed uniformly throughout the interval
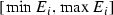 . Set
. Set 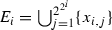 , with
, with 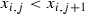 ,
, 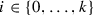 and
and 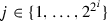 .
. -
(3)
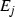 lies to the right of \(E_{l}\) whenever \(j < l\) and
lies to the right of \(E_{l}\) whenever \(j < l\) and 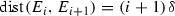 .
. -
(4)
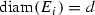 for all i, where \(d < {\delta }/{4}\).
for all i, where \(d < {\delta }/{4}\).
The idea, now, is to associate to each point \(x_{i,j}\) a non-empty compact neighborhood \(E'_{i,j} \subseteq B_{r}(x_{i,j})\), where  . More precisely, take
. More precisely, take  such that
such that  , and set \(E'_{i,j} = B_{r}(x_{i,j}) \cap E{'}\), for
, and set \(E'_{i,j} = B_{r}(x_{i,j}) \cap E{'}\), for  and
and  , and
, and  .
.
Suppose  is a weak contraction. Then
is a weak contraction. Then
-
(i)
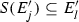 ; that is each
; that is each 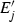 can map into only one \(E'_{l}\) as
can map into only one \(E'_{l}\) as 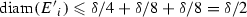 , and the smallest interval in
, and the smallest interval in  complementary to the sets
complementary to the sets 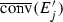 is of length at least
is of length at least 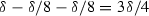 .
. -
(ii)
\(S(E'_{k,j}) \subseteq E'_{l,p}\), so that each \(E'_{k,j}\) can map into only one \(E'_{l,p}\) as
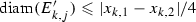 and the smallest interval complementary to the sets
and the smallest interval complementary to the sets 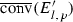 is at least of length
is at least of length 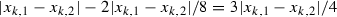 .
. -
(iii)
If \(l >j\) and
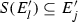 , then
, then 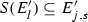 , for some s as
, for some s as 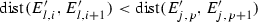 for any i and p.
for any i and p. -
(iv)
If \(S(E'_{l}) \subseteq E'_{l}\), then
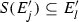 , whenever \(j < l\) as \(S(E'_{l}) \subseteq E'_{l}\) implies that
, whenever \(j < l\) as \(S(E'_{l}) \subseteq E'_{l}\) implies that 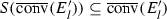 , so that
, so that 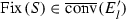 . Now, note that \(S(E{'}) \subseteq E'\), and S is a weak contraction.
. Now, note that \(S(E{'}) \subseteq E'\), and S is a weak contraction.
Let \({\mathscr {S}} = \{S_{1}, S_{2}, \ldots , S_{m}\}\), where each \(S_{i}\) is a weak contraction, m is now a fixed number, and take \(\epsilon >0\). Let  . Since the collection of finite sets is dense in
. Since the collection of finite sets is dense in  , there exists \(F_{2}\) finite such that \({\mathscr {H}}(F_{1}, F_{2}) < {\epsilon }/{2}\). Say
, there exists \(F_{2}\) finite such that \({\mathscr {H}}(F_{1}, F_{2}) < {\epsilon }/{2}\). Say  . Take \(F_{3}\) finite in
. Take \(F_{3}\) finite in  such that
such that
-
(v)
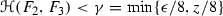 , where
, where 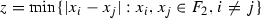 ,
, -
(vi)
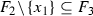 , and
, and -
(vii)
there is a similar copy of E in \(B_{\gamma }(x_{1})\). We take \(k> m \geqslant 2\), so that
-
a.
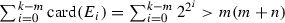 , and
, and -
b.
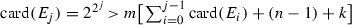 whenever \(k \geqslant j \geqslant k-m\).
whenever \(k \geqslant j \geqslant k-m\).
-
a.
Suppose that \({\mathscr {H}}(F_{4}, F_{3}) < \sigma \), where  ,
,  , and
, and  , the distance between \(E_{0}\) and \(E_{1}\), the first two components of the similar copy of E found in \(B_{\gamma }(x_{1})\). Thus
, the distance between \(E_{0}\) and \(E_{1}\), the first two components of the similar copy of E found in \(B_{\gamma }(x_{1})\). Thus  and
and  . We continue to use the notation of \(F_{3}\), remembering that each point \(x_{i}\) in \(F_{3}\) now represents \(F_{4} \cap B_{\sigma }(x_{i})\), a subset of \(F_{4}\) both open and closed in the relative topology of \(F_{4}\). Suppose \({\mathscr {S}}(F_{4}) = F_{4}\). By our choice of k (see (vii) b), there are so many components of \(E'_{k}\) that it is not possible to cover \(E'_{k}\) with m weak contractions defined on
. We continue to use the notation of \(F_{3}\), remembering that each point \(x_{i}\) in \(F_{3}\) now represents \(F_{4} \cap B_{\sigma }(x_{i})\), a subset of \(F_{4}\) both open and closed in the relative topology of \(F_{4}\). Suppose \({\mathscr {S}}(F_{4}) = F_{4}\). By our choice of k (see (vii) b), there are so many components of \(E'_{k}\) that it is not possible to cover \(E'_{k}\) with m weak contractions defined on  . Thus, there must exist some \(S_{i}\)—say \(S_{1}\)—such that \(S_{1}(E'_{k}) \subseteq E'_{k}\). This implies \(S_{1}(E') \subseteq E'_{k}\). Similarly, there exists some
. Thus, there must exist some \(S_{i}\)—say \(S_{1}\)—such that \(S_{1}(E'_{k}) \subseteq E'_{k}\). This implies \(S_{1}(E') \subseteq E'_{k}\). Similarly, there exists some  —say \(S_{2}\)—such that \(S_{2}(E'_{k-1}) \subseteq E'_{k-1}\), which implies that
—say \(S_{2}\)—such that \(S_{2}(E'_{k-1}) \subseteq E'_{k-1}\), which implies that  . (It is also possible that \(S_{2}(E'_{k}) \subseteq E'_{k-1}\).) Continuing, for each \(0 \leqslant i \leqslant m-1\), we have, with possible renumbering of the elements of \({\mathscr {S}}\), that \(S_{i+1}(E'_{k-i}) \subseteq E'_{k-i}\), so that
. (It is also possible that \(S_{2}(E'_{k}) \subseteq E'_{k-1}\).) Continuing, for each \(0 \leqslant i \leqslant m-1\), we have, with possible renumbering of the elements of \({\mathscr {S}}\), that \(S_{i+1}(E'_{k-i}) \subseteq E'_{k-i}\), so that  . (Analogously to what we noted with \(S_{2}\), it is also possible that there exists
. (Analogously to what we noted with \(S_{2}\), it is also possible that there exists  such that \(S_{i+1}(E'_{l}) \subseteq E'_{k-i}\).) Note that
such that \(S_{i+1}(E'_{l}) \subseteq E'_{k-i}\).) Note that  can intersect at most i components of
can intersect at most i components of  . This follows from (iii). The m contractions \(\{S_{1}, \ldots , S_{m}\}\) acting on the \(n-1\) components of
. This follows from (iii). The m contractions \(\{S_{1}, \ldots , S_{m}\}\) acting on the \(n-1\) components of  can intersect at most \(m(n-1) < mn \) components of \(F_{4}\). We conclude that
can intersect at most \(m(n-1) < mn \) components of \(F_{4}\). We conclude that  and
and  can intersect at most
can intersect at most  components of
components of  . Since
. Since  , we conclude that \(F_{4} \nsubseteq {\mathscr {S}}(F_{4})\). \(\square \)
, we conclude that \(F_{4} \nsubseteq {\mathscr {S}}(F_{4})\). \(\square \)
As a corollary, we have that the set of attractors generated by those IFS with m many contractions is a nowhere dense \(F_{\sigma }\) set in  .
.
Corollary 4.9
The set  is a nowhere dense \(F_{\sigma }\) set in
is a nowhere dense \(F_{\sigma }\) set in  .
.
Proof
We note that  . \(\square \)
. \(\square \)
Remark 4.10
Let l and m be elements of \({\mathbb N}\). Then

where
-
(1)
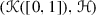 is compact,
is compact, -
(2)
\({({\mathscr {K}}_{2})}^\mathrm{c}\) is a first category and dense \(F_{\sigma }\) subset of
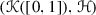 ,
, -
(3)
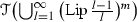 is a nowhere dense \(F_{\sigma }\) subset of \(({\mathscr {K}}([0,1]), {\mathscr {H}})\), and
is a nowhere dense \(F_{\sigma }\) subset of \(({\mathscr {K}}([0,1]), {\mathscr {H}})\), and -
(4)
\({\mathscr {T}}\bigl ({\bigl (\mathrm{Lip}\,\frac{l-1}{l}\bigr )}{}^{m}\bigr )\) is nowhere dense and closed.
In particular, the set of all attractors \({\mathscr {I}}\) is dense in  , but, when we limit ourselves to only m maps, we are able to generate as attractors only a very small subset of
, but, when we limit ourselves to only m maps, we are able to generate as attractors only a very small subset of  .
.
5 The set of attractors with large measure
As in [4], we denote by \({\mathscr {I}R}\) the collection of all points in  with all of the coordinates irrational. Set
with all of the coordinates irrational. Set

We call a rational open interval in  each set
each set  , where \(a_{i}\) and \(b_{i}\) are in
, where \(a_{i}\) and \(b_{i}\) are in  for all i. We say that \(E \cap J\) is a rational portion of
for all i. We say that \(E \cap J\) is a rational portion of  if \(E \cap J\) is non-empty and J a rational open interval. If \(E \in {\mathscr {K}}_{1}\), then there exists some \(\phi \in \Phi \) such that \({\mathscr {H}}^{\phi }(E \cap J) >0\) for every rational portion \(E \cap J\) of E. Moreover, the set
if \(E \cap J\) is non-empty and J a rational open interval. If \(E \in {\mathscr {K}}_{1}\), then there exists some \(\phi \in \Phi \) such that \({\mathscr {H}}^{\phi }(E \cap J) >0\) for every rational portion \(E \cap J\) of E. Moreover, the set  is a dense \(G_{\delta }\) subset of
is a dense \(G_{\delta }\) subset of  [2, 4]. One concludes, then, that the typical element of
[2, 4]. One concludes, then, that the typical element of  has very small measure, and that the elements of
has very small measure, and that the elements of  which comprise the elements of \({\mathscr {K}}_{2}\) in Proposition 4.1 can be taken to have arbitrarily small measure. In what follows it will be convenient to use the following results. We let \(\lambda \) be the Lebesgue measure in \({\mathbb R}\), and denote by \({\Phi }_\mathrm{c}\) the family of concave functions from \(\Phi \).
which comprise the elements of \({\mathscr {K}}_{2}\) in Proposition 4.1 can be taken to have arbitrarily small measure. In what follows it will be convenient to use the following results. We let \(\lambda \) be the Lebesgue measure in \({\mathbb R}\), and denote by \({\Phi }_\mathrm{c}\) the family of concave functions from \(\Phi \).
If f is a finite function of a real variable defined in the neighbourhood of a point \(x_{0}\), we denote the lower limit of \(({f(x) - f(x_{0})})/({x - x_{0}})\) as x tends to \(x_{0}\) by values \(x > x_{0}\), that is the lower right Dini derivate of the function f at the point \(x_{0}\), as \(D_{+}f({x}_{0})\) [14].
Proposition 5.1
([16, Lemmas 3.3, 3.5, Proposition 3.2]) Let \(\phi \in \Phi \).
-
(1)
If the lower right Dini derivate of \(\phi \) at 0 is finite, for instance \(D_{+} \phi (0) = s < \infty \), and
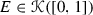 for which \(\lambda (E) =c\), then \({\mathscr {H}}^{\phi }(E) = sc\).
for which \(\lambda (E) =c\), then \({\mathscr {H}}^{\phi }(E) = sc\). -
(2)
If \(D_{+} \phi (0) = + \infty \), then there exists \(\tilde{\phi } \in {\Phi }_\mathrm{c}\) such that \({\mathscr {H}}^{\phi }(E) = {\mathscr {H}}^{\tilde{\phi }}(E)\), for all
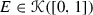 .
. -
(3)
If \(\phi \in {\Phi }_\mathrm{c}\) and
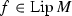 , then \(L = \lim _{\delta \rightarrow 0} {\phi (M \delta )}/{\phi (\delta )} \not =0\) exists, and \({\mathscr {H}}^{\phi }(f(E)) \leqslant L {\mathscr {H}}^{{\phi }}(E)\). Moreover, should \(\vert f(x) - f(y) \vert = M \vert x-y \vert \), then \({\mathscr {H}}^{\phi }(f(E)) = M {\mathscr {H}}^{{\phi }}(E)\).
, then \(L = \lim _{\delta \rightarrow 0} {\phi (M \delta )}/{\phi (\delta )} \not =0\) exists, and \({\mathscr {H}}^{\phi }(f(E)) \leqslant L {\mathscr {H}}^{{\phi }}(E)\). Moreover, should \(\vert f(x) - f(y) \vert = M \vert x-y \vert \), then \({\mathscr {H}}^{\phi }(f(E)) = M {\mathscr {H}}^{{\phi }}(E)\).
For the remainder of this section, we presume that each \(\phi \) taken is concave, so that we can apply Proposition 5.1 to our measures. The next result shows that the mass distribution within elements of \({\mathscr {I}}_{2}\) is relatively uniform.
Lemma 5.2
Let \(X = {\mathbb R}\). Let \(F \in {\mathscr {I}}_{2}\), and \(\phi \in {\Phi }_\mathrm{c}\). Then one of the following is true:
-
(1)
For every portion P of F, \({\mathscr {H}}^{\phi }(P)=0\).
-
(2)
For every portion P of F, \({\mathscr {H}}^{\phi }(P)=\infty \).
-
(3)
For every portion P of F, \(0< {\mathscr {H}}^{\phi }(P) < \infty \).
Proof
Let P, J be portions of F, where \(F = {\mathscr {S}}(F)\) and \({\mathscr {S}} = \{S_{1}, \ldots , S_{N}\}\) and \(\phi \in {\Phi }_\mathrm{c}\). There exists \(i_{1} i_{2} \ldots i_{n}\) such that \(S_{i_{1} i_{2} \ldots i_{n}}(P) \subset J\). Thus, there is some  for which
for which  . There exists \(j_{1} j_{2} \ldots j_{m}\) such that
. There exists \(j_{1} j_{2} \ldots j_{m}\) such that  , which ensures the existence of
, which ensures the existence of  for which
for which  . It follows that
. It follows that  and
and  . \(\square \)
. \(\square \)
In [3, 5] sets of arbitrary Hausdorff dimension are constructed which are not attractors of any finite family of weak contractions in  and, more generally, in
and, more generally, in  . Let \(\phi \in {\Phi }_\mathrm{c}\). In [4] and Theorem 4.1, one sees that the typical element of
. Let \(\phi \in {\Phi }_\mathrm{c}\). In [4] and Theorem 4.1, one sees that the typical element of  has both \({\mathscr {H}}^{\phi }\)-measure zero, and is not an attractor for any IFS. Working on the unit interval, we now show that the typical element of
has both \({\mathscr {H}}^{\phi }\)-measure zero, and is not an attractor for any IFS. Working on the unit interval, we now show that the typical element of  for which \({\mathscr {H}}_{m}^{\phi }\) is bounded away from zero also is not an attractor for any IFS. That is, the remainder of this section is dedicated to showing that while Lemma 5.2 provides a necessary condition for some compact set to be an element of \({\mathscr {I}}_{2}\), that condition is far from sufficient. As with Theorem 4.1, the typical “large” set that satisfies the necessary condition found in Lemma 5.2 is not an attractor for any IFS.
for which \({\mathscr {H}}_{m}^{\phi }\) is bounded away from zero also is not an attractor for any IFS. That is, the remainder of this section is dedicated to showing that while Lemma 5.2 provides a necessary condition for some compact set to be an element of \({\mathscr {I}}_{2}\), that condition is far from sufficient. As with Theorem 4.1, the typical “large” set that satisfies the necessary condition found in Lemma 5.2 is not an attractor for any IFS.
We begin by recalling the following result from [2], which describes a typical element of  .
.
Proposition 5.3
([2, Proposition 2.2 (1)]) Let

Then \({ \Sigma }_{0}\) is a dense \(G_{\delta }\) subset of  , hence topologically complete.
, hence topologically complete.
Lemma 5.4
Let \(\gamma >0\). Then

is dense and open in the complete metric space  .
.
Proof
The density of \({ \Sigma }_{1}\) follows from the fact that each compact set can be approximated by finite sets in the Hausdorff metric. Let \(E \in { \Sigma }_{1}\). To show that \({ \Sigma }_{1}\) is open, take \({\{U_{i} \}}_{i=1}^{\infty }\) such that
-
(1)
 ,
, -
(2)
\(\vert U_{i} \vert \leqslant {1}/{m}\) for all i, and
-
(3)
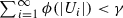 .
.
If \(F \subseteq \bigcup _{i=1}^{\infty } U_{i}\), then \({\mathscr {H}}_{m}^{\phi }(F) < \gamma \), too. \(\square \)
Proposition 5.5
Let \(\gamma >0\). The collection  is topologically complete with respect to the Hausdorff metric \({\mathscr {H}}\).
is topologically complete with respect to the Hausdorff metric \({\mathscr {H}}\).
Proof
Let \(\gamma >0\). Then  , so that \({ \Sigma }_{2}\) is closed in the topologically complete metric space \({ \Sigma }_{0}\). \(\square \)
, so that \({ \Sigma }_{2}\) is closed in the topologically complete metric space \({ \Sigma }_{0}\). \(\square \)
Proposition 5.6
Fix \(F \in { \Sigma }_{2}\). The set  is closed in \({\Sigma }_{2}\).
is closed in \({\Sigma }_{2}\).
Proof
Let \(\{E_{n}\} \subseteq { \Sigma }_{3}\) with  such that \(f_{n}(E_{n}) \supseteq F\). Since
such that \(f_{n}(E_{n}) \supseteq F\). Since  is compact and \(\{f_{n}\}\) is uniformly bounded and equicontinuous, there exist
is compact and \(\{f_{n}\}\) is uniformly bounded and equicontinuous, there exist  in \({\mathbb N}\) and
in \({\mathbb N}\) and  such that
such that  and \(f_{n_{k}}\) converges uniformly to some f. Then
and \(f_{n_{k}}\) converges uniformly to some f. Then

Since \(F \subseteq f_{n_{k}}(E_{n_{k}})\), it follows that \(F \subseteq f(E)\). \(\square \)
Theorem 5.7
Let  . The typical \(E \in { \Sigma }_{2}\) is not an attractor of any system of weak contractions.
. The typical \(E \in { \Sigma }_{2}\) is not an attractor of any system of weak contractions.
Proof
Suppose E and F are nowhere dense subsets of  , and
, and  is such that \(f(E) =F\). If
is such that \(f(E) =F\). If  is complementary to F, then there exists
is complementary to F, then there exists  complementary to E such that \(f((a,b)) \supseteq (c,d)\) and \(({d-c})/({b-a}) \leqslant \rho \). Let \(\{J_{k}\}\) be an enumeration of the intervals complementary to F such that \(\vert J_{k} \vert \geqslant \vert J_{k+1} \vert \) for all k. Similarly, let \(\{I_{k}\}\) be an enumeration of the intervals complementary to E. There exists a subsequence \(\{I_{k_{s}}\}\) such that \({\vert J_{s} \vert }/{\vert I_{k_{s}} \vert } \leqslant \rho \) for all i [16, Lemma 3.6]. This observation provides a necessary condition on the sets E and F in order for there to exist some
complementary to E such that \(f((a,b)) \supseteq (c,d)\) and \(({d-c})/({b-a}) \leqslant \rho \). Let \(\{J_{k}\}\) be an enumeration of the intervals complementary to F such that \(\vert J_{k} \vert \geqslant \vert J_{k+1} \vert \) for all k. Similarly, let \(\{I_{k}\}\) be an enumeration of the intervals complementary to E. There exists a subsequence \(\{I_{k_{s}}\}\) such that \({\vert J_{s} \vert }/{\vert I_{k_{s}} \vert } \leqslant \rho \) for all i [16, Lemma 3.6]. This observation provides a necessary condition on the sets E and F in order for there to exist some  with the property that \(f(E) \supseteq F\). We use this observation below. Let I and J be disjoint rational intervals. Our goal is to show that the typical element of \({ \Sigma }_{2}\) is not an attractor of any system of weak contractions. A critical step in this direction is establishing that given some fixed \(\rho >0\), for the typical \(E \in { \Sigma }_{2}\) and disjoint clopen portions \(E \cap I\) and \(E \cap J\), one has that
with the property that \(f(E) \supseteq F\). We use this observation below. Let I and J be disjoint rational intervals. Our goal is to show that the typical element of \({ \Sigma }_{2}\) is not an attractor of any system of weak contractions. A critical step in this direction is establishing that given some fixed \(\rho >0\), for the typical \(E \in { \Sigma }_{2}\) and disjoint clopen portions \(E \cap I\) and \(E \cap J\), one has that  whenever f is in
whenever f is in  . We restrict our attention to disjoint portions as the identity function \(i_{d}\) is in
. We restrict our attention to disjoint portions as the identity function \(i_{d}\) is in  , and
, and  for all E in \({ \Sigma }_{2}\) and rational intervals I. Set
for all E in \({ \Sigma }_{2}\) and rational intervals I. Set  . Then \({\Sigma }_{4}^{I,J}\) is closed. This can be proved as for \({\Sigma }_{3}\) in Proposition 5.6. We wish to show that \({\Sigma }_{4}^{I,J}\) is nowhere dense. Since \({\Sigma }_{4}^{I,J}\) is closed, it is sufficient to show that its complement, necessarily open in \({ \Sigma }_{2}\), is also dense. Let \(E \in {\Sigma }_{4}^{I,J}\) and \(\epsilon >0\). We modify E to get \(E'\) in \({ \Sigma }_{0}\) such that
. Then \({\Sigma }_{4}^{I,J}\) is closed. This can be proved as for \({\Sigma }_{3}\) in Proposition 5.6. We wish to show that \({\Sigma }_{4}^{I,J}\) is nowhere dense. Since \({\Sigma }_{4}^{I,J}\) is closed, it is sufficient to show that its complement, necessarily open in \({ \Sigma }_{2}\), is also dense. Let \(E \in {\Sigma }_{4}^{I,J}\) and \(\epsilon >0\). We modify E to get \(E'\) in \({ \Sigma }_{0}\) such that
-
(1)
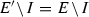 , so that E and \(E'\) are the same outside of I;
, so that E and \(E'\) are the same outside of I; -
(2)
Take \(E'\) on I so that
-
a.
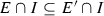 and
and 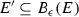 . Thus, \({\mathscr {H}}(E, E') < \epsilon \). Since \(E \subseteq E'\), it follows that
. Thus, \({\mathscr {H}}(E, E') < \epsilon \). Since \(E \subseteq E'\), it follows that 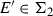 , too.
, too. -
b.
Consider \(\{J_{k}\}\) for \(J \cap E\) and \(\{I_{k}\}\) for \(I \cap E\). Suppose
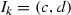 is a complementary interval of \(E \cap I\). Then c and d are elements of E and if \(d-c < \epsilon \), then \((c,d) \subseteq B_{\epsilon }(c) \subseteq B_{\epsilon }(E)\). It follows that there exists some N such that \(\vert I_{k} \vert < \epsilon \) whenever \(k >N\), and hence
is a complementary interval of \(E \cap I\). Then c and d are elements of E and if \(d-c < \epsilon \), then \((c,d) \subseteq B_{\epsilon }(c) \subseteq B_{\epsilon }(E)\). It follows that there exists some N such that \(\vert I_{k} \vert < \epsilon \) whenever \(k >N\), and hence 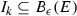 . Take
. Take 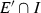 such that if \(\{I_{k}'\}\) are the complementary intervals of
such that if \(\{I_{k}'\}\) are the complementary intervals of 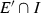 , then
, then 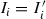 for \(1 \leqslant i \leqslant N\), and \({\vert J_{i} \vert }/{\vert I_{i}' \vert } > \rho \) for all \(i >N\). Thus
for \(1 \leqslant i \leqslant N\), and \({\vert J_{i} \vert }/{\vert I_{i}' \vert } > \rho \) for all \(i >N\). Thus 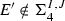 , so \({\Sigma }_{4}^{I,J}\) is nowhere dense.
, so \({\Sigma }_{4}^{I,J}\) is nowhere dense.
-
a.
Set  . Then \({\Sigma }_{5}\) is a first category \(F_{\sigma }\) subset of \({ \Sigma }_{2}\). If
. Then \({\Sigma }_{5}\) is a first category \(F_{\sigma }\) subset of \({ \Sigma }_{2}\). If  , and
, and  , then
, then  whenever I and J are any disjoint rational intervals. In particular,
whenever I and J are any disjoint rational intervals. In particular,  must be nowhere dense in \(E \cap J\) as
must be nowhere dense in \(E \cap J\) as  is a continuous image of the compact set \(E \cap I\), hence is itself compact. We show that E is not the attractor of any weakly contractive system. Since we are interested in weak contractions, in what follows, we may fix \(\rho =1\) so as to work within
is a continuous image of the compact set \(E \cap I\), hence is itself compact. We show that E is not the attractor of any weakly contractive system. Since we are interested in weak contractions, in what follows, we may fix \(\rho =1\) so as to work within  . Let \(\{T_{1}, T_{2}, \ldots , T_{s}\}\) be a set of weak contractions, \(T_{i}:E \rightarrow E\). It suffices to show that \(T_{i}(E)\) is nowhere dense in E, for any i. In fact, if it is so, then
. Let \(\{T_{1}, T_{2}, \ldots , T_{s}\}\) be a set of weak contractions, \(T_{i}:E \rightarrow E\). It suffices to show that \(T_{i}(E)\) is nowhere dense in E, for any i. In fact, if it is so, then  also is nowhere dense in E. Thus
also is nowhere dense in E. Thus  is a proper subset of E, and, hence, E is not an attractor of \(\{T_{1}, T_{2}, \ldots , T_{s}\}\). To this end, fix
is a proper subset of E, and, hence, E is not an attractor of \(\{T_{1}, T_{2}, \ldots , T_{s}\}\). To this end, fix  , a weak contraction, with
, a weak contraction, with  the unique fixed point of T in
the unique fixed point of T in  . Let \(y \not =x\), \(y \in E\). Since T is a weak contraction,
. Let \(y \not =x\), \(y \in E\). Since T is a weak contraction,
Let \(\epsilon = \vert T(y) -y \vert \). Since T is continuous, there exists \(\delta >0\) such that \(\vert T(z) - T(y) \vert < {\epsilon }/{2}\) whenever \(\vert z - y \vert < \delta \). Set  . Then \(T(B_{{\delta }'}(y)) \subseteq B_{{\epsilon }/{2}}(T(y))\), and \(B_{{\delta }'}(y) \cap B_{{\epsilon }/{2}}(T(y)) = \varnothing \). Now, take (a, b) a rational interval of
. Then \(T(B_{{\delta }'}(y)) \subseteq B_{{\epsilon }/{2}}(T(y))\), and \(B_{{\delta }'}(y) \cap B_{{\epsilon }/{2}}(T(y)) = \varnothing \). Now, take (a, b) a rational interval of  such that \(y \in (a,b) \subseteq B_{{\delta }'}(y)\). Since \(E \in {\Sigma }_{2}\), it follows that \(E \cap {\mathbb Q} = \varnothing \), so that a and b are not in E. Now,
such that \(y \in (a,b) \subseteq B_{{\delta }'}(y)\). Since \(E \in {\Sigma }_{2}\), it follows that \(E \cap {\mathbb Q} = \varnothing \), so that a and b are not in E. Now,  . Moreover,
. Moreover,  and \(T((b,1] \cap E)\) are both nowhere dense in \((a,b) \cap E\) since
and \(T((b,1] \cap E)\) are both nowhere dense in \((a,b) \cap E\) since  and \(T((a,b) \cap E) \cap ((a,b) \cap E)= \varnothing \). We conclude that there exists a neighborhood of y, namely (a, b), such that T(E) is nowhere dense in \((a,b) \cap E\). Since this is true for any \(y \not = x\), T(E) is nowhere dense in E. \(\square \)
and \(T((a,b) \cap E) \cap ((a,b) \cap E)= \varnothing \). We conclude that there exists a neighborhood of y, namely (a, b), such that T(E) is nowhere dense in \((a,b) \cap E\). Since this is true for any \(y \not = x\), T(E) is nowhere dense in E. \(\square \)
6 Attractors with non-empty interior
In Proposition 2.3, one sees that when working within \({\mathscr {I}}_{2}\) and \(X = {\mathbb R}^{n}\), an attractor F has non-empty interior if and only if it is the closure of its components with non-empty interior. Simple examples, as our first example below, show that in \({\mathscr {I}}_{2}\) we can have attractors composed of an arbitrarily large number of non-trivial components.
Example 6.1
We show that  is an attractor for
is an attractor for  , where each \(S_{i}\) is a similarity and \({\mathscr {S}}\) satisfies the OSC.
, where each \(S_{i}\) is a similarity and \({\mathscr {S}}\) satisfies the OSC.
Construction. Let \(S_{1}(x)= x/{4}\), \(S_{2}(x) = x/{4} + {1}/{12}\), \(S_{3}(x)= x/{4} + {2}/{3}\), \(S_{4}(x)= x/{4} + {3}/{4}\) and set  . Then
. Then

This gives  . Moreover, \({\mathscr {S}} = \{S_{1}, S_{2}, S_{3}, S_{4}\}\) satisfies the OSC with \(G = (0, {1}/{3}) \cup ({2}/{3}, 1)\).
. Moreover, \({\mathscr {S}} = \{S_{1}, S_{2}, S_{3}, S_{4}\}\) satisfies the OSC with \(G = (0, {1}/{3}) \cup ({2}/{3}, 1)\).
This construction can be generalized to \({\mathbb R}^{n}\) for any number of components k. That is, for any n and k in \({\mathbb N}\), there exists  a disjoint union, where each \(F_{i}\) is an n-cube,
a disjoint union, where each \(F_{i}\) is an n-cube,  where each
where each  is a similarity, \({\mathscr {S}}\) satisfies the OSC, and \(F= {\mathscr {S}}(F)\).
is a similarity, \({\mathscr {S}}\) satisfies the OSC, and \(F= {\mathscr {S}}(F)\).
As we remarked in Proposition 2.5, the only type of attractor with non-empty interior formed by two similarities is an interval. The next example shows that, with three similarities, one can form an attractor that is the closure of the union of countably many disjoint and non-degenerate closed components. In what follows, we use \(\dot{{\bigcup }}\) to indicate the union of pairwise disjoint subsets of  . Each of the intervals
. Each of the intervals  or \((a_{i}, b_{i})\) taken is non-degenerate, so that \(b_{i} > a_{i}\).
or \((a_{i}, b_{i})\) taken is non-degenerate, so that \(b_{i} > a_{i}\).
Example 6.2
We develop an attractor of type  for \({\mathscr {S}} = \{S_{1}, S_{2}, S_{3}\}\) composed of similarities that satisfy the OSC.
for \({\mathscr {S}} = \{S_{1}, S_{2}, S_{3}\}\) composed of similarities that satisfy the OSC.
Construction. Fix \(0< r < 1\).
-
1.
Set
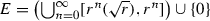 .
. -
2.
Set \(S_{1}(x) = r x\). Then
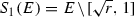 .
. -
3.
Set \(S'_{2}(x) = \sqrt{r} x\). Then
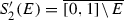 .
. -
4.
Let \(h:{\mathbb R} \rightarrow {\mathbb R}\) be the linear homeomorphism taking
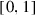 to
to 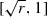 : \(h(0)= \sqrt{r}\) and \(h(1)= 1\) so that
: \(h(0)= \sqrt{r}\) and \(h(1)= 1\) so that 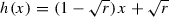 .
. -
5.
Set
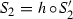 and \(S_{3} = h\). Then
and \(S_{3} = h\). Then 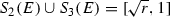 as
as 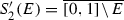 and \(i_{d}(E)= E\) imply that
and \(i_{d}(E)= E\) imply that 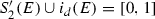 , and
, and 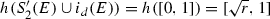 .
. -
6.
We conclude that \(E = {\mathscr {S}}(E)\), with \({\mathscr {S}} = \{S_{1}, S_{2}, S_{3}\}\), where \(S_{1}(x) = rx\),
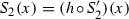 , with \(S'_{2}(x) = \sqrt{r} x\), and
, with \(S'_{2}(x) = \sqrt{r} x\), and 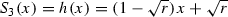 .
. -
7.
The collection \({\mathscr {S}}\) satisfies the OSC with
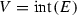 .
. -
8.
If we let \(m_{i}\) be the slope of \(S_{i}\), then
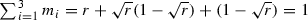 .
.
Let \({\mathscr {I}}\) be the set of attractors contained in  and set
and set  . For A and B subsets of
. For A and B subsets of  , we take
, we take  . In what remains of this section, we study the elements of \({\mathscr {L}}\). Definition 6.3 and Lemma 6.4 provide a topological characterization of the elements of \({\mathscr {L}}\) analogous to that for countable and compact sets described in Theorems 3.1 and 3.2. Definition 6.3 gives us a tool that allows us to relate elements of \({\mathscr {L}}\) with nowhere dense attractors.
. In what remains of this section, we study the elements of \({\mathscr {L}}\). Definition 6.3 and Lemma 6.4 provide a topological characterization of the elements of \({\mathscr {L}}\) analogous to that for countable and compact sets described in Theorems 3.1 and 3.2. Definition 6.3 gives us a tool that allows us to relate elements of \({\mathscr {L}}\) with nowhere dense attractors.
In what follows, let  be a pairwise disjoint enumeration of the components of E in \({\mathscr {L}}\) with non-empty interior. Should the collection be finite, then \(P \in {\mathbb N}\). Otherwise, \(P = \infty \).
be a pairwise disjoint enumeration of the components of E in \({\mathscr {L}}\) with non-empty interior. Should the collection be finite, then \(P \in {\mathbb N}\). Otherwise, \(P = \infty \).
Definition 6.3
(collapse morphism) Let \(E \in {\mathscr {L}}\), with  a pairwise disjoint enumeration of the components of E with non-empty interior. We define \({\phi }\) as the uniform limit of a sequence of functions. Let \({\phi }_{0}(x) = x\) be the identity function. Define \({\phi }_{1}\) such that
a pairwise disjoint enumeration of the components of E with non-empty interior. We define \({\phi }\) as the uniform limit of a sequence of functions. Let \({\phi }_{0}(x) = x\) be the identity function. Define \({\phi }_{1}\) such that

In general, define \({\phi }_{n}\) such that

Should \(P \in {\mathbb N}\), set \(\phi = \phi _{P}\).
By our construction, \(\Vert {\phi }_{n} - {\phi }_{n+1} \Vert = \vert b_{n+1} - a_{n+1} \vert \). Thus, \({\phi }_{n}\) converges uniformly to \(\phi \) on  . The following are consequences of this uniform convergence:
. The following are consequences of this uniform convergence:
-
(1)
Since \({\phi }_{n}\) is continuous for all n, \(\phi \) is continuous.
-
(2)
Since
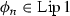 for all n,
for all n, 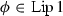 .
. -
(3)
Since \({\phi }_{n}\) is non-decreasing for all n, \(\phi \) is non-decreasing.
-
(4)
Since \({\phi }_{k}\) is constant on
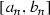 for all \(k \geqslant n\), \(\phi \) is constant on
for all \(k \geqslant n\), \(\phi \) is constant on 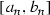 for all n.
for all n. -
(5)
If
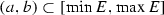 is complementary to E, then \({\phi }_{n}\) is linear with slope \(m=1\) on (a, b), for all n. Thus, \(\phi \) is linear with slope \(m=1\) on (a, b).
is complementary to E, then \({\phi }_{n}\) is linear with slope \(m=1\) on (a, b), for all n. Thus, \(\phi \) is linear with slope \(m=1\) on (a, b). -
(6)
If
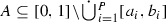 , then \(\lambda (A)= \lambda ({\phi }_{n}(A))\), for all n. Thus, \(\lambda (A)= \lambda (\phi (A))\).
, then \(\lambda (A)= \lambda ({\phi }_{n}(A))\), for all n. Thus, \(\lambda (A)= \lambda (\phi (A))\).
Lemma 6.4
Suppose that the pairwise disjoint sequence  is contained in \(E \in {\mathscr {L}}\) and
is contained in \(E \in {\mathscr {L}}\) and  . Then
. Then  as \(i \rightarrow \infty \) if and only if
as \(i \rightarrow \infty \) if and only if  as \(i \rightarrow \infty \).
as \(i \rightarrow \infty \).
Proof
Suppose  is contained in E and that
is contained in E and that  . By definition, for any \(\epsilon >0\), there is N a natural number so that
. By definition, for any \(\epsilon >0\), there is N a natural number so that  whenever \(i >N\). Since
whenever \(i >N\). Since  for any
for any  , it follows that
, it follows that  whenever \(i >N\). We conclude that
whenever \(i >N\). We conclude that  as \(i \rightarrow \infty \).
as \(i \rightarrow \infty \).
Suppose that  as \(i \rightarrow \infty \). Then, for any \(\epsilon >0\), there exists \(N(\epsilon )\) such that
as \(i \rightarrow \infty \). Then, for any \(\epsilon >0\), there exists \(N(\epsilon )\) such that  whenever \(i >N(\epsilon )\). Since
whenever \(i >N(\epsilon )\). Since  is a pairwise disjoint sequence contained in
is a pairwise disjoint sequence contained in  , the series
, the series  converges. Take M such that
converges. Take M such that  . Let
. Let  , and set
, and set  . If \(i > N(\delta )\) and
. If \(i > N(\delta )\) and  , then \(l >M\). Let \(k > \max \{N(\epsilon ), N(\delta )\}\). Then
, then \(l >M\). Let \(k > \max \{N(\epsilon ), N(\delta )\}\). Then

This follows from (4), (5) and (6) in the observation following Definition 6.3. \(\square \)
Example 6.5
Let F be a countable space homeomorphic to the space  . Suppose \(x \in F\) is isolated; say \(\epsilon >0\) such that \(B_{\epsilon }(x) \cap F = \{x\}\). To each such isolated point x, associate the interval \([x - {\epsilon }/{2},x + {\epsilon }/{2}]\). Let
. Suppose \(x \in F\) is isolated; say \(\epsilon >0\) such that \(B_{\epsilon }(x) \cap F = \{x\}\). To each such isolated point x, associate the interval \([x - {\epsilon }/{2},x + {\epsilon }/{2}]\). Let

Then \(\phi (E)\) is homeomorphic to the space  .
.
Example 6.6
Let Q be the middle thirds Cantor set with C the set of midpoints of the intervals complementary to Q in  . Let \(x \in (c,d)\) be in C, where (c, d) is an interval complementary to Q. Take
. Let \(x \in (c,d)\) be in C, where (c, d) is an interval complementary to Q. Take  so that
so that  . Then
. Then  , and \(\phi (E)\) is uncountable.
, and \(\phi (E)\) is uncountable.
Let \(E \in {\mathscr {L}}\) with  an enumeration of the components of E with non-empty interior and \(\phi \) the collapse morphism defined on E. Say
an enumeration of the components of E with non-empty interior and \(\phi \) the collapse morphism defined on E. Say  . In the following proposition, we make use of \({\phi }^{-1}\) defined on \(E'\), which is intended to reverse the collapse affected by \(\phi \) on
. In the following proposition, we make use of \({\phi }^{-1}\) defined on \(E'\), which is intended to reverse the collapse affected by \(\phi \) on  . If
. If  , then there exists a unique element
, then there exists a unique element  of
of  such that
such that  . This follows from the observations (3)–(6). If \(x \in E'\) and
. This follows from the observations (3)–(6). If \(x \in E'\) and  , then there exists a unique element \(y \in E\) such that \(\phi (y) =x\). This follows from (3), (5) and (6). Let
, then there exists a unique element \(y \in E\) such that \(\phi (y) =x\). This follows from (3), (5) and (6). Let  be the power set of
be the power set of  . We define
. We define  such that
such that  , the unique element of
, the unique element of  such that
such that  , whenever
, whenever  , and \({\phi }^{-1}(x) = y\), the unique point in E such that \(\phi (y) = x\), whenever
, and \({\phi }^{-1}(x) = y\), the unique point in E such that \(\phi (y) = x\), whenever  .
.
Proposition 6.7
If \(E \in {\mathscr {L}}\) is an attractor for some IFS, then \(\phi (E)\) is an attractor, too.
Proof
Suppose \(E \in {\mathscr {L}}\), with  an enumeration of the components of E with non-empty interior, and \(E = {\mathscr {S}}(E)\) where \({\mathscr {S}} = \{ S_{1}, S_{2}, \ldots , S_{N}\}\). Let \(\phi \) be the collapse morphism as in Definition 6.3, and set \(\phi (E) = E'\). Take
an enumeration of the components of E with non-empty interior, and \(E = {\mathscr {S}}(E)\) where \({\mathscr {S}} = \{ S_{1}, S_{2}, \ldots , S_{N}\}\). Let \(\phi \) be the collapse morphism as in Definition 6.3, and set \(\phi (E) = E'\). Take  . We first show that if
. We first show that if  , then
, then  , too. We make frequent reference to the observations following Definition 6.3. Let
, too. We make frequent reference to the observations following Definition 6.3. Let  . Take
. Take  . Then
. Then  from (3),
from (3),

with

and

is the length of  . This follows from (4), (5) and (6). As
. This follows from (4), (5) and (6). As  ,
,

so that

which again follows from (4), (5) and (6). Or, alternatively, we can, again, write

so that

and hence

Therefore

From (5) and (6), one sees that \(\phi \), on  , preserves measure off the set
, preserves measure off the set  . Since \({\mathscr {A}}\) is countable and
. Since \({\mathscr {A}}\) is countable and  is a singleton for each i, we have
is a singleton for each i, we have  . This follows from (6). Thus
. This follows from (6). Thus  .
.
We now show that  . Let \(x \in E'\), and take \(y \in {\phi }^{-1}(x)\). Then \(y \in E\), so there exists \(1 \leqslant j \leqslant N\) such that
. Let \(x \in E'\), and take \(y \in {\phi }^{-1}(x)\). Then \(y \in E\), so there exists \(1 \leqslant j \leqslant N\) such that  . Say \(z \in E\) for which
. Say \(z \in E\) for which  . Then \(\phi (z) \in E'\). Now,
. Then \(\phi (z) \in E'\). Now,  , where
, where  , so that
, so that  , and
, and  . Finally,
. Finally,  . We conclude that
. We conclude that  . Thus,
. Thus,  .
.
We now show that \(S'(E') \subseteq E'\). Let \(x \in E'\). It suffices to show that  , for each \(1 \leqslant j \leqslant N\). From the construction of \(\phi \), one sees that
, for each \(1 \leqslant j \leqslant N\). From the construction of \(\phi \), one sees that  . Since
. Since  for any j, it follows that
for any j, it follows that  , too. Again, by the construction of \(\phi \), \(\phi (E) = E'\), so
, too. Again, by the construction of \(\phi \), \(\phi (E) = E'\), so  . \(\square \)
. \(\square \)
The above proposition allows us to show that certain classes of elements of  are not attractors for any IFS, using Theorem 3.1.
are not attractors for any IFS, using Theorem 3.1.
Corollary 6.8
A compact set \(E \in {\mathscr {L}}\) such that \(\phi (E)\) is of limit Cantor–Bendixon height is not homeomorphic to any IFS-attractor consisting of weak contractions.
As the next example shows, and as one would expect, Corollary 6.8 provides a necessary but not a sufficient condition for a set of the form  to be an attractor for some IFS.
to be an attractor for some IFS.
Example 6.9
A compact set \(E \in {\mathscr {L}} \) with the property that \(\phi (E)\) has height of a successor ordinal can be embedded into the real line so that it is not an attractor of any iterated function system consisting of weak contractions defined on E.
Construction. We begin with the example found in [12, Theorem 2]. Nowak proves that a compact scattered metric space with successor height can be embedded topologically in the real line so that it is not an attractor of any iterated function system consisting of weak contractions. Consider the scattered set  , where \(\{0\} \cap X_{n} = \varnothing \) for all n, each of the \(X_{n}\) is homeomorphic to
, where \(\{0\} \cap X_{n} = \varnothing \) for all n, each of the \(X_{n}\) is homeomorphic to  and
and  whenever \(n \not = m\), and \(d(\{0\}, X_{n}) \rightarrow 0\) as \(n \rightarrow \infty \). Since
whenever \(n \not = m\), and \(d(\{0\}, X_{n}) \rightarrow 0\) as \(n \rightarrow \infty \). Since  , it follows that X is homeomorphic to
, it follows that X is homeomorphic to  . Let
. Let  be the collection of isolated points found in X. Let
be the collection of isolated points found in X. Let  . Take \(E_{1}\) so that
. Take \(E_{1}\) so that  ,
,  is a translation 1 / 2 units to the right of
is a translation 1 / 2 units to the right of  , and
, and  . That is, we start our construction with \(E_{1}\) using \(E_{0}\), replacing \(x_{1}\) with an interval
. That is, we start our construction with \(E_{1}\) using \(E_{0}\), replacing \(x_{1}\) with an interval  of length 1 / 2 so that \(a=x_{1}\), and that part of \(E_{0}\) to the right of \(x_{1}\) is translated to the right a distance of 1 / 2. In general, we take \(E_{n+1}\) so that
of length 1 / 2 so that \(a=x_{1}\), and that part of \(E_{0}\) to the right of \(x_{1}\) is translated to the right a distance of 1 / 2. In general, we take \(E_{n+1}\) so that  ,
,  , and
, and  is a translation \({1}/{2^{n+1}}\) units to the right of
is a translation \({1}/{2^{n+1}}\) units to the right of  .
.
Since \(\{E_{n}\}_{n=0}^{\infty }\) is Cauchy in \(({\mathscr {K}}({\mathbb R}), {\mathscr {H}})\),  exists. Since
exists. Since  , and
, and  , we see that
, we see that  . Moreover, \(\phi (E)= X\), where \(\phi \) is the collapse morphism of E. Now, suppose \(E = {\mathscr {S}}(E)\) for some collection \({\mathscr {S}} = \{ S_{1}, S_{2}, \ldots , S_{N}\}\) of weak contractions. From Proposition 6.7, it follows that \(\phi (E)=X\) is the attractor of the IFS
. Moreover, \(\phi (E)= X\), where \(\phi \) is the collapse morphism of E. Now, suppose \(E = {\mathscr {S}}(E)\) for some collection \({\mathscr {S}} = \{ S_{1}, S_{2}, \ldots , S_{N}\}\) of weak contractions. From Proposition 6.7, it follows that \(\phi (E)=X\) is the attractor of the IFS  . This contradicts the fact that X is not an attractor for any IFS defined on
. This contradicts the fact that X is not an attractor for any IFS defined on  . We conclude that E is not an attractor for any IFS.
. We conclude that E is not an attractor for any IFS.
The next example constructs an attractor E of the form  such that \(\phi (E)\) is homeomorphic to \(Q \cup C\), where Q is the middle thirds Cantor set, and C is the set of midpoints of the intervals complementary to Q in
such that \(\phi (E)\) is homeomorphic to \(Q \cup C\), where Q is the middle thirds Cantor set, and C is the set of midpoints of the intervals complementary to Q in  .
.
Example 6.10
There exists an IFS \({\mathscr {S}} = \{S_{1}, S_{2}, S_{3}, S_{4}\}\) satisfying the OSC for which \( E = \vert {\mathscr {S}} \vert \), and \(\phi (E)\) is homeomorphic to \(Q \cup C\), where Q is the middle thirds Cantor set, and C is the set of midpoints of the intervals complementary to Q in  .
.
Construction. Let \({\mathscr {S}} = \{S_{1}, S_{2}, S_{3}, S_{4}\}\), where \(S_{1}(x) = {1}/{3} x\), \(S_{2}(x) = x/{3} + {2}/{3}\), and \(S_{3}\) and \(S_{4}\) are piecewise linear  functions such that
functions such that  . Let
. Let  . Then
. Then  , and
, and  is composed of three intervals, where K is centered at 1 / 2 of length 1 / 6, \(S_{1}(K)\) is centered at 1 / 6 of length 1 / 18, and \(S_{2}(K)\) is centered at 5 / 6, also of length 1 / 18. Moreover,
is composed of three intervals, where K is centered at 1 / 2 of length 1 / 6, \(S_{1}(K)\) is centered at 1 / 6 of length 1 / 18, and \(S_{2}(K)\) is centered at 5 / 6, also of length 1 / 18. Moreover,  . As one can easily verify,
. As one can easily verify,  , each \(E_{k}\) is composed of
, each \(E_{k}\) is composed of  disjoint closed intervals centered in intervals complementary to Q, the middle thirds Cantor set, and
disjoint closed intervals centered in intervals complementary to Q, the middle thirds Cantor set, and  in
in  .
.
References
Banakh, T., Nowak, M., Strobin, F.: Detecting topological and Banach fractals among zero-dimensional spaces. Topology Appl. 196(part A), 22–30 (2015)
Bruckner, A.M., Steele, T.H.: The Lipschitz structure of continuous self-maps of generic compact sets. J. Math. Anal. Appl. 188(3), 798–808 (1994)
D’Aniello, E.: Non-self-similar sets in \({[0,1]}^{N}\) of arbitrary dimension. J. Math. Anal. Appl. 456(2), 1123–1128 (2017)
D’Aniello, E., Steele, T.H.: Attractors for iterated function schemes on \([0,1]^{n}\) are exceptional. J. Math. Anal. Appl. 424(1), 537–541 (2015)
D’Aniello, E., Steele, T.H.: A non self-similar set. Real Anal. Exchange 41(2), 347–350 (2016)
D’Aniello, E., Steele, T.H.: Attractors for iterated function systems. J. Fractal Geom. 3(2), 95–117 (2016)
De Blasi, F.S., Myjak, J.: Sur la porosité de l’ensemble des contractions sans point fixe. C. R. Acad. Sci. Paris Sér. I Math. 308(2), 51–54 (1989)
Edgar, G.: Measure, Topology and Fractal Geometry. Undergraduate Texts in Mathematics. Springer, New York (1990)
Falconer, K.: Fractal Geometry, 2nd edn. Wiley, Hoboken (2003)
Hutchinson, J.E.: Fractals and self-similarity. Indiana Univ. Math. J. 30(5), 713–747 (1981)
Mazurkiewicz, S., Sierpiński, W.: Contribution à la topologie des ensembles dénombrables. Fund. Math. 1, 17–27 (1920)
Nowak, M.: Topological classification of scattered IFS-attractors. Topology Appl. 160(14), 1889–1901 (2013)
Reich, S., Zaslavski, A.J.: Almost all nonexpansive mappings are contractive. C. R. Math. Acad. Sci. Soc. R. Can. 22(3), 118–124 (2000)
Saks, S.: Theory of the Integral. Dover, New York (2005)
Schief, A.: Separation properties for self-similar sets. Proc. Amer. Math. Soc. 122(1), 111–115 (1994)
Steele, T.H.: Towards a characterization of \(\omega \)-limit sets for Lipschitz functions. Real Anal. Exchange 22(1), 201–212 (1996)
Zajiček, L.: Porosity and \(\sigma \)-porosity. Real Anal. Exchange 13(2), 314–350 (1987/88)
Author information
Authors and Affiliations
Corresponding author
Additional information
This research has been partially supported by the Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM).
Rights and permissions
About this article
Cite this article
D’Aniello, E., Steele, T.H. Attractors for classes of iterated function systems. European Journal of Mathematics 5, 116–137 (2019). https://doi.org/10.1007/s40879-018-0280-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0280-7




 of elements of
of elements of 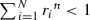 .
.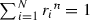 and
and 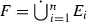 , where each
, where each 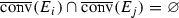 whenever
whenever 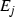 lies to the right of
lies to the right of 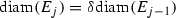 , where
, where 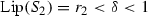 , for any
, for any 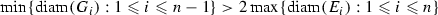 , where
, where 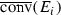 is mapped onto
is mapped onto 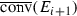 with
with 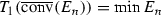 ,
, is closed.
is closed. is a closed and nowhere dense subset of
is a closed and nowhere dense subset of 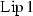 , for all
, for all 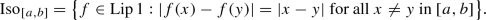
 is closed in
is closed in  . If for any i, j and k in
. If for any i, j and k in  with
with 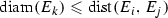 , then for every weak contraction
, then for every weak contraction 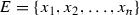 and
and 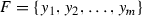 . Suppose that
. Suppose that 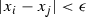 for all
for all 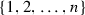 , and
, and 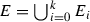 , with
, with 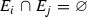 for each
for each 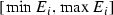 . Set
. Set 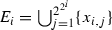 , with
, with 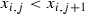 ,
, 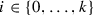 and
and 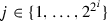 .
.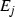 lies to the right of
lies to the right of 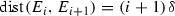 .
.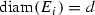 for all i, where
for all i, where 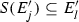 ; that is each
; that is each 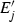 can map into only one
can map into only one 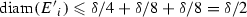 , and the smallest interval in
, and the smallest interval in 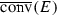 complementary to the sets
complementary to the sets 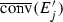 is of length at least
is of length at least 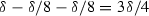 .
.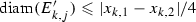 and the smallest interval complementary to the sets
and the smallest interval complementary to the sets 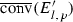 is at least of length
is at least of length 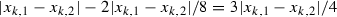 .
.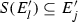 , then
, then 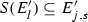 , for some s as
, for some s as 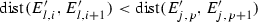 for any i and p.
for any i and p.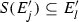 , whenever
, whenever 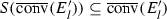 , so that
, so that 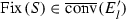 . Now, note that
. Now, note that 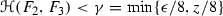 , where
, where 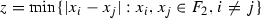 ,
,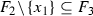 , and
, and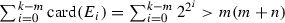 , and
, and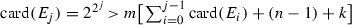 whenever
whenever 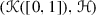 is compact,
is compact,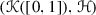 ,
,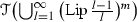 is a nowhere dense
is a nowhere dense 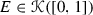 for which
for which 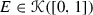 .
.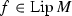 , then
, then  ,
,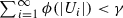 .
.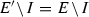 , so that E and
, so that E and 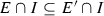 and
and 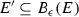 . Thus,
. Thus, 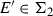 , too.
, too.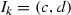 is a complementary interval of
is a complementary interval of 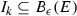 . Take
. Take 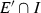 such that if
such that if 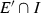 , then
, then 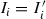 for
for 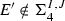 , so
, so 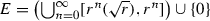 .
.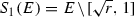 .
.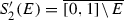 .
.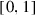 to
to 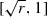 :
: 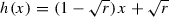 .
.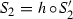 and
and 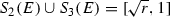 as
as 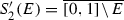 and
and 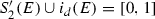 , and
, and 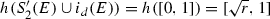 .
.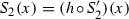 , with
, with 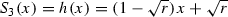 .
.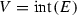 .
.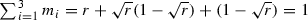 .
. for all n,
for all n, 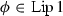 .
.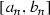 for all
for all 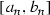 for all n.
for all n.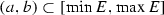 is complementary to E, then
is complementary to E, then 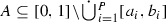 , then
, then