Abstract
We discuss William L. Edge’s approach to Humbert’s curves as a canonical genus 5 curve that is a complete intersection of diagonal quadrics. Moreover, the contribution of Edge to the study of projective curves  that are complete intersections of \(n-1\) quadrics is explained and some results, complementary to Edge’s exposition, are proved.
that are complete intersections of \(n-1\) quadrics is explained and some results, complementary to Edge’s exposition, are proved.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\{p_1,\dots ,p_5 \}\) be a set of five points in general position in \(\mathbb {P}^3\), and  be the family of twisted cubic curves through the fixed five points. Consider another point \(p\in \mathbb {P}^3\) general with respect to \(p_1,\dots ,p_5\) and define
be the family of twisted cubic curves through the fixed five points. Consider another point \(p\in \mathbb {P}^3\) general with respect to \(p_1,\dots ,p_5\) and define

\(\overline{pq}\) stands for the line joining p and q. This variety turns out to be an irreducible curve, and was studied by Humbert in [9]. In [1] Baker considered the curve of contact of a Weddle surface with one of its tangent cones at a node (for the definition of Weddle curve and its basic properties see [14], see also [5], specially Remark 8.6.2).
The aim of this note is to present several results obtained by William L. Edge regarding the geometry of Humbert’s curves and certain generalization that he introduced and to prove some related results. We work over an algebraically closed field of characteristic different form 2. The material discussed here by no means covers the total contribution of Edge to the study of Humbert’s curves and its generalizations, it was a constant topic in his work and even one of his last articles [8], written at his retirement in Nazareth House, was devoted to the study of a particular case of Humbert’s curve. Here we focus our attention on two papers [6] and [7].
In the first of these papers Edge proved the equivalence of the constructions by Humbert and Baker and introduced another equivalent construction that was the core of his treatment: the several geometric realizations of Humbert’s curve can be obtained by projecting a canonical genus 5 curve that is a complete intersection of three diagonal quadrics. In this sense, the Edge approach to Humbert’s curve can be considered as a part of the theory of intersection of quadrics as further developed in [2, 12, 13]. He proved many interesting properties of these curves, including a characterization of its Weierstrass points and a natural isogenous decomposition of its Jacobian as a sum of five elliptic curves (this being noticed before by Humbert and Baker). In Sect. 2 we present these results, the section is principally of an expository nature and the statement and the idea of the proof of Theorem 2.2 is taken from [14], where some of Edge’s results are also reproduced.
In Sect. 3 we focus on the paper [7], in which Edge introduced a generalization of Humbert’s curve by considering curves  that can be expressed as complete intersections of diagonal quadrics, we propose to call these curves Humbert–Edge’s curves of type n. We prove that the diagonality of the quadrics equations defining X is equivalent to X admitting a certain abelian group of order \(2^n\). Strangely enough, in his discussion, Edge did not include a proof that having this group action implies the diagonality of the quadrics. We also provide in Proposition 3.5 a partial equivariant decomposition of the Jacobian variety of X with respect to the action of the above mentioned group. Finally, in Sect. 4 we slightly generalize an Edge’s construction providing a family of special Humbert–Edge’s curves with a larger, non-abelian group of automorphisms.
that can be expressed as complete intersections of diagonal quadrics, we propose to call these curves Humbert–Edge’s curves of type n. We prove that the diagonality of the quadrics equations defining X is equivalent to X admitting a certain abelian group of order \(2^n\). Strangely enough, in his discussion, Edge did not include a proof that having this group action implies the diagonality of the quadrics. We also provide in Proposition 3.5 a partial equivariant decomposition of the Jacobian variety of X with respect to the action of the above mentioned group. Finally, in Sect. 4 we slightly generalize an Edge’s construction providing a family of special Humbert–Edge’s curves with a larger, non-abelian group of automorphisms.
It should be noted that in [3] the authors rediscovered these curves and some of its basic properties and called them generalized Humbert’s curves, they seemed not to be aware of the Edge’s work [7].
2 The classical Humbert’s curve
Let C be a plane, irreducible, degree 6 curve with five nodes, say \(n_1,\dots ,n_5\), in general position. Thus, C has geometric genus 5. Let \(\Gamma \) be the conic passing through the five nodes. Thus, \(\Gamma \) must intersect C in two remaining points p, q. The linear system  of cubics passing through the five nodes defines an immersion \(\phi \) of \(\mathbb {P}^2\) into
of cubics passing through the five nodes defines an immersion \(\phi \) of \(\mathbb {P}^2\) into  , whose image is a degree 4 Del Pezzo surface. This can be defined as a complete intersection of two diagonal quadrics [5, Theorem 8.6.2] and the image X of C is cut out on S by a further quadric hypersurface. In this way, we obtain the canonical curve X as a complete intersection of three quadrics in
, whose image is a degree 4 Del Pezzo surface. This can be defined as a complete intersection of two diagonal quadrics [5, Theorem 8.6.2] and the image X of C is cut out on S by a further quadric hypersurface. In this way, we obtain the canonical curve X as a complete intersection of three quadrics in  . The birational inverse from X to C is obtained by projecting X from the chord \(\overline{p'q'}\), with \(p'\!,q'\) denoting, respectively, the images of p and q under \(\phi \).
. The birational inverse from X to C is obtained by projecting X from the chord \(\overline{p'q'}\), with \(p'\!,q'\) denoting, respectively, the images of p and q under \(\phi \).
In [6] Edge identified Humbert’s curve as one of these projections in the particular case when the canonical curve X is the intersection of three diagonal quadrics.
We briefly recall the basic facts concerning intersections of quadrics (see [2, 12, 13]). Let  be an irreducible, non-singular complete intersection of quadrics \(Q_0,\dots ,Q_{n-2}\). Thus, X can be interpreted as the base locus of the
be an irreducible, non-singular complete intersection of quadrics \(Q_0,\dots ,Q_{n-2}\). Thus, X can be interpreted as the base locus of the  -dimensional linear system \(\lambda _0 Q_0 + \cdots +\lambda _{n-2} Q_{n-2}=0\). Denote by
-dimensional linear system \(\lambda _0 Q_0 + \cdots +\lambda _{n-2} Q_{n-2}=0\). Denote by  the corresponding
the corresponding  -subspace. The discriminant hypersurface \(\Delta \subset \Pi \) is defined by
-subspace. The discriminant hypersurface \(\Delta \subset \Pi \) is defined by

if  . This is a degree \(n+1\) hypersurface parameterizing the singular quadrics in \(\Pi \).
. This is a degree \(n+1\) hypersurface parameterizing the singular quadrics in \(\Pi \).
We have a filtration
where  , \(l=2,\dots ,n-2\). Moreover,
, \(l=2,\dots ,n-2\). Moreover,

see [13] for a proof.
In general \(\Delta \) could be reducible. A hyperplane appears as an irreducible component of \(\Delta \) if and only if an  -dimensional linear system
-dimensional linear system  exists formed by singular quadrics.
exists formed by singular quadrics.
Definition 2.1
(Edge, [6]) Let X be a non-hyperelliptic curve of genus 5 (identified with its canonical model  ). We say that X is a Humbert’s curve if there exists a projective system of coordinates in
). We say that X is a Humbert’s curve if there exists a projective system of coordinates in  and diagonal quadrics
and diagonal quadrics

such that X is the base locus of the net  .
.
In [6] Edge proved that the nodal Humbert’s plane sextic can be obtained as an image of the projection of X from a chord and the cuspidal one as an image of the projection of X from a tangent. Edge’s study is based on the fact that X admits an automorphism subgroup generated by the involutions:

The fundamental properties of X are summarized in the following theorem.
Theorem 2.2
Let  be a canonical curve. The following statements are equivalent:
be a canonical curve. The following statements are equivalent:
-
(i)
X is a Humbert’s curve.
-
(ii)
X admits five involutions \(\sigma _0,\dots , \sigma _4\) such that
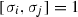 ,
, 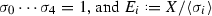 are elliptic curves.
are elliptic curves. -
(iii)
X admits 10 even and effective theta-characteristics.
-
(iv)
The discriminant curve of
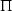 , \(\Delta \subset \mathbb {P}^2\), is a product of five lines.
, \(\Delta \subset \mathbb {P}^2\), is a product of five lines.
That (i) implies (ii) and (iii) was proved (in a rather scattered way) in [6]. Even though the other implications were not explicitly formulated, it is possible that Edge was aware of these equivalences. As formulated here this result and an indication of its proof appear in [14]. We include a proof for the reader’s convenience.
Proof
We start with a non-trigonal canonical curve  which is a complete intersection of three diagonal quadrics \(Q_0,Q_1,Q_2\),
which is a complete intersection of three diagonal quadrics \(Q_0,Q_1,Q_2\),

Note that in order for X to be non-degenerated and non-singular the determinant of any  minor of the matrix \((a_{ij})\) must be different from 0. Denote by \(\{ e_0,\dots ,e_4\}\) the standard frame of reference in
minor of the matrix \((a_{ij})\) must be different from 0. Denote by \(\{ e_0,\dots ,e_4\}\) the standard frame of reference in  , i.e.,
, i.e.,  with 1 on the i-th position. Note that
with 1 on the i-th position. Note that  for \(i=0,\dots ,4\).
for \(i=0,\dots ,4\).
Let  and denote
and denote  , i.e., \(p_{ij}\), \(j=1,\dots ,8\), are the points of intersection of X with the hyperplane
, i.e., \(p_{ij}\), \(j=1,\dots ,8\), are the points of intersection of X with the hyperplane  . Note that, on X, \(p_{i1}+\cdots +p_{i8} \sim K_X\).
. Note that, on X, \(p_{i1}+\cdots +p_{i8} \sim K_X\).
(i) \(\Rightarrow \) (ii). Fix, for instance \(i=0\). Let \(p\in X\) and consider the line \(l_p\) joining \(e_0\) and p. An easy computation shows that there exists another point  . Explicitly in coordinates, if
. Explicitly in coordinates, if  , then
, then  . Let us call this involution \(\sigma _0\) and consider the quotient
. Let us call this involution \(\sigma _0\) and consider the quotient  . The ramification points of this quotient are precisely \(\{p_{01},\dots ,p_{08}\}\). Thus, it follows from the Riemann–Hurwitz formula that \(E_0\) is an elliptic curve. Analogous considerations apply for \(i=1,\dots ,4\).
. The ramification points of this quotient are precisely \(\{p_{01},\dots ,p_{08}\}\). Thus, it follows from the Riemann–Hurwitz formula that \(E_0\) is an elliptic curve. Analogous considerations apply for \(i=1,\dots ,4\).
(ii) \(\Rightarrow \) (iii). Consider the subgroup generated by two involutions, say  , we obtain
, we obtain

This covering is simply ramified in the 16 points \(\{p_{01},\dots ,p_{08},p_{11},\dots , p_{18} \}\). Thus,

Therefore,  and we obtain that \(f^* \mathscr {O}_{\mathbb {P}^1}(1)\) is a theta-characteristic of X. Since \(h^0(X,f^* \mathscr {O}_{\mathbb {P}^1}(1))=2\) we obtain the desired theta-characteristics.
and we obtain that \(f^* \mathscr {O}_{\mathbb {P}^1}(1)\) is a theta-characteristic of X. Since \(h^0(X,f^* \mathscr {O}_{\mathbb {P}^1}(1))=2\) we obtain the desired theta-characteristics.
(iii) \(\Rightarrow \) (iv). Theta-characteristics of dimension at least 2 are in a  correspondence with rank 3 quadrics containing X (see, for instance [13, Section 4]). Taking into account our previous remark on \(\Delta ^{(l)}\) we see that the existence of the 10 theta-characteristics implies that the plane quintic \(\Delta \) has 10 singular points. This implies that \(\Delta \) is a product of five lines.
correspondence with rank 3 quadrics containing X (see, for instance [13, Section 4]). Taking into account our previous remark on \(\Delta ^{(l)}\) we see that the existence of the 10 theta-characteristics implies that the plane quintic \(\Delta \) has 10 singular points. This implies that \(\Delta \) is a product of five lines.
(iv) \(\Rightarrow \) (i). As X is a genus 5 canonical curve it must be contained in the base locus of a net \(\Pi \) of quadrics. We are assuming that the discriminant \(\Delta \) of this net is a product of five lines. We can choose coordinates in such a way that  and the pencil of quadrics in \(\Pi \) containing \(e_i\) is formed by rank 4 quadrics, from this the diagonal form for the \(Q_i\) is deduced. \(\square \)
and the pencil of quadrics in \(\Pi \) containing \(e_i\) is formed by rank 4 quadrics, from this the diagonal form for the \(Q_i\) is deduced. \(\square \)
The following corollary was also central in Edge’s investigation of Humbert’s curves.
Corollary 2.3
Let X be a Humbert’s curve. The set of Weierstrass points of X is formed by the 40 intersections of  with the hyperplanes \(H_i\), that is the set \(\{ p_{ij}\}_{0\leqslant i\leqslant 4, \,1\leqslant j \leqslant 8 }\) defined in the proof of Theorem 2.2. Each of these points has weight 3 and gap sequence
with the hyperplanes \(H_i\), that is the set \(\{ p_{ij}\}_{0\leqslant i\leqslant 4, \,1\leqslant j \leqslant 8 }\) defined in the proof of Theorem 2.2. Each of these points has weight 3 and gap sequence  .
.
Proof
Recall that given a projective curve X of genus g, a general point \(p\in X\) satisfies  for \(l=1,\dots ,g\). Points failing to fulfil this condition are the Weierstrass points. For any point \(p\in X\) the gap sequence is defined by
for \(l=1,\dots ,g\). Points failing to fulfil this condition are the Weierstrass points. For any point \(p\in X\) the gap sequence is defined by  such that
such that  . Thus, p is a Weierstrass point if and only if its gap sequence is not
. Thus, p is a Weierstrass point if and only if its gap sequence is not  . The weight of a Weierstrass point is defined as the sum
. The weight of a Weierstrass point is defined as the sum  and the sum of the weights of all the Weierstrass points equals
and the sum of the weights of all the Weierstrass points equals  (for a complete discussion, see for instance [11]).
(for a complete discussion, see for instance [11]).
Returning to our particular case, consider the quotient \(\sigma _i:X \rightarrow E_i\). Let  be as defined in the proof of Theorem 2.2. Since in the elliptic curve \(E_i\),
be as defined in the proof of Theorem 2.2. Since in the elliptic curve \(E_i\),

for all \(l\geqslant 1\), we have a non-constant meromorphic function on \(E_i\) having exactly a pole of order 2 at \(\sigma _i(p_{ij})\) and two non-constant linearly independent meromorphic functions having exactly a pole of order 3 at \(\sigma _i(p_{ij})\). Composing these functions with \(\sigma _i\), we deduce that
From this we obtain the desired gap sequence. Since each of these 40 points has weight 3, they form the totality of Weierstrass points. \(\square \)
Another important feature of Humbert’s curve is that its Jacobian is isogenous to a product of the five elliptic curves given by the pull-back of the quotients \(X\rightarrow E_i\):
Proposition 2.4
Let X be a Humbert’s curve and \(\pi _i:X\rightarrow E_i\) be the quotient by the involution \(\sigma _i\). Then,

Proof
The proof is elementary. Given  , we can write
, we can write

In this way, for any  ,
,  . Since
. Since  is a divisible group the result follows. \(\square \)
is a divisible group the result follows. \(\square \)
3 Intersection of quadrics and Humbert–Edge’s curves
In [7] Edge considered the following situation: let  be a non-singular, irreducible complete intersection of \(n-1\) diagonal quadrics \(Q_0,\dots ,Q_{n-2}\):
be a non-singular, irreducible complete intersection of \(n-1\) diagonal quadrics \(Q_0,\dots ,Q_{n-2}\):

In [3] such a curve is called a generalized Humbert’s curve. Taking into account the quoted paper [7] we think it is more appropriate to call it a Humbert–Edge’s curve.
Definition 3.1
An irreducible, non-degenerated and non-singular curve  , \(n\geqslant 2\), is a Humbert–Edge’s curve (HE curve for short) of type n if it is the complete intersection of \(n-1\) diagonal quadrics \(Q_0,\dots , Q_{n-2}\).
, \(n\geqslant 2\), is a Humbert–Edge’s curve (HE curve for short) of type n if it is the complete intersection of \(n-1\) diagonal quadrics \(Q_0,\dots , Q_{n-2}\).
The basic properties of an HE curve \(X_n\) are as follows.
Lemma 3.2
Let \(X_n\) be an HE curve. Then:
-
(i)
\(\deg X_n=2^{n-1}\!\).
-
(ii)
The canonical sheaf of \(X_n\) is
$$\begin{aligned} \mathscr {O}_{X_n}(K_{X_n})\simeq \mathscr {O}_{X_n}(n-3), \end{aligned}$$in particular \(g_{X_n}-1\!= 2^{n-2}(n-3)\).
-
(iii)
Every
 -minor of the matrix \((a_{ij})\) is non-degenerated.
-minor of the matrix \((a_{ij})\) is non-degenerated. -
(iv)
The linear involutions of
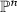 sending \(x_i\) into
sending \(x_i\) into 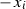 induce involutions \(\sigma _i\) on \(X_n\). These together generate a subgroup of
induce involutions \(\sigma _i\) on \(X_n\). These together generate a subgroup of 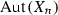 isomorphic to \((\mathbb {Z}/2\mathbb {Z})^n\) with relation \(\sigma _0\cdots \sigma _n=1\).
isomorphic to \((\mathbb {Z}/2\mathbb {Z})^n\) with relation \(\sigma _0\cdots \sigma _n=1\). -
(v)
The quotient of \(X_n\) by each involution \(\sigma _i\) is geometrically interpreted as projection with center \(e_i\) onto the hyperplane
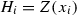 and this quotient is an HE curve of type \(n-1\).
and this quotient is an HE curve of type \(n-1\).
All these properties are stated in [7] and rediscovered in [3]. The cases \(n=2,3\) correspond to a plane conic and an elliptic space quartic curve, respectively, the case \(n=4\) is the classical Humbert’s curve, as presented by Edge.
Definition 3.3
Let \(X_n\) be a non-singular, irreducible, projective curve of genus \(2^{n-2}\) \(\cdot (n-3)+1\). We say that a group E acting on \(X_n\) is an HE group if it is isomorphic to \((\mathbb {Z}/2\mathbb {Z})^n\) and generators \(\sigma _0,\dots ,\sigma _n\) of E exist such that \(\sigma _0\cdots \sigma _n=1\) and the fixed set of each \(\sigma _i\) is of cardinality \(2^{n-1}\) and disjoint from the fixed set of  if \(i\ne j\).
if \(i\ne j\).
The following theorem is not explicitly stated in [7], but probably was implicitly assumed.
Theorem 3.4
An irreducible and non-singular curve of genus  is an HE curve of type n if and only if it admits an action of an HE group. Moreover, in this case the generators \(\sigma _i\) are the restriction to \(X_n\) of the involutions
is an HE curve of type n if and only if it admits an action of an HE group. Moreover, in this case the generators \(\sigma _i\) are the restriction to \(X_n\) of the involutions  .
.
This fact was proved over \(\mathbb {C}\) in [3], using the theory of uniformization and Klenian groups. We give here an algebraic proof valid over any algebraically closed field of characteristic different from 2.
Proof
We make an induction on n (the result being trivial for \(n=2\) and previously proved for \(n=4\)). Assume that a non-singular projective curve \(X_n\) of genus \(2^{n-2}\cdot \) \((n-3)+1\) admits an HE group as a subgroup of  . Then, the quotient
. Then, the quotient  admits a group of automorphisms generated by \(\overline{\sigma }_0,\dots ,\overline{\sigma }_{n-1}\) satisfying \(\overline{\sigma }_0\cdots \overline{\sigma }_{n-1}=1\). Thus, by induction \(X_{n-1}\) is an HE curve of type \(n-1\). Thus, it is expressed as the complete intersection of \(n-2\) diagonal quadrics
admits a group of automorphisms generated by \(\overline{\sigma }_0,\dots ,\overline{\sigma }_{n-1}\) satisfying \(\overline{\sigma }_0\cdots \overline{\sigma }_{n-1}=1\). Thus, by induction \(X_{n-1}\) is an HE curve of type \(n-1\). Thus, it is expressed as the complete intersection of \(n-2\) diagonal quadrics  in
in  .
.
In order to recover the  covering
covering  we must consider the ramified covering associated with the divisor \(E=q_1+\cdots +q_{2^{n-1}}\), where \(q_i\) are the ramification values of \(\pi _n\). We have
we must consider the ramified covering associated with the divisor \(E=q_1+\cdots +q_{2^{n-1}}\), where \(q_i\) are the ramification values of \(\pi _n\). We have

with \(2\eta =E\). Let  be the divisor given by \(X_{n-1}. H_i\) (equivalently
be the divisor given by \(X_{n-1}. H_i\) (equivalently  is the set of fixed points of \(\overline{\sigma }_i\)). Then,
is the set of fixed points of \(\overline{\sigma }_i\)). Then,  and thus
and thus

In this way \(\vert \pi _n^* D_i \vert \) defines a diagram

with \(p_n\) the projection of \(X_n\) with center \(e_n\) onto \(H_n\).
Hence, the equations of  are given by
are given by  and the extra equation defining the
and the extra equation defining the  covering, namely:
covering, namely:
\(s\in \mathbb {P}H^0(\mathscr {O}_{X_{n-1}}(E))=\mathbb {P}H^0(\mathscr {O}_{X_{n-1}}(2D))\). As s is invariant under the action of the HE group induced on \(X_{n-1}\), we see that s can be written as a diagonal quadric in the projective coordinates of \(\mathbb {P}^{n-1}\). \(\square \)
It is not clear to us if the Jacobian of an HE curve X can be written as a sum of elliptic curves. However, a partial decomposition exists: let  be the quotient and
be the quotient and  be the abelian subvariety defined as
be the abelian subvariety defined as

Moreover, let  be the abelian subvariety
be the abelian subvariety

Then we have:
Proposition 3.5
Let  be the Jacobian variety of an HE curve. Then
be the Jacobian variety of an HE curve. Then
-
(i)
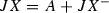 and A and
and A and 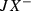 are complementary, in the sense that its intersection is finite.
are complementary, in the sense that its intersection is finite. -
(ii)
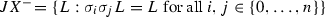 .
.
Proof
Given an abelian subvariety \(B\subset JX\), define

and, for any 

We clearly have

Next, look at the representation of the HE group E in \(T_0X\). As E is abelian a basis exists such that all the matrices representing elements of E are diagonal and with eigenvalues 1 or \(-1\). Write, for each \(\sigma \in E\)

with \(V_{\sigma }^{+}\) (respectively \(V_{\sigma }^{-}\)) denoting the eigenspace associated with 1 (resp. \(-1\)).
Then, we see that  and \(T_0A=\sum V_{\sigma _i}^{+}\). Moreover,
and \(T_0A=\sum V_{\sigma _i}^{+}\). Moreover,

The proposition follows from these considerations. \(\square \)
Remark 3.6
The dimension of some of the spaces appearing in the previous decomposition can be explicitly computed. For instance, if n is even, then the argument in the proof of Proposition 2.4 provides  . It must also be noticed that the obtained decomposition gives a partial solution to the computation of the E-equivariant decomposition in the sense of [10]. Since E induces on
. It must also be noticed that the obtained decomposition gives a partial solution to the computation of the E-equivariant decomposition in the sense of [10]. Since E induces on  the group
the group  the E-simplicity of
the E-simplicity of  is equivalent to its simplicity as abelian variety.
is equivalent to its simplicity as abelian variety.
4 Specializations with larger automorphism group
Recall that by definition, if \(X_n\) is an HE curve of type n there exist \(n-1\) diagonal quadrics,

such that \(X_n\) is the complete intersection of these quadrics. Also, an HE curve admits naturally \(n+1\) involutions  for \(i=0,\dots ,n\). Denote the HE group generated by the involutions \(\sigma _i\) by
for \(i=0,\dots ,n\). Denote the HE group generated by the involutions \(\sigma _i\) by  .
.
Edge found in [7] a convenient representation for an HE curve given as above. In fact, for each \(j=0,\dots ,n\), regard the coefficients \(a_{ij}\) as the homogeneous coordinates of a point  in the projective space
in the projective space  , thus, we have \(n+1\) points. Using the fact that there is a unique rational normal curve
, thus, we have \(n+1\) points. Using the fact that there is a unique rational normal curve  through the \(n+1\) points \(p_0,\dots ,p_n\) in general position and changing the coordinates of
through the \(n+1\) points \(p_0,\dots ,p_n\) in general position and changing the coordinates of  , one may assume that C is given in the standard parametric form and consequently,
, one may assume that C is given in the standard parametric form and consequently,  for every \(j=0,\dots ,n\). Therefore, we can assume that an HE curve \(X_n\) is defined by diagonal quadrics with the form
for every \(j=0,\dots ,n\). Therefore, we can assume that an HE curve \(X_n\) is defined by diagonal quadrics with the form

A direct consequence of this representation noted by Edge is that \(X_n\) has only \(n-2\) moduli.
On the other hand, Edge specialized an HE curve (denoted by \(\Gamma _n\) in his paper) to obtain another curve which has a larger automorphism group and fewer moduli. Edge’s idea was to modify the diagonal quadrics that define the HE curve in such a way that the curve defined by these new quadrics is preserved under the original automorphism group E and under a specific automorphism of finite order. Indeed, he presented three such curves:  admitting an automorphism of order 2, \(\Gamma ''_n\subset \mathbb {P}^{3s-1}\) admitting an automorphism of order 3 and
admitting an automorphism of order 2, \(\Gamma ''_n\subset \mathbb {P}^{3s-1}\) admitting an automorphism of order 3 and  admitting an automorphism of order \(n+1\). The diagonal quadrics that define such curves enabled Edge to conclude that the curve \(\Gamma _n'\) has \(p+1\) moduli, \(\Gamma ''_n\) has s moduli and \(\Delta _n\) has no moduli (see [7, Sections II.8, II.13 and III.17]).
admitting an automorphism of order \(n+1\). The diagonal quadrics that define such curves enabled Edge to conclude that the curve \(\Gamma _n'\) has \(p+1\) moduli, \(\Gamma ''_n\) has s moduli and \(\Delta _n\) has no moduli (see [7, Sections II.8, II.13 and III.17]).
Following the procedure used by Edge, we generalize this process to construct curves admitting the HE group E and other specific automorphism of finite order with fewer moduli. Consider an HE curve  defined by the diagonal quadrics
defined by the diagonal quadrics  , where m and t are positive integers. Fix a primitive \(m^{\text{ th }}\) root \(\xi \) of unity. Let \(H_{m,t}\) be the curve defined as the intersection of the diagonal quadrics
, where m and t are positive integers. Fix a primitive \(m^{\text{ th }}\) root \(\xi \) of unity. Let \(H_{m,t}\) be the curve defined as the intersection of the diagonal quadrics

Definition 4.1
Given an HE curve  , a specialization of \(X_{mt-1}\) is the curve \(H_{m,t}\) given by the intersection of the \(mt-2\) diagonal quadrics \(\Omega _0,\dots ,\Omega _{mt-3}\).
, a specialization of \(X_{mt-1}\) is the curve \(H_{m,t}\) given by the intersection of the \(mt-2\) diagonal quadrics \(\Omega _0,\dots ,\Omega _{mt-3}\).
The next result presents some properties of the specialization \(H_{m,t}\) of an HE curve \(X_{mt-1}\).
Proposition 4.2
The following assertions hold:
-
(i)
The genus
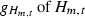 satisfies \(g_{H_{m,t}}\!-1=2^{mt-3}(mt-4)\).
satisfies \(g_{H_{m,t}}\!-1=2^{mt-3}(mt-4)\). -
(ii)
\(H_{m,t}\) has \(t-3\) moduli if \(t> 3\) and has no moduli if \(t\leqslant 3\).
-
(iii)
\(H_{m,t}\) admits the action of a group \(\widehat{E}\) of order
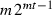 which contains the HE group E, isomorphic to
which contains the HE group E, isomorphic to 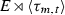 where \(\tau _{m,t}\) is an automorphism of order m.
where \(\tau _{m,t}\) is an automorphism of order m.
Proof
(i) holds since \(H_{m,t}\) is a specialization of \(X_{mt-1}\) and (ii) follows immediately from the equations that define \(H_{m,t}\).
(iii) Note that by construction \(\Omega _i\) is invariant under E for every \(i=0,\dots ,mt-3\). On the other hand, consider the automorphism \(\tau _{m,t}\) of  induced by the following permutation consisting of t m-cycles:
induced by the following permutation consisting of t m-cycles:

\(H_{m,t}\) is invariant under \(\tau _{m,t}\). Indeed, for each \(i=0,\dots ,mt-3\),

Define the group \(\widehat{E}\) as the group spanned by E and \(\tau _{m,t}\). This group is non-abelian, for example, if  , then
, then

while

In \(\widehat{E}\), we have the original relations between the elements of E and also there are new relations coming from the elements \(\tau _{m,t}\) and \(\sigma _i\tau _{m,t}\). The relations in \(\widehat{E}\) are the following:

The relation (1) implies that E is a normal subgroup of \(\widehat{E}\). In addition, the fact that \(\widehat{E}\) is the product of the subgroups E and  and
and  imply that \(\widehat{E}\) is the semidirect product of E by
imply that \(\widehat{E}\) is the semidirect product of E by  , i.e.,
, i.e.,  . So, the order of \(\widehat{E}\) is equal to
. So, the order of \(\widehat{E}\) is equal to  . \(\square \)
. \(\square \)
Remark 4.3
There exist Humbert’s curves admitting larger automorphisms groups than the mentioned before. For example, the automorphism group of the Humbert’s curve given by the equations
where \(\zeta _5\) is a primitive fifth root of unity, has order 160. This curve was recently considered by Cheltsov and Shramov in the context of the study of groups of rigid transformations of \(\mathbb {P}^3\), [4, Remark 4.18].
References
Baker, H.F.: An Introduction to the Theory of Multiply Periodic Functions. Cambridge University Press, Cambridge (1907)
Beauville, A.: Variétés de Prym et jacobiennes intermédiaires. Ann. Sci. Éc. Norm. Super. 10(3), 309–391 (1977)
Carocca, A., González-Aguilera, V., Hidalgo, R.A., Rodríguez, R.E.: Generalized Humbert curves. Israel J. Math. 164, 165–192 (2008)
Cheltsov, I., Shramov, C.: Finite collineation groups and birational rigidity (2017). arXiv:1712.08258
Dolgachev, I.V.: Classical Algebraic Geometry. Cambridge University Press, Cambridge (2012)
Edge, W.L.: Humbert’s plane sextics of genus 5. Proc. Cambridge Philos. Soc. 47, 483–495 (1951)
Edge, W.L.: The common curve of quadrics sharing a self-polar simplex. Ann. Math. Pura Appl. 114, 241–270 (1977)
Edge, W.L.: A plane sextic and its five cusps. Proc. Roy. Soc. Edinburgh Sect. A 118(3–4), 209–223 (1991)
Humbert, G.: Sur un complexe remarquable de coniques et sur la surface de troisième ordre. J. de l’Ecole Poly. 64, 123–149 (1894)
Lange, H., Recillas, S.: Poincaré’s reducibility theorem with \(G\)-action. Bol. Soc. Mat. Mexicana 10(1), 43–48 (2004)
Miranda, R.: Algebraic Curves and Riemann Surfaces. Graduate Studies in Mathematics, vol. 5. American Mathematical Society, Providence (1995)
Reid, M.: The Complete Intersection of Two or More Quadrics. Ph.D. Thesis, Cambridge University (1972)
Tyurin, A.N.: On intersections of quadrics. Russian Math. Surveys 30(6), 51–105 (1975)
Varley, R.: Weddle’s surfaces, Humbert’s curves and a certain 4-dimensional abelian variety. Amer. J. Math. 108(4), 931–951 (1986)
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper was partially supported by CONACyT Grant 257079. The first author acknowledges the financial support of Fondo Institucional de Fomento Regional para el Desarrollo Científico, Tecnológico y de Innovación, FORDECYT 265667.
Rights and permissions
About this article
Cite this article
Frías-Medina, J.B., Zamora, A.G. Some remarks on Humbert–Edge’s curves. European Journal of Mathematics 4, 988–999 (2018). https://doi.org/10.1007/s40879-018-0232-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0232-2




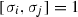 ,
, 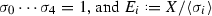 are elliptic curves.
are elliptic curves.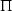 ,
,  -minor of the matrix
-minor of the matrix 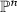 sending
sending 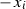 induce involutions
induce involutions 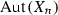 isomorphic to
isomorphic to 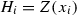 and this quotient is an HE curve of type
and this quotient is an HE curve of type 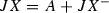 and A and
and A and 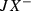 are complementary, in the sense that its intersection is finite.
are complementary, in the sense that its intersection is finite.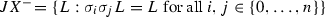 .
.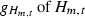 satisfies
satisfies 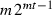 which contains the HE group E, isomorphic to
which contains the HE group E, isomorphic to 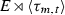 where
where