Abstract
The Lindelöf degree and extent were studied in Buhagiar et al. (Cent Eur J Math 12(8):1249–1264, 2014) in relation to lexicographic products of linearly ordered spaces. In this paper we consider the behaviour of other important cardinal functions, such as spread, density, weight and character, in such lexicographic products. Namely, we study the relation between a particular cardinal function on a lexicographic product of linearly ordered spaces and that cardinal function on each factor of the product.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The lexicographic product  of a collection
of a collection  , \(\mu > 1\), of linearly ordered sets is an unexpectedly useful and ubiquitous set theoretic structure. When each linearly ordered set is given the order topology, it is important to study the behaviour of topological properties when lexicographic products are taken. Such investigations were done, for example, by Faber [3]. In this paper, the behaviour of some cardinal functions is investigated when lexicographic products of linearly ordered spaces are taken.
, \(\mu > 1\), of linearly ordered sets is an unexpectedly useful and ubiquitous set theoretic structure. When each linearly ordered set is given the order topology, it is important to study the behaviour of topological properties when lexicographic products are taken. Such investigations were done, for example, by Faber [3]. In this paper, the behaviour of some cardinal functions is investigated when lexicographic products of linearly ordered spaces are taken.
A linearly ordered topological space (abbreviated LOTS) is a triple \((X,\lambda (\leqslant ),\leqslant )\), where \((X,\leqslant )\) is a linearly ordered set (abbreviated LOS) and \(\lambda (\leqslant )\) is the usual interval topology defined by \(\leqslant \) [7, 8].
An ordered pair (A, B) of disjoint subsets of a LOS X is said to be a jump if (i)  , (ii) \(x<y\) whenever \(x\in A\) and \(y\in B\), and (iii) A has a maximal element a, and B has a minimal element b. Thus \(a<b\) and
, (ii) \(x<y\) whenever \(x\in A\) and \(y\in B\), and (iii) A has a maximal element a, and B has a minimal element b. Thus \(a<b\) and  . For a LOTS X we will let
. For a LOTS X we will let

We use standard notation for the cardinal functions on a topological space X. Namely,

As usual, we require all cardinal functions to take only infinite cardinals as values. The reader is referred to [4,5,6] for a thorough study of cardinal functions. Figure 1 shows the relations between the above cardinal functions in LOTS (see [2, p. 222]).
The behaviour of the cardinal functions \(\ell \) and e in lexicographic products of LOTS was studied in [1], in this paper we study the behaviour of the other cardinal functions.
If X is a LOS and for some \(x\in X\) we write \(x=0\), then this would mean that X has a minimal element denoted by 0. Analogously, \(x=1\) means that x is the maximal element of X denoted by 1. In particular, when we consider the two-point LOS or LOTS  we understand that \(0 < 1\). In the rest of the paper we assume that \(|X| \geqslant 2\) for any LOS X.
we understand that \(0 < 1\). In the rest of the paper we assume that \(|X| \geqslant 2\) for any LOS X.
2 Spread, density, weight and character of the lexicographic product of two LOTS
In this section we consider the lexicographic product  of two LOTS X and Y.
of two LOTS X and Y.
Lemma 2.1
-
(a)
 ,
,  ,
,  and
and  .
. -
(b)
If \(|Y|>2\), then
 .
.
Proof
(a) For \(x\in X\), the subspace  of
of  is order-isomorphic to Y, the order topology of
is order-isomorphic to Y, the order topology of  induces on \(_xL\) the order topology of \(_xL\). The inequalities
induces on \(_xL\) the order topology of \(_xL\). The inequalities  ,
,  and
and  thus follow. The inequality
thus follow. The inequality  follows from the equality \(d=hd\).
follows from the equality \(d=hd\).
(b) Since  , for a non endpoint \(y\in Y\), is a discrete subspace of
, for a non endpoint \(y\in Y\), is a discrete subspace of  we get
we get  . This implies
. This implies  . \(\square \)
. \(\square \)
Theorem 2.2

Proof
Suppose that  . If
. If  , for \(a,b\in X\) with \(a<b\), then
, for \(a,b\in X\) with \(a<b\), then  , hence
, hence  . Moreover, if \(D\subseteq X\) is discrete, then the set
. Moreover, if \(D\subseteq X\) is discrete, then the set  is a discrete set in
is a discrete set in  and
and  follows. Consequently,
follows. Consequently,  . Conversely, consider a cellular family \({{\mathscr {C}}}\) in
. Conversely, consider a cellular family \({{\mathscr {C}}}\) in  , one can assume that each \(I\in {{\mathscr {C}}}\) is an open interval of the form
, one can assume that each \(I\in {{\mathscr {C}}}\) is an open interval of the form  with
with

The image of \({{\mathscr {C}}}\) under the mapping  is a collection of pairwise disjoint open intervals in X. Noting that
is a collection of pairwise disjoint open intervals in X. Noting that  defines a jump in X, one concludes that
defines a jump in X, one concludes that  .
.
If \(|Y| > 2\), the inequality  follows from Lemma 2.1. Conversely, if
follows from Lemma 2.1. Conversely, if  is discrete, then for any \(x\in X\),
is discrete, then for any \(x\in X\),  is discrete in Y, so that \(|D_x| \leqslant s(Y)\). Consequently,
is discrete in Y, so that \(|D_x| \leqslant s(Y)\). Consequently,  and therefore,
and therefore,  . \(\square \)
. \(\square \)
An analogous formula holds for the density.
Theorem 2.3

Proof
If  , then
, then  follows from Theorem 2.2. Suppose
follows from Theorem 2.2. Suppose  is dense and
is dense and  . Then the set
. Then the set  is a dense set in X. Consequently,
is a dense set in X. Consequently,  and therefore,
and therefore,  . Conversely, suppose \(D\subseteq X\) is a dense subset of X satisfying \(|D| \leqslant d(X)\). Let
. Conversely, suppose \(D\subseteq X\) is a dense subset of X satisfying \(|D| \leqslant d(X)\). Let  . Then
. Then  is dense in
is dense in  , adding to P any possible isolated end points. Note that
, adding to P any possible isolated end points. Note that  so that
so that  follows.
follows.
If \(|Y| > 2\), the inequality  follows from Lemma 2.1. Suppose \(D\subseteq Y\) is dense in Y with \(|D| \leqslant d(Y)\), one can assume that \(0,1\in D\) if they exist in Y. Then
follows from Lemma 2.1. Suppose \(D\subseteq Y\) is dense in Y with \(|D| \leqslant d(Y)\), one can assume that \(0,1\in D\) if they exist in Y. Then  is dense in
is dense in  and
and  follows. \(\square \)
follows. \(\square \)
We next consider the weight.
Theorem 2.4
 .
.
Proof
Suppose  and let \({{\mathscr {B}}}\) be a base of open intervals in
and let \({{\mathscr {B}}}\) be a base of open intervals in  with
with  . For any \(x\in X\) choose \(I(x)\in {{\mathscr {B}}}\) with \((x,0)\in I(x)\) and \((x,1)\notin I(x)\). Since \(X\ni x\mapsto I(x)\) is injective, the inequality
. For any \(x\in X\) choose \(I(x)\in {{\mathscr {B}}}\) with \((x,0)\in I(x)\) and \((x,1)\notin I(x)\). Since \(X\ni x\mapsto I(x)\) is injective, the inequality  follows. On the other hand
follows. On the other hand  and therefore,
and therefore,  .
.
If \(|Y| > 2\), the inequality  follows from Lemma 2.1. The inequality
follows from Lemma 2.1. The inequality  easily follows if Y does not have endpoints. Now suppose \(0\in Y\). Given \(x\in X\), a neighbourhood base for (x, 0) must have cardinality
easily follows if Y does not have endpoints. Now suppose \(0\in Y\). Given \(x\in X\), a neighbourhood base for (x, 0) must have cardinality  so that the collection of neighbourhood bases for (x, 0), for all \(x\in X\), must have cardinality
so that the collection of neighbourhood bases for (x, 0), for all \(x\in X\), must have cardinality  . Similarly for the case that \(1\in Y\). Consequently, after considering a neighbourhood base for points (x, y) with \(y\notin \{0,1\}\), it follows that
. Similarly for the case that \(1\in Y\). Consequently, after considering a neighbourhood base for points (x, y) with \(y\notin \{0,1\}\), it follows that  . \(\square \)
. \(\square \)
We end this section by considering  . For a LOS X, we will denote the topology generated by sets of the form
. For a LOS X, we will denote the topology generated by sets of the form

\(a,b\in X\), and \(\{1\}\) (if \(1\in X\)) by \(\tau _{\mathrm{r}}\), and similarly, the topology generated by sets of the form  , \(a,b\in X\), and \(\{0\}\) (if \(0\in X\)) by \(\tau _{\mathrm{l}}\). We will write \(\chi _{\mathrm{r}}(x)\) to mean the character of \(x \in (X,\tau _{\mathrm{r}})\) and \(\chi _{\mathrm{r}}(X)\) for the character of \((X,\tau _{\mathrm{r}})\). Similarly for \(\chi _{\mathrm{l}}(x)\) and \(\chi _{\mathrm{l}}(X)\). If one needs to specify that the character of x is taken in X, then one writes \(\chi (x,X)\) (similarly \(\chi _{\mathrm{r}}(x,X)\) and \(\chi _{\mathrm{l}}(x,X)\)). Recall that as shown in Fig. 1, the character of a LOTS is equal to its pseudo-character. One can also note that for any \(x\in X\),
, \(a,b\in X\), and \(\{0\}\) (if \(0\in X\)) by \(\tau _{\mathrm{l}}\). We will write \(\chi _{\mathrm{r}}(x)\) to mean the character of \(x \in (X,\tau _{\mathrm{r}})\) and \(\chi _{\mathrm{r}}(X)\) for the character of \((X,\tau _{\mathrm{r}})\). Similarly for \(\chi _{\mathrm{l}}(x)\) and \(\chi _{\mathrm{l}}(X)\). If one needs to specify that the character of x is taken in X, then one writes \(\chi (x,X)\) (similarly \(\chi _{\mathrm{r}}(x,X)\) and \(\chi _{\mathrm{l}}(x,X)\)). Recall that as shown in Fig. 1, the character of a LOTS is equal to its pseudo-character. One can also note that for any \(x\in X\),  .
.
Proposition 2.5
For two LOTS X and Y,

Proof
For  we have
we have

Taking the supremum over all  we get the formula for
we get the formula for  . Dually we get the formula for
. Dually we get the formula for  , while
, while  . \(\square \)
. \(\square \)
Example 2.6
Let us look at the following examples:
-
1.
Consider
 . Then \(s(Z) = \aleph _0\) (since \(s({\mathbb {R}}) = {\mathbb {J}}_{{\mathbb {R}}} = \aleph _0\)). But
. Then \(s(Z) = \aleph _0\) (since \(s({\mathbb {R}}) = {\mathbb {J}}_{{\mathbb {R}}} = \aleph _0\)). But  . Analogously, \(d(Z) = \aleph _0\) and
. Analogously, \(d(Z) = \aleph _0\) and  . On the other hand, if one takes
. On the other hand, if one takes  , then
, then  .
. -
2.
Let \(X = {\mathbb {R}}\) and
 . Then
. Then  .
. -
3.
If
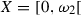 and
and 
then
 . However, if we take
. However, if we take  and
and  , then
, then  .
.
3 Spread, density, weight and character of the lexicographic product of LOTS
In what follows,  is the lexicographic product of \(X_\alpha \), where \(X_\alpha \) is a LOS for every \(\alpha < \mu \) and \(\mu \) is a limit ordinal.
is the lexicographic product of \(X_\alpha \), where \(X_\alpha \) is a LOS for every \(\alpha < \mu \) and \(\mu \) is a limit ordinal.
Theorem 3.1
If  , then
, then

Proof
For every \(0< \alpha < \mu \) we have  , so that, by Theorem 2.2,
, so that, by Theorem 2.2,  . Hence \(s(X) \geqslant \sup _{\alpha< \mu }\bigl |\prod _{\gamma < \alpha } X_\gamma \bigr |\).
. Hence \(s(X) \geqslant \sup _{\alpha< \mu }\bigl |\prod _{\gamma < \alpha } X_\gamma \bigr |\).
Now let us look at the weight of X. We show that \(w(X) \leqslant \sup _{\alpha< \mu }\bigl |\prod _{\gamma < \alpha } X_\gamma \bigr |\) from which the result follows. Let \(z = (z_\alpha )_{\alpha < \mu }\in X\) be defined as follows:
For every \(\gamma < \mu \) let  and let \(D = \bigcup _{\gamma < \mu }Z_\gamma \). Then \(|Z_\gamma | = \bigl |\prod _{\alpha \leqslant \gamma }X_\alpha \bigr |\) and therefore,
and let \(D = \bigcup _{\gamma < \mu }Z_\gamma \). Then \(|Z_\gamma | = \bigl |\prod _{\alpha \leqslant \gamma }X_\alpha \bigr |\) and therefore,

We show that for every \(x\in X\) and every \(c < x\), there exists \(a\in D\) such that \(c\leqslant a < x\). Let \(x = (x_\alpha )_{\alpha < \mu }\) and \(c = (c_\alpha )_{\alpha < \mu }\). Let \(\alpha _0\) be the first index such that  . If \(c_\alpha = 1\) for all \(\alpha > \alpha _0\), then let \(a = c \in D\), otherwise there exists some \(\delta > \alpha _0\) such that \(c_\delta < y\) for some \(y\in X_\delta \), and we define \(a = (a_\alpha )_{\alpha < \mu }\in D\) by
. If \(c_\alpha = 1\) for all \(\alpha > \alpha _0\), then let \(a = c \in D\), otherwise there exists some \(\delta > \alpha _0\) such that \(c_\delta < y\) for some \(y\in X_\delta \), and we define \(a = (a_\alpha )_{\alpha < \mu }\in D\) by
Dually, there exists a subset  with \(|D'| \leqslant \sup _{\gamma< \mu }\bigl |\prod _{\alpha <\gamma }X_\alpha \bigr |\) such that for every \(x\in X\) and every \(d > x\), there exists \(b\in D'\) such that \(d\geqslant b > x\). Consequently, there exists a base of cardinality \(\sup _{\gamma< \mu }\bigl |\prod _{\alpha <\gamma }X_\alpha \bigr |\) as required to show. \(\square \)
with \(|D'| \leqslant \sup _{\gamma< \mu }\bigl |\prod _{\alpha <\gamma }X_\alpha \bigr |\) such that for every \(x\in X\) and every \(d > x\), there exists \(b\in D'\) such that \(d\geqslant b > x\). Consequently, there exists a base of cardinality \(\sup _{\gamma< \mu }\bigl |\prod _{\alpha <\gamma }X_\alpha \bigr |\) as required to show. \(\square \)
We are left with the calculation of the character \(\chi (X)\) of a lexicographic product  , where \(\mu \) is a limit ordinal. We first calculate \(\chi _{\mathrm{r}}(x,X)\) for \(x\in X\) and then \(\chi _{\mathrm{r}}(X)\). By duality we obtain \(\chi _{\mathrm{l}}(x,X)\) and \(\chi _{\mathrm{l}}(X)\). Finally, we get \(\chi (x,X)\) and \(\chi (X)\) as a maximum of \(\chi _{\mathrm{r}}\) and \(\chi _{\mathrm{l}}\).
, where \(\mu \) is a limit ordinal. We first calculate \(\chi _{\mathrm{r}}(x,X)\) for \(x\in X\) and then \(\chi _{\mathrm{r}}(X)\). By duality we obtain \(\chi _{\mathrm{l}}(x,X)\) and \(\chi _{\mathrm{l}}(X)\). Finally, we get \(\chi (x,X)\) and \(\chi (X)\) as a maximum of \(\chi _{\mathrm{r}}\) and \(\chi _{\mathrm{l}}\).
For \(x = (x_\alpha )_{\alpha < \mu }\in X\), let

[We use the following convention: \(\mu _1(x) = \mu \) when  . In other words, \(\inf \varnothing = \mu \), which is true when \(A_1(x)\) is cofinal in \(\mu \). If \(A_1(x)\) is not cofinal in \(\mu \) then
. In other words, \(\inf \varnothing = \mu \), which is true when \(A_1(x)\) is cofinal in \(\mu \). If \(A_1(x)\) is not cofinal in \(\mu \) then  .]
.]
Lemma 3.2
For \(x = (x_\alpha )_{\alpha < \mu }\in X\) we have

Proof
Case I: \(A_1(x)\) is cofinal in \(\mu \). In this case we show that  . Choose \(z_\alpha > x_\alpha \) for every \(\alpha \in A_1(x)\) and let \(y^\gamma = (y^\gamma _\alpha )_{\alpha < \mu }\in X\), for every \(\gamma \in A_1(x)\), be defined by:
. Choose \(z_\alpha > x_\alpha \) for every \(\alpha \in A_1(x)\) and let \(y^\gamma = (y^\gamma _\alpha )_{\alpha < \mu }\in X\), for every \(\gamma \in A_1(x)\), be defined by:
Take any \(A\subseteq A_1(x)\) with  , then \(y^\gamma > x\) for every \(\gamma \in A\) and \(\inf _{\gamma \in A}y^\gamma = x\). Hence \(\chi _{\mathrm{r}}(x,X)\leqslant |A| = \mathrm{cf}(\mu )\). To prove the converse, suppose \(\chi _{\mathrm{r}}(x,X) < \mathrm{cf}(\mu )\). There exists a set B with
, then \(y^\gamma > x\) for every \(\gamma \in A\) and \(\inf _{\gamma \in A}y^\gamma = x\). Hence \(\chi _{\mathrm{r}}(x,X)\leqslant |A| = \mathrm{cf}(\mu )\). To prove the converse, suppose \(\chi _{\mathrm{r}}(x,X) < \mathrm{cf}(\mu )\). There exists a set B with  and elements \(b^\beta = (b^\beta _\alpha )_{\alpha < \mu }\in X\) with \(b^\beta > x\) for all \(\beta \in B\) such that \(\inf _{\beta \in B}b^\beta = x\). Let
and elements \(b^\beta = (b^\beta _\alpha )_{\alpha < \mu }\in X\) with \(b^\beta > x\) for all \(\beta \in B\) such that \(\inf _{\beta \in B}b^\beta = x\). Let  , then
, then  . Therefore, there exists \(\xi <\mu \) such that \(\alpha _\beta < \xi \) for all \(\beta \in B\). Take any \(\gamma \in A_1(x)\) with \(\gamma > \xi \). Then \(x< y^\gamma < b^\beta \) for all \(\beta \in B\), so that \(\inf _{\beta \in B}b^\beta \geqslant y^\gamma > x\), a contradiction.
. Therefore, there exists \(\xi <\mu \) such that \(\alpha _\beta < \xi \) for all \(\beta \in B\). Take any \(\gamma \in A_1(x)\) with \(\gamma > \xi \). Then \(x< y^\gamma < b^\beta \) for all \(\beta \in B\), so that \(\inf _{\beta \in B}b^\beta \geqslant y^\gamma > x\), a contradiction.
Case II: \(A_1(x)\) is not cofinal in \(\mu \). If \(x_\alpha = 1\) for all \(\alpha < \mu \) then x is the greatest element of X, hence \(\chi _{\mathrm{r}}(x,X) = 1\). Otherwise,  , see the proof of Proposition 2.5 for
, see the proof of Proposition 2.5 for  . If \(\mu _1(x)\) is a limit ordinal, then \(\chi _{\mathrm{r}}((x_\alpha )_{\alpha <\mu _1(x)}\),
. If \(\mu _1(x)\) is a limit ordinal, then \(\chi _{\mathrm{r}}((x_\alpha )_{\alpha <\mu _1(x)}\),  by Case I above. Otherwise, let \(\beta <\mu \) satisfy \(\beta + 1 = \mu _1(x)\). Then
by Case I above. Otherwise, let \(\beta <\mu \) satisfy \(\beta + 1 = \mu _1(x)\). Then  and by Proposition 2.5 one obtains
and by Proposition 2.5 one obtains

\(\square \)
For our next corollary we let

Hence, using the above convention, \(\mu _1 = \mu \) if and only if  is cofinal in \(\mu \). For an ordinal \(\alpha \), let us denote by \(\alpha ^-\) the immediate predecessor of \(\alpha \) if it exists; otherwise, if \(\alpha \) is a limit ordinal (or 0) we let \(\alpha ^- = \alpha \). Moreover, in line with our interest in infinite cardinals, we let \(\sup \varnothing = \aleph _0\) (instead of \(\sup \varnothing = 0\)).
is cofinal in \(\mu \). For an ordinal \(\alpha \), let us denote by \(\alpha ^-\) the immediate predecessor of \(\alpha \) if it exists; otherwise, if \(\alpha \) is a limit ordinal (or 0) we let \(\alpha ^- = \alpha \). Moreover, in line with our interest in infinite cardinals, we let \(\sup \varnothing = \aleph _0\) (instead of \(\sup \varnothing = 0\)).
Corollary 3.3
For  we have
we have

To calculate \(\chi _{\mathrm{l}}(x,X)\) and \(\chi _{\mathrm{l}}(X)\) for \(x = (x_\alpha )_{\alpha < \mu }\in X\), let

As above we use the convention: \(\mu _0(x) = \mu \) when  . By duality we have the following two results:
. By duality we have the following two results:
Lemma 3.4
For \(x = (x_\alpha )_{\alpha < \mu }\in X\) we have

Also, if we let  , we have the following corollary.
, we have the following corollary.
Corollary 3.5
For  we have
we have

Using Lemmas 3.2 and 3.4 we can calculate \(\chi (x,X)\) by the formula

Finally, by Corollaries 3.3 and 3.5 and the formula  , we have the following result for the character of a lexicographic product.
, we have the following result for the character of a lexicographic product.
Theorem 3.6
If  , then
, then

where  .
.
Remark 3.7
A particular case of Theorem 3.6 is when \(\delta = \mu _0 = \mu _1\), then

Example 3.8
Let us look at the following examples.
-
1.
Suppose
 for all \(\alpha < \omega _1\) and let
for all \(\alpha < \omega _1\) and let  . Then \(\chi (X) = \aleph _2\).
. Then \(\chi (X) = \aleph _2\). -
2.
Suppose
 for all \(\alpha < \omega _1\) and let
for all \(\alpha < \omega _1\) and let  . Then \(\chi (X) = \aleph _1\).
. Then \(\chi (X) = \aleph _1\). -
3.
Let
 and
and 
If
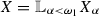 , where \(X_\alpha = Y\) for all \(\alpha <\omega _0\) and \(X_\alpha = Z\) for all \(\omega _0\leqslant \alpha <\omega _1\), then \(\chi (X) = \aleph _1\). However if,
, where \(X_\alpha = Y\) for all \(\alpha <\omega _0\) and \(X_\alpha = Z\) for all \(\omega _0\leqslant \alpha <\omega _1\), then \(\chi (X) = \aleph _1\). However if,  , where \(X_\alpha = Y\) for all \(\alpha \leqslant \omega _0\) and \(X_\alpha = Z\) for all \(\omega _0<\alpha <\omega _1\), then \(\chi (X) = \aleph _2\).
, where \(X_\alpha = Y\) for all \(\alpha \leqslant \omega _0\) and \(X_\alpha = Z\) for all \(\omega _0<\alpha <\omega _1\), then \(\chi (X) = \aleph _2\). -
4.
Let
 for all \(\alpha < \omega _\omega \), \(\alpha \ne \omega _n\) for all \(n < \omega _0\), and
for all \(\alpha < \omega _\omega \), \(\alpha \ne \omega _n\) for all \(n < \omega _0\), and  for all \(\alpha < \omega _\omega \), \(\alpha = \omega _n\) for some \(n<\omega _0\). If
for all \(\alpha < \omega _\omega \), \(\alpha = \omega _n\) for some \(n<\omega _0\). If 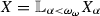 , then
, then  .
.
We end this section by noting that the results of Sect. 2 and of this section give us a way of calculating \(\phi (X)\), where  , \(\mu = \lambda + 1\) is a successor ordinal and \(\phi \) is any of the considered cardinal functions.
, \(\mu = \lambda + 1\) is a successor ordinal and \(\phi \) is any of the considered cardinal functions.
One needs to look into the following four cases to calculate the spread and use Theorems 2.2 and 3.1:
-
(1) \(|X_\lambda |>2\):
 ;
; -
(2a) \(|X_\lambda |=2\), \(\lambda \) is a limit ordinal:
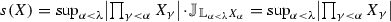 , because
, because ;
; -
(2b) (i) \(|X_\lambda |=2\), \(\lambda = \nu + 1\) with \(|X_\nu |>2\);
-
(2b) (ii) \(|X_\lambda |=2\), \(\lambda = \nu + 1\) with \(|X_\nu |=2\):
In both cases
 .
.In (2b) (ii), in general if \(|X_\nu |\leqslant \aleph _0\), we can simplify to obtain \(s(X) = k(X) = \bigl |\prod _{\alpha < \mu } X_\alpha \bigr |\).
Analogous formulas apply for d(X). If we want to calculate the weight of X we use Theorem 2.4 to conclude

Finally, one uses Proposition 2.5 to calculate the character of X. As above, let \(\mu = \lambda + 1 = \lambda _0 + n\), \(1\leqslant n <\omega _0\), be a successor ordinal, where \(\lambda _0\) is a limit ordinal. Let  and let
and let

Analogously define  . Put
. Put  and \(Z_k = X_{\lambda _0+k}\) for
and \(Z_k = X_{\lambda _0+k}\) for  . Note that \(\chi _{\mathrm{r}}(Z_{-1}),\chi _{\mathrm{l}}(Z_{-1})\) and \(\chi (Z_{-1})\) can be calculated by Corollaries 3.3, 3.5 and Theorem 3.6, respectively. Then
. Note that \(\chi _{\mathrm{r}}(Z_{-1}),\chi _{\mathrm{l}}(Z_{-1})\) and \(\chi (Z_{-1})\) can be calculated by Corollaries 3.3, 3.5 and Theorem 3.6, respectively. Then

Example 3.9
Let us look at a simple example. Suppose  for all \(\alpha < \omega _1\) and let
for all \(\alpha < \omega _1\) and let  .
.
-
1.
Let
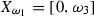 and let
and let  . Then
. Then 
-
2.
Let \(X_{\omega _1} = \{0,1\}\) and let
 . Then
. Then 
References
Buhagiar, D., Chetcuti, E., Weber, H.: \(\kappa \)-compactness, extent and the Lindelöf number in LOTS. Cent. Eur. J. Math. 12(8), 1249–1264 (2014)
Engelking, R.: General Topology, Sigma Series in Pure Mathematics, vol. 6, 2nd edn. Heldermann, Berlin (1989)
Faber, M.J.: Metrizability in Generalized Ordered Spaces. Mathematical Centre Tracts, vol. 53. Mathematisch Centrum, Amsterdam (1974)
Hodel, R.: Cardinal functions I. In: Kunen, K., Vaughan, J. (eds.) Handbook of Set-Theoretic Topology, pp. 1–61. North-Holland, Amsterdam (1984)
Juhász, I.: Cardinal Functions in Topology. Mathematical Centre Tracts, vol. 34. Mathematisch Centrum, Amsterdam (1971)
Juhász, I.: Cardinal Functions in Topology—10 Years Later. Mathematical Centre Tracts, vol. 123. Mathematisch Centrum, Amsterdam (1980)
Lutzer, D.J.: On Generalized Ordered Spaces. Dissertationes Mathematicae, vol. 89. PAN, Warsaw (1971)
Nagata, J.: Modern General Topology. North-Holland Mathematical Library, vol. 33, 2nd edn. North Holland, Amsterdam (1985)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Buhagiar, D., Chetcuti, E. & Weber, H. Some cardinal functions in lexicographic products of LOTS. European Journal of Mathematics 4, 1505–1514 (2018). https://doi.org/10.1007/s40879-017-0198-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0198-5




 ,
,  ,
,  and
and  .
. .
. . Then
. Then  . Analogously,
. Analogously,  . On the other hand, if one takes
. On the other hand, if one takes  , then
, then  .
. . Then
. Then  .
.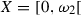 and
and 
 . However, if we take
. However, if we take  and
and  , then
, then  .
. for all
for all  . Then
. Then  for all
for all  . Then
. Then  and
and 
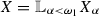 , where
, where  , where
, where  for all
for all  for all
for all 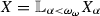 , then
, then  .
. ;
;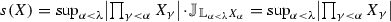 , because
, because ;
; .
.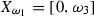 and let
and let  . Then
. Then 
 . Then
. Then 