Introduction

Recent experiments on magnesium (Mg) alloys assert the interacting effects of microstructure and stress state on their macroscopic strength and damage tolerance. Together with high resolution computational modeling and simulation, a quantitative understanding of the underlying micromechanisms is beginning to emerge [14]. One consistent feature as evidenced from multiaxial experiments and modeling is the importance of texture and intrinsic crystallographic plastic anisotropy in their uniaxial and multiaxial responses [1, 3, 6, 11, 23, 27].

Another important effect is the role of loading rate on the macroscopic response of Mg alloys. A number of experimental reports on assessing the rate-dependent behaviors of different Mg alloys have emerged. The reader is referred to the succinct review by Prasad et al. [15]. Key takeaways are: (i) Mg alloys loaded along a direction that causes profuse extension twinning exhibit a lower rate sensitivity of the flow stress compared to the directions along which slip mechanisms dominate the flow stress, (ii) deformation localizes into multiple shear bands, and (iii) texture plays a role on the strain to failure. Experiments conducted at even higher strain rates, \(\sim 10^{4}\) s\(^{-1}\) (using miniaturized Kolsky bar apparatus [8]) and \(\sim 10^{5}\) s\(^{-1}\) (plate impact experiments [28, 31]) assert this assessment by Prasad et al. [15] but also provide deeper insight into the deformation and failure mechanisms as a function of the loading state and initial microstructural details (e.g. texture). For instance, the compressive strain-to-failure (defined empirically as the critical strain beyond which a persistent stress decrease occurs), which is driven by shear localization, increases with increasing strain rate regardless of the loading direction. In comparison, at slower strain rates (\(\sim 10^{-3}\) s\(^{-1}\)) the failure strain is anisotropic with a consistently higher value for specimens loaded along the directions that promote extension twinning [15, 18].

Yet another aspect that has been of interest is the temperature rise at dynamic rates of loading. To that end, we refer to the detailed experiments on AZ31 Mg alloys [5, 10]. Their careful analysis reveals that the average temperature rise even at very high rates of loading (\(\sim 10^{5}\) s\(^{-1}\)) may be modest—on the order of 15–50 \(^\circ\)C (also see [31]). In other words, thermal effects on the material strength may be small at least under the assumption of homogeneous deformations. Shear bands may result in a much larger local temperature rise, which can then affect the strength and activity of the deformation mechanisms [10].

These and similar works provide useful insight into the high rate behavior of Mg alloys under compressive deformation states. In comparison, investigations on Mg alloys under dynamic tensile deformation states are scant [26, 29], although they may set more stringent conditions from the viewpoint of ultimate failure limits. Moreover, the state of stress is nominally uniaxial in most cases (save for the plate impact experiments [28, 31] and the shear-compression experiments [5]). A detailed investigation of the role of stress triaxiality (\({\mathcal {T}} = \Sigma _{{\text {m}}}/ \Sigma _{{\text {eq}}}\) where \(\Sigma _{\text{m}}\) is the macroscopic hydrostatic stress and \(\Sigma _{{\text {eq}}}\) the von Mises equivalent stress) and its interaction with the mechanism-based plastic anisotropy is particularly important to Mg alloys because of the implications on failure [9, 16, 17, 24], let alone when the applied strain rate becomes a factor. Tensile experiments on AZ31 and WE43 notched round bars at slow strain rates (\(\sim 10^{-3}\) s\(^{-1}\)) reveal several discriminating features not commonly observed in ductile metals, which include: (i) shear failure in smooth round bar specimens, and (ii) a non-monotonic dependence of fracture strains on the notch acuity with peak ductility occurring at intermediate values of \({\mathcal {T}}\) [11, 12]. This hints at more complex interactions between texture and failure mechanisms than currently appreciated.

Recent efforts on the rate-dependent uniaxial tensile behavior of rolled Mg alloys [4, 25, 26, 29] indicate that at room temperature both the hardening response and the maximum elongation increase with increasing strain rate along the rolling as well as the in-plane transverse directions, in effect reducing the overall anisotropy in damage that is observed at slow loading rates. Although the material strain rate sensitivity is known to be a stabilizing factor, its coupling with stress triaxiality remains largely unexplored. To our knowledge, only the most recent work by [7] investigates the role of stress triaxiality in the rate-dependent behavior of rolled AZ31 Mg alloys over a range of strain rates, from \(10^{-3} \,{\text {to}} \,10^{4}\) s\(^{-1}.\) Their experiments reveal a qualitative effect on the stress–strain response when the high strain rate is imposed on relatively sharp notched bar specimens. For specimens loaded along the rolling direction at strain rates \(\gtrsim 10^{3}\) s\(^{-1},\) the tensile response switches from a conventional power-law/saturation hardening type to a sigmoidal type, indicating profuse extension twinning. Notably, such a behavior is observed in specimens with a high notch acuity, which suggests an intricate coupling between the stress triaxiality and strain rate. On a broader note, one may posit that there exists a critical combination of strain rate and stress triaxiality which effects a fundamental switch in the dominant deformation mechanism. Granted this postulate, it then becomes imperative to investigate the strain rate–notch acuity combinations that bring about such a qualitative change in the response.

With this in mind, we take a step towards understanding the connections between stress triaxiality and material rate dependence in Mg alloys using a high resolution computational modeling and simulation approach. Recently, we investigated the interplay between the stress triaxiality and intrinsic plastic anisotropy in Mg that revealed complex characteristics of the macroscopic deformation anisotropy and their micromechanical underpinnings in single [19] and polycrystalline [20] notched specimens at a nominal strain rate of \(10^{-3}\) s\(^{-1}.\) Those works clarify the role of the aggregate (intrinsic crystallographic as well as texture-induced) plastic anisotropy in the deformation stability of Mg alloys under triaxial stress states.

Motivated by the experiments of Kale et al. [7], we perform three-dimensional, finite deformation based crystal plasticity finite element simulations over strain rates ranging from \(10^{-3}\) to \(10^{3}\) s\(^{-1}.\) The objective here is to assess the fundamental effect of the material rate sensitivity on the rate-dependent behavior of an Mg alloy under varying levels of induced stress triaxiality conditions. We should note three key limitations of this work: first, it does not consider the effect of material inertia in the rate-dependent response. Second, we ignore the effect of temperature rise on the mechanical response. Third, the framework is based on a damage-free constitutive description and hence, no damage evolution is modeled. With these caveats, the results provide a glimpse of the intrinsic coupling between the strain rate, deformation mechanisms, and the stress triaxiality.

Computational Framework

The crystal plasticity model for hexagonal single crystals developed by [30] and implemented as a User MATerial (UMAT) subroutine in ABAQUS/STANDARD\({\circledR }\) [21] is adopted as the constitutive framework. It comprises 18 slip and 12 twin systems (Table 1).

Table 1 Slip and twin systems considered in this work
Full size table

Crystal Plasticity Formulation

The transversely isotropic elastic response is accounted for by using the following elastic constants (in GPa) [22]: \(C_{11} = 59.4, C_{12} = 25.61, C_{13} = 21.4, C_{33} = 61.6 \ {\text {and}} \ C_{44}= 16.0.\)

The total deformation gradient \({\mathbf {F}}\) is multiplicatively decomposed into elastic \({\mathbf {F}}^{e}\) and plastic \({\mathbf {F}}^{p}\) components, i.e. \({\mathbf {F}} = {\mathbf {F}}^{e}{\mathbf {F}}^{p}.\) The spatial velocity gradient is the sum of an elastic (\({\mathbf {L}}^{e}\)) and a plastic (\({\mathbf {L}}^{p}\)) part

$${\mathbf {L}} = {\dot{{\mathbf {F}}}} {\mathbf {F}}^{-1} = {\mathbf {L}}^{e} + \underbrace{{\mathbf {F}}^{e}{\tilde{{\mathbf {L}}}}^{p}\left( {\mathbf {F}}^{e}\right) ^{-1}}_{{\mathbf {L}}^{p}},$$
(1)

where \({\dot{{\mathbf {F}}}}\) is the material derivative of \({\mathbf {F}}.\) The plastic velocity gradient (\({\mathbf {L}}^{p}\)) is computed in the current configuration as the sum of three parts: slip in the parent region, twin in the parent region

$$\begin{aligned} {\mathbf {L}}^{p}&= {} \underbrace{\left( 1 - \sum _{\beta =1}^{N_{tw}} f^{\beta } \right) \sum _{\alpha = 1}^{N_{s}} {\dot{\gamma }}^{\alpha } ({\mathbf {s}}^{\alpha } \otimes {\mathbf {m}}^{\alpha })}_{\text {slip in parent}} \\&\quad +\underbrace{\sum _{\beta = 1}^{N_{tw}} {\dot{\gamma }}^{\beta } ( {\mathbf {s}}^{\beta } \otimes {\mathbf {m}}^{\beta })}_{\text {twin in parent}}, \end{aligned}$$
(2)

where \(\alpha\) and \(\beta\) respectively refer to slip systems and twin systems in the parent region; the model accounts for \(N_{s} = 18\) slip and \({N}_{tw} = 12\) denote twin systems. The shear rate on the system i is denoted by \({\dot{\gamma }}^{i}\) where \(i = \alpha\) or \(\beta .\) The twin volume fraction of the \(\beta {\text {th}}\) twin system is denoted as \({f}^{\beta }.\) The slip/twin plane normal and direction vector of the \(i{\text {th}}\) system, in the current configuration, are denoted as \(\mathbf{m }^{i}\) and \(\mathbf{s }^{i}\) respectively. Details of the model can be found in [30]; below, we briefly present the constitutive relations.

  1. (1)

    Constitutive equations for slip: The slip rate \({\dot{\gamma }}^{i}\) on the ith slip system is described by a visco-plastic power law:

    $${\dot{\gamma }}^{\alpha} = {\dot{\gamma }}_{0}\left| \frac{\tau ^{\alpha}}{g^{\alpha}}\right| ^{1/m} \ {\text {sign}} (\tau ^{\alpha}) ,$$
    (3)

    where \(\tau ^{\alpha} = {\mathbf {m}}^{\alpha}\cdot {\varvec{\sigma }}\cdot {\mathbf {s}}^{\alpha}\) is the resolved shear stress (RSS) based on the Schmid law and \(g^{\alpha}\) is the current strength of the \(\alpha\text{th}\) slip system. The reference slip rate \({\dot{\gamma }}_0 = 3.0 \ {\text {s}}^{-1}\) and the inverse rate-sensitivity exponent \(1/m = 100.\) \(g^{\alpha}\) is calculated as the sum of the initial strength \(\left( \tau _{0}^{\alpha}\right) ,\) the hardening due to slip–slip \(\left( {\dot{g}}^{\alpha}_{sl{-}sl}\right)\) and twin–slip \(\left( {\dot{g}}^{\alpha}_{tw{-}sl}\right)\) interactions.

    $${g}^{\alpha} = \tau _{0}^{\alpha} + \int _{t_{\circ }}^{t_{i}} ({\dot{g}}^{\alpha}_{sl{-}sl} + {\dot{g}}^{\alpha}_{tw{-}sl})\,{\text {d}}t,$$
    (4)

    where \({\dot{g}}^{\alpha}_{sl{-}sl}\) is given by

    $${\dot{g}}^{\alpha}_{sl{-}sl} = \displaystyle \sum \limits _{j=1}^{N_{s}} h_{ij}(\bar{\gamma }){\dot{\gamma }}^{j}$$
    (5)

    with \(h_{ij}\) the hardening moduli for self (\(i = j\)) and latent (\(i \ne j\)) hardening. \(h_{ij}\) depends on the total accumulated shear strain (\({\bar{\gamma }}\)) on all slip systems, i.e. \({\bar{\gamma }} = \displaystyle \sum \nolimits _{i=1}^{N_{s}} \smallint _{t_{0}}^{t_{i}} {\dot{\gamma }}^{i} {\text {d}}t\) and \(h_{ij}\) is

    $$h_{ij} ={\left\{ \begin{array}{ll} h({\bar{\gamma }}) &{} (i=j), \\ qh({\bar{\gamma }}) &{} (i \ne j). \end{array}\right. }$$
    (6)

    For simplicity, we set \(q = 1.\) The basal and non-basal slip systems harden as follows:

    $$h({\bar{\gamma }}) = {\left\{ \begin{array}{ll} h_{0}, &{} ({\text {basal slip}}), \\ h_{0}^{i} {\text {sech}}^{2}\left| \frac{h_{0}^{i}\bar{\gamma }}{\tau ^{\text {i}}_{s}-\tau ^{\text {i}}_0}\right| , &{} ({\text {non-basal slip}}), \end{array}\right. }$$
    (7)

    where \(h_{0}^{i}\) is the initial hardening modulus and \(\tau ^{i}_{s}\) the saturation stress of the \(i{{\text {th}}}\) slip system.

  2. (2)

    Constitutive equations for twinning: The extension (ET) and contraction (CT) twin volume fraction rates in the parent region are given by

    $${\dot{f}}^{\beta } ={\left\{ \begin{array}{ll} {\dot{f}}^{0}_{et}\left( \frac{\tau ^{\beta }}{s^{\beta }_{et}}\right) ^{1/m_{t}}, &{} ({\text {ET}}), \\ {\dot{f}}^{0}_{ct}\left( \frac{\tau ^{\beta }}{s^{\beta }_{ct}}\right) ^{1/m_{t}}, &{} ({\text {CT}}), \end{array}\right. }$$
    (8)

    where \(\tau ^{\beta }\) is the RSS and \(s^{\beta }\) is the current strength of the \(\beta\text{th}\) twin system. The average reference twin volume fraction rates of ET and CT are \({\dot{f}}^{0}_{et} = 3.0 \ {\text {s}}^{-1}\) and \({\dot{f}}^{0}_{ct} = 0.3 \ {\text {s}}^{-1}.\) The rate-sensitivity exponent \(1/m_{t} = 100\) for both, ET and CT systems. The rate of plastic shear \({\dot{\gamma }}^{\beta }\) on \(\beta {{\text {th}}}\) twin system is related to \({\dot{f}}^{\beta }\) via

    $${\dot{\gamma }}^{\beta } = {\dot{f}}^{\beta }\gamma ^{tw},$$
    (9)

    where \(\gamma ^{tw}\) is the theoretical twinning shear. For Mg, \(\gamma ^{tw} = 0.129 {\text { and }} 0.138\) for ET and CT respectively. \({s}^{\beta }\) is calculated as the sum of the initial CRSS \(\left( \tau _{0}^{\beta }\right) ,\) the hardening due to twin–twin \({\dot{s}}^{\beta }_{tw{-}tw}\) and slip–twin \({\dot{s}}^{\beta }_{sl{-}tw}\) interactions.

    $$s^{\beta } = \tau _{0}^{\beta } + \int _{t_{\circ }}^{t_{i}} \left( {\dot{s}}^{\beta }_{tw{-}tw} + {\dot{s}}^{\beta }_{sl{-}tw}\right) \,{\text {d}}t.$$
    (10)

    The extension twin systems are assumed to follow a saturation type hardening due to twin–twin interaction

    $${\dot{s}}^{\beta }_{tw{-}tw} = h_{\text {et}}^{\beta } {\text {sech}}^{2}\left| \frac{h_{\text {et}}^{\beta }{\bar{\gamma }}_{et}}{\tau ^{\beta }_{s\_et}-\tau ^{\beta }_{0\_et}}\right| {\dot{\gamma }}^{\beta },$$
    (11)

    where \(h_{et}^{\beta }\) is the initial hardening modulus and \(\tau ^{\beta }_{s\_et}\) is the saturation stress for ET. \(\bar{\gamma }_{et}\) is the total shear strain on all ET systems. The hardening of contraction twinning systems is given by

    $${\dot{s}}^{\beta }_{tw{-}tw} = H_{ct} \left( \displaystyle \sum \limits _{m=1}^{N_{ct}} f^{m}\right) ^{b} \ {\dot{\gamma }}^{\beta },$$
    (12)

    where \(N_{ct}\) is the total number of CT systems. \(H_{ct}\) and b are hardening parameters for CT. We assume \({\dot{s}}^{\beta}_{sl{-}tw} = 0\) while \({\dot{g}}^{\beta}_{tw{-}sl}\) in Eq. (4) is given by

    $${\dot{g}}^{\beta }_{tw-sl} = {\left\{ \begin{array}{ll} h_{et\_sl}^{\beta } {\text {sech}}^{2}\left| \frac{h_{et\_sl}^{\beta }{\bar{\gamma }}_{et}}{\tau ^{\beta }_{s\_et}-\tau ^{\beta }_{\circ \_et}}\right| {\dot{\gamma }}^{\beta }, &{} ({\text {ET}}),\\ 0.5H_{ct\_sl} ({\bar{\gamma }}_{ct})^{-0.5}{\dot{\gamma }}_{ct}, &{} ({\text {CT}}). \end{array}\right. }$$
    (13)

For a particular twin mode, when the total twin v.f. on all its twin systems reaches a critical value \(f_{{\text {cr}}}\) (set equal to 0.9) the finite element (FE) volume represented by a Gauss point (GP) is reoriented from its original orientation to the twinned one; the twin system that possesses the largest twin v.f. is chosen as the orientation of the twinned lattice. See Ref. [30] for details.

Simulation Set-Up

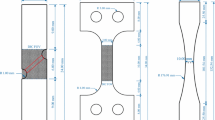
Figure 1a–c depicts typical meshes used in the calculations for the smooth and notched specimens. These are the same geometries adopted in our recent work [20], which mimic the experimental protocol of Kondori and Benzerga [11], which considers rolled AZ31 alloy. The round notched specimens are identified by \({\text {RN}}\mathsf{{x}}\) with \(\mathsf{{x}} = 10{\text {R}}/{\textsf {D}}_{0}\) where \({\text {R}}\) is the notch radius. The rolled plate, from which the specimens are extracted, is defined by three principal directions: transverse \(\left( {\textsf {T}}\right) ,\) rolling \(\left( {\textsf {L}}\right)\) and normal \(\left( {\textsf {S}}\right)\). In our simulations, these directions are aligned with the global \({\textsf {X}},\) \({\textsf {Y}}\) and \({\textsf {Z}}\) axes, respectively. All specimens are loaded in tension along \({\textsf {L}}\) (the global \({\textsf {Y}}\) axis) with a constant velocity \(v_{0}\) applied at the top surface of the specimen keeping the bottom surface fixed along \({\textsf {Y}}\) with sufficient constraints to suppress rigid body motion. The constant nominal strain rate \({\dot{\bar{\varepsilon }}} = v_{0}/L_{0},\) where \(v_{0}\) is the prescribed velocity and \(L_{0}\) is the length of the specimen. Three cases are considered \({\dot{{\bar{\varepsilon }}}} = 1 \times 10^{-3}, 1 \times 10^{1}\) and \(1 \times 10^{3}\) s\(^{-1}.\)

Fig. 1
figure 1

Finite element rendering of smooth and notched round bar geometries. \({\textsf {D}}_{{\text {c}}} = 7\) mm, \({\textsf {D}}_{0}=3.9\) mm

Full size image

For details on creating the polycrystal geometries and their finite element rendering the reader is referred to Ref. [19] together with the mesh sensitivity analysis at slow strain rate. Here we provide a brief outline. For a given geometry (smooth or notched), a grain is defined by grouping a fixed number of elements and assigning a unique crystallographic orientation to that element group. For the smooth specimen, the entire volume is divided into several grains whereas for the notched specimens, only the notch volume is considered for the polycrystalline representation while the remaining region is assigned a fixed single crystal orientation. The number of elements that constitute a grain is different for different specimens; however, the total number of grains \(N_{g}\) in each specimen is kept approximately the same so that a systematic comparison can be made for a family of smooth and notched specimens with the same initial texture (Table 2).

Table 2 Details of polycrystal geometry and finite element mesh density per grain
Full size table

Each grain is defined by an Euler angle set \(\{E\} = \{\varphi _{1},\Phi ,\varphi _{2}\},\) comprising the Euler rotation angles associated with that grain. In a single crystal setting, the \([10{\bar{1}}0]\) and [0001] directions of a grain are aligned with the global \(\mathsf{{X}}\) and \(\mathsf{{Z}}\) directions, respectively. Subsequently, each grain is rotated following the Bunge rotation scheme, which determines its actual orientation with reference to the material principal directions (cf. Table 3). Given \(N_{g}\) grains in a specimen, the required \(N_{g}\) Euler angle sets are generated assuming normal distributions of the Euler angles (with mean value equal to zero) and defining their standard deviations \(\{ E^{\sigma }\} = \{\varphi _{1}^{\sigma }, \Phi ^{\sigma }, \varphi _{2}^{\sigma }\}.\) From the three distributions, an Euler angle set is formed by randomly picking \(\varphi _{1}, \Phi\) and \(\varphi _{2}\) from the distributions with \(- 3\varphi _1^\sigma \le \varphi _1 \le 3\varphi _1^\sigma ,\) \(- 3\Phi ^\sigma \le \Phi \le 3\Phi ^\sigma\) and \(- 3\varphi _2^\sigma \le \varphi _2 \le 3\varphi _2^\sigma ,\) respectively. The so-generated texture is represented as a pole figure plotted using the open source package MTEX [2]. The stress state at a material point (denoted by a position vector \({\varvec{x}}\)) is characterized by the local stress triaxiality, \({\mathcal {T}} ({\varvec{x}})=\sigma _{h} ({\varvec{x}}) /\sigma _{e} ({\varvec{x}})\) where \(\sigma _h ({\varvec{x}})\) is the local hydrostatic stress and \(\sigma _{e} ({\varvec{x}})\) the local von Mises equivalent stress.

Table 3 Effect of Euler rotations on the final orientation of the of the grain
Full size table

The effect of initial texture, stress triaxiality and crystallographic plastic anisotropy on the following macroscopic quantities will be of interest in the remainder of the paper; first, the normalized load is given by \(\left( {F}/A_{0}\right) ,\) where F is the total force along the loading direction and \(A_{0}\) is the initial cross sectional area at the notch root. Second, the deformation anisotropy ratio which is a useful metric to quantify the macroscopic anisotropy. For loading along \({\textsf {L}},\) the anisotropy ratio \({\textsf {R}_{\textsf {L}}}\) is defined as the ratio of the diametric strain along \({\textsf {T}}\) to the diametric strain along \({\textsf {S}};\) i.e. \({\textsf {R}_{\textsf {L}}}= {\varepsilon _{\textsf {T}}}/{\varepsilon _{\textsf {S}}}\) where \(\varepsilon _{\alpha } = \ln \left( {\textsf {D}}_{\alpha }/{\textsf {D}}_{0}\right)\) in the direction \(\alpha ;\) \({\textsf {D}}_{\alpha }\) is the current characteristic specimen diameter and \({\textsf {D}}_{0}\) is the initial characteristic diameter. In addition to these macroscopic quantities, we also highlight the role of initial texture and stress state in determining the deformation micromechanics and texture evolution. The following macroscopic quantities will also be used in the paper: the normalized diametric reduction \(\left( \delta _{\alpha } = {\Delta {\textsf {D}}_{\alpha }}/{{\textsf {D}}_{0}}\right)\) where \(\Delta {\textsf {D}}_{\alpha }\) is the reduction in diameter along direction \(\alpha\) (where \(\alpha = {\textsf {T} }\ {\text {or}}\ {\textsf { S}}\)) and the total areal strain \(\varepsilon _{\textsf {A}} = \varepsilon _{\textsf {S}} + \varepsilon _{\textsf {T}}.\)

The material parameters identified in Eqs. (3)–(13) are given in Table 4 and are representative of an AZ31 Mg alloy [20].

Table 4 Material parameters for Mg alloy
Full size table

Results

For simplicity, results are presented only for a single texture case \(\{E\} = \{\varphi _{1},\Phi ,\varphi _{2}\} = \{10,0,0\},\) which mimics a polycrystalline material with an extremely strong texture close to a single crystal. A more detailed analysis will be presented in a follow-up paper.

Figure 2a and b respectively show the initial \(\left( 10{\bar{1}}0\right)\) and \(\left( 0001\right)\) pole figures for the polycrystal texture considered in this work (\(\{ E^{\sigma }\} = \{10^{\circ }, 0^{\circ }, 0^{\circ }\}\)). For reference, Fig. 2c shows the \(\left( 10{\bar{1}}0\right)\) pole figure for a single crystal. For the polycrystal and single crystal, Fig. 2b is the \(\left( 0001\right)\) pole figure. Note that the \(\left( 0001\right)\) intensity in both cases is unchanged for the chosen \(\{ E^{\sigma }\}.\) On the other hand, the \(\left( 10{\bar{1}}0\right)\) peak intensity of the textured polycrystal (Fig. 2a) is somewhat lower than that of the single crystal (Fig. 2c). In other words, increasing \(\varphi _{1}^{\sigma }\) causes increased spread of \([10{\bar{1}}0]\) of the grains away from \({\textsf {T}}\) in the plane of the sheet while the \(\left( 0001\right)\) pole figures do not change because the rotation is about the [0001] axis of the grains. Such a polycrystalline microstructure roughly resembles a strongly textured material produced by severe plastic deformation, for example, rolling.

Fig. 2
figure 2

Panel a shows the \([10\bar{1}0]\) pole figure of the polycrystal considered in this work. Panel b is the corresponding \([10\bar{1}0]\) pole figure, which also represents a single crystal. Panel c shows the reference \(\left[ 10\bar10\right]\) pole figure for a single crystal \((\varphi_{1}^{\sigma } = \Phi ^{\sigma } = \varphi_{2}^{\sigma } = 0^{\circ })\). Results for the single crystal case are not presented in this work

Full size image

Overall Load–Deformation Response

Figure 3 shows the load versus diametric reduction for the each specimen over six decades of strain rates. Several salient features are observed in the rate-sensitive responses. For smooth specimens the responses are anisotropic at all three rates but the deformation anisotropy is much stronger for \({\dot{{\bar{\varepsilon }}}=10^{-3} \ {\text{s}}^{-1}}\) and \({\dot{{\bar{\varepsilon }}}=10^{1} \ {\text{s}}^{-1}}.\) This is a direct consequence of the deformation anisotropy along the two principal directions \(\textsf{T}\) and \(\textsf{S}\). For instance, at \({\dot{{\bar{\varepsilon }}}=10^{-3} \ {\text{s}}^{-1}},\) \(\delta _{{\textsf{T}}} = 0.038\) and \(\delta _{{\textsf{S}}} \sim 0.0027\) at the peak load \((F/A_{0})_{{\text {peak}}} = 214\) MPa. Similar situation exists for the \({\dot{{\bar{\varepsilon }}}=10^{1} \ {\text{s}}^{-1}}\) case. In comparison, the deformation anisotropy is somewhat tempered at \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}}.\) The precipitous softening is a result of strain localization, which persists over the entire range of strain rates considered here. The strain localization phenomenon at quasi-static strain rate was previously reported by [19].

In comparison, both notched specimens show a tempered response anisotropy, and this improves with increasing notch acuity. In other words, for a given \({\dot{{\bar{\varepsilon }}}}\) the response is less anisotropic for RN2 compared to the RN10 specimen. On the other hand, for a given notch acuity (say RN10), the response is more anisotropic at a higher \({\dot{{\bar{\varepsilon }}}}.\) Interestingly, higher strain rates exhibit a more stable load–deformation response in both notched bars, which alludes to the coupling between the stress triaxiality and strain rate.

Fig. 3
figure 3

Normalized load vs normalized diametric reduction responses for a Smooth, b RN10, and c RN2 specimens as a function of the nominal strain rate (\({\dot{{\bar{\varepsilon }}}}\))

Full size image

Figure 4 shows the normalized load at a nominal axial strain (\(\varepsilon _{{\text {nom}}}\)) of about 0.02 as a function of the nominal applied strain rate. As seen, the apparent rate sensitivity is higher for the RN10 and RN2 specimens compared to the smooth specimen, which quantifies the coupling between the stress triaxiality and the material rate dependence.

Fig. 4
figure 4

Rate-dependence of normalized load (\(F/A_{0}\))

Full size image

Deformation Anisotropy

Figure 5a–c show the variation of \({\textsf {R}_{\textsf {L}}}= \varepsilon _{{\textsf {T}}}/\varepsilon _{{\textsf {S}}}\) for different specimens as a function of imposed strain rate. For the single crystal case, \({\textsf {R}_{\textsf {L}}}\) is not unity and varies with triaxiality at quasi-static loading rates; see [19] for more details. On that backdrop, we observe several interesting features arising from the coupling between the stress-triaxiality effect and the strain rate. First, for a fixed strain rate the deformation anisotropy decreases with increasing notch acuity. This observation is consistent with the previous results based on quasi-static strain rates [11, 19, 20]. In the smooth specimen, \({\textsf {R}_{\textsf {L}}}> 1,\) which means \(\varepsilon _{{\textsf {T}}} > \varepsilon _{{\textsf {S}}}.\) The lateral deformation of the bar is highly anisotropic (\({\textsf {R}_{\textsf {L}}}\gg 1\)) at \({\dot{{\bar{\varepsilon }}}=10^{-3} \ {\text{s}}^{-1}}\) and \({\dot{{\bar{\varepsilon }}}=10^{1} \ {\text{s}}^{-1}}\) and it continues to increase with increasing deformation. However, when the same bar is subjected to \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}},\) the deformation anisotropy is nearly an order of magnitude smaller and exhibits much slower increase, although it still is greater than unity. In RN10 and RN2 specimens, the rate-dependence is reversed. The deformation anisotropy is higher at \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}}.\) In RN10, \({\textsf {R}_{\textsf {L}}}> 1\) but is non-monotonic with the strain rate such that for a fixed \(\varepsilon _{{\text {A}}},\) \({\textsf {R}_{\textsf {L}}}|_{{\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}}}> {\textsf {R}_{\textsf {L}}}|_{{\dot{{\bar{\varepsilon }}}=10^{-3} \ {\text{s}}^{-1}}}> {\textsf {R}_{\textsf {L}}}|_{{\dot{{\bar{\varepsilon }}}=10^{1} \ {\text{s}}^{-1}}}.\) On the other hand, in the RN2 case, \({\textsf {R}_{\textsf {L}}}|_{{\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}}} > {\textsf {R}_{\textsf {L}}}|_{{\dot{{\bar{\varepsilon }}}=10^{-3} \ {\text{s}}^{-1}}} \approx {\textsf {R}_{\textsf {L}}}|_{{\dot{{\bar{\varepsilon }}}=10^{1} \ {\text{s}}^{-1}}}.\) For \({\dot{{\bar{\varepsilon }}}}\le 10 \ {\text {s}}^{-1},\) \({\textsf {R}_{\textsf {L}}}\) rapidly decreases from a value much greater than unity to \({\textsf {R}_{\textsf {L}}}< 1\) in the regime \(\varepsilon _{{\text {A}}} \lesssim 0.03,\) which signifies \(\varepsilon _{{\textsf {T}}} < \varepsilon _{{\textsf {S}}}.\) This behavior is qualitatively distinct from the smooth and RN10 specimens subjected the same strain rates.

Fig. 5
figure 5

Rate-dependent variation of \({\textsf {R}_{\textsf {L}}}\) in a Smooth, b RN10, and c RN2 specimens. Note the remarkably high deformation anisotropy in case of the smooth specimens subjected to relatively slower rates of loading

Full size image

Deformation Micromechanics

The micromechanics that drives the observed dependence of \({\textsf {R}_{\textsf {L}}}\) on initial texture and triaxiality can be understood by studying the underlying deformation mechanisms. The relative activity \(\left( {\overline{\zeta }}^{\alpha }\right)\) is a useful measure to quantify the relative magnitude of rate of strain accrual on one slip/twin system compared to the others. Thus, for each slip/twin system

$${\overline{\zeta }}^{\alpha } = \frac{\displaystyle \sum \nolimits _{i=1}^{N_{{\text {gp}}}} \Delta \gamma ^{\alpha }_{i} \Omega _{i}}{\displaystyle \sum \nolimits _{i=1}^{N_{{\text {gp}}}} \Delta \Gamma _{i} \Omega _{i}}.$$
(14)

Equation (14) quantifies the relative amount of strain accommodated on various slip/twin systems. Here \(N_{{\text {gp}}}\) is the total number of Gauss points in the volume over which averaging is performed, \(\Omega _{{\text {i}}}\) is the FE volume represented by ith Gauss point, \(\Delta \gamma ^{\alpha }_{{\text {i}}}\) is the increment in plastic strain on the \(\alpha {{\text {th}}}\) system and \(\Delta \Gamma _{i} = \sum _{\alpha = 1}^{N} \Delta \gamma _{i}^{\alpha }\) is the increment in the cumulative plastic strain on all \(N = N_{{\text {s}}} + N_{{\text {tw}}}\) deformation systems at that Gauss point. For the smooth specimen, volume averaging is performed over the entire sample whereas for the notched specimens it is performed over the notch volume.

As seen in Fig. 6a–c, prismatic \(\langle a \rangle\) slip dominates the response of the smooth specimen over the range of applied strain rates. At \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}},\) pyramidal \(\langle a \rangle\) and pyramidal \(\langle c+a \rangle\) slip modes emerge as second most important deformation mechanisms indicating the effect of strain rate. At \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}}\) some contraction twinning (CT) is observed although its relative importance decreases as pyramidal \(\langle c + a \rangle\) slip becomes more prominent.

Fig. 6
figure 6

Rate-dependent evolution of averaged relative deformation activity \({\bar{\zeta }}\) in Smooth (a–c), RN10 (d–f), and RN2 (g–i) specimens

Full size image

In notched specimens, the deformation landscape is richer. In RN10 specimens (Fig. 6d–f), the profuse basal slip occurs at yield but quickly recedes paving the way to the prismatic slip. This behavior is observed across all three strain rates. While the prismatic slip remains the primary mechanism, pyramidal \(\langle c + a \rangle\) slip also plays a role while the pyramidal \(\langle a \rangle\) slip plays a tertiary role especially at \({\dot{{\bar{\varepsilon }}}=10^{-3} \ {\text{s}}^{-1}}\) and \({\dot{{\bar{\varepsilon }}}=10^{1} \ {\text{s}}^{-1}}.\) In RN2 specimens (Fig. 6g–i), basal slip remains active over the entire deformation range shown with a stronger presence at slower strain rates. At \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}}\), the CT activity is much tempered in the notched specimens compared to the smooth specimen at the same rate of loading. In all three specimens, the extension twinning (ET) activity remains relatively insignificant across the range of strain rates. This result indicates that for a strongly textured material (closer to a single crystal) the imposed rate does not play a major role in the extension twinning activity.

Distribution of Stress Triaxiality

Figures 7 and 8 show the distribution of stress triaxiality [\({\mathcal {T}}({\varvec{x}})\)] at \(\varepsilon _{{\text {A}}} = 0.05\) along the L–T and L–S planes over the range of strain rates. Note that the sections are taken at the mid-planes and may cut through the grains non-uniformly, which manifests as patchy contour plots. Nevertheless, these distributions give a reasonable idea of the specimen response. The peak stress triaxiality in RN10 specimens is \(\sim 0.70.\) For \({\dot{{\bar{\varepsilon }}}=10^{-3} \ {\text{s}}^{-1}}\) and \({\dot{{\bar{\varepsilon }}}=10^{1} \ {\text{s}}^{-1}},\) the high triaxiality region is in the central portion of the notch whereas at \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}}\) the high triaxiality region is closer to the notch root. In RN2 specimens, the peak stress triaxiality is \(\sim 1\) and appears to be located in the central region of the notch. For the latter case, the region of high triaxiality is rather diffuse at \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}},\) in contrast to those at slower rates.

Fig. 7
figure 7

Distribution of stress triaxiality \({\mathcal {T}}({\varvec{x}})\) in RN10 specimens at \(\varepsilon _{\textsf {A}}=0.05\)

Full size image
Fig. 8
figure 8

Distribution of stress triaxiality \({\mathcal {T}}({\varvec{x}})\) in RN2 specimens at \(\varepsilon _{\textsf {A}}= 0.05\)

Full size image

Discussion

The work reported here is motivated by the experiments of Kale et al. [7], however no attempt is made to quantitatively compare the present results with their experiments. Such an exercise requires an elaborate calibration of the basic material parameters as a function of strain rate, which is beyond the scope of this work. One of the interesting results in the experiments is the sigmoidal response for small notched specimens subjected to \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}},\) which alludes to the significant extension twinning. On that backdrop, the present simulations do not reveal such a characteristic in any of the notched specimens at the same strain rate. It is noted that there may be several variables at play. First, the notch acuity and therefore, the nominal stress triaxiality, is different in the two scenarios. According to their calculations [7], the estimated nominal stress triaxiality is \({\mathcal {T}}_{{\text {nom}}} \sim 1.68\) in the small-notched bars. In comparison, our results indicate that the RN2 specimen induces \({\mathcal {T}}_{{\text {nom}}} \sim 1,\) which is in fact closer to the large-notched bar of Kale et al. [7] that does not exhibit a sigmoidal behavior, consistent with the present observation. Second, texture is expected to play a role in the activation of twinning. Our preliminary analysis indicates that a texture somewhat (\(\sim 20\%\)) weaker than the one adopted in this work does exhibit sufficient extension twinning to render a sigmoidal response in RN2 specimens at high strain rates.

We note here that there are two non-dimensional groups involving both, loading and material parameters [13]

$$\frac{{L_{0} }}{{L_{c} }} = \frac{{v_{0} }}{{c_{0} }}\;{\mkern 1mu} ;{\mkern 1mu} \;\kappa = \frac{{v_{0} /L_{0} }}{{\dot{\varepsilon }_{0} }},$$
(15)

where \(v_{0}\) is the magnitude of the imposed velocity, \(L_{c} = c_{0}/(v_{0}/L_{0})\) the reference length, and \(L_{0}\) the specimen length. The first ratio is a measure of the effect of material inertia while the second signifies the effect of loading rate, independent of material inertia. In the quasi-static limit \(L_{0}/ L_{c} \rightarrow 0\) so that the material inertia effect vanishes although the role of \(\kappa\) still persists. For polycrystalline Mg alloys, the longitudinal wave speed \(c_{0} \approx 5700\) m/s [31], which gives \(L_{c} \approx 5.7\) m (for the largest strain rate considered here, \(v_{0}/L_{0} = 1000 \ {\text {s}}^{-1}\)) so that \(L_{0}/L_{c} = 40/5700 \approx 0.007.\) Likewise, assuming \({{\dot{\varepsilon }}}_{0} \approx {{\dot{\gamma }}}_{0} = 3.0 \ {\text {s}}^{-1},\) \(\kappa = 1000/3.0 \approx 330.\) For this combination of \(L_{0}/L_{c}\) and \(\kappa ,\) the material inertia is expected to play a negligible role and the response is governed by the material rate sensitivity [13].

Another aspect of interest is the local temperature increase (\(\Delta T\)) at high strain rates due to the plastic work

$$\Delta T ({\varvec{x}}) = \frac{\beta W_{p} ({\varvec{x}})}{\rho C_{p}},$$
(16)

where \(W_{p} ({\varvec{x}}) = {\varvec{\sigma }}({\varvec{x}}):{\varvec{\varepsilon }}_{p}({\varvec{x}})\) is the plastic work density at time t with \({\varvec{\varepsilon }}_{p} ({\varvec{x}})\) being the local plastic strain tensor, and \(\rho = 1730 \ {\text {kg m}}^{-3}\) the mass density, \(C_{p} = 1005 \ {\text {J kg}}^{-1} \ ^{\circ } {\text {C}}^{-1}\) the specific heat [31], and \(\beta \approx 0.8\) the Taylor–Quinney factor [5, 10]. With these parameters, Fig. 9a, b show the temperature distribution at an areal strain \(\varepsilon _{{\text {A}}} = 0.05\) calculated using Eq. (16) for the RN10 and RN2 specimens subjected to \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}}.\) Interestingly, the RN10 specimen shows relatively uniform temperature distribution in the notch region while the RN2 specimen exhibits a stronger temperature gradient with the temperature at the notch root being somewhat higher than that of the notch center. Nevertheless, the corresponding volume averaged temperature increase (\(\Delta T_{{\text {avg}}}\)) is relatively modest. For instance, \(\Delta T_{{\text {avg}}} \approx 9\,^{\circ }\)C in the notched region of RN2 specimen and increases to \(\sim 19\,^{\circ }\)C at \(\varepsilon _{{\text {A}}} = 0.1.\) These numbers corroborate with experimental estimates [8].

Fig. 9
figure 9

Snapshot of temperature distribution [Eq. (16)] in a RN10 and b RN2 specimens subjected to \({\dot{{\bar{\varepsilon }}}=10^{3} \ {\text{s}}^{-1}}\) at \(\varepsilon _{{\text {A}}} = 0.05\)

Full size image

Summary

In this work, we present a crystal plasticity based numerical study of the interaction between the material rate sensitivity and stress triaxiality in polycrystalline Mg alloys. The simulations reveal that for strongly textured Mg alloys, strain localization may occur under nominally uniaxial tensile stress states (smooth specimens), which is tempered at high strain rates due to the stabilizing effect of the material rate sensitivity. The resulting diametrical reduction is anisotropic along the two principal lateral directions and this anisotropy decreases with increasing strain rate. In notched geometries, which induce elevated levels of stress triaxialities, the deformation anisotropy is much lower compared to the smooth specimens over the range of strain rates considered here. In specimens with low notch acuity (RN10) the region of high triaxiality appears to shift from the notch center towards the notch root with increasing strain rate. This may have implications on the nucleation and growth of damage. Interestingly, specimens with a high notch acuity (RN2) do not exhibit such a behavior, which merits further investigation. This preliminary effort is a step towards understanding structure–property linkages in such low symmetry materials with an obvious interest in its effect on their failure mechanics at dynamic loading rates. At least for the cases considered here, the material inertia and temperature rise are sufficiently small so that they may not significantly alter the main conclusions. However, a rigorous analysis should account for these effects, which will be our focus in the near future.