Introduction

Most metallic materials such as steel, copper, and aluminum are categorized as ductile materials. One of the unique properties of ductile materials is the ability to experience large deformation without fracture. Due to this ductility, these metals are capable of undergoing metal-forming and fabrication processes such as rolling, forging, and extrusion. In addition, ductile materials such as steel also exhibit a balanced combination of high Young’s modulus, high yield strength, and high ultimate tensile strength. As such, steel has been widely used in several engineering fields, such as aerospace, building construction, and automotive industry. Some of these applications require the material to survive dynamic loading such as crashes, impact, and blast loading. Therefore, it is often necessary to determine the mechanical properties of ductile materials undergoing large deformation at high strain rates.

The compressive mechanical behavior of steel deforming to large strains at various strain rates has been studied by many researchers. For example, ASTM E9-09 [1] is widely used as a reference for the mechanical properties of steel at low engineering strain rates. Fitzsimons and Kuhn [2] modified the MTS servo controlled machine by adding a capacitor discharge circuit to investigate the material behavior at true strain rates between 10−2 and 102 s−1. Cam plastometer had been employed to deform steel at a constant true strain rate which is extremely difficult to control in a conventional testing machine [3]. However, the highest true strain rate that could be achieved is only around 150 s−1 [3, 4]. The Kolsky bar is used to characterized the material properties at high strain rates (102–105 s−1) [5, 6]. Utilizing a Kolsky bar, the dynamic behavior of steel up to engineering strain rate of approximately 103 s−1 have been obtained by several researchers [7–9]. From these studies, most researchers agree that the compressive yield strength and flow stress increase as the strain rate is increased.

As pointed out by Ramesh and Narashimhan [10], the stress–strain curves obtained from Kolsky bar experiments are usually presented as true stress, true strain, and at nearly constant engineering strain rate. However, when performing numerical simulations for predictions at large deformation, the yield and flow stresses are usually expressed in term of true strain rates instead of engineering strain rates [3, 4]. However, the dynamic behavior of stainless steel deforming at high true strain rates has not been reported. Therefore, it is desired to characterize the behavior of the specimens at constant true strain rates. Hence, the purpose of this study is to present a method to characterize the compressive stress–strain behavior of a 304 stainless steel at high, constant true strain rates using a modified Kolsky bar. The obtained behavior is then contrasted with the behavior of the 304 stainless steel deforming at high, constant engineering strain rates.

Materials and Methods

The ductile specimens utilized in this study were made from a commercially available precision ground 304 stainless-steel rod (diameter = 6.35 mm, length = 0.6 m). The rod was cut into disc-shape specimens with final diameter of 6.35 mm and thickness of 2.8 ± 0.01 mm.

Analytical Model

For an incompressible specimen under uniaxial compression loading with the assumption that compression is taken as positive, the true stress (σ) in the specimen can be calculated from Eq. 1, where S is the engineering stress and e is the engineering strain.

$$\sigma = S(1 - e).$$
(1)

The relationship between true strain (ε) and engineering strain (e) can be calculated from Eq. 2.

$$\varepsilon = - \ln (1 - e).$$
(2)

The true strain rate (\(\dot{\varepsilon }\)) is calculated by taking the time derivative of the expression presented in Eq. 2, and the obtained expression is presented in Eq. 3,

$$\dot{\varepsilon } = \frac{{\dot{e}}}{{1 - e}}.$$
(3)

It should be emphasized that if the strain in the specimens is small, the corresponding true strain rate is nearly equal to the engineering strain rate. In addition, Eq. 3 also shows that at large strains, the specimen could either deform at a constant engineering strain rate or constant true strain rate but not both.

To allow the specimen to deform at a constant true strain rate, it is necessary for the history of true strain rate to be trapezoidal shape as sketched in Fig. 1. The reason is that the specimen requires a finite amount of time to reach the desired true strain rate (D in Fig. 1d), similar to a specimen being deformed in a Kolsky bar at constant engineering strain rate [5, 7]. Mathematically, the expression for a trapezoidal shape pulse is given in Eq. 4.

$$\dot{\varepsilon } = \left\{ {\begin{array}{*{20}c} {\frac{D}{{t_{0} }}t~~~,~~t \le t_{0} } \\ {} \\ {D~~~~~,~~t \ge t_{0} } \\ \end{array} } \right.,$$
(4)

where t 0 is the time to reach a constant true strain rate as shown in Fig. 1d. Substituting Eq. 4 into Eq. 3, an expression for engineering strain is obtained (Eq. 5).

$$e = \left\{ {\begin{array}{*{20}c} {1 - \exp \left( { - \frac{{Dt^{2} }}{{2t_{0} }}} \right)~~~~~~~~~~,~~~t \le t_{0} } \\ {} \\ {~1 - \exp \left[ { - D\left( {t - \frac{{t_{0} }}{2}} \right)} \right]~,~~~t \ge t_{0} } \\ \end{array} } \right..$$
(5)

Finally, the engineering strain rate (Eq. 6) is determined by taking time derivative of Eq. 5

$$\dot{e} = \left\{ {\begin{array}{*{20}c} {\frac{{Dt}}{{t_{0} }}\exp ( - \frac{{Dt^{2} }}{{2t_{0} }})~~~~~~~~~~,~~t \le t_{0} } \\ {} \\ {D\exp \left[ { - D\left( {t - \frac{{t_{0} }}{2}} \right)} \right]~,~~t \ge t_{0} } \\ \end{array} } \right..$$
(6)

The corresponding true strain is obtained by substituting Eq. 5 into Eq. 2. Figure 1 presents the time histories of engineering strain (Eq. 5), engineering strain rate (Eq. 6), and true strain (Eq. 2) required to deform the specimen at a constant true strain rate (Eq. 4). In Fig. 1, D = 2700 s− 1 and t0 = 50 µs, which simulates one of the experiments discussed later.

Fig. 1
figure 1

History of a engineering strain b engineering strain rate c true strain and d true strain rate for a specimen deformed at a constant true strain rate of 2700 s−1

Full size image

Experimental Setup and Procedure

Two different experimental apparatus were used to characterize the behavior of 304 stainless steel at low and high strain rates: an MTS 810 universal testing machine and a Kolsky compression bar with pulse shapers.

For low strain rate experiments, Vaseline acting as the lubricant was applied on both ends of the specimen, the specimen then was sandwiched between compression platens as shown in Fig. 2. In order to compress the specimens at a constant engineering strain rates, the lower platen was set to move at 0.28 and 0.028 mm/s resulting in constant engineering strain rates of 0.1 and 0.01 s−1. To determine the mechanical response at a constant true strain rate, the length of the specimen (L) as a function of time should be deformed according to Eq. 7, where L 0 is the specimen original length [2]. Therefore, the bottom part of the platen was set to move with the displacement history that followed Eq. 7, resulting in the specimen being compressed at a constant true strain rate.

$$L\left( t \right) = L_{0} {\text{exp}}(\dot{\varepsilon }t).$$
(7)
Fig. 2
figure 2

Experiment apparatus to characterize mechanical behavior at low strain rates

Full size image

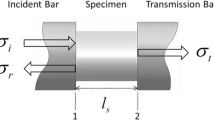
A Kolsky compression bar was employed to characterize the dynamic behavior of the specimen at constant engineering and true strain rates. The Kolsky bar consists of an incident bar, a transmission bar and a momentum trap bar as schematically shown in Fig. 3. All the bars used in this study are maraging steel rods having a common diameter of 19 mm. The specimen was sandwiched between the incident and transmission bars. Similarly, the Vaseline was applied to the specimen ends. A gas gun launched the striker against the incident bar to generate a compressive stress wave. Two pairs of resistance strain gages were attached on the incident and transmission bar surfaces to record the incident (ε I ), reflected (ε R ) and transmitted (ε T ) pulses. These strain gages were connected to Wheatstone bridges. Two differential amplifiers were used to amplified the pulses. An upper bandwidth of 100 KHz was set on the amplifiers to filter and smooth the signals. Utilizing the 1-D wave theory with the assumption that the specimen is in stress equilibrium, the engineering strain rate, engineering strain, and engineering stress can be obtained by using Eq. 8a, b, c, where C b , E b A b and A s are the bar wave speed, bar Young’s modulus, bar cross section area and specimen cross sectional area respectively [5]. Finally, the true stress, true strain and true strain rate are determined by substituting Eq. 8a, b, c into Eqs. 1, 2 and 3, respectively.

$$\dot{e} = - \frac{2 C_b}{L_{0}}\varepsilon _{R} ,$$
(8a)
$$e = \mathop \smallint \nolimits^{} \dot{e}dt,$$
(8b)
$$S = \frac{{A_{b} }}{{A_{S} }}E_{b} \varepsilon _{T} ,$$
(8c)

To deform the specimen at a constant engineering strain rate, the reflected wave should have a plateau region as indicated in Eq. 8a. However, to deform at a constant true strain rate, it is necessary for the reflected pulse to increase in time initially and then have a negative slope afterward as sketched in Fig. 1b. To achieve such a pulse profile for a ductile material, it is essential to employ a pulse shaping technique to generate bi-linear (Fig. 4c) and trapezoidal (Fig. 4d) incident pulses to enable the specimen to deform at constant true strain rates of 600, 2500 and 7000 s−1, respectively [11, 12]. To limit experimental trials, the pulse shaping model developed by Frew et al. [11, 12] was utilized to predict the material and dimensions of the pulse shaper required to generate the desired incident stress wave. The dimensions of the pulse shapers to deform the specimens at nearly constant engineering and true strain rates are summarized in Table 1.

Table 1 Kolsky bar experimental parameters to deform the specimen at constant engineering (Eng.) or true strain rates
Full size table
Fig. 3
figure 3

A Kolsky bar experimental setup

Full size image

Experimental Results

Dynamic compression experiments were performed using the Kolsky bar on the 304 stainless steel specimens at the engineering and true constant strain rates at about 700, 2400, 7000 s−1. For each strain rate, five repeating experiments were conducted. Table 1 summarizes the experimental parameters including striker length, striking velocity, pulse shapers material and dimensions to deform the specimen at constant engineering or true strain rate.

Figure 4 present four sets of the typical experimental outputs obtained from Kolsky bar experiments to deform the specimens at either constant engineering (Fig. 4a, b) or true (Fig. 4c, d) strain rates. The incident (Inc), reflected (Ref) and transmitted (Tra) pulses were plotted in Fig. 4. From these figures, it is verified that the axial forces on the specimens were in equilibrium, since the transmitted pulse is in good agreement with the sum of incident and reflected strain pulse [5].

Fig. 4
figure 4

Typical experimental results obtained from Kolsky bar experiments to deformed specimen at constant engineering (Eng.) or true (True) strain rate at about a Eng. 2080 s−1, b Eng. 6830 s−1, c True 2720 s−1, d True 6700 s−1

Full size image

The strain rate histories for the above four cases are summarized in Fig. 5. It is noted that there are plateau regions in the plots which indicate that the specimens could only deformed at either nearly constant engineering (Fig. 5a, b) or true (Fig. 5c, d) strain rates but not both.

Fig. 5
figure 5

The corresponding strain rate history for specimen that deform at constant engineering (Eng.) or true (True) strain rate at about: a Eng. 2080 s−1, b Eng. 6830 s−1, c True 2720 s−1, d True 6700 s−1

Full size image

In Fig. 6, the flow stress–strain curves at nearly constant engineering and true strain rates are presented [7], the error bars in Fig. 6 represent one standard deviation. This phenomenon is known as strain-rate hardening in ductile metals and has been observed by many researchers [7, 13, 14].

Fig. 6
figure 6

Flow stress strain curves at nearly constant engineering and true strain rates

Full size image

Discussion of Results

In Fig. 6, it is shown that the flow stress–strain curves between constant engineering and true strain rate at similar magnitudes below 3000 s−1 are very close to each other. For example, at about 2400 s−1 strain rate, it was observed that the flow stress at the constant true strain rate of 2720 s−1 nearly overlaps that obtained at constant engineering strain rate of about 2080 s−1. However, the flow stress for the specimens deformed at a constant engineering strain rate of 6830 s−1 shows a clearly difference from that obtained at the true strain rate of 6700 s−1.

One possible explanation for the observed differences in flow stress at higher strain rates is that the average strain rate for a specimen deformed at constant engineering and true strain rates were relatively close at strain rates below 3000 s−1. For example, to deform a specimen at a constant true strain rate at about of 2700 s−1, the average engineering strain rate (average of the decreasing slope in Fig. 5c) that is experienced by the specimen is at about 2200 s−1. As a result, the flow stress for the specimen deformed at a constant engineering strain rate of 2080 s−1 is similar to that specimen deformed at the constant true strain rate of 2720 s−1. However, to deform the specimen at around 6700 s−1 true strain rate, the corresponding engineering strain rate needs to have a much steeper decreasing slope as shown in Fig. 5d, the average engineering strain rate (average of the decreasing slope in Fig. 5d) on the specimen is about 5000 s−1 which is significantly lower than 6830 s−1. As a consequence, the flow stresses for the specimen deformed at 6700 s−1 true strain rate is significantly lower compared to the specimens deformed at 6830 s−1 engineering strain rate.

Material Constitutive Models

We used two material models in an effort to represent these data in an analytical form; namely, Johnson–Cook and Camacho-Ortiz [15, 16]. It should be emphasized that the parameters determined from both models were obtained by curve fitting experimental data at constant engineering and true strain rates from about 0.01 to 7000 s−1. The Johnson–Cook model is expressed in Eq. 9a, b as

$$\sigma = \left[ {A + B\left( {\varepsilon _{{pl}} } \right)^{n} } \right]\left[ {1 + C\ln \dot{\varepsilon }^{*} } \right],$$
(9a)
$$\dot{\varepsilon }^{*} = \left\{ {\begin{array}{*{20}c} {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}~~for~constant~true~strain~rate} \\ {~~~~~~~~~~~~~~\frac{{\dot{e}}}{{\dot{e}_{0} }}~for~constant~engineering~strain~rate} \\ \end{array} } \right..$$
(9b)

For the Johnson–Cook model, the first term represents isotropic hardening where A, B, ε pl and n are equivalent to yield stress, strength coefficient, plastic true strain and strain hardening parameter, respectively. The second term represents the strain rate hardening, where \(\dot{\varepsilon }\) and \(\dot{e}\) are true and engineering strain rates, \(\dot{\varepsilon }_{0}\) and \(\dot{e}_{0}\) are the reference true and engineering strain rates, and C is a fitting parameter [16]. The parameter A was determined from the yield stress at the lowest engineering or true strain rate using a 0.2% offset strain. Parameters B, C and n were determined through curve fitting. The Johnson–Cook parameters obtained from this study are listed in Table 2.

Table 2 Johnson–Cook curve fitting parameters for constant true (True) and engineering (Eng.) strain rate
Full size table

As pointed out by Clausen et al. [14], an issue with Eq. 9a can occur with the logarithmic term if the dimensionless strain rate terms are less than one. To avoid this problem, the second term in Eq. 9a is taken as one for dimensionless strain rates less than one. Thus, for these very low strain rates Eq. 9b is taken as rate-independent.

Like the Johnson–Cook model, the Camacho-Ortiz model has a product form with a strain hardening term and a strain rate term [15]. However, the strain rate term is a power law rather a logarithm term. Thus, the problem with small strain rates is avoided. A slightly modified version of the Camacho-Ortiz material model was used for this study (Eq. 10a, b).

$$\sigma = Y\left( {1 + \frac{{E\varepsilon _{{pl}} }}{Y}} \right)^{n} \left( {1 + \dot{\varepsilon }^{*} } \right)^{C} ,$$
(10a)
$$\dot{\varepsilon }^{*} = \left\{ {\begin{array}{*{20}c} {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}~~for~cons\tan t~true~strain~rate} \\ {~~\frac{{\dot{e}}}{{\dot{e}_{0} }}~for~cons\tan t~engineering~strain~rate} \\ \end{array} } \right.,$$
(10b)

where Y is the yield stress, E is the Young’s modulus, n and C are the curve fitting parameters. Table 3 lists the parameters obtained by curve fitting the average experimental data at different strain rates using Eq. 10a, b. It should be noted that the yield stresses (Y) were obtained by implementing the 0.2% offset strain at the lowest engineering and true strain rates, respectively.

Table 3 Camacho-Ortiz curve fitting parameters for constant true (True) and engineering (Eng.) strain rate
Full size table

The comparison of the flow stress–strain curves obtained from both models with the data obtained from experiments at both constant engineering and true strain rates are presented in Fig. 7. It can be observed that both models are in good agreement with the experimental results.

Fig. 7
figure 7

Comparison between experimental flow stress–strain curves (Exp) with a Johnson–Cook (JC) model at nearly constant true strain rates, b Camacho-Ortiz (CO) model at nearly constant true strain rates, c JC model at nearly constant engineering strain rates and d CO model at nearly constant engineering strain rates

Full size image

Conclusions

Dynamic experiments utilizing a Kolsky bar to characterize the compressive dynamic behavior of 304 stainless steel at high constant engineering and true strain rates are presented and compared in this study. Equations were derived for the engineering strain rate and strain as a function of true strain rate. To deform the specimen at a nearly constant true strain rate, it is necessary for the engineering strain rate to increase in time initially and then have a negative slope afterward. The negative slope becomes much steeper for experiments at high true strain rates. Consequently, to compress a specimen below 3000 s−1 true strain rate, a bi-linear incident pulse was needed. However, to deform a specimen at 7000 s−1 true strain rate, a trapezoidal incident wave was needed. Using these incident pulses, the compressive stress–strain response of 304 stainless steel deformed to large strains at high true strain rates was obtained and compared with the response obtained at constant engineering strain rates. The results indicate that, below a strain rate of 3000 s−1, there is very little difference for the specimens deforming at a particular constant engineering or true strain rate. However, at a high strain rate of 7000 s−1, the flow stress for the specimens deforming at constant engineering strain rate is higher than the stress from a specimen deforming at comparable constant true strain rate. Finally, both the Johnson–Cook and Camacho-Ortiz material models fit the experimental data accurately.