Specimen-Bar Impedance Mismatch Effects on Equilibrium and Rate Constancy for Kolsky Bar Experiments

Abstract

During a Kolsky bar, also known as a split Hopkinson pressure bar (SHPB), experiment, stress equilibrium and strain rate constancy conditions directly contribute to the measurement quality for rate-sensitive materials. A Kolsky bar specimen is initially at rest, and then gradually accelerated to a desired rate. Stress equilibrium is incrementally achieved by multiple stress pulse reflections inside the specimen to reach the desired mean stress. The critical time to achieve constant strain rate and equilibrium stress depends on the impedance mismatch between the bars and the specimen. This paper examined this critical time based on using linear elastic specimens under uniaxial compression. In the first part, the critical time is experimentally measured for PMMA specimens loaded by aluminum, titanium, and steel bars using linear ramp incident pulses. The results show that increasing impedance mismatch increases the time to reach a constant rate, while the time to satisfy equilibrium remains nearly the same. In the second part, optimal bilinear-shaped incident loadings were evaluated and shown to achieve both conditions faster than linear loadings. The time to satisfy both conditions was mapped via simulation using various bilinear pulses over a wide range of impedance mismatches. The analysis shows bilinear loadings with initial rise time between 1.75 and 2.15 transits in the sample require minimum time to equilibrium. There exists an optimum region of bilinear loadings that can reduce the time to reach constant rate. Within such region, the bilinear slope ratio can be approximated to be a reciprocal function of initial rise time.

Introduction

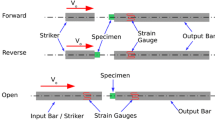
Understanding the mechanical behavior of materials under high-rate loading is essential to model and ensure the integrity of structures subjected to dynamic loading in automotive, aerospace, and civil engineering applications. To acquire accurate material properties, experiments need to be carefully designed and conducted with valid experimental conditions. The Kolsky bar, or split Hopkinson pressure bar (SHPB), originally developed by Kolsky [1], has been widely used by many researchers to characterize material responses for strain rates from 10²/s to 10⁴/s. During a Kolsky bar measurement, a specimen is sandwiched between an incident bar and a transmission bar (schematically shown in Fig. 1). A stress pulse (incident pulse) is applied and propagates from the other end of the incident bar to the specimen. A portion of the incident pulse transmits through the specimen and to the transmission bar and forms the transmitted pulse; and the remainder reflects back in to the incident bar and forms the reflected pulse. The specimen response can then be calculated from the incident, transmitted, and reflected strain pulses based on 1-D wave propagation theory.

Fig. 1

Schematic of specimen-bar interfaces

For a valid Kolsky bar measurement, stress equilibrium must be satisfied. Stress equilibrium implies that the axial stress within the specimen is distributed evenly along the thickness, such that the averaged specimen response can be treated as a point-wise-valid material response. Under stress-pulse loading, the stress inside the specimen is initially unbalanced, and dynamic stress equilibrium is incrementally achieved as the mean stress builds up through wave reflections between the two specimen-bar interfaces [2]. When the Kolsky bar is used to investigate the inelastic behavior of ductile metals, the requirement of stress equilibrium is satisfied fairly rapidly, as compared with the time needed for the entire loading. However, stress equilibrium can be violated when characterizing brittle materials [3] when the specimen may break before equilibrium is achieved, or soft materials [4] when loading may end before equilibrium is achieved. In such cases, Kolsky bar experiments may no longer lead to valid material response measurements.

Furthermore, the specimen needs to be deformed at a nearly constant strain rate to effectively delineate rate dependency of the material behavior. Under dynamic loading, the specimen is initially at rest (zero strain rate) and then deforms gradually to the desired strain rate. Maintaining a constant strain rate during a majority of the experiment duration is essential for rate-effect to be clearly quantified, especially for strain-rate sensitive materials [5]. A rate-dependent constitutive model can then be constructed based on a family of curves at various constant strain rates.

Until stress equilibrium is achieved, the obtained data on the bar is not an accurate representation of the stress in the specimen. Before achieving constant strain rate, the measurement is normally hard to interpret. In an effect to maximize the usability of Kolsky bar data, it is thus desirable to minimize the critical time needed to achieve both conditions on stress equilibrium and strain-rate consistency. This critical time depends on the wave speed of the specimen, the thickness of the specimen, the shape of the incident pulse, and the impedance mismatch between the bars and specimen. For a low-wave-speed material or a thick specimen, the equilibrium process inherently takes longer than for a high-wave-speed material or a thin specimen [4, 6]. This paper studies the impedance mismatch effects. The impedance mismatch is defined as the ratio of the mechanical impedance of the bars to that of the specimen. Loading with a flat-topped incident pulse with a finite rise time, Lee and Park [7] found that a longer rise time creates a better equilibrium condition for soft materials (i.e. a large impedance mismatch), and Zhu et al. [8] reported there exists an optimum rise time for concrete-like materials (a small impedance mismatch). For a brittle material under linear ramp loading, Frew et al. [2] suggested analytically that a larger impedance mismatch leads to faster approach to stress equilibrium, but a slower approach to strain rate constancy.

In this paper, we focus on the effect of impedance mismatch on the time to achieve both stress equilibrium and strain rate constancy in elastic specimens. Linear ramp incident pulses were used by many researchers to characterize elastic or brittle materials [2, 5, 9], due to the ease in obtaining nearly constant strain rates. Such linear loadings outperform trapezoidal loadings for brittle specimens as the former generates a plateau in the reflected pulse, while the latter leads to a triangular reflected pulse where the strain rate is not constant during the entire loading duration. In the first part, such time are measured experimentally under loading by traditional linear ramp incident pulses. To vary the impedance mismatch, three Kolsky bar systems (aluminum, titanium and steel) were used to measure the performance of identical PMMA specimens at an identical strain rate (90/s). Beyond the traditional linear incident ramp loadings, some researchers use inverse methods to iteratively adjust the parameters of the incident pulse for optimum achievement of strain rate constancy [10, 11]. Bi-linear incident loadings were found to be the optimum solution for viscoelastic silicone rubber [10] and work hardening metals [12]. However, the optimized incident loading profiles depend on the properties of the specimen, where the optimizing algorithm needs to run for each type of specimen at each intended strain rate. In the second part, we analyzed bilinear incident loadings for a more general case, trying to provide a guidance for selecting bilinear loadings for brittle specimens without the iterative optimization process. Analytical expressions for equilibrium and strain rate were derived based on 1-D wave propagation theory by tracking the wave propagation history inside an elastic specimen under bilinear loading conditions. Achieving equilibrium and rate constancy were also simulated by a MATLAB program through iterative calculations. The time to reach both conditions was mapped by generating a matrix of bilinear incident pulse shapes with respect to bilinear slope ratio and rise time.

Experimental Study of Linear Incident Loading

Experimental Setup

In this part of our paper, three compressive Kolsky bars were utilized to characterize identical linear-elastic PMMA specimens at an identical strain rate (90/s). Aluminum 7075-T651, grade-5 titanium, and maraging steel Kolsky bars were selected to provide a relative wide range of impedance mismatches. As discussed earlier, for a brittle specimen that exhibits linear-elastic behavior, linear incident loadings were typically used to obtain a nearly constant strain rate. Such linear incident pulses can be readily produced by pulse shaping techniques [9].

Aluminum bars are widely used among many researchers to characterize low to medium impedance materials, such as polymers [13], rubber compounds [14], foams [15], and bio-materials [7, 15], because of aluminum’s high strength-to-weight ratio, relative low Young’s modulus, and stable mechanical properties. The aluminum 7075-T651 used in this study has a Young’s modulus of 70 GPa, a yield strength of about 500 MPa, a density of 2.7 g/cm³, and a measured longitudinal wave speed of 5094 m/s. The striker, incident, and transmission bar lengths for the aluminum setup are 610, 3658, and 1829 mm, respectively. The grade-5 titanium contains 6% aluminum, 4% vanadium, 0.25% iron and 0.2% oxygen. Its Young’s modulus, yield strength, density, and measured wave speed are 110 GPa, 1 GPa, 4.42 g/cm³, and 4956 m/s, respectively. The striker, incident, and transmission bar lengths for the titanium setup are 305, 1829, and 1829 mm, respectively. Kolsky bars made from steel alloys has a long usage history since Bertram Hopkinson’s original experiments to measure the pressure produced during dynamic events in 1914. Due to its high strength and toughness, the steel system was widely used to measure medium to high impedance materials, such as metals [1, 16], limestones [2], ceramics [3], and composites [5]. Maraging steel was used in this study, because it is well known for its superior strength without losing malleability. It contains 17–19% nickel, 8–12% cobalt, 3–5% molybdenum and 0.2–1.6% titanium. Its Young’s modulus, yield strength, density, and measured wave speed are 200 GPa, 2 GPa, 8.1 g/cm³, and 4932 m/s, respectively. The striker, incident, and transmission bar lengths for the steel setup are 610, 4153, and 1372 mm, respectively.

All bars share a common diameter of 19.05 mm. Strain gages were glued on the incident and transmission bars to record the incident, reflected and transmitted pulses. A pulse shaping technique [9, 17] was used in this research. The pulse shapers were stacked double disks punched from annealed C11000 copper plates. The pulse shapers for each Kolsky bar setups were adjusted so the generated incident pulse has a nearly linear ramp shape. The dimensions of the pulse shapers are listed in Table 1. The lengths of the strikers were sufficient for the specimen to reach stable strain rates. Striking velocities were also adjusted so that the stable strain rates were identical and within the range of 80–100/s.

Table 1 Pulse shaper dimensions to generate nearly linear ramp incident pulse

Experimental data were recorded with a high-speed digital oscilloscope. The specimen strain rate $\dot{\varepsilon_s}$ and strain ε_s can be calculated using

$$ \dot{\varepsilon_s}(t)=\frac{v_1-{v}_2}{l_s}=\frac{\sigma_i(t)-{\sigma}_r(t)-{\sigma}_t(t)}{\rho c{l}_s} $$

(1)

$$ {\varepsilon}_s(t)={\int}_0^t\dot{\varepsilon_s}(t) dt $$

(2)

where v₁ and v₂ are the particle velocities at interface-1 and interface-2 (in Fig. 1); σ_i, σ_r, and σ_t are the incident pulse, reflected pulse, and transmitted pulse, respectively; ρ, c, l_s are the bar density, bar wave speed, and specimen length, respectively. The specimen stresses at both interfaces are

$$ {\sigma}_1(t)=\frac{A_b}{A_s}\left[{\sigma}_i(t)+{\sigma}_r(t)\right] $$

(3)

$$ {\sigma}_2(t)=\frac{A_b}{A_s}{\sigma}_t(t) $$

(4)

where the A_b and A_s are the area of the bar and the specimen. The relative stress difference δ between σ₁(t) and σ₂(t) is used to quantify the stress equilibrium process, which is defined as the absolute difference divided by mean stress:

$$ \delta (t)=\frac{\Delta \sigma }{\sigma_{mean}}=2\frac{\sigma_1(t)-{\sigma}_2(t)}{\sigma_1(t)+{\sigma}_2(t)}\times 100\% $$

(5)

The specimen material for this study is Poly(methyl methacrylate) (PMMA) selected, because of its large linear visco-elastic region [18]. Due to the viscosity of PMMA, its dynamic linear modulus differs from its quasi-static Young’s modulus. The linear modulus of PMMA at a strain rate between 80 and 100/s was measured to be 4.93 ± 0.10 GPa and has a density of 1.18 g/cm³, which leads to its 1-D wave speed of 2040 m/s. The specimen was a cylinder of 15.87 mm diameter and 15.87 mm length. The surfaces were carefully grounded to ensure a smooth finish and parallelism between the two ends. The specimen was then annealed at 90 °C for 5 h to relieve the residual stresses induced by machining. Considering the bar-specimen cross-sectional area ratio, the impedance mismatch can be calculated as

$$ r=\frac{A_b{\rho}_b{c}_b}{A_s{\rho}_s{c}_s} $$

(6)

which leads to r = 8.19, 13.14, and 23.67 for the aluminum, titanium and steel bar systems, respectively.

Results and Discussions

Figure 2(a) shows typical raw data for the incident, reflected, and transmitted signals from an aluminum bar measurement. The nearly linearly increasing portion of the incident pulse indicates a linear ramp loading to deform the specimen at a constant strain rate, which is evidenced by the plateau region on the reflected pulse (starting from ~40 μs). Figure 2(b) shows a typical set of data from a titanium bar measurement, where the plateau region of the reflected pulse starts from ~55 μs. Figure 2(c) shows a typical set of data from a steel bar measurement, where the plateau region of the reflected pulse starts from ~140 μs. Under a linear ramp loading, it can be seen that the time to achieve a constant strain rate increases from the aluminum setup to steel setup.

Fig. 2

Typical experimental results showing (a) raw signals of incident, reflected, and transmitted pulses from aluminum setup, (b) raw signals from titanium setup, (c) raw signals from steel setup, (d) incident end and transmission end specimen stresses and relative stress difference history from aluminum setup, (e) normalized strain rate histories from aluminum (a), titanium (b) and steel (c) setups, and (f) resulting specimen stress-strain curve from aluminum setup

Figure 2(d) shows the specimen stress histories at both interfaces (σ₁ and σ₂) and the relative stress difference history δ defined by equation (5). Note that the time is normalized by the transit time t₀, which is defined as the specimen length divided by measured specimen wave speed. When the loading has just begun, the stress at the specimen-transmission interface is zero (where the relative stress difference is 200%) until the wave passes through the specimen (t ≥ t₀). As time passes, the specimen mean stress increases, and the absolute difference ∆σ oscillates and gradually converges to a fixed value. Thus, the relative stress difference δ oscillates and gradually decreases to near zero. We assume that if the relative stress difference can be bounded by an error of ± 10%, then stress equilibrium is satisfied. For this single measurement in Fig. 2(d), the time to reach stress equilibrium is 5.43 t₀.

Figure 2(e) shows the normalized strain rate histories from aluminum, titanium, and steel setups. The strain rate histories are normalized by the average rates within the plateau region (where the strain rate is stable). The average rates for the three cases are 88/s (for aluminum), 85/s (for titanium), and 83/s (for steel). We assume that if the strain rate increases to 90% of its steady value then nearly constant strain rate is achieved. For the three cases, it takes 5.25 t₀, 7.95 t₀, and 18.70 t₀ for the specimens to reach strain rate constancy for aluminum, titanium, and steel setups, respectively. Figure 2(f) shows the resulting stress-strain curve from the aluminum setup, which shows that the specimen has a Young’s modulus of 4.9 GPa. This response matches with those in the literature [18].

A minimum of four experiments were repeated for each condition. The results from the three bar types are summarized in Fig. 3. The time to reach stress equilibrium are 5.38 ± 0.25 t₀, 5.3 ± 0.78 t₀, and 6.24 ± 1.48 t₀ for aluminum, titanium, and steel SHPB, respectively. The time to reach strain rate constancy are 4.77 ± 0.87 t₀, 8.61 ± 1.04 t₀, and 20.14 ± 1.68 t₀ for aluminum, titanium, and steel SHPB, respectively. Thus, the time to reach both conditions are 5.38 t₀, 8.61 t₀, and 20.14 t₀ for the aluminum, titanium, and steel setups, respectively. The corresponding strains (equation (2)) at those time are ~0.2%, ~0.3%, and ~0.7% for ~90/s stable strain rate. Theoretically, the time to reach both conditions are independent of the strain rate, which will be discussed in next section. However, the strain when both conditions are satisfied is strain-rate dependent. The absolute measurement scatter (plotted as one standard deviation in Fig. 3) increased with increasing impedance mismatch. For a smaller impedance mismatch setup, a larger portion of incident pulse would transmit to the specimen, which results in higher signal-to-noise ratio for the specimen stress. This could explain why the smaller impedance mismatch setup leads to a smaller measurement scatter for the time to equilibrium. On the other hand, the relative scatter for the time to reach rate constancy decrease when higher impedance bars are used (18.2% for aluminum, 12.1% for titanium, and 8.3% for steel SHPB system). This is probably due to the fact that a higher impedance bar reflects higher percentage of the pulse from the bar-specimen interfaces and results in higher signal-to-noise ratio for the strain rate. For the aluminum SHPB system, the specimen reached a constant strain rate before it reached stress equilibrium. From an optimization point of view, it is favorable to satisfy both conditions at the same time. The results in Fig. 3 suggest an optimum impedance mismatch of r ≈ 9 for the PMMA specimen loaded with a linear incident pulse. It is noted that such optimum impedance mismatch might vary for a different specimen.

Fig. 3

Time to achieve stress equilibrium and strain rate constancy loaded by linear incident pulses

It was confirmed that a closer impedance mismatch setup requires less time to achieve rate constancy. However, the measured time to equilibrium was found to remain nearly the same. In the analytical derivations by Frew et al. [2] and Ravichandran and Subhash [3], a larger impedance mismatch lead to faster equilibrium. This discrepancy is probably due to the insignificant time difference to achieve equilibrium for the cases studied here, combined with measurement scatter and noise in experimental approach as discussed earlier. Based on the Frew et al. [2] method, the calculated time to equilibrium only differs by 0.2 t₀ between the aluminum and steel bars, which is small compared to the experimental scatter.

As mentioned earlier, some researchers have indicated that the time to equilibrium and rate constancy can be further shortened by optimizing pulse shaper using a bilinear loading [10, 12]. In the next section, we provide general guidance for selecting characteristics in the bilinear loading profiles without using iterative optimization processes.

Modeling of Bilinear Incident Loading

Basic Theory

To describe the shape of an arbitrary bilinear loading, we introduce two parameters β and t₁: β is the ratio of the slope of first ramp α₁ (as shown in Fig. 4(a)) to the slope of second α₂; the t₁ is the time duration of the first ramp (or initial rise time). It is noted that when β is very large (≥ 100) and t₁ is relatively small (≤ 1t₀), the loading profile (type I) is close to a rectangular loading; when β equals to 1, the loading profile (type III) is linear. We further define the loading with β > 1 (and t₁ > 1 t₀) as type II and the loading with β < 1 as type IV.

Fig. 4

Bilinear incident loadings: (a) four typical types of bilinear incident loadings, (b) matrix of bilinear incident loadings for t₁ = 0.1, 1, 4 t₀ and β = 0.1, 1, 10

With the incident pulse σ_i(t) as a function of time, based on 1-D wave propagation theory in a linear elastic specimen, the stress σ₁(t) transmitted to the specimen on the interface-1 (in Fig. 1) is given by

$$ {\sigma}_1(t)=\left(\frac{2\gamma }{r+1}\right){\sigma}_i(t),0\le t<2{t}_0 $$

(7)

where γ is the ratio of bar cross-section area to specimen cross-section area. The stress σ_r(t) reflected back to the incident bar is given by

$$ {\sigma}_r(t)=\left(\frac{1-r}{r+1}\right){\sigma}_i(t),0\le t<2{t}_0 $$

(8)

When t = t₀, the stress wave reaches interface-2. The stress σ_t(t) transmitted to the transmission bar is

$$ {\sigma}_t(t)=\left(\frac{r-1}{r+1}\right){\sigma}_1\left(t-{t}_0\right),{t}_0\le t<3{t}_0 $$

(9)

And the stress σ₂(t) inside the specimen on interface-2 is given by

$$ {\sigma}_2(t)=\left(\frac{2\gamma }{r+1}\right)\left(1+\frac{r-1}{r+1}\right){\sigma}_1\left(t-{t}_0\right),{t}_0\le t<3{t}_0 $$

(10)

To simplify the equations, we define

$$ A=\frac{2\gamma }{r+1},B=\frac{r-1}{r+1}, and\ C=\frac{2r}{\gamma \left(r+1\right)} $$

(11a,b,c)

By iterating equations (7–10), the stresses on both interfaces in the specimen can be obtained

$$ {\sigma}_1(t)=A\left\{{\sigma}_i(t)+\sum \limits_{k=1}^{\frac{n}{2}}\left[\left({B}^{2k-1}+{B}^{2k}\right){\sigma}_i\left(t-2k{t}_0\right)\right]\right\},{nt}_0\le t<\left(n+2\right){t}_0,n= even $$

(12a)

$$ {\sigma}_2(t)=A\sum \limits_{k=1}^{\frac{n+1}{2}}\left[\left({B}^{2k-2}+{B}^{2k-1}\right){\sigma}_i\left(t-\left(2k-1\right){t}_0\right)\right],{nt}_0\le t<\left(n+2\right){t}_0,n= odd $$

(12b)

And the resultant reflected stress and transmitted stress are given by

$$ {\sigma}_r(t)= AC\sum \limits_{k=1}^{\frac{n}{2}}\left[{B}^{2k-1}{\sigma}_i\left(t-2k{t}_0\right)\right]-B{\sigma}_i(t),{nt}_0\le t<\left(n+2\right){t}_0,n= even $$

(13a)

$$ {\sigma}_t(t)= AC\sum \limits_{k=1}^{\frac{n+1}{2}}\left[{B}^{2k-2}{\sigma}_i\left(t-\left(2k-1\right){t}_0\right)\right],{nt}_0\le t<\left(n+2\right){t}_0,n= odd $$

(13b)

It is noted that from equation (12), the stress histories at both interfaces are proportional to the incident pulse. For a given shaped incident pulse, when substituting equation (12) into equation (5), the relative stress difference is independent of the maximum incident amplitude, which indicates that the time to equilibrium is also independent of the maximum incident amplitude. Similarly, from equation (13), the time to rate constancy is also independent of the maximum incident amplitude (or maximum strain rate amplitude). A MATLAB simulation program was developed to implement equations (12–13). The incident pulses were digitized to small steps in the time domain, and the stress difference, reflected stress, and transmitted stress were iteratively calculated for each time step. To verify this method, an experimental incident loading pulse (shown in Fig. 5(a)) was inputted to the program. Shown in Fig. 5(b), the normalized strain rate from simulation was compared against the rate from the experiment, which indicates a very close agreement.

Fig. 5

Model verification: (a) zoom-in view of the incident pulse input from a titanium-bar experiment, and (b) the resulting normalized strain rate histories from simulation and from experiment

Map for Bilinear Loadings to Equilibrium and Rate Constancy

We generated various bilinear incident pulses for simulations based on β and t₁, where β was varied exponentially from 1E-3 to 1E + 4 with an interval of $\sqrt[7]{10}$, and t₁ was varied linearly from 0 to 4 t₀ with an interval of 0.05 t₀. The highest amplitude and total time duration were identical for every loading. The arbitrary incident pulses were then inputted to the MATLAB program to simulate the resulting stress difference histories and strain rate histories, based on four different impedance mismatches (r = 3, 6, 12, and 24). The same error allowance of 10% was used to determine the time to stress equilibrium and strain rate constancy.

Figure 6 shows the resultant time maps to stress equilibrium. The color bar on the right represents the scale for all four impedance mismatch cases, where the color dark blue indicates the shortest time to reach equilibrium. With increasing time to equilibrium, the colors showed in Fig. 6 change from dark blue to light blue, green, lime, yellow, orange and red. For a type III loading (linear loading, shown on the horizontal line at β = 1), the case of impedance mismatch r = 3 requires longer time to reach equilibrium than the other three cases of higher impedance mismatches; while there is little difference between the cases of r = 6, 12 and 24, which matches the experimental study presented before. For a type I loading (step loading, shown on top left corner in the maps), the time to reach equilibrium increases with increasing impedance mismatch. A type III loading outperforms type I loading in the cases of impedance mismatches of 6, 12 and 24, but underperforms type I loading for impedance mismatch of 3 (with 1.8 t₀ longer to equilibrium). A type II loading (β > 1 and t₁ > 1 t₀) is complex and sensitive with respect to t₁. For example, consider the case with r = 24 and β = 10: the time to equilibrium a) ranges from 5.01–5.24 t₀ when t₁ < 1.3 t₀; b) decreases apparently to 1.83–1.9 t₀ when 1.75 t₀ ≤ t₁ ≤ 2.15 t₀, which is the region that takes minimum time to equilibrium; c) increases slightly to 3.9–4.03 t₀ when 2.9 t₀ ≤ t₁ < 3.1 t₀; and d) decrease slight to 3.46 t₀ when t₁ > 3.4 t₀, which is the same when comparing to type III loading. In general, for a type II bilinear loading with higher first ramp slope than the second, when the rise time is around 2 transit time of the specimen, it takes minimun time to equilibrium. This finding matchs the specific case reported in literature [8] for a flat-topped loading with finite rise time. A possible explaination is that the sudden slop decline at 2 t₀ in the incident pulse can reduce the specimen stress increment at incident end for the period of 2–3 t₀, while the specimen stress increment at the transmission end remains the same. As initially the incident end stress is much higher than the transmission end, such reduction of the incident end stress will promote faster equilibrium. And for type IV loading (β < 1), it generally requires a longer time to equilibrium comparing to linear loading and type II loading, and such time increases with increasing t₁.

Fig. 6

Time to achieve stress equilibrium from simulated bilinear loadings for impedance mismatch of (a) r = 3, (b) r = 6, (c) r = 12, and (d) r = 24

Figure 7 shows the time maps to rate constancy. It is noted that the color bar is shown in log scale, where the blue indicates the shortest and red the longest time to reach a constant rate. The color contours (the dependency of β and t₁ for each r case) are similar, but the scales (the time to rate constancy) are increasing with respect to increasing impedance mismatch. For majority of cases considered, the time to constant rate is longer than to equilibrium, especially for high impedance mismatch. The time to constant rate is also sensitive to β and t₁, and reaches a minimum within a reciprocal-function-shaped region indicated by the blue in the maps. In this region, the time to rate constancy can be significantly reduced compared to linear loading, and the time reduction increases with increasing impedance mismatch. The optimum region can be empirically approximated by a power law:

$$ \beta ={c}_1\bullet {\left(\frac{t_1}{t_0}\right)}^{c_2}+{c}_3,{t}_0\le {t}_1<4{t}_0 $$

(14)

where the fitted parameters (c₁, c₂, and c₃) are listed in Table 2.

Fig. 7

Time to achieve strain rate constancy from simulated bilinear loadings for impedance mismatch of (a) r = 3, (b) r = 6, (c) r = 12, and (d) r = 24

Table 2 Optimum regions to constant rate, fitted with power law lines

To achieve the rate constancy optimally, the results in Table 2 indicate that a higher β is needed for a higher impedance mismatch case, and a higher β is required for a bilinear loading pulse with shorter rise time. It is noted that the parameter c₂ is approximately −1, which leads the fitting very close to a reciprocal function. For further illustration, Fig. 8 plots the simulated bar signals from four cases with r = 12: cases (a) and (b) are within the optimum region, where the t₁ and β are 2 t₀ and 3.52 for case (a) while 4 t₀ and 2.05 for case (b), respectively; case (c) is linear loading; and case (d) is a bilinear loading with the same t₁ but much higher β to case (a). The time to rate constancy is the time for the transmitted pulse slope to catch up with the incident. For cases (a) and (b), a higher slope in the first ramp of incident pulse can increase the initial slope of the transmitted pulse, thus the specimen can reach the convergence strain rate faster. However, for case (d), the strain rate overshoots the convergence rate and needs a considerable amount of time to decrease back, which indicates either t₁ or β is higher than the optimum.

Fig. 8

Simulated bar signals from impedance mismatch r = 12 of (a) t₁ = 2 t₀ and β = 3.52, (b) t₁ = 4 t₀ and β = 2.05, (c) β = 1, and (d) t₁ = 2 t₀ and β = 7

It is noted that for the cases within the optimum region (Figures 8(a) and (b)), the second ramp of the incident pulses share very similar slopes $\overset{\sim }{\alpha_2}$ and y-intercepts $\overset{\sim }{b_2}$ (as indicated in Figure 4). To provide an initial guess to design experiments around the optimum region, such $\overset{\sim }{\alpha_2}$ can be approximated to the slope of the transmitted pulse $\dot{\sigma_t}$ at a given strain rate $\dot{\varepsilon}$:

$$ \overset{\sim }{\alpha_2}\approx \dot{\sigma_t}=\frac{\overset{\sim }{E_s}\dot{\varepsilon}}{\gamma } $$

(15)

where $\overset{\sim }{E_s}$ is the expected Young’s Modulus of the specimen. Assuming equilibrium, the $\overset{\sim }{b_2}$ can be estimated by the reflected pulse amplitude minus the y-intercept of the transmitted pulse:

$$ \overset{\sim }{b_2}\approx \frac{1}{2}\dot{\varepsilon}\left({\rho}_b{c}_b{l}_s-\frac{t_1\overset{\sim }{E_s}}{\gamma}\right) $$

(16)

And the optimum slope ratios $\overset{\sim }{\beta }$ can be calculated as a function of rise time:

$$ \overset{\sim }{\beta }=\frac{\overset{\sim }{b_2}}{\overset{\sim }{\alpha_2}{t}_1}+1 $$

(17)

For a β > 1 bilinear loading with large impedance mismatch, the reflected pulse amplitude is generally much larger than the y-intercept of the transmitted pulse. Thus $\overset{\sim }{\beta }$ can be approximated to a reciprocal function of t₁, which explains the shape of optimum regions in Figure 7.

To validate a bi-linear incident pulse around the optimum region can indeed shorten the time to rate constancy, an experimental bi-linear incident pulse was generated for the steel bar setup. As mentioned earlier, for a fast achievement rate constancy, (a) the second slope α₂ and the transmitted pulse slope should be similar, and (b) the y-intercepts b₂ should be close to reflected pulse amplitude minus the y-intercept of the transmitted pulse. A single hardened copper pulse shaper (L-3.0 mm and D-5.7 mm) was used to generate such a bilinear incident pulse with a relative short initial rise time t₁ = ~3t₀. As shown in Figure 9(b), the bi-linear loading reduces the time to reach constant rate from 18.7 t₀ to 3.8 t₀.

Fig. 9

Experimental bi-linear incident loading on steel SHPB setup: (a) a set of raw signals of incident, reflected and transmitted pulses, and (b) the normalized strain rate from bi-linear loading VS the strain rate from linear loading in Fig. 2(c)

Conclusions

In this study, the effect of impedance mismatch on the time to achieve the stress equilibrium and strain rate constancy was investigated for an elastic specimen. For conventional linear incident loading, we used aluminum, titanium and steel SHPB systems to examine identical specimens of PMMA loaded at ~90/s strain rate. Results show that the time to equilibrium remains nearly the same while the time to constant rate increases with increasing impedance mismatch. Experimental data also suggests an optimum impedance mismatch of ~9.

To further improve equilibrium and rate constancy, we mapped the performance of various bilinear incident loadings. Arbitrary bilinear incident pulses were generated based on two parameters: initial rise time and slope ratio. Then the pulses were inputted to a numerical program to iteratively implement equations (12–13). The results show a β > 1 bilinear loading with t₁ between 1.75 and 2.15 t₀ has the minimum time to equilibrium. A bilinear loading with its second ramp parallel to the transmitted pulse is found capable of achieving rate constancy. Improved from linear loading, bilinear loadings within an optimum region can significantly reduce the time to rate constancy, where optimum slope ratios $\overset{\sim }{\beta }$ can be approximated to be a reciprocal function of t₁.