1 Introduction

Heart rate variability (HRV) is a powerful tool for assessing neural control of heart activities. Linear methods, such as time-domain analysis and the Fourier transform, have been widely used to characterize HRV signals for diagnosing heart disease or analyzing physiological states in humans [1, 2]. However, traditional linear approximation methods may not be sufficient for resolving the complex nature of HRV signals. Methods based on nonlinear dynamics are required to further uncover the intricate and subtle properties of HRV [3–7]. The concept of entropy, which is associated with the rate of information production, was usually used to quantify the complexity of physiological data [3, 4]. Chaotic parameters have been used to analyze the time evolution of HRV in the phase space for implications in clinical cardiology [5–7].

Recently, a time series analysis technique called coarse grained average (CGA) has been proposed for calculating entropy-based complexity measures from HRV signals in multiple scales [8, 9]. This category of complexity measures, termed multiscale sample entropy (MSE), has been demonstrated to successfully differentiate HRV signals of young subjects from those of elderly subjects [8]. However, when applying MSE to differentiate HRV signals of the normal sinus rhythm (NSR) and two pathological states, namely congestive heart failure (CHF) and atrial fibrillation (AF), one may need to consider not only the specific values of the entropy measure but also their dependence on resolution (scale) to better characterize the physiological processes [8].

By using the CGA method, the original time series of length N is first dissected into segments of length τ, the scale, and then the average values of individual segments are calculated to construct a shrunken time series of length N/τ. The averaging process is actually a low-pass filter. Thus, CGA is similar to passing a signal through a low-pass filter followed by a down-sampler, a process comparable to the use of the discrete wavelet transform (DWT) for signal decomposition [10]. Compared to CGA, multi-level DWT can only generate subband components in a dyadic manner such that the scales are limited to be numbers that are powers of two, i.e., the output of the d-th level DWT has a scale of 2 d and a data length 2 −d times the original data length.

Our recent study [11] investigated the discrimination power of MSE features based on CGA and DWT for recognizing CHF. The results demonstrated the superiority of using MSE features calculated from the five dyadic scales using the two multiscale analysis methods to that based on all 20 scales using CGA. However, the recognition rates were not high enough for practical use and the method had room for improvement. Therefore, other nonlinear features, such as chaotic features, and other multiscale analysis methods that can provide longer multiscale lengths, such as DWT with reconstruction (RDWT), were evaluated as possible solutions to further enhance system performance.

The present study explores the discrimination power of wavelet-based multiscale analysis methods in characterizing nonlinear features for CHF recognition. Two DWT paradigms, namely standard DWT and RDWT, were employed to decompose HRV signals into multiple scales for further analysis. Sample entropy (SE) [12] and four chaotic measures, namely time delay (TD), embedding dimension (ED), correlation dimension (CD), and largest Lyapunov exponent (LLE) [7], that characterize the dynamics of the signal in the phase space, were employed as features. Theoretically, SE has some connection with the other four chaotic measures since the calculation of SE also requires embedded reconstruction [7–9]. However, since SE features have been applied successfully to multiscale analysis methods such as CGA [8, 9] and DWT [11] for characterizing HRV signals, SE and the other four chaotic measures are treated separately in order to compare the discriminatory capability of these two categories of nonlinear features.

The following hypotheses were tested: (1) DWT, with its orthogonality property, has better resolution power than that of CGA in multiscale analysis, (2) RDWT, which reconstructs subband components back to the original data length, can better characterize length-sensitive SE and chaotic features for CHF recognition, and (3) the four chaotic features, which describe the evolution of HRV signals in the phase space, have better CHF differentiation power than that of SE features. The discrimination power of the wavelet-based multiscale analysis methods were compared to that obtained using the tradition CGA method. Experiments were designed to clarify the roles of different multiscale analysis methods and different categories of nonlinear features in the recognition of CHF. The performance of the proposed method was also compared to that of well-known CHF classifiers found in the literature [2, 13, 14].

2 Multiscale Analysis of Signals

Two categories of multiscale signal analysis method were employed in the study. One was CGA, which has been successfully used [8, 9] with SE for characterizing CHF and AF based on HRV sequences. The other was the DWT, which decomposes signals into subbands (scales) to uncover the hidden information that is otherwise buried in the original signals [11].

2.1 Coarse Grained Average Analysis

Consider a time series of length N, {x i } = {x 1 , x 2 ,…, x N }. One can construct a coarse grained averaged time series {v j (τ)} [8], where τ is the scale factor, such that:

$$v_{j} \left( \tau \right) = \frac{1}{\tau }\sum\limits_{i = (j - 1)\tau + 1}^{j\tau } {x_{i} ,\;1 \le j \le Round\;\left( {N/\tau } \right)}$$
(1)

where Round(N/τ) rounds N/τ to the nearest integer less than or equal to N/τ.

For scale 1, the time series {v j (1)} is simply the original time series. For scale factors τ larger than unity, the original time series shrinks into a coarse grained sequence of length N/τ with values calculated from the N/τ non-overlapping segments of length τ. In this manner, CGA smoothes and de-correlates a time series into sequences of different scales. The CGA method proposed in another study [8] is used here to generate the first twenty consecutive scales of signal suggested by the paper for calculating the SE features.

2.2 Discrete Wavelet Transform

The DWT has been widely used in signal processing tasks [10]. The major advantage of the DWT is its great time and frequency localizations. Moreover, the DWT allows the decomposition of the signal into different scales, each of which represents a particular coarseness of a signal. Among the various wavelet bases, the db4 wavelet was reported to provide maximum energy localization in analyzing HRV signals [15]. It was thus chosen as the mother wavelet in our recent [11] and present studies.

In this study, a 4-level DWT was employed for signal decomposition. Each level of the DWT signal decomposer contained a pair of complementary high- and low-pass filters, each of which was followed by a two-point down-sampler [10]. After the first level of DWT, a signal was decomposed into detail (D1) and approximation (A1) components, which represent the signal parts in the higher- and lower-half subbands of the spectrum, respectively. The approximation component A1 was further decomposed by the second level DWT using the same pair of filters. This process continued until all the four levels of the DWT were processed.

The four approximation components, Ai, i = 1, 2, 3, and 4, corresponding to the lower frequency part in the four levels of the DWT decomposition were used for further feature calculation. Because a low-pass filter followed by a two-point down-sampler was used, each of the Ai (i = 2, 3, 4) components contained the information of the lower-half subband and was half the length of its input Ai−1. Therefore, components A1 through A4 were comparable to CGA at scales 21 (=2), 22 (=4), 23 (=8), and 24 (=16), respectively. The only difference is that CGA at each dyadic scale replaces the low-pass filter of the multiscale DWT with a first-order moving average filter. The first-order moving average filter is actually the low-pass filter of the DWT with a Haar basis, except that the coefficients of the first-order moving average filter are scaled down by a factor of 2−1/2 [10]. Therefore, CGA at dyadic scales 2i, i > 0, can be considered as the 2−i/2 scaled version of the approximation component Ai of an i-level DWT with a Haar basis. The frequency response of the first-order moving average filter can be easily derived to have a magnitude of cos(0.5 Ω) for −π ≤ \({\widehat{{\upomega }}}\) ≤ π, where \({\widehat{{\upomega }}}\) = 2πf/f s is the digital frequency of the analog frequency f with a sampling frequency f s [16]. The Haar wavelet has the shortest support among all orthogonal wavelets and is not well suited to approximating smooth functions. Comparatively, many well-known wavelets, such as Daubechies wavelets, need to be carefully designed to ensure minimum support for any given numbers of vanishing moments and, thus, usually result in DWT low-pass filters with narrower transition bands [10].

Since 24 (=16) was the largest dyadic integer that was smaller than the largest scale 20 used in CGA, applying the DWT up to level 4 was adequate to extract the largest subset of components to be compared to its counterpart using CGA. As a result, by using the 4-level DWT, the original signal and the subband components A1 through A4 were used to analyze the signal in five dyadic scales, i.e., 1, 2, 4, 8, and 16.

2.3 Discrete Wavelet Transform with Reconstruction

By using DWT, subband components with dyadically (with powers of 2) shortened data lengths were acquired. However, it has been pointed out that data length is critical in calculating accurate nonlinear, especially chaotic, features [7, 8]. Therefore, the RDWT was applied to convert the shrunken subband components back to their original signal length. The procedure was as follows. The signal was first decomposed with the regular DWT. Each subband component was converted back to the original length by first filling all the other subbands with zero and performing the inverse DWT. In this manner, subband components A1 through A4 were converted back to the original length. The four components, together with the original signal, were the outputs of the 5-scale RDWT method for further analysis.

3 Features Used in Study

Two categories of features were used to test the capability of the multiscale representation of RR interval (RRI) sequences in discriminating CHF from NSR. The first category was the SE features based on information theory. The second category of features was calculated from the chaotic analysis of the RRI sequences. As pointed out in the introduction section, although SE has some connection with the chaotic measures [7–9], it and the other four chaotic features were treated separately in order to compare the discriminatory capability of these two categories of nonlinear features in CHF recognition. These two categories of features are described below.

3.1 Sample Entropy Features

The concept of entropy has been widely used to quantify the complexity of a signal [7]. Traditional entropy-based algorithms usually require an infinite data series with infinitely accurate precision and resolution [12]. To deal with short and noisy time series, Pincus [17, 18] introduced approximate entropy (AE). However, AE is a biased statistic which makes it dependent on the data length [12]. Therefore, Richmann and Moorman [12] modified AE and developed a related complex measure, SE, to cope with this problem [12]. Costa et al. [8] combined CGA analysis with SE to characterize the complexity of physiologic time series in multiple scales.

In the applications of AE or SE, a critical parameter is the length of the pattern vectors that are to be analyzed and compared [17, 18]. The present study adopted SE measures with pattern vector lengths of one and two, denoted as SE1 and SE2, respectively, as features. The two entropy measures were consistent with previously suggested values from the literature [17, 18] and were employed by Pincus [19] to characterize heart rate for human aging studies. Other important parameters of the two SE features include a unity time delay and a tolerance of 0.15 times the standard deviation of the original sequence, as utilized elsewhere [8].

3.2 Chaotic Features

The notion that the normal human heartbeat sequence is chaotic was first proposed by Goldberger and West [20]. Numerous studies have supported this concept [5–7]. Researchers mapped time series signals into the phase space domain and successfully uncovered the chaotic nature of biological signals. The phase space is a coordination system used to demonstrate the behavior of a dynamic system, in which the trajectory of the dynamic system usually converges to a stationary state, called an attractor. Takens [21] proposed the embedding theorem, which states that an m-dimensional attractor can be reconstructed from one-dimensional projected data while preserving the topological properties of the original attractor. For a time series x i , i = 1, 2,…, N, the m-dimensional vector in the phase space with time delay τ is expressed as y = [y 1 , y 2 ,…, y L ]T, where L = N−(m−1)τ is the number of time delay vectors and each time delay vector is expressed as y i  = [x i , x i+τ ,…, x i+(m−1)τ ]T. Both TD τ and ED m must be carefully determined in order to successfully unfold the attractor.

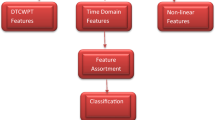
This study employed four chaotic features to characterize the chaotic nature of the HRV signal, namely TD, ED, CD, and LLE. The relationship among these features is depicted in Fig. 1. Among these features, TD and ED were first determined to adequately map the time series into the phase space. Then, CD was calculated to symbolize the geometric complexity of the system and LLE was calculated to describe the divergence of nearby trajectories in the phase space [22, 23].

Fig. 1
figure 1

Chaotic feature extraction

Full size image

3.2.1 Time Delay and Embedding Dimension

A good choice of time delay (τ) provides low correlation between adjacent elements in the embedding vector. One method detects the delay time based on linear correlation [24]. Considering the nonlinear nature of the chaotic system, the method proposed by Fraser and Swinney [25] that alternatively uses mutual information to characterize the nonlinear correlation was applied here.

The ED (m) is used to properly unfold an attractor in m-dimensions. Many algorithms have been proposed to estimate this quantity [26–28]. Cao [29] proposed an objective and computationally effective method for estimating the minimum ED, especially for short time series. It is adopted here.

3.2.2 Correlation Dimension and Largest Lyapunov Exponent

Before calculating CD and LLE, one needs first to reconstruct the attractor dynamics in a phase space with properly estimated TD and ED. CD gives an estimate of system complexity in chaos. This study adopted Grassberger and Procaccia’s method [22] to compute CD.

Lyapunov exponents are quantitative measures of exponential separation of nearby trajectories in the phase space [23]. Wolf et al. [30] proposed a practical method for the estimation of LLEs. Rosenstein [23] further modified Wolf’s method and proposed an efficient LLE method especially suitable for short data series. Therefore, Rosenstein’s method is applied in this study.

4 Experimental Design

The block diagram of the experimental design is depicted in Fig. 2. The details of the functional blocks are described below.

Fig. 2
figure 2

Block diagram of experimental design

Full size image

4.1 Database

Records from 44 CHF subjects (19 male and 25 female; aged 55.30 ± 11.38 years) and 72 NSR subjects (35 male and 37 female; aged 54.6 ± 16.2 years) were obtained from CHF and NSR databases, respectively, both of which are available on PhysioNet [31]. Each record also contained a beat annotation file which specifies the occurrence times of individual R peaks. The 15-minute segment data recorded in the early morning of each record were extracted and the RRI sequences for experiments were generated based on the annotation files of individual records. Selecting a 15-minute data length was motivated by a recent study [32] which explored the influence of segment length in differentiating CHF from NSR and suggested that 15-minute record segments are sufficient for CHF recognition. The 15-minute data segments were confined to be extracted in the same time period of day to minimize the possible influence of the physiological cycle. Figure 3 shows the representative heartbeat (RR) interval (RRI) time series from a healthy subject (a) and a subject with CHF (b). The RRI time series usually also contain slowly changing trends and impulse-type artifacts, such as the two drastic dips in Fig. 3b. These phenomena can cause false interpretation of the RRI time series and mistakes in feature extraction. Therefore, preprocessing techniques such as de-trending and artifact removal filters are usually used.

Fig. 3
figure 3

Representative heartbeat (RR) interval time series from a health subject and b subject with congestive heart failure (CHF) (showing two artifacts)

Full size image

4.2 Preprocessing and Feature Extraction

Our earlier study [33] developed simple preprocessors for removing ectopic beats and trends in the original RRI sequences. This procedure eliminates outliers, especially extremely small-valued data possibly induced by artifacts. The results in our previous study [33] demonstrated the effectiveness of the proposed preprocessors in reducing the effect of artifacts while preserving the major properties of the RRI sequences for CHF recognition. Moreover, the DWT requires input data that are evenly sampled, but the RRI sequence is unevenly spaced. To standardize the RRI sequence for all multiscale analysis methods, the filtered RRI sequence was interpolated with the cubic-spline method and re-sampled at a rate of 4 samples/s. The evenly spaced RRI sequences were first analyzed by different multiscale analysis methods. The two SE and four chaotic features were then calculated from each of the multiscale signals.

4.3 Support Vector Machine Classifier

Support vector machine (SVM) maps the training samples from the input space into a higher-dimensional feature space via a mapping (kernel) function [34]. Any product between vectors in the optimization process can be implicitly computed to generate a hyper-plane to categorize two classes. Numerous studies have demonstrated the superiority of using an SVM classifier over other classifiers in pattern classification tasks. In this study, SVM was employed as the classifier and the radial basis function (RBF) was empirically selected as the kernel function.

4.4 Performance Measures and Validation

The performance of the classifier was measured in terms of sensitivity (SEN), specificity (SPE), and accuracy (ACC). SEN is defined as the ratio of the number of correctly recognized CHF to the total number of CHF records. SPE is defined as the ratio of the number of correctly recognized NSR to the total number of NSR records. ACC is the percentage of all test data that are correctly classified.

The leave-one-out cross-validation method was employed to evaluate the performance of a classifier. This method uses all, except one, samples to train the classifier and then uses the excluded sample to test the performance of the classifier. This procedure repeats until all the samples have been excluded once as the testing sample. The percentage of true results is calculated as a measure of classifier performance. This method tests over the entire database and allows each sample the same opportunity to serve as a training or testing sample. Many CHF recognition systems published in the literature were evaluated using the leave-one-out method [1, 2, 13, 14], and thus it is applied here to also facilitate comparison.

4.5 Experimental Protocol

All 116 records of the database (44 CHF and 72 NSR) were used in the study. All features were extracted from the records and normalized by first subtracting the mean and then dividing by the standard deviation and passing through a tangent sigmoid function, such that all the features were normalized to the range [−1, +1]. The normalization process was performed prior to classification to eliminate the influence of bias due to different feature scales. SVM was then employed as a classifier with leave-one-out cross-validation. The discrimination capabilities of the two SE and four chaotic features in CHF recognition under different multiscale analysis schemes were investigated.

5 Results

In recent studies [8, 9], researchers applied CGA as a multiscale analysis method to characterize SE and distinguish CHF from NSR. The present study first compares the discrimination power of wavelet-based multiscale SE features to that obtained using CGA in recognizing CHF. Then, the discrimination power of wavelet-based multiscale chaotic features and the combination of wavelet-based multiscale SE and chaotic features in CHF recognition is investigated.

5.1 Performance of Multiscale Sample Entropy Features

A previously reported method [8] was followed to calculate two SE features (SE1 and SE2) from each of the 20 CGA scales. This process resulted in a total of 40 SE features. The wavelet-based multiscale analysis methods were based on 4-level DWT and RDWT, both of which provided five dyadic scales, i.e., scales 1, 2, 4, 8, and 16, for feature calculation. The five dyadic scales was chosen because the largest scale (16) generated in this manner is the largest dyadic number that is smaller than the number (20) of applied CGA scales. To assess the influence of decreasing the number of scales from 20 to 5 dyadic numbers, the SE features were also extracted from the five dyadic CGA scales for comparison. As a result, with two SE features calculated from each of the five scales, the 5-scale CGA, DWT, and RDWT methods each has ten SE features. The discrimination power of the SE features calculated using different multiscale analysis methods are summarized in Table 1. The recognition rates obtained using SE features calculated only from the scale 1 (original) signals are also included in the table for comparison.

Table 1 Performance of SE features calculated from various multiscale analysis methods for CHF recognition
Full size table

It is notable that using only two SE features calculated from the original signal achieved SEN, SPE, and ACC values of 47.71, 87.50, 72.41 %, respectively. Comparatively, applying SE features calculated from the CGA method with all 20 scales achieved SEN, SPE, and ACC values of 59.09, 70.83, and 66.37 %, respectively. Using the 5-scale CGA, DWT, and RDWT methods remarkably improved the performance of the classifier (i.e., increased ACC). The 5-scale CGA and 5-scale DWT methods achieved the same ACC of 85.34 %, with the 5-scale RDWT method attaining a slightly lower ACC of 82.75 %. All three 5-scale multiscale analysis methods outperformed the 20-scale traditional CGA method in characterizing SE features for CHF recognition.

5.2 Performance of Multiscale Chaotic Features

Since the 5-dyadic-scale approach effectively improved the recognition rates of SE features, the possibility of using this approach to improve the recognition power of chaotic features was explored. As mentioned in previous sections, four chaotic features were used in the study, namely TD, ED, CD, and LLE. The four chaotic features calculated from each of the five scales resulted in a total of twenty chaotic features used in the CGA, DWT, and RDWT methods, respectively. The recognition rates of the multiscale chaotic features are summarized in Table 2. The results obtained using chaotic features calculated solely from the scale 1 HRV sequences are also included in the table for comparison.

Table 2 Performance of chaotic features calculated from various multiscale analysis methods for CHF recognition
Full size table

By using the four chaotic features calculated from the scale 1 HRV sequences, the classifier achieved SEN, SPE, and ACC values of 38.64, 88.89, and 69.82 %, respectively. Applying 5-scale CGA increased ACC to 77.58 %. Comparatively, 5-scale DWT increased ACC to a slightly lower level of 75 %. However, if the chaotic features were calculated from the 5-scale RDWT, ACC was boosted to a very high level of 96.55 %, with SEN and SPE values of 95.45 and 97.22 %, respectively.

5.3 Performance of Combined Multiscale Sample Entropy and Chaotic Features

Considering the high recognition rates obtained using multiscale SE features and chaotic features in CHF recognition, the performance of the classifier with the two categories of features combined was evaluated. The results are summarized in Table 3. The results obtained using SE and chaotic features calculated solely from the scale 1 HRV sequences are also included in the table for comparison.

Table 3 Performance of combining SE and chaotic features calculated from various multiscale analysis methods for CHF recognition
Full size table

By using the two SE and four chaotic features calculated from the original HRV sequences, the classifier achieved an ACC of 72.41 %, which was slightly higher than that obtained using only the chaotic features and was the same as that obtained using only the SE features calculated solely from the original signals. However, this value was inferior to that for the combined SE and chaotic features using either of the three 5-scale methods. For the three 5-scale multiscale analysis methods, similar to the results in Table 2, multiscale features calculated using the 5-scale RDWT method achieved the highest recognition rates. Compared to the 5-scale CGA and DWT methods, 5-scale RDWT outperformed them by 13.79 and 18.96 % in terms of ACC, respectively. However, when compared to the performance of chaotic features, the ACC for the combination of SE and chaotic features was only slightly higher (+2.59 %) than that obtained using CGA, the same as that obtained using DWT, and slightly lower (−2.59 %) than that obtained using RDWT.

5.4 Comparison with Existing Methods

The results in previous sections demonstrated that chaotic features extracted from the 5-scale RDWT provide superior performance with the proposed scheme. Therefore, this set of features was used for further comparison. To evaluate the performance of the proposed method with existing CHF classifiers, the discriminating capability of the proposed classifier was compared to that of CHF classifiers proposed by Asyali [2], Isler and Kuntalp [13], and Melillo et al. [14], referred to as Asyali’s, Isler’s, and Melillo’s methods, respectively. The comparison results are summarized in Table 4.

Table 4 Comparison of proposed system with three existing methods
Full size table

Asyali’s method applies nine time-domain features calculated from long-term HRV signals. It achieved an ACC of 93.24 %. However, SEN was only 81.92 %. Isler’s method uses short-term HRV signals for CHF recognition with a k-nearest neighbor (KNN) classifier. A genetic algorithm is applied as a feature selector. The best SEN and ACC values were 96.43 and 96.39 %, respectively. Melillo et al. proposed a simple framework which applies only three features and a regression tree (CART) to categorize CHF from NSR. Their system achieved a SEN of 89.74 % and an ACC of 96.36 %. All three studies used the leave-one-out cross-validation method to evaluate the performance of the system.

The proposed method with 5-scale SE and chaotic features based on RDWT had ACC values 3.31, 0.16, and 0.19 % higher than those of Asyali’s, Isler’s, and Melillo’s methods, respectively. The SEN value, which is believed to be the most crucial in clinical diagnosis, was 13.69 and 5.71 % higher than those of Asyali’s and Melillo’s methods, respectively. Compared to Isler’s method, which employs a genetic algorithm as a feature selector, the proposed method achieved the same levels of recognition without the application of any time-consuming feature selectors.

6 Discussion

This study investigated the performance of several multiscale analysis methods in characterizing SE and chaotic features from HRV signals for CHF recognition. The concept of multiscale analysis stems from the CGA analysis of SE features [8]. The concept of multiscale analysis was extended here to the subband decomposition of signals based on DWT. Four chaotic features were used to further characterize the HRV signals in the phase space.

In the analysis of multiscale analysis methods for calculating SE features for CHF recognition, it was unexpected to find that the CGA method with all 20 scales did not improve the performance obtained using SE features, but showed inferior results when compared to those obtained using only SE features calculated from the scale 1 (original) signals. The 5-scale CGA, DWT, and RDWT, even with a smaller number of SE features, showed superior discrimination power when compared to that of the 20-scale CGA method.

These results imply that although multiscale SE has been successfully employed to analyze various categories of signals, such as HRV time series [8, 9], complex rainfall time series [35], and pattern synchronization in cardio-respiratory coupling [36], it may not provide an efficient and compact feature set for recognition tasks. Without orthogonality between scales, SE features extracted from some of the CGA scales may be redundant and may even deteriorate the performance of the classifier, as observed in the present study. This phenomenon was confirmed by the superiority of recruiting the five dyadic scales, as a subset of the 20 scales, over the 20-scale SE features calculated from CGA, no matter which of the three multiscale analysis methods were used. However, there is currently no evidence that the SE features calculated from the five dyadic scales are an optimal subset of multiscale SE features.

Moreover, standard SE measures with unity time delay and pattern vector lengths of one and two were recruited. However, Kaffashi et al. [37] pointed out that SE with unity time delay may only be suitable for characterizing signals with rapidly decaying autocorrelation functions. For a signal with other kinds of autocorrelation functions, the time delay should be carefully selected to more appropriately quantify the complex aspects of the signal. The suitability of using pattern vector lengths of one and two in calculating SE for CHF recognition may need to be justified [38]. Optimization techniques may be applied to simultaneously optimize the pattern vector length and the time lag such that the most suitable SE can be selected for CHF recognition [38]. Several approaches have been proposed in recent studies to solve these problems, such as systematically testing the influence of time delay on SE [37], investigating the effect of the pattern vector length on entropy values [35], applying empirical mode decomposition to decompose data into scale-dependent intrinsic mode functions [39], and estimating entropy values over the adaptive scales of the signal [40]. This important issue will be considered in our future work to develop an efficient and reliable clinical heartbeat recognition system based on ECG.

In the evaluation of 5-scale chaotic features for CHF recognition, RDWT outperformed CGA and DWT in characterizing chaotic features for the SVM classifier. The use of inverse DWT to reconstruct the subband components back to the length of the original signal contributed to the effective calculation of chaotic features for the recognition of CHF. The superiority of RDWT over CGA and DWT might be explained by the distinct characteristics of chaotic features that require longer data to construct the trajectory in the phase space for the calculation of reliable values [7].

Compared to SE features, the chaotic features were more discriminative in CHF recognition. One of the reasons is that the chaotic features were extracted optimally. Contrary to the use of a unity time lag and pattern vector lengths of one and two in calculating the SE features, optimal values of the time lag and embedding dimension were estimated for the reconstruction of the phase space and the calculation of CD and the Lyapunov exponent. In this manner, nonlinear dynamics were appropriately characterized. Therefore, in order to enhance the discrimination power of SE features, optimization techniques should be applied to the parameters of SE features [38]. Moreover, an effective feature selector, such as the genetic algorithm applied in Isler’s method [13], may be employed to select an optimal subset of multiscale SE features to further improve the performance of multiscale SE. With parameter optimization and feature selection processes, an efficient and compact multiscale SE feature set can be constructed.

When SE features were combined with the chaotic features, not all the multiscale analysis methods showed increases in recognition rates. Combining SE and chaotic features only slightly increased the ACC of CGA, yet showed the same ACC by using DWT and even showed a slightly (2.59 %) decrease in ACC using RDWT. These results elucidate the significance of using RDWT and chaotic features in characterizing HRV signals for CHF recognition. Adding SE features into the feature vector did not further enhance the discriminality of the feature space, which further confirms the disadvantage of using SE features of inadequately assigned parameters in CHF recognition, as pointed out earlier in this section. Optimization techniques are required to allocate the most suitable SE features for CHF recognition. Better results can then be expected when combining SE and chaotic features. This topic will be considered in our future work to develop an effective heartbeat recognition system based on ECG.

Compared to three existing CHF classifiers, the proposed method using 5-scale SE and chaotic features based on RDWT outperformed all of them in terms of ACC and SEN. Considering the crucial importance of correctly detecting suspicious CHF from NSR HRV (high SEN), the proposed method is more suitable than the three existing methods for practical clinical services. Even without feature selectors, the proposed method achieved the same high level of recognition compared to that of Isler’s method, which employs a time-consuming genetic algorithm as a feature selector.

7 Conclusion

This study applied three multiscale analysis methods, namely CGA, DWT, and RDWT, to explore the capability of two categories of nonlinear features, namely SE and chaotic features, for CHF recognition. The chaotic features calculated from 5-scale RDWT were the most promising in differentiating CHF from NSR. The proposed method outperforms three existing methods in terms of ACC and SEN. This method can be readily applied to photoplethysmography (PPG) signals with little modification [41].

The SE features employed in this study were standard SE measures with predefined parameters that may not be optimal for characterizing signals such as HRV. In contrast, the chaotic features were estimated to optimally characterize the nonlinear dynamics of the HRV in the phase space. The RDWT preserves the length of the original data and enables the generation of more reliable chaotic features that are length-sensitive for CHF recognition.