1 Introduction

In the past few years, fractional diffusion equations become a popular research topic for their wide applications, such as finance [1], physics [2], medicine [3], and so on. The direct problems of fractional diffusion equation have been extensively studied [4,5,6,7,8,9,10,11]. Nevertheless, in many application, initial information, boundary information, coefficient information, source term information might not be given and then we need to recover them by extra measured information which is able to yield some fractional diffusion inverse problems [12,13,14,15,16,17,18,19,20]. In recent years, inverse problems for fractional diffusion equation have become very active in various fields of sciences and engineering, such as biology [21, 22], physics [23, 24], chemistry [25], and hydrology [26].

To our knowledge, the researches on inverse source problems for space-fractional diffusion equation are still lack of wide attention. For inverse source problem for the space-fractional diffusion equation \(u_{t}(x,t)-~_{x}D^{\alpha }_{\theta }u(x,t)=F(x,t)\), we assume the source term \(F=F(x,t)\) can be split into f(x)q(t), if \(q(t)\ne 1\), we can see reference [27], if \(q(t)=1\), we can see references [28, 29]. In this work, we shall study an inverse source problem for the Riesz–Feller space-fractional diffusion equation as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{t}(x,t)-~_{x}D^{\alpha }_{\theta }u(x,t)=f(x), \quad &{}x\in \mathbb {R},\quad 0<t<1,\\ u(x,0)=0, \quad &{}x\in \mathbb {R},\\ u(x,1)=g(x), \quad &{}x\in \mathbb {R},\\ \end{array}\right. } \end{aligned}$$
(1.1)

where the space-fractional derivative \(_{x}D^{\alpha }_{\theta }\) is the Riesz–Feller fractional derivative of order \(\alpha (0<\alpha <2)\) and skewness \(\theta (|\theta |\le \min \{\alpha ,2-\alpha \},\theta \ne \pm 1)\) which is defined by the Fourier transform in [30],

$$\begin{aligned} \widehat{_{x}D^{\alpha }_{\theta }f(x)}=-\psi _{\alpha }^{\theta }(\xi )\hat{f}(\xi ), \end{aligned}$$
(1.2)

where

$$\begin{aligned} \psi _{\alpha }^{\theta }(\xi )=|\xi |^{\alpha }e^{i(\mathrm {sign}(\xi ))\frac{\theta \pi }{2}}. \end{aligned}$$
(1.3)

From [30], the Riesz–Feller fractional derivative can be written as

$$\begin{aligned} {}_{x}D^{\alpha }_{\theta }f(x)=&\frac{\Gamma (1+\alpha )}{\pi }\bigg \{\sin \frac{(\alpha +\theta )\pi }{2} \int ^{\infty }_{0}\frac{f(x+\xi )-f(x)}{\xi ^{1+\alpha }}\text {d}\xi \\&\quad +\sin \frac{(\alpha -\theta )\pi }{2}\int ^{\infty }_{0}\frac{f(x+\xi )-f(x)}{\xi ^{1+\alpha }}\text {d}\xi \bigg \}, \quad 0<\alpha <2, \\ {}_{x}D^{2}_{0}f(x)&=\frac{d^{2}f(x)}{dx^{2}},\quad \alpha =2, \end{aligned}$$

where \(\Gamma (\cdot )\) is a gamma function. The function f(x) denotes the source term. Our aim is to identify f(x) from the additional data \(u(x,1)=g(x)\). Since the data g(x) is based on physical observation, there must exist measurement errors, and we assume the measured data \(g^{\delta }\in L^{2}(\mathbb {R})\), which satisfies

$$\begin{aligned} \Vert g^{\delta }-g\Vert \le \delta , \end{aligned}$$
(1.4)

where \(\Vert \cdot \Vert \) denotes \(L^{2}\)-norm and the constant \(\delta >0\) is a noise level.

Our main purposes are as follows. By using the simplified generalized Tikhonov regularization method, we give the convergence estimates under a priori and a posteriori regularization parameter choice rules, respectively. Next, the numerical results are based on a posteriori parameter choice rule which is independent of a priori bound of the exact solution is more useful in practical issues.

Finally, we list the content of the paper. In Sect. 2, we will analyze the ill-posedness of inverse source problem (1.1). In Sect. 3, we propose the simplified generalized Tikhonov regularization method and prove convergence estimates under a priori parameter choice rule and a posteriori parameter choice rule. In Sect. 4, we give two numerical examples to show the effectiveness of the proposed method. Section 5 puts an end to this paper with a brief conclusion.

2 Ill-Posedness of Identifying an Unknown Source

In order to apply the Fourier transform, we assume all the functions involving x variable belong to \(L^{2}(\mathbb {R})\). Here, and in the following sections, \(\Vert \cdot \Vert \) denotes the \(L^{2}\)-norm,

$$\begin{aligned} \Vert f\Vert =\bigg (\int ^{+\infty }_{-\infty }\big |f(x)\big |^{2}\text {d}x\bigg )^{\frac{1}{2}}. \end{aligned}$$

Let

$$\begin{aligned} \widehat{f}(\xi )=\frac{1}{\sqrt{2\pi }}\int ^{\infty }_{-\infty }f(x)e^{-i\xi x}\text {d}x,\quad \xi \in \mathbb {R} \end{aligned}$$
(2.1)

be the Fourier transform of the function \(f(x)\in L^{2}(\mathbb {R})\), the solution of problem (1.1) is obtained in the frequency domain

$$\begin{aligned} \widehat{f}(\xi )=\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\widehat{g}(\xi ), \end{aligned}$$
(2.2)

or equivalently,

$$\begin{aligned} f(x)=\frac{1}{\sqrt{2\pi }}\int ^{\infty }_{-\infty }e^{i\xi x}\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\widehat{g}(\xi )\text {d}\xi . \end{aligned}$$
(2.3)

Note that \(\psi ^{\theta }_{\alpha }(\xi ) (\theta \le \min \{\alpha ,2-\alpha \},\theta \ne 1)\) has a positive real part \(|\xi |^{\alpha }\). It can be seen that \(|\xi |^{\alpha }\rightarrow \infty \) as \(|\xi |\rightarrow \infty \), the small error in the high-frequency components will be amplified. Therefore, inverse source problem (1.1) is ill-posed. It is impossible to solve the problem (1.1) by using classical methods, the regularization methods are needed. Before doing that, we need to impose a priori bound on the given data

$$\begin{aligned} \Vert f(\cdot )\Vert _{H^{p,2}}\le M, \quad p>0, \end{aligned}$$
(2.4)

where \(M>0\) is a constant, and \(\Vert \cdot \Vert _{H^{p,2}}\) denotes the norm in the Sobolev space \(H^{p,2}(\mathbb {R})\) defined by

$$\begin{aligned} \Vert f(\cdot )\Vert _{H^{p,2}}:=\bigg (\int ^{\infty }_{-\infty }\big |\widehat{f}(\xi )\big |^{2}(1+\xi ^{2})^{p}\text {d}\xi \bigg )^{\frac{1}{2}}. \end{aligned}$$
(2.5)

3 Simplified Generalized Tikhonov Regularization Method and Convergence Estimates

In this section, we solve problem (1.1) by using generalized Tikhonov regularization method that minimizes the quadratic functional

$$\begin{aligned} \Vert g^{\delta }(\cdot )-g(\cdot )\Vert ^{2}+\mu \Vert f(\cdot )\Vert _{H^{p,2}}^{2}, \end{aligned}$$
(3.1)

where \(\mu >0\) is the regularization parameter. Let \(\widehat{f}_{\mu }^{\delta }(\cdot )\) be the solution of the above problem, the unique solution of the minimization problem (3.1) is equal to the following Euler equation:

$$\begin{aligned} \bigg (\bigg (\frac{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}{\psi ^{\theta }_{\alpha }(\xi )}\bigg )^{2}+\mu (1+|\xi |^{2})^{p}\bigg ) \widehat{f}_{\mu }^{\delta }(\xi )=\frac{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}{\psi ^{\theta }_{\alpha }(\xi )}\widehat{g}^{\delta }(\xi ). \end{aligned}$$
(3.2)

The generalized Tikhonov regularization solution \(\widehat{f}^{\delta }_{\mu }(\xi )\) in frequency domain can be given

$$\begin{aligned} \widehat{f}_{\mu }^{\delta }(\xi )=\frac{\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}}{1+\mu (1+|\xi |^{2})^{p}\bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{2}}\widehat{g}^{\delta }(\xi ), \end{aligned}$$
(3.3)

or equivalently,

$$\begin{aligned} f_{\mu }^{\delta }(x)=\frac{1}{\sqrt{2\pi }}\int ^{\infty }_{-\infty }\frac{\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}}{1+\mu (1+|\xi |^{2})^{p}\bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{2}}\widehat{g}^{\delta }(\xi )e^{i\xi x}\text {d}\xi . \end{aligned}$$
(3.4)

Now, we use the new filter \(\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\) to replace the original filter \(\frac{1}{1+\mu (1+|\xi |^{2})^{p}\bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{2}}\). Thus, we get a simplified generalized Tikhonov regularization solution of (3.4), that is,

$$\begin{aligned} \widehat{f}_{\mu }^{\delta }(\xi )=\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi ), \end{aligned}$$
(3.5)

or equivalently,

$$\begin{aligned} f_{\mu }^{\delta }(x)=\frac{1}{\sqrt{2\pi }}\int ^{\infty }_{-\infty }\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )e^{i\xi x}\text {d}\xi . \end{aligned}$$
(3.6)

In the following subsection, the convergence estimates will be given under a priori regularization parameter choice and a posteriori regularization parameter choice.

3.1 A Priori Choice Rule

In order to obtain our main results, we first give some important lemmas.

Lemma 3.1

[28] If \(x>1\), the following inequality holds

$$\begin{aligned} \frac{1}{1-e^{-x}}<2. \end{aligned}$$
(3.7)

Lemma 3.2

[29] If \(\xi \in \mathbb {R}\), the following inequality holds

$$\begin{aligned} \bigg |\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg |\le \frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}. \end{aligned}$$
(3.8)

Lemma 3.3

If \(\xi \in \mathbb {R}\), and \(0<\alpha <2\), the following inequality holds

$$\begin{aligned}&\sup _{\xi \in \mathbb {R}}\bigg (\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\bigg )\nonumber \\&\le \max \bigg \{\frac{e}{\cos \frac{\theta \pi }{2}}, \frac{(2p+4-\alpha )^{\frac{2p+4-\alpha }{2p+4}}}{p+2}\bigg (\frac{\alpha }{\mu }\bigg )^{\frac{\alpha }{2(p+2)}}\bigg \}. \end{aligned}$$
(3.9)

Proof

Let

$$\begin{aligned} A(\xi ):=\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}. \end{aligned}$$
(3.10)

Let \(s=|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})\), and we know \(|\xi |^{\alpha }=\frac{s}{\cos (\frac{\theta \pi }{2})}\) and \(|\xi |=\big (\frac{s}{\cos (\frac{\theta \pi }{2})}\big )^{\frac{1}{\alpha }}\), then \(A(\xi )\) can be written as

$$\begin{aligned} B(s)=\frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}\frac{1}{1+\mu (1+(\frac{s}{\cos (\frac{\theta \pi }{2})})^{\frac{2}{\alpha }})^{(p+2)}}. \end{aligned}$$
(3.11)

We need to estimate the function B(s) in three cases.

Case 1. If \(0\le s\le 1\), we obtain

$$\begin{aligned} B(s)\le \frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}=\frac{s e^{s}}{\cos (\frac{\theta \pi }{2})(e^{s}-1)}\le \frac{e^{s}}{\cos (\frac{\theta \pi }{2})}\le \frac{e}{\cos (\frac{\theta \pi }{2})}. \end{aligned}$$
(3.12)

Case 2. If \(-1\le s< 0\), we have

$$\begin{aligned} B(s)\le \frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}=\frac{-s}{\cos (\frac{\theta \pi }{2})(e^{-s}-1)}\le \frac{1}{\cos (\frac{\theta \pi }{2})}\le \frac{e}{\cos (\frac{\theta \pi }{2})}. \end{aligned}$$
(3.13)

Case 3. If \(|s|> 1\), we get

$$\begin{aligned} B(s)<\frac{2|s|}{\cos (\frac{\theta \pi }{2})}\frac{1}{1+\mu (1+(\frac{s}{\cos (\frac{\theta \pi }{2})})^{\frac{2}{\alpha }})^{(p+2)}}\le \frac{2|s|}{\cos (\frac{\theta \pi }{2})}\frac{1}{1+\mu (\frac{s}{\cos (\frac{\theta \pi }{2})})^{\frac{2(p+2)}{\alpha }}}. \end{aligned}$$
(3.14)

Let

$$\begin{aligned} \eta (s)=\frac{s}{\cos (\frac{\theta \pi }{2})(1+\mu (\frac{s}{\cos (\frac{\theta \pi }{2})})^{\frac{2(p+2)}{\alpha }})}. \end{aligned}$$
(3.15)

By elementary calculation, we can obtain that \(s^{*}=(\frac{\alpha }{(2p+4-\alpha )\mu })^{\frac{\alpha }{2(p+2)}}\cos (\frac{\theta \pi }{2})\) such that \(\frac{d\eta (s)}{ds}(s^{*})=0\). If \(s>s^{*}\), then \(\frac{d\eta (s)}{ds}<0\); If \(s<s^{*}\), then \(\frac{d\eta (s)}{ds}>0\), and then \(\eta (s)\) attains the maximum at \(s^{*}\), i.e.,

$$\begin{aligned} \eta (s)\le \eta (s^{*})&=\eta \bigg (\bigg (\frac{\alpha }{(2p+4-\alpha )\mu }\bigg )^{\frac{\alpha }{2(p+2)}}\cos (\frac{\theta \pi }{2})\bigg )\nonumber \\&= \frac{(2p+4-\alpha )^{\frac{2p+4-\alpha }{2p+4}}}{2p+4}\bigg (\frac{\alpha }{\mu }\bigg )^{\frac{\alpha }{2(p+2)}}. \end{aligned}$$
(3.16)

Therefore, we know

$$\begin{aligned} B(s)\le 2\frac{(2p+4-\alpha )^{\frac{2p+4-\alpha }{2p+4}}}{2p+4}\bigg (\frac{\alpha }{\mu }\bigg )^{\frac{\alpha }{2(p+2)}}= \frac{(2p+4-\alpha )^{\frac{2p+4-\alpha }{2p+4}}}{p+2}\bigg (\frac{\alpha }{\mu }\bigg )^{\frac{\alpha }{2(p+2)}}. \end{aligned}$$
(3.17)

Finally, combining (3.10), (3.11), (3.12), (3.13) and (3.17), we have

$$\begin{aligned}&\sup _{\xi \in \mathbb {R}}\bigg (\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\bigg )\nonumber \\&\qquad \le \max \bigg \{\frac{e}{\cos \frac{\theta \pi }{2}}, \frac{(2p+4-\alpha )^{\frac{2p+4-\alpha }{2p+4}}}{p+2}\bigg (\frac{\alpha }{\mu }\bigg )^{\frac{\alpha }{2(p+2)}}\bigg \}. \end{aligned}$$
(3.18)

\(\square \)

Lemma 3.4

If \(\xi \in \mathbb {R}\), the following inequality holds

$$\begin{aligned} \sup _{\xi \in \mathbb {R}}\frac{(1+|\xi |^{2})^{\frac{p}{2}+2}}{1+\mu (1+|\xi |^{2})^{p+2}}\le \frac{p}{2p+4}\bigg (\frac{p}{p+4}\bigg )^{-\frac{p+4}{2p+4}}\mu ^{-\frac{p+4}{2p+4}}. \end{aligned}$$
(3.19)

Proof

Let

$$\begin{aligned} D(\xi ):=\frac{(1+|\xi |^{2})^{\frac{p}{2}+2}}{1+\mu (1+|\xi |^{2})^{p+2}}. \end{aligned}$$
(3.20)

Let \(z=1+|\xi |^{2}\), then \(D(\xi )\) can be written as

$$\begin{aligned} \phi (z)=\frac{z^{\frac{p}{2}+2}}{1+\mu z^{p+2}}. \end{aligned}$$
(3.21)

By elementary calculation, we can obtain that \(z^{*}=(\frac{4+p}{\mu p})^{\frac{1}{p+2}}\) such that \(\frac{d\phi (z)}{dz}(z^{*})=0\). If \(z>z^{*}\), then \(\frac{d\phi (z)}{dz}<0\). If \(z<z^{*}\), then \(\frac{d\phi (z)}{dz}>0\), and hence, \(\phi (z)\) attains its maximum at \(z^{*}\), i.e.,

$$\begin{aligned} \phi (z)=\frac{z^{\frac{p}{2}+2}}{1+\mu z^{p+2}}\le \frac{p}{2p+4}\bigg (\frac{p}{p+4}\bigg )^{-\frac{p+4}{2p+4}}\mu ^{-\frac{p+4}{2p+4}}. \end{aligned}$$
(3.22)

\(\square \)

Theorem 3.5

Suppose that \(f_{\mu }^{\delta }(x)\) is the regularization solution for problem (1.1) with the noisy data \(g^{\delta }(x)\), and \(f_{\mu }(x)\) is the simplified generalized Tikhonov regularization solution for problem (1.1) with the exact data g(x). Assumptions (1.4) and (2.4) are satisfied, then we obtain

$$\begin{aligned} \Vert f^{\delta }_{\mu }(\cdot )-f_{\mu }(\cdot )\Vert \le \frac{e}{\cos \frac{\theta \pi }{2}}\delta +\frac{2p+4-\alpha }{p+2}\bigg (\frac{1}{2p+4-\alpha }\bigg )^{\frac{\alpha }{2(p+2)}} \bigg (\frac{\alpha }{\mu }\bigg )^{\frac{\alpha }{2(p+2)}}\delta .\qquad \end{aligned}$$
(3.23)

Proof

By using the Parseval equality, and Lemmas 3.2 and 3.3, we have

$$\begin{aligned} \begin{aligned} \Vert f^{\delta }_{\mu }(\cdot )-f_{\mu }(\cdot )\Vert&=\Vert \widehat{f}^{\delta }_{\mu }(\cdot )-\widehat{f}_{\mu }(\cdot )\Vert \\&=\bigg (\int ^{\infty }_{-\infty }\bigg |\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )\\&\quad -\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}(\xi )\bigg |^{2}\text {d}\xi \bigg )^{\frac{1}{2}}\\&\le \sup _{\xi \in \mathbb {R}}\bigg |\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\bigg |\Vert \widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\Vert \\&\le \sup _{\xi \in \mathbb {R}}\bigg (\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\bigg )\delta \\&\le \max \bigg \{\frac{e}{\cos \frac{\theta \pi }{2}},\frac{2(2p+4-\alpha )}{2p+4}\bigg (\frac{1}{2p+4-\alpha }\bigg )^{\frac{\alpha }{2(p+2)}} \bigg (\frac{\alpha }{\mu }\bigg )^{\frac{\alpha }{2(p+2)}}\bigg \}\delta \\&\le \frac{e}{\cos \frac{\theta \pi }{2}}\delta +\frac{2p+4-\alpha }{p+2}\bigg (\frac{1}{2p+4-\alpha }\bigg )^{\frac{\alpha }{2(p+2)}} \bigg (\frac{\alpha }{\mu }\bigg )^{\frac{\alpha }{2(p+2)}}\delta . \end{aligned} \end{aligned}$$
(3.24)

\(\square \)

Theorem 3.6

Suppose that \(f_{\mu }(x)\) is the simplified generalized Tikhonov regularization solution for problem (1.1) with the exact data g(x) and f(x) is the exact solution of problem (1.1) with the exact data g(x). Assumptions (1.4) and (2.4) are satisfied, then we have

$$\begin{aligned} \Vert f_{\mu }(\cdot )-f(\cdot )\Vert \le \frac{p}{2p+4}\bigg (\frac{p}{p+4}\bigg )^{-\frac{p+4}{2p+4}}\mu ^{\frac{p}{2p+4}}M. \end{aligned}$$
(3.25)

Proof

By using the Parseval equality, and Lemma 3.4, we have

$$\begin{aligned} \Vert f_{\mu }(\cdot )-f(\cdot )\Vert= & {} \Vert \widehat{f}_{\mu }(\cdot )-\widehat{f}(\cdot )\Vert \nonumber \\= & {} \bigg (\int ^{\infty }_{-\infty }\bigg |\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}(\xi )\nonumber \\&-\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\widehat{g}(\xi )\bigg |^{2}\text {d}\xi \bigg )^{\frac{1}{2}}\nonumber \\= & {} \bigg (\int ^{\infty }_{-\infty }\bigg |\frac{\mu (1+|\xi |^{2})^{p+2}}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{f}(\xi )\bigg |^{2}\text {d}\xi \bigg )^{\frac{1}{2}}\nonumber \\= & {} \bigg (\int ^{\infty }_{-\infty }\bigg |\frac{\mu (1+|\xi |^{2})^{\frac{p}{2}+2}}{1+\mu (1+|\xi |^{2})^{p+2}}(1+|\xi |^{2})^{\frac{p}{2}}\widehat{f}(\xi )\bigg |^{2}\text {d}\xi \bigg )^{\frac{1}{2}}\nonumber \\\le & {} \sup _{\xi \in \mathbb {R}}\frac{\mu (1+|\xi |^{2})^{\frac{p}{2}+2}}{1+\mu (1+|\xi |^{2})^{p+2}}\Vert \widehat{f}(\cdot )\Vert _{H^{p,2}}\nonumber \\\le & {} \sup _{\xi \in \mathbb {R}}\frac{\mu (1+|\xi |^{2})^{\frac{p}{2}+2}}{1+\mu (1+|\xi |^{2})^{p+2}}M\nonumber \\\le & {} \frac{p}{2p+4}\bigg (\frac{p}{p+4}\bigg )^{-\frac{p+4}{2p+4}}\mu ^{\frac{p}{2p+4}}M. \end{aligned}$$
(3.26)

\(\square \)

Theorem 3.7

Suppose that \(f_{\mu }^{\delta }(x)\) is the regularization solution for problem (1.1) with the noisy data \(g^{\delta }(x)\), and \(f_{\mu }(x)\) is the exact solution for problem (1.1) with the exact data g(x). Assumptions (1.4) and (2.4) are satisfied. If we choose

$$\begin{aligned} \mu =\bigg (\frac{\delta }{M}\bigg )^{\frac{2(p+2)}{p+\alpha }}, \end{aligned}$$
(3.27)

then we obtain the following convergence estimate

$$\begin{aligned} \begin{aligned} \Vert f^{\delta }_{\mu }(\cdot )-f(\cdot )\Vert \le&\frac{e}{\cos \frac{\theta \pi }{2}}\delta +\bigg (\frac{2p+4-\alpha }{p+2}\bigg (\frac{\alpha }{2p+4-\alpha }\bigg )^{\frac{\alpha }{2(p+2)}}\\&+\frac{p}{2p+4}\bigg (\frac{p}{p+4}\bigg )^{-\frac{p+4}{2p+4}}\bigg ) \delta ^{\frac{p}{p+\alpha }}M^{\frac{\alpha }{p+\alpha }}. \end{aligned} \end{aligned}$$
(3.28)

Proof

According to the Parseval identity and triangle inequality, we get

$$\begin{aligned} \Vert f^{\delta }_{\mu }(\cdot )-f(\cdot )\Vert =\Vert \widehat{f}^{\delta }_{\mu }(\cdot )-\widehat{f}(\cdot )\Vert \le \Vert \widehat{f}^{\delta }_{\mu }(\cdot ) -\widehat{f}_{\mu }(\cdot )\Vert +\Vert \widehat{f}_{\mu }(\cdot )-\widehat{f}(\cdot )\Vert . \end{aligned}$$
(3.29)

Then, using Theorems 3.5 and 3.6, the proof of Theorem 3.7 is completed. \(\square \)

3.2 A Posteriori Choice Rule

In this subsection, we prove the convergence estimate between the exact solution and the regularized solution by using a posteriori choice rule for a regularization parameter, i.e., Morozov’s discrepancy principle.

According to the Morozov’s discrepancy principle [31], we choose the regularization parameter \(\mu \) as the solution of the following equation

$$\begin{aligned} \bigg \Vert \frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}^{\delta }(\xi )\bigg \Vert =\tau \delta . \end{aligned}$$
(3.30)

Here, \(\tau >1\) is a constant. To establish the main result, we need the following lemmas and remark.

Lemma 3.8

Let \(\rho (\mu ):=\Vert \frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}^{\delta }(\xi )\Vert \), the following results hold

(a) \(\rho (\mu )\) is a continuous function;

(b) \(\lim _{\mu \rightarrow 0}\rho (\mu )=0;\)

(c) \(\lim _{\mu \rightarrow +\infty }\rho (\mu )=\Vert \widehat{g}^{\delta }\Vert ;\)

(d) \(\rho (\mu )\) is a strictly increasing function over \((0,+\infty )\).

The proof of Lemma 3.8 is very easy and we omit it here.

Remark 3.9

To establish the existence and uniqueness of the solution for Eq. (3.30), we always suppose \(0<\tau \delta <\Vert g^{\delta }\Vert \).

Lemma 3.10

If \(\mu \) is the solution of Eq. (3.30), then the following inequality holds

$$\begin{aligned} \bigg \Vert \frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg \Vert \le (\tau +1)\delta . \end{aligned}$$
(3.31)

Proof

Using the triangle inequality, we obtain

$$\begin{aligned} \begin{aligned}&\bigg \Vert \frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg \Vert \\&\quad =\bigg \Vert \frac{1}{1+\mu (1+|\xi |^{2})^{p+2}} \widehat{g}^{\delta }(\xi )-\widehat{g}^{\delta }(\xi )+\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg \Vert \\&\quad \le \bigg \Vert \frac{1}{1+\mu (1+|\xi |^{2})^{p+2}} \widehat{g}^{\delta }(\xi )-\widehat{g}^{\delta }(\xi )\bigg \Vert +\bigg \Vert \widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg \Vert \\&\quad \le (\tau +1)\delta . \end{aligned} \end{aligned}$$

\(\square \)

Lemma 3.11

If \(\mu \) is the solution of Eq. (3.30), then the following inequality holds

$$\begin{aligned} \frac{1}{\mu }\le \bigg (\frac{e 2^{(p+2)}M}{(\tau -1)\delta }\bigg )^{\frac{2p+4}{p+\alpha }}. \end{aligned}$$
(3.32)

Proof

Using the triangle inequality, the formula (3.30) and the condition (2.4), we have

$$\begin{aligned} \tau \delta= & {} \bigg \Vert \frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}^{\delta }(\xi )\bigg \Vert \nonumber \\= & {} \bigg \Vert \frac{\mu (1+|\xi |^{2})^{(p+2)}}{1+\mu (1+|\xi |^{2})^{(p+2)}}\widehat{g}^{\delta }(\xi )\bigg \Vert \nonumber \\= & {} \bigg \Vert \frac{\mu (1+|\xi |^{2})^{(p+2)}}{1+\mu (1+|\xi |^{2})^{(p+2)}}\widehat{g}^{\delta }(\xi )-\frac{\mu (1+|\xi |^{2})^{(p+2)}}{1+\mu (1+|\xi |^{2})^{(p+2)}} \widehat{g}(\xi )\nonumber \\&+\frac{\mu (1+|\xi |^{2})^{(p+2)}}{1+\mu (1+|\xi |^{2})^{(p+2)}} \widehat{g}(\xi )\bigg \Vert \nonumber \\\le & {} \bigg \Vert \frac{\mu (1+|\xi |^{2})^{(p+2)}}{1+\mu (1+|\xi |^{2})^{(p+2)}}(\widehat{g}^{\delta }(\xi )- \widehat{g}(\xi ))\bigg \Vert +\bigg \Vert \frac{\mu (1+|\xi |^{2})^{(p+2)}}{1+\mu (1+|\xi |^{2})^{(p+2)}} \widehat{g}(\xi )\bigg \Vert \nonumber \\\le & {} \delta +\bigg \Vert \frac{\mu (1+|\xi |^{2})^{(p+2)}}{1+\mu (1+|\xi |^{2})^{(p+2)}}(1+|\xi |^{2})^{-\frac{p}{2}}\frac{1-e^{-\psi ^{\theta }_{\alpha }}(\xi )}{\psi ^{\theta }_{\alpha }(\xi )}\widehat{f}(\xi )(1+|\xi |^{2})^{\frac{p}{2}} \bigg \Vert \nonumber \\\le & {} \delta +\sup _{\xi \in \mathbb {R}}\bigg |\frac{\mu (1+|\xi |^{2})^{(p+2)}}{1+\mu (1+|\xi |^{2})^{(p+2)}}(1+|\xi |^{2})^{-\frac{p}{2}}\frac{1-e^{-\psi ^{\theta }_{\alpha }}(\xi )}{\psi ^{\theta }_{\alpha }(\xi )}\bigg |M. \end{aligned}$$
(3.33)

Let

$$\begin{aligned} G(\xi ):=\bigg |\frac{\mu (1+|\xi |^{2})^{(p+2)}}{1+\mu (1+|\xi |^{2})^{(p+2)}}(1+|\xi |^{2})^{-\frac{p}{2}}\frac{1-e^{-\psi ^{\theta }_{\alpha }}(\xi )}{\psi ^{\theta }_{\alpha }(\xi )}\bigg |, \quad \xi \in \mathbb {R}. \end{aligned}$$

We need to estimate the function \(G(\xi )\) in three cases.

Case 1. If \(\xi =0\), then we have

$$\begin{aligned} G(0)=\lim _{\xi \rightarrow 0}G(\xi )=\frac{\mu }{1+\mu }. \end{aligned}$$
(3.34)

Case 2. If \(|\xi |\le 1\) and \(\xi \ne 0\), then we get

$$\begin{aligned} G(\xi )\le \frac{\mu e 2^{(p+2)}}{1+\mu }. \end{aligned}$$
(3.35)

Case 3. If \(|\xi |>1\), then we obtain

$$\begin{aligned} G(\xi )\le \frac{\mu (2|\xi |^{2})^{(p+2)}}{1+\mu |\xi |^{2(p+2)}}\frac{1}{|\xi |^{p}}\frac{2}{|\xi |^{\alpha }} = 2^{p+3}\frac{\mu |\xi |^{2(p+2)}}{1+\mu |\xi |^{2(p+2)}}\frac{1}{|\xi |^{p+\alpha }}. \end{aligned}$$
(3.36)

Let \(m=\mu |\xi |^{2(p+2)}\), then \(|\xi |^{(p+\alpha )}=(\frac{m}{\mu })^{\frac{p+\alpha }{2(p+2)}}\), and we know \(\frac{p+4-\alpha }{2(p+2)}<1\), then

$$\begin{aligned} G(\xi )\le 2^{(p+3)} \frac{m}{1+m} \frac{\mu ^{\frac{p+\alpha }{2(p+2)}}}{m^{\frac{p+\alpha }{2(p+2)}}} = 2^{(p+3)} \mu ^{\frac{p+\alpha }{2(p+2)}} \frac{m^{\frac{p+4-\alpha }{2(p+2)}}}{1+m}\le 2^{(p+3)} \mu ^{\frac{p+\alpha }{2(p+2)}}. \end{aligned}$$
(3.37)

Combining (3.34), (3.35), (3.36) and (3.37), we can get

$$\begin{aligned} \sup _{\xi \in \mathbb {R}}G(\xi )\le \max \bigg \{\frac{\mu e 2^{(p+2)}}{1+\mu }, 2^{(p+3)} \mu ^{\frac{p+\alpha }{2(p+2)}}\bigg \}. \end{aligned}$$
(3.38)

According to the condition \(0<\mu<1, 0<\alpha <2\), we have

$$\begin{aligned} \frac{\mu }{1+\mu }<\mu <\mu ^{\frac{p+\alpha }{2(p+2)}}. \end{aligned}$$

So, we know

$$\begin{aligned} \sup _{\xi \in \mathbb {R}}G(\xi )\le e 2^{(p+2)} \mu ^{\frac{p+\alpha }{2(p+2)}}. \end{aligned}$$
(3.39)

Therefore, combining (3.33) and (3.39), we can obtain

$$\begin{aligned} \tau \delta \le \delta + e 2^{(p+2)} \mu ^{\frac{p+\alpha }{2(p+2)}}M. \end{aligned}$$

By elementary calculation, the following inequality holds

$$\begin{aligned} \frac{1}{\mu }\le \bigg (\frac{e 2^{(p+2)}M}{(\tau -1)\delta }\bigg )^{\frac{2p+4}{p+\alpha }}. \end{aligned}$$

\(\square \)

Lemma 3.12

If  \(0<\alpha <2\), \(p>0\), then the following inequality holds

$$\begin{aligned} \sup _{\xi \in \mathbb {R}}\bigg |\bigg (\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\bigg )^{\frac{p}{\alpha }} (1+\xi ^{2})^{-\frac{p}{2}}\bigg |\le \max \bigg \{\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }},2^{\frac{p}{\alpha }}\bigg \}. \end{aligned}$$
(3.40)

Proof

Let

$$\begin{aligned} H(\xi ):=\bigg (\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\bigg )^{\frac{p}{\alpha }} (1+\xi ^{2})^{-\frac{p}{2}}, \end{aligned}$$
(3.41)

and \(s=|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})\), and we know \(|\xi |^{\alpha }=\frac{s}{\cos (\frac{\theta \pi }{2})}\) and \(|\xi |=(\frac{s}{\cos (\frac{\theta \pi }{2})})^{\frac{1}{\alpha }}\), then \(H(\xi )\) can be written as

$$\begin{aligned} H(s)=\bigg (\frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}\bigg )^{\frac{p}{\alpha }}\bigg (1+\bigg (\frac{s}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{2}{\alpha }}\bigg )^{-\frac{p}{2}}. \end{aligned}$$
(3.42)

If \(0\le s\le 1\), we have

$$\begin{aligned} H(s)&\le \bigg (\frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}\bigg )^{\frac{p}{\alpha }}\le \bigg (\frac{s e^{s}}{\cos (\frac{\theta \pi }{2})(e^{s}-1)}\bigg )^{\frac{p}{\alpha }}\nonumber \\&\le \bigg (\frac{e^{s}}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }}\le \bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }}. \end{aligned}$$
(3.43)

If \(-1\le s <0\), we get

$$\begin{aligned} H(s)&\le \bigg (\frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}\bigg )^{\frac{p}{\alpha }}\le \bigg (\frac{-s}{\cos (\frac{\theta \pi }{2})(e^{-s}-1)}\bigg )^{\frac{p}{\alpha }}\nonumber \\&\le \bigg (\frac{1}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }}\le \bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }}. \end{aligned}$$
(3.44)

If \(|s|>1\), we obtain

$$\begin{aligned} H(s)&\le \bigg (\frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}\bigg )^{\frac{p}{\alpha }}\bigg (\frac{|s|}{\cos (\frac{\theta \pi }{2})}\bigg )^{-\frac{p}{\alpha }}\nonumber \\&\le \bigg (\frac{2|s|}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }}\bigg (\frac{|s|}{\cos (\frac{\theta \pi }{2})}\bigg )^{-\frac{p}{\alpha }}= 2^{\frac{p}{\alpha }}. \end{aligned}$$
(3.45)

Hence, the proof of Lemma 3.12 is completed. \(\square \)

Lemma 3.13

If  \(0<\alpha <2\), \(p>0\), then the following inequality holds

$$\begin{aligned}&\sup _{\xi \in \mathbb {R}}\bigg |\bigg (\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\bigg )^{\frac{p+\alpha }{\alpha }}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\bigg |\nonumber \\&\qquad \le \max \bigg \{\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }},C\bigg (\frac{1}{\mu }\bigg )^{\frac{p+\alpha }{2p+4}}\bigg \}. \end{aligned}$$
(3.46)

Here, \(C=2^{\frac{p+\alpha }{\alpha }}(\frac{1}{\cos (\frac{\theta \pi }{2})})^{\frac{p}{\alpha }}\frac{p+\alpha -4}{2p+2\alpha -4} (\frac{p+\alpha }{p+4-\alpha })^{\frac{p+\alpha }{2p+4}}\).

Proof

Let

$$\begin{aligned} L(\xi ):=\bigg (\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\bigg )^{\frac{p+\alpha }{\alpha }}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}, \end{aligned}$$
(3.47)

and \(s=|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})\), and we know \(|\xi |^{\alpha }=\frac{s}{\cos (\frac{\theta \pi }{2})}\) and \(|\xi |=(\frac{s}{\cos (\frac{\theta \pi }{2})})^{\frac{1}{\alpha }}\), then \(L(\xi )\) can be written as

$$\begin{aligned} \begin{aligned} L(s)&=\bigg (\frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}\bigg )^{\frac{p+\alpha }{\alpha }}\frac{1}{1+\mu (1+(\frac{s}{\cos {\frac{\theta \pi }{2}}})^{\frac{2}{\alpha }})^{p+2}}\\&\le \bigg (\frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}\bigg )^{\frac{p+\alpha }{\alpha }}\frac{1}{1+\mu (\frac{s}{\cos {\frac{\theta \pi }{2}}})^{\frac{2p+4}{\alpha }}}=Q(s). \end{aligned} \end{aligned}$$
(3.48)

If \(0\le s\le 1\), we have

$$\begin{aligned} Q(s)&\le \bigg (\frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}\bigg )^{\frac{p+\alpha }{\alpha }}= \bigg (\frac{s e^{s}}{\cos (\frac{\theta \pi }{2})(e^{s}-1)}\bigg )^{\frac{p+\alpha }{\alpha }}\nonumber \\&\le \bigg (\frac{e^{s}}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }} \le \bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }}. \end{aligned}$$
(3.49)

If \(-1\le s< 0\), we have

$$\begin{aligned} Q(s)&\le \bigg (\frac{s}{\cos (\frac{\theta \pi }{2})(1-e^{-s})}\bigg )^{\frac{p+\alpha }{\alpha }}= \bigg (\frac{-s}{\cos (\frac{\theta \pi }{2})(e^{-s}-1)}\bigg )^{\frac{p+\alpha }{\alpha }}\nonumber \\&\le \bigg (\frac{1}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }} \le \bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }}. \end{aligned}$$
(3.50)

If \(|s|>1\), we obtain

$$\begin{aligned} Q(s)\le \bigg (\frac{2|s|}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }}\frac{1}{1+\mu (\frac{s}{\cos {\frac{\theta \pi }{2}}})^{\frac{2p+4}{\alpha }}}=\bigg (\frac{2}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }}\frac{|s|^{\frac{p+\alpha }{\alpha }}}{1+\mu (\frac{s}{\cos {\frac{\theta \pi }{2}}})^{\frac{2p+4}{\alpha }}}. \end{aligned}$$
(3.51)

Let

$$\begin{aligned} N(s)=\frac{s^{\frac{p+\alpha }{\alpha }}}{1+\mu (\frac{s}{\cos {\frac{\theta \pi }{2}}})^{\frac{2p+4}{\alpha }}}, \quad (s>0). \end{aligned}$$
(3.52)

By elementary calculation, we can obtain that \(s^{*}=\cos (\frac{\theta \pi }{2})(\frac{p+\alpha }{p+4-\alpha })^{\frac{\alpha }{2p+4}} (\frac{1}{\mu })^{\frac{\alpha }{2p+4}}\), such that \(\frac{d N(s)}{ds}(s^{*})=0\). If \(s>s^{*}\), then \(\frac{d N(s)}{ds}<0\). If \(s<s^{*}\), then \(\frac{d N(s)}{ds}>0\), and hence, N(s) attains its maximum at \(s^{*}\), i.e.,

$$\begin{aligned} Q(s)\le 2^{\frac{p+\alpha }{\alpha }}\frac{p+\alpha -4}{2p+4} \bigg (\frac{p+\alpha }{p+4-\alpha }\bigg )^{\frac{p+\alpha }{2p+4}}\bigg (\frac{1}{\mu }\bigg )^{\frac{p+\alpha }{2p+4}}=C\bigg (\frac{1}{\mu }\bigg )^{\frac{p+\alpha }{2p+4}}. \end{aligned}$$
(3.53)

Here, \(C=2^{\frac{p+\alpha }{\alpha }}\frac{p+\alpha -4}{2p+4} (\frac{p+\alpha }{p+4-\alpha })^{\frac{p+\alpha }{2p+4}}\). Hence, combining (3.48), (3.49) and (3.53), the proof of Lemma 3.13 is completed. \(\square \)

Theorem 3.14

Suppose that \(f_{\mu }^{\delta }(x)\) is the regularization solution for problem (1.1) with the noisy data \(g^{\delta }(x)\), and \(f_{\mu }\) is the exact solution for problem (1.1) with the exact data g(x). Assumptions (1.4) and (2.4) are satisfied. Then, we obtain the following convergence estimate

$$\begin{aligned} \Vert f^{\delta }_{\mu }(\cdot )-f(\cdot )\Vert \le D \delta ^{\frac{p}{p+\alpha }}M^{\frac{\alpha }{p+\alpha }}. \end{aligned}$$
(3.54)

Here, \(D=\left( \left( \frac{e}{\cos (\frac{\theta \pi }{2})}\right) ^{\frac{p+\alpha }{\alpha }}\delta M^{-1}+C\frac{e 2^{(p+2)}}{\tau -1} +\left( \frac{e}{\cos (\frac{\theta \pi }{2})}\right) ^{\frac{p}{\alpha }}+2^{\frac{p}{\alpha }}\right) ^{\frac{\alpha }{p+\alpha }}(\tau +1)^{\frac{p}{p+\alpha }}.\)

Proof

According to the Parseval identity and the Hölder inequality, we have

$$\begin{aligned}&\Vert f^{\delta }_{\mu }(\cdot )-f(\cdot )\Vert ^{2}\nonumber \\&\quad = \Vert \widehat{f}^{\delta }_{\mu }(\cdot )-\widehat{f}(\cdot )\Vert ^{2}\nonumber \\&\quad =\bigg \Vert \frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\widehat{g}(\xi )\bigg \Vert ^{2}\nonumber \\&\quad = \bigg \Vert \frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg )\bigg \Vert ^{2}\nonumber \\&\quad = \int ^{\infty }_{-\infty }\bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{2}\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg )^{\frac{2\alpha }{p+\alpha }}\nonumber \\&\qquad \times \bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg )^{2-\frac{2\alpha }{p+\alpha }}\text {d}\xi \nonumber \\&\quad \le \bigg [\int ^{\infty }_{-\infty }\bigg (\bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{2}\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg )^{\frac{2\alpha }{p+\alpha }}\bigg )^{\frac{p+\alpha }{\alpha }}\text {d}\xi \bigg ]^{\frac{\alpha }{p+\alpha }}\nonumber \\&\qquad \times \bigg [\int ^{\infty }_{-\infty }\bigg (\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg )^{2(1-\frac{\alpha }{p+\alpha })}\bigg )^{\frac{p+\alpha }{p}}\text {d}\xi \bigg ]^{\frac{p}{p+\alpha }}\nonumber \\&\quad = \bigg [\int ^{\infty }_{-\infty }\bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{\frac{2(p+\alpha )}{\alpha }}\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg )^{2}\text {d}\xi \bigg ]^{\frac{\alpha }{p+\alpha }}\nonumber \\&\qquad \times \bigg [\int ^{\infty }_{-\infty }\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg )^{2}d\xi \bigg ]^{\frac{p}{p+\alpha }}\nonumber \\&\quad = \bigg \Vert \bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{\frac{p+\alpha }{\alpha }}\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg )\bigg \Vert ^{\frac{2\alpha }{p+\alpha }}\nonumber \\&\qquad \times \bigg \Vert \frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg \Vert ^{\frac{2p}{p+\alpha }}\nonumber \\&\quad = I_{1}\times I_{2}. \end{aligned}$$
(3.55)

Firstly, we estimate \(I_{1}\),

$$\begin{aligned} I_{1}\le & {} \bigg \Vert \bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{\frac{p+\alpha }{\alpha }}\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}(\xi )\nonumber \\&+\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}(\xi )-\widehat{g}(\xi )\bigg )\bigg \Vert ^{\frac{2\alpha }{p+\alpha }}\nonumber \\\le & {} \bigg (\bigg \Vert \bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{\frac{p+\alpha }{\alpha }}\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}(\xi )\bigg )\bigg \Vert \nonumber \\&+\bigg \Vert \bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{\frac{p+\alpha }{\alpha }}\bigg (\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}(\xi )-\widehat{g}(\xi )\bigg )\bigg \Vert \bigg )^{\frac{2\alpha }{p+\alpha }}\nonumber \\\le & {} \bigg (\sup _{\xi \in \mathbb {R}}\bigg |\bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{\frac{p+\alpha }{\alpha }}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\bigg |\delta +\bigg \Vert \bigg (\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}}\bigg )^{\frac{p}{\alpha }}\nonumber \\&\bigg (1-\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\bigg )(1+\xi ^{2})^{-\frac{p}{2}}(1+\xi ^{2})^{\frac{p}{2}}\frac{\psi ^{\theta }_{\alpha }(\xi )}{1-e^{-\psi ^{\theta }_{\alpha }(\xi )}} \widehat{g}(\xi )\bigg \Vert \bigg )^{\frac{2\alpha }{p+\alpha }}\nonumber \\\le & {} \bigg (\sup _{\xi \in \mathbb {R}}\bigg |\bigg (\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\bigg )^{\frac{p+\alpha }{\alpha }}\frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\bigg |\delta +\bigg \Vert \bigg (\frac{|\xi |^{\alpha }}{1-e^{-|\xi |^{\alpha }\cos (\frac{\theta \pi }{2})}}\bigg )^{\frac{p}{\alpha }}\nonumber \\&(1+\xi ^{2})^{-\frac{p}{2}}(1+\xi ^{2})^{\frac{p}{2}} \widehat{f}(\xi )\bigg \Vert \bigg )^{\frac{2\alpha }{p+\alpha }}. \end{aligned}$$
(3.56)

From Lemmas 3.12 and 3.13, we know

$$\begin{aligned} I_{1}\le & {} \bigg (\max \bigg \{\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }},C\bigg (\frac{1}{\mu }\bigg )^{\frac{p+\alpha }{2p+4}}\bigg \}\delta +\max \bigg \{\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }},2^{\frac{p}{\alpha }}\bigg \}M\bigg )^{\frac{2\alpha }{p+\alpha }}\nonumber \\\le & {} \bigg (\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }}\delta +C\bigg (\frac{1}{\mu }\bigg )^{\frac{p+\alpha }{2p+4}}\delta +\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }}M+2^{\frac{p}{\alpha }}M\bigg )^{\frac{2\alpha }{p+\alpha }}, \end{aligned}$$
(3.57)

and using Lemma 3.11, we can get

$$\begin{aligned} I_{1}&\le \bigg (\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }}\delta +C\bigg (\frac{e 2^{(p+2)}M}{\tau -1}\bigg )+\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }}M+2^{\frac{p}{\alpha }}M\bigg )^{\frac{2\alpha }{p+\alpha }}\nonumber \\&= \bigg (\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }}\delta M^{-1}+C\frac{e 2^{(p+2)}}{\tau -1}+\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }}+2^{\frac{p}{\alpha }}\bigg )^{\frac{2\alpha }{p+\alpha }}M^{\frac{2\alpha }{p+\alpha }}. \end{aligned}$$
(3.58)

For \(I_{2}\), using Lemma 3.10, we have

$$\begin{aligned} I_{2}=\bigg \Vert \frac{1}{1+\mu (1+|\xi |^{2})^{p+2}}\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi )\bigg \Vert ^{\frac{2p}{p+\alpha }}=((\tau +1)\delta )^{\frac{2p}{p+\alpha }}. \end{aligned}$$
(3.59)

Therefore, combining (3.55), (3.58), and (3.59), we obtain

$$\begin{aligned} \begin{aligned} \Vert f^{\delta }_{\mu }(\cdot )-f(\cdot )\Vert \le&\bigg (\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p+\alpha }{\alpha }}\delta M^{-1}+C\frac{e 2^{(p+2)}}{\tau -1}+\bigg (\frac{e}{\cos (\frac{\theta \pi }{2})}\bigg )^{\frac{p}{\alpha }}+2^{\frac{p}{\alpha }}\bigg )^{\frac{\alpha }{p+\alpha }}\\&\times (\tau +1)^{\frac{p}{p+\alpha }} \delta ^{\frac{p}{p+\alpha }}M^{\frac{\alpha }{p+\alpha }}. \end{aligned} \end{aligned}$$
(3.60)

\(\square \)

4 Numerical Experiments

In this section, we present some numerical results for two examples for showing the effectiveness of the proposed method.

The numerical examples are constructed in the following way: First, we select the exact solution f(x) and obtain the exact data function g(x) through solving the forward problem. Then, we add a normally distributed perturbation to each data function and obtain vectors \(g^{\delta }(x)\), i.e.,

$$\begin{aligned} g^{\delta }=g+\epsilon \mathrm{randn(size(g))}, \end{aligned}$$
(4.1)

where

$$\begin{aligned} g=(g(x_{1}),g(x_{2}),\ldots ,g(x_{n}))^{T}, \quad x_{i}=-5+(i-1)\Delta x, \Delta x=\frac{10}{n-1}, i=1,2,\ldots ,n. \end{aligned}$$
(4.2)

Here, the function “\(\mathrm{{randn(\cdot )}}\)” generates arrays of random numbers whose elements are normally distributed with mean 0, variance \(\sigma ^{2}=1\) and standard deviation \(\sigma =1\), “\(\mathrm{{randn(size(g))}}\)” returns array of random entries that is the same size as g, the magnitude \(\epsilon \) indicates a relative noise level. Here, the total noise \(\delta \) can be measured in the sense of the root mean square error according to

$$\begin{aligned} \delta :=\Vert g^{\delta }-g\Vert _{l^{2}}=\sqrt{\frac{1}{n}\sum \nolimits ^{n}_{i=1}(g^{\delta }_{i}-g_{i})^{2}}. \end{aligned}$$
(4.3)

Finally, we obtain the regularization solution through solving an inverse problem, and the regularized solution is compared with the exact solution.

In our experiments, we only consider the regularization parameter \(\mu \) is chosen by (3.30) with \(\tau =1.1\) under a posteriori regularization parameter choice rule, which is independent of a priori bound of the exact solution is more useful in practical issues.

Example 4.1

Consider a piecewise smooth source:

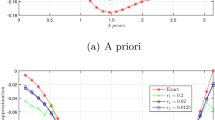
$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} 0, \quad &{} {-\infty \le x \le -1},\\ 1-x^{2}, \quad &{} {-1< x\le 1 },\\ 0, \quad &{} {1 < x \le \infty }. \end{array}\right. \end{aligned}$$

In Fig. 1, the numerical results for simplified generalized Tikhonov regularization method under a posteriori parameter choice rule for various noise levels \(\epsilon =0.001, 0.01\) in case of \(\alpha =0.5,\theta =0.1, p=2\) with Example 4.1 are shown.

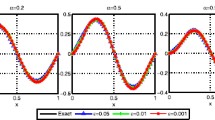
In Fig. 2, the numerical results for simplified generalized Tikhonov regularization method under a posteriori parameter choice rule for various noise levels \(\alpha =1.4, 0.4\) in case of \(\theta =0.1, \epsilon =0.001, p=2\) with Example 4.1 are shown.

Fig. 1
figure 1

The comparison of the numerical effects between the exact solution and its approximation solution, \(\alpha =0.5, \theta =0.1, p=2\): \(\epsilon =0.001, 0.01\) with Example 4.1

Full size image
Fig. 2
figure 2

The comparison of the numerical effects between the exact solution and its approximation solution, \(\theta =0.1, \epsilon =0.001, p=2\): \(\alpha =1.4, 0.4\) with Example 4.1

Full size image

Example 4.2

Consider the following discontinuous source:

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} 0, \quad &{} {-\infty \le x \le -\frac{5}{2} },\\ 1, \quad &{} {-\frac{5}{2}< x \le \frac{5}{2} },\\ 0, \quad &{} {\frac{5}{2} < x \le \infty }. \end{array}\right. \end{aligned}$$

In Fig. 3, the numerical results for simplified generalized Tikhonov regularization method under a posteriori parameter choice rule for various noise levels \(\epsilon =0.001, 0.01\) in case of \(\alpha =0.5,\theta =0.1, p=2\) with Example 4.2 are shown.

In Fig. 4, the numerical results for simplified generalized Tikhonov regularization method under a posteriori parameter choice rule for various noise levels \(\alpha =1.4, 0.4\) in case of \(\theta =0.1, \epsilon =0.001, p=2\) with Example 4.2 are shown.

Fig. 3
figure 3

The comparison of the numerical effects between the exact solution and its approximation solution, \(\alpha =0.5, \theta =0.1, p=2\): \(\epsilon =0.001, 0.01\) with Example 4.2

Full size image
Fig. 4
figure 4

The comparison of the numerical effects between the exact solution and its approximation solution, \(\theta =0.1, \epsilon =0.001, p=2\): \(\alpha =1.4, 0.4\) with Example 4.2

Full size image

Figures 1 and 3 show that the smaller the parameter \(\epsilon \) is, the better the computed approximation is, and Figs. 2 and 4 show the smaller the parameter \(\alpha \) is, the better the computed approximation is. Moreover, Figs. 1, 2, 3, and 4 also show that the posteriori parameter choice rule works well. Finally, these tests illustrate that the proposed method is not only effective for the continuous example, but it works well for the discontinuous example.

5 Conclusion

In this paper, we provide a simplified generalized Tikhonov regularization method to solve an inverse space-dependent source of space-fractional diffusion equation. The convergence estimates are proved based on a priori and a posteriori parameter choice rules, respectively. From Theorems 3.7 and 3.14, we know that the convergence order of the proposed method under a posteriori parameter choice rule is better than one of the proposed method under a priori parameter choice rule. Numerical examples show that the proposed method is effective and stable.