The Mostar Index of Fibonacci and Lucas Cubes

Abstract

The Mostar index of a graph was defined by Došlić, Martinjak, Škrekovski, Tipurić Spužević and Zubac in the context of the study of the properties of chemical graphs. It measures how far a given graph is from being distance-balanced. In this paper, we determine the Mostar index of two well-known families of graphs: Fibonacci cubes and Lucas cubes.

1 Introduction

We consider what is termed the Mostar index of Fibonacci and Lucas cubes. These two families of graphs are special subgraphs of hypercube graphs. They were introduced as alternative interconnection networks to hypercubes and have been studied extensively because of their interesting graph theoretic properties. The Mostar index of a graph was introduced in [4].

Let $G = (V(G),E(G))$ be a graph with vertex set V(G) and edge set E(G). For any $uv\in E(G)$, let $n_{u,v}(G)$ denote the number of vertices in V(G) that are closer (w.r.t. the standard shortest path metric) to u than to v, and let $n_{v,u}(G)$ denote the number of vertices in V(G) that are closer to v than to u. The Mostar index of G is defined in [4] as

$$\begin{aligned} \mathrm{Mo}(G) = \sum _{uv\in E(G)}|n_{u,v}(G)-n_{v,u}(G)|~. \end{aligned}$$

When G and uv is clear from the context, we will write $n_u = n_{u,v}(G)$ and $n_v = n_{v,u}(G).$

Distance-related properties of graphs such as the Wiener index, irregularity and Mostar index have been studied for various families of graphs in the literature.

The Wiener index W(G) of a connected graph G is defined as the sum of distances over all unordered pairs of vertices of G. It is determined for Fibonacci cubes and Lucas cubes in [9]. The irregularity of a graph is another distance invariant measuring how much the graph differs from a regular graph, and Albertson index (irregularity) is defined as the sum of $|deg(u)-deg(v)|$ over all edges uv in the graph [1]. The irregularity of Fibonacci cubes and Lucas cubes is studied in [2, 5]. The relation between the Mostar index and the irregularity of graphs and their difference is investigated in [6]. Recently, the Mostar index of trees and product graphs has been investigated in [3].

In this work, we determine the Mostar index of Fibonacci cubes and Lucas cubes. As a consequence, we derive a relation between the Mostar and the Wiener indices for Fibonacci cubes, giving an alternate expression to the closed formula for $W(\varGamma _n)$ calculated in [9].

2 Preliminaries

We use the notation $[n]=\{1,2, \ldots ,n\}$ for any $n\in {{\mathbb {Z}}}^+$. Let $B=\{0,1\}$ and

$$\begin{aligned} B_n=\{b_1 b_2 \ldots b_n\mid \forall i\in [n]\ \ b_i\in B\} \end{aligned}$$

denote the set of all binary strings of length n. Special subsets of $B_n$ defined as

$$\begin{aligned} \mathcal{F}_n=\{b_1 b_2 \ldots b_n\mid \forall i\in [n-1]\ \ b_i\cdot b_{i+1}=0\} \end{aligned}$$

and

$$\begin{aligned} \mathcal{L}_n=\{b_1b_2 \ldots b_n\mid \forall i\in [n-1]\ \ b_i\cdot b_{i+1}=0 \text{ and } b_1\cdot b_{n}=0 \} \end{aligned}$$

are the set of all Fibonacci strings and Lucas strings of length n, respectively.

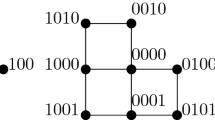
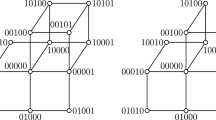
The n-dimensional hypercube $Q_n$ has vertex set $B_n$. Two vertices are adjacent if and only if they differ in exactly one coordinate in their string representation. For $n\ge 1$, the Fibonacci cube $\varGamma _n$ and the Lucas cube $\varLambda _n$ are defined as the subgraphs of $Q_n$ induced by the Fibonacci strings $\mathcal{F}_n$ and Lucas strings $\mathcal{L}_n$ of length n [7, 10]. For convenience, we take $\varGamma _0 = K_1$ whose only vertex is represented by the empty string.

One can classify the binary strings defining the vertices of $\varGamma _n$ by the value of $b_1$. In this way, $\varGamma _n$ decomposes into a subgraph $\varGamma _{n-1}$ whose vertices start with 0 and a subgraph $\varGamma _{n-2}$ whose vertices start with 10 in $\varGamma _n$. This decomposition can be denoted by

$$\begin{aligned} \varGamma _n= 0\varGamma _{n-1}+10\varGamma _{n-2}~. \end{aligned}$$

Furthermore, $0\varGamma _{n-1}$ in turn has a subgraph $00\varGamma _{n-2}$ and there is a perfect matching between $00\varGamma _{n-2}$ and $10\varGamma _{n-2}$, whose edges are called link edges. This decomposition is the fundamental decomposition of $\varGamma _n$. In a similar way, we can also decompose $\varGamma _n$ as

$$\begin{aligned} \varGamma _n= \varGamma _{n-1}0+\varGamma _{n-2}01~. \end{aligned}$$

We refer to [8] for further details on $\varGamma _n$ .

For $n\ge 2$, $\varLambda _n$ is obtained from $\varGamma _n$ by deleting the vertices that start and end with 1. This gives the fundamental decomposition of $\varLambda _n$ as

$$\begin{aligned} \varLambda _n= 0\varGamma _{n-1}+10\varGamma _{n-3}0~. \end{aligned}$$

Here, $0\varGamma _{n-1}$ has a subgraph $00\varGamma _{n-3}0$ and there is a perfect matching between $00\varGamma _{n-3}0$ and $10\varGamma _{n-3}0$.

Fibonacci numbers $f_n$ are defined by the recursion $f_n = f_{n-1} + f_{n-2}$ for $n\ge 2$, with $f_0 = 0$ and $f_1 = 1$. Similarly, the Lucas numbers $L_n$ are defined by $L_n = L_{n-1} + L_{n-2}$ for $n\ge 2$, with $L_0 = 2$ and $L_1 = 1$. It is well known that $|V(Q_n)|=|B_n|=2^n$, $|V(\varGamma _n)|=|\mathcal{F}_n|=f_{n+2}$ and $|V(\varLambda _n)|=|\mathcal{L}_n|=L_{n}$.

For any binary string s, let $w_H(s)$ denote the Hamming weight of s, that is, the number of its nonzero coordinates. The XOR of two binary strings $s_1$ and $s_2$ of length n, denoted by $s_1 \oplus s_2$, is defined as the string of length n whose coordinates are the modulo 2 sum of the coordinates of $s_1$ and $s_2$. The distance d(u, v) between two vertices u and v of the hypercube, the Fibonacci cube and the Lucas cube is equal to the Hamming distance between the string representations of u and v. In other words, $d(u,v)=d_H(s_1,s_2)=w_H(s_1 \oplus s_2)$ for any of these graphs, by assuming u and v have string representations $s_1$ and $s_2$, respectively.

3 The Mostar Index of Fibonacci Cubes

For any $uv\in E(\varGamma _{n})$, let the string representations of u and v be $u_1 u_2\ldots u_n$ and $v_1 v_2\ldots v_n$, respectively. By the structure of $\varGamma _{n}$, we know that $d(u,v)=1$; that is, there is only one index k for which $u_k\ne v_k$.

Lemma 1

For $n\ge 2$, assume that $uv\in E(\varGamma _n)$ with $u_k=0$ and $v_k=1$ for some $k\in [n]$. Then, $n_{u,v}(\varGamma _n)=f_{k+1}f_{n-k+2}$ and $n_{v,u}(\varGamma _n)=f_{k}f_{n-k+1}$.

Proof

The result is clear for $n=2$. Assume that $n\ge 3$, $1<k<n$ and let $\alpha \in V(\varGamma _{n})$ have string representation $b_1 b_2 \ldots b_n$. Since $uv\in E(\varGamma _n)$, u and v must be of the form $a_1\ldots a_{k-1}0a_{k+1}\ldots a_n$ and $a_1\ldots a_{k-1}1a_{k+1}\ldots a_n$, respectively. Since $v\in V(\varGamma _n)$, we must have $a_{k-1}=a_{k+1}=0$. From these representations, we observe that the difference between $d(\alpha ,u)$ and $d(\alpha ,v)$ depends on the value of $b_k$ only. If $b_k=0$, we have $d(\alpha ,u)=d(\alpha ,v)-1$, and if $b_k=1$, we have $d(\alpha ,u)=d(\alpha ,v)+1$. Therefore, the vertices whose kth coordinate is 0 are closer to u than v, and the vertices whose kth coordinate is 1 are closer to v than u. Hence, $n_{u,v}(\varGamma _n)$ is equal to the number of vertices in $\varGamma _n$ whose kth coordinate is 0. These vertices have string representation of the form $\beta _10\beta _2$ where $\beta _1$ is any Fibonacci string of length $k-1$ and $\beta _2$ is any Fibonacci string of length $n-k$. Consequently, $n_{u,v}(\varGamma _n)=f_{k+1}f_{n-k+2}$. Similarly, $n_{v,u}(\varGamma _n)$ is number of vertices of the form $\beta _3010\beta _4$, and this is equal to $f_{k}f_{n-k+1}$.

For the case $k=1$, we have $u\in V(0\varGamma _{n-1})$ and $v\in V(10\varGamma _{n-2})$. Then, $n_{u,v}(\varGamma _n)=|V(0\varGamma _{n-1})|=f_{n+1}$ and $n_{v,u}(\varGamma _n)=|V(10\varGamma _{n-2})|=f_{n}$. Similarly, for $k=n$ we have $u\in V(\varGamma _{n-1}0)$ and $v\in V(\varGamma _{n-2}01)$. This gives again $n_{u,v}(\varGamma _n)=f_{n+1}$ and $n_{v,u}(\varGamma _n)=f_{n}$ for $k=n$. As $f_1=f_2=1$, these are also of the form claimed. $\square$

To find the Mostar index of Fibonacci cubes, we only need to find the number of edges uv in $\varGamma _n$ for which $u_k=0$ and $v_k=1$ for a fixed $k\in [n]$ and add up these contributions over k.

Lemma 2

For $n\ge 2$, assume that $uv\in E(\varGamma _n)$ with $u_k=0$ and $v_k=1$ for some $k\in [n]$. Then, the number of such edges in $\varGamma _n$ is equal to $f_{k}f_{n-k+1}$.

Proof

As in the proof of Lemma 1, the result is clear for $n=2$. Assume that $n\ge 3$. For $1<k<n$, we know that u and v are of the form $a_1\ldots a_{k-2}000a_{k+2}\ldots a_n$ and $a_1\ldots a_{k-2}010a_{k+2}\ldots a_n$. Then, the number of edges uv in $\varGamma _n$ satisfying $u_k=0$ and $v_k=1$ is equal to the number of vertices of the form $a_1\ldots a_{k-2}000a_{k+2}\ldots a_n$, which gives the desired result.

For the boundary cases $k=1$ and $k=n$, we need to find the number of vertices of the form $00a_3\ldots a_n$ and $a_1\ldots a_{n-2}00$, respectively. Clearly, this number is equal to $|V(00\varGamma _{n-2})|=f_n$ and $f_1=1$. This completes the proof. $\square$

Using Lemma 1 and Lemma 2, we obtain the following main result.

Theorem 1

The Mostar index of Fibonacci cube $\varGamma _n$ is given by

$$\begin{aligned} \mathrm{Mo}(\varGamma _n) = \sum _{k=1}^{n} f_{k}f_{n-k+1}\left( f_{k+1}f_{n-k+2}-f_{k}f_{n-k+1}\right) ~. \end{aligned}$$

(1)

Proof

Let $uv\in E(\varGamma _n)$ with $u_k=0$ and $v_k=1$ for some $k\in [n]$. Then, from Lemma 1 we know that

$$\begin{aligned} |n_u-n_v|=f_{k+1}f_{n-k+2}-f_{k}f_{n-k+1} \end{aligned}$$

and therefore using Lemma 2, we have

$$\begin{aligned} \mathrm{Mo}(\varGamma _n)= & {} \sum _{uv\in E(\varGamma _n)}|n_u-n_v| \\= & {} \sum _{k=1}^{n} f_{k}f_{n-k+1}\left( f_{k+1}f_{n-k+2}-f_{k}f_{n-k+1}\right) ~. \end{aligned}$$

$\square$

Note that $f_{k+1}f_{n-k+2}-f_{k}f_{n-k+1}= f_{k}f_{n-k}+f_{k-1}f_{n-k+2}$ so that we can equivalently write

$$\begin{aligned} \mathrm{Mo}(\varGamma _n) = \sum _{k=1}^{n} f_{k}f_{n-k+1}\left( f_{k}f_{n-k}+f_{k-1}f_{n-k+2}\right) ~. \end{aligned}$$

In Sect. 5, Theorem 3, we present a closed-form formula for $\mathrm{Mo}(\varGamma _n)$ obtained by using the theory of generating functions.

Next, we consider the Mostar index of Lucas cubes.

4 The Mostar Index of Lucas Cubes

We know that $\varLambda _{2}=\varGamma _2$ and therefore $\mathrm{Mo}(\varGamma _2)=\mathrm{Mo}(\varLambda _2)=2$.

For any $uv\in E(\varLambda _{n})$, let the string representations of u and v be $u_1 u_2\ldots u_n$ and $v_1v_2\ldots v_n$, respectively. We know that $d(u,v)=1$ and there is only one index k for which $u_k\ne v_k$. Similar to Lemma 1 and Lemma 2, we have the following result.

Lemma 3

For $n\ge 3$, assume that $uv\in E(\varLambda _n)$ with $u_k=0$ and $v_k=1$ for some $k\in [n]$. Then, $n_{u,v}(\varLambda _n)=f_{n+1}$ and $n_{v,u}(\varLambda _n)=f_{n-1}$.

Proof

Assume that $1<k<n$ and let $\alpha \in V(\varLambda _n)$ having string representation $b_1b_2\ldots b_n$. Since $uv\in E(\varLambda _n)$, u must be of the form $a_1\ldots a_{k-2}000a_{k+2}\ldots a_n$ and v must be of the form $a_1\ldots a_{k-2}010a_{k+2}\ldots a_n$. Then, if $b_k=0$, we have $d(\alpha ,u)=d(\alpha ,v)-1$ and if $b_k=1$, we have $d(\alpha ,u)=d(\alpha ,v)+1$. Therefore, $n_{u,v}(\varLambda _n)$ and $n_{v,u}(\varLambda _n)$ are equal to the number of vertices in $\varLambda _n$ whose kth coordinate is 0 and 1, respectively. Therefore, we need to count the number of Lucas strings of the form $\beta _10\beta _2$ and $\beta _3010\beta _4$ which gives $n_{u,v}(\varLambda _n)=f_{n+1}$ and $n_{v,u}(\varLambda _n)=f_{n-1}$.

For the case $k=1$, using the fundamental decomposition of $\varLambda _n$ we have $u\in V(0\varGamma _{n-1})$ and $v\in V(10\varGamma _{n-3}0)$. Then, $n_{u,v}(\varLambda _n)=|V(0\varLambda _n)|=f_{n+1}$ and $n_{v,u}(\varLambda _n)=|V(10\varGamma _{n-3}0)|=f_{n-1}$. Similarly, for $k=n$ we have the same results $n_{u,v}(\varLambda _n)=f_{n+1}$ and $n_{v,u}(\varLambda _n)=f_{n-1}$. $\square$

For any $uv\in E(\varLambda _{n})$ using Lemma 3, we have

$$\begin{aligned} |n_{u,v}(\varLambda _n)-n_{v,u}(\varLambda _n)|=f_{n+1}-f_{n-1}=f_n~. \end{aligned}$$

Since the number of edges in $\varLambda _n$ is $nf_{n-1}$ [10], similar to Theorem 1 we have the following result.

Theorem 2

The Mostar index of Lucas cube $\varLambda _n$ is given by

$$\begin{aligned} \mathrm{Mo}( \varLambda _n) = n f_n f_{n-1}~. \end{aligned}$$

Here, we remark that the vertices of Lucas cubes are represented by Lucas strings which are circular binary strings that avoid the pattern “11." Because of this symmetry, the derivation of a closed formula of Theorem 2 for the Mostar index of Lucas cube $\varLambda _n$ is easier than the one for $\varGamma _n$, in which the first and the last coordinates behave differently from the others.

5 A Closed Formula for $\mathrm{Mo}(\varGamma _n)$

By the fundamental decomposition of $\varGamma _n$, the set of edges $E(\varGamma _n)$ consists of three distinct types:

• 1. The edges in $0\varGamma _{n-1}$, which we denote by $E(0\varGamma _{n-1})$.

• 2. The link edges between $10\varGamma _{n-2}$ and $00\varGamma _{n-2}$, denoted by $C_{n}$.

• 3. The edges in $10\varGamma _{n-2}$, which we denote by $E(10\varGamma _{n-2})$ .

In other words, we have the partition

$$\begin{aligned} E(\varGamma _n)=E(0\varGamma _{n-1}) \cup C_{n} \cup E(10\varGamma _{n-2}) ~. \end{aligned}$$

We keep track of the contribution of each part of this decomposition by setting for $n\ge 2$,

$$\begin{aligned} M_n(x,y,z)= & {} \sum _{uv\in E(0\varGamma _{n-1})}|n_u-n_v|x+ \sum _{uv\in C_{n}}|n_u-n_v|y \nonumber \\&+ \sum _{uv\in E(10\varGamma _{n-2})}|n_u-n_v|z ~. \end{aligned}$$

(2)

Clearly, $\mathrm{Mo}(\varGamma _{n})=M_n(1,1,1)$. By direct inspection, we observe that

$$\begin{aligned} M_2= & {} x+y \\ M_3= & {} 4x+2y+z \\ M_4= & {} 16x+6y+6z \\ M_5= & {} 54x+15y+23z \end{aligned}$$

which gives

$$\begin{aligned} \mathrm{Mo}(\varGamma _{2})= & {} M_2(1,1,1)=2 \\ \mathrm{Mo}(\varGamma _{3})= & {} M_3(1,1,1)=7 \\ \mathrm{Mo}(\varGamma _{4})= & {} M_4(1,1,1)=28 \\ \mathrm{Mo}(\varGamma _{5})= & {} M_5(1,1,1)=92~, \end{aligned}$$

consistent with the values that are calculated using Theorem 1.

By using the fundamental decomposition of $\varGamma _n$, we obtain the following useful result.

Proposition 1

For $n\ge 2$, the polynomial $M_n(x,y,z)$ satisfies

$$\begin{aligned} M_n(x,y,z)= & {} M_{n-1}(x+z,0,x)+M_{n-2}(2x+z,x+z,x+z)\\&+f_{n-1}\left( f_{n}+f_{n-2}\right) x+f_nf_{n-1}y \end{aligned}$$

where $M_0(x,y,z)=M_1(x,y,z)=0$.

Proof

By the definition (2), there are three cases to consider:

• 1. Assume that $uv\in C_{n}$ such that $u\in V(0\varGamma _{n-1})$ and $v\in V(10\varGamma _{n-2})$:

  We know that $d(u,v)=1$ and the string representations of u and v must be of the form $00b_3\ldots b_n$ and $10b_3\ldots b_n$, respectively. Then, using Lemma 1 with $k=1$ we have $|n_u-n_v|=f_{n+1}-f_n=f_{n-1}$ for each edge uv in $C_{n}$. As $|C_n|=f_n$, all of these edges contribute $f_nf_{n-1}y$ to $M_n(x,y,z)$.

• 2. Assume that $uv\in E(10\varGamma _{n-2})$:

  Let the string representations of u and v be $10u_3\ldots u_n$ and $10v_3\ldots v_n$, respectively. Using the fundamental decomposition of $\varGamma _n$, there exist vertices of the form $u'=0u_3\ldots u_n$ and $v'=0v_3\ldots v_n$ in $V(\varGamma _{n-1})$; $u''=u_3\ldots u_n$ and $v''=v_3\ldots v_n$ in $V(\varGamma _{n-2})$. Then, $n_u$ counts the number of vertices $0\alpha \in V(0\varGamma _{n-1})$ and $10\beta \in V(10\varGamma _{n-2})$ satisfying

  $$\begin{aligned} d(0\alpha ,u)<d(0\alpha ,v) \text{ and } d(10\beta ,u)<d(10\beta ,v)~. \end{aligned}$$

  For any $0\alpha \in V(0\varGamma _{n-1})$, we know that $d(0\alpha ,u)=d(\alpha ,u')+1$ and $d(0\alpha ,v)=d(\alpha ,0v')+1$. Therefore, for a fixed $0\alpha \in V(0\varGamma _{n-1})$, $d(\alpha ,u')<d(\alpha ,v')$ if and only if $d(0\alpha ,u)<d(0\alpha ,v)$. Similarly, for any $10\beta \in V(10\varGamma _{n-2})$ we have $d(10\beta ,u)=d(\beta ,u'')$ and $d(\beta ,v)=d(\beta ,v'')$. Then, we can write

  $$\begin{aligned} \sum _{uv\in E(10\varGamma _{n-2})}\big |n_{u,v}(\varGamma _n)-n_{v,u}(\varGamma _n)\big |= & {} \sum _{u'v'\in E(\varGamma _{n-1})}\big |n_{u',v'}(\varGamma _{n-1})-n_{v',u'}(\varGamma _{n-1})\big | \\&+\sum _{u''v''\in E(\varGamma _{n-2})}\big |n_{u'',v''}(\varGamma _{n-2})-n_{v'',u''}(\varGamma _{n-2})\big |~. \end{aligned}$$

  Note that $\varGamma _{n-1}=0\varGamma _{n-2}+10\varGamma _{n-3}$ and the edge $u'v'\in E(\varGamma _{n-1})$ is an edge in the set $E(0\varGamma _{n-2})$. Furthermore, $u''v''\in E(\varGamma _{n-2})$ is an arbitrary edge. Then, by the definition (2) of $M_n$ we have

  $$\begin{aligned} \sum _{u'v'\in E(\varGamma _{n-1})}\big |n_{u',v'}(\varGamma _{n-1})-n_{v',u'}(\varGamma _{n-1})\big |= M_{n-1}(1,0,0) \end{aligned}$$

  and

  $$\begin{aligned} \sum _{u''v''\in E(\varGamma _{n-2})}\big |n_{u'',v''}(\varGamma _{n-2})-n_{v'',u''}(\varGamma _{n-2})\big |= M_{n-2}(1,1,1)~. \end{aligned}$$

  Hence, all of these edges $uv\in E(10\varGamma _{n-2})$ contribute $\big (M_{n-1}(1,0,0)+M_{n-2}(1,1,1)\big )z$ to $M_n(x,y,z)$.

• 3. Assume that $uv\in E(0\varGamma _{n-1})$:

  Since $0\varGamma _{n-1}=00\varGamma _{n-2}+010\varGamma _{n-3}$, we have three subcases to consider here.

  • 1. Assume that $uv\in C_{n-1}$ such that $u\in 00\varGamma _{n-2}$ and $v\in 010\varGamma _{n-3}$ .

    Then, using Lemma 1 with $k=2$ we have

    $$\begin{aligned} |n_u-n_v|=f_3f_{n}-f_2f_{n-1}=2f_n-f_{n-1}=f_n+f_{n-2} \end{aligned}$$

    for each edge uv in $C_{n}$. As $|C_{n-1}|=f_{n-1}$, all of these edges contribute $f_{n-1}(f_n+f_{n-2})x$ to $M_n(x,y,z)$.

  • 2. Assume that $uv\in E(010\varGamma _{n-3})$:

    Let the string representations of u and v are of the form $010u_4\ldots u_n$ and $010v_4\ldots v_n$, respectively. Using the fundamental decomposition of $\varGamma _n$, there exist vertices of the form $u'=000u_4\ldots u_n$ and $v'=000v_4\ldots v_n$ in $V(0\varGamma _{n-1})$; $u''=0u_4\ldots u_n$ and $v''=0v_4\ldots v_n$ in $V(\varGamma _{n-2})$. Then, for any $10\alpha \in V(10\varGamma _{n-2})$ we know that $d(10\alpha ,u)=d(10\alpha ,u')+1=d(\alpha ,u'')+2$ and we know that $d(10\alpha ,v)=d(10\alpha ,v')+1=d(\alpha ,v'')+2$. Therefore, for all $10\alpha \in V(10\varGamma _{n-2})$ we count their total contribution to $M_n$ by $M_{n-2}(1,0,0)x$ in this case. Furthermore, as $uv\in E(010\varGamma _{n-3})$, we have $uv\in E(0\varGamma _{n-1})$, and for all $0\alpha \in V(0\varGamma _{n-1})$, we count their total contribution to $M_n$ by $M_{n-1}(0,0,1)x$ by using the definition of $M_{n-1}$. Hence, the edges $uv\in E(010\varGamma _{n-3})$ contribute $\big (M_{n-1}(0,0,1)+M_{n-2}(1,0,0)\big )x$ to $M_n(x,y,z)$.

  • 3. Assume that $uv\in E(00\varGamma _{n-2})$.

    These edges are the ones of $E(0\varGamma _{n-1})$ that are not in $E(010\varGamma _{n-3})$ and $C_{n-1}$ (not created during the connection of $00\varGamma _{n-2}$ and $010\varGamma _{n-3}$). Then, similar to the Case 2 and using the definition (2) of $M_n$ these edges contribute $\big (M_{n-1}(1,0,0)+M_{n-2}(1,1,1)\big )x$ to $M_n(x,y,z)$.

Combining all of the above cases and noting $M_{n-1}(0,0,1)x=M_{n-1}(0,0,x)$, $M_{n-2}(1,0,0)x=M_{n-2}(x,0,0)$, $M_{n-2}(1,1,1)x=M_{n-2}(x,x,x)$, we complete the proof. $\square$

If we write $M_n(x,y,z)=a_nx+b_ny+c_nz$, then from the recursion in Proposition 1, we obtain for $n \ge 2$

$$\begin{aligned} a_n= & {} a_{n-1} + c_{n-1} + 2 a_{n-2} + b_{n-2} + c_{n-2} +f_{n-1} (f_n + f_{n-2}) \\ b_n= & {} f_n f_{n-1} \\ c_n= & {} a_{n-1}+ a_{n-2} + b_{n-2} + c_{n-2} ~. \end{aligned}$$

Eliminating $b_n$, this is equivalent to the system

$$\begin{aligned} a_n= & {} a_{n-1} + 2 a_{n-2} + c_{n-1}+c_{n-2} + f_{n-2}f_{n-3} + f_{n-1} f_{n-2} + f_n f_{n-1} \nonumber \\ c_n= & {} a_{n-1}+ a_{n-2} + c_{n-2} + f_{n-2}f_{n-3} ~. \end{aligned}$$

(3)

Let A(t), B(t), C(t) be the generating functions of the sequences $a_n, b_n , c_n$, ($n \ge 2$), respectively. We already know that ( [11, A001654])

$$\begin{aligned} B(t) = \sum _{n \ge 2} f_n f_{n-1} t^n = \frac{t^2}{(1+t) (1-3t+t^2)} ~. \end{aligned}$$

(4)

From (3), we obtain

$$\begin{aligned} A(t)= & {} (t + 2 t^2) A(t) + (t +t^2) C(t) + (1 + t + t^2 ) B(t) \nonumber \\ C(t)= & {} (t + t^2) A(t) + t^2 C (t) + t^2 B(t) ~. \end{aligned}$$

(5)

Solving the system of equations (5) and using (4), we calculate

$$\begin{aligned} A(t)= & {} \frac{t^2}{(1+t)^2 (1-3t+t^2)^2} ~,\nonumber \\ C(t)= & {} \frac{t^3 + 2 t^4 - t^5}{(1+t)^2 (1-3t+t^2)^2 } ~. \end{aligned}$$

(6)

Since $\mathrm{Mo}(\varGamma _n) = M_n(1,1,1) = a_n + b _n + c_n$, adding the generating functions A(t), B(t), C(t) we obtain

$$\begin{aligned} \sum _{n \ge 2 } \mathrm{Mo}(\varGamma _n) t^n = \frac{(2-t)t^2}{(1+t)^2 (1-3t+t^2)^2} ~. \end{aligned}$$

(7)

Using partial fractions decomposition in (7) and the expansions

$$\begin{aligned} \frac{1}{1-3t + t^2}= & {} \sum _{n\ge 0} f_{2n+2} t^n ~, \end{aligned}$$

(8)

$$\begin{aligned} \frac{1}{(1-3t + t^2)^2}= & {} \sum _{n\ge 0} \frac{1}{5} \big ( (4n+2) f_{2n+2} + (3n+3) f_{2n+1} \big ) t^n, \end{aligned}$$

(9)

we obtain

$$\begin{aligned} \mathrm{Mo}( \varGamma _n) = \frac{1}{25} \Big ( (3n+2) (-1)^n + (4n-5) f_{2n+2} + (3n+3) f_{2n+1} - (4n-3) f_{2n} - 3n f_{2n-1} \Big )~, \end{aligned}$$

which can be simplified to the closed-form expression for $\mathrm{Mo}( \varGamma _n)$ in Theorem 3. This is another way of writing the sum given in Theorem 1.

Theorem 3

The Mostar index of Fibonacci cube $\varGamma _n$ is

$$\begin{aligned} \mathrm{Mo}(\varGamma _n) = \frac{1}{25} \big ((3n-2)f_{2n+2} + n f_{2n+1} + (3n+2)(-1)^n \big )~. \end{aligned}$$

6 The Wiener Index and Remarks

In [9], it is shown that

$$\begin{aligned} W(\varGamma _n)=\sum _{k=1}^{n} f_{k}f_{k+1}f_{n-k+1}f_{n-k+2}~ \end{aligned}$$

(10)

and that this sum can be evaluated as

$$\begin{aligned} W(\varGamma _n)= \frac{1}{25} \big ( 4 (n+1) f_n^2 +(9n+2) f_n f_{n+1} +6n f_{n+1}^2 \big ) ~. \end{aligned}$$

(11)

In view of our formula (1) of Theorem 1 and (10), this means that

$$\begin{aligned} W(\varGamma _n)= \mathrm{Mo}(\varGamma _n) + \sum _{k=1}^{n} (f_{k}f_{n-k+1})^2 ~. \end{aligned}$$

The sum above is the sequence [11, A136429] with generating function

$$\begin{aligned} \frac{t(1-t)^2}{(1+t)^2 (1-3t+t^2)^2}~. \end{aligned}$$

Adding the generating function (7) to this, we get

$$\begin{aligned} \sum _{n\ge 1} W(\varGamma _n) t^n = \frac{t}{(1+t)^2 ( 1 - 3t + t^2)^2} ~. \end{aligned}$$

(12)

Using partial fractions and the expansions (8) and (9), $W(\varGamma _n)$ ($n \ge 2$) is found to be

$$\begin{aligned} W(\varGamma _n) = \frac{1}{25} \big ( (3n+2)f_{2n+3} + (n-2) f_{2n+2} -(n+2)(-1)^n\big ) \end{aligned}$$

which is a somewhat simpler expression than (11).

It is also curious that in view of their generating functions (6) and (12) which differ only by factor of t, we have

$$\begin{aligned} a_n = M_n(1,0,0) = W(\varGamma _{n-1})~. \end{aligned}$$