Well-Balanced Numerical Schemes for Shallow Water Equations with Horizontal Temperature Gradient

Abstract

A class of well-balanced numerical schemes for the one-dimensional shallow water equations with temperature gradient is constructed. The construction of the schemes is based on two steps: the first step to absorb the nonconservative term and the second step to deal with the evolution of the system. Algorithms for computing contact waves which absorb the nonconservative term are developed. Furthermore, to improve the accuracy, the underlying numerical fluxes can be formed as convex combinations of a pair of numerical fluxes of a low and stable scheme and a higher and fast scheme. The schemes are well balanced and can retain the positivity of the water height and the water temperature. Numerical tests show that the schemes are stable and have a good accuracy.

1 Introduction

In this paper, we will construct a class of well-balanced numerical schemes for the following one-dimensional shallow water equations with variable topography and temperature gradient (see Ripa [25, 26])

$$\begin{aligned}&h_t + (hu)_x = 0,\nonumber \\&(hu)_t + \left( hu^2 + \dfrac{g}{2}h^2\theta \right) _x = -gh\theta a_x,\nonumber \\&(h\theta )_t + (uh\theta )_x = 0, \end{aligned}$$

(1.1)

where h is the height of the water from the bottom to surface, u is the velocity, g is the gravity constant, $\theta$ is the temperature and a is the height of the bottom from a given level.

System (1.1) is a hyperbolic system of balance laws with a nonconservative source term on the right-hand side. Often, nonconservative terms cause lots of inconvenience for standard numerical schemes. For example, errors may be increasing when the mesh sizes get smaller. Therefore, the study on numerical approximations for systems of balance laws containing nonconservative terms is interesting and attracts many authors.

It has been shown that, by supplementing with the trivial equation

$$\begin{aligned} a_t=0, \end{aligned}$$

(1.2)

one can rewrite system (1.1) in the form of nonconservative system of conservation laws

$$\begin{aligned} {\mathbf U}_t+{\mathbf A}({\mathbf U}){\mathbf U}_x=0. \end{aligned}$$

(1.3)

Recall that solutions of (1.3) can be understood in the sense of nonconservative products; see [12]. Recently, the Riemann problem for the shallow water equations with horizontal temperature gradients (1.1)–(1.2) was investigated in [33].

To deal with the nonconservativeness of system (1.1), we use the stationary waves. These waves result in equilibrium states, which are independent of time. The equilibrium states are incorporated into a suitable numerical flux. To improve the efficiency, we form a class of numerical fluxes to be convex combinations of a pair of numerical fluxes, where the first one is of a first-order (stable) scheme and the second one is of a high-order (fast) scheme. For example, such a pair can be the numerical fluxes of the Lax–Friedrichs (first-order, stable) scheme and of the Lax–Wendroff (second-order, fast) scheme. Schemes of this kind are fast and well balanced in the sense that they can capture exactly stationary waves. Many numerical tests are conducted, which all show that the schemes can give a good accuracy. Furthermore, we will show that the scheme using the underlying numerical flux of the Lax–Friedrichs scheme possesses interesting properties: The positivity of the water height and water temperature is conserved.

We note that numerical schemes for the Ripa system were constructed in [7, 16, 28, 36]. Well-balanced schemes for shallow water equations with variable topography were considered in [13, 14, 22,23,24, 27]. Positively conservative schemes were built in [11, 35]. Godunov-type schemes for hyperbolic systems of balance laws in nonconservative forms are considered in [2, 9, 21, 29]. Well-balanced numerical schemes for a single conservation law with source term were studied in [3, 5, 6, 15]. Well-balanced schemes for the model of a fluid flow in a nozzle with variable cross section were constructed in [18, 19]. Numerical schemes for two-phase flow models were presented in [1, 4, 8, 10, 30]. The Riemann problem for other hyperbolic systems in nonconservative form is considered in [17, 20, 31, 32]. See also the references therein.

The organization of this paper is as follows. Section 2 is devoted to basic properties of system (1.1)–(1.2). Numerical schemes will be constructed in Sect. 3. Furthermore, properties of the schemes are also established. Numerical tests are conducted in Sect. 4, where the errors are computed for different mesh sizes. Finally, we will make several conclusions and discussions in Sect. 5.

2 Basic Properties and Stationary Waves

In this section, we recall basic properties and investigate the admissible stationary waves of system (1.1).

2.1 Basic Properties of System

To study basic properties of system (1.1), one often supplement the system with the trivial equation

$$\begin{aligned} a_t=0. \end{aligned}$$

Then, the system can be transformed to the following system

$$\begin{aligned}&h_t + uh_x + hu_x = 0,\nonumber \\&u_t+uu_x + g\theta h_x + \dfrac{gh}{2}\theta _x+g\theta a_x = 0,\nonumber \\&\theta _t + u\theta _x = 0,\nonumber \\&a_t=0. \end{aligned}$$

(2.1)

Thus, if one formally sets the unknown function in the form $\mathbf {U}=(h,u,\theta ,a)^\mathrm{T}$, one can rewrite system (2.1) in the nonconservative form

$$\begin{aligned} \mathbf {U}_t + \mathbf {A}(\mathbf {U})\mathbf {U}_x = 0, \end{aligned}$$

(2.2)

where the matrix $\mathbf {A}(\mathbf {U})$ is given by

$$\begin{aligned} \mathbf {A}(\mathbf {U})=\left( \begin{matrix} u &{}\quad h &{}\quad 0 &{}\quad 0\\ g\theta &{}\quad u &{}\quad \dfrac{gh}{2} &{}\quad g\theta \\ 0 &{}\quad 0 &{}\quad u &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{matrix}\right) . \end{aligned}$$

(2.3)

The characteristic equation of the matrix $\mathbf {A}(\mathbf {U})$ is given by

$$\begin{aligned} |\mathbf {A}(\mathbf {U})-\lambda I|=0, \end{aligned}$$

which gives us four eigenvalues

$$\begin{aligned} \lambda _1=u-\sqrt{g\theta h},\quad \lambda _2=u,\quad \lambda _3=u+\sqrt{g\theta h}, \quad \lambda _4=0. \end{aligned}$$

(2.4)

The corresponding eigenvectors can be chosen as

$$\begin{aligned} \mathbf {r}_1= & {} \left( -\sqrt{gh\theta },g\theta ,0,0\right) ^\mathrm{T},\nonumber \\ \mathbf {r}_2= & {} \left( -h,0,2\theta ,0\right) ^\mathrm{T},\nonumber \\ \mathbf {r}_3= & {} \left( \sqrt{gh\theta },g\theta ,0,0\right) ^\mathrm{T},\nonumber \\ \mathbf {r}_4= & {} \left( gh\theta ,-g\theta u,0,u^2-gh\theta \right) ^\mathrm{T}. \end{aligned}$$

(2.5)

From these formulas, one can see that the first and the fourth characteristic fields may coincide. Indeed, letting

$$\begin{aligned} (\lambda _1(\mathbf {U}),\mathbf {r}_1(\mathbf {U}))=(\lambda _4(\mathbf {U}), \mathbf {r}_4(\mathbf {U})), \end{aligned}$$

we obtain a hypersurface of the space $(h,u,\theta ,a)$ on which the first and the fourth characteristic fields coincide

$$\begin{aligned} \mathbf {C}_{+}=\{(h,u,\theta ,a)|u=\sqrt{g\theta h}\}. \end{aligned}$$

(2.6)

Similarly, the third and the fourth characteristic fields may coincide:

$$\begin{aligned} (\lambda _3(\mathbf {U}),\mathbf {r}_3(\mathbf {U}))=(\lambda _4 (\mathbf {U}),\mathbf {r}_4(\mathbf {U})) \end{aligned}$$

on the hypersurface of the space $(h,u,\theta ,a)$

$$\begin{aligned} \mathbf {C}_{-}=\{(h,u,\theta ,a)|u=-\sqrt{g\theta h}\}. \end{aligned}$$

(2.7)

Furthermore, the second and the fourth eigenvalues may coincide when $u=0$:

$$\begin{aligned} \mathbf {C}_{0}=\{(h,u,\theta ,a)|u=0\}. \end{aligned}$$

(2.8)

Therefore, system (2.2) may not be strictly hyperbolic in the entire domain.

On the other hand, it holds that

$$\begin{aligned}&D\lambda _2(\mathbf {U})\cdot \mathbf {r}_2(\mathbf {U}) =D\lambda _4(\mathbf {U})\cdot \mathbf {r}_4(\mathbf {U})=0,\\&D\lambda _1(\mathbf {U})\cdot \mathbf {r}_1(\mathbf {U}) =D\lambda _3(\mathbf {U})\cdot \mathbf {r}_3(\mathbf {U})=\dfrac{3}{2}g\theta \ne 0,\quad h>0. \end{aligned}$$

This means that the second and the fourth characteristic fields $(\lambda _2,\mathbf {r}_2),(\lambda _4,\mathbf {r}_4)$ are linearly degenerate, and the first and the third characteristic fields $(\lambda _1,\mathbf {r}_1),(\lambda _3,\mathbf {r}_3)$ are genuinely nonlinear in the open half-space $\{(h,u,\theta ,a)|h>0\}$.

From (2.6), (2.7), (2.8), it is convenient to set

$$\begin{aligned} \mathbf {C}=\mathbf {C}_{+}\cup \mathbf {C}_{0}\cup \mathbf {C}_{-} \end{aligned}$$

which is the hypersurface on which the system fails to be strictly hyperbolic. We have seen that the system lacks strict hyperbolicity only on the surface $\mathbf {C}$. However, this surface divides the phase domain into three sub-domains which are disjoint regions, or areas, denoted by $\mathbf {G}_1, \mathbf {G}_2$ and $\mathbf {G}_3$, so that in each region the system is strictly hyperbolic. More precisely,

$$\begin{aligned}&\mathbf {G}_1 = \{(h,u,\theta ,a)\in {\mathbb {R}}_{+}\times {\mathbb {R}}\times {\mathbb {R}}_{+} \times {\mathbb {R}}_{+}|\lambda _4<\lambda _1<\lambda _2<\lambda _3\},\\&\mathbf {G}_2^{+} = \{(h,u,\theta ,a)\in {\mathbb {R}}_{+}\times {\mathbb {R}}\times {\mathbb {R}}_{+} \times {\mathbb {R}}_{+}|\lambda _1<\lambda _4<\lambda _2<\lambda _3\},\\&\mathbf {G}_2^{-} = \{(h,u,\theta ,a)\in {\mathbb {R}}_{+}\times {\mathbb {R}}\times {\mathbb {R}}_{+} \times {\mathbb {R}}_{+}|\lambda _1<\lambda _2<\lambda _4<\lambda _3\},\\&\mathbf {G}_2=\mathbf {G}_2^{+} \cup \mathbf {G}_2^{-},\\&\mathbf {G}_3 = \{(h,u,\theta ,a)\in {\mathbb {R}}_{+}\times {\mathbb {R}}\times {\mathbb {R}}_{+} \times {\mathbb {R}}_{+}|\lambda _1<\lambda _2<\lambda _3<\lambda _4\}; \end{aligned}$$

see Fig. 1.

Fig. 1

Projection of strictly hyperbolic areas in the (h, u) plane

Let us recall the concept of supercritical and subcritical regions in the water resource engineering. The Froude number is defined by

$$\begin{aligned} Fr(\mathbf {U})=\frac{|u|}{\sqrt{gh\theta }}. \end{aligned}$$

If a state $\mathbf {U}$ such that $Fr(\mathbf {U})=1$, then it is said to be a critical state. If $Fr(\mathbf {U})>1$, then $\mathbf {U}$ is said to be a supercritical state. If $Fr(\mathbf {U})<1$, then $\mathbf {U}$ is said to be a subcritical state.

2.2 The Curve of Stationary Waves

First, consider stationary smooth solutions of system (1.1), which are time-independent solutions. It is not difficult to check that such a stationary smooth solution satisfies the following ordinary differential equations

$$\begin{aligned}&(hu)' = 0,\nonumber \\&\left( \dfrac{u^2}{2}+g\theta (h+a)\right) ' = 0,\nonumber \\&\theta ' = 0, \end{aligned}$$

(2.9)

where $(.)'=\mathrm{d}/\mathrm{d}x$. Thus, the trajectory of the system of three differential equations (2.9) passing through a fixed point $(h_0,u_0,\theta _0,a_0)$ satisfy the following algebraic equations

$$\begin{aligned}&hu = h_0u_0,\nonumber \\&\dfrac{u^2}{2}+g\theta (h+a) = \dfrac{u_0^2}{2}+g\theta (h_0+a_0),\nonumber \\&\theta = \theta _0. \end{aligned}$$

(2.10)

Stationary contact discontinuities associated with the fourth characteristic field $\lambda _4$ can be obtained as the limit of stationary smooth solutions; see [33]. Precisely, one can take a sequence of stationary smooth solutions of (1.1), which can be parameterized in terms of the water height h in the form $u=u(h), \theta =\theta (h),a=a(h)$. Then, by letting the water height h tend to a jump $h_\pm$, that is,

$$\begin{aligned} h\longrightarrow h_{\pm }, \end{aligned}$$

and setting

$$\begin{aligned} u_{\pm }=u(h_{\pm }), \quad \theta _{\pm }=\theta (h_{\pm }),\quad a_{\pm }=a(h_{\pm }), \end{aligned}$$

we can see that the states $\mathbf {U}_\pm =(h_{\pm },u_{\pm },\theta _{\pm },a_{\pm })^\mathrm{T}$ satisfy the jump conditions

$$\begin{aligned}&{[}hu{]} = 0,\nonumber \\&\left[ \dfrac{u^2}{2}+g\theta (h+a)\right] = 0,\nonumber \\&{[}\theta {]} = 0. \end{aligned}$$

(2.11)

This implies that the curve of stationary contact waves which consists of all right-hand states $\mathbf {U}$ that can be connected to a given left-hand state $\mathbf {U}_0$ by a four-contact wave can be parameterized in h:

$$\begin{aligned} \begin{array}{ll} \mathcal {W}_0(\mathbf {U}_0): &{}u = u(h) = \dfrac{h_0u_0}{h},\\ &{}\theta = \theta (h) = \theta _0,\\ &{}a = a(h) = \dfrac{u_0^2-u^2}{2g\theta _0}+h_0-h+a_0. \end{array} \end{aligned}$$

(2.12)

Substituting for u in the third equation of system (2.12), and re-arranging terms, we obtain

$$\begin{aligned} u= & {} u(h) = \dfrac{h_0u_0}{h},\nonumber \\ \theta= & {} \theta (h)= \theta _0,\nonumber \\ a= & {} a(h) = \dfrac{u_0^2}{2g\theta _0}\left( 1-\dfrac{h_0^2}{h^2} \right) +h_0-h+a_0. \end{aligned}$$

(2.13)

Therefore, if the topography levels on both sides of a discontinuity are known, we can determine the water height from the nonlinear algebraic equation

$$\begin{aligned} a-a_0+\dfrac{u_0^2}{2g\theta _0}\left( \dfrac{h_0^2}{h^2}-1\right) +h-h_0=0. \end{aligned}$$

Thus, given a state $\mathbf {U}_0$ on the one side of a four-contact discontinuity, we can determine the state $\mathbf {U}$ on the other side by first evaluating the water height to be a zero of the function

$$\begin{aligned} \varphi (h)=a-a_0+\dfrac{u_0^2}{2g\theta _0} \left( \dfrac{h_0^2}{h^2}-1\right) +h-h_0. \end{aligned}$$

(2.14)

The other quantities of that state will follow from (2.13).

Let us now discuss about the finding zeros of the function $\varphi$ in (2.14). Set

$$\begin{aligned}&h_{\min }(\mathbf {U}_0) := \left( \dfrac{u_0^2h_0^2}{g\theta _0}\right) ^{\frac{1}{3}},\\&a_{\max }(\mathbf {U}_0) := \dfrac{u_0^2}{2g\theta _0}\left( 1-\dfrac{h_0^2}{h_{\min }^2} \right) +h_0-h_{\min }+a_0. \end{aligned}$$

It is easy to verify that

$$\begin{aligned} a_{\max }(\mathbf {U}_0)= \dfrac{h_0}{2}\left( \dfrac{u_0^{\frac{2}{3}}}{g^{\frac{1}{3}}\theta _0^{\frac{1}{3}}h_0^{\frac{1}{3}}} -1\right) ^2\left( 2+\dfrac{u_0^{\frac{2}{3}}}{g^{\frac{1}{3}} \theta _0^{\frac{1}{3}}h_0^{\frac{1}{3}}}\right) +a_0. \end{aligned}$$

(2.15)

We can see from Eq. (2.15) that $a_{\max }(\mathbf {U}_0)\ge a_0$ and the equality happens only along the curve $u^2=gh\theta$ on which the system is not strictly hyperbolic.

Interesting properties of the function $\varphi$ defined by (2.14) are obtained in the following lemma.

Lemma 2.1

Suppose $u_0\ne 0$. The function $\varphi (h), h>0$ is smooth, is convex, is decreasing in the interval $(0,h_{\min })$ and is increasing in the interval $(h_{\min },+\infty )$, and satisfies the limit conditions

$$\begin{aligned} \lim \limits _{h\rightarrow 0}\varphi (h)=\lim \limits _{h\rightarrow +\infty }\varphi (h)=+\infty . \end{aligned}$$

(2.16)

Consequently, if $a\le a_{\max }$, the function $\varphi$ has two zeros $h_{*}(\mathbf {U}_0,a),h^{*}(\mathbf {U}_0,a)$ such that $h_{*}(\mathbf {U}_0,a)\le h_{\min }(\mathbf {U}_0)\le h^{*}(\mathbf {U}_0,a)$. The inequalities are strict whenever $a<a_{\max }(\mathbf {U}_0)$.

Proof

The smoothness of the function $\varphi$ and the limit conditions at infinity (2.16) are obvious. Moreover, we have

$$\begin{aligned} \varphi '(h)=1-\dfrac{u_0^2h_0^2}{g\theta _0h^3} \end{aligned}$$

(2.17)

(for $u_0\ne 0$). Thus, $\varphi '(h)$ is positive if

$$\begin{aligned} h>\left( \dfrac{u_0^2h_0^2}{g\theta _0}\right) ^{\frac{1}{3}} =h_{\min }(\mathbf {U}_0), \end{aligned}$$

and $\varphi '(h)<0$ if $0<h<h_{\min }(\mathbf {U}_0)$. This establishes the monotonicity properties of $\varphi$. Furthermore, we have

$$\begin{aligned} \varphi ''(h)=3\dfrac{u_0^2h_0^2}{g\theta _0h^4}\ge 0 \end{aligned}$$

which establishes the convexity of $\varphi$. Consequently, $\varphi$ attains its minimum value at $h_{\min }(\mathbf {U}_0)$. That is,

$$\begin{aligned} \min \varphi = \varphi (h_{\min }(\mathbf {U}_0)). \end{aligned}$$

If $a<a_{\max }(\mathbf {U}_0)$, then the minimum value $\varphi (h_{\min }(\mathbf {U}_0))$ is negative. It is derived from the limit conditions (2.16) that the equation $\varphi (h)=0$ has exactly two distinct roots. In addition, it is not difficult to see that the two roots of the equation $\varphi (h)=0$ coincide when $a=a_{\max }(\mathbf {U}_0)$. $\square$

It is arisen from the above lemma that there are two choices of a contact wave from a given state. To select a physical contact wave, we need to impose an additional admissibility criterion as follows:

• (MC) (Monotonicity criterion)—Along any stationary curve $\mathcal {W}_0(\mathbf {U}_0)$, the bottom level a is monotone as a function of h. The total variation in the bottom-level component of any Riemann solution must not exceed $| a_L -a_R |$, where $a_L$ and $a_R$ are left-hand and right-hand bottom levels.

Note that a similar condition was used in [20, 33]. Under the monotonicity criterion, a stationary contact wave always remain in the closure of each of the strictly hyperbolic domains. That is, if a state on the one side of an admissible four-contact discontinuity $\mathbf {U}_0\in {\bar{\mathbf{G}}}_i,$ where ${\bar{\mathbf{G}}}_i$ denotes the closure of the region $\mathbf {G}_i$, then the state on the other side of that contact $\mathbf {U}$ still belongs to ${\bar{\mathbf{G}}}_i$, $i=1,2,3$; see [33]. Since the point $(h_{\min }(\mathbf {U}_0),h_0u_0/h_{\min }(\mathbf {U}_0))$ is critical, we deduce the following algorithm for the computation of the admissible contact wave with a given state on the one side and given left-hand and right-hand levels of topography.

• (i) If $\mathbf {U}_0$ is a supercritical state, then the smaller root $h_{*}(\mathbf {U}_0,a)$ of $\varphi$ defined by (2.14) is selected and can be computed by Newton’s method with a starting point in the interval $(0,h_{\min }(\mathbf {U}_0))$;

• (ii) If $\mathbf {U}_0$ is a subcritical state, then the larger root $h^{*}(\mathbf {U}_0,a)$ of $\varphi$ defined by (2.14) is selected and can be computed by Newton’s method with a starting point in the interval $(h_{\min }(\mathbf {U}_0),+\infty )$.

3 Numerical Schemes

In this section, we construct well-balanced numerical schemes for approximating solutions of system (1.1), relying on the arguments in the previous sections. Given a uniform time step $\bigtriangleup t$ and a special mesh size $\bigtriangleup x$, define $x_j=j\bigtriangleup x,j\in {\mathbb {Z}}$, $t_n=n\bigtriangleup t,n\in {\mathbb {N}}$, and denote by $\mathbf {U}_j^n$ the approximate value of the exact solution $\mathbf {U}=(h,hu,h\theta )^\mathrm{T}$ of system (1.1) at the time $t^n$ in the interval $(x_{j-1/2},x_{j+1/2})$. Set

$$\begin{aligned} \lambda =\dfrac{\bigtriangleup t}{\bigtriangleup x}, \end{aligned}$$

where $\lambda$ is required to satisfy the CFL condition

$$\begin{aligned} \lambda< \dfrac{\text {CFL coefficient}}{\max _{h,u}\{|u|+\sqrt{gh\theta }\}},\quad 0<\text {CFL coefficient}\le 1. \end{aligned}$$

3.1 Constructing the Well-Balanced Schemes

The method we use to construct the well-balanced scheme consists of two steps:

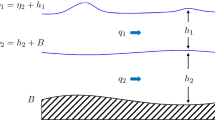
• Step 1: First, the source term on the right-hand side of system (1.1) will be absorbed in stationary contact waves at each grid node: For each state $\mathbf {U}_j^n$ at the time $t^n$ in the interval $(x_{j-1/2},x_{j+1/2})$, there is a state $\mathbf {U}_{j-1,+}^n$ on the left and a state $\mathbf {U}_{j+1,-}^n$ on the right of that interval that can be connected to $\mathbf {U}_j^n$ by a contact wave.

• Step 2: Second, the states on both sides of the contact waves in Step 1 will be incorporated in a standard numerical flux for conservation laws: $\mathbf {U}_{j-1,+}^n$ and $\mathbf {U}_{j+1,-}^n$ which will replace $\mathbf {U}_{j-1}^n$ and $\mathbf {U}_{j+1}^n$, respectively, in a standard numerical flux for conservation laws.

Precisely, the scheme is defined by

$$\begin{aligned} \mathbf {U}_j^{n+1}=\mathbf {U}_j^n-\lambda \left( k(\mathbf {U}_j^n,\mathbf {U}_{j+1,-}^n) -k(\mathbf {U}_{j-1,+}^n,\mathbf {U}_j^n)\right) , \end{aligned}$$

(3.1)

where k, which will be referred to as the underlying numerical flux, can be any standard numerical flux for conservation laws. For example, one may take the underlying numerical flux to be the one of the Lax–Friedrichs schemes:

$$\begin{aligned} k_{LF}(\mathbf {U},\mathbf {V})=\dfrac{1}{2}(\mathbf {f}(\mathbf {U}) +\mathbf {f}(\mathbf {V})) - \dfrac{1}{2\lambda }(\mathbf {V}-\mathbf {U}). \end{aligned}$$

(3.2)

The computation of the states $\mathbf {U}_{j+1,-}^n,\mathbf {U}_{j-1,+}^n$ is now discussed. In scheme (3.1), the states

$$\begin{aligned} \mathbf {U}_{j+1,-}^n=[(h,hu,h\theta )^\mathrm{T}]_{j+1,-}^n, \mathbf {U}_{j-1,+}^n=[(h,hu,h\theta )^\mathrm{T}]_{j-1,+}^n \end{aligned}$$

are defined by observing that the entropy is constant across each stationary jump, and by computing $h_{j+1,-}^n,u_{j+1,-}^n, \theta _{j+1,-}^n$ from the system

$$\begin{aligned}&h_{j+1}^n u_{j+1}^n = h_{j+1,-}^nu_{j+1,-}^n,\nonumber \\&\dfrac{(u_{j+1}^n)^2}{2}+g\theta _{j+1}^n(h_{j+1}^n+a_{j+1}) = \dfrac{(u_{j+1,-}^n)^2}{2}+g\theta _{j+1}^n(h_{j+1,-}^n+a_j),\nonumber \\&\theta _{j+1}^n = \theta _{j+1,-}^n, \end{aligned}$$

(3.3)

and computing $h_{j-1,+}^n,u_{j-1,+}^n, \theta _{j-1,+}^n$ from the system

$$\begin{aligned}&h_{j-1}^n u_{j-1}^n = h_{j-1,+}^nu_{j-1,+}^n,\nonumber \\&\dfrac{(u_{j-1}^n)^2}{2}+g\theta _{j-1}^n(h_{j-1}^n+a_{j-1}) = \dfrac{(u_{j-1,+}^n)^2}{2}+g\theta _{j-1}^n(h_{j-1,+}^n+a_j),\nonumber \\&\theta _{j-1}^n = \theta _{j-1,+}^n. \end{aligned}$$

(3.4)

Observe that from Eq. (2.15), we have

$$\begin{aligned} a_{\max }(\mathbf {U}_{j+1}^n)&= \dfrac{h_{j+1}^n}{2}\left( \dfrac{(u_{j+1}^n)^{\frac{2}{3}}}{g^{\frac{1}{3}}(\theta _{j+1}^n)^{\frac{1}{3}}(h_{j+1}^n)^{\frac{1}{3}}} -1\right) ^2\left( 2+\dfrac{(u_{j+1}^n)^{\frac{2}{3}}}{g^{\frac{1}{3}}(\theta _{j+1}^n)^{\frac{1}{3}}(h_{j+1}^n)^{\frac{1}{3}}} \right) +a_{j+1}^n. \end{aligned}$$

(3.5)

Thus, $a_{\max }(\mathbf {U}_{j+1}^n)\ge a_{j+1}$ and therefore system (3.3) have a solution provided

$$\begin{aligned} a_{\max }(\mathbf {U}_{j+1}^n)\ge a_j. \end{aligned}$$

To ensure that the scheme always works, we may modify the value $a_j$ and re-assign it to a new value $a_{\max }(\mathbf {U}_{j+1}^n)$, if necessary. A similar procedure is used for system (3.4). In particular, the bottom function a is expected not to have too large jumps near the critical surface.

Scheme (3.1) is well balanced in the sense that it can capture exactly stationary waves. Indeed, it holds for any stationary waves that

$$\begin{aligned}&h_{j+1}^n u_{j+1}^n = h_ju_j,\nonumber \\&\dfrac{(u_{j+1}^n)^2}{2}+g\theta _{j+1}^n(h_{j+1}^n+a_{j+1}) = \dfrac{u_j^2}{2}+g\theta _{j+1}^n(h_j+a_j),\nonumber \\&\theta _{j+1}^n = \theta _j, \end{aligned}$$

(3.6)

and

$$\begin{aligned}&h_{j-1}^n u_{j-1}^n = h_ju_j,\nonumber \\&\dfrac{(u_{j-1}^n)^2}{2}+g\theta _{j-1}^n(h_{j-1}^n+a_{j-1}) = \dfrac{u_j^2}{2}+g\theta _{j-1}^n(h_j+a_j),\nonumber \\&\theta _{j-1}^n = \theta _j. \end{aligned}$$

(3.7)

This yields

$$\begin{aligned}&h_{j+1,-}^n=h_j, u_{j+1,-}^n=u_j, \theta _{j+1,-}^n=\theta _j,\\&h_{j-1,+}^n=h_j, u_{j-1,+}^n=u_j, \theta _{j-1,+}^n=\theta _j. \end{aligned}$$

Thus,

$$\begin{aligned} \mathbf {U}_{j+1,-}^n=\mathbf {U}_j^n,\quad \mathbf {U}_{j-1,+}^n=\mathbf {U}_j^n, \end{aligned}$$

and therefore, the scheme gives

$$\begin{aligned} \mathbf {U}_j^{n+1}=\mathbf {U}_j^n. \end{aligned}$$

This means that the solution is stationary.

Now, it is interesting to observe that a particular choice of scheme (3.1), which takes the underlying numerical flux (3.2), can preserve the positivity of the height and temperature of water.

Theorem 3.1

Scheme (3.1)–(3.2) is positively conservative for the water height. That is, if $h_j^0\ge 0$ for all $j\in {\mathbb {Z}}$, then $h_j^n\ge 0$ for all $n\in {\mathbb {N}}, j\in {\mathbb {Z}}$.

Proof

We need only to verify that for an arbitrary fixed n, if $h_j^n\ge 0, \forall j$, then $h_j^{n+1}\ge 0, \forall j$. Indeed, it is not to difficult to check that $h_{j-1,+}^n$ and $h_{j+1,-}^n$ are also nonnegative for all j. Moreover, it follows from Eq. (3.1) that

$$\begin{aligned} h_j^{n+1}&=\dfrac{h_{j-1,+}^n+h_{j+1,-}^n}{2}+\dfrac{\lambda }{2} \left( h_{j-1,+}^n u_{j-1,+}^n-h_{j+1,-}^n u_{j+1,-}^n\right) \\&\ge \dfrac{h_{j-1,+}^n+h_{j+1,-}^n}{2}-\dfrac{\lambda }{2} \max \{|u_{j-1,+}^n|,|u_{j+1,-}^n|\}\left( h_{j-1,+}^n+h_{j+1,-}^n \right) \\&\ge \dfrac{h_{j-1,+}^n+h_{j+1,-}^n}{2}\left( 1-\lambda \max \{|u_{j-1,+}^n|,|u_{j+1,-}^n|\}\right) \\&\ge 0 \end{aligned}$$

due to the CFL condition. This completes the proof of Theorem 3.1.

Theorem 3.2

Scheme (3.1)–(3.2) is positively conservative for the water temperature: if $\theta _j^0\ge 0$ for all $j\in {\mathbb {Z}}$, then $\theta _j^n\ge 0$ for all $n\in {\mathbb {N}}, j\in {\mathbb {Z}}$.

Proof

By induction, we need only to show that for any fixed $n\ge 0$, if $\theta _j^n\ge 0$ for all integers j, then $\theta _j^{n+1}\ge 0$ for all integers j. Indeed, since the temperature $\theta$ remains constant across stationary waves, it holds that

$$\begin{aligned} \theta _{j-1,+}^n=\theta _{j-1}^n\ge 0, \quad \theta _{j+1,-}^n=\theta _{j+1}^n\ge 0, \end{aligned}$$

for all integers j. It therefore follows from Eq. (3.1) that

$$\begin{aligned} h_j^{n+1}\theta _j^{n+1}&=\dfrac{h_{j-1,+}^n\theta _{j-1,+}^n+h_{j+1,-}^n\theta _{j+1,-}^n}{2}\nonumber \\&\quad +\dfrac{\lambda }{2}\left( h_{j-1,+}^n\theta _{j-1,+}^n u_{j-1,+}^n-h_{j+1,-}^n\theta _{j+1,-}^n u_{j+1,-}^n\right) \\&\ge \dfrac{h_{j-1,+}^n\theta _{j-1,+}^n+h_{j+1,-}^n\theta _{j+1,-}^n}{2}-\dfrac{\lambda }{2}\max \{|u_{j-1,+}^n|,|u_{j+1,-}^n|\}\nonumber \\&\quad \left( h_{j-1,+}^n\theta _{j-1,+}^n+h_{j+1,-}^n\theta _{j+1,-}^n\right) \\&\ge \dfrac{h_{j-1,+}^n\theta _{j-1,+}^n+h_{j+1,-}^n\theta _{j+1,-}^n}{2}\left( 1-\lambda \max \{|u_{j-1,+}^n|,|u_{j+1,-}^n|\}\right) \\&\ge 0 \end{aligned}$$

due to the CFL condition. Since $h_j^{n+1}\ge 0$, we get $\theta _j^{n+1}\ge 0$. $\square$

3.2 Fast and Stable Schemes by Underlying Numerical Fluxes

In general, one may choose any standard numerical flux k in (3.1) as the underlying numerical flux. To make the scheme fast and stable, we form the underlying numerical flux to be any convex combination of the numerical fluxes of a first-order and stable scheme and a high-order one. For example, one can take the following convex combinations

$$\begin{aligned} k(\mathbf {U},\mathbf {V})=\theta k_{LF}(\mathbf {U},\mathbf {V})+(1-\theta )k_{LW}(\mathbf {U}, \mathbf {V}), \end{aligned}$$

(3.8)

for $0\le \theta \le 1$, where $k_{LW}$ is the Lax–Wendroff numerical flux:

$$\begin{aligned} k_{LW}(\mathbf {U},\mathbf {V})=\dfrac{1}{2}(\mathbf {f}(\mathbf {U}) +\mathbf {f}(\mathbf {V}))-\dfrac{\lambda }{2}\mathbf {A}^2(\mathbf {U}, \mathbf {V})(\mathbf {V}-\mathbf {U}), \end{aligned}$$

(3.9)

and

$$\begin{aligned}&\mathbf {U}=(h,hu,h\theta )^\mathrm{T},\\&\mathbf {f}(\mathbf {U})=\left( hu,hu^2+\dfrac{gh^2\theta }{2}, uh\theta \right) ^\mathrm{T},\\&\mathbf {A}(\mathbf {U},\mathbf {V})={\hat{\mathbf {A}}}_{j -\frac{1}{2}} \text { is a Roe matrix}. \end{aligned}$$

In particular, taking $\theta =1/2$ in (3.8) leads us to the one of the FORCE schemes (see [34]):

$$\begin{aligned} k_{FORCE}(\mathbf {U},\mathbf {V})=\dfrac{1}{2}k_{LF}(\mathbf {U}, \mathbf {V})+\dfrac{1}{2}k_{LW}(\mathbf {U}.\mathbf {V}). \end{aligned}$$

(3.10)

Let us construct a Roe matrix of system (1.1) as follows. The matrix ${\hat{\mathbf {A}}}_{j-\frac{1}{2}}=\mathbf {A}(\mathbf {U}_{j-1},\mathbf {U}_j)$ is chosen to be some approximation to $\mathbf {f}'(\mathbf {U})$ valid a neighborhood of the data $\mathbf {U}_{j-1}$ and $\mathbf {U}_{j}$. So ${\hat{\mathbf {A}}}_{j-\frac{1}{2}}$ satisfies condition:

$$\begin{aligned} \mathbf {f}(\mathbf {U}_{j})-\mathbf {f}(\mathbf {U}_{j-1})= {\hat{\mathbf {A}}}_{j-\frac{1}{2}}(\mathbf {U}_{j}-\mathbf {U}_{j-1}). \end{aligned}$$

(3.11)

Parameter vector $\mathbf {Z}$: $\mathbf {U}=\mathbf {U}(\mathbf {Z})$ invertible $\mathbf {Z}=\mathbf {Z}(\mathbf {U})$. We will integrate along the path

$$\begin{aligned} \mathbf {Z}(\xi )=\mathbf {Z}_{j-1}+(\mathbf {Z}_{j}-\mathbf {Z}_{j-1})\xi ,\quad 0\le \xi \le 1, \end{aligned}$$

(3.12)

where $\mathbf {Z}_i=\mathbf {Z}(\mathbf {U}_i)$ for $i=j-1,j$. Then $\mathbf {Z}'(\xi )=\mathbf {Z}_{j}-\mathbf {Z}_{j-1}$ is independent of $\xi$, and so

$$\begin{aligned} \mathbf {f}(\mathbf {U}_{j})-\mathbf {f}(\mathbf {U}_{j-1})= \int _0^1\dfrac{d}{d\xi } \mathbf {f}(\mathbf {U}(\mathbf {Z}(\xi )))d\xi =\int _0^1 \mathbf {f}'(\mathbf {U}(\mathbf {Z}(\xi )))d\xi (\mathbf {Z}_{j} -\mathbf {Z}_{j-1}). \end{aligned}$$

(3.13)

We also have

$$\begin{aligned} \mathbf {U}_{j}-\mathbf {U}_{j-1}=\int _0^1\dfrac{d}{d\xi } \mathbf {U}(\mathbf {Z}(\xi ))d\xi =\int _0^1\mathbf {U}'(\mathbf {Z}(\xi )) d\xi (\mathbf {Z}_{j}-\mathbf {Z}_{j-1}). \end{aligned}$$

(3.14)

Setting

$$\begin{aligned}&{\hat{\mathbf {C}}}_{j-\frac{1}{2}}=\int _0^1\mathbf {f}'(\mathbf {U} (\mathbf {Z}(\xi )))d\xi ,\end{aligned}$$

(3.15)

$$\begin{aligned}&{\hat{\mathbf {B}}}_{j-\frac{1}{2}}=\int _0^1\mathbf {U}'(\mathbf {Z} (\xi ))d\xi . \end{aligned}$$

(3.16)

From (3.13), (3.14), we obtain

$$\begin{aligned} \mathbf {f}(\mathbf {U}_{j})-\mathbf {f}(\mathbf {U}_{j-1})&={\hat{\mathbf {C}}}_{j-\frac{1}{2}}(\mathbf {Z}_{j}-\mathbf {Z}_{j-1}),\end{aligned}$$

(3.17)

$$\begin{aligned} \mathbf {U}_{j}-\mathbf {U}_{j-1}&={\hat{\mathbf {B}}}_{j-\frac{1}{2}} (\mathbf {Z}_{j}-\mathbf {Z}_{j-1}). \end{aligned}$$

(3.18)

From (3.18), and from using

$$\begin{aligned} {\hat{\mathbf {A}}}_{j-\frac{1}{2}}={\hat{\mathbf {C}}}_{j-\frac{1}{2}} {\hat{\mathbf {B}}}_{j-\frac{1}{2}}^{-1}, \end{aligned}$$

we obtain the relation (3.11). Now, set in system (1.1),

$$\begin{aligned} \mathbf {U}=\left[ \begin{matrix} h\\ hu\\ h\theta \end{matrix}\right] =\left[ \begin{matrix} U^1\\ U^2\\ U^3 \end{matrix}\right] . \end{aligned}$$

(3.19)

It holds that

$$\begin{aligned} \mathbf {f}(\mathbf {U})=\left[ \begin{matrix} hu\\ hu^2+\dfrac{gh^2\theta }{2}\\ uh\theta \end{matrix}\right] =\left[ \begin{matrix} U^2\\ \dfrac{(U^2)^2}{U^1}+\dfrac{gU^1U^3}{2}\\ \dfrac{U^2U^3}{U^1} \end{matrix}\right] . \end{aligned}$$

(3.20)

From (3.19), (3.20), we obtain Jacobian matrix for the shallow equations with flat bottom (a is constant):

$$\begin{aligned} \dfrac{\partial \mathbf {f}(\mathbf {U})}{\partial \mathbf {U}}&=\left[ \begin{matrix} 0 &{}\quad 1 &{}\quad 0\\ -\left( \dfrac{U^2}{U^1}\right) ^2+\dfrac{gU^3}{2} &{}\quad \dfrac{2U^2}{U^1} &{}\quad \dfrac{gU^1}{2}\\ -\dfrac{U^2U^3}{(U^1)^2} &{}\quad \dfrac{U^3}{U^1} &{}\quad \dfrac{U^2}{U^1} \end{matrix}\right] =\left[ \begin{matrix} 0 &{}\quad 1 &{}\quad 0\\ -u^2+\dfrac{gh\theta }{2} &{}\quad 2u &{}\quad \dfrac{gh}{2}\\ -u\theta &{}\quad \theta &{}\quad u \end{matrix}\right] . \end{aligned}$$

(3.21)

As a parameter vector, one may choose

A straight calculation gives us

$$\begin{aligned} \dfrac{\partial \mathbf {U}(\mathbf {Z})}{\partial \mathbf {Z}}=\left[ \begin{matrix} 2Z^1 &{}\quad 0 &{}\quad 0\\ Z^2 &{}\quad Z^1 &{}\quad 0\\ Z^3 &{}\quad 0 &{}\quad Z^1 \end{matrix}\right] , \end{aligned}$$

(3.22)

and

$$\begin{aligned} \dfrac{\partial \mathbf {f}(\mathbf {U}(\mathbf {Z}))}{\partial \mathbf {Z}}=\left[ \begin{matrix} Z^2 &{}\quad Z^1 &{}\quad 0\\ \dfrac{3g(Z^1)^2Z^3}{2} &{}\quad 2Z^2 &{} \quad \dfrac{g(Z^1)^3}{2}\\ 0 &{}\quad Z^3 &{}\quad Z^2 \end{matrix}\right] . \end{aligned}$$

(3.23)

From (3.12), it holds for each component $p=1,2,3$ that

$$\begin{aligned} Z^p=Z_{j-1}^p+(Z_j^p-Z_{j-1}^p)\xi ,\quad p=\overline{1,3}, 0\le \xi \le 1. \end{aligned}$$

This yields

$$\begin{aligned} \begin{aligned} \int _0^1 Z^p(\xi )d\xi =&\dfrac{1}{2}(Z_{j-1}^p+Z_j^p)={\overline{Z}}^p,\\ \int _0^1 (Z^1)^2Z^3 d\xi =&\dfrac{1}{4}(Z_{j-1}^1)^2Z_{j-1}^3+\dfrac{1}{12}(Z_{j-1}^1)^2Z_{j}^3 +\dfrac{1}{6}Z_{j-1}^1Z_{j}^1Z_{j-1}^3+\dfrac{1}{6} Z_{j-1}^1Z_{j}^1Z_{j}^3\\&+\dfrac{1}{12}(Z_{j}^1)^2Z_{j-1}^3+\dfrac{1}{4}(Z_{j}^1)^2Z_{j}^3 = \overline{{\overline{Z}}},\\ \int _0^1 (Z^1)^3 d\xi =&\dfrac{1}{2}(Z_{j}^1+Z_{j-1}^1).\dfrac{1}{2}\left[ (Z_{j}^1)^2 +(Z_{j-1}^1)^2\right] ={\overline{Z}}^1\overline{h}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\overline{h}=\dfrac{h_{j-1}+h_j}{2},\\&\overline{{\overline{Z}}} = \dfrac{h_{j-1}^\frac{3}{2}\theta _{j-1}}{4}+\dfrac{h_{j-1} \sqrt{h_j}\theta _j}{12}+\dfrac{\sqrt{h_j}h_{j-1}\theta _{j-1}}{6} +\dfrac{\sqrt{h_{j-1}}h_j\theta _j}{6}+\dfrac{h_j\sqrt{h_{j-1}} \theta _{j-1}}{12}+\dfrac{h_j^\frac{3}{2}\theta _j}{4}. \end{aligned} \end{aligned}$$

Substituting (3.22) into (3.16), we have

$$\begin{aligned} {\hat{\mathbf {B}}}_{j-\frac{1}{2}}=\left[ \begin{matrix} 2{\overline{Z}}^1 &{}\quad 0 &{}\quad 0\\ {\overline{Z}}^2 &{}\quad {\overline{Z}}^1 &{}\quad 0\\ {\overline{Z}}^3 &{}\quad 0 &{}\quad {\overline{Z}}^1 \end{matrix}\right] , \end{aligned}$$

which yields the inverse matrix

Similarly, substituting (3.23) into (3.16), we have

$$\begin{aligned} {\hat{\mathbf {C}}}_{j-\frac{1}{2}}=\left[ \begin{matrix} {\overline{Z}}^2 &{}\quad {\overline{Z}}^1 &{}\quad 0\\ \dfrac{3g\overline{{\overline{Z}}}}{2} &{}\quad 2{\overline{Z}}^2 &{}\quad \dfrac{g{\overline{Z}}^1\overline{h}}{2}\\ 0 &{}\quad {\overline{Z}}^3 &{} \quad {\overline{Z}}^2 \end{matrix}\right] . \end{aligned}$$

So

$$\begin{aligned} \begin{aligned} {\hat{\mathbf {A}}}_{j-\frac{1}{2}}&=\mathbf {A}(\mathbf {U}_{j-1}, \mathbf {U}_{j})=\mathbf {A}(\mathbf {U}_{j},\mathbf {U}_{j-1}) ={\hat{\mathbf {C}}}_{j-\frac{1}{2}}{\hat{\mathbf {B}}}_{j -\frac{1}{2}}^{-1}\\&= \left[ \begin{matrix} 0 &{}\quad 1 &{}\quad 0\\ \dfrac{3g\overline{{\overline{Z}}}}{4{\overline{Z}}^1} -\left( \dfrac{{\overline{Z}}^2}{{\overline{Z}}^1}\right) ^2 -\dfrac{g\overline{h}}{4}\dfrac{{\overline{Z}}^3}{{\overline{Z}}^1} &{}\quad \dfrac{2{\overline{Z}}^2}{{\overline{Z}}^1} &{}\quad \dfrac{g\overline{h}}{2}\\ -\dfrac{{\overline{Z}}^2}{{\overline{Z}}^1}\dfrac{{\overline{Z}}^3}{{\overline{Z}}^1} &{}\quad \dfrac{{\overline{Z}}^3}{{\overline{Z}}^1} &{}\quad \dfrac{{\overline{Z}}^2}{{\overline{Z}}^1} \end{matrix}\right] , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\dfrac{{\overline{Z}}^2}{{\overline{Z}}^1}=\dfrac{\sqrt{h_{j-1}} u_{j-1}+\sqrt{h_{j}}u_{j}}{\sqrt{h_{j-1}}+\sqrt{h_{j}}},\\&\dfrac{{\overline{Z}}^3}{{\overline{Z}}^1}=\dfrac{\sqrt{h_{j-1}} \theta _{j-1}+\sqrt{h_{j}}\theta _{j}}{\sqrt{h_{j-1}}+\sqrt{h_{j}}},\\&{\overline{Z}}^1=\dfrac{\sqrt{h_{j-1}}+\sqrt{h_{j}}}{2}. \end{aligned} \end{aligned}$$

Specially, if $\mathbf {U}_{j-1}=\mathbf {U}_{j}$ then ${\hat{\mathbf {A}}}_{j-\frac{1}{2}}$ is Jacobian matrix in (3.21) where $h=h_j, u=u_j, \theta =\theta _j$.

Fig. 2

Exact stationary wave (4.1) approximated by the well-balanced scheme with 250 mesh points

4 Numerical Tests

This section is devoted to numerical tests, where the exact solutions and the approximate solutions are computed and compared. The errors are computed for different mesh sizes, where we take the underlying numerical flux in our well-balanced scheme (3.1) to be the one of the Lax–Friedrichs schemes (3.2) and the FORCE scheme (3.10). The exact solution is denoted by $\mathbf {U}=(h,u,\theta )^\mathrm{T}$, and the approximate solution at the step size h is denoted by $\mathbf {U}_h^{\mathrm{LF}},\mathbf {U}_h^{\mathrm{FORCE}}$ corresponding to the scheme using the numerical flux of the Lax–Friedrichs scheme and of the FORCE scheme, respectively.

Exact solutions and approximate solutions of the Riemann problem for (1.1) will be computed on the interval $x\in [-1,1]$ at the time $t=0.1$. The CFL constant is chosen to be $\lambda =0.5$ in all of the tests.

4.1 Stationary Waves

In the last section, scheme (3.1) is shown to be well balanced in the sense that it can capture exactly stationary waves. It is interesting to see the numerical demonstration of this property. One can see that the errors are very small and almost stable, since they are caused by the errors from the input data.

Table 1 Errors of numerical approximations for different mesh sizes for test case of height bottom discontinuous

4.1.1 Test 1: Stationary Contact Discontinuities

This test is devoted to a stationary discontinuity of system (1.1)

$$\begin{aligned} (h,u,\theta ,a)(x,t)={\left\{ \begin{array}{ll} (h_L,u_L,\theta _L,a_L), &{} \text {if } x<0,\\ (h_R,u_R,\theta _R,a_R), &{} \text {if } x>0, \end{array}\right. } \end{aligned}$$

(4.1)

Fig. 3

Exact stationary wave with bottom height continuous approximated by the well-balanced scheme with 250 mesh points

Table 2 Errors of numerical approximations for different mesh sizes for test case of height bottom continuous

Table 3 States for the exact solution near dry zone in Test 3

Fig. 4

Test 3: Exact Riemann solution with Riemann data (4.3) approximated by the well-balanced scheme with Lax–Friedrichs and FORCE flux

where the left-hand and the right-hand states of the wave are approximately given by

$$\begin{aligned}&(h_L,u_L,\theta _L,a_L) = (0.2, 3, 3, 1.2),\\&(h_R,u_R,\theta _R,a_R) = (0.118727337921731, 5.053595999899697, 3, 1). \end{aligned}$$

As mentioned above, the approximate solutions are computed by the well-balanced scheme with the numerical fluxes (3.2) and (3.10). The exact solution, which is a stationary contact discontinuity, and the approximate solutions are plotted in Fig. 2. The errors for different mesh sizes are given in Table 1.

Figure 2 and Table 1 show that the approximate solutions almost coincide with the exact solution. The very errors are caused by the errors from the input data and the tolerance of the code iterative algorithm.

4.1.2 Test 2: Smooth Stationary Waves

Let us take the exact solution to be a smooth stationary wave. The solution is thus independent of time. Precisely, let us take the smooth topography as

$$\begin{aligned} a(x)=2+\text {tan}^{-1}(x), \end{aligned}$$

(4.2)

and the initial water height, water velocity and water temperature as

$$\begin{aligned} (h_0,u_0,\theta _0)=(3, 1.5, 3). \end{aligned}$$

Then, the exact solution is given by algebraic system (2.10). Note that the values of the exact solution at any mesh point $x_j$ can be computed by the exact solution and the approximate solutions are displayed in Fig. 3. The corresponding errors are given in Table 2.

From this test, one can see that the approximate solutions almost coincide with the exact solution. The errors are stable and caused by the input data and the tolerance of the code for iterative algorithms.

Table 4 Errors of numerical approximations for different mesh sizes for Test 3

Fig. 5

Test 4: Exact Riemann solution with Riemann data (4.4) approximated by the well-balanced scheme with Lax–Friedrichs and FORCE flux

4.2 Nonstationary Solutions

4.2.1 Test 3: Solutions Near Dry Zone and in the Supercritical Region

This test is aimed to show the convergence in the supercritical region and the positive conservation for the water height of the scheme, as demonstrated by Theorem 3.1. For this purpose, we take an exact nonstationary solution of the Riemann problem for (1.1) near the dry zone, i.e.,

$$\begin{aligned} h\approx 0, \end{aligned}$$

in an interval. Then, we will check that the scheme still gives the approximate solutions whose water height remains well above zero. Precisely, the Riemann data are given by

$$\begin{aligned} (h,u,\theta ,a)(x,0)={\left\{ \begin{array}{ll} (0.01, 4, 3, 1.2), &{} \text {if } x<0,\\ (0.02, 2, 4, 1), &{} \text {if } x>0. \end{array}\right. } \end{aligned}$$

(4.3)

The exact solution begins with a stationary contact wave from $U_L$ to $U_1$, followed by a 1-shock wave from $U_1$ to $U_2$, a 2-contact from $U_2$ to $U_3$, and finally a 3-shock wave from $U_3$ to $U_R$; see Table 3. It is not difficult to check that both left-hand and right-hand states $U_L, U_R$ belong to the supercritical region.

Table 5 Errors of numerical approximations for different mesh sizes for Test 4

The exact solution of the Riemann problem for (1.1) and the approximate solutions by our scheme are plotted in Fig. 4. The corresponding errors are given in Table 4. The errors become smaller as the mesh sizes are smaller.

The picture on the left upper corner of Fig. 4 shows approximate values of the water height by the scheme for different mesh sizes, which all remain well positive.

4.2.2 Test 4: Solutions in Both Supercritical and Subcritical Regions

In this test, we consider the approximation for the Riemann problem when the left-hand state is supercritical and the right-hand state is subcritical. Precisely, the Riemann data are given by

$$\begin{aligned} (h,u,\theta ,a)(x,0)={\left\{ \begin{array}{ll} (0.2, 3, 3, 1), &{} \text {if } x<0,\\ (0.195816152469433, 0.182801122801997, 5, 1.1), &{} \text {if } x>0. \end{array}\right. } \end{aligned}$$

(4.4)

See Fig. 5 and Table 5 for the comparison of the errors of the well-balanced scheme with Lax–Friedrichs and FORCE flux.

In this test, one can see that the errors are small and decrease significantly when the mesh sizes tends to zero.

Fig. 6

Test 5: Exact Riemann solution with Riemann data (4.5) approximated by the well-balanced scheme with Lax–Friedrichs and FORCE flux

4.2.3 Test 5: Approximation in Subsonic Region

In this test, we consider the approximation of the exact solution of the Riemann problem when the left-hand and right-hand states are subcritical. Precisely, the Riemann data are given by

$$\begin{aligned} (h,u,\theta ,a)(x,0)=\left\{ \begin{array}{l@{\quad }l} (1, 3, 2, 1), &{} \text {if } x<0,\\ (0.912012600264880, -0.176048159061341, 3, 1.1), &{} \text {if } x>0. \end{array}\right. \end{aligned}$$

(4.5)

Table 6 Errors and orders of accuracy of well-balanced scheme using Lax–Friedrichs and FORCE flux in Test 5

The exact solution and the approximate solutions are plotted in Fig. 6. The errors and orders of accuracy are given in Table 6.

Again, in this test, the scheme still possesses a very good accuracy. When using the underlying numerical flux of the FORCE scheme, the scheme has a much better accuracy than using the one of the Lax–Friedrichs schemes.

5 Conclusions

Numerical scheme (3.1) for the shallow water equations with variable topography and horizontal temperature gradient is constructed and tested. It is well balanced in the sense that it can capture stationary waves. In addition, the scheme with a particular choice of the underlying numerical flux to be the one of the Lax–Friedrichs schemes possesses interesting properties: it preserves the positivity of the water height and the positivity of the temperature. This well-balanced scheme provides us with very reasonable accuracy. It is interesting to note that we can improve the accuracy of the scheme by using the underlying numerical flux obtained as a convex combination of the numerical fluxes of a first-order and stable scheme and a high-order one, such as the FORCE scheme. Tests show that the scheme is convergent for all the circumstances when the exact solution belongs to either the supercritical region or the subcritical region, or expands in both supercritical and subcritical regions.