A Stabilized Characteristic-Nonconforming Finite Element Method for Time-Dependent Incompressible Navier–Stokes Equations

Abstract

In this paper, we study a stabilized characteristic-nonconforming finite element method to solve the time-dependent incompressible Navier–Stokes equations. The characteristic scheme is used to deal with advection term and temporal differentiation, which avoid some difficulties caused by trilinear terms. The space discretization utilizes the nonconforming lowest equal-order pair of mixed finite elements (i.e. $\textit{NCP}_1-{\mathbf {P}}_1$). The stability analysis and optimal-order error estimates for velocity and pressure are presented. Numerical results are also provided to verify theory analysis.

1 Introduction

The time-dependent incompressible Navier–Stokes equations are one of the most important equations in mathematical physics and fluid mechanics. To solve them, a variety of numerical methods are proposed. Among them, the characteristics methods (or the Lagrange–Galerkin methods) have proved their efficiency for the problem when advection dominates diffusion. These methods are based on combining a Galerkin finite element procedure with a special discretization of the material derivative along trajectories, which have some common features, such as better stability, larger time steps, etc. [1]. On the other hand, if standard finite element methods are used to solve the incompressible Navier–Stokes equations, the approximations for velocity and pressure must satisfy the LBB conditions to be stable. This cause some difficulties in using low-order finite element pairs because of the lack of LBB condition. However, the equal-order pairs for velocity and pressure are of practical important in scientific computation because they are computationally convenient and efficient in a parallel or multi-grid context [2]. To compensate the lack of LBB stability, all kinds of stabilized techniques have been proposed, such as residual-based stabilized methods in [3–9], non-residual stabilized methods in [5–8], polynomial pressure-stabilized methods [10–15]. For the non-stationary Navier–Stokes equations, characteristic methods combining with pressure projection stabilized method and macro-element technique, respectively, is proposed in [16, 17]. In the above methods, the standard conforming finite element methods are used. Compared with the conforming finite element methods, the nonconforming finite element possesses more favorable stability properties and less support sets [18, 19]. Hence, we will focus on the application of the nonconforming finite elements in characteristic methods for non-stationary Navier–Stokes equations.

A lot of work has been devoted to study the lowest order nonconforming finite elements. For example, the nonconforming elements proposed by Douglas et al. [20] for the piecewise velocity and a piecewise constant element for the pressure were used for the stationary Stokes and Navier–Stokes equations in [21], and the nonconforming and conforming piecewise linear polynomial approximations for the velocity and pressure were used for the Navier–Stokes equations in [22]. In 2002, Chen proposed characteristic mixed discontinuous finite element methods for advection-dominated diffusion problems in [23]. Two years later, characteristic-nonconforming finite elements for advection-dominated diffusion problems are proposed in [24]. In [23, 24], advection-dominated diffusion problems were both solved by characteristic technique and nonconforming finite element methods, but the different nonconforming finite elements were used. In this paper, the method we proposed is to combine the characteristic-nonconforming finite element methods developed in [24] and characteristic stabilized finite element methods developed in [16] to solve the non-stationary incompressible Navier–Stokes equations. The method is based on the $\textit{NCP}_1-{\mathbf {P}}_1$ approximations for velocity and pressure, respectively, where $\textit{NCP}_1$ is the space of the nonconforming ${\mathbf {P}}_1$ elements. The optimal-order error estimates are derived. Numerical results agreeing with the error estimates are obtained. Furthermore, numerical comparisons with characteristic stabilized finite element also show the better performance of the present method.

The outline of the paper is as follows. In next section, we introduce the notation used in the paper and give a description of the model and method we study. In Sect. 3, the characteristic-nonconforming stabilized finite element method is proposed and the stability analysis is done. In Sect. 4, optimal-order error estimates for the stabilized characteristic-nonconforming finite element solution are derived. Some numerical experiments for illustrating the theoretical results are given in Sect. 5. The article is concluded in final section.

2 Problem Setting

Let $\Omega$ be a bounded domain in $R^2$, with Lipschitz-continuous boundary $\Gamma$. Throughout the paper, the standard notations for Sobolev space and their associated norms and seminorms are used. The symbol C denotes a generic positive constant whose value may change from place to place.

The governing equations we study read:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial \mathbf{u}}{\partial t}-\mu \Delta \mathbf{u}+(\mathbf{u}\cdot \nabla )\mathbf{u}+\nabla p=\mathbf{f} &{}\quad \text{ in } \, \Omega _T,\\ \text{ div }\mathbf{u}=0 &{}\quad \text{ in } \, \Omega _T,\\ \mathbf{u}(0)=\mathbf{u}_0&{}\quad \text{ in } \, \Omega , \\ \mathbf{u}=0&{}\quad \text{ on } \, \Gamma \times (0,T], \end{array}\right. \end{aligned}$$

(2.1)

where $\Omega _T=\Omega \times (0,T]$, $0<T\le +\infty$. $\mathbf{u}=(u_1, u_2)$ and $\mathbf{f}=(f_1,f_2)$ denote the flow velocity and the external force, respectively, p(x, t) denotes the pressure, $\mu >0$ is the viscous coefficient, and T is the given final time.

To obtain a mixed variational form of problem (2.1), the following spaces are introduced

$$\begin{aligned}&X =H_0^1(\Omega )^2,\quad Y=L^2(\Omega )^2,\quad M=L_0^2(\Omega ),\quad V=\{\mathbf{v}\in X:\mathrm{div} v=0\},\\&D(A) =(H^2(\Omega ))^2\cap V\quad H=\{\mathbf{v}\in H_0^1(\Omega )^2|\nabla \cdot \mathbf{v}=0\quad \text{ in }\,\Omega \quad \text{ and }\quad \mathbf{v}\cdot \mathbf{n}=0\}, \end{aligned}$$

and

$$\begin{aligned} L^P(0,T;X)= & {} \{v:\{t_1\ldots ,t_M\}\rightarrow X|\Vert v\Vert _{L^p(0,T;x)}\\= & {} \left[ \Delta t\sum \limits _{i=1}^M\Vert v(t_i)\Vert _X^p\right] ^{\frac{1}{p}}<\infty \},\quad 1\le p<\infty ,\\ L^\infty (0,T;X)= & {} \{v:\{t_1,...,t_M\}\rightarrow X|\Vert v\Vert _{L^\infty (0,T;X)}\\&= \max \limits _{1\le i\le M}\Vert v(t_i)\Vert _X<\infty \},\quad 1\le p<\infty . \end{aligned}$$

The bilinear forms $a(\cdot ,\cdot ), d(\cdot ,\cdot )$ on $X\times X , X\times M$ are defined by

$$\begin{aligned} a(\mathbf{u},\mathbf{v})=\mu (\nabla \mathbf{u},\nabla \mathbf{v}),\quad d(\mathbf{v},q)=(\mathrm{div}{} \mathbf{v},q)=-(\mathbf{v},\nabla p)\,, \end{aligned}$$

and trilinear form $b(\cdot ,\cdot ,\cdot )$ on$X\times X\times X$ by

$$\begin{aligned} b(\mathbf{u},\mathbf{v},\mathbf{w})=((\mathbf{u}\cdot \nabla \mathbf{v}),\mathbf{w}). \end{aligned}$$

So, we can define a generalized bilinear form on $(X,M)\times (X,M)$ as follows:

$$\begin{aligned} B((\mathbf{u},p);(\mathbf{v},q))=a(\mathbf{u},\mathbf{v})-d(\mathbf{v},p)+d(\mathbf{u},q), \end{aligned}$$

which has the following properties [25, 26]:

• (1) $|B((\mathbf{u},p);(\mathbf{u},p))|=\mu \Vert \mathbf{u}\Vert ^2_1$;

• (2) $|B((\mathbf{u},p);(\mathbf{v},q))|\le c(\Vert \mathbf{u}\Vert _1+\Vert p\Vert _0)(\Vert \mathbf{v}\Vert _1+\Vert q\Vert _0)$;

• (3) $\beta _0(\Vert \mathbf{u}\Vert _1+\Vert p\Vert _0)\le \sup \limits _{(\mathbf{v},q)\in (X\times M)}\frac{|B((\mathbf{u},p);(\mathbf{v},q))|}{\Vert \mathbf{v}\Vert _1+\Vert q\Vert _0}$.

The solution (u,p) of problem (2.1) satisfys the following regularity hypotheses:

• (A) $\mathbf{u}\in L^\infty (0,T,H^2(\Omega )^2\cap C(C^{0,1}({\bar{\Omega }})^2)\cap C(V)$,

• (B) $\frac{\mathrm{d}{} \mathbf{u}}{\mathrm{d}t}\in L^2(H^2(\Omega )^2\cap L^2(H),\qquad D_t^2\mathbf{u}\in L^2(H)$,

• (C) $p\in L^\infty (H^1(\Omega )\cap L^\infty (L_0^2(\Omega )),\frac{\mathrm{d}p}{\mathrm{d}t}\in L^2(H^1(\Omega ))$.

The mixed variational formulation of problem (2.1) reads: find $(\mathbf{u},p)\in L^2(0,T;X)\times L^2(0,T;M)$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} (\mathbf{u}_t,\mathbf{v})+b(\mathbf{u},\mathbf{u},\mathbf{v})+B((\mathbf{u},p);(\mathbf{v},q))=(\mathbf{f},\mathbf{v})&{}\forall (\mathbf{v},q)\in X\times M,\\ \mathbf{u}(0)=\mathbf{u}_0. \end{array}\right. \end{aligned}$$

(2.2)

The characteristic method is based on the fact that the term $\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u}\cdot \triangledown )\mathbf{u}$ can be written as $D\mathbf{u}/Dt$, the total derivative of $\mathbf{u}$ in the direction of flow u. Let $\psi =(1+|\mathbf{u}|^2)^{\frac{1}{2}}$, then characteristic direction of operator $\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u}\cdot \triangledown )\mathbf{u}$ can be defined as follows:

$$\begin{aligned} \frac{\partial }{\partial \tau }=\frac{1}{\psi }\frac{\partial }{\partial t}+\sum \limits _{i=1}^{n}\frac{\mathbf{u}_i}{\psi }\frac{\partial }{\partial x_i}. \end{aligned}$$

Thus

$$\begin{aligned} D_t\mathbf{u}=\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u}\cdot \triangledown )\mathbf{u}=\psi \frac{\partial \mathbf{u}}{\partial \tau }. \end{aligned}$$

Accordingly, an equivalent variational form of (2.2) has the following form:

$$\begin{aligned} \left\{ \begin{array}{ll} (D_t\mathbf{u},\mathbf{v})+B((\mathbf{u},p);(\mathbf{v},q))=(\mathbf{f},\mathbf{v})&{}\forall (\mathbf{v},q)\in X\times M,\\ \mathbf{u}(0)=\mathbf{u}_0. \end{array}\right. \end{aligned}$$

(2.3)

The core of the characteristic method lies in the discretization of $D_t\mathbf{u}$. To achieve this, let $X(x,t_{m+1};t)$ denote the characteristic curves associated with the material derivative, so

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}X(x,t_{m+1};t)}{\mathrm{d}t}=\mathbf{u}(X(x,t_{m+1};t),t),\\ X(x,t_{m+1};t_{m+1})=x. \end{array} \right. \end{aligned}$$

(2.4)

Noting that $X(x,t_{m+1};t)$ is the departure point and represents the position at time t of a particle which locates at x at time $t_{m+1}$. Hence, for all $(x,t)\in \Omega \times [t_m,t_{m+1}]$, we have

$$\begin{aligned} x-X(x,t_{m+1};t_m)=\int _{t_m}^{t_{m+1}}{} \mathbf{u}(X(x,t_{m+1};t),t)\mathrm{d}t \end{aligned}$$

Accurate estimation of the characteristic curve $X(x,t_{m+1};t)$ is crucial to the overall accuracy of the method of characteristic. If the integral approximation is first order, it yields

$$\begin{aligned} X(x,t_{m+1};t_m)\approx x-\Delta t\mathbf{u}(x,t_{m+1}). \end{aligned}$$

(2.5)

Therefore, an approximation can be obtained:

$$\begin{aligned} D_t\mathbf{u}(x,t_{m+1})= & {} \psi \displaystyle \frac{\partial \mathbf{u}}{\partial \tau }(x,t_{m+1})\\\approx & {} \psi \displaystyle \frac{\mathbf{u}_h^{m+1}-\mathbf{u}_h^m(X_h^m(x,t_{m+1};t_m),t_m)}{\{|x-X(x,t_{m+1};t_m)|^2+|t_{m+1}-t_m|^2\}^\frac{1}{2}}\\= & {} \displaystyle \frac{\mathbf{u}(x,t_{m+1})-\mathbf{u}(X(x,t_{m+1};t_m),t_m)}{\Delta t}. \end{aligned}$$

3 The Characteristic-Nonconforming Stabilized Finite Element Approximation

Let $K_h$ be a regular triangulation of $\Omega$ into elements $\{K_j\}:{\bar{\Omega }}=\cup \bar{K_j}$, where ${\bar{\Omega }}$ and $\bar{K_j}$ stand for the closure of $\Omega$ and K, respectively. The boundary of $K_j$ on $\partial \Omega$ is denoted by $\Gamma _j=\partial \Omega \cap \partial K_j$. Denote an interior boundary between elements $K_j$ and $K_k$ by

$$\begin{aligned} \Gamma _{jk}=\Gamma _{kj}=\partial K_j\cap \partial K_k. \end{aligned}$$

and the centers of $\Gamma _j$ and $\Gamma _{jk}$ by $\xi _j$ and $\xi _{jk}$, respectively. Therefore, the nonconforming finite element space for the velocity and conforming finite element space are defined as follows:

$$\begin{aligned} \textit{NCP}_1= & {} \{\mathbf{v}\in Y:\mathbf{v}|_K\in (P_1(K))^2 \forall K\in K_h;\mathbf{v}(\xi _{jk})=\mathbf{v}(\xi _{kj}),\mathbf{v}(\xi _j)=0 \quad \forall j,k \},\\ {\mathbf {P}}_1= & {} \{p\in H^1(\Omega )\cap M:p|_K\in P_1(K) \quad \forall K\in K_h\}. \end{aligned}$$

Notably, the nonconforming finite element space $\textit{NCP}_1$ for the velocity is not a subspace of X. For $\forall \mathbf{v}\in \textit{NCP}_1$, the following compatibility conditions hold for all j and k:

$$\begin{aligned} \int _{\Gamma _{jk}}[\mathbf{v}]\mathrm{d}t=0 \quad \mathrm{and} \int _{\Gamma _j}{} \mathbf{v}\mathrm{d}t=0, \end{aligned}$$

where $[\mathbf{v}]=\mathbf{v}|_{\Gamma _{jk}}-\mathbf{v}|_{\Gamma _j}$ denotes the jump of the function $\mathbf{v}$ across the interface $\Gamma _{jk}$.

These two finite element spaces $\textit{NCP}_1$ and ${\mathbf {P}}_1$ have the following property: for any $(\mathbf{v},q)\in ((H^2(\Omega ))^2\cap X)\times (H^1(\Omega )\cap M)$, there exists$(\mathbf{v}_I,q_I)\in (\textit{NCP}_1\times {\mathbf {P}}_1)$ such that

$$\begin{aligned} \Vert \mathbf{v}-\mathbf{v}_I\Vert _0+h (\Vert \mathbf{v}-\mathbf{v}_I\Vert _{1,h}+\Vert q-q_I\Vert _0)\le Ch^2 (\Vert \mathbf{v}\Vert _2+\Vert q\Vert _1). \end{aligned}$$

where $\Vert \cdot \Vert _{1,h}$ denotes the (broken) energy norm:$\Vert \cdot \Vert _{1,h}=(\sum _j|\mathbf{v}|_{1,K_j}^2)^\frac{1}{2},\forall \mathbf{v}\in \textit{NCP}_1.$

Hence, we can define the discrete bilinear forms as follows:

$$\begin{aligned} a_h(\mathbf{u},\mathbf{v})= & {} \nu \sum \limits _j(\nabla \mathbf{u},\nabla \mathbf{v})_j, \ \mathbf{u},\mathbf{v}\in \textit{NCP}_1,\\ d_h(\mathbf{u},\mathbf{v})= & {} \sum \limits _j(div \mathbf{u},q)_j,\ \mathbf{v}\in \textit{NCP}_1,q\in {\mathbf {P}}_1, \end{aligned}$$

where $(\cdot ,\cdot )_j=(\cdot ,\cdot )_{K_j}$and $\langle \cdot ,\cdot \rangle _j=\langle \cdot ,\cdot \rangle _{\partial K_j}$denote the$L^2$-inner products on $K_j$ and $\partial K_j$, respectively.

It is well known that the $\textit{NCP}_1-{\mathbf {P}}_1$ pair does not satisfy the LBB condition. However, as in [15], we introduce a standard $L^2$-projection operator $\Pi _h$:

$$\begin{aligned} \Pi _h:L^2(\Omega )\rightarrow {\mathbf {P}}_0, \end{aligned}$$

where ${\mathbf {P}}_0=\{p\in M:p|_K\in P_0(K) \ \forall K\in K_h\}.$ Then a simple effective stabilization term $G_h(\cdot ,\cdot )$ can be defined as

$$\begin{aligned} G_h(p,q)=(p-\Pi _h p,q-\Pi _h q), \end{aligned}$$

and the projection operator $\Pi _h$ has the following properties [10]:

$$\begin{aligned} (p,q_h)= & {} (\Pi _h p,q_h)\quad \forall p\in M,q_h\in {\mathbf {P}}_0,\end{aligned}$$

(3.1)

$$\begin{aligned} \Vert \Pi _h p\Vert _0\le & {} c\Vert p\Vert _0\quad \forall p\in M,\end{aligned}$$

(3.2)

$$\begin{aligned} \Vert p-\Pi _h p\Vert _0\le & {} Ch\Vert p\Vert _1\quad \forall p\in H_1(\Omega )\cap M. \end{aligned}$$

(3.3)

In conclusion, a stabilized nonconforming mixed finite element approximation of problem (2.3) reads

Definition

Assume that $\mathbf{u}_h^m$ and $p_h^m$ are the approximations of velocity and pressure at the point $(x,t_m)$, respectively, seek $(\mathbf{u}_h^{m+1},p_h^{m+1})\in \textit{NCP}_1\times {\mathbf {P}}_1$, such that

$$\begin{aligned} (d_t \mathbf{u}_h^{m+1},\mathbf{v}_h)+{{\mathcal {B}}}_h(( \mathbf{u}_h^{m+1},p_h^{m+1});(\mathbf{v}_h,q_h))=(\mathbf{f}^{m+1},\mathbf{v}_h),\,\forall \mathbf{v}_h\in \textit{NCP}_1,q_h\in {\mathbf {P}}_1, \end{aligned}$$

(3.4)

where

$$\begin{aligned} d_t \mathbf{u}_h^{m+1}(x)=\frac{\mathbf{u}_h^{m+1}(x)-\mathbf{u}_h^m(X_h^m(x,t_{m+1};t_m))}{\Delta t}, \end{aligned}$$

and

$$\begin{aligned} {{\mathcal {B}}}_h((\mathbf{u},p);(\mathbf{v},q))=a_h(\mathbf{u},\mathbf{v})-d_h(\mathbf{v},p)+d_h(\mathbf{u},q)+\alpha G_h(p,q) \end{aligned}$$

is the stabilized bilinear form defined on $\{\textit{NCP}_1\times {\mathbf {P}}_1\}\times \{\textit{NCP}_1\times {\mathbf {P}}_1\}$, where the $\alpha$ is a positive stabilization parameter and determined by numerical trials. The following theorem establishes the weak coercivity of the bilinear form ${{\mathcal {B}}}_h((\mathbf{u},p);(\mathbf{v},q))$ for the lowest equal-order nonconforming finite element pairs.

Lemma 3.1

[27] The bilinear form ${\mathcal {B}}_h((\cdot ,\cdot );(\cdot ,\cdot ))$ satisfies the continuous property

$$\begin{aligned} |{{\mathcal {B}}}_h((\mathbf{u}_h,p_h);(\mathbf{v}_h,q_h))|\le & {} c(\Vert \mathbf{u}_h\Vert _{1,h}+\Vert p_h\Vert _0)(\Vert \mathbf{v}_h\Vert _{1,h}+\Vert q_h\Vert _0),\quad \\&\quad \forall (\mathbf{u}_h,p_h),(\mathbf{v}_h,q_h)\in \textit{NCP}_1\times {\mathbf {P}}_1 \end{aligned}$$

and the coercive property

$$\begin{aligned} \beta (\Vert \mathbf{u}_h\Vert _{1,h}+\Vert p_h\Vert _0)\le & {} \sup \limits _{0\ne (\mathbf{v}_h,q_h)\in \textit{NCP}_1\times P_1}\frac{{{\mathcal {B}}}_h((\mathbf{u}_h,p_h);(\mathbf{v}_h,q_h))}{\Vert \mathbf{v}_h\Vert _{1,h}+\Vert q_h\Vert _0},\quad \\&\quad \forall (\mathbf{u}_h,p_h)\in \textit{NCP}_1\times {\mathbf {P}}_1 \end{aligned}$$

where the constants $c>0$ and $\beta >0$ are independent of h.

Lemma 3.2

[10] There exists a positive constant C such that

$$\begin{aligned} Ch\Vert \nabla p_h\Vert _0\le \Vert p_h-\Pi _h p_h\Vert _0 \quad \forall p_h\in {\mathbf {P}}_1. \end{aligned}$$

Existence and uniqueness of the approximate solution of problem (3.4) can be easily checked as in [15].

Lemma 3.3

[28] It holds that

$$\begin{aligned} ({\overline{u}},{\overline{u}})-(u,u)\le C\Delta t(u,u) \forall u\in X, \end{aligned}$$

where ${\overline{u}}=u(x-u(x,t)\Delta t)$.

Now, we present the stability of the numerical solutions for problem (3.4).

Theorem 3.1

Under the assumptions of $f\in L^2(0,T;L^2(\Omega )^2)$, for $1\le m\le k+1$, the solution $(u_h^{m+1},p_h^{m+1})$ of (3.4) satisfies

$$\begin{aligned} \Vert \mathbf{u}_h^{k+1}\Vert _0^2+\mu \sum _{m=0}^k\Vert \nabla u_h^{m+1}\Vert _0^2\Delta t+2h^2\sum _{m=0}^k\Vert p_h^{m+1}\Vert _0^2\Delta t\le C. \end{aligned}$$

Proof. At $t=t^{m+1}$, choosing $(v_h,q_h)=(u_h^{m+1},p_h^{m+1})$ in (3.4), we get

$$\begin{aligned} \left( \frac{\mathbf{u}_h^{m+1}-\overline{\mathbf{u}}_h^m}{\Delta t},\mathbf{u}_h^{m+1}\right) +\mu \Vert \nabla \mathbf{u}_h^{m+1}\Vert _0^2+G(p_h^{m+1},p_h^{m+1})=(\mathbf{f}^{m+1},\mathbf{u}_h^{m+1}). \end{aligned}$$

(3.5)

Noting that

$$\begin{aligned}&\frac{1}{\Delta t}(\mathbf{u}_h^{m+1}-\overline{\mathbf{u}}_h^m,\mathbf{u}_h^{m+1})\nonumber \\&\quad =\frac{1}{2\Delta t}(\mathbf{u}_h^{m+1}-\overline{\mathbf{u}}_h^m,\mathbf{u}_h^{m+1}+\overline{\mathbf{u}}_h^m+\mathbf{u}_h^{m+1}-\overline{\mathbf{u}}_h^m)\nonumber \\&\quad \ge \frac{1}{2\Delta t}[(\mathbf{u}_h^{m+1},\mathbf{u}_h^{m+1})-(\overline{\mathbf{u}}_h^m,\overline{\mathbf{u}}_h^m)]\nonumber \\&\quad =\frac{1}{2\Delta t}\{[(\mathbf{u}_h^{m+1},\mathbf{u}_h^{m+1})-(\mathbf{u}_h^{m},\mathbf{u}_h^{m})]+[(\mathbf{u}_h^{m},\mathbf{u}_h^{m})-(\overline{\mathbf{u}}_h^m,\overline{\mathbf{u}}_h^m)]\}, \end{aligned}$$

(3.6)

and by Lemma 3.2, we obtain

$$\begin{aligned} Ch\Vert \nabla p_h^{m+1}\Vert _0\le \Vert (I-\Pi )p_h^{m+1}\Vert _0, \end{aligned}$$

together with the Poincar$\acute{e}$-Friedrichs inequality: $\Vert p_h^{m+1}\Vert _0\le C\Vert \nabla p_h^{m+1}\Vert _0$, we have

$$\begin{aligned} h^2\Vert p_h^{m+1}\Vert _0^2\le G(p_h^{m+1},p_h^{m+1}). \end{aligned}$$

(3.7)

For the right terms of (3.5), using the Young inequality, we have

$$\begin{aligned} |(\mathbf{f}^{m+1},\mathbf{u}_h^{m+1})|\le & {} C\Vert \mathbf{f}^{m+1}\Vert _0\Vert \mathbf{u}_h^{m+1}\Vert _0\le C\Vert \mathbf{f}^{m+1}\Vert _0\Vert \nabla \mathbf{u}_h^{m+1}\Vert _0\nonumber \\\le & {} \frac{1}{2\mu }C\Vert \mathbf{f}^{m+1}\Vert _0^2+\frac{\mu }{2}\Vert \nabla \mathbf{u}_h^{m+1}\Vert _0^2. \end{aligned}$$

(3.8)

Substituting (3.6)–(3.8) into (3.5), multiplying by $2\Delta t$, and summing from $m=0$ to $m=k$, we get

$$\begin{aligned}&\Vert \mathbf{u}_h^{k+1}\Vert _0^2+\mu \sum _{m=0}^k\Vert \nabla u_h^{m+1}\Vert _0^2\Delta t+2h^2\sum _{m=0}^k\Vert p_h^{m+1}\Vert _0^2\Delta t\\&\quad \le C\sum _{m=0}^k\Vert \mathbf{f}^{m+1}\Vert _0^2\Delta t+\Vert \mathbf{u}_h^0\Vert _0^2+C\sum _{m=0}^k\Vert \mathbf{u}_h^{m}\Vert _0^2\Delta t. \end{aligned}$$

Applying the discrete Gronwall inequality, we arrive at

$$\begin{aligned}&\Vert \mathbf{u}_h^{k+1}\Vert _0^2+\mu \sum _{m=0}^k\Vert \nabla u_h^{m+1}\Vert _0^2\Delta t+2h^2\sum _{m=0}^k\Vert p_h^{m+1}\Vert _0^2\Delta t\\&\quad \le C\left( \sum _{m=0}^k\Vert \mathbf{f}^{m+1}\Vert _0^2\Delta t+\Vert \mathbf{u}_h^0\Vert _0^2\right) . \end{aligned}$$

according to the assumptions, the proof is completed.

4 Error Analysis

To obtain error estimates for the finite element solution $(\mathbf{u}_h,p_h)$, we define the Galerkin projection operator $R_h,Q_h$:$X\times M\rightarrow \textit{NCP}_1\times {\mathbf {P}}_1$ as follows

$$\begin{aligned}&{{\mathcal {B}}}_h((R_h(\mathbf{u},p),Q_h(\mathbf{u},p);(\mathbf{v}_h,p_h)) =B_h((\mathbf{u},p);(\mathbf{v}_h,p_h)) \nonumber \\&\forall (\mathbf{u},p)\in X\times M , (\mathbf{v}_h,p_h)\in \textit{NCP}_1\times {\mathbf {P}}_1, \end{aligned}$$

(4.1)

which is well defined and have the following properties.

Lemma 4.1

[27] For $\forall (\mathbf{u},p)\in (H^2(\Omega )^2\cap X)\times (H^1(\Omega )\cap M)$, there holds

$$\begin{aligned} \Vert R_h(\mathbf{u},p)-{} \mathbf{u}\Vert _0+h(\Vert R_h(\mathbf{u},p)-\mathbf{u}\Vert _{1,h}+\Vert Q_h(\mathbf{u},p)-p\Vert _0)\le Ch^2(\Vert \mathbf{u}\Vert _2+\Vert p\Vert _1). \end{aligned}$$

And we define $(\mathbf{u}_h^0,p_h^0)=(R_h(\mathbf{u}_0,p_0),Q_h(\mathbf{u}_0,p_0))$.

As in [29], the initial approximation velocity $\mathbf{u}_h^0$ will be chosen and have the following estimates

$$\begin{aligned} \Vert \mathbf{u}(\cdot ,t_0)-\mathbf{u}_h^0\Vert _0+h\Vert \mathbf{u}(\cdot ,t_0)-\mathbf{u}_h^0\Vert _{1,h}\le Ch^2. \end{aligned}$$

(4.2)

Lemma 4.2

[21] For any $\mathbf{s},\mathbf{w}\in X\cup \textit{NCP}_1,$

$$\begin{aligned} \left| \sum _j\left\langle \frac{\partial \mathbf{w}}{\partial \mathbf{n}_j},\mathbf{s}\right\rangle _j\right|\le & {} Ch\Vert \mathbf{w}\Vert _2\Vert \mathbf{s}\Vert _{1,h}\ \forall \mathbf{w}\in X\cap (H^2(\Omega ))^2,\\ \left| \sum _j\left\langle q,\mathbf{s}\cdot \mathbf{n}_j\right\rangle _j\right|\le & {} Ch\Vert q\Vert _1\Vert \mathbf{s}\Vert _{1,h}\ \forall q\in H^1(\Omega ). \end{aligned}$$

Theorem 4.1

Under assumption (A-C) and $\Delta t=O(h)$, it holds that

$$\begin{aligned} \Vert \mathbf{u}-\mathbf{u}_h\Vert _{L^\infty (0,T;L^2(\Omega )^2)}\le C(\Delta t+h^2). \end{aligned}$$

Proof

According to (4.2),

$$\begin{aligned} \Vert \mathbf{u}(\cdot ,t_0)-\mathbf{u}_h^0\Vert _0\le & {} C(\Delta t+h^2),\nonumber \\ \Vert \mathbf{u}(\cdot ,t_0)-\mathbf{u}_h^0\Vert _{1,h}\le & {} C(\Delta t+h). \end{aligned}$$

(4.3)

Let m be an integer, $0\le k\le M-1$, we suppose the below conclusion already holds for $\forall \,0\le m\le k,$

$$\begin{aligned} \max \limits _{0\le i\le m}\Vert \mathbf{u}(\cdot ,t_i)-\mathbf{u}_h^i\Vert _0\le C(\Delta t+h^2). \end{aligned}$$

(4.4)

We shall prove that (4.4) holds for $m=k+1$ and by induction.

Subtracting (3.4) from (4.1) gives

$$\begin{aligned}&{{\mathcal {B}}}_h(R_h(\mathbf{u},p)-\mathbf{u}_h^{m+1},Q_h(\mathbf{u},p)-p_h^{m+1};(\mathbf{v}_h,q_h))-(d_t\mathbf{u}_h^{m+1},\mathbf{v}_h)\\&\quad =B_h((\mathbf{u},p);(\mathbf{v}_h,q_h))-(\mathbf{f}^{m+1},\mathbf{v}_h)\\&\qquad \forall (\mathbf{v}_h,q_h)\in \textit{NCP}_1\times {\mathbf {P}}_1. \end{aligned}$$

Combining (2.1) and with the fact $D_t\mathbf{u}=\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u}\cdot \triangledown )\mathbf{u}$ yields

$$\begin{aligned} (\mathbf{f}^{m+1},\mathbf{v}_h)=\sum _j\{(D_t\mathbf{u},\mathbf{v}_h)_j-\mu (\Delta \mathbf{u},\mathbf{v}_h)_j+(\nabla p,\mathbf{v}_h)_j\}. \end{aligned}$$

Using the Green formula on each element in $K_h$, we see that

$$\begin{aligned} (\mathbf{f}^{m+1},\mathbf{v}_h)=(D_t\mathbf{u},\mathbf{v}_h)+B_h((\mathbf{u},p);(\mathbf{v}_h,q_h))-\mu \sum _j \left\langle \frac{\partial \mathbf{u}}{\partial n_j},\mathbf{v}_h\right\rangle _j+ \sum _j\langle p,\mathbf{v}_h\cdot n_j\rangle _j. \end{aligned}$$

Let $\mathbf{\xi }=\mathbf{u}-\mathbf{u}_h,\mathbf{\eta }=\mathbf{u}-R_h(\mathbf{u},p),\mathbf{\sigma }=\mathbf{\eta }-\mathbf{\xi }=\mathbf{u}_h-R_h(\mathbf{u},p),\lambda =p_h-Q_h(\mathbf{u},p)$, and using these three equations, we have

$$\begin{aligned}&(d_t\mathbf{\sigma }^{m+1},\mathbf{v}_h)+a(\mathbf{\sigma }^{m+1},\mathbf{v}_h)-d(\mathbf{v}_h,\lambda ^{m+1})+d(\mathbf{\sigma }^{m+1},q_h)+G(\lambda ^{m+1},q_h)\nonumber \\&\quad =(D_t\mathbf{u}(\cdot ,t_{m+1})-d_t\mathbf{u}(\cdot ,t_{m+1}),v_h)+(d_t\mathbf{\eta }(\cdot ,t_{m+1}),\mathbf{v}_h)\nonumber \\&\qquad -\,\mu \sum _j\left\langle \frac{\partial \mathbf{u}}{\partial n_j},v_h\right\rangle _j+\sum _j\langle p,v_h\cdot n_j\rangle _j. \end{aligned}$$

(4.5)

Taking $\mathbf{v}_h=\sigma ^{m+1},q_h=\lambda ^{m+1}$, yields

$$\begin{aligned}&(d_t\mathbf{\sigma }^{m+1},\mathbf{\sigma }^{m+1})+\mu \Vert \nabla \mathbf{\sigma }^{m+1}\Vert _0^2+\Vert (I-\Pi )\lambda ^{m+1}\Vert ^2_0\\&\quad =(D_t\mathbf{u}(\cdot ,t_{m+1})-d_t\mathbf{u}(\cdot ,t_{m+1}),\mathbf{\sigma }^{m+1})\\&\qquad +\,(d_t\mathbf{\eta }(\cdot ,t_{m+1}),\mathbf{\sigma }^{m+1})-\mu \sum _j \left\langle \frac{\partial \mathbf{u}}{\partial n_j},\mathbf{\sigma }^{m+1}\right\rangle _j+\sum _j\langle p,\mathbf{\sigma }^{m+1}\cdot \mathbf{n}_j\rangle _j. \end{aligned}$$

Thus

$$\begin{aligned}&\frac{1}{2\Delta t}(\Vert \sigma ^{m+1}\Vert _0^2-\Vert \sigma ^m\Vert _0^2+\Vert \sigma ^{m+1}-\sigma ^m\Vert _0^2)+\mu \Vert \nabla \sigma ^{m+1}\Vert _0^2+\Vert (I-\Pi )\lambda ^{m+1}\Vert ^2_0\nonumber \\&\quad \le \left| \left( D_t\mathbf{u}(\cdot ,t_{m+1})-\frac{\mathbf{u}(\cdot ,t_{m+1})-\mathbf{u}(X(\cdot ,t_{m+1};t_m),t_m)}{\Delta t},\sigma ^{m+1}\right) \right| \nonumber \\&\qquad +\left| \left( \frac{\mathbf{u}(X(\cdot ,t_{m+1};t_m),t_m)-\mathbf{u}(X_h^m(\cdot ,t_{m+1};t_m),t_m)}{\Delta t},\sigma ^{m+1}\right) \right| \nonumber \\&\qquad +\left| \left( \frac{\eta (\cdot ,t_{m+1})-\eta (\cdot ,t_m)}{\Delta t},\sigma ^{m+1}\right) \right| \nonumber \\&\qquad + \left| \left( \frac{\eta (\cdot ,t_m)-\eta (X(\cdot ,t_{m+1};t_m),t_m)}{\Delta t},\sigma ^{m+1}\right) \right| \nonumber \\&\qquad +\left| \left( \frac{\eta (X(\cdot ,t_{m+1};t_m),t_m)-\eta (X_h^m(\cdot ,t_{m+1};t_m),t_m)}{\Delta t},\sigma ^{m+1}\right) \right| \nonumber \\&\qquad +\left| \left( \frac{\sigma ^m(\cdot )-\sigma ^m(X(\cdot ,t_{m+1};t_m))}{\Delta t},\sigma ^{m+1}\right) \right| \nonumber \\&\qquad +\left| \left( \frac{\sigma ^m(X(\cdot ,t_{m+1};t_m))-\sigma ^m(X_h^m(\cdot ,t_{m+1};t_m))}{\Delta t},\sigma ^{m+1}\right) \right| \nonumber \\&\qquad +\left| \mu \sum _j\left\langle \frac{\partial \mathbf{u}}{\partial n_j},\sigma ^{m+1}\right\rangle _j\right| + \left| \sum _j\langle p,\sigma ^{m+1}\cdot n_j\rangle _j\right| =\sum \limits _{i=1}^9B_i. \end{aligned}$$

(4.6)

In order to estimate term $B_i,i=1\ldots 9$, we use the conclusion in [29] and Lemma 4.2 to obtain

$$\begin{aligned} B_1\le & {} \frac{\varepsilon }{3}\Vert \sigma ^{m+1}\Vert _0^2+C\Delta t \Vert D_t^2 \mathbf{u}\Vert ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2}),\nonumber \\ B_2\le & {} \frac{\varepsilon }{3}\Vert \sigma ^{m+1}\Vert _0^2+ C\left( \Vert \xi ^m\Vert _0^2+\Delta t \left\| \frac{\mathrm{d}{} \mathbf{u}}{\mathrm{d}t}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2}\right) ,\nonumber \\ B_3\le & {} \frac{\varepsilon }{3}\Vert \sigma ^{m+1}\Vert _0^2+\frac{C}{\Delta t} \left\| \frac{\mathrm{d}\eta }{\mathrm{d}t}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2)},\nonumber \\ B_4\le & {} \frac{\varepsilon _1}{6}\Vert \nabla \sigma ^{m+1}\Vert _0^2+C\Vert \eta \Vert ^2_{L^\infty (L^2(\Omega )^2)},\nonumber \\ B_5\le & {} \frac{\varepsilon _1}{6}\Vert \nabla \sigma ^{m+1}\Vert _0^2+ C\left( \Vert \xi ^m\Vert _0^2+\Delta t \left\| \frac{\mathrm{d}{} \mathbf{u}}{\mathrm{d}t}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2}\right) ,\nonumber \\ B_6\le & {} \frac{\varepsilon _1}{6}\Vert \nabla \sigma ^{m+1}\Vert _0^2+C\Vert \sigma ^m\Vert _0^2,\nonumber \\ B_7\le & {} \frac{\varepsilon _1}{6}\Vert \nabla \sigma ^{m+1}\Vert _0^2+C \left( \Vert \xi ^m\Vert _0^2+\Delta t \left\| \frac{\mathrm{d}{} \mathbf{u}}{\mathrm{d}t}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2}\right) , \end{aligned}$$

For the terms $B_8,B_9$, under the condition of $\Delta t=O(h)$, we have

$$\begin{aligned} B_8\le & {} Ch\Vert \mathbf{u}\Vert _2\Vert \sigma ^{m+1}\Vert _{1,h}\le C\Delta t^2\Vert \mathbf{u}\Vert _2^2+\frac{\varepsilon _1}{6}\Vert \nabla \sigma ^{m+1}\Vert _0^2,\nonumber \\ B_9\le & {} Ch\Vert p\Vert _1\Vert \sigma ^{m+1}\Vert _{1,h}\le C\Delta t^2\Vert p\Vert _1^2+\frac{\varepsilon _1}{6}\Vert \nabla \sigma ^{m+1}\Vert _0^2. \end{aligned}$$

Substituting the above estimates into (4.6), multiplying by $2\Delta t$, summing from $m=0$ to $m=k$ and choosing $\varepsilon =\frac{1}{4}T,\varepsilon _1=\frac{\mu }{2}$, we obtain the recursion relation

$$\begin{aligned}&\Vert \sigma ^{k+1}\Vert _0^2+\mu \left( \Delta t\sum \limits _{m=0}^{k+1}\Vert \nabla \sigma ^{m}\Vert _0^2\right) +2\Delta t\sum \limits _{m=0}^kG(\lambda ^{m+1},\lambda ^{m+1})\\&\quad \le C\Delta t^2\left( \Vert D_t^2 \mathbf{u}\Vert ^2_{L^2(L^2(\Omega )^2)}+ \left\| \frac{\mathrm{d}{} \mathbf{u}}{\mathrm{d}t}\right\| ^2_{L^2(L^2(\Omega )^2}\right) \\&\qquad +\,C\left( \Vert \eta \Vert ^2_{L^{\infty }(L^2(\Omega )^2)}+ \left\| \frac{\mathrm{d}\eta }{\mathrm{d}t}\right\| ^2_{L^2(L^2(\Omega )^2)}\right) \\&\qquad +\,C\Delta t\sum \limits _{m=0}^k\Vert \xi ^m\Vert _0^2+C\Delta t\sum \limits _{m=0}^k\Vert \sigma ^m\Vert _0^2 +C\Delta t^2\Vert \mathbf{u}\Vert ^2_{L^2(H^2(\Omega )^2)}\nonumber \\&\qquad +\,C\Delta t^2\Vert p\Vert ^2_{L^2(H^1(\Omega )^2)}. \end{aligned}$$

By the discrete version of Gronwall’s lemma, (4.2) and Lemma 4.1

$$\begin{aligned} \Vert \xi ^{k+1}\Vert _0^2\le & {} 2\Vert \sigma ^{k+1}\Vert _0^2+2\Vert \eta ^{k+1}\Vert _0^2\\\le & {} C\Delta t^2\left( \Vert D_t^2 \mathbf{u}\Vert ^2_{L^2(L^2(\Omega )^2)}+ \left\| \frac{\mathrm{d}{} \mathbf{u}}{\mathrm{d}t}\right\| ^2_{L^2(L^2(\Omega )^2}\right) \\&+\,Ch^4\left( \Vert \mathbf{u}\Vert ^2_{L^\infty (H^2(\Omega )^2)}+ \left\| \frac{\mathrm{d}{} \mathbf{u}}{\mathrm{d}t}\right\| ^2_{L^2(L^2(\Omega )^2)}+\Vert p\Vert ^2_{L^\infty (H^1(\Omega )^2)} \right. \\&\left. +\, \left\| \frac{\mathrm{d}p}{\mathrm{d}t}\right\| ^2_{L^2(H^1(\Omega ))}\right) \\&+\,C\Delta t^2(\Vert \mathbf{u}\Vert ^2_{L^2(H^2(\Omega )^2)}+\Vert p\Vert ^2_{L^2(H^1(\Omega )^2)})+C\Delta t\sum \limits _{m=0}^k\Vert \xi ^m\Vert _0^2. \end{aligned}$$

Finally, the discrete Gronwall’s Lemma yields (4.4), which holds for $m=k+1$. $\square$

Theorem 4.2

Under assumption (A–C) and under condition $\frac{1}{2C_0}\le \frac{h^2}{\Delta t}\le C_{\Delta t}$, it holds that

$$\begin{aligned} \Vert \mathbf{u}-\mathbf{u}_h\Vert _{L^\infty (0,T;H^1(\Omega )^2)}\le C(\Delta t+h). \end{aligned}$$

where $C_{\Delta t}=min\{\Delta t^2,\frac{1}{C_0}\}$.

Proof

According to (4.2)

$$\begin{aligned} \Vert \mathbf{u}(\cdot ,t_0-\mathbf{u}_h^0)\Vert _{1,h}\le C(\Delta t+h). \end{aligned}$$

Let us suppose that k is an integer, $0\le k\le M-1,$ and that we have already shown the estimate

$$\begin{aligned} \max \limits _{0\le i\le m}\Vert \mathbf{u}(\cdot ,t_i)-\mathbf{u}_h^i\Vert _{1,h}\le C (\Delta t+h), \end{aligned}$$

(4.7)

for all m, $0\le m\le k,$ we shall prove that (4.7) holds for $m=k+1$ and by induction, this will complete the proof.

Taking $\mathbf{v}_h=\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}$.$q_h=\frac{\lambda ^{m+1}}{\Delta t}$ in the formula (4.5), we have

$$\begin{aligned}&\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right\| _0^2+\frac{\mu }{2\Delta t}(\Vert \nabla \sigma ^{m+1}\Vert _0^2-\Vert \nabla \sigma ^m\Vert _0^2)+d \left( \frac{\sigma ^m}{\Delta t},\lambda ^{m+1}\right) \nonumber \\&\qquad +\frac{1}{\Delta t}G(\lambda ^{m+1},\lambda ^{m+1})+\frac{\mu }{2} \left| \frac{\sigma ^{m+1}-\sigma ^m}{(\Delta t)^{\frac{1}{2}}}\right| _{1,h}^2\nonumber \\&\quad \le \left| \left( D_t\mathbf{u}(\cdot ,t_{m+1})-\frac{\mathbf{u}(\cdot ,t_{m+1})-\mathbf{u}(X(\cdot ,t_{m+1};t_m),t_m)}{\Delta t},\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right) \right| \nonumber \\&\qquad +\left| \left( \frac{\mathbf{u}(X(\cdot ,t_{m+1};t_m),t_m)-\mathbf{u}(X_h^m(\cdot ,t_{m+1};t_m),t_m)}{\Delta t},\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right) \right| \nonumber \\&\qquad +\left| \left( \frac{\eta (\cdot ,t_{m+1})-\eta (\cdot ,t_m)}{\Delta t},\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right) \right\| _0\nonumber \\&\qquad +\left\| \left( \frac{\eta (\cdot ,t_m)-\eta (X(\cdot ,t_{m+1};t_m),t_m)}{\Delta t},\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right) \right| \nonumber \\&\qquad +\left| \left( \frac{\eta (X(\cdot ,t_{m+1};t_m),t_m)-\eta (X_h^m(\cdot ,t_{m+1};t_m),t_m)}{\Delta t},\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right) \right| \nonumber \\&\qquad +\left| \left( \frac{\sigma ^m(\cdot )-\sigma ^m(X(\cdot ,t_{m+1};t_m))}{\Delta t},\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right) \right| \nonumber \\&\qquad + \left| \left( \frac{\sigma ^m(X(\cdot ,t_{m+1};t_m))-\sigma ^m(X_h^m(\cdot ,t_{m+1};t_m))}{\Delta t},\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right) \right| \nonumber \\&\qquad +\left| \mu \sum _j\left\langle \frac{\partial \mathbf{u}}{\partial \mathbf{n}_j},\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t} \right\rangle _j\right| \nonumber \\&\qquad +\left| \sum _j\langle p,\frac{\sigma ^{m+1}-\sigma ^m}{\Delta t} \cdot \mathbf{n}_j\rangle _j\right| =\sum \limits _{i=10}^{18}B_i. \end{aligned}$$

(4.8)

using Lemma 3.2, the term $\frac{1}{\Delta t}G(\lambda ^{m+1},\lambda ^{m+1})$ can be treated as below, for a positive constant $C_0$

$$\begin{aligned} C_0\frac{h^2}{\Delta t}\Vert \nabla \lambda ^{m+1}\Vert _0\le \frac{1}{\Delta t}\Vert (I-\Pi )\lambda ^{m+1}\Vert ^2_0 \end{aligned}$$

for the term $d(\frac{\sigma ^m}{\Delta t},\lambda ^{m+1})$, using $\varepsilon$-inequality, with $\varepsilon =2C_0h^2$

$$\begin{aligned} d\left( \frac{\sigma ^m}{\Delta t},\lambda ^{m+1}\right) =-\frac{1}{\Delta t}(\sigma ^m,\nabla \lambda ^{m+1})\ge -C_0\frac{h^2\Vert \nabla \lambda ^{m+1}\Vert _0^2}{\Delta t}-\frac{\Delta t}{4C_0h^2} \left\| \frac{\sigma ^m}{\Delta t}\right\| _0^2. \end{aligned}$$

So the left side of (4.8) can be bounded from below by

$$\begin{aligned}&\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t} \right\| _0^2+\frac{\mu }{2\Delta t} (\Vert \nabla \sigma ^{m+1}\Vert _0^2-\Vert \nabla \sigma ^m\Vert _0^2)\\&\quad -\frac{\Delta t}{4C_0h^2} \left\| \frac{\sigma ^m}{\Delta t}\right\| _0^2 +\frac{\mu }{2}\left| \frac{\sigma ^{m+1}-\sigma ^m}{(\Delta t)^{\frac{1}{2}}} \right| _{1,h}^2 \end{aligned}$$

For the term $\Vert \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\Vert _0^2$, we have

$$\begin{aligned}&\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t} \right\| _0^2=\left\| \frac{\sigma ^{m+1}}{\Delta t}\right\| _0^2+ \left\| \frac{\sigma ^m}{\Delta t}\right\| _0^2-2\frac{(\sigma ^{m+1},\sigma ^m)}{\Delta t^2}\\&\quad \ge \left( 1-\frac{C_0h^2}{\Delta t}\right) \left\| \frac{\sigma ^{m+1}}{\Delta t}\right\| _0^2+ \left( 1-\frac{\Delta t}{4C_0h^2}\right) \left\| \frac{\sigma ^m}{\Delta t}\right\| _0^2 \end{aligned}$$

Then the left side of (4.8) can be bounded from below by

$$\begin{aligned}&\frac{\mu }{2\Delta t}(\Vert \nabla \sigma ^{m+1}\Vert _0^2-\Vert \nabla \sigma ^m\Vert _0^2)+ \left( 1-\frac{C_0h^2}{\Delta t}\right) \left\| \frac{\sigma ^{m+1}}{\Delta t}\right\| _0^2\nonumber \\&\quad + \left( 1-\frac{\Delta t}{2C_0h^2}\right) \left\| \frac{\sigma ^m}{\Delta t}\right\| _0^2+\frac{\mu }{2} \left| \frac{\sigma ^{m+1}-\sigma ^m}{(\Delta t)^{\frac{1}{2}}}\right| _1^2. \end{aligned}$$

(4.9)

For $C_0<\frac{\Delta t}{h^2}<2C_0$, choosing ${\tilde{C}}=min\{1-\frac{C_0h^2}{\Delta t},1-\frac{\Delta t}{2C_0h^2}\}$, together with (4.8), (4.9), it yields

$$\begin{aligned}&\frac{\mu }{2\Delta t}(\Vert \nabla \sigma ^{m+1}\Vert _0^2-\Vert \nabla \sigma ^m\Vert _0^2)\\&\quad +\,{\tilde{C}}\left\| \frac{\sigma ^{m+1}}{\Delta t}\right\| _0^2+{\tilde{C}}\left\| \frac{\sigma ^m}{\Delta t}\right\| _0^2+\frac{\mu }{2}\left| \frac{\sigma ^{m+1}-\sigma ^m}{ (\Delta t)^{\frac{1}{2}}}\right| _1^2\le \sum \limits _{i=10}^{18}B_i \end{aligned}$$

For the estimates of right term of (4.8), similar to [29]:

$$\begin{aligned} B_{10}\le & {} \frac{\epsilon }{7}\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right\| _0^2+C\Delta t\Vert D_t^2\mathbf{u}\Vert ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2)}\\ B_{11}\le & {} \frac{\epsilon }{7}\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right\| _0^2+ C\left( \Vert \xi \Vert _0^2+\Delta t\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2)}\right) \\ B_{12}\le & {} \frac{\epsilon }{7}\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right\| _0^2+\frac{C}{\Delta t}\left\| \frac{d\eta }{dt}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2)} \\ B_{13}\le & {} \frac{\epsilon }{7}\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right\| _0^2+C\Vert \eta \Vert ^2_{L^\infty (H^1(\Omega )^2)}\\ B_{14}\le & {} \frac{\epsilon }{7}\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right\| _0^2+\frac{\epsilon _1}{4}\left| \frac{\sigma ^{m+1}-\sigma ^m}{ (\Delta t)^{\frac{1}{2}}}\right| _1^2+ C\left( 1+\frac{\alpha _m}{\Delta t}\right) \Vert \eta \Vert ^2_{L^\infty (H^1(\Omega )^2)}\\ B_{15}\le & {} \frac{\epsilon }{7}\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t }\right\| _0^2+C\Vert \nabla \sigma \Vert _0^2\\ B_{16}\le & {} \frac{\epsilon }{7}\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t }\right\| _0^2+\frac{\epsilon _1}{4}\left| \frac{\sigma ^{m+1}-\sigma ^m}{ (\Delta t)^{\frac{1}{2}}}\right| _1^2+ C\left( 1+\frac{\alpha _k}{\Delta t}\right) \Vert \nabla \sigma ^m\Vert ^2_0 \end{aligned}$$

where $\alpha _m=D_N(h)^2 (\Delta t^2+\Delta t\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^N)})$, $D_N(h)=h^{1-\frac{N}{2}}(log\frac{1}{h})^{1-\frac{1}{N}}$.

By lemma 4.2 and the equivalence of norm, we have

$$\begin{aligned} B_{17}\le & {} Ch\Vert \mathbf{u}\Vert _2\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right\| _{1,h}\le Ch\Vert \mathbf{u}\Vert _2 \left| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right| _{1,h}\nonumber \\\le & {} C\frac{\Delta t^2}{2\epsilon _1}\Vert \mathbf{u}\Vert _2^2+\frac{\epsilon _1h^2}{4\Delta t^3} \left| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t^\frac{1}{2}}\right| _{1.h}^2,\\ B_{18}\le & {} Ch\Vert p\Vert _1\left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right\| _{1,h}\le Ch\Vert p\Vert _1\left| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right| _{1,h}\nonumber \\\le & {} C\frac{\Delta t^2}{2\epsilon _1}\Vert p\Vert _1^2+\frac{\epsilon _1h^2}{4\Delta t^3} \left| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t^\frac{1}{2}}\right| _{1,h}^2. \end{aligned}$$

Now we assume that $\frac{1}{2C_0}\le \frac{h^2}{\Delta t}\le C_{\Delta t},$ where $C_{\Delta t}=min\left\{ \Delta t^2,\,\frac{1}{C_0}\right\}$

$$\begin{aligned} B_{17}\le & {} C\frac{\Delta t^2}{2\epsilon _1}\Vert \mathbf{u}\Vert _2^2+\frac{\epsilon _1}{4}\left| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t^\frac{1}{2}}\right| _{1,h}^2,\\ B_{18}\le & {} C\frac{\Delta t^2}{2\epsilon _1}\Vert p\Vert _1^2+\frac{\epsilon _1}{4}\left| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t^\frac{1}{2}}\right| _{1,h}^2. \end{aligned}$$

Substituting the above estimates into (4.8), multiplying by $2\Delta t$, summing from $m=0$ to $m=k$, and choosing $\epsilon =\frac{1}{4}{\tilde{C}},\epsilon _1=\frac{\mu }{4},$ we obtain

$$\begin{aligned}&\Vert \nabla \sigma ^{k+1}\Vert _0^2+\Delta t\frac{{\tilde{C}}}{\mu }\sum \limits _{m=0}^k\left\| \frac{\sigma ^m}{\Delta t}\right\| _0^2+\Delta t\frac{{\tilde{C}}}{\mu }\sum \limits _{m=0}^k\left\| \frac{\sigma ^{m+1}}{\Delta t}\right\| _0^2+\frac{1}{2}\Delta t\sum \limits _{m=0}^k\left| \frac{\sigma ^{m+1}-\sigma ^m}{(\Delta t)^{\frac{1}{2}}}\right| _1^2\nonumber \\&\quad \le C\Delta t^2 \left( \Vert D_t^2\mathbf{u}\Vert ^2_{L^2(L^2(\Omega )^2)}+\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(L^2(\Omega )^2)}\right) \nonumber \\&\qquad +\,C\left( 2T+\sum \limits _{m=0}^k\alpha _m\right) \Vert \eta \Vert ^2_{L^\infty (H^1(\Omega )^2)}+C\left\| \frac{d\eta }{dt}\right\| ^2_{L^2(L^2(\Omega )^2)}\nonumber \\&\qquad +\,C\left( \Delta t\sum \limits _{m=0}^k\Vert \xi ^m\Vert _0^2\right) +C\sum \limits _{m=0}^k(\alpha _m+2\Delta t)\Vert \nabla \sigma ^m\Vert _0^2\nonumber \\&\qquad +\,Ch^2\Vert \mathbf{u}\Vert ^2_{L^2(H^2(\Omega )^2)}+Ch^2\Vert p\Vert ^2_{L^2(H^1(\Omega )^2)}. \end{aligned}$$

(4.10)

Since

$$\begin{aligned} \sum \limits _{m=0}^k\alpha _m=D_2(h)^2\Delta t \left( T+\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(L^2(\Omega )^2)}\right) , \end{aligned}$$

together with the discrete Gronwall’s Lemma, Lemma 4.1 and (4.2) imply that

$$\begin{aligned}&\Vert \nabla \xi ^{k+1}\Vert _0^2\le 2\Vert \nabla \eta ^{k+1}\Vert _0^2+2\Vert \nabla \sigma ^{k+1}\Vert _0^2\\&\quad \le C\Delta t^2 \left( \Vert D_t^2\mathbf{u}\Vert ^2_{L^2(L^2(\Omega )^2)}+\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(L^2(\Omega )^2)}\right) \\&\qquad +\,Ch^2\left( \Vert \mathbf{u}\Vert ^2_{L^\infty (H^2(\Omega )^2)}+C\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(H^2(\Omega )^2)}+\Vert p\Vert ^2_{L^\infty (H^1(\Omega )^2)}\right. \nonumber \\&\left. \qquad + \left\| \frac{dp}{dt}\right\| _{L^2(H^1(\Omega )^2)}\right) +C\Delta t\sum \limits _{m=0}^k\Vert \xi ^m\Vert _0^2. \end{aligned}$$

By the Poincar$\acute{e}$-Friedrichs inequality$\Vert \xi ^m\Vert _0\le C\Vert \nabla \xi ^m\Vert _0,$ the discrete Gronwall’s Lemma yields (4.7) hold for m $=$ k $+$ 1. $\square$

Theorem 4.3

Under assumption (A-C) and under condition $\frac{1}{2C_0}\le \frac{h^2}{\Delta t}\le C_{\Delta t}$, it holds that

$$\begin{aligned} \Vert p-p_h\Vert _{L^2(0,T;L^2(\Omega )}\le C(\Delta t+h). \end{aligned}$$

Proof

From the formulation (4.5), we obtain the following expression:

$$\begin{aligned}&{{\mathcal {B}}}_h((\sigma ^{m+1},\lambda ^{m+1});(\mathbf{v}_h,q_h))\\&\quad =(D_t\mathbf{u}(\cdot ,t_{m+1})-d_t\mathbf{u}(\cdot ,t_{m+1}),\mathbf{v}_h)+(d_t\eta (\cdot ,t_{m+1}),\mathbf{v}_h)-(d_t\sigma ^{m+1},\mathbf{v}_h)\\&\qquad -\mu \sum _j \left\langle \frac{\partial \mathbf{u}}{\partial \mathbf{n}_j},\mathbf{v}_h\right\rangle _j+\sum _j\langle p,\mathbf{v}_h\cdot \mathbf{n}_j\rangle _j. \end{aligned}$$

From Lemma 3.1, yields

$$\begin{aligned}&\beta (\Vert \sigma ^{m+1}\Vert _1+\Vert \lambda ^{m+1}\Vert _0)\\&\quad \le \sup \limits _{(\mathbf{v}_h,q_h)\in \textit{NCP}_1\times {\mathbf {P}}_1}\frac{{{\mathcal {B}}}_h((\sigma ^{m+1},\lambda ^{m+1});(\mathbf{v}_h,q_h))}{\Vert \mathbf{v}_h\Vert _{1,h}+\Vert q_h\Vert _0}\\&\quad \le \sup \limits _{(\mathbf{v}_h,q_h)\in \textit{NCP}_1\times {\mathbf {P}}_1}\\&\qquad \times \frac{(D_t\mathbf{u}(\cdot ,t_{m+1})-d_t\mathbf{u}(\cdot ,t_{m+1}), \mathbf{v}_h)+(d_t\eta (\cdot ,t_{m+1}),\mathbf{v}_h)-(d_t\sigma ^{m+1},\mathbf{v}_h) -\mu \sum _j \left\langle \frac{\partial \mathbf{u}}{\partial \mathbf{n}_j},\mathbf{v}_h\right\rangle _j +\sum _j\langle p,\mathbf{v}_h\cdot \mathbf{n}_j\rangle _j}{\Vert \mathbf{v}_h\Vert _{1,h}+\Vert q_h\Vert _0}. \end{aligned}$$

we can obtain

$$\begin{aligned} \beta \Vert \lambda ^{m+1}\Vert _0\le & {} \left\| D_t\mathbf{u}(\cdot ,t_{m+1})-\frac{\mathbf{u}(\cdot ,t_{m+1})-\mathbf{u}(X(\cdot ,t_{m+1};t_m),t_m)}{\Delta t}\right\| _0\\&+\left\| \frac{\mathbf{u}(X(\cdot ,t_{m+1};t_m),t_m)-\mathbf{u}(X_h^m(\cdot ,t_{m+1};t_m),t_m)}{\Delta t}\right\| _0\\&+\left\| \frac{\eta (\cdot ,t_{m+1})-\eta (\cdot ,t_m)}{\Delta t}\right\| _0+ \left\| \frac{\eta (\cdot ,t_m)-\eta (X(\cdot ,t_{m+1};t_m),t_m)}{\Delta t}\right\| _{-1} \\&+\, C\left\| \frac{\eta (X(\cdot ,t_{m+1};t_m),t_m)-\eta (X_h^m(\cdot ,t_{m+1};t_m),t_m)}{\Delta t}\right\| _{0,1}\\&+\left\| \frac{\sigma ^m(\cdot )-\sigma ^m(X(\cdot ,t_{m+1};t_m))}{\Delta t}\right\| _{-1}\\&+\,C \left\| \Bigg (\frac{\sigma ^m(X(\cdot ,t_{m+1};t_m)) -\sigma ^m(X_h^m(\cdot ,t_{m+1};t_m))}{\Delta t} \right\| _{0,1}\\&+\, \left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t} \right\| _0+Ch\Vert \mathbf{u}\Vert _2+Ch\Vert p\Vert _1. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \Vert \lambda ^{m+1}\Vert _0^2\le & {} C\left\| D_t\mathbf{u}(\cdot ,t_{m+1})-\frac{\mathbf{u}(\cdot ,t_{m+1})-\mathbf{u}(X(\cdot ,t_{m+1};t_m),t_m)}{\Delta t}\right\| _0^2\nonumber \\&+\,C\left\| \frac{\mathbf{u}(X(\cdot ,t_{m+1};t_m),t_m)-\mathbf{u}(X_h^m(\cdot ,t_{m+1};t_m),t_m)}{\Delta t}\right\| _0^2\nonumber \\&+\,C\left\| \frac{\eta (\cdot ,t_{m+1})-\eta (\cdot ,t_m)}{\Delta t}\right\| _0+C \left\| \frac{\eta (\cdot ,t_m)-\eta (X(\cdot ,t_{m+1};t_m),t_m)}{\Delta t}\right\| _{-1}^2 \nonumber \\&+\,C \left\| \frac{\eta (X(\cdot ,t_{m+1};t_m),t_m)-\eta (X_h^m(\cdot ,t_{m+1};t_m),t_m)}{\Delta t} \right\| _{0,1}^2\nonumber \\&+\,C\left\| \frac{\sigma ^m(\cdot )-\sigma ^m(X(\cdot ,t_{m+1};t_m))}{\Delta t}\right\| _{-1}^2\nonumber \\&+\,C \left\| \Bigg (\frac{\sigma ^m(X(\cdot ,t_{m+1};t_m))-\sigma ^m(X_h^m (\cdot ,t_{m+1};t_m))}{\Delta t}\right\| _{0,1}^2\nonumber \\&+\,C \left\| \frac{\sigma ^{m+1}-\sigma ^m}{\Delta t}\right\| _0^2\nonumber \\&+\,Ch^2\Vert \mathbf{u}\Vert _2^2+Ch^2\Vert p\Vert _1^2= \sum \limits _{i=19}^{26} B_i+Ch^2\Vert \mathbf{u}\Vert _2^2+Ch^2\Vert p\Vert _1^2. \end{aligned}$$

(4.11)

By similar argument in [29], we have

$$\begin{aligned} B_{19}\le & {} C\Delta t\Vert D_t^2 \mathbf{u}\Vert ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2}),\\ B_{20}\le & {} C\left( \Vert \xi ^m\Vert _0^2+\Delta t\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2}\right) ,\\ B_{21}\le & {} \frac{C}{\Delta t}\left\| \frac{d\eta }{dt}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2)},\\ B_{22}\le & {} C\Vert \eta \Vert ^2_{L^\infty (L^2(\Omega )^2)},\\ B_{23}\le & {} C\left( \Vert \xi ^m\Vert _0^2+\Delta t\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2}\right) ,\\ B_{24}\le & {} C\Vert \sigma ^m\Vert _0^2,\\ B_{25}\le & {} C\left( \Vert \xi ^m\Vert _0^2+\Delta t\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(t_m,t_{m+1};L^2(\Omega )^2}\right) , \end{aligned}$$

and

$$\begin{aligned} B_{26}\le C\left\| \frac{\sigma ^{m+1}}{\Delta t}\right\| _0^2+C\left\| \frac{\sigma ^m}{\Delta t}\right\| _0^2. \end{aligned}$$

Substituting the above estimates into (4.11), multiplying by $\Delta t$, and summing from $m=0$ to $m=M-1$, we obtain

$$\begin{aligned}&\Vert (p-p_h)\Vert _{L^2(0,T;L^2(\Omega ))}^2 \le 2\Vert \lambda \Vert _{L^2(0,T;L^2(\Omega ))}^2+2\Vert p-Q_h(\mathbf{u},p)\Vert _{L^2(0,T;L^2(\Omega ))}^2\\&\quad \le C\Delta t^2 \left( \Vert D_t^2\mathbf{u}\Vert ^2_{L^2(L^2(\Omega )^2)}+C\left\| \frac{d\mathbf{u}}{dt}\right\| ^2_{L^2(L^2(\Omega )^2}\right) \\&\qquad +\,C\left( \Vert \eta \Vert ^2_{L^{\infty }(L^2(\Omega )^2)}+\left\| \frac{d\eta }{dt}\right\| ^2_{L^2(L^2(\Omega )^2)}\right) \\&\qquad +\,Ch^2(\Vert \mathbf{u}\Vert ^2_{L^2(H^2(\Omega )^2)}+\Vert p\Vert ^2_{L^2(H^1(\Omega )^2)})+C\Delta t\sum \limits _{m=0}^{M-1}\Vert \xi ^m\Vert _0^2+C\Delta t\sum \limits _{m=0}^{M-1}\Vert \sigma ^m\Vert _0^2\\&\qquad +\,C\Delta t\sum \limits _{m=0}^{M-1}\left\| \frac{\sigma ^{m+1}}{\Delta t}\right\| _0^2+C\Delta t\sum \limits _{m=0}^{M-1}\left\| \frac{\sigma ^m}{\Delta t}\right\| _0^2 +2\Delta t\sum \limits _{m=0}^M\Vert p-Q_h(\mathbf{u},p)\Vert _0^2. \end{aligned}$$

Together with (4.2), (4.10), Theorem 4.1 and Lemma 4.1, yields

$$\begin{aligned} \Vert p-p_h\Vert _{L^2(0,T;L^2(\Omega ))}\le C(\Delta t+h) \end{aligned}$$

$\square$

5 Numerical Results

In this section, we present numerical results to compare the stabilized characteristic-nonconforming finite element method for the non-stationary incompressible Navier–Stokes equation described in Sect. 3. The software Freefem++ developed by Hecht et al. is used in our experiments.

Fig. 1

The domain $\Omega$

In this paper, we consider the problem (2.1) in the fixed domain $[0,1]\times [0,1]$. The exact solution is given by

$$\begin{aligned} \mathbf{u}(x,y)= & {} (u_1(x,y),u_2(x,y)),\quad p(x,y)=10(2x-1)(2y-1)\mathrm{cos}(t), \\ u_1(x,y)= & {} 10x^2y(x-1)^2(y-1)(2y-1)\mathrm{cos}(t),\quad \\ u_2(x,y)= & {} -10xy^2(x-1)(2x-1)(y-1)^2\mathrm{cos}(t) . \end{aligned}$$

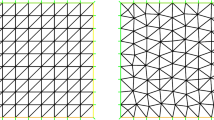
Let the natural projection of exact solution onto $\textit{NCP}_1\times {\mathbf {P}}_1$ to be the initial condition and f is computed by evaluating the momentum equation of problem (2.1) for the exact solution. The domain is divided into triangles; see Fig 1. For simplicity, the Reynolds number for this problem is defined as $\mathrm{Re}=1/\mu$. We choose $\alpha =0.1$ in our experiments. Result is shown by the below table and figure, in which $K_{div}:=\mathrm{max}_{K\in K_h}|\int _K\mathrm{div}{} \mathbf{u}_h\mathrm{d}x|$.

We first compare the stabilized characteristic-nonconforming finite element method with characteristic stabilized finite element method for $\mathrm{Re}=1,\,T=1,$ dt = 0.1 in Tables 1 and 2. Secondly, computations are made on a fixed mesh size with different time steps (mesh size $60\times 60$, $\mathrm{Re}=10$, $T=1.5$), and the result is presented in Tables 3 and 4. The numerical order of accuracy for stabilized characteristic-nonconforming finite element method we plot in Fig. 2. Finally, the error contours of streamline, pressure, velocity, and velocity divergence are presented in Figs. 3, 4, 5 (mesh size $50\times 50$, $T=1,\,\hbox {dt} = 0.01,\,\mathrm{Re} = 10).$

Table 1 Characteristic stabilized ${\mathbf {P}}_1-{\mathbf {P}}_1$ element with different mesh sizes

Table 2 Stabilized characteristic-nonconforming $\textit{NCP}_1-{\mathbf {P}}_1$ element with different mesh size

Table 3 Characteristic stabilized ${\mathbf {P}}_1-{\mathbf {P}}_1$ element with different time step

Table 4 Stabilized characteristic-nonconforming $\textit{NCP}_1-{\mathbf {P}}_1$ element with different time step

Fig. 2

The numerical order of accuracy for stabilized characteristic-nonconforming finite element method

Fig. 3

The error contours for characteristic stabilized finite element: ${\mathbf {P}}_1-{\mathbf {P}}_1$ $T=1$ dt = 0.01

Fig. 4

The error contours for stabilized characteristic-nonconforming finite element: $\textit{NCP}_1-{\mathbf {P}}_1$ $T=1$ dt = 0.01

Fig. 5

The error contours of velocity divergence for two methods: $T=1$ dt = 0.01

From the Tables 1 and 2, we can observe that there are some minor differences for the relative error of velocity and pressure between two methods. However, the convergence rate of the $L^2$ norm of velocity in the mesh size are more close to the theoretical results. The pressure approximation show a supper convergence behavior in both two methods. From the Tables 3 and 4, as the time size is decreasing, there is a deterioration in the velocity and pressure approximation by these two methods. Observing the convergence rates depending the time size, we find that the convergence rate of velocity of the stabilized characteristic-nonconforming finite element method is in a good agreement with the theoretical analysis. However, on pressure, the convergence rate present badly deteriorated for both these two methods. Simultaneously, comparing Table 1 with Tables 2 and 3 with Table 4, we can conclude that the stabilized characteristic-nonconforming finite element method is more efficient than the characteristic stabilized finite method when they have the same order convergence rate. We can obtain the numerical order of accuracy for stabilized characteristic-nonconforming finite element method intuitively in Fig. 2. From Figs. 3 and 4, it can be found that the error of approximate solution and exact solution for two methods is small and also has the same accuracy. In addition, from Tables 1, 2, 3, 4, and Fig 5, we can observe that the velocity divergence is approximates to zero for two methods, and in other words, same as the characteristic stabilized finite element method, the stabilized characteristic-nonconforming finite element method can also maintain the flow incompressibility.

6 Conclusion

In this paper, we have studied a stabilized characteristic-nonconforming finite element method for the non-stationary incompressible Navier–Stokes equations based on pressure projection and characteristic-nonconforming finite element method. The discretization uses a pair of spaces of nonconforming finite element $\textit{NCP}_1-{\mathbf {P}}_1$ over triangles. This method has a number of attractive computational properties, such as the difficulties caused by trilinear terms can be avoided. Compared with some established methods, numerical result shows that new method exhibited good shape, and even large time steps are used in computation. In addition, it can save a lot of CPU time.