Introduction

Rotavirus is a double-stranded RNA virus that is the major cause of diarrheal disorder amongst toddlers and older children. The viruses enter via the fecal-oral route, where it mainly poisons gut cells and reasons gastroenteritis. In 1973, Ruth Bishop first detected rotavirus [1]. Rotaviruses can communicate a disease to humans in addition to different animals. Rotavirus contamination occurs most frequently in kids below five years. The inclusive diversity of diarrhea cases resulting from rotavirus [2] is estimated to be 151,714 in 2019. Rotavirus-caused diarrhea is surprisingly contagious. An unmarried inflamed person can unfold greater than 10 trillion infectious debris per gram [3], among which one hundred transmit the contamination to some other prone character [4]. Because the virus survives for nine to 19 days [5], good enough sanitization can control the rotavirus. In the year 2000, rotavirus vaccination was applied in the U.S.A., and on account of that then, hospitalization instances have been considerably reduced [6]. There are nine forms of rotavirus, with A being the most not unusual for rotavirus contamination, in line with Leung. Oral rehydration remedy can control inflamed kids, and proper vaccination can prevent the disease, and a brand new infection [7]. Rotavirus contamination incidence and severity have failed in international locations that have protected rotavirus vaccine in recurring early life immunization policies [8].

There are eight types of rotavirus species named A to H, and this result is based on the VP6 antigen [9]. Primary rotavirus-caused diarrhea is caused by species A. Africa, Asia, and Latin America are the most high-risk regions for rotavirus infection. Because this region lacks proper sanitation, the health care system cites Cortese. In pathology, a polymerase chain reaction (PCR) test is used to diagnose rotavirus infection [10]. At a very early stage, severe symptoms are observed in children. The World Health Organization recommended the rotavirus vaccine in 2013 in all childhood immunization plans to protect from the threat of rotavirus epidemics [11]. This results in a reduction of rotavirus cases and low mortality rates among infants caused by rotavirus infection. However, consistent evidence of lower vaccine efficacy is a significant source of concern for us, according to Zaman. Many questions have been raised on the basis of different quality rotavirus vaccines for developing and developed countries. The significant burdens, as with other infectious diseases such as HIV, malaria, and hepatitis, are high implementation costs and distribution system difficulties (WHO 2013). Overcoming this hurdle is a tremendous challenge for controlling the infection, and various research centers are working on it [12].

A mathematical model plays a significant role in predicting the behaviour of epidemics, and it also helps to take preventive measures. Mathematical modeling is a quantitative measure that can be used to take the initiative to formulate health policy by providing conceptual results. Mathematical modeling also helps us justify the model parameters, variables, and contact rate. Several mathematical models have been studied to analyze the dynamics of rotavirus infection. Chan et al. [13] established a rotavirus infection model in 1998 to calculate and estimate disease burden. Effeltrerre et al. [14] studied the dynamics of rotavirus to verify the secondary effect of vaccination in 2009. Atchison et al. [15] formulated an age structure model to investigate the disease transmission and impact of the rotavirus vaccine in England and Wales in 2010. In 2014, Lin et al. [16] studied the reasons for the diarrheal infectious disease rotavirus (Rotarix and Rotateq). In 2015, Omondi et al. [17] formulated and analyzed a mathematical model of rotavirus to verify the effectiveness of the vaccine. The effect of vaccination and child care is suggested by Shumetie et al. [18]. The effectiveness of the rotavirus vaccine and immunization was presented by Payne et al. [19]. Llmi et al. [20] investigated the dynamics of a rotavirus epidemic model with the effect of crowing infected people. Ahmed et al. [21] proposed a mathematical model to study the epidemic modeling of diarrhea viruses such as rotavirus. Folorunso et al. [22] examined the oral rotavirus vaccine for developed countries, and its implications. In 2015, Namawejje et al. formulated a three-dose vaccination model along with a bilinear incidence rate [23]. The bilinear incidence rate and vaccination effect have been studied by Omondi et al. [24]. Shuaib and Riyapan [25] formulated the mathematical model incorporating breastfeeding and immunization.

The deterministic mathematical model has certain limitations. Because the real world contains randomness, such as instabilities, a deterministic approach cannot completely predict the dynamics of the model. The stochastic modeling of the infectious disease is more physical and realistic, enriching it with more realistic properties [26,27,28,29,30,31]. In recent years, many mathematical models have been developed for studying stochastic contagious disease modeling, giving good results. Beretta et al. [32] developed a SIRS stochastic model with time delay. An SIS epidemic model with a saturation effect was developed by Liu et al. [33] and Zhao et al. [34]. The authors investigated the system’s persistence and existence in this study. In 2014, Zhou et al. [35] analyzed a stochastic SIR model considering the stationary distribution of the solution under specific parameter constraints. In 2016, Zhou et al. [36] established the stochastic SIS model with Levy jump. Zhou et al. [37] studied a stochastic SIS model considering the media effect and environmental variations. Ding and Zhang [38] have considered a stochastic SIRS epidemic model with information intervention. Djordjevic et al. [39] formulated a stochastic SICA epidemic model for HIV transmission by considering environmental white noise.

In this article, we have formulated a mathematical model for the dynamics of rotavirus infection based on the study [40]. The human population’s natural birth and death rates are also considered here. We categorize the human population into four subcategories: susceptible, infected, vaccinated, and recovered. Here we believe in the media’s impact on disease transmission. Our model also focuses on the effects of vaccination. We have also formulate a stochastic mathematical model to analyse the rotavirus infection during vaccination and the effect of media awareness with parametric perturbation. Also, the parameters’ sensitivity via the model’s stochastic extension is analyzed.

The impact of media awareness is studied in detail for the deterministic model. The analytical studies are performed using boundedness, reproduction number, equilibria and their stability analysis. The proposed stochastic version of the model is analyzed using various theorems. An in-depth numerical simulation is performed to verify our analytical results and large sample based iteration method also used to study the long term dynamics of the stochastic system.

The paper is organised in the following manner: In Section “Epidemic Modelling”, we have formulated an ordinary differential equation model. In this section, we have also derived the boundedness and positivity of the system and analysed the proposed model on the basis of the basic reproduction number. In Section “Stochastic Model”, we formulated a stochastic differential equation model with parametric perturbations. In Section “Numerical Simulations”, the model results have been verified with the help of numerical simulation. Finally, in Section “Discussion”, we have finished with a brief conclusion.

Epidemic Modelling

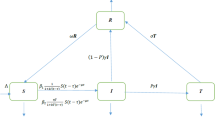
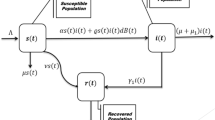
In this modelling S(t) be the number of susceptiable individuals, V(t) the vaccinated individuals, I(t) the infected individual and R(t) the recovered individuals at time t respectively. Here we assume the population mix homogeneous to formulate the system of ordinary differential equations. Thus, our model becomes:

$$\begin{aligned} \frac{d S}{d t}= & {} (1 - \rho ) \Lambda - \frac{\beta S I}{1+pI} - (\nu +\mu ) S, \nonumber \\ \frac{d V}{d t}= & {} \rho \Lambda +\nu S- \frac{ \epsilon \beta V I}{1+pI} - \mu V,\nonumber \\ \frac{d I}{d t}= & {} \frac{\beta S I}{1+pI}+ \frac{\epsilon \beta V I}{1+pI} - (\tau + \kappa + \mu )I,\\ \frac{d R}{d t}= & {} \kappa I - \mu R.\nonumber \end{aligned}$$
(1)

We assume that \(\Lambda \) is the birth rate of S(t) by adult and \(\beta \) is the rate of contact. Here we introduce the media impact \(\frac{1}{1+p I}\) where p denotes the strength media effect. \(I_c\) is the threshold value which decides whether media awareness is needed or not. We also consider \(\varphi (I)=I-I_c\) to show the media factor. Recruitment rate of vaccination individual is denoted as \(\rho \). Due to vaccination the contact rate reduced at a rate \(\epsilon \) and \(\nu \) is the vaccine coverage rate. Here \(\mu \) is the natural death rate and \(\kappa \) is the recovery rate. \(\tau \) is the death rate due to rota virus.

Here \(\hat{\beta }(I,p)=\frac{\beta }{1+ pI}\), p represents the media effects with

$$\begin{aligned} p= & {} \left\{ \begin{array}{ll} 0, &{} \varphi (I)\le 0; \\ 1, &{} \varphi (I)> 0. \end{array} \right. \end{aligned}$$
(2)

When \(p=0\) then the transmission rate \(\hat{\beta }=\beta \), constant and when \(p\ne 1\), the transmission rate is \(\hat{\beta }=\frac{\beta }{1+p I}\).

Analysis

The feasible region of the model can be supported by the non negativeness of the model variables S(t),  V(t),  I(t),  and R(t). In this section, we discuss feasible region of the model. Therefore, the results of the epidemic model should be bounded in the region \(\mathcal {B}=\{(S, V, I, R)\in R^4_+: N(t)\le \frac{\Lambda }{\mu }, S(t)\ge 0, V(t)\ge 0, I(t)\ge 0, R(t)\ge 0\}\) at any time \(t\ge 0\).

Non-negativity of Solutions

Theorem 1

The solution of the system (1) is positive at any time \(t\ge 0\) with non negative initial condition.

Proof

From (1) we can write

$$\begin{aligned} \frac{dS}{dt}|_{S=0}= & {} (1-\rho )\Lambda \ge 0,~~~\frac{dV}{dt}|_{V=0}=\rho \Lambda +\nu S\ge 0\\ \frac{dI}{dt}|_{I=0}= & {} 0,~~~\frac{dR}{dt}|_{R=0}=\kappa I\ge 0. \end{aligned}$$

Hence, the system (1) is positive at any time with positive initial conditions.

Boundedness

Theorem 2

The system (1) is bounded in the feasible region \(\mathcal {B}\).

Proof

Let us consider the population density function as follows:

$$\begin{aligned} N(t)= & {} S(t)+V(t)+I(t)+R(t),\\ \frac{dN}{dt}= & {} \Lambda -\mu N. \end{aligned}$$

By using Gronwall’s inequality,

$$\begin{aligned} N(t)= & {} N(0)e^{-\Lambda t}+\frac{\Lambda }{\mu },~~ t\ge 0\nonumber \\ \lim _{t\rightarrow \infty }&\sup&N(t)\le \frac{\Lambda }{\mu }. \end{aligned}$$
(3)

So, we can say that the system (1) is bounded in the region \(\mathcal {B}\).

Equilibria

Assuming the state variable of the system (1) are constant, we choose

$$\begin{aligned} (1 - \rho ) \Lambda - \frac{\beta S I}{1+pI} - (\nu +\mu ) S= & {} 0, \nonumber \\ \rho \Lambda +\nu S- \frac{\epsilon \beta V I}{1+pI} - \mu V= & {} 0,\nonumber \\ \frac{\beta S I}{1+pI}+ \frac{\epsilon \beta V I}{1+pI} - (\tau + \kappa + \mu )I= & {} 0,\\ \kappa I - \mu R= & {} 0.\nonumber \end{aligned}$$
(4)

From Eq. (4) we get the endemic equilibrium \(E^*(S^*,V^*,I^*,R^*)\) where

$$\begin{aligned} S^*= & {} \frac{(1-\rho )\Lambda (1+pI^*)}{\beta I^*+(\nu +\mu )(1+pI^*)},~~ V^*=\frac{(\rho \Lambda +\nu S^*)(1+pI^*)}{\epsilon \beta I^*+\mu (1+pI^*)}\nonumber \\ R^*= & {} \frac{\kappa I^*}{\mu }, \end{aligned}$$
(5)

and \(I^*\) is defined as

$$\begin{aligned} I^*= & {} \frac{a_5-(a_0 \mu +\epsilon \beta \rho \Lambda a_5)}{a_0 a_2+\epsilon \beta (\rho \Lambda a_1+a_3 p)} \end{aligned}$$
(6)

where

$$\begin{aligned} a_0= & {} \beta (1-\rho ) \Lambda ,~~ a_1=\beta +p(\nu +\mu ),~a_2= \epsilon \beta +\mu p,\nonumber \\ a_3= & {} (1-\rho ) \Lambda \nu ,~~a_4=\nu +\mu ,~~a_5=\tau +\kappa +\mu . \end{aligned}$$
(7)

Also when \(I=0,~~R=0\) we have the disease free equilibrium \(\hat{E}(\hat{S},\hat{V},0,0)\) where

$$\begin{aligned} \hat{S}= & {} \frac{(1-\rho )\Lambda }{\nu +\mu },~~\hat{V}=\frac{(\nu +\rho \mu )\Lambda }{\mu (\nu +\mu )}. \end{aligned}$$
(8)

Reproduction Number

In this section, we investigate the reproduction number by using the next-generation matrix method. The transmission and transition matrices (P and Q respectively) of the system (1) after substituting the disease-free equilibrium are as follows [41]:

$$\begin{aligned} \left[ \begin{array}{c} I' \\ R' \end{array}\right]= & {} \left[ \begin{array}{cc} \beta (S+\epsilon V) &{} 0 \\ 0 &{} 0 \end{array}\right] \left[ \begin{array}{c} I \\ R \end{array}\right] -\left[ \begin{array}{cc} (\tau +\kappa +\mu ) &{} 0 \\ -\kappa &{} \mu \end{array}\right] \left[ \begin{array}{c} I \\ R \end{array}\right] \end{aligned}$$
(9)

Now,

$$\begin{aligned} P= & {} \left[ \begin{array}{cc} \beta (S+\epsilon V) &{} 0 \\ 0 &{} 0 \end{array}\right] ,~~Q=\left[ \begin{array}{cc} (\tau +\kappa +\mu ) &{} 0 \\ -\kappa &{} \mu \end{array}\right] \end{aligned}$$
(10)
$$\begin{aligned} |Q|= & {} \mu (\tau +\kappa +\mu ), Q^{-1}=\left[ \begin{array}{cc} \frac{1}{\tau +\kappa +\mu } &{} 0 \\ \frac{\kappa }{\mu (\tau +\kappa +\mu )}&{} \frac{1}{\mu } \end{array}\right] \nonumber \\ U= & {} PQ^{-1}=\left[ \begin{array}{cc} \beta (S+\epsilon V)&{} 0 \\ 0 &{} 0 \end{array}\right] \times \left[ \begin{array}{cc} \frac{1}{\tau +\kappa +\mu } &{} 0 \\ \frac{\kappa }{\mu (\tau +\kappa +\mu )}&{} \frac{1}{\mu } \end{array}\right] =\left[ \begin{array}{cc} \frac{\beta (\hat{S}+\epsilon \hat{V})}{(\tau +\kappa +\mu )} &{} 0 \\ 0 &{} 0 \end{array}\right] \nonumber \\ |U-\lambda I_2|_{\hat{E}}= & {} \left| \begin{array}{cc} \frac{\beta (\hat{S}+\epsilon \hat{V})}{(\tau +\kappa +\mu )} -\lambda &{} 0 \\ 0 &{} -\lambda \end{array}\right| =0,\nonumber \\{} & {} \implies \lambda \left( \frac{\beta (\hat{S}+\epsilon \hat{V})}{(\tau +\kappa +\mu )} -\lambda \right) =0. \end{aligned}$$
(11)

The dominant eigenvalue of the matrix \(P Q^{-1}\) is called the reproduction number and is denoted as

$$\begin{aligned} R_0= & {} \frac{\beta (1-\rho )\Lambda }{(\nu +\mu )(\tau +\kappa +\mu )}+\frac{\epsilon \beta (\nu +\rho \mu )\Lambda }{\mu (\nu +\mu )(\tau +\kappa +\mu )}\nonumber \\= & {} R_{01}+R_{02} \end{aligned}$$
(12)

\(R_0\) is a combination of two terms here. \(R_{01}\) refers to human-to-human transmission. The second term, \(R_{02}\), represents the human to human disease transmission after vaccination. If \(R_0\) crosses the value 1, the system transitions from disease-free to endemic.

Local Stability

In this section, we consider two theorems for local stability. The functions X, Y, Z, W are considered for the system (1) given as follows:

$$\begin{aligned} X= & {} (1 - \rho ) \Lambda - \frac{\beta S I}{1+pI} - (\nu +\mu ), \nonumber \\ Y= & {} \rho \Lambda +\nu S- \frac{\epsilon \beta V I}{1+pI} - \mu V,\nonumber \\ Z= & {} \frac{\beta S I}{1+pI}+ \frac{\epsilon \beta V I}{1+pI} - (\tau + \kappa + \mu )I,\\ W= & {} \kappa I - \mu R.\nonumber \end{aligned}$$
(13)

The partial derivatives of the function regarding state variables are as follows:

$$\begin{aligned} \frac{\partial X}{\partial S}= & {} -\frac{\beta I}{1+p I}-(\nu +\mu );~\frac{\partial X}{\partial V}=0;~ \frac{\partial X}{\partial I}=-\frac{\beta S}{(1+pI)^2};~\frac{\partial X}{\partial R}=0,\\ \frac{\partial Y}{\partial S}= & {} \nu ; ~\frac{\partial Y}{\partial V}=-\frac{\epsilon \beta I}{1+p I}-\mu ;~\frac{\partial Y}{\partial I}=-\frac{\epsilon \beta V}{(1+p I)^2}; \frac{\partial Y}{\partial R}=0;\\ \frac{\partial Z}{\partial S}= & {} \frac{\beta I}{1+p I};~\frac{\partial Z}{\partial V}=\frac{\epsilon \beta I}{1+p I};~\frac{\partial Z}{\partial I}=\frac{\beta (S+\epsilon V)}{(1+p I)^2}-(\tau +\kappa +\mu );~\frac{\partial Z}{\partial R}=0;\\ \frac{\partial W}{\partial S}= & {} 0;\frac{\partial W}{\partial V}=0;\frac{\partial W}{\partial I}=\kappa ;\frac{\partial W}{\partial R}=-\mu . \end{aligned}$$

Thus the Jacobian of the system becomes

$$\begin{aligned} J= \left( \begin{array}{cccc} -\{\frac{\beta I}{1+p I}+(\nu +\mu )\} &{} 0 &{} -\frac{\beta S}{(1+pI)^2} &{} 0\\ \nu &{} -\{\frac{\epsilon \beta I}{1+p I}+\mu \} &{} -\frac{\beta S}{(1+p I)^2} &{} 0\\ \frac{\beta I}{1+p I} &{} \frac{\epsilon \beta I}{1+p I} &{} \frac{\beta (S+\epsilon V)}{(1+p I)^2}-(\tau +\kappa +\mu ) &{} 0\\ 0 &{} 0 &{} \kappa &{} -\mu \end{array}\right) \end{aligned}$$
(14)

Theorem 3

The disease free equilibrium \(\hat{E}\) is locally asymptotically stable if \(R_0<1\). Otherwise the system is unstable when \(R_0>1\).

Proof

The Jacobian matrix at \(\hat{E}\) is as follows

$$\begin{aligned} J_1= \left( \begin{array}{cccc} -(\nu +\mu ) &{} 0 &{} -\beta \hat{S} &{} 0 \\ \nu &{} -\mu &{} -\epsilon \beta \hat{V} &{} 0\\ 0 &{} 0 &{} \beta (\hat{S}+\epsilon \hat{V})-(\tau +\kappa +\mu ) &{} 0\\ 0 &{} 0 &{} \kappa &{} -\mu \end{array}\right) \end{aligned}$$
(15)

Hence, from the characteristic equation \(|J_1-\lambda I|=0\), we have \(\lambda _1=-(\mu +\nu ),~\lambda _2=-\mu ,~\lambda _3=-\mu \), and \(\lambda _4<0\) if

$$\begin{aligned} \beta (\hat{S}+\epsilon \hat{V})< & {} (\tau +\kappa +\mu )~\implies R_0<1. \end{aligned}$$
(16)

Hence the disease-free equilibrium is stable for \(R_0<1\).

Theorem 4

The endemic equilibrium \(E^*\) is is locally asymptotically stable if \(R_0>1\).

Proof

The Jacobian matrix of the system at \(E^*\) is as follows:

$$\begin{aligned} J_{E^*}= & {} \left[ \begin{array}{cccc} a_{11} &{} a_{12} &{} a_{13} &{} a_{14} \\ a_{21} &{} a_{22} &{} a_{23} &{} a_{24} \\ a_{31} &{} a_{32} &{} a_{33} &{} a_{34} \\ a_{41} &{} a_{42} &{} a_{43} &{} a_{44} \end{array}\right] , \end{aligned}$$
(17)

where,

$$\begin{aligned} a_{11}= & {} -\left( \frac{\beta I^*}{1+pI^*}+\nu +\mu \right) ,~a_{12}=0,~a_{13}=-\frac{\beta S^*}{(1+p I^*)^2},~a_{14}=0,\nonumber \\ a_{21}= & {} \nu ,~a_{22}=-\left( \frac{\epsilon \beta I^*}{1+p I^*}+\mu \right) ,~a_{23}=-\frac{\epsilon \beta V^*}{(1+p I^*)^2},~a_{24}=0,\nonumber \\ a_{31}= & {} \frac{\beta I^*}{1+pI^*},~a_{32}=\frac{\epsilon \beta I^*}{1+pI^*},~a_{33}=\frac{\beta (S^*+\epsilon V^*)}{(1+p I^*)^2}-(\tau +\kappa +\mu ),~a_{34}=0,\nonumber \\ a_{41}= & {} 0,~a_{42}=0,~a_{43}=\kappa ,~a_{44}=-\mu . \end{aligned}$$
(18)

Consequently, the characteristic equation becomes

$$\begin{aligned} (\lambda -a_{11})(\lambda ^3+b_1 \lambda ^2+b_2 \lambda +b_4)= & {} 0, \end{aligned}$$
(19)

where,

$$\begin{aligned} b_1= & {} -(a_{11}+a_{22}+a_{33})>0,\nonumber \\\ b_2= & {} [a_{22}a_{33}-a_{23}a_{32}+a_{11}(a_{22}+a_{33})-a_{13}a_{31}],\nonumber \\ b_3= & {} -a_{11}(a_{22}a_{33}-a_{23}a_{32})-a_{21}a_{13}a_{32}+a_{13}a_{31}a_{22}. \end{aligned}$$
(20)

Here, \(\lambda _1=a_{11}<0\). Now, we observe that Routh-Hurwitz criterion for the 3rd-degree polynomial is also satisfied, since \(b_1>0,b_2>0,~b_1 b_2-b_3>0\) for \(R_0>1\). Hence the system is locally asymptotically stable.

Stochastic Model

All natural systems are mostly susceptible to stochastic perturbations. The stochastic model exists on the basis of small changes in populations and the dynamical changes due to the small changes in the parameters. For the initial phase of infection, the stochastic model plays a pivotal role in small geographical regions. To get the relevant and important information, we formulate the stochastic model of the (1)

Possible state changes in the stochastic process are based on deterministic models. Consider the system (1) vector \(\mathcal {G}\), which is defined as \(\mathcal {G}=[S, V, I, R]^T\). Table 1 defines the probability of transition under the assumption that \(\Delta t\) is very small. As a result, \(\Delta \mathcal {G}=\mathcal {G}(t+\Delta t)-\mathcal {G}(t)\) with \(t \in [0,\infty )\) is obtained.

Table 1 Possible changes in the process of the model
Full size table

Here the expectation and variance are defined as \(E^*[\Delta \mathcal {G}]\) and \(E^*[\Delta \mathcal {G} \Delta \mathcal {G}^T]\) where,

  • Expectation:

    $$\begin{aligned} E^*[\Delta \mathcal {G}]= & {} \Sigma ^{10}_{i=1} P_i (\Delta \mathcal {G})_i\\= & {} \left[ \begin{array}{c} (1-\rho )\Lambda -\frac{\beta SI}{1+pI}-(\nu +\mu )S\\ \rho \Lambda +\nu S-\frac{\epsilon \beta V I}{1+pI}-\mu V\\ \frac{\beta S I}{1+p I}+\frac{\epsilon \beta V I}{1+p I}-(\tau +\kappa +\mu ) I\\ \kappa I-\mu R \end{array}\right] \Delta t; \end{aligned}$$

  • Variance=

    $$\begin{aligned} E^*[\Delta \mathcal {G} \Delta \mathcal {G}^T]= & {} \Sigma ^{10}_{i=1} P_i [(\Delta \mathcal {G})_i][(\Delta \mathcal {G})_i]^T\\= & {} {\left[ \begin{array}{cccc} P_1+P_2+P_3+P_4 &{} -P_4 &{} -P_2 &{} 0 \\ -P_4&{} P_4+P_5+P_6+P_7 &{} -P_6 &{} 0\\ -P_2 &{} -P_6 &{} P_2+P_6+P_8+P_9 &{} -P_8 \\ 0 &{} 0 &{} -P_8 &{} P_8+P_{10} \end{array}\right] }\Delta t\\= & {} {\left[ \begin{array}{cccc} M_{11} &{} M_{12} &{} M_{13} &{} M_{14} \\ M_{21} &{} M_{22} &{} M_{23} &{} M_{24} \\ M_{31} &{} M_{32} &{} M_{33} &{} M_{34} \\ M_{41} &{} M_{42} &{} M_{43} &{} M_{44} \\ \end{array}\right] \Delta t,} \end{aligned}$$

where,

$$\begin{aligned} M_{11}= & {} (1-\rho )\Lambda +\frac{\beta S I}{1+p I}+(\nu +\mu ) S; M_{12}=-\nu S; M_{13}=-\frac{\beta S I}{1+p I}; M_{14}=0\\ M_{21}= & {} -\nu S; M_{22}= \rho \Lambda +\nu S+\frac{\epsilon \beta V I}{1+pI}+\mu V; M_{23}=-\frac{\epsilon \beta V I}{1+pI}; M_{24}=0\\ M_{31}= & {} -\frac{\beta S I}{1+p I}; M_{32}= -\frac{\epsilon \beta V I}{1+pI}; M_{33}=\frac{\beta S I}{1+pI}+\frac{\epsilon \beta V I}{1+pI}+(\tau +\kappa +\mu )I;\\ M_{34}= & {} -\kappa I; M_{41}= 0; M_{42}= 0; M_{43}=-\kappa I; M_{44}=\kappa I+\mu R. \end{aligned}$$

Now, we define

$$\begin{aligned} Drift= & {} \mathcal {C}(\mathcal {G},t)=\frac{E^*[\Delta \mathcal {G}]}{\Delta t}\nonumber \\= & {} \left[ \begin{array}{c} (1 - \rho ) \Lambda - \frac{\beta S I}{1+pI} - (\nu +\mu ) \\ \rho \Lambda +\nu S- \frac{\epsilon \beta V I}{1+pI} - \mu V\\ \frac{\beta S I}{1+pI}+ \frac{\epsilon \beta V I}{1+pI} - (\tau + \kappa + \mu )I,\\ \kappa I - \mu R \end{array}\right] , \end{aligned}$$
(21)

and the diffusion is defined as

$$\begin{aligned} Diffusion= & {} \mathcal {D}(\mathcal {G},t)\nonumber \\= & {} \sqrt{\frac{E^*[\Delta \mathcal {G} \Delta \mathcal {G}^T]}{\Delta t}}=\sqrt{\left[ \begin{array}{cccc} M_{11} &{} M_{12} &{} M_{13} &{} M_{14} \\ M_{21} &{} M_{22} &{} M_{23} &{} M_{24} \\ M_{31} &{} M_{32} &{} M_{33} &{} M_{34} \\ M_{41} &{} M_{42} &{} M_{43} &{} M_{44} \end{array}\right] }. \end{aligned}$$
(22)

Using (24) and (22), we have the stochastic differential equation as follows:

$$\begin{aligned} d \mathcal {G}(t)= & {} \mathcal {C}(\mathcal {G},t)+\mathcal {D}(\mathcal {G},t)dB(t),\nonumber \\ d\left[ \begin{array}{c} S \\ V \\ I \\ R \end{array}\right]= & {} \left[ \begin{array}{c} (1-\rho )\Lambda -\frac{\beta SI}{1+pI}-(\nu +\mu )S\\ \rho \Lambda +\nu S-\frac{\epsilon \beta V I}{1+pI}-\mu V\\ \frac{\beta S I}{1+p I}+\frac{\epsilon \beta V I}{1+p I}-(\tau +\kappa +\mu ) I\\ \kappa I-\mu R \end{array}\right] dt\nonumber \\{} & {} {+\sqrt{\left[ \begin{array}{cccc} (1-\rho )\Lambda +\frac{\beta SI}{1+pI}+(\nu +\mu )S &{} -\nu S &{} -\frac{\beta SI}{1+pI} &{} 0 \\ -\nu S &{} \rho \Lambda +\nu S+\frac{\epsilon \beta V I}{1+pI}+\mu V &{} -\frac{\epsilon \beta V I}{1+p I} &{} 0 \\ -\frac{\beta SI}{1+pI} &{} -\frac{\epsilon \beta V I}{1+p I} &{} \frac{\beta S I}{1+p I}+\frac{\epsilon \beta V I}{1+p I}+(\tau +\kappa +\mu ) I &{} -\kappa I \\ 0 &{} 0 &{} -\kappa I &{} \kappa I+\mu R \end{array}\right] }}dB(t)\nonumber \\ \end{aligned}$$
(23)

Here, B(t) is the Brownian motion with the initial condition \(\mathcal {G}(0)=\mathcal {G}_0,~~0\le t \le \mathcal {G}\).

Euler Maruyama Scheme

In this section, we utilize the Euler Maruyama scheme to determine the numerical solution of the stochastic differential equation (23). The employed model parameters are reported in Table 2. The following computational procedure holds:

$$\begin{aligned} d \mathcal {G}_n(t)= & {} \mathcal {C}(\mathcal {G}_n,t)+\mathcal {D}(\mathcal {G}_n,t)dB(t),\\ d\left[ \begin{array}{c} S^{n+1} \\ V^{n+1} \\ I^{n+1} \\ R^{n+1} \end{array}\right]= & {} \left[ \begin{array}{c} S^n \\ V^n \\ I^n \\ R^n \end{array}\right] +\left[ \begin{array}{c} (1-\rho )\Lambda -\frac{\beta SI}{1+pI}-(\nu +\mu )S\\ \rho \Lambda +\nu S-\frac{\epsilon \beta V I}{1+pI}-\mu V\\ \frac{\beta S I}{1+p I}+\frac{\epsilon \beta V I}{1+p I}-(\tau +\kappa +\mu ) I\\ \kappa I-\mu R \end{array}\right] dt \\{} & {} \tiny {+\sqrt{\left[ \begin{array}{cccc} (1-\rho )\Lambda +\frac{\beta SI}{1+pI}+(\nu +\mu )S &{} -\nu S &{} -\frac{\beta SI}{1+pI} &{} 0 \\ -\nu S &{} \rho \Lambda +\nu S+\frac{\epsilon S I}{1+pI}+\mu V &{} -\frac{\epsilon \beta V I}{1+p I} &{} 0 \\ -\frac{\beta SI}{1+pI} &{} -\frac{\epsilon \beta V I}{1+p I} &{} \frac{\beta S I}{1+p I}+\frac{\epsilon \beta V I}{1+p I}+(\tau +\kappa +\mu ) I &{} -\kappa I \\ 0 &{} 0 &{} -\kappa I &{} \kappa I+\mu R \end{array}\right] }}\delta B_n, \end{aligned}$$

where \(\Delta t\) stands for the discretization parameter.

Parametric Perturbation of the Model

In what follows, we introduce parametric perturbation in the system (23). In this way, the epidemic model (23) with a saturated transmission rate and stochastic fluctuations will be reduced to the following form:

$$\begin{aligned} dS(t)= & {} \{(1-\rho )\Lambda -\frac{\beta SI}{1+pI}-(\nu +\mu )S\}dt+\sigma _1 (S-S^*) dB(t), \nonumber \\ dV(t)= & {} \{\rho \Lambda -\nu S-\frac{\epsilon \beta V I}{1+pI}-\mu V\} dt+\sigma _2 (V-V^*) dB(t),\nonumber \\ dI(t)= & {} \{\frac{\beta S I}{1+p I}+\frac{\epsilon \beta V I}{1+p I}-(\tau +\kappa +\mu ) I\}dt+\sigma _3 (I-I^*) dB(t),\\ dR(r)= & {} \{\kappa I-\mu R\} dt +\sigma _4 (R-R^*) dB(t),\nonumber \end{aligned}$$
(24)

where \(\sigma _1, ~\sigma _2,~\sigma _3,~\sigma _4\) are real constants and known as the intensity of the stochastic environment and B(t) standard Brownian motion.

Positivity and Boundedness of the Stochastic Model

Let \((\Upsilon , \mathcal {F}, \mathcal {D})\) be a complete probability space with a filtration \(\{\mathcal {F}_t\}_{t\in \mathcal {R}_+}\) satisfying the usual conditions; that is, it is right continuous and increasing while \(\mathcal {F}_0\) contains all \(\mathcal {D}\)-null sets. Denote

$$\begin{aligned} \Psi (t)= & {} (S(t), V(t), I(t), R(t))\triangleq (\psi _1(t),\psi _2(t),\psi _3(t),\psi _4(t)) \end{aligned}$$
(25)

and the norm \(|\Psi (t)|=\sqrt{S^2(t)+V^2(t)+I^2(t)+R^2(t)}\).

Table 2 Variables and biological relevant parameters values used for numerical simulations of the system (1)
Full size table

Let \(C^{2,1}(\mathbb {R}^3 \times (0,\infty ); \mathbb {R}_+)\) as the family of all nonnegative functions \(V(\Psi ,t)\) defined on \(\mathbb {R}^3 \times (0,\infty )\) such that they are continuously twice differentiable in \(\Psi \) and once in t.

We define the differential operator L associated with four-dimensional stochastic differential equation

$$\begin{aligned} d \Psi =\mathcal {G}(\Psi ,t)dt+\mathcal {H}(\Psi ,t) d B(t), \end{aligned}$$
(26)

where \(\mathcal {G}\) and \(\mathcal {H}\) are defined as

$$\begin{aligned} \mathcal {G}= & {} \left( \begin{array}{c} (1-\rho )\Lambda -\frac{\beta SI}{1+pI}-(\nu +\mu )S \\ \rho \Lambda -\nu S-\frac{\epsilon \beta V I}{1+pI}-\mu V\\ \frac{\beta S I}{1+p I}+\frac{\epsilon \beta V I}{1+p I}-(\tau +\kappa +\mu ) I\\ \kappa I-\mu R \end{array}\right) \end{aligned}$$
(27)

and

$$\begin{aligned} \mathcal {H}= & {} diag\left( \sigma _1(S-S^*),\sigma _2(V-V^*),\sigma _3(I-I^*),\sigma _4(R-R^*)\right) \end{aligned}$$
(28)

We have

$$\begin{aligned} L= & {} \frac{\partial }{\partial t}+\Sigma ^4_{i=1} \mathcal {G}_i (\Psi ,t) \frac{\partial }{\partial \psi _i}+\frac{1}{2}\Sigma ^4_{i=1}(\mathcal {H}^T(\Psi ,t)\mathcal {H}(\Psi ,t))_{i,j} \frac{\partial ^2}{\partial \psi _i \partial \psi _j} \end{aligned}$$
(29)

The action of the operator L on a function \(\chi \in C^{2,1} (\mathcal {R}^4 \times (0,\infty ): \mathcal {R}^4_+)\) then we have

$$\begin{aligned} L \chi (\Psi ,t)= & {} \chi _t(\Psi ,t)+\chi _{\psi } (\Psi ,t)\mathcal {G}(\Psi ,t)\nonumber \\{} & {} + \frac{1}{2} trace (\mathcal {H}^T(\Psi ,t) \chi _{\psi \psi } (\Psi ,t)\mathcal {H}(\Psi ,t)) \end{aligned}$$
(30)

T means transposition.

In this subsection, we first show the existence of a unique positive global solution of the stochastic model (24).

Theorem 5

The system (24) with the initial conditions \((S(0), V(0), I(0), R(0))\in R^4_+\) there is a unique solution \((S(t), V(t), I(t), R(t)),~t\ge 0\) which remain \(R^4_+\) having probability is one.

Proof

Using Ito’s formula, (24) admits a non-negative solution in the form of unique local on \((0,\tau _e)\), where explosion time is denoted \(\tau _e\) due to the local Lipschitz coefficients of the model.

Next, we shall prove that the Eq. (24) assume this solution in a global sense - meaning that \(\tau _e=\infty \).

Let \(q_0>0\) is sufficiently large for (S(0), V(0), I(0), R(0)) lying with in the interval \([1/q_0,q_0]\). For each integer \(q \ge q_0\), define a sequence of stopping times by

$$\begin{aligned} \tau _q= & {} inf \left\{ t\in [0,\tau _e]: S(t) \in \left( \frac{1}{q},q\right) ~or ~V(t) \in \left( \frac{1}{q},q\right) \right. \nonumber \\{} & {} \left. ~or ~I(t)\in \left( \frac{1}{q},q\right) ~or~R(t)\in \left( \frac{1}{q},q\right) \right\} \end{aligned}$$
(31)

We set \(\phi =\infty \) where \(\phi \) is an empty set. \(\tau _q\) is non decreasing as \(q \rightarrow \infty \) we get

$$\begin{aligned} \tau _\infty= & {} \lim _{q\rightarrow \infty } \tau _p; \end{aligned}$$
(32)

Thus \(\tau _\infty \le \tau _e\). Now, we would like to verify \(\tau _\infty =\infty \). There exist \(\mathcal {T}>0\) and \(\jmath \in (0,1)\) such that

$$\begin{aligned} P\{\tau _\infty \le \mathcal {T}\}> & {} \jmath , \forall q\ge q_1 \nonumber \\ P\{\tau _q \le \mathcal {T}\}\ge & {} \jmath , \forall q\ge q_1 \end{aligned}$$
(33)

Let us consider a function \(\chi : R^3_+ \rightarrow R_+\) defined as

$$\begin{aligned} \chi (S,V,I,R)= & {} (S-1-\ln S)+(V-1-\ln V)\nonumber \\{} & {} +(I-1-\ln I)+(R-1-\ln R), \end{aligned}$$
(34)

a nonnegative function. If \((S(t), V(t), I(t), R(t))\in R^4_+\), by using Ito’s formula, we compute

$$\begin{aligned} d \chi (S,V,I,R)= & {} \big (1-\frac{1}{S}\big )dS+ \big (1-\frac{1}{V}\big )dV+ \big (1-\frac{1}{I}\big )dI+ \big (1-\frac{1}{R}\big )dR\nonumber \\{} & {} +\big (\frac{\sigma ^2_1}{2}\big (1-\frac{S^*}{S}\big )^2+\frac{\sigma ^2_2}{2}\big (1-\frac{V^*}{V}\big )^2+\frac{\sigma ^2_3}{2}\big (1-\frac{I^*}{I}\big )^2+\frac{\sigma ^2_4}{2}\big (1-\frac{R^*}{R}\big )^2\big )dt\nonumber \\{} & {} +\big ( \sigma _1\big ( 1-\frac{1}{S}\big )(S-S^*)+\sigma _2\big ( 1-\frac{1}{V}\big )(V-V^*)\nonumber \\{} & {} +\sigma _3\big ( 1-\frac{1}{I}\big )(I-I^*)+\sigma _4\big ( 1-\frac{1}{R}\big )(R-R^*)\big )d B(t)\nonumber \\= & {} \big (\Lambda +\nu +\tau +\kappa +4\mu +\frac{\sigma ^2_1}{2}\big (1-\frac{S^*}{S}\big )^2+\frac{\sigma ^2_2}{2}\big (1-\frac{V^*}{V}\big )^2\nonumber \\{} & {} +\frac{\sigma ^2_3}{2}\big (1-\frac{I^*}{I}\big )^2+\frac{\sigma ^2_4}{2}\big (1-\frac{R^*}{R}\big )^2-\mu (S+V+I+R)\nonumber \\{} & {} -\tau I -\frac{(1-\rho )\Lambda }{S}-\frac{\beta }{1+pI}(S+\epsilon V)+\frac{\beta I}{1+p I}(1+\epsilon )\big )dt\nonumber \\{} & {} +\big ( \sigma _1\big ( 1-\frac{1}{S}\big )(S-S^*)+\sigma _2\big ( 1-\frac{1}{V}\big )(V-V^*)\nonumber \\{} & {} +\sigma _3\big ( 1-\frac{1}{I}\big )(I-I^*)+\sigma _4\big ( 1-\frac{1}{R}\big )(R-R^*)\big )d B(t)\nonumber \\\le & {} \big (\Lambda +\nu +\tau +\kappa +4\mu +\frac{\sigma ^2_1}{2}\big (1-\frac{S^*}{S}\big )^2+\frac{\sigma ^2_2}{2}\big (1-\frac{V^*}{V}\big )^2\nonumber \\{} & {} +\frac{\sigma ^2_3}{2}\big (1-\frac{I^*}{I}\big )^2+\frac{\sigma ^2_4}{2}\big (1-\frac{R^*}{R}\big )^2\big ) dt\nonumber \\{} & {} +\big ( \sigma _1\big ( 1-\frac{1}{S}\big )(S-S^*)+\sigma _2\big ( 1-\frac{1}{V}\big )(V-V^*)\nonumber \\{} & {} +\sigma _3\big ( 1-\frac{1}{I}\big )(I-I^*)+\sigma _4\big ( 1-\frac{1}{R}\big )(R-R^*)\big )d B(t). \end{aligned}$$
(35)

Considering

$$\begin{aligned} \Pi= & {} \Lambda +\nu +\tau +\kappa +4\mu +\frac{\sigma ^2_1}{2}\big (1-\frac{S^*}{S}\big )^2+\frac{\sigma ^2_2}{2}\big (1-\frac{V^*}{V}\big )^2\\{} & {} +\frac{\sigma ^2_3}{2}\big (1-\frac{I^*}{I}\big )^2+\frac{\sigma ^2_4}{2}\big (1-\frac{R^*}{R}\big )^2, \end{aligned}$$

we have

$$\begin{aligned} d \chi (S,V,I,R)\le & {} \Pi dt+\big ( \sigma _1\big ( 1-\frac{1}{S}\big )(S-S^*)+\sigma _2\big ( 1-\frac{1}{V}\big )(V-V^*)\nonumber \\{} & {} +\sigma _3\big ( 1-\frac{1}{I}\big )(I-I^*)+\sigma _4\big ( 1-\frac{1}{R}\big )(R-R^*)\big )d B(t) \end{aligned}$$
(36)

Where \(\Pi \) is positive constant.

Integrating (36) yields

$$\begin{aligned} \int ^{\tau _q \wedge \mathcal {T}}_0 d \chi (S, V, I, R)\le & {} \int ^{\tau _q \wedge \mathcal {T}}_0 \Pi ds+\int ^{\tau _q \wedge \mathcal {T}}_0 \big ( \sigma _1\big ( 1-\frac{1}{S}\big )(S-S^*)+\sigma _2\big ( 1-\frac{1}{V}\big )(V-V^*)\nonumber \\{} & {} +\sigma _3\big ( 1-\frac{1}{I}\big )(I-I^*)+\sigma _4\big ( 1-\frac{1}{R}\big )(R-R^*)\big )d B(t), \end{aligned}$$
(37)

where, \({\tau _q \wedge \mathcal {T}}=min(\tau _q, \mathcal {T} )\). Then taking the expectations leads to

$$\begin{aligned} E\chi (S(\tau _q \wedge \mathcal {T}),V(\tau _q \wedge \mathcal {T}), I(\tau _q \wedge \mathcal {T}), R(\tau _q \wedge \mathcal {T}))\le & {} \chi (S(0), V(0), I(0), R(0))+ \Pi \mathcal {T}\nonumber \\ \end{aligned}$$
(38)

Setting \(\zeta _q=\{\tau _q\le \mathcal {T}\}\) for \(q>q_1\) and taking into account we have \(P(\zeta _q \ge \jmath )\). For every \(\zeta _1\in \zeta _q\) there are some I such that \(\Psi _i(\tau _q, \zeta _1)\) equals either q or 1/q for \(i=1,2,3,4\). Hence we have

$$\begin{aligned} \Psi= & {} \chi (S(\tau _q, \zeta _1),V(\tau _q, \zeta _1),I(\tau _q, \zeta _1),R(\tau _q, \zeta _1)). \end{aligned}$$
(39)

It is less than \(min(q-1-ln ~q, \frac{1}{q}-1-ln\frac{1}{q})\), then we have

$$\begin{aligned} \chi (S(0),V(0),I(0),R(0))+\Pi \mathcal {T}\ge & {} E\big ( I_{\zeta _q} \chi (S(\tau _q),V(\tau _q),I(\tau _q),R(\tau _q))\big )\nonumber \\\\le & {} \left\{ \min \left\{ q-1-ln q, \frac{1}{q}-1-ln\frac{1}{q}\right\} \right\} \end{aligned}$$
(40)

Here \(I_\zeta \) of \(\zeta _q\) is an indicator function. Consider \(q\rightarrow \infty \) leads to the contradiction \(\infty =\chi (S(0),V(0),I(0),R(0))+\Pi \mathcal {T}<\infty \), as desired. This completes the proof.

Theorem 5 shows that the solution to model (24) will remain in \(R^4_+\).The property makes us continue to discuss how the solution varies in \(R^3_+\) in more detail. Here, we present that the definition of stochastic ultimate boundedness [5] is one of the important topics in population dynamics and is defined as follows.

Definition 1

The solutions \(\Psi (t)=(S(t), V(t), I(t), R(t))\) of the model (24) are said to be stochastically ultimately bounded, if for any \(\epsilon \in (0,1)\) there is a positive constant \(\delta =\delta (\epsilon )\), such that for any initial value \((S(0),V(0), I(0), R(0))\in R^4_+\) the solution \(\Psi (t)\) of the model (24) has the property that

$$\begin{aligned} \lim _{t \rightarrow \infty } \sup P\{|\Psi (t)|>\delta \}< & {} \epsilon . \end{aligned}$$
(41)

Theorem 6

The solutions of model (24) are stochastically ultimately bounded for any initial value \((S(0),V(0), I(0), R(0))\in R^4_+\).

Proof

Define a function

$$\begin{aligned} \chi (S, V, I, R)= & {} e^t (S^\omega +V^\omega +I^\omega +R^\omega ) \end{aligned}$$
(42)

for \((S,I,R,V)\in R^4_+\) and \(\omega >1\). By Ito’s formula

$$\begin{aligned} d\chi (S, V, I, R )= & {} e^t\Big (\omega S^{\omega -1}\left( (1-\rho )\Lambda -\frac{\beta SI}{1+pI}-(\nu +\mu )S\right) \nonumber \\{} & {} +\omega V^{\omega -1}\left( \rho \Lambda -\nu S-\frac{\epsilon \beta V I}{1+pI}-\mu V\right) \nonumber \\{} & {} +\omega I^{\omega -1}\left( \frac{\beta S I}{1+p I}+\frac{\epsilon \beta V I}{1+p I}-(\tau +\kappa +\mu ) I\right) \nonumber \\{} & {} +\omega R^{\omega -1}\left( \kappa I-\mu R\right) \\{} & {} +\frac{\omega (\omega -1)}{2}\Big (\sigma ^2_1 S^\omega \Big (1-\frac{S^*}{S}\Big )^2+\sigma ^2_2 V^\omega \Big (1-\frac{V^*}{V}\Big )^2\nonumber \\{} & {} +\sigma ^2_3 I^\omega \Big (1-\frac{I^*}{I}\Big )^2+\sigma ^2_4 R^\omega \Big (1-\frac{R^*}{R}\Big )^2\Big )dt\nonumber \\{} & {} +e^t\omega \Big ( \sigma _1 S^\omega \Big (1-\frac{S^*}{S}\Big )+\sigma _2 V^\omega \Big (1-\frac{V^*}{V}\Big )\nonumber \\{} & {} +\sigma _3 I^\omega \Big (1-\frac{I^*}{I}\Big )+\sigma _4 R^\omega \Big (1-\frac{R^*}{R}\Big )\Big ) dB(t)\nonumber \\\le & {} \mathcal {K} e^t dt+e^t \omega \Big ( \sigma ^2_1 S^\omega \Big (1-\frac{S^*}{S}\Big )+\sigma ^2_2 V^\omega \Big (1-\frac{V^*}{V}\Big )\nonumber \\{} & {} +\sigma ^2_3 I^\omega \Big (1-\frac{I^*}{I}\Big )+\sigma ^2_4 R^\omega \Big (1-\frac{R^*}{R}\Big )\Big )d B(t)\nonumber \end{aligned}$$
(43)

where \(\mathcal {K}\) is a constant.

Based on Theorem () and from (43), we have

$$\begin{aligned} E\Big ( e^{\tau _q \wedge \mathcal {T}} \chi \Big ( S(\tau _q \wedge \mathcal {T}),V(\tau _q \wedge \mathcal {T}),I(\tau _q \wedge \mathcal {T}),R(\tau _q \wedge \mathcal {T})\Big )\Big )\le & {} \chi \Big (S(0),V(0),I(0),R(0)\Big )\nonumber \\{} & {} +\mathcal {K} E \int ^{\tau _q \wedge \mathcal {T}}_0e^s ds. \end{aligned}$$
(44)

Letting \(t\rightarrow \infty \), we have

$$\begin{aligned} e^t E \chi (S(t), V(t), I(t), R(t))\le & {} \chi (S(0),V(0), I(0),R(0))+\mathcal {K}(e^t-1), \end{aligned}$$
(45)

which implies

$$\begin{aligned} E \chi (S(t), V(t), I(t), R(t))\le & {} e^{-t} \chi (S(0),V(0),I(0),R(0))+\mathcal {K}. \end{aligned}$$
(46)

Note that

$$\begin{aligned} |\Psi (t)|^\omega= & {} (S^2(t)+V^2(t)+I^2(t)+R^2(t))^{\frac{\omega }{2}}\nonumber \\\le & {} 3^{\frac{\omega }{2}} max\Big (S^\omega (t)+V^\omega (t)+I^\omega (t)+R^\omega (t)\Big )\\\le & {} 3^{\frac{\omega }{2}}\Big (S^\omega +V^\omega +I^\omega +R^\omega \Big ).\nonumber \end{aligned}$$
(47)

Then we have

$$\begin{aligned} E|\Psi (t)|^\omega\le & {} 3^{\omega /2}\Big ( e^{-t}\chi \Big ( S(0),V(0),I(0),R(0)\Big )+\mathcal {K}\Big ), \end{aligned}$$
(48)

which means

$$\begin{aligned} \lim _{t \rightarrow \infty } \sup E|\chi (t)|^\omega\le & {} 3^{\omega /2}\mathcal {K} <\infty . \end{aligned}$$
(49)

Therefore, there exist a positive constant \(\hat{\delta }\) such that

$$\begin{aligned} \lim _{t \rightarrow \infty } \sup E|\sqrt{\chi (t)}|< & {} \hat{\delta }. \end{aligned}$$
(50)

For any \(\epsilon >0\), set \(\delta =\hat{\delta }^2/\epsilon ^2\), then according to Chebyshev’s inequality,

$$\begin{aligned} P\{\chi (t)>\delta \}\le & {} \frac{E|\sqrt{\chi (t)}|}{\sqrt{\delta }}. \end{aligned}$$
(51)

Then we have

$$\begin{aligned} \lim _{t \rightarrow \infty } P\{\chi (t)>\delta \}< & {} \frac{\hat{\delta }}{\sqrt{\delta }}=\epsilon . \end{aligned}$$
(52)

Which proves the theorem.

Generally speaking, the nonexplosion property, the existence, and the uniqueness of the solution are not enough but the property of permanence is more desirable since it means the long time survival in a population dynamics. Now, the definition of stochastic permanence [39] will be given below.

Theorem 7

The solution of the system (S(t), V(t), I(t), R(t)) with the initial condition (S(0), V(0), I(0), R(0)) and \(\mu <\Lambda \) satisfies

$$\begin{aligned} \lim _{t\rightarrow \infty } \sup E(|\chi (t)|^{-\omega })\le & {} \Theta , \end{aligned}$$
(53)

where \(\omega \) is an arbitrary positive constant satisfying

$$\begin{aligned} \frac{\omega +1}{2} \max \{\sigma ^2_1,\sigma ^2_2,\sigma ^2_3,,\sigma ^2_4\}< & {} \Lambda -\mu , \end{aligned}$$
(54)

where,

$$\begin{aligned} \Theta= & {} \frac{3^\omega (4\omega \Phi _1+\Phi _2)}{4 \omega \Phi _1}\times \max \Big \{ 1, \Big (\frac{2 \Phi _1+\Phi _2+\sqrt{\Phi ^2_2+4\Phi _1 \Phi _2}}{2 \Phi }\Big )^{\omega -1}\Big \}, \end{aligned}$$
(55)

in which \(\xi \) is an arbitrary positive constant satisfying

$$\begin{aligned} \xi< & {} \Lambda -\mu -\frac{\omega +1}{2} \max \{\sigma ^2_1,\sigma ^2_2,\sigma ^2_3,\sigma ^2_4\}\nonumber \\ \Phi _1= & {} \Lambda -\mu -\frac{\omega +1}{2}\max \{\sigma ^2_1,\sigma ^2_2,\sigma ^2_3,\sigma ^2_4\}-\xi \\ \Phi _1= & {} \mu +\max \{\sigma ^2_1,\sigma ^2_2,\sigma ^2_3,\sigma ^2_4\}+2\xi \nonumber \end{aligned}$$
(56)

Proof

Define function

$$\begin{aligned} \chi (S,V,I,R)= & {} \frac{1}{S+V+I+R}, \end{aligned}$$
(57)

for \((S(t),V(t),I(t),R(t))\in R^4_+\), using Ito’s formula, we get

$$\begin{aligned} d\chi (S,V,I,R)= & {} -\chi ^2(\Lambda -\mu (S+V+I+R))dt+\chi ^3\Big (\sigma ^2_1(S-S^*)^2+\sigma ^2_2(V-V^*)^2\nonumber \\{} & {} +\sigma ^2_3(I-I^*)^2+\sigma ^2_4(R-R^*)^2\Big )dt\\{} & {} -\chi ^2\Big ( \sigma _1(S-S^*)+\sigma _2(V-V^*)+\sigma _3(I-I^*)+\sigma _4(R-R^*)\Big )dB(t)\nonumber \end{aligned}$$
(58)

Choosing a positive constant \(\omega \) that satisfies and applying Itˆo’s formula, we obtain

$$\begin{aligned} L(1+\chi )^\omega= & {} \omega (1+\chi )^{\omega -1}\times \Big (-\chi ^2(\Lambda -\mu (S+V+I+R))\nonumber \\{} & {} \Big (\sigma ^2_1(S-S^*)^2+\sigma ^2_2(V-V^*)^2+\sigma ^2_3(I-I^*)^2+\sigma ^2_4(R-R^*)^2\Big )\nonumber \\{} & {} +\frac{\omega (\omega -1)}{2}\chi ^4(1+\chi )^{\omega -2}\Big ( \sigma ^2_1(S-S^*)^2+\sigma ^2_2(V-V^*)^2\nonumber \\{} & {} +\sigma ^2_3(I-I^*)^2+\sigma ^2_4(R-R^*)^2\Big )\nonumber \\= & {} \omega (1+\chi )^{\omega -2}\times \Big (-\chi ^2(\Lambda -\mu (S+V+I+R))-\chi ^3(\Lambda -\mu (S+V+I+R))\nonumber \\{} & {} +\chi ^3(\chi ^2_1(S-S^*)^2+\chi ^2_2(V-V^*)^2+\chi ^2_3(I-I^*)^2+\chi ^2_4(R-R^*)^2)\nonumber \\{} & {} \frac{\omega +1}{2} \chi ^4(\chi ^2_1(S-S^*)^2+\chi ^2_2(V-V^*)^2+\chi ^2_3(I-I^*)^2+\chi ^2_4(R-R^*)^2)\Big )\nonumber \\= & {} \omega (1+\chi )^{\omega -1} \mathcal {W}, \end{aligned}$$
(59)

where

$$\begin{aligned} \mathcal {W}= & {} \Big (-\chi ^2(\Lambda -\mu (S+V+I+R))-\chi ^3(\Lambda -\mu (S+V+I+R))\nonumber \\{} & {} +\chi ^3(\chi ^2_1(S-S^*)^2+\chi ^2_2(V-V^*)^2+\chi ^2_3(I-I^*)^2+\chi ^2_4(R-R^*)^2)\nonumber \\{} & {} \frac{\omega +1}{2} \chi ^4(\chi ^2_1(S-S^*)^2+\chi ^2_2(V-V^*)^2+\chi ^2_3(I-I^*)^2\nonumber \\{} & {} +\chi ^2_4(R-R^*)^2)\Big ) \end{aligned}$$
(60)
Fig. 1
figure 1

The relationship between S, I and \(g(S,I)=\frac{\beta S I}{1+p I}\) for \(\Lambda =1,\beta =0.005\) where a \(p=0.5\), b \(p=0.9\), c \(p=0.1\). The other parameters are same as in Table 2

Full size image
Fig. 2
figure 2

The time series plot of the model (1) for a \(p=0.5\), b \(p=0.1\), and c \(p=0.01\). The other parameters are same as in Table 2 with \(A=1,\beta =0.005\)

Full size image

Numerical Simulations

In this section, we perform numerical simulations to support our analytical findings. The parameters used for simulation (see Table 2) are taken from the study [40]. The newly introduced parameter p (media effect) takes the value in [0,1]. For \(p=0\) i.e. no media effect leads to transmission rate (\(\beta \)) and for \(p=1\) i.e. maximum media effect reduces transmission rate (\(\frac{\beta }{1+I}\)). In our study, we have analyzed the system with several values of p, from very small (0.01) to small (0.1) to moderate (0.5) to high value (0.9) so that the entire scenario can be studied with respect to this parameter. We have taken most of the parameter values from Table 2 and demonstrated the system dynamics for both \(R_0\) greater and less than 1. For the parameter set \(\Lambda =1,~\beta =0.005,~p=0.5\), it is observed that \(R_0=5.835 (>1)\) which implies the disease persist in the deterministic system (1). First, we have plotted the function \(g(S, I)=\frac{\beta S I}{1+p I}\) concerning S, I for various values of the parameters p. We fixed \(\Lambda =1,\beta =0.005\) and took other parameter values from Table 2. This g(S,I) shows the spread pattern of infection with respect to S, I. This surface plot mainly visualize the spread of disease for different values of the media parameter p. We have drawn the relationship for \(p=0.5,0.9,0.1\) in Fig. 1a–c, respectively. It is observed that the curve is sigmoidal for I and exponential for S. For the above mentioned parameter values together with \(p=0.5\), two equilibrium exists: disease free equilibrium (DFE) \(E'(49.6,5.96,0,0)\) and endemic equilibrium (EE) \(E^*(35.89,4.43,6.45,7.16)\). Similarly, for \(p=0.1,~0.01\) the DFE are same and EE are (20.24, 2.69, 13.82, 15.35), (10.08, 1.56, 18.6, 20.67) respectively. As \(R_0=5.835\) in all the cases, so by Theorems 3 and 4 the DFE unstable and EE stable for all the case i.e. \(p=0.5,0.1,0.01\). We have drawn a time series diagram to visualize these three scenario in Fig. 2a–c. The Runge-Kutta (RK) method (of order 4) is used to simulate the deterministic model. For the high order RK methods it is possible to obtaining good accuracy even if for a moderate step size but algorithms stability requires the step size not becomes large [42]. Here it is clear that all four compartments go towards a stable equilibrium. So in Fig. 2a, the susceptible population (green) goes to stable equilibrium density 35.89, the vaccinated population (purple) goes to stable equilibrium density 4.43, infected population (red) goes to stable equilibrium density 6.45 and recovered population (blue) goes to stable equilibrium density 7.16. Similarly, in Fig. 2b, the susceptible population (green) goes to stable equilibrium density 20.24, the vaccinated population (purple) goes to stable equilibrium density 2.69, the infected population (red) goes to stable equilibrium density 13.82 and recovered population (blue) goes to stable equilibrium density 15.35. In Fig. 2c, the susceptible population (green) goes to stable equilibrium density 10.08, the vaccinated population (purple) goes to stable equilibrium density 1.56, the infected population (red) goes to stable equilibrium density 18.6 and recovered population (blue) goes to stable equilibrium density 20.67. In Fig. 2, we have observed that for low value of media effect parameter the infected component dominant the susceptible. As we increase the impact of media effect, we notice that the susceptible component get higher equilibrium density than the infected equilibrium. So the media effect significantly impact the spread of rotavirus infection.

Fig. 3
figure 3

The path S(t),  V(t),  I(t) and R(t) for the stochastic model (23) with initial values \((S(0), V(0), I(0),R(0)) = (2, 1.5, 1, 0.5)\). The parameters are taken from Table 2 and \(A=1,\beta =0.005\) with a) \(\sigma _1=0.1, \sigma _2=0.2, \sigma _3=0.1, \sigma _4=0.1\), b) \(\sigma _1=0.1, \sigma _2=0.3, \sigma _3=0.1, \sigma _4=0.3\), c) \(\sigma _1=0.3, \sigma _2=0.3, \sigma _3=0.2, \sigma _4=0.3\) and d) \(\sigma _1=0.3, \sigma _2=0.1, \sigma _3=0.3, \sigma _4=0.1\)

Full size image
Fig. 4
figure 4

The four different sample paths and their average path of S(t),  V(t),  I(t) and R(t) for the stochastic model (23). The parameters are taken from Fig. 3 with \(\sigma _1=0.2, \sigma _2=0.2, \sigma _3=0.1, \sigma _4=0.2\)

Full size image
Fig. 5
figure 5

Histogram of the densities at the time point 200 of the system (23). The parameters are taken from Fig. 3 with \(\sigma _1=0.1, \sigma _2=0.2, \sigma _3=0.1, \sigma _4=0.1\)

Full size image
Fig. 6
figure 6

The time series plot of the model (1) and the path S(t),  V(t),  I(t) and R(t) for the stochastic model (23) with initial values \((S(0), V(0), I(0),R(0)) = (10, 2, 5, 3)\). The parameters are taken from Table 2 with \(A=0.8,\beta =0.001,p=0.5\) and \(\sigma _1=0.3, \sigma _2=0.1, \sigma _3=0.3, \sigma _4=0.1\)

Full size image
Fig. 7
figure 7

The four different sample paths and their average path of S(t),  V(t),  I(t) and R(t) for the stochastic model (23). The parameters are taken from Fig. 6

Full size image
Fig. 8
figure 8

Histogram of the densities at the time point 200 of the system (23). The parameters are taken from Fig. 6

Full size image

Next, we have simulated the stochastic version of the model (23) through the Euler Maruyama method. It is the simplest stochastic numerical approximation method for the Ito scheme. The convergence and accurace for this scheme requires a small step size [43]. This scheme represents the order 0.5 strong Taylor scheme [43]. For the stochastic model, we have used several values of intensity parameter (\(\sigma _i\)) ranges from [0.1,0.3]. However, in most of the case we have fixed three (or, two) intensity parameters at the same value and study the dynamics of sample path due to the non-fixed parameter(s). To simulate the path of S(t),  V(t),  I(t) and R(t) for the model (23), we fixed the initial values \((S(0), V(0), I(0),R(0)) = (2, 1.5, 1, 0.5)\) throughout the stochastic simulation. The parameter values are taken from Table 2 with \(A=1,\beta =0.005\). In Fig. 3a, we consider the intensity parameters \(\sigma _1=0.1, \sigma _2=0.2, \sigma _3=0.1, \sigma _4=0.1\) and generated the stochastic densities for susceptible (green), vaccinated (purple), infected (red) and recovered population (blue). We further generated the stochastic densities corresponding to \(\sigma _1=0.1, \sigma _2=0.3, \sigma _3=0.1, \sigma _4=0.3\) in Fig. 3b; \(\sigma _1=0.3, \sigma _2=0.3, \sigma _3=0.2, \sigma _4=0.3\) Fig. 3c and \(\sigma _1=0.3, \sigma _2=0.1, \sigma _3=0.3, \sigma _4=0.1\) in Fig. 3d. We observed that all the Fig. 3a–d are stochastically bounded (Theorem 6) and have positive, unique solution converges in probability (Theorem 5). Figure 4a–d represents four different sample path and their average path of S(t),  V(t),  I(t) and R(t) respectively for the stochastic model (23). The parameters are taken from Fig. 3 with \(\sigma _1=0.2, \sigma _2=0.2, \sigma _3=0.1, \sigma _4=0.2\). In Fig. 4a (i.e. stochastic densities with respect to S), we observed that the second sample path (purple) goes to extinction. The other paths have positive flow, as does the middle path (black). Note that, as other compartment does not solely depend upon S, they don’t need to be extinct due to S. However, they can be extinct due to stochastic fluctuations. Similarly, in Fig. 4b (i.e., stochastic densities with respect to V), we observed that the fourth sample path (blue) might undergo extinction after some time. The other paths have positive flow, as does the average path (black). We observed non-extinct sample paths for the I and R compartments (see Fig. 4c, d). To get more detailed on the distribution of the densities of various compartments, we have drawn histograms (see Fig. 5a–d) of the densities at the time point 200 for 5000 runs of the system (23). These histograms show the distribution of densities at a particular time point for a large number of sample path simulation. The parameters are taken from Fig. 3 with \(\sigma _1=0.1, \sigma _2=0.2, \sigma _3=0.1, \sigma _4=0.1\). We have observed that maximum extinction occurs on S and R population. The average densities lies in the approximate range (1.5, 3), (1, 2), (0.75, 1.25) and (0.25, 0.75) for S, V, I and R respectively. For V and I the histogram shows a near symmetric distribution. However, for S and I it shows a skewed distribution due to a large times of extinction in samle path near or, before the mentioned time point.

We again simulate the deterministic model (1) and stochastic model (23) for the parameters taken from Table 2 with \(A=0.8,\beta =0.001,p=0.5\). It is observed that \(R_0=0.934 (<1)\), which implies the disease dies out in the deterministic system (1). These histograms show the distribution of densities at a particular time point for a large number of sample path simulation.

Only disease-free equilibrium (DFE) \(E'(39.7,4.76,0,0)\) for the parameter mentioned above. As \(R_0=0.934\), so by Theorem 3, the DFE is stable. We have drawn the time series diagram to visualize the scenario in Fig. 6a. Here it is clear that the S, V compartments go towards a stable equilibrium concerning time, and I, R compartments go to zero. To simulate the path of S(t),  V(t),  I(t) and R(t) for the stochastic model (23), we fixed the initial values \((S(0),V(0),I(0),R(0))=(10, 2, 5, 3)\) throughout the simulation with \(\sigma _1=0.3, \sigma _2=0.1, \sigma _3=0.3, \sigma _4=0.1\). We have simulated three different runs (see Fig. 6b–d) to observe any similar phenomena like the deterministic system. We observed that the I, R simultaneously do not reveal any kind of extinction in all runs. We also simulate four different sample paths and their average path of S(t),  V(t),  I(t), and R(t) for the stochastic model (23). It reveals there is no extinction scenario on the average run (see Fig. 7b–d), although a downward trend is observed in the average run of I(t). Also, various histograms of the densities (see Fig. 8a–d) at the time point 200 shows S and R compartments have more chance to extinct in the present scenario.

Discussion

In this article, our main focus is to study the SVIR epidemic model for rotavirus and the role of media awareness for vaccination and rotavirus infection. The deterministic model has two solutions, which are disease-free equilibrium and endemic equilibrium. The basic reproduction number of the system has two parts: one is after vaccination, and another is after vaccination. It is established that when \(R_0<1\), the system becomes virus-free and returns to its disease-free state. But when \(R_0>1\), the virus’s extinction probability becomes less than one. Thus, the system moves to its endemic state.

We have also investigated an stochastic SVIR model of the proposed SVIR ODE model. We demonstrated that for relatively small noise, the solution of the stochastic model oscillates around the solution of the ODE model. In this context, we would like to mentioned that most of previous studies [44,45,46] mainly focused on the vaccine efficiency. Some recent studies [47,48,49] focused on modelling the breast feeding and vaccine efficiency through ordinary and fractional differential equation. However, the impact of media is missing and we have studied this part to enrich the rotavirus model. Specific impact of media on the system dynamics has been studied through deterministic as well as stochastic setup.

So the important findings of our study includes the analysis of boundedness, reproduction number, equilibrium point and their stability analysis for the deterministic system. The impact of media on the spread of rotavirus transmission also investigated and we concluded that media awareness has a great potential to control the disease. The stochastic model is designed for the dynamics of rotaviruses. We use the Euler–Maruyama scheme to find the solution to the stochastic differential equation. Theorems 5 and 6 show the positivity and bounds of the stochastic system. Our analysis suggests that media campaigns can be used to understand the present condition of the rotavirus infection and the effective inhibition and control measures proposed by experts. Additionally, the numerical simulation suggests that as the intensity of informational intervention increases, the infected population diminishes.

Also, analysis of the dynamics of the stochastic model suggests that it does not fully depend on \(R_0\) like the deterministic model. The present study confirms a significant advantage over the other methods in effectiveness and unconditional convergence. However, the optimal cost of rapid disease control due to the combined effect of media awareness and vaccination will be an interesting area of study in our future work.