Analysis of Casson Nanofluid Flow and Heat Transfer Across a Non-linear Stretching Sheet Adopting Keller Box Finite Difference Scheme

Abstract

In this paper, chemical reaction of MHD Casson nanofluid flow and heat transfer over a non-linearly stretching sheet under convective and radiative effects with velocity and temperature slip boundary conditions have been analyzed. The governing equations have been transformed into non-dimensional form by employing similarity transformations. Non dimensional boundary value problem have been solved numerically using Keller Box Finite difference scheme. Velocity, temperature, concentration profiles have been obtained and presented graphically. Illustrations for Nusselt number, skin friction coefficient and Sherwood number etc. have been tabulated.

Introduction

Mainly fluids have been classified into two types as Newtonian and non-Newtonian. Both have wide range of variety of applications. Several non-Newtonian fluid models are present in the literature such as Casson, Williamson, Powel-eyring, Micro polar etc.As far researchers gone through experiments they have found some imperfection in expectations from fluids.They try to enhance conductivity of fluids as a result nanofluid’s discovery came into existence. Firstly Choi [1] introduced nanofluid. To enhance the thermal conductivity nanosized metal particles are poured into base fluid, such a mixture is referred as nanofluid. A numerical study of nanofluid over a sheet has been done by Dodda Ramya et al. [2]. An analytical modelling of nanofluid flow with second law analysis has been explored by Mohammad Hossein Abolbashari et al. [3]. Zahir Shah et al. [4] have been studied radiative Casson nanofluid with activation energy via Homotopy analysis method over stretching sheet. Casson nanofluid flow in porous medium with chemical reaction via a fast convergent method has been explained by Adebowale Martins Obalalu [5]

Flow due to stretched surface has variety of utilizations as extruction of plastic sheets, paper and glass fiber generation, cooling of electronic chips and sheets of metals etc. Several authors have been investigated flow over stretching sheet with stretched in various dimensions taking different type of fluids and produced useful results. Abd El-Aziz and Afify [6] have been investigated Casson fluid flow along with entropy generation analysis and observed effect of various parameters. Gopal et al. [7] have been explored chemically reacting Casson fluid over stretching sheet taking into account multiple slips with Runge–Kutta method. They have found that slip have proclivity to control the boundary layer flow. An unsteady flow of nanofluid flow with the help of Keller-box method has been evaluated by Wasim Jamshed et al. [8]. Boundary layer flow over inclined stretching sheet has been studied by Susmay Nandi et al. [9] using the Runge–Kutta Cash-Karp method.

Thermal radiation is one of the mode of heat transfer. It transfer the energy in the form of electromagnetic waves. It finds applications in various science fields as physics, engineering science as well as industrial science. When two bodies are at large temperature difference then we have to take non-linear radiation effect into account to explain the phenomenon of heat transfer.At lower temperature difference between two bodies linear thermal radiation is sufficient to describe the heat transfer phenomenon. A number of authors have been illustrated the effect of linear radiation as well as non linear radiation on various fluids taking a plenty of different geometries [10,11,12,13].

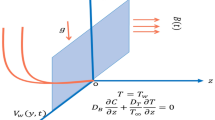
After reviewing the literature carefully we have noticed that convective Casson nanofluid flow with non linear magnetic field considering radiative and chemical reaction effect with thermal as well as velocity slip boundary condition have not been yet discovered properly. Also we have used a finite difference scheme to tackle the problem mathematically.We have taken stretching sheet as geometry for boundary layer flow. This study will help in several engineering processes as we have discussed earlier in the starting of this section in the view of geometry, fluid and other aspects. We have been explored the results with figures and tables and disused the effect of distinct parameters in detail. All observations have been summarized. Figure 1explain the flow pattern and boundary layers.

Formulation

We have considered a steady and incompressible two dimensional radiative and chemically reactive, magnetohydrodynamic flow of Casson nanofluid over a sheet which is stretched with non-linear velocity $U_w=ax^n$, where a and n denote a constant and non-linear parameter of stretching respectively. And stretching coordinate is denoted by $'x'$. The variable magnetic field $B=B_0 x^{{n-1}/2}$ is applied in transverse (y- direction). Convective effect is also considered in the modelling of this flow problem. u and v are velocities in x and y directions respectively. $T_w$ and $C_w$ represent wall temperature and nanoparticles fraction respectively while ambient nanoparticles fraction and temperature are represented by $C_\infty$ and $T_\infty$ respectively. Velocity, thermal and concentration boundary layers have been shown in Fig. 1

Fig. 1

Flow diagram of the model

Mathematical equations for the model are described as [follow [2, 3, 7]]-

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0 \end{aligned}$$

(1)

$$\begin{aligned}&u \frac{\partial u}{\partial x}+ v \frac{\partial u}{\partial y}=\nu \left( 1+\frac{1}{\beta }\right) \frac{\partial ^2 u}{\partial y^2}-\frac{\sigma B^2 u}{\rho }+ g \beta _T (T-T_\infty )+g \beta _C (C-C_\infty ) \end{aligned}$$

(2)

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{\partial ^2 T}{\partial y^2}+\frac{\nu }{C_p}\left( 1+\frac{1}{\beta }\right) \left( \frac{\partial u}{\partial y}\right) ^2-\frac{1}{\rho C_p}\frac{\partial q_r}{\partial y}+\tau \biggl \{D_B \frac{\partial T}{\partial y}\frac{\partial C}{\partial y}+\frac{D_T}{T_\infty } \bigg (\frac{\partial T}{\partial y}\bigg )^2 \biggl \} \end{aligned}$$

(3)

$$\begin{aligned}&u \frac{\partial C}{\partial x}+ v \frac{\partial C}{\partial y}= D_B \frac{\partial ^2 C}{\partial y^2}+ \frac{D_T}{T_\infty }\left( \frac{\partial ^2 T}{\partial y^2}\right) -k_0 (C-C_\infty ) \end{aligned}$$

(4)

Equation (1) represents conservation of mass. Equation (2) denotes velocity distribution in which fluid friction, magnetic field and convective terms are included. Equation (3) is energy equation in which last term in right hand side represents radiative term. Equation (4) denotes mass transfer in which first term in right hand side due to Brownian motion, second due to thermophoresis and third due to chemical reaction. Boundary conditions Dodda et al. [2] are-

$$\begin{aligned} u&=u_w +N \nu \frac{\partial u}{\partial y},\hspace{0.4 cm} v=0,\hspace{0.4 cm} T=T_w +D \frac{\partial T}{\partial y},\hspace{0.4 cm} C=C_w \hspace{1cm} at \hspace{0.5cm} y=0 \end{aligned}$$

(5)

$$\begin{aligned} u&\longrightarrow 0,\hspace{0.4 cm} T\longrightarrow T_\infty ,\hspace{0.4 cm} C {\longrightarrow } C_{\infty } \hspace{1 cm} as \hspace{0.5cm} y\longrightarrow \infty \end{aligned}$$

(6)

Where mathematical symbols have their own meanings as $\beta$ Casson Parameter, $\sigma$ Stefan Boltzmann coefficient, $B=B_0 x^\frac{n-1}{2}$ Variable magnetic field, g gravitational acceleration, $\beta _T$ and $\beta _C$ are thermal and solutal expansion coefficient, $\alpha$ thermal diffusivity, $\tau =\frac{(\rho C)_p}{(\rho C)_f}$ is the ratio of the effective heat capacity of the nanoparticle material to the effective heat capacity of the base fluid, $C_p$ specific heat at constant pressure, $\rho$ density of fluid, $q_r$ denotes radiative heat flux, $D_B$ and $D_T$ are Brownian and thermophoretic diffusion, $k_0$ is in reference to chemical reaction. $u_w =ax^n$ is stretching velocity of sheet, N and D are velocity and thermal slip factor respectively, both depands on x and n as $N=N_1 x^{-(\frac{n-1}{2})}$, $D=D_1 x^{-(\frac{n-1}{2})}$,(for no slip case $N=D=0$). Where $N_1$ and $D_1$ are initial values of velocity and thermal slip factors respectively. $T_w=T_\infty +bx^{2n}$ is the temperature of the wall i.e. sheet.

The similarity transformations for this flow problem referring Dodda et al [2] are introduced as-

$$\begin{aligned} \eta&=y\sqrt{\frac{a(n+1)}{2\nu _f}}x^\frac{n-1}{2}, \end{aligned}$$

(7)

$$\begin{aligned} u&=ax^n f'(\eta ), \end{aligned}$$

(8)

$$\begin{aligned} v&=-\sqrt{\frac{(n+1)a \nu _f}{2}}x^\frac{n-1}{2}\big [f(\eta )+\frac{n-1}{n+1} \eta f'(\eta )\big ], \end{aligned}$$

(9)

$$\begin{aligned} T&=T_\infty +bx^{2n} \theta (\eta ), \end{aligned}$$

(10)

$$\begin{aligned} \phi (\eta )&=\frac{C-C_\infty }{C_w-C_\infty } \end{aligned}$$

(11)

Using these similarity transformations (7)–(11) Eq. (1) (continuity equation) satisfies identically and Eqs. (2)–(6) are reduced in the following equations-

$$\begin{aligned}&\left( 1+\frac{1}{\beta }\right) f^{'''}-Mf' +f f^{''} -\frac{2n}{n+1} f'^2+\frac{2}{n+1}Gr \theta +\frac{2}{n+1}Gc \phi =0 \end{aligned}$$

(12)

$$\begin{aligned}&\left( 1+\frac{4R}{3}\right) \frac{1}{Pr} \theta ^{''} +\left( 1+\frac{1}{\beta }\right) Ec f{''}^2+f \theta '-\frac{4n}{n+1}f' \theta +N_b \theta ' \phi ' +N_t \theta '^2 =0 \end{aligned}$$

(13)

$$\begin{aligned}&\phi ^{''}+ \frac{N_t}{N_b}\theta ^{''} - \Gamma Sc \frac{2}{n+1} \phi + Sc f \phi '=0 \end{aligned}$$

(14)

Boundary conditions become-

$$\begin{aligned} f'(0)&=1+\lambda f^{''}(0),\hspace{0.4cm} f(0)=0,\hspace{0.4cm}\theta (0)=1+\delta \theta '(0),\hspace{0.4cm}\phi (0)=1 \end{aligned}$$

(15)

$$\begin{aligned} f'&\longrightarrow 0,\hspace{0.4cm} \theta \longrightarrow 0, \hspace{0.4cm}\phi \longrightarrow 0 \hspace{2cm } as \hspace{1cm } \eta \longrightarrow \infty \end{aligned}$$

(16)

Where,$M=\frac{2\sigma B^2}{\rho a x^{n-1}(n+1)}$ magnetic parameter, $Gr=\frac{g \beta _T (T_w-T_\infty )}{a^2 x^{2n-1}}$ thermal Grashoff number, $Gc=\frac{g \beta _c (C_w-C_\infty )}{a^2 x^{2n-1}}$ concentration Grashoff number, $R=\frac{4\sigma T_\infty ^3}{k^* k}$ radiation parameter, $Pr=\frac{\nu }{\alpha }$ Prandtl number, $Ec=\frac{u_w^2}{C_p (T_w-T_\infty )}$ Eckert number, $N_b=\frac{(\rho C)_p D_B (C_w-C_\infty )}{(\rho C)_f \alpha }$ Brownian diffusion coefficient, $N_t=\frac{(\rho C)_p D_T (T_w-T_\infty )}{(\rho C)_f T_\infty \alpha }$ thermal diffusion coefficient, $\Gamma =\frac{k_0}{a x^{n-1}}$ chemical reaction parameter, $Sc=\frac{\nu }{D_B}$ Schmidth number, $\lambda =N x^\frac{n-1}{2} \sqrt{\frac{a(n+1)\nu }{2}}$ velocity slip parameter, $\delta =D x^\frac{n-1}{2} \sqrt{\frac{a (n+1)}{2 \nu }}$ thermal slip parameter.

The quantities of practical interest are as follows,

local skin friction coefficient,

$$\begin{aligned} {Cf}_x=\frac{\tau _w}{\rho u_w^2} \end{aligned}$$

local Nusselt number,

$$\begin{aligned} Nu_x=\frac{x q_w}{k (T_w-T_\infty )} \end{aligned}$$

local Sherwood number,

$$\begin{aligned} Sh_x=\frac{x q_m}{D_B (C_w-C_\infty )} \end{aligned}$$

Where, $\tau _w=\mu \left( 1+\frac{1}{\beta }\right) \left( \frac{\partial u}{\partial y}\right) _{y=0}$, $q_w=-k\left( 1+\frac{16}{3}\frac{\sigma T_\infty ^3}{k^* k }\right) \left( \frac{\partial T}{\partial y}\right) _{y=0}$ heat flux, $q_m=-D_B \left( \frac{\partial C}{\partial y}\right) _{y=0}$ mass flux at the surface, k is thermal conductivity of the nanofluid.

Using these fluxes in above formulae we get the expressions in non dimensional form as-

$$\begin{aligned} Re_x^{\frac{1}{2}}Cf_x= & {} \sqrt{\frac{n+1}{2}}\left( 1+\frac{1}{\beta }\right) f^{"}(0) \\ Re_x^{-\frac{1}{2}} Nu_x= & {} -\sqrt{\frac{n+1}{2}}\left( 1+\frac{4R}{3}\right) \theta ^{'}(0) \\ Re_x^{-\frac{1}{2} }Sh_x= & {} -\sqrt{\frac{n+1}{2}}\phi ^{'}(0) \end{aligned}$$

Where, $Re_x=\frac{u_w x}{\nu }$ indicates the local Reynolds number.

Solution

The non-dimensional Eqs. (12)–(14) are non-linear in the form so it is quite difficult to solve them manually. Consequently we have used the finite difference scheme named as ’Keller-Box’ which was developed by Keller [14], to solve them numerically. Keller-Box method is based on four principal steps as-

• Transformation of given non-dimensional equations into a system of first order ordinary differential equations.

• Use of central differences to reduce them in finite differences.

• Use of Newton’s method to linearize the algebraic equations and put them into vector form.

• Use of block tri-diagonal elimination method to solve the system of linear equations.

Solution Procedure

Conversion into System of ODE’s

In order to solve the problem via Keller-Box method the first step is to reduce the transformed non-dimensional equations into first order system of ordinary differential equations along with boundary conditions, we introduce new variables as $p(\eta ), q(\eta ),\theta (\eta ),t(\eta ),\phi (\eta ),v(\eta )$ so that the system of equations can be written as-

$$\begin{aligned}&f' =p \end{aligned}$$

(17)

$$\begin{aligned}&p' =q \end{aligned}$$

(18)

$$\begin{aligned}&\theta ' =t \end{aligned}$$

(19)

$$\begin{aligned}&\phi ' =v \end{aligned}$$

(20)

$$\begin{aligned}&\left( 1+\frac{1}{\beta }\right) q^{'}+fq-\frac{2n}{n+1}p^2-Mp+\frac{2}{n+1}Gr \theta +\frac{2}{n+1}Gc \phi =0 \end{aligned}$$

(21)

$$\begin{aligned}&\left( 1+\frac{4R}{3}\right) \frac{1}{Pr}t^{'}+ \left( 1+\frac{1}{\beta }\right) Ec q^2 +N_b t v+N_t t^2 +ft-\frac{4n}{n+1}p \theta =0 \end{aligned}$$

(22)

$$\begin{aligned}&v^{'} +\frac{N_t}{N_b}t^{'}-\frac{2}{n+1} \Gamma Sc \phi + Sc f v=0 \end{aligned}$$

(23)

and boundary conditions-

$$\begin{aligned}&at\hspace{0.2cm} \eta =0,\hspace{0.5cm} p(0)=1+\lambda q(0), \hspace{0.4cm}f(0)=0,\hspace{0.4cm} \theta (0)=1+\delta t(0),\hspace{0.4cm} \phi (0)=1, \end{aligned}$$

(24)

$$\begin{aligned}&at \hspace{0.2cm} n\longrightarrow \infty \hspace{3cm} p(\eta )\longrightarrow 0,\hspace{0.4cm}\theta (\eta )\longrightarrow 0,\hspace{0.4cm} \phi (\eta ) \longrightarrow 0 \end{aligned}$$

(25)

Finite Difference Method

Now to convert into finite difference, consider

$$\begin{aligned} \eta _0=0,\hspace{0.3cm} \eta _j=\eta _{j-1} +h_j,\hspace{0.3cm}\eta _j=\eta _\infty \end{aligned}$$

(26)

Where $h_j$ is the $\Delta \eta$ spacing and $\Delta \eta =1,2,...,J$ is a sequence number indicating coordinate location. $\eta _{j-1/2}$ is the midpoint. Introducing the finite differences $f^{'}=\frac{f_j-f_{j-1}}{h_j}$,     $f=\frac{f_j+f_{j-1}}{2}$ applying these finite differences upon equations (17)–(23) we get,

$$\begin{aligned}&f_j-f_{j-1}-\frac{h_j}{2}(p_j+p_{j+1})=0 \end{aligned}$$

(27)

$$\begin{aligned}&p_j-p_{j-1}-\frac{h_j}{2}(q_j+q_{j+1})=0 \end{aligned}$$

(28)

$$\begin{aligned}&\theta _j-\theta _{j-1}-\frac{h_j}{2}(t_j+t_{j+1})=0 \end{aligned}$$

(29)

$$\begin{aligned}&\phi _j-\phi _{j-1}-\frac{h_j}{2}(v_j+v_{j+1})=0 \end{aligned}$$

(30)

$$\begin{aligned}&\left( 1+\frac{1}{\beta }\right) (q_j-q_{j-1})+\frac{h_j}{4}(q_j+q_{j-1})(f_j+f_{j-1})-\frac{2n}{n+1} \frac{h_j}{4} (p_j+p_{j-1})^2\nonumber \\&\quad -\frac{Mh_j}{2}(p_j+p_{j-1})+ \frac{h_j}{n+1}Gr (\theta _j+\theta _{j-1})+ \frac{h_j}{n+1}Gc (\phi _j+\phi _{j-1})=0 \end{aligned}$$

(31)

$$\begin{aligned}&\left( 1+\frac{4R}{3}\right) \frac{1}{Pr}(t_j-t_{j-1})+\frac{h_j}{4}\left( 1+\frac{1}{\beta }\right) Ec (q_j+q_{j-1})^2+ \frac{h_j}{4}N_b (t_j+t_{j-1})(v_j+v_{j-1})+\frac{h_j}{4}\nonumber \\&\quad N_t(t_j+t_{j-1})^2+\frac{h_j}{4}(t_j+t_{j-1})(f_j+f_{j-1})-\frac{n}{n+1}(p_j+p_{j-1})(\theta _j+\theta _{j-1})=0 \end{aligned}$$

(32)

$$\begin{aligned}&v_j-v_{j-1}+h_j \frac{N_t}{N_b}-\frac{h_j}{n+1}\Gamma Sc (\phi _j+\phi _{j-1})+Sc\frac{h_j}{4}(f_j+f_{j-1}) (v_j+v_{j-1})=0 \end{aligned}$$

(33)

and boundary conditions-

$$\begin{aligned} f_0=0, p_0=1+\lambda q_0, \theta _0=1+\delta t_0, \phi _0=1,p_J=0, \phi _J=0 \end{aligned}$$

(34)

Newton’s Method

To linearize the non-linear system (27)–(33) we use Newton’s method-

$$\begin{aligned}&f_j^{(k+1)}=f_j^{(k)}+\delta f_j^{(k)},\hspace{0.5cm} p_j^{(k+1)}=p_j^{(k)}+\delta p_j^{(k)},\hspace{0.5cm} q_j^{(k+1)}=q_j^{(k)}+\delta q_j^{(k)}, \hspace{0.5cm} \theta _j^{(k+1)}=\\&\theta _j^{(k)}+\delta \theta _j^{(k)},\hspace{0.5cm} t_j^{(k+1)}=t_j^{(k)}+\delta t_j^{(k)},\hspace{0.5cm} \phi _j^{(k+1)}=\phi _j^{(k)}+\delta \phi _j^{(k)}, \hspace{0.5cm} v_j^{(k+1)}=v_j^{(k)}+\delta v_j^{(k)} \end{aligned}$$

where, $k=0,1,2,3,...$ after inserting these expressions i.e we insert $f_j+\delta f_j$ in place of $f_j$ (we leave k here, for simplicity) and same for others, we get,

$$\begin{aligned}&\delta f_j-\delta f_{j-1}-\frac{h_j}{2} (\delta p_j +\delta p_{j-1})=(r_1)_{j-1/2} \end{aligned}$$

(35)

$$\begin{aligned}&\delta p_j-\delta p_{j-1}-\frac{h_j}{2} (\delta q_j +\delta q_{j-1})=(r_2)_{j-1/2} \end{aligned}$$

(36)

$$\begin{aligned}&\delta \theta _j-\delta \theta _{j-1}-\frac{h_j}{2} (\delta t_j +\delta t_{j-1})=(r_3)_{j-1/2} \end{aligned}$$

(37)

$$\begin{aligned}&\delta \phi _j-\delta \phi _{j-1}-\frac{h_j}{2} (\delta v_j +\delta v_{j-1})=(r_4)_{j-1/2} \end{aligned}$$

(38)

$$\begin{aligned}&(a_1) \delta q_j +(a_2) \delta q_{j-1}+(a_3)\delta f_j +(a_4) \delta f_{j-1}+(a_5) \delta p_j+(a_6) \delta p_{j-1}+(a_7) \delta \theta _j \nonumber \\&\quad +(a_8) \delta \theta _{j-1}+(a_9) \delta \phi _{j}+(a_{10}) \delta \phi _{j-1}=(r_5)_{j-1/2} \end{aligned}$$

(39)

$$\begin{aligned}&(b_1) \delta t_j +(b_2) \delta t_{j-1}+(b_3) \delta f_j+ (b_4) \delta f_{j-1}+(b_5) \delta p_j+(b_6) \delta p_{j-1}+(b_7) \delta \theta _j+(b_8)\nonumber \\&\quad \delta \theta _{j-1}+(b_9) \delta v_j+(b_{10}) \delta v_{j-1}+ (b_{11}) \delta q_j+(b_{12}) \delta q_{j-1}=(r_6)_{j-1/2} \end{aligned}$$

(40)

$$\begin{aligned}&(c_1) \delta v_j+(c_2) \delta v_{j-1}+(c_3) \delta f_{j}+(c_4) \delta f_{j-1}+(c_5) \delta t_{j}+(c_6) \delta t_{j-1}\nonumber \\&+(c_7) \delta \phi _{j}+(c_8) \delta \phi _{j-1}=(r_7)_{j-1/2} \end{aligned}$$

(41)

Where,

$$\begin{aligned} (a_1)_j&=\left( 1+\frac{1}{\beta }\right) +\frac{h_j}{2} f_{j-1/2},\hspace{0.5cm} (a_2)_j=-\left( 1+\frac{1}{\beta }\right) +\frac{h_j}{2} f_{j-1/2},\\ (a_3)_j&=\frac{h_j}{2}q_{j-1/2},\\ (a_4)_j&=(a_3)_j,\hspace{0.5cm} (a_5)_j=-\frac{2n}{n+1} h_j p_{j-1/2} -M \frac{h_j}{2},\hspace{0.5cm} (a_6)_j=(a_5)_j, \\ (b_1)_j&=\left( 1+\frac{4R}{3}\right) \frac{1}{Pr}+N_b \frac{h_j}{2}v_{j-1/2}+h_j N_t t_{j-1/2}+\frac{h_j}{2}f_{j-1/2},\\ (b_2)_j&=-\left( 1+\frac{4R}{3}\right) \frac{1}{Pr} + N_b \frac{h_j}{2}v_{j-1/2}+ h_j N_t t_{j-1/2}+\frac{h_j}{2}f_{j-1/2},\\ (b_3)_j&=\frac{h_j}{2}t_{j-1/2},\hspace{0.5cm} (b_4)_j=(b_3)_j,\hspace{0.5cm}\\ (b_5)_j&=-\frac{2n}{n+1}h_j \theta _{j-1/2},\hspace{0.5cm} (b_6)_j=(b_5)_j,\hspace{0.5cm} (b_7)_j=-\frac{2n}{n+1}h_j p_{j-1/2},\\ (b_8)_j&=(b_7)_j, (b_9)_j=\frac{h_j}{2}N_b t_{j-1/2},\hspace{0.5cm} (b_{10})_j=(b_9)_j,\\ (b_{11})_j&=\left( 1+\frac{1}{\beta }\right) h_j Ec q_{j-1/2},\hspace{0.5cm} (b_{12})_j=(b_{11})_j, \hspace{1cm} \\ (c_1)_j&=1+ Sc \frac{h_j}{2} f_{j-1/2},\hspace{0.5cm} (c_2)_j=(c_1)_j-2,\hspace{0.5cm} (c_3)_j=Sc \frac{h_j}{2}v_{j-1/2},\\ (c_4)_j&=(c_3)_j,\hspace{0.5cm}\\ (c_5)_j&=\frac{N_t}{N_b}, \hspace{0.5cm}(c_6)_j=-(c_5)_j,\hspace{0.5cm} (c_7)_j=-\frac{1}{n+1} h_j \Gamma Sc,\hspace{0.5cm} (c_8)_j=(c_7)_j \\ (r_1)_{j-1/2}&=f_{j-1}-f_j +h_j p_{j-1/2},\\ (r_2)_{j-1/2}&=p_{j-1}-p_j +h_j q_{j-1/2},\\ (r_3)_{j-1/2}&=\theta _{j-1}-\theta _j +h_j t_{j-1/2},\\ (r_4)_{j-1/2}&=\phi _{j-1}-\phi _j +h_j v_{j-1/2},\\ (r_5)_{j-1/2}&=\left( 1+\frac{1}{\beta }\right) (q_{j-1}-q_j) -h_j (fq)_{j-1/2}+\frac{2n}{n+1}h_j p_{j-1/2}^2 \\&\quad +Mh_j p_{j-1/2}-\frac{1}{n+1}h_j Gr \theta _{j-1/2} -\frac{1}{n+1}h_j Gc \phi _{j-1/2},\\ (r_6)_{j-1/2}&=\left( 1+\frac{4R}{3}\right) \frac{1}{Pr}(t_{j-1}-t_j) -h_j \left( 1+\frac{1}{\beta }\right) Ec q_{j-1/2}^2 -h_j (ft)_{j-1/2}\\&\quad -h_j N_b (tv)_{j-1/2}-h_j N_t t_{j-1/2}^2 +\frac{4n}{n+1}(p\theta )_{j-1/2}, \end{aligned}$$

and the boundary conditions become-

$$\begin{aligned}&\delta f_0=0, \hspace{0.5cm} \delta p_0=0, \hspace{0.5cm} \delta q_0=0, \hspace{0.5cm} \delta \theta _0=0, \hspace{0.5cm} \delta \phi _0=0,\hspace{0.5cm} \delta p_J=0, \hspace{0.5cm} \delta \theta _J=0,\\&\delta \phi _J=0 \end{aligned}$$

Block Elimination Method

To solve the linearized finite difference equations (35)–(41) numerically we use the block tridiagonal elimination method which was described by Cebeci and Bradshaw [15] as-

$$\begin{aligned} A \delta =r, \end{aligned}$$

(42)

Where

$$\begin{aligned} {A}= \begin{bmatrix} [A_1]&{} [C_1] &{} &{} &{} &{} &{} &{} &{}\\ [B_2]&{} [A_2] &{}[C_2]&{} &{} &{} &{} &{} &{}\\ &{} &{} &{} . &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} . &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} . &{} &{} &{} &{} \\ &{} &{} &{} . &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} . &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} . &{} &{} &{} &{} \\ &{} &{} &{} . &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} . &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} . &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} [B_{j-1}] &{} [A_{j-1}] &{} [C_{j-1}] &{} \\ &{} &{} &{} &{} &{} &{} &{} [B_j] &{} [A_j] &{} \\ \end{bmatrix}, \delta = \begin{bmatrix} [\delta _1]\\ [\delta _2]\\ .\\ .\\ .\\ [\delta _{j-1}]\\ [\delta _{j}] \end{bmatrix}, {r}= \begin{bmatrix} [r_1]\\ [r_2]\\ .\\ .\\ .\\ [r_{j-1}]\\ [r_{j}] \end{bmatrix} \end{aligned}$$

and the elements of the matrices are given as-

$[A_1]= \begin{bmatrix} 0&{}0&{}0&{}1&{}0&{}0&{}0\\ \frac{-h_j}{2}&{}0&{}0&{}0&{}\frac{-h_j}{2}&{}0&{}0\\ 0&{}\frac{-h_j}{2}&{}0&{}0&{}0&{}\frac{-h_j}{2}&{}0\\ 0&{}0&{}\frac{-h_j}{2}&{}0&{}0&{}0&{}\frac{-h_j}{2}\\ (a_2)_1&{}0&{}0&{}(a_3)_1&{}(a_1)_1&{}0&{}0\\ (b_{12})_1&{}(b_{2})_1&{}(b_{10})_1&{}(b_{3})_1&{}(b_{11})_1&{}(b_{1})_1&{}(b_{9})_1\\ 0&{}(c_6)_1&{}(c_2)_1&{}(c_3)_1&{}0&{}(c_5)_1&{}(c_1)_1\\ \end{bmatrix}$

$[A_j]= \begin{bmatrix} \frac{-h_j}{2}&{}0&{}0&{}1&{}0&{}0&{}0\\ -1&{}0&{}0&{}0&{}\frac{-h_j}{2}&{}0&{}0\\ 0&{}-1&{}0&{}0&{}0&{}\frac{-h_j}{2}&{}0\\ 0&{}0&{}-1&{}0&{}0&{}0&{}\frac{-h_j}{2}\\ (a_6)_j&{}(a_8)_j&{}(a_{10})_j&{}(a_3)_j&{}(a_1)_j&{}0&{}0\\ (b_{6})_j&{}(b_{8})_j&{}0&{}(b_{3})_j&{}(b_{11})_j&{}(b_{1})_j&{}(b_{9})_j\\ 0&{}0&{}(c_8)_j&{}(c_3)_j&{}0&{}(c_5)_j&{}(c_1)_j\\ \end{bmatrix}$

$[B_j]=$ $\begin{bmatrix} 0&{}0&{}0&{}-1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}\frac{-h_j}{2}&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}\frac{-h_j}{2}&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}\frac{-h_j}{2}\\ 0&{}0&{}0&{}(a_4)_j&{}(a_2)_j&{}0&{}0\\ 0&{}0&{}0&{}(b_4)_j&{}(b_{12})_j&{}(b_2)_j&{}(b_{10})_j\\ 0&{}0&{}0&{}(c_4)_j&{}0&{}(c_6)_j&{}(c_2)_j \end{bmatrix}$ $[C_j]= \begin{bmatrix} \frac{-h_j}{2}&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}0&{}0&{}0\\ (a_5)_j&{}(a_7)_j&{}(a_9)_j&{}0&{}0&{}0&{}0\\ (b_5)_j&{}(b_7)_j&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}(c_7)_j&{}0&{}0&{}0&{}0 \end{bmatrix}$;$1\le j\le J-1$

$[\delta _1]=$ $\begin{bmatrix} \delta q_0\\ \delta \theta _0\\ \delta \phi _0\\ \delta f_1\\ \delta q_1\\ \delta t_1\\ \delta v_1 \end{bmatrix}$ $[\delta _j]=$ $\begin{bmatrix} \delta q_{j-1}\\ \delta \theta _{j-1}\\ \delta \phi _{j-1}\\ \delta f_j\\ \delta q_j\\ \delta t_j\\ \delta v_j \end{bmatrix}$, $2\le j\le J$ $[r_j]=$ $\begin{bmatrix} (r_1)_{j-1/2}\\ (r_2)_{j-1/2}\\ (r_3)_{j-1/2}\\ (r_4)_{j-1/2}\\ (r_5)_{j-1/2}\\ (r_6)_{j-1/2}\\ (r_7)_{j-1/2}\\ \end{bmatrix}$

by factorizing A as a lower and an upper triangular matrices as- $A=LU$ where,

$L=\begin{bmatrix} [\alpha _1]&{} &{} &{} &{} &{} &{} &{}\\ [\beta _2]&{}[\alpha _1] &{}[c_2] &{} &{} &{} &{} &{}\\ &{} &{} &{} &{}.&{} &{} &{} &{}\\ &{} &{} &{} &{} &{}.&{} &{} &{}\\ &{} &{} &{} &{} &{} &{}.&{} &{}\\ &{} &{} &{} &{}.&{} &{} &{} &{}\\ &{} &{} &{} &{} &{}.&{} &{} &{}\\ &{} &{} &{} &{} &{} &{}.&{} &{}\\ &{} &{} &{} &{} &{} &{} &{}[\alpha _{j-1}] &{}\\ &{} &{} &{} &{} &{} &{} &{}[\beta _j] &{}[\alpha _j] \end{bmatrix}$ $U= \begin{bmatrix} [I_1] &{} [\Gamma _{j-1}] &{} &{} &{} &{} &{} &{} &{}\\ &{} [I_1]&{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} .&{} &{} &{} &{}\\ &{} &{} &{} &{} &{}. &{} &{} &{}\\ &{} &{} &{} &{} &{} &{}. &{} &{}\\ &{} &{} &{} &{} .&{} &{} &{} &{}\\ &{} &{} &{} &{} &{}. &{} &{} &{}\\ &{} &{} &{} &{} &{} &{}. &{} &{}\\ &{} &{} &{} &{} &{} &{} &{}[I_{j-1}] &{}[\Gamma _{j-1}]\\ &{} &{} &{} &{} &{} &{} &{} &{}[I]\\ \end{bmatrix}$

where [I] is a $7\times 7$ identity matrix, while $[\alpha _i]$ and $[\Gamma _i]$ are $7\times 7$ matrices in which the aforementioned equations determine components:

$$\begin{aligned} {[}\alpha _i]&=[A_1] \end{aligned}$$

(43)

$$\begin{aligned} {[}A_1][\Gamma _1]&=[C_1] \end{aligned}$$

(44)

$$\begin{aligned} {[}\alpha _i]&=[A_1]-[B_j][\Gamma _{j-1}],\hspace{1cm} j=2,3,....J \end{aligned}$$

(45)

$$\begin{aligned} {[}\alpha _j][\Gamma _j]&=[C_j],\hspace{1cm} j=2,3,....J-1 \end{aligned}$$

(46)

substituting Eq (43) into (42), we obtain $LU\delta =r$ if we let,

$$\begin{aligned} U\delta =W \end{aligned}$$

(47)

then Eq. (47) becomes

$LW=r$ where, $W= \begin{bmatrix} [W_1]\\ [W_2]\\ .\\ .\\ .\\ [W_{j-1}]\\ [W_{j}] \end{bmatrix}$

The following relations can be used to derive the components of W: $[\alpha _1][W_1]=[r_1], [\alpha _i][W_j]=[r_j]-[B_i][W_{j-1}],$         $2\le j \le J$

Once the components of W have been identified, the equation above provides the delta solution in which the components are identified from the relationships shown below: $[\delta _J]=[W_J],$ $[\delta _i]=[W_J]-[\Gamma _j][\delta _{j+1}],$         $1\le j \le J-1$

These calculations are repeated until some convergence criterion is satisfied and calculations are stopped when $|\delta \nu _0|\le \epsilon _1$ where $\epsilon _1$ is a very small prescribed value. The precision of the method’s early estimations is one of the elements influencing accuracy. Choosing the right first assumptions will determine how accurate the process is. The boundary conditions and convergence criteria both influence the first predictions that are made.

In this study, we used a uniform grid of size $\Delta \eta =0.006$ which is found to fulfil convergence and yield solutions with an error tolerance of $10^{-5}$ in all circumstances.

Results and Analysis

The governing equations along with variable slip boundary conditions of the present mathematical model under the effect of various parameters as Casson, velocity and thermal slip,magnetic, chemical reaction, radiation, thermophoresis, convection etc. have been solved using finite difference scheme. The results of this study have been described by Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 and 23 and Tables 1, 2 and 3.

Figures 2, 3 and 4 describes the effect of Casson parameter on velocity, temperature and concentration respectively. Natural phenomena decrease in velocity with respect to Casson parameter is observed clearly, because fluid become more viscous with increase in Casson parameter so less movable while we observe that thermal and concentration boundary layer enhances via enhancing Casson parameter. We also noticed a very natural phenomena with magnetic parameter i.e. decrease in velocity profile with enlarged magnetic parameter due to Lorentz force Fig. 5. On the another side we observed that concentration and temperature profiles are showing directly proportional behaviour with magnetic parameter shown via Figs. 6 and 7.

Influence of velocity slip parameter $\lambda$ on velocity has been portrayed by Fig. 8 and it is concluded that velocity profile receives a decrement with increasing velocity slip parameter. This happen because when we apply slip condition then the velocities of stretching sheet and flow near the sheet are not same. Temperature and concentration profiles have been plotted via Figs. 9 and 10 and found an increasing nature with respect to velocity slip parameter. Thermal slip parameter $\delta$ downturn the dimensionless temperature and concentration profiles. Even when just a little quantity of heat is transported from the sheet to the fluid, the thermal boundary layer thickness falls as the value of the thermal slip parameter rises.

Fig. 2

Velocity distribution with respect to Casson parameter

Fig. 3

Temperature distribution with respect to Casson parameter

Fig. 4

Concentration distribution with respect to Casson parameter

Fig. 5

Velocity distribution with respect to magnetic parameter

Fig. 6

Temperature distribution with respect to magnetic parameter

Fig. 7

Concentration distribution with respect to magnetic parameter

Fig. 8

Velocity distribution with respect to velocity slip parameter

Gr thermal Grashoff number illustrate the ratio of the buoyancy to viscous force acting on fluid. Higher Gr denotes the laminar flow and vice versa. In fact enhanced Gr add up more thermal energy into the fluid molecules, make weaker the intermolecular forces within the fluid particles and therefore accelerate the fluid velocity Fig. 13 and local rate of heat transfer of the fluid. Same behavior of velocity profile is noticed with respect to concentration Grashoff number Gc i.e proportional nature Fig. 14.

Physically larger $N_b$ is referred to produce the collision between nanoparticles. Due to this phenomena the species between nanoparticles diminishes which are responsible for decrease in concentration profile Fig. 15 and because collision in fluid enhances due to high $N_b$, it leads to increase in temperature profile showed in Fig. 16. Increment in $N_t$ means increase of the thermophoretic phenomena. Thermophoresis enhances the concentration and temperature profiles showed via Figs. 17, 18 respectively. For increasing values of Eckert number Ec thermal boundary layer thickness increases plotted via Fig. 19. Eckert number is a useful factor in the view of the study of thermal behaviour of the fluid flow. Thermal boundary layer reduces the heat dissipation.

Fig. 9

Temperature distribution with respect to velocity slip parameter

Fig. 10

Concentration distribution with respect to velocity slip parameter

Fig. 11

Temperature distribution with respect to thermal slip parameter

Fig. 12

Concentration distribution with respect to thermal slip parameter

Fig. 13

Velocity distribution with respect to thermal Grashoff number

Fig. 14

Velocity distribution with respect to concentration Grashoff number

Fig. 15

Concentration distribution with respect to $N_b$

Fig. 16

Temperature distribution with respect to $N_b$

Fig. 17

Concentration distribution with respect to $N_t$

Fig. 18

Temperature distribution with respect to $N_t$

Fig. 19

Temperature distribution with respect to Eckert number

We know that increasing Schmidt number Sc means lesser or lower mass diffusivity so concentration profile declines portrayed by Fig. 20. Temperature profile for constituted model shows decreasing relation with increasing values of Prandtl number Pr Fig. 21. Effect of radiation parameter on thermal profile have been shown by Fig. 22 it is concluded that temperature profile rises when radiation is increased as thermal radiation supplies more heat into the fluid and consequently thermal boundary layer intensified.

Concentration profile with respect to chemical reaction parameter is sketched in Fig. 23 illustrates an inversely proportional relationship. The reasoning behind this is that increase in chemical reaction parameter enlarges the number of solute molecules in chemical reaction which give rise to decrement in concentration profile.

Tables 1 and 2 represent the comparison of our present results with Dodda et al [2] and Hammad et al [16] for $-\phi '(0)$, $-\theta '(0)$ and $-f''(0)$ respectively in no slip case. This validate the accuracy of our present results. Table 3 illustrates some numerical values of skin friction coefficient, local Nusselt number and Shrewood number with variation in magnetic and Casson parameter for the present research problem. By calculating these quantities we get the rate of heat and mass transfer of the flow. We observed that for higher Casson parameter i.e. when fluid gets more viscous a least change is observed in numerical values of velocity, temperature and concentration.

Fig. 20

Concentration distribution with respect to Schmidt number

Conclusion

In this article, the numerical study of MHD Casson nanofluid havebeen pursued over a non-linear stretching sheet and some very useful outcomes are concluded and these are listed below-

Fig. 21

Temperature distribution with respect to Prandtl number

Fig. 22

Temperature distribution with respect to radiation parameter

Fig. 23

Concentration distribution with respect to chemical reaction parameter

Table 1 Comparison of results for $-\theta '(0)$ and $-\phi '(0)$ when $Sc=10$, $Pr=10$, $Nt=0.3$, $n=10$,$\lambda =\delta =M=Gr=Gc=R=\Gamma =0$ and $\beta \longrightarrow \infty$

Table 2 Comparison of results for $-f''(0)$ when $Sc=1, Pr=6.8, Nb=Nt, Ec=\lambda =\delta =M=Gr=Gc=R=\Gamma =0$

Table 3 Results for $-f''(0)$, $-\theta '(0)$, $-\phi '(0)$ when $Sc=1, Pr=0.5, Nb=Nt=0.3, Ec=0.1=\lambda =\delta =R, Gr=Gc=0.3,\Gamma =0.2$ and varying values of $\beta$ and M

• Casson nanofluid parameter and magnetic parameter exhibit same attitude towards velocity, temperature and concentration profiles show inversely relation with velocity and directly proportional relation with temperature and concentration profiles.

• Velocity slip parameter declines velocity profile but enhances thermal and concentration distribution profiles.

• Thermal slip parameter diminish the temperature and concentration profiles.

• Velocity profile raises with raised thermal and concentration Grashoff numbers.

• Concentration profiles diminishes with increasing Brownian motion parameter while shows opposite nature with thermophoresis parameter.

• Temperature profile shows a very slight increment with respect to increasing Brownian motion and thermophoresis parameter.

• Thermal boundary layer enhances with Eckert number.

• Concentration profile shows decrement with respect to Schmidt number.

• Prandtl number reduces temperature profiles while Radiation Parameter enhances the thermal profile.