Application of Caputo Fractional Operator to Analyse the Fractional Model of Brain Tumour Via Modified Technique

Abstract

In this article, the fractional model of brain tumour is investigated. The numerical solution of this model is obtained by the modified technique called as Natural transform homotopy perturbation technique. The existence and uniqueness of the solution is discussed with the help of the fixed point theorem, also the stability is analysed using the Lyapunov function. The convergence and error are also analysed with help of Cauchy sequence. Finally, the effectiveness of the proposed technique is tested by three different test examples and the results are compared with the existing methods.

Introduction

Fractional calculus (FC) is considered as the generalisation of the traditional integer order calculus to the modern calculus that contains integrals and derivatives of fractional order. Fractional calculus has a powerful tool to model a wide range of real-life phenomena in wide areas of science and technology. The Caputo derivative [1] is the most helpful among the various derivatives that are listed in the literature. Several researchers investigated many fractional models such as the Parkinson’s disease fractional model [2,3,4], the fractional competition model [5] of bank data, fractional order Cahn–Allen model [6], the fractional HBV immune model [7], the fractional Lana fever model [8], the fractional Leukemia model [9], the Caputo fractional operator is applied to the blood alcohol model [10], the fractional order Zika virus model [11], the generalised time fractional Cattaneo model [12], the fractional model of Babesiosis disease [13], fractional operators with Mittag–Leffler kernel [14], the Aboodh transform is applied to solve proportional delay TFPDE [15], the time-fractional Navier–Stokes equations [16], fractional dynamical systems [17], the non-linear fractional glucose–insulin regulatory dynamical system [18], and the fractional immunogenetic tumour model [19].

For the sake of society, it is crucial to investigate fractional order mathematical models, however doing so can occasionally be quite challenging. In order to obtain approximate analytic solutions for these models, a numerical technique must be developed. Numerous methods have been used to research these fractional models such as; ADM [20], FEM [21], ABM [22], HATM [23], STM [24], FHPTM [25], Collocation method [26], FRDTM [27], FVIM [28], Sumudu transform method [29], q-HAM [29], Sumudu transform perturbation method [29], and Modified computational technique [6] etc.

For the appropriate treatment of the tumour, the information about the growth profile of the tumour cells is very crucial. So, the study of the fractional model of brain tumour is very crucial for the proper treatment of the patient suffering from the brain tumour. Mathematically, the geometry of the tumour is considered as spherical as shown in Fig. 1. The two-dimensional tumour model was investigated by many researchers [30,31,32,33], they consider the equation as:

$$ \partial_{t} B\left( {x,\tau } \right) = D\nabla^{2} B\left( {x,\tau } \right) + \rho B\left( {x,\tau } \right). $$

where $B\left(x,\tau \right)$ represents the cell density at time $\tau$ and radius $x$ and ${\nabla }^{2}$ is the Laplacian operator. $\rho$ is the net rate of growth of cells and is expressed as a decimal fraction per day. $D$ is the diffusion coefficient, expressed as ${cm}^{2}$ per day.

Fig. 1

Glioblastoma tumour in the parietal lobe [20]

In this model, the two main key processes of a diffusive brain tumour are taken into consideration, these are cell proliferation (ρ) and diffusion (D), and then merge to give the form of reaction–diffusion equation [34]:

$$ \partial_{t} B\left( {x,\tau } \right) = D\frac{1}{{x^{2} }}\partial_{x} \left( {{\text{x}}^{2} \partial_{x} B\left( {x,\tau } \right)} \right) + \rho B\left( {x,\tau } \right). $$

The fractional order model of brain tumour is developed by Ganzi et al. [35] in the form of the fractional Burgess equation which is given by

$$_{0}^{c} D_{t}^{\alpha } Q\left( {x,t} \right) = \frac{1}{2}Q_{xx} \left( {x,t} \right) + S\left( {x,t} \right), \alpha \in \left( {0,1} \right], $$

(1.1)

having initial conditions $Q\left(x,0\right)=h\left(x\right).$ Here, $Q(x,t)$ is growth profile and $S\left(x,t\right)=\frac{\rho -{k}_{t}}{2D}Q\left(x,t\right),$ where, $\rho$ is cell proliferation, ${k}_{t}$ is killing rate of tumour cells and $x$ and $t$ are the growth profile parameter. The symbol ${{}_{ 0}{}^{c}D}_{t}^{\alpha }$ is Caputo derivative of order $\alpha$ with respect to time.

The integer order model was originally developed for simulation of a case of recurrent anaplastic astrocytoma which is under chemotherapy and then extended to study the effects of the scale of surgical resection and of the variation in growth and diffusion to cover the complete extent of glioma growth. The mathematical model with fractional derivatives seem very helpful in explaining the growth of tumour and the interaction between tumour cells and host cells as compared to the integer order derivatives. The use of fractional derivative gives a possible answer to the question on how the neoplasm cells appear arbitrarily far from the main (primary) tumour in the case of solid tumour. Mutation of single cell or groups of cells is the cause of the generation of the tumour. Gliomas are diffusive brain tumours which are very difficult to cure in spite of major surgical resections. The main characteristic of the mutated cells is that they show rapid and uncontrolled growth, which is the main cause of the malfunctioning of normal tissues.

In this article, our main objective is to analyse the fractional model of brain tumour (glioblastomas) and analyse the variation of growth profile of tumour with respect to time. Natural transform homotopy perturbation technique (NTHPT) is used for solving fractional model of brain tumour. Natural transform is an advanced transformation which is a generalisation of Laplace and Sumudu transformation. Natural transform handles the non-linearity and other restrictions very smoothly as compared to Laplace transform. Natural transform converges to both Laplace and Sumudu transform. So, Natural transform is more reliable and effective than Laplace or Sumudu transform. The existence and uniqueness of the solution are discussed by using fixed-point theorem, also the stability analysed is discussed with the help of the Lyapunov function. The convergence and error are analysed with help of Cauchy sequence.

This work is innovative in that it makes an accurate prediction about how the tumor's growth profile will change over time. It has been demonstrated that the modified numerical technique, Natural transform homotopy perturbation technique, decreases the computational effort required to solve non-linear fractional models, which are useful in a wide range of engineering and scientific fields. The main objective of this research is the development of a very accurate numerical method for solving the fractional model of a brain tumour. The findings in this research may have significant applications in biotechnology, diffusion theory, computational biology, and medical science, among other fields. Additionally, we simulate three separate test cases to demonstrate that the suggested technique, NTHPT, allows us to investigate the variation of the tumor's growth profile with regard to time much more accurately than the other methods do.

Preliminaries

Definition 2.1

Let $n$ be a natural number and $f\left(t\right)$ is a continuous function in interval $[0,t]$ then its Riemann–Liouville derivative of the order $\alpha >0,$ is defined as [1]:

$$ D_{t}^{\alpha } f\left( t \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{{\Gamma \left( {n - \alpha } \right)}}\frac{{d^{n} }}{{dt^{n} }}\int\limits_{0}^{t} {(t - s)^{{\left( {n - \alpha - 1} \right)}} f\left( s \right)ds,} } & {{\text{ if}}\;{ n} - 1{ < }\alpha { < n, }} \\ {f^{\left( n \right)} \left( t \right),} & {{\text{ if}}\;{ }\alpha {= n } \in { }{\mathbb{N}},} \\ \end{array} } \right. $$

where $\Gamma (\alpha )$ denote Gamma function.

Definition 2.2

The Caputo derivative of function $f\left(t\right),$ is defined as [1]:

$$ {\text{D}}^{{\upalpha }} f\left( t \right) = I^{m - \alpha } D^{m} f\left( t \right) = \frac{1}{{\Gamma \left( {m - \alpha } \right)}}\mathop \int \limits_{0}^{t} \left( {t - x} \right)^{m - \alpha - 1} f^{\left( m \right)} \left( x \right)dx, $$

where $m-1<\alpha \le m.$

Definition 2.3

The Caputo integral of $f\left(t\right)$ is defined as [36]:

$$ {}_{0}^{c} I_{t}^{{\upalpha }} \left\{ {f\left( t \right)} \right\} = \frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{t} \left( {t - x} \right)^{\alpha - 1} f\left( x \right)dx, $$

where $0<\alpha \le 1.$

Definition 2.4

Let $f(t)$ be a function defined on $t \ge 0$. Then Natural transformation of the function $f(t)$ is $R(s,v)$ and is given as [37]:

$$ NT\left[ {f\left( t \right)} \right] = \mathop \int \limits_{ - \infty }^{\infty } e^{ - st} f\left( {vt} \right)dt, s,v \in \left( { - \infty ,\infty } \right). $$

Definition 2.5

If $R(s,v)$ is the Natural transformation of $f(t)$, then the inverse natural transformation of $R(s,v)$ is $f(t)$ and given as [37]:

$$ NT^{ - 1} \left[ {R\left( {s,v} \right)} \right] = \frac{1}{2\pi i}\mathop \int \limits_{ - \infty }^{\infty } e^{\frac{st}{v}} R\left( {s,v} \right)dt, \;\;s,v \in \left( { - \infty ,\infty } \right) . $$

Definition 2.6

The Natural transformation of fractional Caputo operator is given as [37]:

$$ NT\left[ {{}_{0}^{c} D_{t}^{\alpha } f\left( t \right)} \right] = \frac{{s^{\alpha } }}{{v^{\alpha } }}N\left[ {f\left( t \right)} \right] - \mathop \sum \limits_{k = 0}^{m - 1} \frac{{s^{{\left( {\alpha - k - 1} \right)}} }}{{v^{\alpha - k} }}f^{\left( k \right)} \left( 0 \right),\;{ }m - 1 < \alpha \le m. $$

Definition 2.7

The Caputo operator of any constant number is always zero.

Theorem 2.1

[37] If $f(t)$ is sectionally continuous in every finite interval $0\le t\le k$ and of the exponential order δ for $t>k$, then its Natural transform exists for all $s>\delta ,v>\delta .$

Theorem 2.2

[36] The fractional differential equation $_{0}^{c} D_{t}^{\alpha } f(t) = e(t)$ has a unique solution given as:

$$ f\left( t \right) = \frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{t} \left( {t - x} \right)^{\alpha - 1} e\left( x \right)dx, $$

where $0<\alpha \le 1.$

Stability Analysis

In this segment, we analyse the asymptotically stability of the fractional model of brain tumour with the help of the Lyapunov function.

We can rewrite the given equation (1.1) as:

$$ _{0}^{c} D_{t}^{\alpha } Q\left( {x,t} \right) = \psi \left( {x,t,Q} \right), Q\left( {x,0} \right) = h\left( x \right). $$

(3.1)

For analysing the stability of Eq. (3.1), we have to prove that the following equation has positive solution and $lim\to 0$ as $t\to \infty$

$$ {}_{0}^{c} D_{t}^{\alpha } Q = \delta Q, Q\left( 0 \right) = a, \delta < 0. $$

(3.2)

We can transform the Eq. (3.2) into an integral one

$$ Q = Q\left( 0 \right) + \delta I_{{0^{ + } }}^{\alpha } Q, Q\left( 0 \right) = a. $$

(3.3)

Picard’s method is used to solve Eq. (3.3). The approximating formula is defined as

$$ Q_{n + 1} = Q_{0} + \delta I_{{0^{ + } }}^{\alpha } Q_{n} , \;\;0 \le n, $$

(3.4)

where ${Q}_{0}=Q\left(0\right)=a,$ we get

$$ \begin{array}{*{20}l} {Q_{1} = Q_{0} + \delta I_{{0^{ + } }}^{\alpha } Q_{0} = Q_{0} + \frac{{\delta Q_{0} }}{{\Gamma \left( {1 + \alpha } \right)}}t^{\alpha } ,} \hfill \\ {Q_{2} = Q_{0} \sum\limits_{m = 0}^{\infty } {\delta^{m} } \frac{{t^{m\alpha } }}{{\Gamma \left( {1 + m\alpha } \right)}},} \hfill \\ \vdots \hfill \\ {Q_{m} = Q_{0} \sum\limits_{m = 0}^{m} {\delta^{m} } \frac{{t^{m\alpha } }}{{\Gamma \left( {1 + m\alpha } \right)}}. } \hfill \\ \end{array} $$

(3.5)

Hence, we get the Mittag–Leffler function as given below

$$ E_{\alpha ,1} \left( {\delta ,1} \right) = \mathop \sum \limits_{m = 0}^{m} \delta^{m} \frac{{t^{m\alpha } }}{{{\Gamma }\left( {1 + m\alpha } \right)}},\;\;0 < t. $$

(3.6)

The one parameter Mittag–Leffler function is given by

$$ E_{\alpha } \left( { - t^{\alpha } } \right) = \mathop \sum \limits_{m = 0}^{m} \left( { - 1} \right)^{m} \frac{{t^{m\alpha } }}{{{\Gamma }\left( {1 + m\alpha } \right)}}, 0 < t. $$

(3.7)

We approximate the Mittag–Leffler function like [38]:

$$ E_{\alpha } \left( { - t^{\alpha } } \right)\sim \frac{{t^{ - \alpha } }}{{{\Gamma }\left( {1 - \alpha } \right)}}, t \to \infty . $$

(3.8)

So, we get

$$ \mathop {{\text{lim}}}\limits_{ t \to \infty } E_{\alpha ,1} \left( {\delta ,t} \right) = 0. $$

(3.9)

Moreover, it’s clear that ${E}_{\alpha ,1}\left(\delta ,t\right)$ is positive and yields the results which are monotonically identical to ${E}_{\alpha }\left(-{t}^{\alpha }\right)$.

Lemma 3.1

[39] Assume that $x=0,$ is an equilibrium point (EP). It is Luapunov stable if $\forall \epsilon >0,$ there exist $\mathrm{a} \lambda =\lambda \left({t}_{0},\epsilon \right),$ s.t. if

$$ \left\| {x\left( {t_{0} } \right)} \right\| < \lambda \Rightarrow \left\| {x\left( {t_{0} } \right)} \right\|\left\langle {\epsilon , \forall t} \right\rangle t_{0} $$

Lemma 3.2

[39] An EP, $x=0,$ is asymptotically stable if $\ \forall$ $\epsilon >0, \mathrm{there} \ \mathrm{exist } \ \mathrm{ a } \ \lambda =\lambda \left({t}_{0}\right)>0,$ then

$$\Vert x({t}_{0})\Vert <\lambda \Rightarrow \underset{t\to \infty }{\mathrm{lim}}x\left(t\right)=0.$$

Lemma 3.3

[39] For $x\left(t\right), z\left(t\right) \epsilon {C}^{1}\left[a,b\right], x\left(a\right)=z(a)$, $0<m,$ s.t. if

$$ {}_{{a^{ + } }}^{c} \!D_{t}^{\alpha } x\left( t \right) \le - kx\left( t \right), 0 < \alpha \le 1, $$

(3.10)

And

$$ {}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } z\left( t \right) = - kz\left( t \right), $$

(3.11)

then $x(t)\le z(t)$ hold $\forall t \epsilon \left[a,b\right].$

Theorem 3.1

Let us suppose that $x=0$ is an EP. If there exist a $+\,ve$ definite function $V\left(t,x\left(t\right)\right), t\in {\mathbb{R}}$, class $-{\rm K}$ function ${\beta }_{1}, { \beta }_{2}$ and ${\beta }_{3}$ such that

$$ \beta_{1} \left( {\left\| {x\left( t \right)} \right\|} \right) \le V\left( {t,x\left( t \right)} \right) \le \beta_{2} \left( {\left\| {x\left( t \right)} \right\|} \right), $$

(3.12)

$$ {}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } V\left( {t,x\left( t \right)} \right) \le - \beta_{3} \left\| {x\left( t \right)} \right\|, $$

(3.13)

then EP is asymptotically stable.

Proof

From the given Eqs. (3.12) and (3.13). we have.

$$ {}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } V\left( {t,x\left( t \right)} \right) \le - \beta_{3} \left( {\beta_{2}^{ - 1} V\left( {t,x\left( t \right)} \right)} \right), $$

(3.14)

where ${{\beta }_{2}}^{-1}$ is the inverse of ${\beta }_{2}.$ Let us consider the given equation as

$$ {}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } h\left( t \right) \le - \beta_{3} \left( {\beta_{2}^{ - 1} V\left( t \right)} \right), $$

(3.15)

having initial condition $h\left(a\right)=V\left(a,h\left(a\right)\right).$ Eq. (3.15) have a solution similar to the Mittag–Leffler function, $\underset{t\to \infty }{\mathrm{lim}}h\left(t\right)=0,$ and by using lemma $\left(3.3\right),$ it is evident that $V(t,x(t))$ bounded by $h\left(t\right),$ so $\underset{t\to \infty }{\mathrm{lim}}x\left(t\right)=0.$

Lemma 3.4

[39] If ${}_{{a^{ + } }}^{c}\! {D}_{t}^{\alpha }x(t)\ge {}_{{a^{ + } }}^{c}\! {D}_{t}^{\alpha }z\left(t\right), 1<\alpha \le 2, \forall t>a$ and $x(a)=z(a)$ then

$$ x\left( t \right) \ge z\left( t \right). $$

(3.16)

Lemma 3.5

The given below inequality always true

$$ {}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } x^{2} \left( t \right) \le 2x\left( t \right){}_{{a^{ + } }}^{c} D_{t}^{\alpha } x\left( t \right). $$

(3.17)

Proof

We proceed like [40], so, we have to prove that

$$ {}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } x^{2} \left( t \right) - 2x\left( t \right){}_{{a^{ + } }}^{c} D_{t}^{\alpha } x\left( t \right) = \frac{1}{{{\Gamma }\left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{\frac{{dx^{2} \left( f \right)}}{ds} - \frac{2x\left( t \right)dx\left( f \right)}{{ds}}}}{{\left( {t - f} \right)^{\alpha } }} df \le 0. $$

(3.18)

From definition $(2.7)$ and putting the term $\frac{d{x}^{2}\left(t\right)}{df}$ inside the integral $(3.18)$, so

$$ {}_{{a^{ + } }}^{c} \! D_{t}^{\alpha } x^{2} \left( t \right) - 2x\left( t \right){}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } x\left( t \right) = \frac{1}{{{\Gamma }\left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{\frac{{dx^{2} \left( f \right)}}{df} - \frac{2x\left( t \right)dx\left( f \right)}{{df}} + \frac{{dx^{2} \left( t \right)}}{df} { }}}{{\left( {t - f} \right)^{\alpha } }} df. $$

(3.19)

Let $H\left( f \right) = \left( {x\left( f \right) - x\left( t \right)} \right)^{2} ,$ so we have

$$ {}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } x^{2} \left( t \right) - 2x\left( t \right){}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } x\left( t \right) = \frac{1}{{{\Gamma }\left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{H^{\prime } \left( f \right) { }}}{{\left( {t - f} \right)^{\alpha } }} df. $$

(3.20)

Integrating equation (3.20), we get

$$ \mathop \int \limits_{0}^{t} \frac{{H^{\prime } \left( f \right) { }}}{{\left( {t - f} \right)^{\alpha } }}df = \left. {\frac{G\left( f \right)}{{\left( {t - f} \right)^{\alpha } }}} \right]_{f = a}^{t} - \mathop \int \limits_{0}^{t} \frac{{\alpha H\left( f \right) { }}}{{\left( {t - f} \right)^{\alpha + 1} }}df. $$

(3.21)

Next, we have to find the value of $\underset{f\to t}{\mathrm{lim}}\frac{H(f)}{{\left(t-f\right)}^{\alpha }},$ so

$$ \begin{aligned} \mathop {{\text{lim}}}\limits_{f \to t} \frac{H\left( f \right)}{{\left( {t - f} \right)^{\alpha } }} = & \mathop {\lim }\limits_{f \to t} \frac{{\left( {x\left( f \right) - x\left( t \right)} \right)^{2} }}{{\left( {t - f} \right)^{\alpha } }}, \\ & = \mathop {\lim }\limits_{f \to t} \frac{{2\left( {x\left( f \right) - x\left( t \right)} \right)x^{\prime } \left( f \right)}}{{\alpha \left( {t - f} \right)^{\alpha - 1} }} = 0, \\ \end{aligned} $$

$$ {}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } x^{2} \left( t \right) - 2x\left( t \right){}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } x\left( t \right) = \frac{ - 1}{{{\Gamma }\left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{H\left( a \right){ }}}{{\left( {t - a} \right)^{\alpha } }} - \frac{\alpha }{{{\Gamma }\left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{H\left( f \right){ }}}{{\left( {t - f} \right)^{\alpha + 1} }} df. $$

(3.22)

Hence, proved.

Theorem 3.2

If $x=0$is an EP of Eq. (1.1)and $x\left(t\right)\psi \left(t,x\left(t\right)\right)<0,$then Eq. (1.1)is asymptotically stable.

Proof

Let us consider the Lyapunov function as:

$$ V = \frac{{x^{2} \left( t \right)}}{2}, $$

(3.23)

so, we get

$$ {}_{{a^{ + } }}^{c}\! D_{t}^{\alpha } V \le x\left( t \right){}_{{a^{ + } }}^{c} D_{t}^{\alpha } x\left( t \right) = x\left( t \right)\psi \left( {t,x\left( t \right)} \right) < 0. $$

(3.24)

Hence, form theorem (3.1), Eq. (1.1) is asymptotically stable.

Existance and Uniqueness of the solution of fractional model of Brain Tumour

The fractional model of brain tumour given by Eq. (1.1) can be transform to the following form

$$_{0}^{c} D_{t}^{\alpha } Q\left( {x,t} \right) = \varphi \left( {x,t,Q} \right), $$

(4.1)

where $\varphi \left( {x,t,Q} \right) = \frac{1}{2}Q_{xx} \left( {x,t} \right) + \frac{{\rho - k_{t} }}{2D}Q\left( {x,t} \right).$

The e Eq. (4.1) can be converted into the Voltera equation by using the theorem $(2.2)$ as:

$$ { }Q\left( {x,t} \right) - Q\left( {x,0} \right) = \frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{t} \left( {t - s} \right)^{\alpha - 1} \varphi \left( {x,t,Q} \right)ds. $$

(4.2)

Next, we have to prove that $\varphi \left(x,t,Q\right)$ satisfy Lipschitz condition.

Theorem 4.1

The function, $\varphi (x,t,Q)$ in the given Voltera equation satisfy the Lipschitz condition and also satisfy the contraction if $0<\eta \le 1$, where $\eta =\frac{{\delta }^{2}}{2}+\lambda$.

Proof

We suppose that the function $Q(x, t)$ is bounded. So, we have

$$ \begin{aligned} \left\| {\varphi \left( {x,t,Q} \right) - \varphi \left( {x,t,Q_{1} } \right)} \right\| = & \left\| {\frac{1}{2}\frac{{\partial^{2} Q\left( {x,t} \right)}}{{\partial x^{2} }} + \frac{{\rho - k_{t} }}{2D}Q\left( {x,t} \right) - \frac{1}{2}\frac{{\partial^{2} Q\left( {x,t_{1} } \right)}}{{\partial x^{2} }} - \frac{{\rho - k_{t} }}{2D}Q\left( {x,t_{1} } \right)} \right\|, \\ & = \left\| {\frac{1}{2}\frac{{\partial^{2} }}{{\partial x^{2} }}\left\{ {Q\left( {x,t} \right) - Q\left( {x,t_{1} } \right)} \right\} + \frac{{\rho - k_{t} }}{2D}\left\{ {Q\left( {x,t} \right) - Q\left( {x,t_{1} } \right)} \right\},} \right\| \\ & \le \left\| {\frac{1}{2}\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\rho - k_{t} }}{2D}} \right\|\left\| {Q\left( {x,t} \right) - Q\left( {x,t_{1} } \right)} \right\|, \\ & \le \left( {\frac{{\delta^{2} }}{2} + \lambda } \right)\left\| {Q\left( {x,t} \right) - Q\left( {x,t_{1} } \right)} \right\|. \\ \end{aligned} $$

Now by letting $\eta =\frac{{\delta }^{2}}{2}+\lambda$, we get

$$ \left\| {\varphi \left( {x,t,Q} \right) - \varphi \left( {x,t,Q_{1} } \right)} \right\| \le \eta \left\| {Q\left( {x,t} \right) - Q\left( {x,t_{1} } \right)} \right\|. $$

(4.3)

Thus, $\varphi \left(x,t,Q\right)$ meet the requirement of the Lipschitz condition and contraction if $0<\eta \le 1.$

The iterative formula taken for the existence of the solution is given below

$$ Q_{n + 1} \left( {x,t} \right) = \frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{t} \left( {t - s} \right)^{\alpha - 1} \varphi \left( {x,t,Q_{n} } \right)ds, $$

(4.4)

with initial condition as $Q(x, 0)=Q(x, {t}_{0}).$

The difference between two consecutive terms is given by

$$ \begin{aligned} \varphi_{n} \left( {x,t} \right) = & Q_{n} \left( {x,t} \right) - Q_{n - 1} \left( {x,t} \right), \\ & = \frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{t} \left( {t - s} \right)^{\alpha - 1} \left\{ {\varphi \left( {x,t,Q_{n - 1} } \right) - \varphi \left( {x,t,Q_{n - 2} } \right)} \right\}ds. \\ \end{aligned} $$

(4.5)

It can be observed that

$$ Q_{n} \left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{n} \varphi_{i} \left( {x,t} \right), $$

(4.6)

so, from Eq. (4.5), we have

$$ \left\| {\varphi_{n} \left( {x,t} \right)} \right\| = \left\| {Q_{n} \left( {x,t} \right) - Q_{n - 1} \left( {x,t} \right)} \right\|. $$

(4.7)

Now, we apply the triangular inequality on Eq. (4.4), we get

$$ \left\| {\varphi_{n} \left( {x,t} \right)} \right\| \le \frac{1}{\Gamma \left( \alpha \right)}\eta \left\| {\mathop \int \limits_{0}^{t} \left( {t - s} \right)^{\alpha - 1} \varphi_{n - 1} \left( {x,s} \right)ds} \right\| . $$

(4.8)

Theorem 4.2

The solution of fractional Burgess equation exist if $\exists$,${t}_{0}$,which satisfy.

$$ \frac{1}{{{\Gamma }\left( \alpha \right)}}\eta t_{0}^{\alpha } \le 1.$$

Proof

Let $Q(x, t)$ is a bounded function that also satisfies the Lipschitz condition then from Eq. (4.8) we have.

$$ \left\| {\varphi_{n} \left( {x,t} \right)} \right\| \le \left\| {\varphi_{n} \left( {x,t} \right)} \right\|\left[ {\frac{1}{{{\Gamma }\left( \alpha \right)}}\eta .t^{\alpha } } \right]^{n} . $$

(4.9)

So, the existence and continuousness of the obtained solution is established.

$$ Q\left( {x,t} \right) - Q\left( {x,0} \right) = Q_{n} \left( {x,t} \right) - \chi_{n} \left( {x,t} \right). $$

(4.10)

Here, we consider that

$$ \begin{aligned} \left\| {\chi_{n} \left( {x,t} \right)} \right\| = & \left\| {\frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{t} \left( {t - s} \right)^{\alpha - 1} \left\{ {\varphi \left( {x,t,Q_{n} } \right) - \varphi \left( {x,t,Q_{n - 1} } \right)} \right\}ds} \right\| , \\ & \le \frac{1}{\Gamma \left( \alpha \right)}\left\| {\mathop \int \limits_{0}^{t} \left( {t - s} \right)^{\alpha - 1} \left\{ {\varphi \left( {x,t,Q_{n} } \right) - \varphi \left( {x,t,Q_{n - 1} } \right)} \right\}ds} \right\| , \\ & \le \frac{1}{\Gamma \left( \alpha \right)}\eta \left\| {Q_{n} \left( {x,t} \right) - Q_{n - 1} \left( {x,t} \right)} \right\|t. \\ \end{aligned} $$

In the same way at ${t}_{0}$, we obtain

$$ \left\| {\chi_{n} \left( {x,t} \right)} \right\| \le \left[ {\frac{1}{{{\Gamma }\left( \alpha \right)}}t_{0}^{\alpha } } \right]^{n + 1} \eta^{n + 1} M, $$

(4.11)

as $n\to \infty$, we can clearly see that $\Vert {\chi }_{n}\left(x,t\right)\Vert \to 0.$

Theorem 4.3

The fractional Burgess equation possesses a unique solution if the following condition holds

$$\left( {1 - \frac{1}{{{\Gamma }\left( \alpha \right)}}\eta t^{\alpha } } \right)> 0. $$

Proof

Suppose ${Q}^{*}\left(x,t\right)$ is another solution of the given fractional brain tumour model, then

$$ \begin{aligned} \left\| {Q\left( {x,t} \right) - Q^{*} \left( {x,t} \right)} \right\| = & \left\| {\frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{t} \left( {t - s} \right)^{\alpha - 1} \left\{ {\varphi \left( {x,t,Q} \right) - \varphi \left( {x,t,Q^{*} } \right)} \right\}ds} \right\|, \\ & \le \frac{1}{\Gamma \left( \alpha \right)}\eta \left\| {Q\left( {x,t} \right) - Q^{*} \left( {x,t} \right)} \right\|. \\ \end{aligned} $$

(4.12)

Now, on simplifying above equation, we gethence, if

$$ \left\| {Q\left( {x,t} \right) - Q^{*} \left( {x,t} \right)} \right\|\left( {1 - \frac{1}{{{\Gamma }\left( \alpha \right)}}\eta t^{\alpha } } \right) \le 0, $$

$$ \left( {1 - \frac{1}{{{\Gamma }\left( \alpha \right)}}\eta t^{\alpha } } \right) > 0, $$

(4.13)

so, $Q\left( {x,t} \right) = Q^{*} \left( {x,t} \right).$

Which shows the uniqueness condition of the solution of the fractional model of brain tumour.

Description of Proposed Technique NTHPT

The fractional-order model of brain tumour is given by

$$ {}_{0}^{c} D_{t}^{\alpha } Q\left( {x,t} \right) = \frac{1}{2}Q_{xx} \left( {x,t} \right) + S\left( {x,t} \right), $$

(5.1)

with initial condition $Q\left(x,0\right)=h(x)$.

Now, we apply Natural transform on Eq. (5.1), we get

$$ \begin{aligned} NT\left[ {{}_{0}^{c} D_{t}^{\alpha } Q\left( {x,t} \right)} \right] = & NT\left[ {\frac{1}{2}Q_{xx} \left( {x,t} \right) } \right] + NT\left[ {S\left( {x,t} \right)} \right], \\ \left( \frac{s}{v} \right)^{\alpha } NT\left[ {Q\left( {x,t} \right)} \right] - \frac{{s^{\alpha - 1} }}{{v^{\alpha } }}\left[ {Q\left( {x,0} \right)} \right] = & NT\left[ {\frac{1}{2}Q_{xx} \left( {x,t} \right)} \right] + NT\left[ {S\left( {x,t} \right)} \right], \\ \left( \frac{s}{v} \right)^{\alpha } NT\left[ {Q\left( {x,t} \right)} \right] - \frac{{s^{\alpha - 1} }}{{v^{\alpha } }}h\left( x \right) = & NT\left[ {\frac{1}{2}Q_{xx} \left( {x,t} \right)} \right] + NT\left[ {S\left( {x,t} \right)} \right], \\ NT\left[ {Q\left( {x,t} \right)} \right] = & \frac{1}{{\text{s}}}h\left( x \right) + \left( \frac{v}{s} \right)^{\alpha } NT\left[ {\frac{1}{2}Q_{xx} \left( {x,t} \right) + S\left( {x,t} \right)} \right]. \\ \end{aligned} $$

Now, we apply inverse Natural transform to above equation, we get

$$ Q\left( {x,t} \right) = h\left( x \right) + NT^{ - 1} \left\{ {\left( \frac{v}{s} \right)^{\alpha } NT\left[ {\frac{1}{2}Q_{xx} \left( {x,t} \right) + S\left( {x,t} \right)} \right]} \right\}. $$

(5.2)

Next, we use the Homotopy perturbation technique to solve the above equation, so for the linear term we put

$$ Q\left( {x,t} \right) = \mathop \sum \limits_{m = 0}^{\infty } p^{m} Q_{m} \left( {x,t} \right), $$

(5.3)

and the nonlinear term $N\left\{Q(x,t)\right\}$ is decomposed by the use of He’s polynomial as

$$ N\left\{ {Q\left( {x,t} \right)} \right\} = \mathop \sum \limits_{m = 0}^{\infty } p^{m} H_{m} \left( Q \right), $$

(5.4)

where

$$ H_{m} \left( Q \right) = \frac{1}{n!}\frac{{d^{m} }}{{dp^{m} }}\left[ {f\left( {\mathop \sum \limits_{j = 0}^{m} p^{j} Q_{j} \left( {x,t} \right)} \right)} \right]_{p = 0} . $$

(5.5)

Here if $S(x,t)$ is linear in $Q(x,t)$ then it is replaced by using Eq. (5.3) and if it is nonlinear in $Q(x,t)$ then it is replaced by using Eq. (5.4).

Case-I When $S(x,t)$ is linear. So, we can write $S\left(x,t\right)=c.Q(x,t)$, here c is a constant.

Now using Eq. (5.3) in Eq. (5.2), we get

$$ \mathop \sum \limits_{m = 0}^{\infty } p^{m} Q_{m} \left( {x,t} \right) = h\left( x \right) + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\left( {\mathop \sum \limits_{m = 0}^{\infty } p^{m} \frac{1}{2}\left( {Q_{m} } \right)_{xx} + \mathop \sum \limits_{m = 0}^{\infty } c.Q_{m} } \right)} \right)} \right]. $$

(5.6)

Now, we compare coefficients of equal power of p, so

$$ \begin{aligned} Q_{0} \left( {x,t} \right) =\, & h\left( x \right), \\ Q_{1} \left( {x,t} \right) =\, & NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{0} } \right)_{xx} + c.Q_{0} } \right)} \right], \\ Q_{2} \left( {x,t} \right) =\, & NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{1} } \right)_{xx} + c.Q_{1} } \right)} \right], \\ & \vdots \\ Q_{m} \left( {x,t} \right) =\, & NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{m - 1} } \right)_{xx} + c.Q_{m - 1} } \right)} \right], \\ \end{aligned} $$

and the final solution is given by

$$ Q\left( {x,t} \right) = \mathop {\lim }\limits_{k \to \infty } \mathop \sum \limits_{m = 0}^{k} Q_{m} \left( {x,t} \right). $$

Case-II When $S(x,t)$ is nonlinear. So, we can write $S\left(x,t\right)=N\left\{Q(x,t)\right\}$.

Now usingEq. (5.4) in Eq. (5.2) we get

$$ \mathop \sum \limits_{m = 0}^{\infty } p^{m} Q_{m} \left( {x,t} \right) = h\left( x \right) + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\mathop \sum \limits_{m = 0}^{\infty } p^{m} \frac{1}{2}\left( {Q_{m} } \right)_{xx} + \mathop \sum \limits_{m = 0}^{\infty } p^{m} H_{m} } \right)} \right]. $$

(5.7)

Now, we compare coefficients of equal power of p, soand the final solution is given by

$$ \begin{aligned} Q_{0} \left( {x,t} \right) =\, & h\left( x \right), \\ Q_{1} \left( {x,t} \right) =\, & NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{0} } \right)_{xx} + H_{0} } \right)} \right], \\ Q_{2} \left( {x,t} \right) =\, & NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{1} } \right)_{xx} + H_{1} } \right)} \right], \\ & \vdots \\ Q_{m} \left( {x,t} \right) =\, & NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{m - 1} } \right)_{xx} + H_{m - 1} } \right)} \right], \\ \end{aligned} $$

$$ Q\left( {x,t} \right) = \mathop {\lim }\limits_{k \to \infty } \mathop \sum \limits_{m = 0}^{k} Q_{m} \left( {x,t} \right). $$

(5.8)

Convergence and Error Analysis

For the given NTHPT technique, the convergence and error can be analysed from the following theorem.

Theorem 6.1

The NTHPT is applied to get the solution of Eq. (1.1) is similar to the given below sequence.

$$ \begin{aligned}A_{i} =\, & Q_{1} + Q_{2} + Q_{3} + \ldots Q_{i} , \\ A_{0} =\, &Q_{0} . \\ \end{aligned}$$

By the iterating scheme

$$ A_{i + 1} = NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\mathop \sum \limits_{m = 0}^{\infty } p^{m} \frac{1}{2}\left( {Q_{m} } \right)_{xx} + \mathop \sum \limits_{m = 0}^{\infty } p^{m} H_{m} } \right)} \right]. $$

(6.1)

Proof

For i = 0, eEq. (6.1). gives.

$$ A_{1} = NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{0} } \right)_{xx} + H_{0} } \right)} \right]. $$

then as ${A}_{1}={Q}_{1}$, so we have

$$ Q_{1} = NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{0} } \right)_{xx} + H_{0} } \right)} \right]. $$

Now for i = 1, we have

$$ \begin{aligned} A_{2} = & NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{0} + Q_{1} } \right)_{xx} + H_{0} + H_{1} } \right)} \right] \\ & = NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{0} } \right)_{xx} + H_{0} } \right)} \right] + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{1} } \right)_{xx} + H_{1} } \right)} \right], \\ \end{aligned} $$

as, ${A}_{2}={Q}_{1}+{Q}_{2}$, so we have

$$ Q_{1} + { }Q_{2} = { }A_{1} + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{1} } \right)_{xx} + H_{1} } \right)} \right], $$

thus,

$$ Q_{2} = NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{1} } \right)_{xx} + H_{1} } \right)} \right]. $$

Proceeding in the same way, we get

$$ Q_{{\text{k}}} = NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{k - 1} } \right)_{xx} + H_{k - 1} } \right)} \right], $$

where $k=\mathrm{1,2},3\dots \dots i,$ so we get

$$ \begin{aligned} A_{i + 1} &= NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\mathop \sum \limits_{i = 0}^{m} \frac{1}{2}\left( {Q_{i} } \right)_{xx} + \mathop \sum \limits_{i = 0}^{m} H_{i} } \right)} \right], \\ & = NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{0} } \right)_{xx} + H_{0} } \right)} \right] \\ & \quad + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{1} } \right)_{xx} + H_{1} } \right)} \right] \\ & \quad + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{2} } \right)_{xx} + H_{2} } \right)} \right] \\ & \quad + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{3} } \right)_{xx} + H_{3} } \right)} \right] \\ & \vdots \\ & \quad + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{i - 1} } \right)_{xx} + H_{i - 1} } \right)} \right] \\ & \quad + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{i} } \right)_{xx} + H_{i} } \right)} \right] \\ A_{i + 1} &= Q_{1} + Q_{2} + Q_{3} + \ldots Q_{i} + NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{i} } \right)_{xx} + H_{i} } \right)} \right], \\ \end{aligned} $$

as we know that

$$ A_{i} = Q_{1} + Q_{2} + Q_{3} + \ldots Q_{i} , $$

so, we get

$$ Q_{i + 1} = NT^{ - 1} \left[ {\left( \frac{v}{s} \right)^{\alpha } NT\left( {\frac{1}{2}\left( {Q_{i} } \right)_{xx} + H_{i} } \right)} \right]. $$

Which is identical to the solution given by NTHPT and hence proved.

Theorem 6.2

Let ${Q}_{i}\left(t\right)$and $Q\left(t\right)$are defined in Banach space $\left(C\left[\mathrm{0,1}\right],\Vert .\Vert \right)$. If $\exists 0<\delta <1$, such that $\Vert {Q}_{i+1}\left(t\right)\Vert \le \delta \Vert {Q}_{i}\left(t\right)\Vert , \forall i\in N$ then the NTHPT solution $\sum_{i=0}^{\infty }{Q}_{i}\left(t\right)$converges to the solution $Q\left(t\right)$of the fractional model of the brain tumour $(1.1).$

Proof

Assume that the sequence of partial sums of the series $(5.8)$ is represented by ${\{u}_{i}\}$, then.

$$ \left\| {u_{i + 1} - u_{i} } \right\| = \left\| {Q_{i + 1} } \right\| \le \delta \left\| {Q_{i} } \right\| \le \delta^{2} \left\| {Q_{i + 1} } \right\| \le \ldots \le \delta^{i + 1} \left\| {Q_{0} } \right\|. $$

For any $i,j\in N, i\ge j$,

$$ \begin{aligned} \left\| {u_{i} - u_{j} } \right\| &= \left\| {(u_{i} - u_{i - 1} ) + (u_{i - 1} - u_{i - 2} ) + \ldots + \left( {u_{j + 1} - u_{j} } \right)} \right\| \\ & \le \left\| {(u_{i} - u_{i - 1} )} \right\| + \left\| {(u_{i - 1} - u_{i - 2} )} \right\| + \ldots + \left\| {\left( {u_{j + 1} - u_{j} } \right)} \right\| \\& \le \delta^{i} \left\| {Q_{0} } \right\| + \delta^{i - 1} \left\| {Q_{0} } \right\| + \ldots + \delta^{j + 1} \left\| {Q_{0} } \right\| \\ &\le \delta^{j + 1} \left( {1 + \delta + \delta^{2} + \ldots + \delta^{i - j - 1} } \right)\left\| {Q_{0} } \right\| \le \frac{{1 - \delta^{i - j} }}{1 - \delta }\delta^{j + 1} \left\| {Q_{0} } \right\|,\end{aligned} $$

since $0<\delta <1$, we have $1-{\delta }^{j-i}<1,$ then

$$ u_{i} - u_{j} \le \frac{{\delta^{j + 1} }}{1 - \delta }Q_{0} , $$

(6.2)

so, $\Vert {u}_{i}-{u}_{j}\Vert \to 0$ as $i,j\to \infty$ as ${Q}_{0}$ is bounded. So, $\left\{{u}_{i}\right\}$ is the Cauchy sequence in the Banach space and is convergent. So, $\exists Q(t)\in B$ such that $\sum_{i=0}^{\infty }{Q}_{i}(t)=\varphi (t)$.

Theorem 6.3

If $\exists 0<\delta <1$ in such a manner that $\Vert {Q}_{i+1}\left(t\right)\Vert \le \delta \Vert {Q}_{i}\left(t\right)\Vert , \forall i\in N$ then the truncation error of the NTHPT solution $(5.8)$of the system $(1.1)$is estimated as

$$ \left| {Q\left( t \right) - \mathop \sum \limits_{i = 0}^{j} \varphi_{i} \left( t \right)} \right| \le \frac{{\delta^{j + 1} }}{1 - \delta }\left\| {Q_{0} } \right\|.$$

Proof

From equation (6.2) and theorem (6.2) as $j \to \infty$, $u_{i} \to Q\left( t \right)$, we have

$$ \left| {Q\left( t \right) - \mathop \sum \limits_{i = 0}^{j} \varphi_{i} \left( t \right)} \right| \le \frac{{\delta^{j + 1} }}{1 - \delta }\left\| {Q_{0} } \right\|. $$

Numerical Simulation

In this section, to show the effectiveness of the proposed technique, NTHPT, we simulate three types of fractional Burgess equations (Fig. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12, Table 1).

Fig. 2

Variation of initial growth profile $Q(x,0$) with $x$ for Ex. 7.1

Fig. 3

Absolute Error at $x=1$ for distinct values of $\alpha ,$ for Ex. 7.1

Fig. 4

Absolute Error at $x=1$ for different values of $\alpha ,$ for Ex. 7.1

Fig. 5

Approximate growth profile $Q(x,t)$ at $x=1$ for different values of $\alpha ,$ for Ex. 7.1

Fig. 6

Approximate growth profile $Q(x,t)$ at $x=1$ for distinct values of $\alpha ,$ for Ex. 7.1

Fig. 7

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=0.25$, for Ex. 7.1

Fig. 8

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=0.50$, for Ex. 7.1

Fig. 9

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=0.75$, for Ex. 7.1

Fig. 10

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=0.90$, for Ex. 7.1

Fig. 11

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=1$, for Ex. 7.1

Fig. 12

Exact growth profile $Q(x,t)$ at $\mathrm{\alpha }=1$, for Ex.7.1

Table 1 Absolute error for distinct values of $\alpha$ at $x=1,$ for Ex. 7.1

Example 7.1

Let us consider $S\left(x,t\right)=\frac{1}{2}Q(x,t)$ then, Eq. (1.1) becomes.

$$ {}_{0}^{c} D_{t}^{\alpha } Q\left( {x,t} \right) = \frac{1}{2}Q_{xx} \left( {x,t} \right) + \frac{1}{2}Q\left( {x,t} \right). $$

(7.1)

The exact solution of equation $(7.1)$ for $\alpha =1$ is $Q\left(x,t\right)={e}^{(x+t)}.$

Solution From the exact solution $Q\left(x,0\right)={e}^{x}$. Now, we apply NTHPT to equation $(7.1)$ so, we have ${Q}_{0}\left(x,t\right) = {e}^{x}$. Therefore

$$ \begin{aligned} Q_{0} \left( {x,t} \right) =\, & e^{x} , \\ Q_{1} \left( {x,t} \right) =\, & e^{x} \frac{{t^{\alpha } }}{{{\Gamma }\left( {\alpha + 1} \right)}}, \\ Q_{2} \left( {x,t} \right) =\, & e^{x} \frac{{t^{2\alpha } }}{{{\Gamma }\left( {2\alpha + 1} \right)}}, \\ Q_{3} \left( {x,t} \right) =\, & e^{x} \frac{{t^{3\alpha } }}{{{\Gamma }\left( {3\alpha + 1} \right)}}, \\ \vdots \\ Q_{m} \left( {x,t} \right) =\, & e^{x} \frac{{t^{m\alpha } }}{{{\Gamma }\left( {m\alpha + 1} \right)}}. \\ \end{aligned} $$

Hence, the solution by NTHPT is given by

$$ Q\left( {x,t} \right) = \mathop {\lim }\limits_{k \to \infty } \mathop \sum \limits_{m = 0}^{k} e^{x} \frac{{t^{m\alpha } }}{{{\Gamma }\left( {m\alpha + 1} \right)}}. $$

Example 7.2

Let us consider $S\left(x,t\right)=Q(x,t)$ then, Eq. (1.1) becomes.

$$ {}_{0}^{{{ }c}} D_{t}^{\alpha } Q\left( {x,t} \right) = \frac{1}{2}Q_{xx} \left( {x,t} \right) + Q\left( {x,t} \right). $$

(7.2)

The exact solution of equation $\left( {7.2} \right)$ for $\alpha = 1$ is $Q\left( {x,t} \right) = xe^{t} .$

Solution From the exact solution, $Q\left( {x,0} \right) = x.$ Now, applying NTHPT to Eq. (7.2) so, we have $Q_{0} \left( {x,t} \right) = x$, (Figs. 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 and 23, Tables 2 and 3) therefore

$$ \begin{aligned} Q_{0} \left( {x,t} \right) = & x, \\ Q_{1} \left( {x,t} \right) = & x\frac{{t^{\alpha } }}{{{\Gamma }\left( {\alpha + 1} \right)}}, \\ Q_{2} \left( {x,t} \right) = & x\frac{{t^{2\alpha } }}{{{\Gamma }\left( {2\alpha + 1} \right)}}, \\ Q_{3} \left( {x,t} \right) = & x\frac{{t^{3\alpha } }}{{{\Gamma }\left( {3\alpha + 1} \right)}}, \\ & \vdots \\ Q_{m} \left( {x,t} \right) = & x\frac{{t^{m\alpha } }}{{{\Gamma }\left( {m\alpha + 1} \right)}}. \\ \end{aligned} $$

Fig. 13

Variation of initial growth profile (x, 0) with x, for Ex. 7.2

Fig. 14

Absolute Error at $x=1$ for distinct values of $\alpha ,$ for Ex. 7.2

Fig. 15

Absolute Error at $x=1$ for different values of $\alpha ,$ for Ex. $7.2$

Fig. 16

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=0.25$, for Ex. 7.2

Fig. 17

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=0.50$, for Ex. 7.2

Fig. 18

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=0.75$, for Ex. 7.2

Fig. 19

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=0.90$, for Ex. 7.2

Fig. 20

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=1$, for Ex. 7.2

Fig. 21

Exact growth profile $Q(x,t)$ at $\mathrm{\alpha }=1$, for Ex. 7.2

Fig. 22

Approximate growth profile $Q(x,t)$ at $x=1$ for distinct values of $\alpha ,$ for Ex. 7.2

Fig. 23

Approximate growth profile $Q(x,t)$ at $x=1$ for distinct values of $\alpha ,$ for Ex. 7.2

Table 2 Absolute error for distinct values of $\alpha$ at $x=1,$ for Ex. 7.2

Table 3 Comparison of absolute error between NTHPT and Collocation method at$x=1$, and$\alpha =1$, for Ex. $7.1,$ and Ex $. 7.2$

Hence, the solution by NTHPT is given by

$$ Q\left( {x,t} \right) = \mathop {\lim }\limits_{k \to \infty } \mathop \sum \limits_{m = 0}^{k} x\frac{{t^{m\alpha } }}{{{\Gamma }\left( {m\alpha + 1} \right)}}. $$

Example 7.3

Let us consider $S\left(x,t\right)={e}^{-Q(x,t)}+\frac{1}{2}{e}^{-2Q(x,t)}$ then, Eq. (1.1) becomes

$$ {}_{0}^{c} D_{t}^{\alpha } Q\left( {x,t} \right) = \frac{1}{2}Q_{xx} \left( {x,t} \right) + e^{{ - Q\left( {x,t} \right)}} + \frac{1}{2}e^{{ - 2Q\left( {x,t} \right)}} . $$

(7.3)

The exact solution of equation $(7.3)$ for $\alpha =1$ is $Q\left(x,t\right)=\mathrm{log}(x+t+2)$.

Solution From the exact solution, $Q\left(x,0\right)=\mathrm{log}(x+2)$. Now, we apply NTHPT to equation $(7.3)$ so, we have ${ Q}_{0}\left(x,t\right) = \mathrm{log}(x+2)$.

The two nonlinear terms in the equation $(7.3$) are ${e}^{-Q(x,t)}$ and ${e}^{-2Q(x,t)}$ are replaced by using He’s polynomials ${H}_{m}$ and ${{H}^{*}}_{m},$ respectively. (Figs. 24, 25, 26, 27, 28, 29, 30, 31, 32, 33 and 34, Tables 4 and 5) Some of them are given below

$$ \begin{aligned} H_{0} = & \frac{1}{x + 2}, \\ H_{1} = & \frac{ - 1}{{\left( {x + 2} \right)^{2} }}\frac{{t^{\alpha } }}{{{\Gamma }\left( {\alpha + 1} \right)}}, \\ H_{2} = & \frac{ - 1}{{2\left( {x + 2} \right)^{3} }}\frac{{t^{2\alpha } }}{{{\Gamma }\left( {2\alpha + 1} \right)}}, \\ \end{aligned} $$

and

$$ \begin{aligned} H^{*}_{0} = & \frac{1}{{\left( {x + 2} \right)^{2} }}, \\ H^{*}_{1} = & \frac{ - 2}{{\left( {x + 2} \right)^{3} }}\frac{{t^{\alpha } }}{{{\Gamma }\left( {\alpha + 1} \right)}}, \\ H^{*}_{2} = & \frac{6}{{\left( {x + 2} \right)^{4} }}\frac{{t^{2\alpha } }}{{{\Gamma }\left( {2\alpha + 1} \right)}}. \\ \end{aligned} $$

Fig. 24

Variation of initial growth profile $Q(x,0)$ with $x,$ for Ex. 7.3

Fig. 25

Absolute Error at $x=25$ for distinct values of $\alpha ,$ for Ex. 7.3

Fig. 26

Absolute Error at $x=25$ for distinct values of $\alpha ,$ for Ex. 7.3

Fig. 27

Approximate growth profile $Q(x,t)$ at $\alpha =0.25$, for Ex. 7.3

Fig. 28

Approximate growth profile $Q(x,t)$ at $\mathrm{\alpha }=0.50$, for Ex. 7.3

Fig. 29

Approximate growth profile $Q(x,t)$ at $\alpha =0.75$, for Ex. 7.3

Fig. 30

Approximate growth profile $Q(x,t)$ at $\alpha =0.90$, for Ex. 7.3

Fig. 31

Approximate growth profile $Q(x,t)$ at $\alpha =1$, for Ex. 7.3

Fig. 32

Exact growth profile $Q(x,t)$ at $\mathrm{\alpha }=1$, for Ex. 7.3

Fig. 33

Approximate growth profile $Q(x,t)$ at $x=25$ for different values of $\alpha ,$ for Ex. 7.3

Fig. 34

Approximate growth profile $Q(x,t)$ at $x=25$ for different values of $\alpha ,$ for Ex. 7.3

Table 4 Absolute error at $x=1$, and distinct values of $\alpha ,$ for Ex. 7.3

Table 5 Absolute Error for different values of $\alpha$ and $x$ at $t=0.1$ for, Ex. 7.3

So, after putting all these values, we get

$$ \begin{aligned} Q_{0} \left( {x,t} \right) = & {\text{log}}\left( {x + 2} \right), \\ Q_{1} \left( {x,t} \right) = & \frac{1}{x + 2}\frac{{t^{\alpha } }}{{{\Gamma }\left( {\alpha + 1} \right)}}, \\ Q_{2} \left( {x,t} \right) = & \frac{ - 1}{{\left( {x + 2} \right)^{2} }}\frac{{t^{2\alpha } }}{{{\Gamma }\left( {2\alpha + 1} \right)}}, \\ Q_{3} \left( {x,t} \right) = & \frac{1}{{\left( {x + 2} \right)^{3} }}\frac{{t^{3\alpha } }}{{{\Gamma }\left( {3\alpha + 1} \right)}}, \\ & \vdots \\ Q_{m} \left( {x,t} \right) = & \frac{{\left( { - 1} \right)^{m + 1} }}{{\left( {x + 2} \right)^{m} }}\frac{{t^{m\alpha } }}{{{\Gamma }\left( {m\alpha + 1} \right)}}. \\ \end{aligned} $$

Hence, the solution by NTHPT is given by

$$ Q\left( {x,t} \right) = \mathop {\lim }\limits_{k \to \infty } \mathop \sum \limits_{m = 0}^{k} \frac{{\left( { - 1} \right)^{m + 1} }}{{\left( {x + 2} \right)^{m} }}\frac{{t^{m\alpha } }}{{{\Gamma }\left( {m\alpha + 1} \right)}}. $$

Numerical Result Discussion

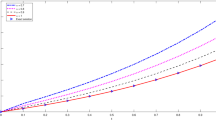
The variation of the initial growth profile $Q(x, 0)$ for Ex. 7.1, 7.2 and 7.3 is illustrated in Figs. 2, 13 and 24, respectively. The absolute error for distinct values of $\alpha$ and $t$ at $x=1$ for Ex. 7.1 and 7.2 is demonstrated in Figs. 3, 4 and 14, 15, respectively, and for Ex. $7.3$ at $x=25$ in Figs. 25, 26. The approximate and exact growth profile $Q(x, t)$ for different values of $\alpha$ for Ex. $7.1,$ Ex. $7.2,$ and Ex. $7.3$ is demonstrated through 2D graphical representation in Figs. 5, 6, 22, 23 and 33, 34, respectively, and through 3D graphical representation in Figs. 7, 8, 9, 10, 11, 12, 16, 17, 18, 19, 20, 21 and 27, 28, 29, 30, 31, 32, respectively. From the graphical representation of the approximate and exact growth profile, it is observed that for $\alpha =1$ the approximate growth profile is almost similar to the exact growth profile.

The effectiveness and accuracy of the proposed technique, NTHPT, are shown in the Tables 1, 2 and 4, by computing absolute error for distinct values of $\alpha$ and $t$ for Ex. 7.1, 7.2 and 7.3. Here, we have observed that the absolute error is very less and the numerical solution is almost equal to the exact solution. In the Table 3 we compare the absolute error of the proposed technique, NTHPT, and Collocation method for Ex. $7.1$ and Ex. $7.2,$ and it is observed that the proposed technique, NTHPT, gives a more accurate solution than the existing technique. In the Table 5$,$ it can be clearly seen that proposed technique, NTHPT, also gives very less error for the higher values of $x=20, 30$ and$40$. Hence, the effectiveness of the proposed techniques is illustrated and it can be applied to solve non-linear fractional models with high accuracy.

Conclusion

In this work, we investigate the potential of the NTHPT to investigate the non-linear fractional model of brain tumour. The existence and uniqueness of the solution of the fractional model of brain tumour are analysed with the help of fixed point theory, also the stability analysis is discussed with the help of Lyapunov function. The convergence and error are also discussed by using Cauchy sequence. Also, we solve three examples, and it is observed that the proposed technique, NTHPT, gives more accurate solution than the existing techniques. So, we can study the variation of growth profile of tumour with respect to time very accurately than the other existing methods. It has been demonstrated that combining the numerical method with the Natural transform speeds up the computation required to solve non-linear fractional models.

Hence, it is proved that the proposed technique, NTHPT, is a powerful technique which can be applied to solve the non-linear fractional model of natural phenomena of science and engineering.