A Higher Order Finite Difference Method for a Singularly Perturbed Boundary Value Problem with a Small Negative Shift

Abstract

This study proposes a uniformly convergent finite difference scheme on a uniform mesh to solve singularly perturbed boundary value problems for second-order ordinary differential-difference equation of the convection-diffusion type. Error estimates are produced for the proposed numerical scheme. The theoretical results are supported by numerical simulations of test problems.

Introduction

Singularly perturbed differential-difference equations (SPDDEs) are the outcomes in mathematical models of practical importance such as those in the fields of physics and biology [1, 2]. Due to the presence of the perturbation parameter and the delay term, the solution to such a class of problems may exhibit boundary or interior layers. Due to the dependence of the solution profile on the singular perturbation parameter, the numerical approaches designed for addressing regular problems turn out to be inapplicable. Also, the traditional numerical schemes on uniform meshes do not produce uniformly convergent results for SPDDEs. The first advancements in the study of singularly perturbed differential-difference equations have been initiated by Lange and Miura [3, 4]. They carried out the analytical work for solving the boundary-value problems for singularly perturbed linear second-order differential-difference equations with small shifts. The problems with solutions that display layer behaviour at one or both of the boundaries were studied. It has been discovered that the size of the shifts compared to the perturbation parameter plays a vital role in the solution profile of the problem. Kadalbajoo and Sharma [5,6,7] provided numerical methods for boundary value problems with delay argument comparable to perturbation parameter. Kadalbajoo and Ramesh [8] discussed numerical schemes to approximate the solution of the boundary value problem, which is defined on Shishkin meshes. Kadalbajoo and Devendra Kumar [9] obtained the scheme for the singularly perturbed boundary value problem by using the B-spline collocation technique with piecewise uniform meshes. Mohapatra and Natesan [10] proposed adaptive grid computational techniques for solving singularly perturbed differential-difference equations on a nonuniform mesh. Nageshwar Rao and Chakravarthy [11, 12] presented a tridiagonal fitted finite difference technique for singularly perturbed linear second-order differential-difference equations and focused on how shift affects the behaviour of the boundary layer or the oscillatory behaviour of the solution. Sahihi et al. [13] solved singularly perturbed second-order differential-difference equations using the reproducing kernel Hilbert space method based on a collocation approach. Swamy et al. [14] presented a computational technique for singularly perturbed delay differential equations exhibiting twin-layers or oscillatory solution. kiltu et al. [15] presented a higher-order numerical scheme for solving reaction-diffusion-type singularly perturbed delay differential equation with solution exhibiting layer or oscillatory behaviour. Sirisha et al. [16] proposed a mixed finite difference approach to solve singularly perturbed differential-difference equations with mixed shifts by using domain decomposition. Ravi Kanth and Murali [17] presented a numerical method for nonlinear singularly perturbed delay differential equations by fitted splines method. Rai and Sharma [18] focused on the interpolation technique for singularly perturbed delay differential equation with or without a turning point, on a piecewise uniform Shishkin mesh. Chakravarthy and Kumar [19] presented a fitted operator finite difference scheme for a reaction-diffusion-type singularly perturbed delay differential equation based on Numerov’s technique. Subburayan and Ramanujam [20] presented uniformly convergent finite difference method with piecewise linear interpolation on Shishkin meshes. Woldaregay and Duressa [21] considered the exponentially fitted operator mid-point upwind finite difference method to solve the singularly perturbed boundary value problem.

It is well known that when traditional numerical methods are used, these types of problems with smaller values of perturbation parameter generate erroneous results. So, it is essential to develop numerical techniques that could provide higher precision, despite the smaller values of the perturbation parameter, i.e., techniques that are parameter uniform convergent. Studying how the shift parameter affects the thin layer structure of the solution is another crucial component for these kinds of problems. To deal with these issues, in the present paper, we used a fitting parameter on a higher-order finite difference scheme for a singularly perturbed boundary value problem with a small negative shift. Briefly, the outline is as follows: In Sect. 2, we state the continuous problem and the problem is replaced with an approximate boundary value problem for computational feasibility. Also, some important properties of the analytical solution of the modified problem are presented. In Sect. 3, an exponentially fitted finite difference method is presented for the modified problem. Convergence analysis of the numerical scheme is discussed in Sect. 4. Section 5 presents numerical results and graphs for the solutions to the test problems. Discussion on the efficiency of the method and the conclusions are given in Sect. 6.

Statement of the Problem

Consider the singularly perturbed two point boundary value problem of convection-diffusion type with a small negative shift in the first derivative term

$$\begin{aligned} \epsilon v^{\prime \prime }(x)+ p(x) v^{\prime }(x-\delta )+q(x) v(x)=r(x), x\in (0, 1) \end{aligned}$$

(1)

under the interval condition

$$\begin{aligned} v(x)=\phi (x), x\in [-\delta ,0], \end{aligned}$$

(2a)

and the boundary condition

$$\begin{aligned} v(1)=\beta , \end{aligned}$$

(2b)

where $0<\epsilon \ll 1$ is the pertutbation parameter, and $\delta$ is the delay (shift) parameter. As $\delta <\epsilon$, for $p(x)\ge M > 0$, $(\epsilon -\delta p(x))>0$, $\forall$ $x\in [0,1]$ and the solution exhibits a boundary layer near $x=0$, while for $p(x)\le {{\overline{M}}} < 0$, the solution exhibits a boundary layer near $x=1$. We assume $q(x)\le -{{\hat{\theta }}}<0$ where ${{\hat{\theta }}}$ is a positive constant, q(x), $\phi (x)$ and r(x) are functions which are sufficiently smooth, $\beta$ is a constant. The function v(x) will be a smooth solution to the problem (1-2), when it satisfies (1) and (2), being continuous in the underlying interval [0, 1] and also continuously differentiable in (0, 1).

As $\delta <\epsilon$, the use of Taylor’s series expansion for the term containing delay is valid [3] and hence the approximation to the boundary value problem (1) and (2) is

$$\begin{aligned} {\mathscr {L}}(w(x))=r(x), 0< x< 1, \end{aligned}$$

(3)

subject to

$$\begin{aligned} \begin{aligned} w(0)&=\phi (0)=\phi _0, \\ w(1)&=\beta , \end{aligned} \end{aligned}$$

(4)

where, ${\mathscr {L}}(w(x))=\mu w^{\prime \prime }(x)+ p(x) w^{\prime }(x)+q(x) w(x)$, $\mu (x)= \epsilon -\delta p(x)$, $w(x) \approx v(x)$. The following Lemma shows that ${\mathscr {L}}$ satisfies the minimum principle:

Lemma 1

Suppose w(x) is a function, sufficiently smooth and satisfying $\{w(0), w(1)\}\ge 0$, then $w(x) \ge 0$, $0\le x \le 1$, whenever $\mathscr {L} (w(x))\le 0$, $0\le x \le 1$.

Proof

Let $0\le {{\bar{z}}}\le 1$ be such that $w({{\bar{z}}}) = \min _{x\in [0,1]} w(x)$ and assume that $w({{\bar{z}}}) <0$. Clearly ${{\bar{z}}}\notin \{0,1 \}$, therfore $w^\prime ({{\bar{z}}})=0$ and $w^{\prime \prime }({{\bar{z}}}) \ge 0.$

Now we have, ${\mathscr {L}}(w({{\bar{z}}})) =\mu ({{\bar{z}}}) w^{\prime \prime }({{\bar{z}}})+p(x) w^\prime ({{\bar{z}}})) + q(x) w({{\bar{z}}}) > 0,$ which is a contradiction to our assumption that $w({{\bar{z}}}) <0$. Therefore, $w({{\bar{z}}}) \ge 0$ and hence $w(x) \ge 0 \; \forall x \in [0,1]$. $\square$

The stability estimate for the solution of the continuous problem (3) is given in the following Lemma:

Lemma 2

If w(x) is the solution of the problem (3) and (4), then we have $\Vert w \Vert \le {\hat{\theta }}^{-1} \Vert r \Vert + \max (\vert \phi _0 \vert , \vert \beta \vert )$, where $\Vert . \Vert$ is the $l_\infty$ norm given by $\Vert w \Vert =\max _{s\in [0,1]} \vert w(x) \vert$.

Proof

We consider two barrier functions $\psi ^{\pm }$ as below:

$$\begin{aligned} \psi ^{\pm } (x) ={\hat{\theta }}^{-1} \Vert r \Vert + max (\vert \phi _0 \vert , \vert \beta \vert ) \pm w(x) \end{aligned}$$

Then we have

$$\begin{aligned} \psi ^{\pm } (0) ={\hat{\theta }}^{-1} \Vert r \Vert + max (\vert \phi _0 \vert , \vert \beta \vert ) \pm w(0), \text { since } w(0)=\phi _0 \ge 0. \end{aligned}$$

and

$$\begin{aligned} \psi ^{\pm } (1) ={\hat{\theta }}^{-1} \Vert r \Vert + max (\vert \phi _0 \vert , \vert \beta \vert ) \pm w(1), \text { since } w(1)=\beta \ge 0. \end{aligned}$$

Also

$$\begin{aligned} \begin{aligned} {\mathscr {L}} \psi ^{\pm } (x) =&\mu (x) (\psi ^{\pm } (x))^{\prime \prime }+ p(x) (\psi ^{\pm } (s))^\prime + q(s) \psi ^{\pm } (x) \\ =&q(x) \left[ {\hat{\theta }}^{-1} \Vert r \Vert + \max (\vert \phi _0 \vert , \vert \beta \vert )\right] \pm {\mathscr {L}} w(x) \\ =&q(x) \left[ {\hat{\theta }}^{-1} \Vert r \Vert + \max (\vert \phi _0 \vert , \vert \beta \vert )\right] \pm r(x) \end{aligned} \end{aligned}$$

We have $q(x) {\hat{\theta }}^{-1} \le -1, \text { since } q(x) \le - {{\hat{\theta }}} < 0$, using in the above inequality, we get,

$$\begin{aligned} \begin{aligned}&{\mathscr {L}} \psi ^{\pm } (x) \le \left( -\Vert r \Vert \pm r(x) \right) +q(x) \max (\vert \phi _0 \vert , \vert \beta \vert ) \le 0 \\&\forall \;x \in (0,1), \text { since } \Vert r \Vert \ge r(x). \end{aligned} \end{aligned}$$

By the minimum principle [22], we know that $\psi ^{\pm } (x) \ge 0 \forall x \in (0,1)$, and we find the stability estimate. $\square$

The uniqueness of the solution of (3-4) is guarenteed by Lemma 1 and as the problem is linear, the existence also is implied. Furthermore, the boundedness of the solution of the problem is implied by lemma 2.

Lemma 3

Let the zeroth order approximate solution to (3) and (4) be $w(x)=w_0^o +w_0^i$, where $w_0^o$ is the approximate solution in the outer region of zeroth order and that in the layer region be $w_0^i$. Then for a fixed positive integer j,

$$\begin{aligned} \lim \limits _{h \rightarrow 0 }w(jh) \approx w_0^o(0)+(\phi (0)-w_0^o(0)) e^{-p(0)j \rho }, \rho =\frac{h}{(\mu (0))} \end{aligned}$$

Proof

The outer(reduced) region problem is given by

$$\begin{aligned} p(x) {(w_0^o(x))}^\prime +q(x)w_0^o(x)=r(x), w_0^o(1)= \beta \end{aligned}$$

and the inner(layer) region problem

$$\begin{aligned} (w_0^i({{\hat{x}}}))^{\prime \prime }+p(0)(w_0^i({{\hat{x}}}))^\prime =0, w_0^i(0)=\phi _0-w_0^o(0), w_0^i(\infty )=0, \text { where } {{\hat{x}}}=\frac{x}{(\epsilon -\delta M)}. \end{aligned}$$

From [23], we know that the zeroth order asymptotic approximations to the solution to the problem is

$$\begin{aligned} w(x)=w_0^o(x)+ \frac{p(0)}{p(x)}(\phi _0-w_0^o(0)) e^{- \int \limits _{0}^{x} \frac{p(x)}{(\mu (x))} dx } \end{aligned}$$

Assuming the coefficients to be locally constant on a fine mesh,

$$\begin{aligned} w(x)\approx w_0^o(x)+ (\phi _0-\nu _0^o(0)) e^{- \frac{p(0)}{(\mu (0))} x } \end{aligned}$$

and hence, at the mesh points,

$$\begin{aligned} \begin{aligned} w(x_j)\approx&w_0^o(x_j)+ (\phi _0-w_0^o(0)) e^{- \frac{p(0)}{(\mu (0))} x_j }, j=0, 1, \cdots , N.\\ w(jh)\approx&w_0^o(jh)+ (\phi _0-w_0^o(0)) e^{- \frac{p(0)}{(\mu (0))} jh } \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned}&\lim \limits _{h \rightarrow 0 }w(jh) \approx w_0^o(0)+(\phi _0-w_0^o(0)) e^{-p(0)j \rho } \text { for } j=0, 1, \cdots , N,\\&\text { where } \rho = \frac{h}{(\mu (0))}. \end{aligned} \end{aligned}$$

$\square$

Lemma 4

Let w(x) is the solution of the problem (3) and (4) then

$\vert \vert w^{(k)} \vert \vert \le C (\epsilon -\delta M)^{-k}$ for $k=1,2,3$.

Proof

Given any $x\in (0,1)$, we can construct the neighborhood $N_x=(c,c+\gamma )$, where $\gamma$ is some combination of $\epsilon$ and $\delta$ yet to be determined, such that $N_x\in (0,1)$.Then by mean value theorem there exists $\zeta \in N_x$ such that

$$\begin{aligned} w^\prime (\zeta )=\frac{w(c+\gamma )-w(c)}{\gamma }, \end{aligned}$$

so

$$\begin{aligned} \vert \vert w^\prime (\zeta ) \vert \vert \le \frac{2\vert \vert y\vert \vert }{\gamma }. \end{aligned}$$

(5)

Now integrating Eq.(3) from $\zeta$ to x and taking the modulus from both sides we get

$$\begin{aligned} (\epsilon -\delta M) \vert w^\prime (x) \vert \le (\epsilon -\delta M) \vert w^\prime (\zeta ) \vert +\vert \vert r\vert \vert \vert x-\zeta \vert + \int _{\zeta }^{x} \vert p(t) w^\prime (t) \vert dt +\vert \vert q \vert \vert \vert \vert w\vert \vert \vert x-\zeta \vert , \end{aligned}$$

this gives

$$\begin{aligned} \vert w^\prime (x) \vert\le & {} \vert w^\prime (\zeta ) \vert +(\epsilon -\delta M)^{-1}\vert \vert r\vert \vert \vert x-\zeta \vert +(\epsilon -\delta M)^{-1} \int _{\zeta }^{x} \vert p(t) w^\prime (t) \vert dt \\{} & {} +(\epsilon -\delta M)^{-1} \vert \vert q \vert \vert \vert \vert w\vert \vert \vert x-\zeta \vert . \end{aligned}$$

Using Eq.(5) and the fact that $x-\zeta \le \gamma$, after simplification we have following bound:

$$\begin{aligned} \begin{aligned} \vert w^\prime (x) \vert&\le C \left( \zeta ^{-1}+(\epsilon -\delta M)^{-1} \zeta +(\epsilon -\delta M)^{-1}\right) \vert \vert w\vert \vert +(\epsilon -\delta M)^{-1} \zeta \vert \vert r\vert \vert \\&\le C \left( \zeta ^{-1}+(\epsilon -\delta M)^{-1} \zeta +(\epsilon -\delta M)^{-1}\right) max\{ \vert \vert y\vert \vert ,\vert \vert r\vert \vert \}. \end{aligned} \end{aligned}$$

The right side is a minimum iff $\gamma =(\epsilon -\delta M)^{1/2}$. For this value of $\gamma$, we have

$$\begin{aligned} \vert w^\prime (x) \vert \le C (\epsilon -\delta M)^{-1}. \end{aligned}$$

Thus the result is true for $k=1$. Using Eq.(3) for w, we can obtain required bounds for $k=2$ and on differentiating Eq.(3) the result for $k=3$ follows. $\square$

Lemma 5

Let w is the solution of (3) and (4) and let $w=w^o+w^i$. For $0\le k \le 3$ and for sufficiently small $\epsilon$, $w^o$, $w^i$ and their derivatives satisfy the following bounds:

$$\begin{aligned} \begin{aligned} \vert \vert ({w^o})^{k} \vert \vert&\le C (\epsilon -\delta M)^{2-k},\\ \vert \vert w^i(x) \vert \vert&\le C e^{(-Mx/(\epsilon -\delta M))}, x\in (0,1),\\ \vert \vert ({w^i})^{k} \vert \vert&\le C (\epsilon -\delta M)^{-k} e^{(-Mx/(\epsilon -\delta M))}, x\in (0,1),\\ \end{aligned} \end{aligned}$$

Proof

For proof of this theorem the reader can refer [24]. $\square$

Numerical Method

We write Eq.(3) as

$$\begin{aligned} \mu (x) w^{\prime \prime }(x)=g(x,w,w^\prime ) \end{aligned}$$

(6)

where

$$\begin{aligned} g(x,w,w^\prime )=r(x)-p(x)w^{\prime }(x)-q(x) w(x). \end{aligned}$$

(7)

We divide the interval [0, 1] into N equal parts with constant mesh length h. Let $0=x_0,x_1,x_2,\cdots ,x_n=1$ be the mesh points, so that $x_i=ih,i=0,1,2,\cdots ,N.$

We consider the sixth order finite difference method by Chawla [25] for the general non-linear boundary value problem of the form $y^{\prime \prime }=g(x,y,y^\prime )$ as below:

$$\begin{aligned}{} & {} {{\overline{y}}}_k^\prime =\frac{1}{2h} [ y_{k+1}-y_{k-1} ], \\{} & {} {{\overline{y}}}_{k+1}^\prime =\frac{1}{2h} [3y_{k+1}-4 y_k +y_{k-1}], \\{} & {} {{\overline{y}}}_{k-1}^\prime =\frac{1}{2h} [-y_{k+1}+4 y_k -3y_{k-1}], \\{} & {} {\overline{{{\overline{y}}}}}_{k+1}^\prime =\frac{1}{2h} [y_{k+1}-y_{k-1}] +\frac{h}{3}[2 {{\overline{g}}}_k + \overline{g}_{k+1}], \\{} & {} {\overline{{{\overline{y}}}}}_{k-1}^\prime =\frac{1}{2h} [y_{k+1}-y_{k-1}] -\frac{h}{3}[2 {{\overline{g}}}_k + \overline{g}_{k-1}], \\{} & {} {{\overline{y}}}_{k+\frac{1}{2}}= \frac{1}{32}[15 y_{k+1}+18 y_k- y_{k-1}]- \frac{h^2}{64} [3 {{\overline{g}}}_{k+1}+4 {{\overline{g}}}_k- {{\overline{g}}}_{k-1}], \\{} & {} {{\overline{y}}}_{k-\frac{1}{2}}= \frac{1}{32}[-y_{k+1}+18 y_k+15 y_{k-1}]- \frac{h^2}{64} [-{{\overline{g}}}_{k+1}+4 \overline{g}_k+3{{\overline{g}}}_{k-1}], \\{} & {} {\overline{{{\overline{y}}}}}_{n+\frac{1}{2}}^\prime =\frac{1}{4h}[5 y_{k+1}-6 y_k+ y_{k-1}]- \frac{h}{48} [3 \overline{g}_{k+1}+8{{\overline{g}}}_k+ {{\overline{g}}}_{k-1}], \\{} & {} {\overline{{{\overline{y}}}}}_{k-\frac{1}{2}}^\prime =\frac{1}{4h}[- y_{k+1}+6 y_k-5 y_{k-1}]- \frac{h}{48} [ \overline{g}_{k+1}+8{{\overline{g}}}_k+3 {{\overline{g}}}_{k-1}], \\{} & {} {{\hat{y}}}_k^\prime ={{\overline{y}}}_k^\prime +h \left[ \frac{1}{78}({{\overline{g}}}_{k+1}- {{\overline{g}}}_{k-1}) -\frac{1}{52} ({\overline{{{\overline{g}}}}}_{k+1} -{\overline{{{\overline{g}}}}}_{k-1} )-\frac{2}{13} ({\overline{{{\overline{g}}}}}_{k+\frac{1}{2}} -{\overline{{{\overline{g}}}}}_{k-\frac{1}{2}} ) \right] , \end{aligned}$$

$$\begin{aligned} \left[ y_{k-1}-2y_k+ y_{k+1}\right] =\frac{h^2}{60} \left[ 26 {{\hat{g}}}_k +{\overline{{{\overline{g}}}}}_{k+1}+{\overline{\overline{g}}}_{k-1}+16 ({\overline{{{\overline{g}}}}}_{k+\frac{1}{2}}+{\overline{{{\overline{g}}}}}_{k-\frac{1}{2}}) \right] , \end{aligned}$$

(8)

where

$$\begin{aligned} \begin{aligned} {\overline{{{\overline{g}}}}}_{k\pm 1}&= g( x_{k\pm 1},y_{k\pm 1},{\overline{{{\overline{y}}}}}_{k\pm 1}^\prime ), \\ {\overline{{{\overline{g}}}}}_{k\pm \frac{1}{2}}&= g( x_{k\pm \frac{1}{2}},y_{k\pm \frac{1}{2}},{\overline{{{\overline{y}}}}}_{k\pm \frac{1}{2}}^\prime ), \\ {{\hat{g}}}_k&= g(x_k,y_k, {{\hat{y}}}_k^\prime ). \end{aligned} \end{aligned}$$

By introducing fitting parameter $\sigma (\rho )$ for the second derivative and applying the above scheme to (6), we get the tridiagonal scheme

$$\begin{aligned} E_n w_{n-1}+F_n w_n+G_n w_{n+1}=H_n\;, n=1, 2,\cdots , N-1, \end{aligned}$$

(9)

where

$$\begin{aligned} \begin{aligned} E_n=&\mu _n \sigma _n+\frac{hp_{n+1/2}}{15} -\frac{hp_{n+1}}{120} -\frac{hp_{n-1/2}}{3} -\frac{hp_{n-1}}{120} +\frac{h^2q_{n-1}}{60} +\frac{h^2q_{n-1/2}}{8} \\ {}&-\frac{h^2q_{n+1/2}}{120} -\frac{13hp_{n}}{60} -\frac{h^2p_{n-1}^2}{120} -\frac{h^2p_{n+1}^2}{360} -\frac{7h^2p_{n-1}p_{n}}{720} -\frac{h^2p_{n+1}p_{n}}{720} \\ {}&+\frac{19h^2p_{n-1/2}p_{n}}{180} -\frac{h^2p_{n+1/2}p_{n}}{180} -\frac{h^3q_{n-1}p_{n}}{360} -\frac{19h^3q_{n-1/2}p_{n}}{480} -\frac{h^3q_{n+1/2}p_{n}}{96} \\ {}&+\frac{h^2p_{n-1}p_{n-1/2}}{40} -\frac{h^2p_{n-1}p_{n+1/2}}{120} -\frac{h^2p_{n+1}p_{n-1/2}}{360} +\frac{h^2p_{n+1}p_{n+1/2}}{120} +\frac{h^3p_{n-1}p_{n}^2}{360} \\ {}&+\frac{h^3p_{n+1}p_{n}^2}{360} +\frac{h^3p_{n-1}^2p_{n}}{240} -\frac{h^3p_{n+1}^2p_{n}}{720} -\frac{h^3p_{n-1/2}p_{n}^2}{180} -\frac{h^3p_{n+1/2}p_{n}^2}{180} \\ {}&+\frac{h^3p_{n-1}q_{n-1}}{180} -\frac{3h^3p_{n-1}q_{n-1/2}}{160} +\frac{h^3p_{n-1}q_{n+1/2}}{160} -\frac{h^3p_{n+1}q_{n-1/2}}{480} +\frac{h^3p_{n+1}q_{n+1/2}}{160} \\ {}&-\frac{h^3p_{n-1/2}q_{n-1}}{60} +\frac{h^3p_{n+1/2}q_{n-1}}{180} +\frac{h^4q_{n-1/2}p_{n}^2}{480} -\frac{h^4q_{n+1/2}p_{n}^2}{480} +\frac{h^4q_{n-1}q_{n-1/2}}{80} \\ {}&-\frac{h^4q_{n-1}q_{n+1/2}}{240} -\frac{h^3p_{n-1}p_{n-1/2}p_{n}}{160} -\frac{h^3p_{n-1}p_{n+1/2}p_{n}}{480} +\frac{h^3p_{n+1}p_{n-1/2}p_{n}}{1440} \\ {}&+\frac{h^3p_{n+1}p_{n+1/2}p_{n}}{480} -\frac{h^4p_{n-1}q_{n-1}p_{n}}{360} +\frac{3h^4p_{n-1}q_{n-1/2}p_{n}}{640} +\frac{h^4p_{n-1}q_{n+1/2}p_{n}}{640} \\ {}&+\frac{h^4p_{n+1}q_{n-1/2}p_{n}}{1920} +\frac{h^4p_{n+1}q_{n+1/2}p_{n}}{640} +\frac{h^4p_{n-1/2}q_{n-1}p_{n}}{240} +\frac{h^4p_{n+1/2}q_{n-1}p_{n}}{720} \\ {}&-\frac{h^5q_{n-1}q_{n-1/2}p_{n}}{320} -\frac{h^5q_{n-1}q_{n+1/2}p_{n}}{960}, \end{aligned} \\ \begin{aligned} F_n=&- 2\mu _n \sigma _n +\frac{2hp_{n-1/2}}{5} -\frac{2hp_{n+1/2}}{5} +\frac{13h^2q_{n}}{30} +\frac{3h^2q_{n-1/2}}{20} +\frac{3h^2q_{n+1/2}}{20} \\ {}&+\frac{h^2p_{n-1}^2}{90} +\frac{h^2p_{n+1}^2}{90} +\frac{h^2p_{n-1}p_{n}}{90} +\frac{h^2p_{n+1}p_{n}}{90} -\frac{h^2p_{n-1/2}p_{n}}{10} -\frac{h^2p_{n+1/2}p_{n}}{10} \\ {}&+\frac{h^3p_{n-1}q_{n}}{90} -\frac{h^3p_{n+1}q_{n}}{90} -\frac{2h^3p_{n-1/2}q_{n}}{45} +\frac{2h^3p_{n+1/2}q_{n}}{45} -\frac{3h^3q_{n-1/2}p_{n}}{80} \\ {}&+\frac{3h^3q_{n+1/2}p_{n}}{80} +\frac{h^4q_{n-1/2}q_{n}}{60} +\frac{h^4q_{n+1/2}q_{n}}{60} -\frac{h^2p_{n-1}p_{n-1/2}}{30} +\frac{h^2p_{n-1}p_{n+1/2}}{90} \\ {}&+\frac{h^2p_{n+1}p_{n-1/2}}{90} -\frac{h^2p_{n+1}p_{n+1/2}}{30} -\frac{h^3p_{n-1}^2p_{n}}{180} +\frac{h^3p_{n+1}^2p_{n}}{180} +\frac{h^3p_{n-1}q_{n-1/2}}{40} \\ {}&-\frac{h^3p_{n-1}q_{n+1/2}}{120} +\frac{h^3p_{n+1}q_{n-1/2}}{120} -\frac{h^3p_{n+1}q_{n+1/2}}{40} -\frac{h^4p_{n-1}p_{n}q_{n}}{180} -\frac{h^4p_{n+1}p_{n}q_{n}}{180} \\ {}&+\frac{h^4p_{n-1/2}p_{n}q_{n}}{90} +\frac{h^4p_{n+1/2}p_{n}q_{n}}{90} -\frac{h^5q_{n-1/2}p_{n}q_{n}}{240} +\frac{h^5q_{n+1/2}p_{n}q_{n}}{240} \\ {}&+\frac{h^3p_{n-1}p_{n-1/2}p_{n}}{120} +\frac{h^3p_{n-1}p_{n+1/2}p_{n}}{360} -\frac{h^3p_{n+1}p_{n-1/2}p_{n}}{360} -\frac{h^3p_{n+1}p_{n+1/2}p_{n}}{120} \\ {}&-\frac{h^4p_{n-1}q_{n-1/2}p_{n}}{160} -\frac{h^4p_{n-1}q_{n+1/2}p_{n}}{480} -\frac{h^4p_{n+1}q_{n-1/2}p_{n}}{480} -\frac{h^4p_{n+1}q_{n+1/2}p_{n}}{160}, \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} G_n=&\mu _n \sigma _n +\frac{hp_{n-1}}{120} +\frac{hp_{n+1}}{120} -\frac{hp_{n-1/2}}{15} +\frac{hp_{n+1/2}}{3} +\frac{h^2q_{n+1}}{60} -\frac{h^2q_{n-1/2}}{120} \\ {}&+\frac{h^2q_{n+1/2}}{8} +\frac{13hp_{n}}{60} -\frac{h^2p_{n-1}^2}{360} -\frac{h^2p_{n+1}^2}{120} -\frac{h^2p_{n-1}p_{n}}{720} -\frac{7h^2p_{n+1}p_{n}}{720} \\ {}&-\frac{h^2p_{n-1/2}p_{n}}{180} +\frac{19h^2p_{n+1/2}p_{n}}{180} +\frac{h^3q_{n+1}p_{n}}{360} +\frac{h^3q_{n-1/2}p_{n}}{96} +\frac{19h^3q_{n+1/2}p_{n}}{480} \\ {}&+\frac{h^2p_{n-1}p_{n-1/2}}{120} -\frac{h^2p_{n-1}p_{n+1/2}}{360} -\frac{h^2p_{n+1}p_{n-1/2}}{120} +\frac{h^2p_{n+1}p_{n+1/2}}{40} -\frac{h^3p_{n-1}p_{n}^2}{360} \\ {}&-\frac{h^3p_{n+1}p_{n}^2}{360} +\frac{h^3p_{n-1}^2p_{n}}{720} -\frac{h^3p_{n+1}^2p_{n}}{240} +\frac{h^3p_{n-1/2}p_{n}^2}{180} +\frac{h^3p_{n+1/2}p_{n}^2}{180} \\ {}&-\frac{h^3p_{n+1}q_{n+1}}{180} -\frac{h^3p_{n-1}q_{n-1/2}}{160} +\frac{h^3p_{n-1}q_{n+1/2}}{480} -\frac{h^3p_{n+1}q_{n-1/2}}{160} \\ {}&+\frac{3h^3p_{n+1}q_{n+1/2}}{160} -\frac{h^3p_{n-1/2}q_{n+1}}{180} +\frac{h^3p_{n+1/2}q_{n+1}}{60} -\frac{h^4q_{n-1/2}p_{n}^2}{480} \\ {}&+\frac{h^4q_{n+1/2}p_{n}^2}{480} -\frac{h^4q_{n+1}q_{n-1/2}}{240} +\frac{h^4q_{n+1}q_{n+1/2}}{80} -\frac{h^3p_{n-1}p_{n-1/2}p_{n}}{480} \\ {}&-\frac{h^3p_{n-1}p_{n+1/2}p_{n}}{1440} +\frac{h^3p_{n+1}p_{n-1/2}p_{n}}{480} +\frac{h^3p_{n+1}p_{n+1/2}p_{n}}{160} -\frac{h^4p_{n+1}q_{n+1}p_{n}}{360} \\ {}&+\frac{h^4p_{n-1}q_{n-1/2}p_{n}}{640} +\frac{h^4p_{n-1}q_{n+1/2}p_{n}}{1920} +\frac{h^4p_{n+1}q_{n-1/2}p_{n}}{640} +\frac{3h^4p_{n+1}q_{n+1/2}p_{n}}{640} \\ {}&+\frac{h^4p_{n-1/2}q_{n+1}p_{n}}{720} +\frac{h^4p_{n+1/2}q_{n+1}p_{n}}{240} +\frac{h^5q_{n+1}q_{n-1/2}p_{n}}{960} +\frac{h^5q_{n+1}q_{n+1/2}p_{n}}{320} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} H_n=&\frac{13h^2r_{n}}{30} +\frac{h^2r_{n-1}}{60} +\frac{h^2r_{n+1}}{60} +\frac{4h^2r_{n-1/2}}{15} +\frac{4h^2r_{n+1/2}}{15} +\frac{h^3p_{n-1}r_{n}}{90} -\frac{h^3p_{n+1}r_{n}}{90} \\ {}&-\frac{h^3r_{n-1}p_{n}}{360} +\frac{h^3r_{n+1}p_{n}}{360} -\frac{2h^3p_{n-1/2}r_{n}}{45} +\frac{2h^3p_{n+1/2}r_{n}}{45} -\frac{h^3r_{n-1/2}p_{n}}{15} \\ {}&+\frac{h^3r_{n+1/2}p_{n}}{15} +\frac{h^4q_{n-1/2}r_{n}}{60} +\frac{h^4q_{n+1/2}r_{n}}{60} +\frac{h^3p_{n-1}r_{n-1}}{180} -\frac{h^3p_{n+1}r_{n+1}}{180} \\ {}&-\frac{h^3p_{n-1/2}r_{n-1}}{60} -\frac{h^3p_{n-1/2}r_{n+1}}{180} +\frac{h^3p_{n+1/2}r_{n-1}}{180} +\frac{h^3p_{n+1/2}r_{n+1}}{60} \\ {}&+\frac{h^4q_{n-1/2}r_{n-1}}{80} -\frac{h^4q_{n-1/2}r_{n+1}}{240} -\frac{h^4q_{n+1/2}r_{n-1}}{240} +\frac{h^4q_{n+1/2}r_{n+1}}{80} -\frac{h^4p_{n-1}p_{n}r_{n}}{180} \\ {}&-\frac{h^4p_{n+1}p_{n}r_{n}}{180} +\frac{h^4p_{n-1/2}p_{n}r_{n}}{90} +\frac{h^4p_{n+1/2}p_{n}r_{n}}{90} -\frac{h^5q_{n-1/2}p_{n}r_{n}}{240} +\frac{h^5q_{n+1/2}p_{n}r_{n}}{240} \\ {}&-\frac{h^4p_{n-1}r_{n-1}p_{n}}{360} -\frac{h^4p_{n+1}r_{n+1}p_{n}}{360} +\frac{h^4p_{n-1/2}r_{n-1}p_{n}}{240} +\frac{h^4p_{n-1/2}r_{n+1}p_{n}}{720} \\ {}&+\frac{h^4p_{n+1/2}r_{n-1}p_{n}}{720} +\frac{h^4p_{n+1/2}r_{n+1}p_{n}}{240} -\frac{h^5q_{n-1/2}r_{n-1}p_{n}}{320} +\frac{h^5q_{n-1/2}r_{n+1}p_{n}}{960} \\ {}&-\frac{h^5q_{n+1/2}r_{n-1}p_{n}}{960} +\frac{h^5q_{n+1/2}r_{n+1}p_{n}}{320}. \end{aligned} \end{aligned}$$

The above tri-diagonal scheme, along with the boundary conditions (4) is evaluated using Thomas Algorithm. The procedure followed for finding the fitting parameter $\sigma _n$ is as follows:

• A fitting parameter $\sigma (\rho )$ is introduced into the second derivative term of (6) and is determined such that the solution of (8) converges uniformly in $\mu$ to the solution of (3-4), which is illustrated in the subsequent steps.

• The numerical scheme (9) obtained after intoducing the fitting parameter, when multiplied by h, as $h\rightarrow 0$ is

  $$\begin{aligned} \lim \limits _{h \rightarrow 0}\left[ \frac{\sigma }{\rho }(w_{n-1}-2 w_n+w_{n+1})+{\frac{p(0)}{2}}(w_{n-1}- w_{n+1})\right] =0 \end{aligned}$$

• Using lemma (3), we get the fitting parameter, $\sigma (\rho )=\frac{p(0)\rho }{2}\coth \left( \frac{p(0)\rho }{2}\right)$, which is a constant fitting factor.

• In general we consider the variable fitting parameter

  $$\begin{aligned} \sigma _n=\frac{p(x_n)\rho _n}{2}\coth \left( \frac{p(x_n)\rho _n}{2}\right) , \end{aligned}$$

  (10)

  where $\rho _n=\frac{h}{\mu _n }$.

Convergence Analysis

Multipying Eq. (9) by h and incorporating the boundary conditions, we obtain the system of equations in the matrix form as

$$\begin{aligned} ({\mathscr {D}}+{\mathscr {J}}){\mathcal {W}}+{\mathcal {K}}+{\mathcal {T}}(h)=0, \end{aligned}$$

(11)

where

and

$$\begin{aligned} \begin{aligned} {\mathcal {K}}&={\left[ {\mathcal {k}} _1+\left( \frac{\mu _1 \sigma _1}{h}+r_1 \right) \phi _0, {\mathcal {k}}_2, {\mathcal {k}}_3,\cdots , {\mathcal {k}}_{N-2},{\mathcal {k}}_{N-1} +\left( \frac{\mu _{N-1} \sigma _{N-1}}{h}+t_{N-1} \right) \beta \right] }^T, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\mathcal {K}}_n=&\frac{13hr_{n}}{30} +\frac{hr_{n-1}}{60} +\frac{hr_{n+1}}{60} +\frac{4hr_{n-1/2}}{15} +\frac{4hr_{n+1/2}}{15} +\frac{h^2p_{n-1}r_{n}}{90} -\frac{h^2p_{n+1}r_{n}}{90} \\ {}&-\frac{h^2r_{n-1}p_{n}}{360} +\frac{h^2r_{n+1}p_{n}}{360} -\frac{2h^2p_{n-1/2}r_{n}}{45} +\frac{2h^2p_{n+1/2}r_{n}}{45} -\frac{h^2r_{n-1/2}p_{n}}{15} \\ {}&+\frac{h^2r_{n+1/2}p_{n}}{15} +\frac{h^3q_{n-1/2}r_{n}}{60} +\frac{h^3q_{n+1/2}r_{n}}{60} +\frac{h^2p_{n-1}r_{n-1}}{180} -\frac{h^2p_{n+1}r_{n+1}}{180} \\ {}&-\frac{h^2p_{n-1/2}r_{n-1}}{60} -\frac{h^2p_{n-1/2}r_{n+1}}{180} +\frac{h^2p_{n+1/2}r_{n-1}}{180} +\frac{h^2p_{n+1/2}r_{n+1}}{60} \\ {}&+\frac{h^3q_{n-1/2}r_{n-1}}{80} -\frac{h^3q_{n-1/2}r_{n+1}}{240} -\frac{h^3q_{n+1/2}r_{n-1}}{240} +\frac{h^3q_{n+1/2}r_{n+1}}{80} \\ {}&-\frac{h^3p_{n-1}p_{n}r_{n}}{180} -\frac{h^3p_{n+1}p_{n}r_{n}}{180} +\frac{h^3p_{n-1/2}p_{n}r_{n}}{90} +\frac{h^3p_{n+1/2}p_{n}r_{n}}{90} \\ {}&-\frac{h^4q_{n-1/2}p_{n}r_{n}}{240} +\frac{h^4q_{n+1/2}p_{n}r_{n}}{240} -\frac{h^3p_{n-1}r_{n-1}p_{n}}{360} -\frac{h^3p_{n+1}r_{n+1}p_{n}}{360} \\ {}&+\frac{h^3p_{n-1/2}r_{n-1}p_{n}}{240} +\frac{h^3p_{n-1/2}r_{n+1}p_{n}}{720} +\frac{h^3p_{n+1/2}r_{n-1}p_{n}}{720} +\frac{h^3p_{n+1/2}r_{n+1}p_{n}}{240} \\ {}&-\frac{h^4q_{n-1/2}r_{n-1}p_{n}}{320} +\frac{h^4q_{n-1/2}r_{n+1}p_{n}}{960} -\frac{h^4q_{n+1/2}r_{n-1}p_{n}}{960} +\frac{h^4q_{n+1/2}r_{n+1}p_{n}}{320}, \\&n=1, 2,\cdots , N-1. \end{aligned} \end{aligned}$$

Here, ${\mathcal {W}}= [{\mathcal {W}}_1,{\mathcal {W}}_2,\cdots , {\mathcal {W}}_{N-1}]^T$, the truncation errors at the mesh points ${\mathcal {T}}(h)=[{\mathcal {T}}_1, {\mathcal {T}}_2, \cdots , {\mathcal {T}}_{N-1}]^T.$

Let $W=[{{\overline{w}}}_1, {{\overline{w}}}_2, \cdots , {{\overline{w}}}_{N-1}]^T \cong {\mathcal {Y}}$ which satisfies the equation

$$\begin{aligned} ({\mathscr {D}}+{\mathscr {J}}) {{\overline{w}}}+{\mathcal {K}}=0 \end{aligned}$$

(12)

Let $e_n={{\overline{w}}}_n-{\mathcal {W}}_n, n=1, 2, \cdots , N-1$ be the discretization error, so that ${\mathcal {E}}=[e_1, e_2, \cdots , e_{N-1}]^T={{\overline{w}}}-{\mathcal {W}}$.

Now subtracting (12) from (11), we get

$$\begin{aligned} (\mathscr {D}+\mathscr {J}){\mathcal {E}}={\mathcal {T}}(h) \end{aligned}$$

(13)

Considering $|p(x)|\le c_1$, $|q(x)|\le c_2$ and ${\mathscr {J}}_{i,j}$, the $(i, j)^{th}$ element of the matrix ${\mathscr {J}}$, we have

When h is sufficiently small,

$$\begin{aligned} \frac{\mu _n \sigma _n}{h}+\vert {\mathscr {J}}_{n, n+1} \vert \le \left( \frac{\mu _n \sigma _n}{h}+\frac{ c_1}{2}\right) \ne 0, \ n=1, 2, \cdots , N-2, \\ \frac{\mu _n \sigma _n}{h}+\vert {\mathscr {J}}_{n, n-1} \vert \le \left( \frac{\mu _n \sigma _n}{h}-\frac{ c_1}{2}\right) \ne 0, \ n=1, 2, \cdots , N-1. \end{aligned}$$

Hence the matrix is irreducible [26].

Let ${\mathcal {S}}_n$ be the sum of the elements of the $n^{th}$ row of the matrix $(\mathscr {D}+\mathscr {J})$, then we have

$$\begin{aligned} \begin{aligned} {\mathcal {S}}_n=&-\frac{\mu _n \sigma _n}{h} +\frac{hp_{n-1}}{120} +\frac{hp_{n+1}}{120} +\frac{hp_{n-1/2}}{3} -\frac{hp_{n+1/2}}{15} +\frac{13hq_{n}}{30} +\frac{hq_{n+1}}{60} \\ {}&+\frac{17hq_{n-1/2}}{120} +\frac{11hq_{n+1/2}}{40} +\frac{13p_{n}}{60} +\frac{hp_{n-1}^2}{120} +\frac{hp_{n+1}^2}{360} +\frac{7hp_{n-1}p_{n}}{720} \\ {}&+\frac{hp_{n+1}p_{n}}{720} -\frac{19hp_{n-1/2}p_{n}}{180} +\frac{hp_{n+1/2}p_{n}}{180} +\frac{h^2q_{n+1}p_{n}}{360} +\frac{h^2p_{n-1}q_{n}}{90} -\frac{h^2p_{n+1}q_{n}}{90} \\ {}&-\frac{2h^2p_{n-1/2}q_{n}}{45} +\frac{2h^2p_{n+1/2}q_{n}}{45} -\frac{13h^2q_{n-1/2}p_{n}}{480} +\frac{37h^2q_{n+1/2}p_{n}}{480} -\frac{hp_{n-1}p_{n-1/2}}{40} \\ {}&+\frac{h^3q_{n-1/2}q_{n}}{60} +\frac{h^3q_{n+1/2}q_{n}}{60} +\frac{hp_{n-1}p_{n+1/2}}{120} +\frac{hp_{n+1}p_{n-1/2}}{360} -\frac{7hp_{n+1}p_{n+1/2}}{240} \\ {}&-\frac{h^2p_{n-1}p_{n}^2}{360} -\frac{h^2p_{n+1}p_{n}^2}{360} -\frac{h^2p_{n-1}^2p_{n}}{240} +\frac{h^2p_{n+1}^2p_{n}}{720} +\frac{h^2p_{n-1/2}p_{n}^2}{180} +\frac{h^2p_{n+1/2}p_{n}^2}{180} \\ {}&-\frac{h^2p_{n+1}q_{n+1}}{180} +\frac{3h^2p_{n-1}q_{n-1/2}}{160} -\frac{h^2p_{n-1}q_{n+1/2}}{160} +\frac{h^2p_{n+1}q_{n-1/2}}{480} -\frac{h^2p_{n+1}q_{n+1/2}}{160} \\ {}&-\frac{h^3p_{n-1}p_{n}q_{n}}{180} -\frac{h^3p_{n+1}p_{n}q_{n}}{180} -\frac{h^2p_{n-1/2}q_{n+1}}{180} +\frac{h^2p_{n+1/2}q_{n+1}}{60} +\frac{h^3p_{n-1/2}p_{n}q_{n}}{90} \\ {}&+\frac{h^3p_{n+1/2}p_{n}q_{n}}{90} -\frac{h^3q_{n-1/2}p_{n}^2}{480} +\frac{h^3q_{n+1/2}p_{n}^2}{480} -\frac{h^3q_{n+1}q_{n-1/2}}{240} +\frac{h^3q_{n+1}q_{n+1/2}}{80} \\ {}&-\frac{h^4q_{n-1/2}p_{n}q_{n}}{240} +\frac{h^4q_{n+1/2}p_{n}q_{n}}{240} +\frac{h^2p_{n-1}p_{n-1/2}p_{n}}{160} +\frac{h^2p_{n-1}p_{n+1/2}p_{n}}{480} \\ {}&-\frac{h^2p_{n+1}p_{n-1/2}p_{n}}{1440} -\frac{h^2p_{n+1}p_{n+1/2}p_{n}}{480} -\frac{h^3p_{n+1}q_{n+1}p_{n}}{360} -\frac{3h^3p_{n-1}q_{n-1/2}p_{n}}{640} \\ {}&-\frac{h^3p_{n-1}q_{n+1/2}p_{n}}{640} -\frac{h^3p_{n+1}q_{n-1/2}p_{n}}{1920} -\frac{h^3p_{n+1}q_{n+1/2}p_{n}}{640} +\frac{h^3p_{n-1/2}q_{n+1}p_{n}}{720} \\ {}&+\frac{h^3p_{n+1/2}q_{n+1}p_{n}}{240} +\frac{h^4q_{n+1}q_{n-1/2}p_{n}}{960} +\frac{h^4q_{n+1}q_{n+1/2}p_{n}}{320}, \ \text { for} \ n=1, \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} {\mathcal {S}}_n=&-\frac{\mu _n\sigma _n}{h} -\frac{p_{n-1}}{120} -\frac{p_{n+1}}{120} -\frac{p_{n+1/2}}{3} +\frac{p_{n-1/2}}{15} +\frac{hq_{n-1}}{60} +\frac{13hq_{n}}{30} \\ {}&+\frac{11hq_{n-1/2}}{40} +\frac{17hq_{n+1/2}}{120} -\frac{13p_{n}}{60} +\frac{hp_{n-1}^2}{360} +\frac{hp_{n+1}^2}{120} +\frac{hp_{n-1}p_{n}}{720} \\ {}&+\frac{7hp_{n+1}p_{n}}{720} +\frac{hp_{n-1/2}p_{n}}{180} -\frac{19hp_{n+1/2}p_{n}}{180} -\frac{h^2q_{n-1}p_{n}}{360} +\frac{h^2p_{n-1}q_{n}}{90} -\frac{h^2p_{n+1}q_{n}}{90} \\ {}&-\frac{2h^2p_{n-1/2}q_{n}}{45} +\frac{2h^2p_{n+1/2}q_{n}}{45} -\frac{37h^2q_{n-1/2}p_{n}}{480} +\frac{13h^2q_{n+1/2}p_{n}}{480} +\frac{h^3q_{n-1/2}q_{n}}{60} \\ {}&+\frac{h^3q_{n+1/2}q_{n}}{60} -\frac{hp_{n-1}p_{n-1/2}}{120} +\frac{hp_{n-1}p_{n+1/2}}{360} +\frac{hp_{n+1}p_{n-1/2}}{120} -\frac{hp_{n+1}p_{n+1/2}}{40} \\ {}&+\frac{h^2p_{n-1}p_{n}^2}{360} +\frac{h^2p_{n+1}p_{n}^2}{360} -\frac{h^2p_{n-1}^2p_{n}}{720} +\frac{h^2p_{n+1}^2p_{n}}{240} -\frac{h^2p_{n-1/2}p_{n}^2}{180} -\frac{h^2p_{n+1/2}p_{n}^2}{180} \\ {}&+\frac{h^2p_{n-1}q_{n-1}}{180} +\frac{h^2p_{n-1}q_{n-1/2}}{160} -\frac{h^2p_{n-1}q_{n+1/2}}{480} +\frac{h^2p_{n+1}q_{n-1/2}}{160} -\frac{3h^2p_{n+1}q_{n+1/2}}{160} \\ {}&-\frac{h^2p_{n-1/2}q_{n-1}}{60} +\frac{h^2p_{n+1/2}q_{n-1}}{180} +\frac{h^3q_{n-1/2}p_{n}^2}{480} -\frac{h^3q_{n+1/2}p_{n}^2}{480} +\frac{h^3q_{n-1}q_{n-1/2}}{80} \\ {}&-\frac{h^3q_{n-1}q_{n+1/2}}{240} -\frac{h^3p_{n-1}p_{n}q_{n}}{180} -\frac{h^3p_{n+1}p_{n}q_{n}}{180} +\frac{h^3p_{n-1/2}p_{n}q_{n}}{90} +\frac{h^3p_{n+1/2}p_{n}q_{n}}{90} \\ {}&-\frac{h^4q_{n-1/2}p_{n}q_{n}}{240} +\frac{h^4q_{n+1/2}p_{n}q_{n}}{240} +\frac{h^2p_{n-1}p_{n-1/2}p_{n}}{480} +\frac{h^2p_{n-1}p_{n+1/2}p_{n}}{1440} \\ {}&-\frac{h^2p_{n+1}p_{n-1/2}p_{n}}{480} -\frac{h^2p_{n+1}p_{n+1/2}p_{n}}{160} -\frac{h^3p_{n-1}q_{n-1}p_{n}}{360} -\frac{h^3p_{n-1}q_{n-1/2}p_{n}}{640} \\ {}&-\frac{h^3p_{n-1}q_{n+1/2}p_{n}}{1920} -\frac{h^3p_{n+1}q_{n-1/2}p_{n}}{640} -\frac{39h^3p_{n+1}q_{n+1/2}p_{n}}{640} +\frac{h^3p_{n-1/2}q_{n-1}p_{n}}{240} \\ {}&+\frac{h^3p_{n+1/2}q_{n-1}p_{n}}{720} -\frac{h^4q_{n-1}q_{n-1/2}p_{n}}{320} -\frac{h^4q_{n-1}q_{n+1/2}p_{n}}{960}, \ \text { for} \ n=N-1, \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} {\mathcal {S}}_n=&\frac{hq_{n-1}}{60} +\frac{13hq_{n}}{30} +\frac{hq_{n+1}}{60} +\frac{4hq_{n-1/2}}{15} -\frac{hq_{n+1/2}}{30} -\frac{h^2q_{n-1}p_{n}}{360} +\frac{h^2q_{n+1}p_{n}}{360} \\ {}&+\frac{h^2p_{n-1}q_{n}}{90} -\frac{h^2p_{n+1}q_{n}}{90} -\frac{2h^2p_{n-1/2}q_{n}}{45} +\frac{2h^2p_{n+1/2}q_{n}}{45} -\frac{h^2q_{n-1/2}p_{n}}{15} \\ {}&+\frac{h^2q_{n+1/2}p_{n}}{15} +\frac{h^3q_{n-1/2}q_{n}}{60} +\frac{h^3q_{n+1/2}q_{n}}{60} +\frac{h^2p_{n-1}q_{n-1}}{180} -\frac{h^2p_{n+1}q_{n+1}}{180} \\ {}&-\frac{h^2p_{n-1/2}q_{n-1}}{60} +\frac{h^2p_{n+1/2}q_{n-1}}{180} -\frac{h^2p_{n-1/2}q_{n+1}}{180} +\frac{h^2p_{n+1/2}q_{n+1}}{60} +\frac{h^3q_{n-1}q_{n-1/2}}{80} \\ {}&-\frac{h^3q_{n-1}q_{n+1/2}}{240} -\frac{h^3q_{n+1}q_{n-1/2}}{240} +\frac{h^3q_{n+1}q_{n+1/2}}{80} -\frac{h^3p_{n-1}p_{n}q_{n}}{180} -\frac{h^3p_{n+1}p_{n}q_{n}}{180} \\ {}&+\frac{h^3p_{n-1/2}p_{n}q_{n}}{90} +\frac{h^3p_{n+1/2}p_{n}q_{n}}{90} -\frac{h^4q_{n-1/2}p_{n}q_{n}}{240} +\frac{h^4q_{n+1/2}p_{n}q_{n}}{240} \\ {}&-\frac{h^3p_{n-1}q_{n-1}p_{n}}{360} -\frac{h^3p_{n+1}q_{n+1}p_{n}}{360} +\frac{h^3p_{n-1/2}q_{n+1}p_{n}}{720} +\frac{h^3p_{n+1/2}q_{n+1}p_{n}}{240} \\ {}&+\frac{h^4q_{n+1}q_{n-1/2}p_{n}}{960} +\frac{h^4q_{n+1}q_{n+1/2}p_{n}}{320} +\frac{h^3p_{n-1/2}q_{n-1}p_{n}}{240} +\frac{h^3p_{n+1/2}q_{n-1}p_{n}}{720} \\ {}&-\frac{h^4q_{n-1}q_{n-1/2}p_{n}}{320} -\frac{h^4q_{n-1}q_{n+1/2}p_{n}}{960}, \ \text { for} \ n=2\,3\,...\,N-2. \end{aligned} \end{aligned}$$

Let $c_{1^*}=\min \vert p(x)\vert$, $c^*_1=\max \vert p(x)\vert$,

Let $c_{2^*}=\min \vert q(x)\vert$, $c^*_2=\max \vert q(x)\vert$,

then $0< c_{1^*}\le c_1 \le c^*_1, 0< c_{2^*}\le c_2 \le c^*_2$

It can be easily verified that $({\mathscr {D}}+{\mathscr {J}})$ is monotone ( [26, 27]).

Table 1 Maximum absolute errors for Example 1 when $\delta =0.5\epsilon$

Table 2 Maximum absolute errors for Example 2 when $\delta =0.5\epsilon$

Table 3 Maximum absolute errors for Example 3 when $\delta =0.5\epsilon$

Table 4 Maximum absolute errors for Example 4 when $\delta =0.5\epsilon$

Table 5 Maximum absolute errors for Example 5 when $\delta =0.5\epsilon$

Table 6 The numerical rate of convergence for the considered examples for various of $\epsilon$ with $\delta =0.3\epsilon$

Table 7 The numerical rate of convergence for the considered examples for various of $\delta$ with $\epsilon =0.01$

Fig. 1

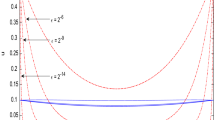
Numerical solution for Example 1 with $\epsilon =0.1$

Hence $({\mathscr {D}}+{\mathscr {J}})^{-1}$ exists and $({\mathscr {D}}+{\mathscr {J}})^{-1} \ge 0$.

From the error equation (13), we have

$$\begin{aligned} \vert \vert {\mathcal {E}} \vert \vert =\vert \vert {({\mathscr {D}}+{\mathscr {J}})}^{-1} \vert \vert .\vert \vert {\mathcal {T}} \vert \vert \end{aligned}$$

For sufficiently small h, we have

$$\begin{aligned} {\mathcal {S}}_n>&\frac{h^4}{80} c_1 c_2^2 \ \ \text {for} \ n=1, \nonumber \\ {\mathcal {S}}_n>&\frac{h^4}{80} c_1 c_2^2 \ \ \text {for}\ n=N-1 \ \text {and} \nonumber \\ {\mathcal {S}}_n>&\frac{h^4}{80} c_1 \left( c_2^2 +c_A^2+c_B^2 \right) \ \text {for} \ n=2, 3, \cdots , N-2 \nonumber \\ \text {where} \ c_A=\vert q_{n+1}q_{n-\frac{1}{2}}-q_{n-1}q_{n+\frac{1}{2}} \vert ,\nonumber \\ \ c_B=\vert q_{n+1}q_{n+\frac{1}{2}}-q_{n-1}q_{n-\frac{1}{2}} \vert . \end{aligned}$$

(14)

Let ${({\mathscr {D}}+{\mathscr {J}})}_{(n,i)}^{-1}$ be the $(n,i)^{th}$ element of ${({\mathscr {D}}+{\mathscr {J}})}^{-1}$ and we define

$$\begin{aligned} \vert \vert {({\mathscr {D}}+{\mathscr {J}})}^{-1} \vert \vert =\max _{1 \le n \le N-1} \sum \limits _{i=1}^{N-1} {({\mathscr {D}}+{\mathscr {J}})}_{n,i}^{-1} \text { and } \vert \vert {\mathcal {T}}(h) \vert \vert =\max _{1 \le n \le N-1} \vert \mathcal {T_n} \vert , \end{aligned}$$

since ${({\mathscr {D}}+{\mathscr {J}})}_{(n,i)}^{-1} \ge 0$ and $\sum \limits _{i=1}^{N-1} {({\mathscr {D}}+{\mathscr {J}})}_{(n,i)}^{-1}\cdot {\mathcal {S}}_i =1$ for $n=1, 2,\cdots , N-1$.

Hence

$$\begin{aligned} \begin{aligned} {({\mathscr {D}}+{\mathscr {J}})}_{(n,1)}^{-1} \le&\frac{1}{{\mathcal {S}}_1} \le \frac{80}{h^4 c_1c_2^2}, \\ {({\mathscr {D}}+{\mathscr {J}})}_{(n,N-1)}^{-1} \le&\frac{1}{{\mathcal {S}}_{N-1}} \le \frac{80}{h^4 c_1c_2^2}. \end{aligned} \end{aligned}$$

Further

$$\begin{aligned} \sum \limits _{i=2}^{N-2} {({\mathscr {D}}+{\mathscr {J}})}_{(n,i)}^{-1} \le \frac{1}{\min \limits _{2 \le i \le N-2} \mathcal {S_i}} \le \frac{80 }{h^4 c_1 [ c_2^2+c_A^2+c_B^2] } \ \text {for} \ n=1,2,\cdots ,N-1. \end{aligned}$$

Hence from Eqs.(13) and (14), we get

$$\begin{aligned} \vert \vert {\mathcal {E}} \vert \vert =\frac{80}{h^4 c_1} \left[ \frac{2}{c_1 c_2^2}+\frac{1}{c_2^2}+\frac{1}{c_A^2}+\frac{1}{c_B^2}\right] \times O(h^6)=O(h^2). \\ \end{aligned}$$

This establishes the convergence of the finite difference scheme (9).

Fig. 2

Numerical solution for Example 1 with $\epsilon =0.01$

Fig. 3

Numerical solution for Example 2 with $\epsilon =0.1$

Fig. 4

Numerical solution for Example 2 with $\epsilon =0.01$

Fig. 5

Numerical solution for Example 3 with $\epsilon =0.1$

Fig. 6

Numerical solution for Example 3 with $\epsilon =0.01$

Fig. 7

Numerical solution for Example 4 with $\epsilon =0.1$

Fig. 8

Numerical solution for Example 4 with $\epsilon =0.01$

Fig. 9

Numerical solution for Example 5 with $\epsilon =0.1$

Fig. 10

Numerical solution for Example 5 with $\epsilon =0.01$

Numerical Results

To check the efficiency of the present method, it is applied on five problems of singularly perturbed linear differential equation with small shift. Three problems with solutions exhibiting boundary layer to the left of the interval [0,1] and two problems with right layer.

Since the exact solutions of these problems for different values of $\delta$ are not known, the maximum absolute errors for the test problems are evaluated using the following double mesh principle:

$$\begin{aligned} E_N=\max _{0\le i\le N} \vert w^N_i -w^{2N}_{2i} \vert . \end{aligned}$$

The numerical rate of convergence for all the examples have been calculated by the formula

$$\begin{aligned} R_N=\frac{log \vert E_N/E_{2N} \vert }{log 2}. \end{aligned}$$

The maximum absolute errors are given in Tables 1, 2, 3, 4 and 5 for the considered test problems with $\delta =(0.5) \epsilon$. The numerical rate of convergence for the considered problems for various values of $\epsilon$ and $\delta$ are given in Tables 6 and 7. The graphical solutions of the examples are depicted in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 for different values of the shift parameter, where-in the effects of the shifts on the layer behaviour of the solutions can be examined.

Example 1

$\epsilon v^{\prime \prime }(x)+ v^{\prime }(x-\delta )+v(x)=0$ subject to the interval and boundary conditions $v(x)=1;-\delta \le x\le 0,v(1)=1$.

Example 2

$\epsilon v^{\prime \prime }(x)+(1+x) v^{\prime }(x-\delta )- e^{-x}v(x)=1$ subject to the interval and boundary conditions $v(x)=0;-\delta \le x\le 0,v(1)=1$.

Example 3

$\epsilon v^{\prime \prime }(x)+0.25 v^{\prime }(x-\delta )-v(x)=0$ subject to the interval and boundary conditions $v(x)=1;-\delta \le x\le 0,v(1)=0$.

Example 4

$\epsilon v^{\prime \prime }(x)- v^{\prime }(x-\delta )+v(x)=0$ subject to the interval and boundary conditions $v(x)=1;-\delta \le x\le 0,v(1)=-1$.

Example 5

$\epsilon v^{\prime \prime }(x)- e^x v^{\prime }(x-\delta )-v(x)=0$ subject to the interval and boundary conditions $v(x)=1;-\delta \le x\le 0,v(1)=1$.

Discussion and Conclusion

In this paper, a higher-order fitted finite difference method is presented for singularly perturbed boundary value problems of second-order ordinary differential-difference equation of the convection-diffusion type. The method is devised for the problems with shifts smaller than the petrubation parameter. The method is shown to be second-order uniformly convergent for various values of $\epsilon$ and $\delta$, which can also be observed from the numerical results. Computations are carried out to examine the efficiency of the present method and also the effects of the shifts on the layer behaviour of the solution. The graphs of the solutions of the considered problems are plotted for various values of $\epsilon$ and $\delta$ and they are found to be in good agreement with those in existing literature. From the figures, we conclude that as the shifts increase in magnitude, the layer thickness decreases in the case where the solution exhibits layer behaviour near left of the underlying interval, while it increases in the case where the solution exhibits boundary layer behaviour on the right side.

While classical finite difference methods fail to provide good results when the mesh parameter exceeds the perturbation parameter and lead to round-off errors, the fitted finite difference method developed in this paper gives uniformly convergent solutions, independent of the perturbation parameter and with considerably larger value of the mesh parameter. Also it provides a higher rate of convergence. An extensive numerical work has been carried out on MATLAB R2023a in double precision and presented in the form of tables which exhibit the efficiency of the method.