A Robust Iterative Approach for Space-Time Fractional Multidimensional Telegraph Equation

Abstract

The aim of the study is to analyze space-time fractional multidimensional telegraph equation using a generalized transform method. Fractional derivative are considered in Liouville-Caputo sense. The idea is to combine New iterative method with Aboodh transform to get approximate-analytical solution in form of fast convergent series. Uniqueness and existence of the proposed problem is shown using Banach fixed point theorem. Stability analysis is stated using Ulam–Hyres stability theorem. The convergent of solution obtain by generalized transform is shown by Cauchy convergent theorem. Four test problem are considered to shows the efficiency of the proposed method.

Introduction

Most of the physical processes rely on their past behavior; thus, to understand their past behavior, fractional calculus is a vital tool. The memory effect and non-local nature of fractional calculus help to capture the past behavior of physical processes. This property of fractional calculus is explained in the transmission of dengue model [1]. It states that mosquito doesn’t look for their host randomly, but they use the prior experience of host location [2, 3]. Thus in the transmission of dengue, the history of the transmission process will affect its future state. Fractional differential operator trajectory is non-local [4]. This property is useful in including memory in physical process. Du et al. [5] provide justification of memory effect by taking $\eta \in (0,1)$ as order of fractional derivative, where $\eta \rightarrow 0$ states an ideal memory and $\eta \rightarrow 1$ states no memory. Hence these properties of fractional calculus attract many researchers in this area. The fractional calculus have various applications in field of fluid dynamics [6], diffusion [7], control [8], relaxation processes [9, 10] and so on.

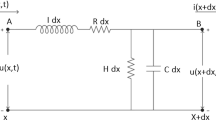
In today’s world communication system is a vital tool to transfer information from source to receiver. Every engineering problem requires the transmission of signals from one point to another. The system together is known as transmission media which transfers data from one point to another. All transmission methods undoubtedly experience signal loss. Sorting out signal losses is necessary to optimise the transmission medium. The study of how electrical impulses spread along a transmission line’s cable and wave phenomena gives rise to telegraph equations. Oliver Heaviside [11] created the transmission line model and discovered telegraph equations. This model shows how electromagnetic waves are magnified on wires and how wave patterns can be seen along the length of a transmission line. There are several applications for telegraph equations, including electrical signal propagation in transmission line cables [12], wave propagation [13], random walks [14], signal analysis [15], etc. Mainly, the telegraph equation occurs in fractional order than integer order. The main benefit of fractional derivatives is their memory character. Hence every successive stage of the physical system will also depend on its past stage. Therefore the physical system with fractional derivative is more realistic.

There are several methods accessible in literature for the study of fractional-order telegraph equations. Bansu and Kumar [16] combine radial basis function with chebyshev polynomial to get approximate solution of fractional telegraph equations. Kumar et al. [17] applied local meshless method for approximation of the fractional telegraph equation.

The 1-dimensional space-time fractional telegraph equation given as,

$$\begin{aligned} \frac{\partial ^{2\eta }w}{\partial \tau ^{2\eta }}+2a_{0}\frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}+a_{1}^{2}w=\frac{\partial ^{2\alpha }w}{ \partial \chi ^{2\alpha }}+h(\chi ,\tau ),~~0<\alpha ,\eta \le 1, \end{aligned}$$

(1)

with conditions,

$$\begin{aligned} w(\chi ,0)&= f_{1}(\chi ), ~~w_{t}(\chi ,0)= f_{2}(\chi ),\\ w(0,\tau )&= g_{1}(\tau ), ~~w_{\chi }(0,\tau )= g_{2}(\tau ). \end{aligned}$$

2-dimensional time fractional telegraph equation given as,

$$\begin{aligned} \frac{\partial ^{2\eta }w}{\partial \tau ^{2\eta }}+2a_{0}\frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}+a_{1}^{2}w=\frac{\partial ^{2}w}{\partial \chi ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}},~~0<\eta \le 1, \end{aligned}$$

(2)

subject to conditions,

$$\begin{aligned} w(\chi ,\gamma ,0)=\phi _{1},~~ w_{\tau }(\chi ,\gamma ,0)=\phi _{2}. \end{aligned}$$

3-dimensional fractional telegraph equation is given by,

$$\begin{aligned} \frac{\partial ^{2\eta }w}{\partial \tau ^{2\eta }}+2a_{0}\frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}+a_{1}^{2}w= \frac{\partial ^{2}w}{\partial \chi ^{2}}+ \frac{\partial ^{2}w}{\partial \gamma ^{2}}+\frac{\partial ^{2}w}{\partial \theta ^{2}}+h(\chi ,\gamma ,\theta ,\tau ),~0<\eta \le 1, \end{aligned}$$

(3)

subject to,

$$\begin{aligned} w(\chi ,\gamma ,\theta ,0)= \psi _{1},~~w_{\tau }(\chi ,\gamma ,\theta ,0)=\psi _{2}. \end{aligned}$$

In Eqs. (1) to (3) $a_{0},a_{1}$ are positive constant. $f_{1},f_{2},g_{1},g_{2},\phi _{1},\phi _{2},\psi _{1},\psi _{2}$ are continuous function.

Integral transform has always remain a helpful tool in solving fractional differential equations (FDEs). There are several integral transform like Laplace transform, Sumudu transform, Elzaki transform available in literature [18, 19]. Combining these integral transform with semi-analytical methods is very helpful in dealing with FDEs [20]. Day by day these transform are refine by several researcher. Aboodh transform a generalized form of Fourier integral developed by Khalid [23]. The Aboodh transform has several properties, but the most useful property over the other integral transforms is its ‘unity’ feature which plays an essential role [21]. Noting these refinement Jena and Chakraverty [21] combines Aboodh transform with Q-Homotopy Analysis method to solve delay time-fractional partial differential equations. Jani and T singh [22] combines Aboodh transform with Homotopy perturbation method for solving regularized long wave equations.

The motivation of the paper is to employ a semi-analytical method namely New iterative method (NIM) [24] coupled with Aboodh transform to find the solution of the space-time fractional multidimensional telegraph equation. NIM is free from arbitrary parameters like the homotopy perturbation method and also does not require tedious calculations like Adomain decomposition method or finding langrange multipliers like in the variational parameter method. Aboodh transform coupled with NIM takes very less computation work and less C.P.U memory. Also, this coupled method is new and still not used for solving this problem. So, the Aboodh transform iterative method (ATIM) reduce computation size compare to other method and give a solution in the form of fast convergent series. Also, the uniqueness and existence of the proposed problem are shown using Banach’s fixed point theorem and Schaefer–Krasnoselskii fixed point theorem. Stability analysis is stated using Ulam–Hyre’s stability theorem. The efficiency of the solution obtained by ATIM is shown by comparing it with the exact solution and previously published work.

This paper consists 7 sections. Section 2 consists basic definitions of fractional calculus and Aboodh transform which is useful in dealing of space-time fractional telegraph equation. Section 3 consists existence, uniqueness and stability analysis of the proposed problem. Section 4 contains general procedure of ATIM with its convergence analysis. Section 5 consists numerical illustrations. Section 6 gives the explanation of the results obtained with help of graphs. Finally, Sect. 7 concludes the findings.

Preliminaries

This section consists fundamental definitions of fractional calculus and their properties which is useful for studying FDEs.

Definition 1.1

[25,26,27] For order $\eta$ the fractional order Reimann-Liouville integral is defined as,

$$\begin{aligned} {I}^{\eta }g(x)=\frac{1}{\Gamma (\eta )} \int _0 ^{t} ({x}-{\tau })^{\eta -1} g(\tau )d{\tau }, ~&\text {if } \eta>0 ,x>0. \end{aligned}$$

Definition 1.2

[28] For order $\eta >0$ the Caputo fractional derivatives (Cfd) is defined as,

$$\begin{aligned} {D}_{t}^{\eta }g(x,t)=\frac{1}{\Gamma (s-\eta )} \int _0^{t}({t}-{\tau })^{l-\eta -1}\frac{\partial ^{s}g(x,\tau )}{\partial \tau ^s}d{\tau }, ~~s-1 \le \eta <s, \end{aligned}$$

Lemma 1

[26] Let $I_{t}^{\eta }$ is an integral operator then for $t>0$ and $n-1<\eta \le n$, $n\in {\mathbb {N}}$

$$\begin{aligned}&(i) D_{t}^{\eta }I_{t}^{\eta }g(x,t)=g(x,t), \\&(ii) I_{t}^{\eta }D_{t}^{\eta }g(x,t)=g(x,t)-\sum _{p=0}^{n}g(x,0)\frac{t^{p}}{p!}. \end{aligned}$$

Definition 1.3

[29] In a set A, consider function which is piece wise continuous and of exponential order given by,

$$\begin{aligned} A=\{v(t): \exists M, ~k_{1},~k_{2}>0,~|z(t)|<Me^{-vt}\}, \end{aligned}$$

where $k_1$ and $k_2$ maybe finite or infinite and M is constant. The Aboodh transform is defined as,

$$\begin{aligned} T(v) ={\mathscr {A}}[z(t)](v)= \frac{1}{v}\int _{0}^{\infty }z(\tau )e^{-v\tau }\partial \tau , \quad \tau \ge 0, ~~ k_1\le v \le k_2. \end{aligned}$$

Definition 1.4

[30] For a function z(t) where $t \in (0,\infty )$, the inverse Aboodh transform is given as,

$$\begin{aligned} if ~T(v)={\mathscr {A}}[z(t)],~ then ~ z(t) = {\mathscr {A}}^{-1} [T(v)]. \end{aligned}$$

Definition 1.5

[30] The Aboodh transform of a Cfd is given as,

$$\begin{aligned} {\mathscr {A}}[(D_{t}^{\eta }z(t));v]=v^{\eta }{\mathscr {A}}[z(t)]-\sum _{p=0}^{n}\frac{z^{(p)}(0)}{v^{2-\eta +p}},\quad ~n-1<\eta \le n, n \in N. \end{aligned}$$

Existence, Uniqueness, and Stability

This section consists existence, uniqueness, and stability analysis of proposed problem. First we state some definitions and theorems which is useful in proving existence and uniqueness of the proposed problem.

Definition 1.6

Consider a norm space as $(X,\vert \vert . \vert \vert )$. Then a map $\phi : X\rightarrow X$ is a contraction of X if for every $x_{1}$, $x_{2}$ $\in X$,

$$\begin{aligned} \vert \vert Q(x_{1})-Q(x_{2})\vert \vert \le \delta \vert \vert x_{1}-x_{2}\vert \vert , \end{aligned}$$

where $0\le \delta <1$.

Definition 1.7

[31] Banach fixed point theorem: On a complete metric space every contraction mapping has a unique fixed point.

Definition 1.8

[32] Arzela–Ascoli theorem: Consider a compact metric space X. Let $C(X, {\mathbb {R}})$ be a metric with sup norm. Then a set $Q\subset C(X,{\mathbb {R}})$ is compact iff Q is bounded, equicontinuous, and closed.

Definition 1.9

[33] Schaefer–Krasnoselskii fixed point theorem: If X is bounded and closed convex subset of a Banach space Y and $Q:X\rightarrow X$ is completely continuous, then Q has a fixed point in Q.

Existence and Uniqueness of Proposed Problem

Let $[0,b]\times (0,T]= \phi$ and consider $C(\phi ,{\mathbb {R}})$ as a Banach space of all continuous function from $\phi$ into ${\mathbb {R}}$ with sup norm define as $\vert \vert x \vert \vert _{\infty }$:= sup$\left( \vert x \vert , (\chi ,\tau ) \in \phi \right)$. We consider a generalized fractional partial differential equation (FPDE) for proposed problem as,

$$\begin{aligned} \partial _{\tau }^{\eta }w(\chi ,\tau )+G(w,w_{\chi }, w_{\chi \chi })= H(\chi ,\tau ), ~\chi \in [0,b],~ \tau \in (0,T],~ 0<\eta \le 1, \end{aligned}$$

(4)

subject to conditions as,

$$\begin{aligned} w(\chi ,0)&= f_{1}(\chi ), ~~w_{t}(\chi ,0)= f_{2}(\chi ),\nonumber \\ w(0,\tau )&= g_{1}(\tau ), ~~w_{\chi }(0,\tau )= g_{2}(\tau ). \end{aligned}$$

(5)

Definition 1.10

Let $w(\chi ,\tau )$ be a function in $C(\phi ,{\mathbb {R}})$ is said to be a solution of (4)–(5) if $\eta$ derivative exists on (0, T] and $w(\chi ,\tau )$ satisfies(4)–(5) on (0, T].

Theorem 1.1

[34] Assuming following condition holds.

• (R1) $\exists$ constant $K_{1}, K_{2}>0$ such that

  $$\begin{aligned}&\vert w_{1 \chi }-w_{2\chi }\vert \le K_{1}\vert w_{1}-w_{2}\vert , \nonumber \\&\vert w_{1\chi \chi }-w_{2\chi \chi } \le K_{2}\vert w_{1}-w_{2}\vert , ~\forall (\chi ,\tau ) \in \phi ,~ w\in C(\phi , {\mathbb {R}}). \end{aligned}$$

• (R2) $\exists$ constant $M_{1}, M_{2}$, and $M_{3}$ such that,

  $$\begin{aligned}&\vert G(w_{1}, w_{1\chi },w_{1\chi \chi })- G(w_{2}, w_{2\chi },w_{2\chi \chi })\vert \\&\quad \le M_{1}\vert w_{1}-w_{2}\vert + M_{2}\vert w_{1\chi }-w_{2\chi }\vert +M_{3}\vert w_{1\chi \chi }-w_{2\chi \chi }\vert \end{aligned}$$

  If

  $$\begin{aligned} \frac{T^{\eta }}{\Gamma (\eta +1)}(M_{1}+M_{2}K_{1}+M_{3}K_{2})<1. \end{aligned}$$

  (6)

Then on $C(\phi ,{\mathbb {R}})$ (4)–(5) has a unique solution.

Proof

Consider a operator $\Psi : C(\phi ,{\mathbb {R}})\rightarrow C(\phi ,{\mathbb {R}})$ define as,

$$\begin{aligned} \Psi (w(\chi ,\tau ))= \sum _{p=0}^{n}\frac{w^{(p)}(\chi ,0)\tau ^{p}}{p!}+I_{\tau }^{\eta }\Big (H(\chi ,\tau )-G(w,w_{\chi },w_{\chi ,\chi })\Big ), n-1<\eta \le n. \end{aligned}$$

The fixed points of operator $\Psi$ are solution of the (4)–(5). Using Banach fixed point theorem we show that $\Psi$ has a fixed point. Finally, show $\Psi$ is a contraction. Consider $w_{1}, w_{2}$ $\in C(\phi , {\mathbb {R}})$ where $(\chi ,\tau ) \in \phi$, then

$$\begin{aligned} \vert \Psi (w_{1}(\chi ,\tau ))-\Psi (w_{2}(\chi ,\tau ))\vert&= I_{\tau }^{\eta }\vert G(w_{1},w_{1\chi },w_{1\chi \chi })-G(w_{2},w_{2\chi },w_{2\chi \chi })\vert , \nonumber \\&\le I_{\tau }^{\eta }\big (M_{1}\vert w_{1}-w_{2}\vert +M_{2}\vert w_{1\chi }-w_{2\chi }\vert +M_{3}\vert w_{1\chi \chi }-w_{2\chi \chi }\vert \big ),\nonumber \\&\le I_{\tau }^{\eta }\big (M_{1}\vert w_{1}-w_{2}\vert +M_{2}K_{1}\vert w_{1}-w_{2}\vert +M_{3}K_{2}\vert w_{1}-w_{2}\vert \big ), \nonumber \\&\le \frac{\tau ^{\eta }}{\Gamma (\eta +1)}\Big (M_{1}+M_{2}K_{1}+M_{3}K_{2}\Big )\vert w_{1}-w_{2}\vert , \nonumber \\&\le \frac{T^{\eta }}{\Gamma (\eta +1)}\Big (M_{1}+M_{2}K_{1}+M_{3}K_{2}\Big )sup\vert w_{1}-w_{2}\vert . \end{aligned}$$

(7)

Hence from Eq. (6), $\Psi$ operator is contraction. As a result of Banach fixed point theorem $\Psi$ has a unique fixed point which is also solution of (4)–(5). $\square$

Theorem 1.2

[34] For existence we assume that:

• (E1) $\exists$ a constant $A_{1}$ such that,

  $$\begin{aligned} \vert H(\chi ,\tau )\vert \le A_{1}, \forall (\chi ,\tau ) \in \phi . \end{aligned}$$

• (E2) $\exists$ a constant $A_{2}$ such that,

  $$\begin{aligned} \vert G(w,w_{\chi },w_{\chi \chi })\vert \le A_{2}, \forall (\chi ,\tau ) \in \phi , w\in C(\phi ,{\mathbb {R}}). \end{aligned}$$

• (E3) Assume $w:\phi \rightarrow {\mathbb {R}}$ is continuous.

• (E4) $\exists$ constants $\beta _{1},\beta _{2}$, and $\beta _{3}$ such that

  $$\begin{aligned}&\vert G(w(\chi _{1},\tau _{1}),w_{\chi _{1}}(\chi _{1},\tau _{1}), w_{\chi _{1}\chi _{1}}(\chi _{1},\tau _{1}))-G(w(\chi _{2},\tau _{2}),w_{\chi _{2}}(\chi _{2},\tau _{2}), w_{\chi _{2}\chi _{2}}(\chi _{2},\tau _{2}))\vert \\&\quad \le \beta _{1}\vert w(\chi _{1},\tau _{1})-w(\chi _{2},\tau _{2})\vert +\beta _{2}\vert w_{\chi _{1}}(\chi _{1},\tau _{1})-w_{\chi _{2}}(\chi _{2},\tau _{2})\vert \\&\qquad + \beta _{3}\vert w_{\chi _{1} \chi _{1}}(\chi _{1},\tau _{1})-w_{\chi _{2} \chi _{2}}(\chi _{2},\tau _{2})\vert , \end{aligned}$$

• (E5) $\exists$ constants $\alpha _{1}$,$\alpha _{2}>0$ such that

  $$\begin{aligned}&\vert w_{\chi _{1}}(\chi _{1},\tau _{1})-w_{\chi _{2}}(\chi _{2},\tau _{2})\vert \le \alpha _{1}\vert w(\chi _{1},\tau _{1})-w(\chi _{2},\tau _{2})\vert ,\\&\vert w_{\chi _{1} \chi _{1}}(\chi _{1},\tau _{1})-w_{\chi _{2} \chi _{2}}(\chi _{2},\tau _{2})\vert \le \alpha _{2}\vert w(\chi _{1},\tau _{1})-w(\chi _{2},\tau _{2})\vert , \\&\forall (\chi _{1},\tau _{1}),(\chi _{2},\tau _{2}) \in \phi , w\in C(\phi ,{\mathbb {R}}). \end{aligned}$$

• (E6) $\exists$ constants $\gamma _{1},\gamma _{2}>0$ such that

  $$\begin{aligned} \vert w(\chi _{1},\tau _{1})-w(\chi _{2},\tau _{2})\vert \le \gamma _{1}\vert \chi _{1}-\chi _{2}\vert +\gamma _{2}\vert \tau _{1}-\tau _{2}\vert ~\forall (\chi _{1},\tau _{1}),(\chi _{2},\tau _{2}) \in \phi , w\in C(\phi ,{\mathbb {R}}). \end{aligned}$$

If assumptions (E1)–(E6) satisfied, then problem (4)–(5) have atleast one solution in space $C(\phi , {\mathbb {R}})$

Proof

The existence of the proposed problem is shown in 4 steps.

Step 1 The map $\phi$ is continuous. Consider $w_{n}$ a sequence in $C(\phi ,{\mathbb {R}})$ such that $w_{n}\rightarrow w$, then

$$\begin{aligned} \vert \Psi w_{n}(\chi ,\tau )-\Psi w(\chi ,\tau )\vert =I_{\tau }^{\eta }\vert G(w_{n},w_{n\chi },w_{n\chi \chi })-G(w,w_{\chi },w_{\chi \chi })\vert . \end{aligned}$$

Using Eq. (6),

$$\begin{aligned} \vert \Psi w_{n}(\chi ,\tau )-\Psi w(\chi ,\tau )\vert \le \frac{T^{\eta }}{\Gamma (\eta +1)}\left( M_{1}+M_{2}K_{1}+M_{3}K_{2}\right) \Vert w_{n}-w\Vert _{\infty }. \end{aligned}$$

From (E3) w is continuous, thus as $n\rightarrow 0$ $\Vert \Psi w_{n}(\chi ,\tau )-\Psi w(\chi ,\tau )\Vert _{\infty }\rightarrow 0$.

Step 2 Operator $\Psi$ maps bounded set into bounded set $C(\phi ,{\mathbb {R}})$. We show for any $\epsilon _{0}>0$ $\exists$ a constant f such that for each $w\in \lambda _{\epsilon _{0}}$=$\{ w\in C(\phi ,{\mathbb {R}}):\Vert w(\chi ,\tau )\Vert _{\infty }<\epsilon _{0}$, we have $\vert \Psi w\vert <f$.

$$\begin{aligned} \vert \Psi w(\chi ,\tau )\vert&= \Big |\sum _{p=0}^{n}\frac{w^{(p)}(\chi ,0)\tau ^{p}}{p!}+I_{\tau }^{\eta }\left( H(\chi ,\tau )-G(w,w_{\chi },w_{\chi \chi })\right) \Big |, \nonumber \\&\le \Big |\sum _{p=0}^{n}\frac{w^{(p)}(\chi ,0)\tau ^{p}}{p!}\Big |+ I_{\tau }^{\eta }(A_{1}+A_{2}),\nonumber \\&\le \Big |\sum _{p=0}^{n}w^{(p)}(\chi ,0)\Big |\frac{\vert \tau ^{p}\vert }{p!}+\frac{\tau ^{\eta }}{\Gamma (\eta +1)}(A_{1}+A_{2}), \nonumber \\&\le \Big |\sum _{p=0}^{n}w^{(p)}(\chi ,0)\Big |\frac{\Vert \tau ^{p}\Vert _{\infty }}{p!}+\frac{T^{\eta }}{\Gamma (\eta +1)}(A_{1}+A_{2}). \end{aligned}$$

(8)

Finally,

$$\begin{aligned} \Vert \Psi w(\chi ,\tau )\Vert _{\infty }\le \Big |\sum _{p=0}^{n}w^{(p)}(\chi ,0)\Big |\frac{\Vert \tau ^{p}\Vert _{\infty }}{p!}+\frac{T^{\eta }}{\Gamma (\eta +1)}(A_{1}+A_{2})= D. \end{aligned}$$

(9)

Implies $\Vert \Psi w(\chi ,\tau )\Vert _{\infty }\le \infty$.

Step 3 $\Psi$ is equicontinuous on $C(\phi ,{\mathbb {R}})$. Consider $(\chi _{1},\tau _{1}),(\chi _{2},\tau _{2})\in \phi$, $\chi _{1}<\chi _{2}$, $\tau _{1}<\tau _{2}$ and $\lambda _{\epsilon _{0}}$ be bounded set of $C(\phi ,{\mathbb {R}})$ and let $w\in \lambda _{\epsilon _{0}}$, then

$$\begin{aligned}&\vert \Psi (w_{1}(\chi ,\tau )-\Psi (w_{2}(\chi ,\tau )\vert \nonumber \\&\quad =\Big | I_{\tau }^{\eta } \Big (G(w(\chi _{1},\tau _{1}),w_{\chi _{1}}(\chi _{1},\tau _{1}), w_{\chi _{1}\chi _{1}}(\chi _{1},\tau _{1}))\nonumber \\&\qquad -G(w(\chi _{2},\tau _{2}),w_{\chi _{2}}(\chi _{2},\tau _{2}), w_{\chi _{2}\chi _{2}}(\chi _{2},\tau _{2}))\Big )\Big |, \nonumber \\&\quad \le I_{\tau }^{\eta }\Big (\beta _{1}\vert w(\chi _{1},\tau _{1})- w(\chi _{2},\tau _{2})\vert +\beta _{2}\vert w_{\chi _{1}}(\chi _{1},\tau _{1})-w_{\chi _{2}}(\chi _{2},\tau _{2})\vert \nonumber \\&\qquad + \beta _{3}\vert w_{\chi _{1}\chi _{1}}(\chi _{1},\tau _{1})-w_{\chi _{2}\chi _{2}}(\chi _{2},\tau _{2}) \vert \Big )\nonumber \\&\quad \le I_{\tau }^{\eta }\Big (\beta _{1}\vert w(\chi _{1},\tau _{1})- w(\chi _{2},\tau _{2})\vert +\beta _{2}\alpha _{1}\vert w(\chi _{1},\tau _{1})- w(\chi _{2},\tau _{2})\vert \nonumber \\&\qquad + \beta _{3}\alpha _{2}\vert w(\chi _{1},\tau _{1})- w(\chi _{2},\tau _{2}) \vert \Big ) , \nonumber \\&\quad \le \frac{\tau ^{\eta }}{\Gamma (\eta +1)}\Big (\Big (\beta _{1}+\beta _{2}\alpha _{1}+\beta _{3}\alpha _{2}\Big )\Big (\gamma _{1}\vert \chi _{1}-\chi _{2}\vert +\gamma _{2}\vert \tau _{1}-\tau _{2}\vert \Big )\Big )\nonumber \\&\quad \le \frac{T^{\eta }}{\Gamma (\eta +1)}\Big (\Big (\beta _{1}+\beta _{2}\alpha _{1}+\beta _{3}\alpha _{2}\Big )\Big (\gamma _{1}\Vert \chi _{1}-\chi _{2}\Vert _{\infty }+\gamma _{2}\Vert \tau _{1}-\tau _{2}\Vert _{\infty } \Big )\Big ). \end{aligned}$$

(10)

Hence as Eq. (10) is free from w and as $\chi _{1}\rightarrow \chi _{2}$, $\tau _{1}\rightarrow \tau _{2}$ right hand side of Eq. (10) tends to zero. From above steps and Arzela–Ascoli theorem, we concludes $\Psi :(\phi ,{\mathbb {R}})\rightarrow (\phi ,{\mathbb {R}})$ is continuous and completely continuous.

Step 4 We show that the set

$$\begin{aligned} \Omega =\{w\in C(\phi ,{\mathbb {R}}):w =\zeta \Psi (w(\chi ,\tau ))~for some~ 0<\zeta <1\} \end{aligned}$$

is bounded.

Let $w\in \Omega$, then

$$\begin{aligned} \vert w(\chi ,\tau )\vert&= \vert \zeta \Psi (w(\chi ,\tau ))\vert ,\nonumber \\&=\zeta \vert \Psi (w(\chi ,\tau ))\vert . \end{aligned}$$

(11)

Using Eq. (9) in Eq. (11), we get

$$\begin{aligned} \vert w(\chi ,\tau )\vert \le \zeta \Bigg (\sum _{p=0}^{n}w^{(p)}(\chi ,0)\Big |\frac{\Vert \tau ^{p}\Vert _{\infty }}{p!}+\frac{T^{\eta }}{\Gamma (\eta +1)}(A_{1}+A_{2})\Big |\Bigg )=D^{1}, \end{aligned}$$

which states that $\Omega$ is bounded set. From Schaefer’s fixed point theorem, operator $\Psi$ has a fixed point which is solution of (4)–(5). $\square$

Stability Analysis

This subsection consists the stability analysis of proposed problem with the help of Ulam-Hyres stability theorem which states,

Definition 1.11

Let $w \in C(\phi , {\mathbb {R}})$ be any solution of (4)–(5) and for any $\epsilon _{0}$ the (4)–(5) is Ulam- Hyres stable if inequality holds,

$$\begin{aligned} \vert \vert \partial _{\tau }^{\eta }w(\chi ,\tau )- (H(\chi ,\tau )-G(w,w_{\chi },w_{\chi \chi }))\vert \vert \le \epsilon _{0}. \end{aligned}$$

(12)

Lemma 2

The following inequality hold to problem (4)–(5),

$$\begin{aligned} \vert w(\chi ,\tau )-\Delta w(\chi ,\tau )\vert \le \left[ \frac{T^{\eta }}{\Gamma (\eta +1)}\right] \epsilon _{0}. \end{aligned}$$

Theorem 1.3

Assuming Lemma 2 holds then the solution of problem (4)–(5) is Ulam-Hyres stable.

Proof

For proof please refer [35]. $\square$

General Procedure of ATIM

This section consists general procedure of ATIM and further its convergences analysis of solution is obtained using Cauchy convergences theorem.

Aboodh Transform Iterative Method

Consider a nonlinear FPDE as,

$$\begin{aligned} D_{t}^{\eta }w(\chi ,\tau )= R(w(\chi ,\tau ))+ Q(w(\chi ,\tau ))+ g(\chi ,\tau ), n-1< \eta \le n, \end{aligned}$$

(13)

with initial conditions,

$$\begin{aligned} w^{(p)}(\chi ,0)=j_{p}(\chi ), p=0,1,2\dots (n-1). \end{aligned}$$

Caputo fractional derivative operator is defined by $D_{t}^{\eta }$ and source term is $g(\chi ,\tau )$, R and Q are linear and nonlinear operator respectively. Operating Aboodh transform on Eq. (13) leads to

$$\begin{aligned} {\mathscr {A}}[D_{t}^{\eta }w(\chi ,\tau )]= {\mathscr {A}}[R(w(\chi ,\tau ))+ Q(w(\chi ,\tau ))+ g(\chi ,\tau )]. \end{aligned}$$

(14)

Using Definition 2.5 and taking inverse of Aboodh transform leads to,

$$\begin{aligned} w(\chi ,\tau )={\mathscr {A}}^{-1}\left[ \frac{1}{v^{\eta }}\left( \sum _{p=0}^{n}\frac{w^{(p)}(0)}{v^{2-\eta +s}}\right) +\frac{1}{v^{\eta }}({\mathscr {A}}[R(w(\chi ,\tau ))+ Q(w(\chi ,\tau ))+ g(\chi ,\tau )])\right] . \end{aligned}$$

(15)

As, through the iterative technique,

$$\begin{aligned} w(\chi ,\tau )=\sum _{p=0}^{\infty } w_{p}(\chi ,\tau ). \end{aligned}$$

(16)

Linear part decompose as,

$$\begin{aligned} R\left( \sum _{p=0}^{\infty } w_{p}(\chi ,\tau )\right) =\sum _{p=0}^{\infty }R\left( w_{p}(\chi ,\tau )\right) . \end{aligned}$$

(17)

The decomposition of nonlinear operator Q is done by NIM,

$$\begin{aligned} Q(w(\chi ,\tau ))&=Q\Bigl (\sum _{p=0}^{\infty }w_{p}(\chi ,\tau )\Bigl ) \nonumber \\&=Q(w_{0}(\chi ,\tau ))+\sum _{p=1}^{\infty }\left( {Q\left( \sum _{j=0}^{p}w_{j}(\chi ,\tau )\right) -Q\left( \sum _{j=0}^{p-1}w_{j}(\chi ,\tau )\right) }\right) . \end{aligned}$$

(18)

Putting Eqs. (17) and (18) in Eq. (16) we get,

$$\begin{aligned} \sum _{p=0}^{\infty } w_{p}(\chi ,\tau )&={\mathscr {A}}^{-1}\left[ \frac{1}{v^{\eta }}\left( \sum _{p=0}^{n} \frac{w^{(p)}(0)}{v^{2-\eta +p}}\right) \right. \nonumber \\&\quad \left. +{\mathscr {A}}[g(\chi ,\tau )]\right] +{\mathscr {A}}^{-1}\left[ \frac{ 1 }{ v ^ { \eta } } {\mathscr {A}}\left[ R(w_{0}(\chi ,\tau )+Q(w_{0}(\chi ,\tau ))\right. \right. \nonumber \\&\quad \left. \left. +\sum _{p=1}^{\infty }R(w_{p}(\chi ,\tau ))+Q\left( \sum _{j=0}^{p} w_{j}(\chi ,\tau )\right) -Q\left( \sum _{j=0}^{p-1} w_{j}(\chi ,\tau )\right) \right] \right] . \end{aligned}$$

(19)

From above scheme, we obtain following iterations,

$$\begin{aligned} w_{0}(\chi ,\tau )&={\mathscr {A}}^{-1}\left[ \frac{1}{v^{\eta }}\left( \sum _{p=0}^{n} \frac{w^{(p)}(0)}{v^{2-\eta +p}}\right) +{\mathscr {A}}[g(\chi ,\tau )]\right] , \quad n-1<\eta \le n . \end{aligned}$$

(20)

$$\begin{aligned} w_{1}(\chi ,\tau )&={\mathscr {A}}^{-1}\left[ \frac{1}{v^{\eta }} A \left[ R(w_{0}(\chi ,\tau ))+Q(w_{0}(\chi ,\tau ))\right] \right] , \end{aligned}$$

(21)

likewise,

$$\begin{aligned} w_{p+1}(\chi ,\tau )&={\mathscr {A}}^{-1}\left[ \frac{1}{v^{\eta }}A \left[ R(w_{p}(\chi ,\tau )+Q\left( \sum _{j=0}^{p}w_{j}(\chi ,\tau )\right) -Q\left( \sum _{j=0}^{p-1} w_{j}(\chi ,\tau )\right) \right] \right] . \end{aligned}$$

(22)

This series solution converges. For convergences analysis following theorem is discussed.

Convergences Analysis

Theorem 1.4

[36] Consider a Banach space B, if there exists L such that $0< L < 1$, $\vert \vert w_{n} \vert \vert$ $\le L \vert \vert w_{n-1} \vert \vert$, then the series solution obtain from ATIM converges to $R_{i} \in B$.

Proof

Consider a sequence $R_{i}$, $i=0,1,...,n.$ given as,

$$\begin{aligned} \left. \begin{aligned}&R_{0}=w_{0}, \\&R_{1}=w_{0}+w_{1}, \\&R_{2}=w_{0}+w_{1}+w_{2},\\&.... \\&R_{n}=w_{0}+w_{1}+w_{2}+...+w_{n}. \end{aligned} \right\} \end{aligned}$$

(23)

We show that this $R_{i}$ is a Cauchy sequence. Using assumption we have,

$$\begin{aligned} \vert \vert R_{n}-R_{n-1} \vert \vert \le \vert \vert w_{n} \vert \vert \le L^{n}w_{0}. \end{aligned}$$

(24)

For all p, q $\in N$,

$$\begin{aligned} \vert \vert R_{p}-R_{q} \vert \vert&= \vert \vert R_{p}-R_{p-1}+R_{p-1}-R_{p-2}+....+R_{q+1}-R_{q} \vert \vert \nonumber \\&\le \vert \vert R_{p}-R_{p-1} \vert \vert + \vert \vert R_{p-1}-R_{p-2} \vert \vert +...+ \vert \vert R_{q+1}-R_{q} \vert \vert \nonumber \\&\le (L_{p}+L^{p-1}+...+L^{q+1})w_{0} \nonumber \\&\le \vert \vert \frac{L^{q+1}(1-L^{p-q})}{1-L} \vert \vert w_{0}, \end{aligned}$$

(25)

where $w_{0}$ is bounded, so

$$\begin{aligned} \lim _{p,q \rightarrow \infty } \vert \vert R_{p}-R_{q} \vert \vert =0. \end{aligned}$$

(26)

So, considered $R_{i}$ is Cauchy sequence in Banach space B, hence solution in Eq. (22) is convergent. $\square$

Numerical Illustrations

Example 5.1

Consider a homogeneous space fractional telegraph equation as [37]

$$\begin{aligned} \frac{\partial ^{2\eta }w}{\partial \chi ^{2\eta }}= \frac{\partial ^{2}w}{\partial \tau ^{2}}+\frac{dw}{\partial \tau }+ w , ~~ \tau \ge 0, 0<\eta \le 1, \end{aligned}$$

(27)

subject to conditions,

$$\begin{aligned} w(\chi ,0)=e^{\chi }, ~w(0,\tau )= e^{-\tau }, ~ w_{\chi }(0,\tau )=e^{-\tau } ,~ {0<\chi <1,}~\tau \ge 0 . \end{aligned}$$

(28)

Exact solution of Eq. (27) is $w(\chi ,\tau )=e^{\chi -\tau }$.

Applying Aboodh Transform on both side Eq. (27) leads to,

$$\begin{aligned} {\mathscr {A}}\left[ \frac{\partial ^{2\eta }w}{\partial \chi ^{2\eta }}\right] = {\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \tau ^{2}}+\frac{dw}{\partial \tau }+ w\right] . \end{aligned}$$

(29)

Using Definition 2.5 on Eq. (29),

$$\begin{aligned} {\mathscr {A}}\left[ w(\chi ,\tau )\right] = \frac{1}{v^{2}}w(0,\tau )+\frac{1}{v^{3}}w_{\chi }(0,\tau )+ \frac{1}{v^{2\eta }} {\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \tau ^{2}}+\frac{dw}{\partial \tau }+ w\right] . \end{aligned}$$

(30)

Inverse Aboodh transform on Eq. (30) leads to,

$$\begin{aligned} w(\chi ,\tau )={\mathscr {A}}^{-1}\left[ e^{-\tau }\left( \frac{1}{v^{2}}+\frac{1}{v^{3}}\right) \right] +{\mathscr {A}}^{-1}\left[ \frac{1}{v^{2\eta }} {\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \tau ^{2}}+\frac{dw}{\partial \tau }+ w \right] \right] . \end{aligned}$$

(31)

Now solving Eq. (31) by procedure of NIM,

$$\begin{aligned} w_{0}(\chi ,\tau )&= e^{-\tau }+ \chi e^{-\tau }, \end{aligned}$$

(32)

$$\begin{aligned} w_{1}(\chi ,\tau )&= {\mathscr {A}}^{-1}\left[ \frac{1}{v^{2\eta }} A\left[ \frac{\partial ^{2}w_{0}}{\partial \tau ^{2}}+\frac{dw_{0}}{\partial \tau }+ w_{0} \right] \right] , \nonumber \\ w_{1}(\chi ,\tau )&= e^{-\tau }\frac{\chi ^{2\eta }}{\Gamma (2\eta +1)}+ e^{-\tau } \frac{\chi ^{2\eta +1}}{\Gamma (2\eta +2)}. \end{aligned}$$

(33)

Similarly,

$$\begin{aligned} w_{2}(\chi ,\tau )&= e^{-\tau }\frac{\chi ^{4\eta }}{\Gamma (4\eta +1)}+ e^{-\tau } \frac{\chi ^{4\eta +1}}{\Gamma (4\eta +2)}. \end{aligned}$$

(34)

Likewise, next approximation,

$$\begin{aligned} w_{3}(\chi ,\tau )&= e^{-\tau }\frac{\chi ^{6\eta }}{\Gamma (6\eta +1)}+ e^{-\tau } \frac{\chi ^{6\eta +1}}{\Gamma (6\eta +2)}. \end{aligned}$$

(35)

In similar manner we can get further approximation. Hence, the approximate solution commuted as,

$$\begin{aligned} w(\chi ,\tau )=e^{-\tau }\left( 1+x+ \frac{\chi ^{2\eta }}{\Gamma (2\eta +1)}+ \frac{\chi ^{2\eta +1}}{\Gamma (2\eta +2)} +\frac{\chi ^{4\eta }}{\Gamma (4\eta +1)} + \frac{\chi ^{4\eta +1}}{\Gamma (4\eta +2)} +\ldots \right) . \end{aligned}$$

(36)

Fig. 1

3-dimensional plot of Example 5.1

Table 1 Comparison of obtained results by ATIM with exact and q-HATM [38] with $\chi =1$ and $\eta =1$

Example 5.2

Considering time fractional telegraph equation in absence of source term as [37],

$$\begin{aligned} \frac{\partial ^{2\eta }w}{\partial \tau ^{2\eta }}+ 2\frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}+w= \frac{\partial ^{2}w}{\partial \chi ^{2}} , ~~ \tau \ge 0,~ 0<\eta \le 1, \end{aligned}$$

(37)

subject to conditions,

$$\begin{aligned} w(\chi ,0)=e^{\chi }, ~ w_{\tau }(\chi ,0)= -2e^{\chi },~ {0<\chi <1} ,~\tau \ge 0. \end{aligned}$$

(38)

Exact solution of Eq. (37) is $w(\chi ,\tau )=e^{\chi -2\tau }$.

Taking Aboodh transform of Eq. (37) leads to,

$$\begin{aligned} {\mathscr {A}}\left[ \frac{\partial ^{2\eta }w}{\partial \tau ^{2\eta }}+2 \frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}+w\right] = {\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \chi ^{2}}\right] . \end{aligned}$$

(39)

Using Definition 2.5 on Eq. (39),

$$\begin{aligned} {\mathscr {A}}\left[ w(\chi ,\tau )\right] = \frac{1}{v^{2}}e^{\chi }-\frac{1}{v^{3}}(2e^{\chi })+\frac{1}{v^{2\eta }}{\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \chi ^{2}}-2 \frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}-w\right] . \end{aligned}$$

(40)

Applying inverse Aboodh transform leads to,

$$\begin{aligned} w(\chi ,\tau )={\mathscr {A}}^{-1}\left[ \frac{e^{\chi }}{v^{2}}-\frac{2e^{\chi }}{v^{3}}\right] +{\mathscr {A}}^{-1}\left[ \frac{1}{v^{2\eta }} {\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \chi ^{2}}-2 \frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}-w\right] \right] , \end{aligned}$$

(41)

now applying procedure of NIM on Eq. (41),

$$\begin{aligned} w_{0}(\chi ,\tau )&= e^{\chi }(1-2\tau ). \end{aligned}$$

(42)

$$\begin{aligned} w_{1}(\chi ,\tau )&= {\mathscr {A}}^{-1}\left[ \frac{1}{v^{2\eta }} {\mathscr {A}}\left[ \frac{\partial ^{2}w_{0}}{\partial \chi ^{2}}-2 \frac{\partial ^{\eta }w_{0}}{\partial \tau ^{\eta }}-w_{0}\right] \right] , \nonumber \\ w_{1}(\chi ,\tau )&= \frac{4e^{\chi }}{\Gamma (\eta +2)}\tau ^{\eta +1}. \end{aligned}$$

(43)

Similarly,

$$\begin{aligned} w_{2}(\chi ,\tau )&= -\frac{8e^{\chi }}{\Gamma (2\eta +2)}\tau ^{2\eta +1}, \end{aligned}$$

(44)

$$\begin{aligned} w_{3}(\chi ,\tau )&= \frac{16e^{\chi }}{\Gamma (3\eta +2)}\tau ^{3\eta +1}. \end{aligned}$$

(45)

In similar manner we can get further approximation.

Hence, the approximate solution commuted as,

$$\begin{aligned} w(\chi ,\tau )=e^{\chi }\left( 1-2\tau + \frac{4e^{\chi }}{\Gamma (\eta +2)}\tau ^{\eta +1}-\frac{8e^{\chi }}{\Gamma (2\eta +2)}\tau ^{2\eta +1}+ \frac{16e^{\chi }}{\Gamma (3\eta +2)}\tau ^{3\eta +1} +\ldots \right) . \end{aligned}$$

(46)

Fig. 2

3-dimensional plot of Example 5.2

Table 2 Comparison of obtained results by ATIM with Exact and q-HATM [38] with $\chi =1$ and $\eta =1$

Example 5.3

Considering 2-dimensional time-fractional telegraph equation [38],

$$\begin{aligned} \frac{\partial ^{2\eta }w}{\partial \tau ^{2\eta }}+3\frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}+2w= \frac{\partial ^{2}w}{\partial \chi ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}},~~ \tau \ge 0,~ 0<\eta \le 1, \end{aligned}$$

(47)

subject to conditions,

$$\begin{aligned} w(\chi ,\gamma ,0)&=e^{\chi +\gamma },~ w_{t}(\chi ,\gamma ,0)=-3e^{\chi +\gamma }, ~ {0<\chi<1, ~0<\gamma <1.} \end{aligned}$$

(48)

Operating Aboodh transform on the both side of Eq. (47) leads to,

$$\begin{aligned} {\mathscr {A}}\left[ \frac{\partial ^{2\eta }w}{\partial \tau ^{2\eta }}+3\frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}+2w\right] = {\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \chi ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}}\right] . \end{aligned}$$

(49)

Using Definition 2.5 on Eq. (49),

$$\begin{aligned} {\mathscr {A}}[w(\chi ,\gamma ,\tau )]= \frac{e^{\chi +\gamma }}{v^2}-\frac{3 e^{\chi +\gamma }}{v^3} + \frac{1}{v^{2\eta }}{\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \chi ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}}-3\frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}-2w \right] . \end{aligned}$$

(50)

Operating inverse Aboodh transform on both side of Eq. (50) leads to,

$$\begin{aligned} w(\chi ,\gamma ,\tau )= e^{\chi +\gamma } -3\tau e^{\chi +\gamma } + {\mathscr {A}}^{-1}\left[ \frac{1}{v^{2\eta }}{\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \chi ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}}-3\frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}-2w \right] \right] . \end{aligned}$$

(51)

Applying procedure of NIM on Eq. (50),

$$\begin{aligned} w_{0}(\chi ,\gamma ,\tau )&=e^{\chi +\gamma }(1-3\tau ), \end{aligned}$$

(52)

$$\begin{aligned} w_{1}(\chi ,\gamma ,\tau )&={\mathscr {A}}^{-1}\left[ \frac{\partial ^{2}w_{0}}{\partial \chi ^{2}}+\frac{\partial ^{2}w_{0}}{\partial \gamma ^{2}}-3\frac{\partial ^{\eta }w_{0}}{\partial \tau ^{\eta }}-2w_{0} \right] , \nonumber \\ w_{1}(\chi ,\gamma ,\tau )&=\frac{9e^{\chi +\gamma }}{\Gamma (\eta +2)}\tau ^{\eta +1}. \end{aligned}$$

(53)

Similarly,

$$\begin{aligned} w_{2}(\chi ,\gamma ,\tau )&=-\frac{27 e^{\chi +\gamma }}{\Gamma (2\eta +2)} \tau ^{2\eta +1}, \end{aligned}$$

(54)

$$\begin{aligned} w_{3}(\chi ,\gamma ,\tau )&=\frac{81 e^{\chi +\gamma }}{\Gamma (3\eta +2)}\tau ^{3\eta +1}. \end{aligned}$$

(55)

Hence, the approximate solution commuted as,

$$\begin{aligned} w(\chi ,\gamma ,\tau )=e^{\chi +\gamma }\left( 1-3\tau + \frac{9}{\Gamma (\eta +2)}\tau ^{\eta +1}-\frac{27}{\Gamma (2\eta +2)}\tau ^{2\eta +1}+\frac{81 }{\Gamma (3\eta +2)}\tau ^{3\eta +1} +\ldots \right) , \end{aligned}$$

(56)

whose exact solution is $w(\chi ,\gamma ,\tau )=e^{\chi +\gamma -3\tau }$.

Fig. 3

3-dimensional plot of Example 5.3

Table 3 Comparison of obtained results by ATIM with Exact and q-HATM [38] with $\chi =\gamma = 1$ and $\eta =1$

Example 5.4

Considering 3-dimensional fractional order time fractional equation as [38],

$$\begin{aligned} \frac{\partial ^{2\eta }w}{\partial \tau ^{2\eta }} +2 \frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}+3w= \frac{\partial ^{2}w}{\partial \chi ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}}+\frac{\partial ^{2}w}{\partial \theta ^{2}},~~ \tau \ge 0,~ 0<\eta \le 1, \end{aligned}$$

(57)

subject to conditions,

$$\begin{aligned} w(\chi ,\gamma ,\theta ,0)&=\sinh \chi {\cdot }\sinh \gamma {\cdot }\sinh \theta ,~ w_{t}(\chi ,\gamma ,\theta ,0)\nonumber \\&=-2\sinh \chi {\cdot }\sinh \gamma {\cdot }\sinh \theta , ~ {0<\chi ,\gamma ,\theta < 1.} \end{aligned}$$

(58)

Operating Aboodh transform on Eq. (57) leads to,

$$\begin{aligned} {\mathscr {A}}\left[ \frac{\partial ^{2\eta }w}{\partial \tau ^{2\eta }} +2 \frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}+3w\right]&= {\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \chi ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}}\right] , \nonumber \\ {\mathscr {A}}\left[ w(\chi ,\gamma ,\theta ,\tau )\right]&= \frac{sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta }{v^2}-\frac{2sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta }{v^{3}}\nonumber \\ {}&\quad +\frac{1}{v^{2\eta }}{\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \chi ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}}+\frac{\partial ^{2}w}{\partial \theta ^{2}}-2 \frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}-3w\right] . \end{aligned}$$

(59)

Inverse Aboodh transform on Eq. (59) leads to,

$$\begin{aligned} w(\chi ,\gamma ,\theta ,\tau )&=sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta -2\tau sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta \nonumber \\&\quad + {\mathscr {A}}^{-1}\left[ \frac{1}{v^{2\eta }}{\mathscr {A}}\left[ \frac{\partial ^{2}w}{\partial \chi ^{2}}+\frac{\partial ^{2}w}{\partial \gamma ^{2}}+\frac{\partial ^{2}w}{\partial \theta ^{2}}-2 \frac{\partial ^{\eta }w}{\partial \tau ^{\eta }}-3w\right] \right] . \end{aligned}$$

(60)

Applying NIM procedure leads to,

$$\begin{aligned} w_{0}(\chi ,\gamma ,\theta ,\tau )&=sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta -2\tau sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta , \end{aligned}$$

(61)

$$\begin{aligned} w_{1}(\chi ,\gamma ,\theta ,\tau )&= \frac{4sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta }{\Gamma (\eta +2)}\tau ^{\eta +1}. \end{aligned}$$

(62)

Similarly,

$$\begin{aligned} w_{2}(\chi ,\gamma ,\theta ,\tau )&=-\frac{8sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta }{\Gamma (2\eta +2)}\tau ^{2\eta +1}, \end{aligned}$$

(63)

$$\begin{aligned} w_{3}(\chi ,\gamma ,\theta ,\tau )&=\frac{16sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta }{\Gamma (3\eta +2)}\tau ^{3\eta +1}. \end{aligned}$$

(64)

Likewise, other approximation can be commuted. Hence, the approximate solution commuted as,

$$\begin{aligned} w(\chi ,\gamma ,\theta ,\tau )&=sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta \Big (1-2\tau + \frac{4}{\Gamma (\eta +2)}\tau ^{\eta +1}-\frac{8}{\Gamma (2\eta +2)}\tau ^{2\eta +1}\nonumber \\&\quad +\frac{16}{\Gamma (3\eta +2)}\tau ^{3\eta +1} +\ldots \Big ). \end{aligned}$$

(65)

The exact solution is $w(\chi ,\gamma ,\theta ,\tau )=e^{-2\tau }sinh\chi {\cdot }sinh\gamma {\cdot }sinh\theta$.

Table 4 Comparison of obtained results by ATIM with Exact and q-HATM [38] with $\chi =\gamma =\theta = 1$ and $\eta =1$

Fig. 4

Approximate solution behavior at distinct order of $\eta$ for Examples 5.1 to 5.4

Fig. 5

Plot of error between successive approximation for Examples 5.1 to 5.4

Results and Discussion

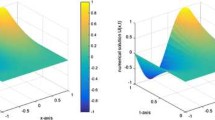
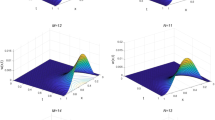
Figure 1a and b shows comparison between obtained approximate solution and exact solution at $\chi =1$, $\eta =1$, for Example 5.1. We have consider the approximation upto 3rd order. It is clear from the graph that the solution obtained from the proposed ATIM coincides with the exact solution. Similarly, for Example 5.2 Figs. 2a and b elaborates the comparison between obtained approximate solution and exact solution for $\chi =1$ and $\eta =1$. It also shows the nature of approximate solution is similar to exact solution. Figures 3a and b elaborate the comparison between obtained approximate solution and exact solution at $\chi =\gamma =1$ and $\eta =1$, for Example 5.3. Likewise, Fig. 3 shows that the approximate and exact solutions coincide. Figures 4a–d explains the nature of approximate solution for different order $\eta =0.7,0.8,0.9,0.98$, and 1. Figure 4a states that with increase in fractional order $\eta$ the approximate solution tends to exact solution at $\eta =1$, for Example 5.1. Similarly, for Example 5.2, Fig. 4b shows that with increasing value of fractional order $\eta$, the approximate solution tends to exact solution at $\eta =1$. Figures 4c and d shows that the approximate solution tends to exact solution as $\eta$ tends to 1, for Examples 5.3 and 5.4, respectively. Figure 5a shows the error between successive approximation at $\chi =0.5$, which elaborates that as number of approximation increase error between successive approximation decreases. Hence solution obtained by the proposed method converges. A similar results are elaborated by Fig. 5b–d for Examples 5.2 to 5.4. Hence, the solution obtained by ATIM in all 4 examples converges. The efficiency of proposed ATIM method is shown from Tables 1, 2, 3 and 4 by comparing it with exact solution and previously published works.

Conclusions

We have successfully implemented the ATIM for multidimensional telegraph equation. The proposed method doesn’t require tedious calculation and is free from linearization or perturbation parameter, which makes it more useful for nonlinear problems. It also takes significantly less memory and less calculation time. Uniqueness and existence of proposed method is shown. Also, stability is stated using Ulam-Hyres theorem. Cauchy theorems give convergent analysis of the solution obtained by ATIM. Graphs and tabular representation show that the proposed method is efficient in solving fractional differential equations. The successive error between approximations states the convergence of the solution.