New Fractional Modelling and Simulations of Prey–Predator System with Mittag–Leffler Kernel

Abstract

Predator–prey models are regarded as the structural blocks of the bio- and ecosystems as biomasses are headed by their resource masses. During the current investigation, we examine the impact of a contagious disease on the growth of ecological varieties. We study a non-integer-order predator–prey system by applying the Atangana–Baleanu–Caputo derivative. We use an effective techniqueto get the numerical solutions and to discover the system’s dynamical behavior using different values of fractional order which indicates that how how the proposed scheme is suitable to solve the dynamical systems containing the derivatives with non-singular kernels. Moreover, the existence of the results is given utilizing the fixed-point theorem. Also, diagrams via numerical simulations of the approximate solutions are shown in different dimensions.

Introduction

The evolution of the qualitative investigation of ODEs is arising to analyze various enigmas in mathematical biology and related areas. Designing the model to the community dynamics of a prey–predator problem is an example of the significant and impressive aim in mathematical biology, that has undergone comprehensive reflection by many scholars [1,2,3,4,5,6]. During real universe, several classes of prey and predator classes possess a living past which is formed of at least couple steps: immature and mature, and every step possesses various behavioral characteristics. Therefore, some activities of step-building prey–predator systems are presented in many articles in the literature [7,8,9,10,11,12]. Contagious diseases occur if infected external bodies penetrate into the individual body.

Table 1 Vital parameters involved in the eco-epidemiological system

Fig. 1

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=1.5, \xi _3=0.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$

Fig. 2

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=1.5, \xi _3=0.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$

Fig. 3

Chaotic behaviour of solutions for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=1.5, \xi _3=0.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$

Fig. 4

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=0.5, \xi _3=0.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$

Fig. 5

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=0.5, \xi _3=0.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$

Fig. 6

Chaotic behaviour of solutions for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=0.5, \xi _3=0.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$

Fig. 7

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=3.5, \xi _2=3.05, \xi _3=0.8, \xi _4=2.5, \xi _5=0.15, \xi _6=0. 5$ and $\xi _7=0.3$

The mentioned pathogens could be bacteria, microorganisms, and parasites. These bodies are transferred by virus from a different individual, creatures, polluted food, or disposal to any of the environmental constituents which are infected by any of the mentioned organisms. These diseases have several signs in body, containing raised one warmth and anxiety, moreover to additional traits which vary regarding the position of contamination, nature, and hardness of the infection. It is permissible to possess a disease that produces moderate signs, and hence it does not require to be solved. Indeed, there are severe situations that may affect mortality. Also, they probably influence the population scale of several kinds. In a more dangerous situation, some species probably indeed become dead because of some fatal infections that occurred in some extremely rational populations. Mathematical systems for foretelling the progression of varieties of such pathogen have been utilized in an escalating way in the latest decades. The biological species are most susceptible to any disease that can affect the development of species. We study the predator–prey interplay. Such disease is able to influence the power of predators and performance of shooting, which places some predators at threat of extirpation. During the literature review, several investigations were examined on the predator–prey interplay in bearing the contagious infections [12,13,14,15,16].

Fig. 8

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=3.5, \xi _2=3.05, \xi _3=0.8, \xi _4=2.5, \xi _5=0.15, \xi _6=0. 5$ and $\xi _7=0.3$

Fig. 9

Chaotic behaviour of solutions for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=3.5, \xi _2=3.05, \xi _3=0.8, \xi _4=2.5, \xi _5=0.15, \xi _6=0. 5$ and $\xi _7=0.3$

Fig. 10

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=0.55, \xi _2=0.5, \xi _3=3.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 11

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=0.55, \xi _2=0.5, \xi _3=3.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 12

Chaotic behaviour of solutions for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=0.55, \xi _2=0.5, \xi _3=3.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 13

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=0.75, \xi _2=0.5, \xi _3=3.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 14

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=0.75, \xi _2=0.5, \xi _3=3.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 15

Chaotic behaviour of solutions for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=0.75, \xi _2=0.5, \xi _3=3.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 16

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=0.95, \xi _2=0.5, \xi _3=3.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 17

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=0.95, \xi _2=0.5, \xi _3=3.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 18

Chaotic behaviour of solutions for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=0.95, \xi _2=0.5, \xi _3=3.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 19

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.2, \xi _2=0.5, \xi _3=3.5, \xi _4=0.05, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 20

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.2, \xi _2=0.5, \xi _3=3.5, \xi _4=0.05, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 21

Chaotic behaviour of solutions for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.2, \xi _2=0.5, \xi _3=3.5, \xi _4=0.05, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 22

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=3.5, \xi _2=1.5, \xi _3=3.5, \xi _4=0.05, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 23

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=3.5, \xi _2=1.5, \xi _3=3.5, \xi _4=0.05, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 24

Chaotic behaviour of solutions for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=3.5, \xi _2=1.5, \xi _3=3.5, \xi _4=0.05, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=1.5$

Fig. 25

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=1.5, \xi _3=0.5, \xi _4=0.05, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$

Fig. 26

Numerical simulations for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=1.5, \xi _3=0.5, \xi _4=0.05, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$

Fig. 27

Chaotic behaviour of solutions for $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=1.5, \xi _3=0.5, \xi _4=0.05, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$

On the other hand, there are various approaches that the predators examine for reaching prosperous hunting. Predator assistance is an efficient approach that several predators seek a unique prey. Such an approach can be so beneficial in degrading the hunting failure scale. Numerous anglers perform in the aforementioned approach. For instance, some animals such as lions, and dogs are distinguished for the great ability scale in this manner. Numerical solution of two- sided space-fractional wave equation using finite difference method in [17]. Modelling of such particular performance of predator was firstly formed in [18]. wherein an uncomplicated pattern was employed for representing such collaboration. There were studies that investigated such performance in the predator–prey interplay [19,20,21,22,23,24,25,26,27]. Regarding the achieved outcomes in [28], time-fractional derivative possesses wide applicability for explaining various real-life conditions, that is recognized with memory impact for the dynamical model; memory speed is named for non-integer order, memory function of kernel of non-integer derivative. The mentioned derivative Atangana–Baleanu–Caputo (ABC) is applied to model several phenomena [29,30,31,32]. More studies about the applications of fractional operators can be found in [33,34,35,36,37]. Regarding the mentioned inclinations, we examine the eco-epidemiological system given below:

$$\begin{aligned} \begin{aligned}&\frac{\textrm{d}u_1}{\textrm{d}t}=f_1(u_1,u_2,u_3)=\xi _1 (u_1(t)+u_2(t))-(\xi _2+\xi _3 u_3(t))u_3(t)u_1(t)\\&\qquad \qquad -\xi _4 u_1(t)u_2(t)-\xi _5 u_1(t) ,\\&\frac{\textrm{d}u_2}{\textrm{d}t}=f_2(u_1,u_2,u_3)=\xi _4 u_1(t)u_2(t)-(\xi _2+\xi _3 u_3(t))u_3(t)u_2(t) - \xi _5 u_2(t),\\&\frac{\textrm{d}u_3}{\textrm{d}t}=f_3(u_1,u_2,u_3)=\xi _6 (\xi _2+\xi _3 u_3(t))u_3(t)(u_1(t)+u_2(t))-\xi _7 u_3(t), \end{aligned} \end{aligned}$$

(1)

where it may be noted that the state variables $u_1 (t), u_2 (t),$ and $u_3 (t)$ respectively stand for densities of susceptible prey, infected prey, and the predator populations. Regarding initial conditions (ICs), we have $u_1(0)=u_{1,0}(t), u_2(0)=u_{2,0}(t)$ and $u_3(0)=u_{3,0}(t)$. Moreover, one can see that there are 7 parameters playing the vital role for the dynamics of the model’s behavior. Description of these parameters is detailed in the Table 1.

The next section is selected to implement some fundamental definitions to comprehend remaining analysis carried out in other forthcoming sections.

Essential Definitions

Definition 2.1

Assume that $X \in H^1 ( a, b ), a < b$ and $\sigma \in [0, 1].$ Therefore, the Atangana-Baleanu derivative for X in the Caputo structure is written as

$$\begin{aligned} {{}^{ABC}}{\mathcal {D}}^\sigma X(t)= \frac{W(\sigma )}{1-\sigma }\int _a^t X^{\prime }(y)E_\sigma \left[ -\sigma \frac{(t-\zeta )^\sigma }{1-\sigma }\right] \textrm{d}\zeta , \end{aligned}$$

(2)

where $E_\sigma$ is known as the Mittag–Leffler function explained in [33, 34].

$$\begin{aligned} E_\sigma (z)=\sum _{n=0}^\infty \frac{z^n}{\Gamma (n\sigma +1)}, \end{aligned}$$

Theorem 2.2

We take into consideration the differential equation containing the Atangana-Baleanu differential operator [35]:

$$\begin{aligned} {{}^{ABC}}_0{\mathcal {D}}_t^\sigma f(t)=u(t). \end{aligned}$$

(3)

The foregoing equation possesses a unique answer if the subsequent theorem is performed

$$\begin{aligned} f(t)= \frac{1-\sigma }{W(\sigma )}u(t)+\frac{\sigma }{W(\sigma )\Gamma (p)}\int _0^t u(\zeta )(t-\zeta )^{\sigma -1}\textrm{d}\zeta , \end{aligned}$$

The common time-fractional order of the differential equation described in (7) is a problem of the form

$$\begin{aligned} {\mathcal {D}}^\sigma X(t)=F(X(t),t), \sigma \in (0,1), \end{aligned}$$

(4)

Analysis by Non-integer Order

We suppose that $\mathfrak {B}= {\mathcal {B}}(L) \times {\mathcal {B}}(L)$, which ${\mathcal {B}}(L)$ named continuous Branch function on interval L containing

$$\begin{aligned} \Vert u_1,u_2,u_3 \Vert = \Vert u_1 \Vert +\Vert u_2 \Vert +\Vert u_3 \Vert \Vert , \end{aligned}$$

which $\Vert u_1 \Vert = \sup \left\{ \vert u_1(t): t\in L\right\}$, $\Vert u_2 \Vert = \sup \left\{ \vert u_2(t): t\in L\right\}$ and $\Vert u_3 \Vert = \sup \left\{ \vert u_3(t): t\right. \left. \in L\right\}$, Following, we develop the problem (1) by interchanging the traditional derivative by ABC one:

$$\begin{aligned} \begin{aligned}&{{}^{ABC}}_0{\mathcal {D}}_t^\sigma u_1(t)=\xi _1 (u_1(t)+u_2(t))-(\xi _2+\xi _3 u_3)u_3(t)u_1(t)-\xi _4 u_1(t)u_2(t)-\xi _5 u_1(t),\\&{{}^{ABC}}_0{\mathcal {D}}_t^\sigma u_2(t)=\xi _4 u_1(t)u_2(t)-(\xi _2+\xi _3 u_3)u_3(t)u_2(t),\\&{{}^{ABC}}_0{\mathcal {D}}_t^\sigma u_3(t)=\xi _5 (\xi _2+\xi _3 u_3(t))u_3(t)(u_1(t)+u_2(t))-\xi _5, \end{aligned} \end{aligned}$$

(5)

Regarding ICs

$$\begin{aligned} u_1(0)=u_{1,0}(t), u_2(0)=u_{2,0}(t), u_3(0)=u_{3,0}(t), \end{aligned}$$

(6)

We have

$$\begin{aligned} u_1(t)-u_1(0)= & {} \frac{1-\sigma }{W(\sigma )}\left[ \xi _1 (u_1(t)+u_2(t))-(\xi _2+\xi _3 u_3)u_3(t)u_1(t)-\xi _4 u_1(t)u_2(t)-\xi _5 u_1(t)\right] \nonumber \\{} & {} +\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t (t-\zeta )^{\sigma -1} \times \left[ \xi _1 (u_1(t)+u_2(t))-(\xi _2+\xi _3 u_3)u_3(t)u_1(t)\right. \nonumber \\ {}{} & {} \left. -\xi _4 u_1(t)u_2(t)-\xi _5 u_1(t)\right] \textrm{d}\zeta , \nonumber \\ u_2(t)-u_2(0)= & {} \frac{1-\sigma }{W(\sigma )}\left[ \xi _4 u_1(t)u_2(t)-(\xi _2+\xi _3 u_3)u_3(t)u_2(t)\right] \nonumber \\{} & {} +\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t (t-\zeta )^{\sigma -1} \times \left[ \xi _4 u_1(t)u_2(t)-(\xi _2+\xi _3 u_3)u_3(t)u_2(t)\right] \textrm{d}\zeta , \nonumber \\ u_3(t)-u_3(0)= & {} \frac{1-\sigma }{W(\sigma )}\left[ \xi _5 (\xi _2+\xi _3 u_3(t))u_3(t)(u_1(t)+u_2(t))-\xi _5\right] \nonumber \\{} & {} +\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t (t-\zeta )^{\sigma -1} \times \left[ \xi _6 (\xi _2+\xi _3 u_3(t))u_3(t)(u_1(t)+u_2(t))-\xi _7 u_3(t)\right] \textrm{d}\zeta , \quad \end{aligned}$$

(7)

Now, we take

$$\begin{aligned} \begin{aligned}&{\mathcal {B}}_1(u_1,t)=\xi _1 (u_1(t)+u_2(t))-(\xi _2+\xi _3 u_3)u_3(t)u_1(t)-\xi _4 u_1(t)u_2(t)-\xi _5 u_1(t)\\&{\mathcal {B}}_2(u_2,t)=[\xi _4 u_1(t)u_2(t)-(\xi _2+\xi _3 u_3)u_3(t)u_2(t)\\&{\mathcal {B}}_3(u_3,t)=\xi _6 (\xi _2+\xi _3 u_3(t))u_3(t)(u_1(t)+u_2(t))-\xi _7 u_3(t)\\ \end{aligned} \end{aligned}$$

(8)

Beside, we provide the subsequent result.

Lemma 3.1

The kernels ${\mathcal {B}}_i(u_i,t)$, for $i = 1, 2, 3$ hold the Lipschitz condition for $0 \le {\mathcal {B}}_i(u_i,t) < 1, i = 1, 2, 3$.

Proof

Opening by $i = 2$ we own ${\mathcal {B}}_2(u_1,t)= \xi _4 u_1(t)u_2(t)-(\xi _2+\xi _3 u_3)u_3(t)u_2(t)$. Let $u_1$ and $u_1^{*}$, the we own

$$\begin{aligned}{} & {} \Vert {\mathcal {B}}_2(u_1,t)-{\mathcal {B}}_2(u_1^{*},t)\Vert =\Vert - \xi _4 \left\{ u_2(t) - u_2^{*}(t)\right\} \Vert \nonumber \\{} & {} \quad \le \Vert \xi _4 \Vert \Vert u_2(t)- u_2^{*}(t)\Vert \le G_2 \Vert u_2(t)- u_2^{*}(t)\Vert \end{aligned}$$

(9)

which $G_2 = \xi _4$. Take $m_1 = \max _{t\in L}\Vert u_1(t)\Vert$, $m_2 = \max _{t\in L}\Vert u_2(t)\Vert$ and $m_3 = \max _{t\in L}\Vert u_3(t)\Vert$ be limited functions, so

$$\begin{aligned} \Vert {\mathcal {B}}_1(u_2,t) - {\mathcal {B}}_1(u_2^{*},t)\Vert \le G_2 \Vert u_2(t)- u_2^{*}(t) \Vert \end{aligned}$$

resembling phrases for components $x_i$, for $i = 1, 3$ to get $\Vert {\mathcal {B}}_i(u_i,t) - {\mathcal {B}}_i(u_i^{*},t)\Vert \le G_i \Vert u_i(t), u_i^{*}(t) \Vert$, for $i = 1, 3$. Hence, the Lipschitz condition works for ${\mathcal {B}}_2$, and contraction works for $0 \le G_2 < 1$. Using the considered kernels (7) gives

$$\begin{aligned} \begin{aligned} u_1(t)=u_1(0)+\frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_1(u_1,t)+\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t(t-\zeta )^{\sigma -1}{\mathcal {B}}_1(\zeta ,u_1)\textrm{d}\zeta ,\\ u_2(t)=u_2(0)+\frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_2(u_2,t)+\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t(t-\zeta )^{\sigma -1}{\mathcal {B}}_2(\zeta ,u_2)\textrm{d}\zeta ,\\ u_3(t)=u_3(0)+\frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_3(u_3,t)+\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t(t-\zeta )^{\sigma -1}{\mathcal {B}}_3(\zeta ,u_3)\textrm{d}\zeta , \end{aligned} \end{aligned}$$

(10)

and

$$\begin{aligned} \begin{aligned}&u_{1,n}(t)=\frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_1(u_{1,n-1},t)+\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t(t-\zeta )^{\sigma -1}{\mathcal {B}}_1(\zeta ,u_{1,n-1})\textrm{d}\zeta ,\\&u_{2,n}(t)=\frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_2(u_{2.n-1},t)+\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t(t-\zeta )^{\sigma -1}{\mathcal {B}}_2(\zeta ,u_{2,n-1})\textrm{d}\zeta ,\\&u_{3,n}(t)=\frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_3(u_{3,n-1},t)+\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t(t-\zeta )^{\sigma -1}{\mathcal {B}}_3(\zeta ,u_{}3,n-1)\textrm{d}\zeta , \end{aligned} \end{aligned}$$

(11)

Then, we have

$$\begin{aligned} Z1_n(t)\equiv u_{1,n}(t)-u_{1,n-1}(t)= & {} \, \frac{1-\sigma }{W(\sigma )}\left[ {\mathcal {B}}_1(u_{1,n-1},t)-{\mathcal {B}}_1(u_{1,n-2},t)\right] \nonumber \\{} & {} +\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t (t-\zeta )^{\sigma -1}\left[ {\mathcal {B}}_1(\zeta ,u_{1,n-1})-{\mathcal {B}}_1(\zeta ,u_{1,n-2})\right] \textrm{d}\zeta ,\nonumber \\ Z2_n(t)\equiv u_{2,n}(t)-u_{2,n-1}(t)= & {} \, \frac{1-\sigma }{W(\sigma )}\left[ {\mathcal {B}}_2(u_{2,n-1},t)-{\mathcal {B}}_2(u_{2,n-2},t)\right] \nonumber \\{} & {} +\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t (t-\zeta )^{\sigma -1}\left[ {\mathcal {B}}_2(\zeta ,u_{2,n-1})-{\mathcal {B}}_2(\zeta ,u_{2,n-2})\right] \textrm{d}\zeta ,\nonumber \\ Z3_n(t)\equiv u_{3,n}(t)-u_{3,n-1}(t)= & {} \,\frac{1-\sigma }{W(\sigma )}\left[ {\mathcal {B}}_3(u_{3,n-1},t)-{\mathcal {B}}_3(u_{3,n-2},t)\right] \nonumber \\{} & {} +\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t (t-\zeta )^{\sigma -1}\left[ {\mathcal {B}}_3(\zeta ,u_{3,n-1})-{\mathcal {B}}_3(\zeta ,u_{3,n-2})\right] \textrm{d}\zeta ,\nonumber \\ \end{aligned}$$

(12)

we state that

$$\begin{aligned} u_{i,n}=\sum _{j=1}^n Zi_j (t), i=1,2,3. \end{aligned}$$

Now, we take (12) and use the norm to have

$$\begin{aligned} \begin{aligned} \Vert Z1_n \Vert&= \Vert u_{1,n}(t)-u_{1,n-1}(t)\Vert \le \frac{1-\sigma }{W(\sigma )}\Vert {\mathcal {B}}_1(u_{1,n-1},t)-{\mathcal {B}}_1(u_{1,n-2},t)\Vert +\frac{p}{W(\sigma )\Gamma (\sigma )}\\&\quad \times \Vert \int _0^t (t-\zeta )^{\sigma -1}\left[ {\mathcal {B}}_1(u_{1,n-1},t)-{\mathcal {B}}_1(u_{1,n-2},t) \right] \textrm{d}\zeta \Vert . \end{aligned} \end{aligned}$$

(13)

To satisfy the Lipschitz condition, we have

$$\begin{aligned} \begin{aligned}&\Vert u_{1,n}(t)- u_{1,n-1}(t)\Vert \le \frac{1-\sigma }{W(\sigma )}\chi _1 \Vert u_{1,n-1}-u_{1,n-2}\Vert \\&\quad +\frac{p}{W(\sigma )\Gamma (\sigma )}\times \chi _1 \int _0^t (t-\zeta )^{\sigma -1}\Vert u_{1,n-1}-u_{1,n-2}\Vert \textrm{d}\zeta , \end{aligned} \end{aligned}$$

(14)

and

$$\begin{aligned} \Vert Z1_n\Vert \le \frac{1-\sigma }{W(\sigma )}\chi _1 \Vert Z1_{n-1}\Vert +\frac{\sigma }{W(\sigma )\Gamma (\sigma )} \times \chi _1 \int _0^t (t-\zeta )^{\sigma -1}\Vert Z1_{n-1}(\zeta )\Vert \textrm{d}\zeta , \end{aligned}$$

(15)

Equivalent expressions guard for rest elements:

$$\begin{aligned} \Vert Zi_n\Vert \le \frac{1-\sigma }{W(\sigma )}\chi _1 \Vert Zi_{n-1}\Vert +\frac{\sigma }{W(\sigma )\Gamma (\sigma )} \times \chi _1 \int _0^t (t-\zeta )^{\sigma -1}\Vert Zi_{n-1}(\zeta )\Vert \textrm{d}\zeta , \ \ i= 2,3, \nonumber \\ \end{aligned}$$

(16)

We take solutions $X_1 ( t ), X_2 ( t )$ and $X_3 ( t )$ exist for model (5) that indicates

$$\begin{aligned} \begin{aligned}&\Vert u_1(t)-X_1(t)\Vert \le \frac{1-\sigma }{W(\sigma )}\left[ {\mathcal {B}}_1(u_1,t)-{\mathcal {B}}_1(X_1,t)\right] \\&\qquad + \frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t (t-\zeta )^{\sigma -1}\left[ {\mathcal {B}}_1(u_1,t)-{\mathcal {B}}_1(X_1,t)\right] \textrm{d}\zeta \\&\quad \le \frac{1-\sigma }{W(\sigma )}\Vert {\mathcal {B}}_1(u_1,t)-{\mathcal {B}}_1(X_1,t)\Vert \\&\qquad +\frac{\sigma }{W(\sigma )\Gamma (\sigma )}\int _0^t (t-\zeta )^{\sigma -1}\Vert [{\mathcal {B}}_1(u_1,t)-{\mathcal {B}}_1(X_1,t)\Vert \textrm{d}\zeta , \end{aligned} \end{aligned}$$

(17)

By regarding traits of the Lipschitz condition yields in

$$\begin{aligned} \Vert u_1(t)-X_1(t)\Vert \le \frac{1-\sigma }{W(\sigma )}\chi _1\Vert u_1(t)-X_1(t)\Vert +\frac{\chi _1 t^\sigma }{W(\sigma )\Gamma (\sigma )}\Vert u_1(t)-X_1(t)\Vert \end{aligned}$$

(18)

which results

$$\begin{aligned} \Vert u_1(t)-X_1(t)\Vert \left[ 1- \frac{\chi _1 (1-\sigma )}{W(\sigma )}+\frac{\chi _1 t^\sigma }{W(\sigma )\Gamma (\sigma )}\right] \le 0 \end{aligned}$$

(19)

with $\Vert u_1(t)-X_1(t)\Vert =0$, it indicates $u_1 (t) = X_1 (t)$. Alike phrases exist for segments $u_i (t), i = 2, 3$.Consequently, the fractional problem (5) owns a unique answer. $\square$

Numerical Scheme

Now, we will apply the numerical technique to resolve the problem for simulations. The method has the following form:

$$\begin{aligned} \begin{aligned} u_{n+1}&=u_0 + \frac{1-\sigma }{W(\sigma )}f(u(t_n),t_n)+\frac{\sigma }{W(\sigma )}\sum _{q=0}^n\left\{ \frac{h^\sigma f(u_q , t_q)}{\Gamma (\sigma +2)}a_n\right. \\&\quad \left. -\frac{h^\sigma f(u_{q-1},t_{q-1})}{\Gamma (\sigma +2)}b_n \right\} +E_n^\sigma , \end{aligned} \end{aligned}$$

(20)

where $a_n=(n+1-q)^\sigma (n-q+2+\sigma )-(n-q)^\sigma (n-q+2+2\sigma )$ and $b_n=(n+1-q)^{\sigma +1}-(n-1)^\sigma (n-q+1+\sigma )$ and the remaining term $E_n^p$ is expressed by

$$\begin{aligned} E_n^\sigma = \frac{\sigma }{W(\sigma )\Gamma (\sigma )}\sum _{q=0}^n\int _{t_q}^{t_{q-1}}\frac{(\zeta -t_q)(\zeta -t_{q-1})}{2}\frac{\partial ^2}{\partial \zeta ^2}\times \left[ f(u(\zeta ),\zeta )\right] _{\zeta =\lambda _\zeta }(t_{n+1 }-\zeta )^{\sigma -1}\textrm{d}\zeta , \nonumber \\ \end{aligned}$$

(21)

So, exercising the kernels, Eq. (10) changes to the following

$$\begin{aligned} \begin{aligned} u_1(t)=u_1(0)+\frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_1(u_1(t),t)+\frac{\sigma }{W(\sigma )\Gamma (\sigma )} \int _0^t (t-\zeta )^{\sigma -1}{\mathcal {B}}_1(\zeta ,u_1(\zeta ))\textrm{d}\zeta ,\\ u_2(t)=u_2(0)+\frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_2(u_2(t),t)+\frac{\sigma }{W(\sigma )\Gamma (\sigma )} \int _0^t (t-\zeta )^{\sigma -1}{\mathcal {B}}_2(\zeta ,u_2(\zeta ))\textrm{d}\zeta ,\\ u_3(t)=u_3(0)+\frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_3(u_3(t),t)+\frac{\sigma }{W(\sigma )\Gamma (\sigma )} \int _0^t (t-\zeta )^{\sigma -1}{\mathcal {B}}_3(\zeta ,u_3(\zeta ))\textrm{d}\zeta . \end{aligned} \end{aligned}$$

(22)

Thus, exercising the technique given in (20) at $t=t_{n+1}$, we own

$$\begin{aligned} \begin{aligned} u_{1,n+1}&=u_{1,0}+ \frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_1(u_1(t_n),t_n)+\frac{\sigma }{W(\sigma )}\sum _{q=0}^n\left\{ \frac{h^\sigma {\mathcal {B}}_1(u_{1,q},t_q)}{\Gamma (\sigma +2)}a_n \right. \\&\quad \left. - \frac{h^\sigma {\mathcal {B}}_1(u_{1,q-1},t_{q-1})}{\Gamma (\sigma +2)} b_n \right\} +{{}^1}E_n^\sigma ,\\ u_{2,n+1}&=u_{2,0}+ \frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_2(u_2(t_n),t_n)+\frac{\sigma }{W(\sigma )}\sum _{q=0}^n\left\{ \frac{h^\sigma {\mathcal {B}}_2(u_{2,q},t_q)}{\Gamma (\sigma +2)}a_n \right. \\&\quad \left. - \frac{h^p{\mathcal {B}}_2(u_{2,s-1},t_{s-1})}{\Gamma (p+2)} b_n \right\} +{{}^2}E_n^\sigma ,\\ u_{3,n+1}&=u_{3,0}+ \frac{1-\sigma }{W(\sigma )}{\mathcal {B}}_3(u_3(t_n),t_n)+\frac{\sigma }{W(\sigma )}\sum _{q=0}^n\left\{ \frac{h^\sigma {\mathcal {B}}_3(u_{3,q},t_q)}{\Gamma (\sigma +2)}a_n \right. \\&\quad \left. - \frac{h^p{\mathcal {B}}_3(u_{3,q-1},t_{q-1})}{\Gamma (\sigma +2)} b_n \right\} +{{}^3}E_n^\sigma ,\\ \end{aligned} \end{aligned}$$

(23)

by $a_n=(n+1-q)^\sigma (n-q+2+\sigma )-(n-q)^\sigma (n-q+2+2\sigma )$, $b_n=(n+1-q)^{\sigma +1}-(n-q)^p(n-q+1+\sigma )$ and ${{}^i} E_n^\sigma$ for $i = 1, 2, 3$ is depicted as

$$\begin{aligned} {{}^i}E_n^\sigma =\frac{\sigma }{W(\sigma )\Gamma (p)}\sum _{q=0}^n \int _{t_q}^{t_{q-1}}\frac{(\zeta -t_q)(\zeta -t_{q-1})}{2}\frac{\partial ^2}{\partial \zeta ^2}\left[ {\mathcal {B}}_i(u(\zeta ),\zeta )\right] _{\zeta =\lambda _\zeta }(t_{n+1}-\zeta )^{\sigma -1}\textrm{d}\zeta , \nonumber \\ \end{aligned}$$

(24)

Numerical Experiments

Now, we use the proposed numerical scheme [38] as discussed in the above-mentioned section to get the approximate solutions of the eco-epidemiological system as suggested in the present study under the novel fractional operator with the name of ABC. We solve the system for different values of fractional order $\sigma$. Figures 1, 2 and 3 show the results for different values of $\sigma$ and also for different values of the ICs including $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, v_2=1.5, \xi _3=0.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$. The fractional orders taken for these figures are 0.95, 0.96, 0.97 and 0.98. Indeed, the Figs. 4, 5 and 6 are dedicated to depict the results for $\sigma$ values and with ICs given as $u_1(0)=0.01, u_2(0)=1.1$ and $u_3(0)=0.05$ for $\xi _1=1.5, \xi _2=0.5, \xi _3=0.5, \xi _4=0.5, \xi _5=0.5, \xi _6=0.5$ and $\xi _7=0.5$; successfully. Similarly, Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 and 27 are obtained to show the results for $\xi _1, \xi _2, \xi _3, \xi _4, \xi _5, \xi _6$ and $\xi _7$ along with the selected fractional orders for the parameter $\sigma >0$.

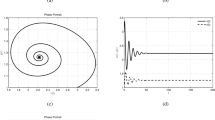
In the Fig. 1, each state variable is simulated over considerably large time interval [0, 500] to understand dynamics of their behaviour. It is observed that the densities of susceptible prey, and predator populations highly fluctuate under selected ICs and the parameters whereas the density of the infected prey sharply decrease over a very small time interval and then goes to vanish as quickly as possible and this situation occurs because susceptible and the predator population are at greater variation.

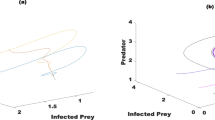
If we closely look at the Fig. 2 then we realize that that patterns like limit cycles occur in the phase portrait forms under different values of $\sigma$ and the parameters. Some strange chaotic type behavior is observed in the figure which is not possible to obtain with classical version of the eco-epidemiological system, that is, when $\sigma = 1$. Similarly, Fig. 3 shows 3-dimensional plot for the underlying system wherein, once again, chaotic type behavior with predator–prey limit cycles is observed. This phenomenon is highly obvious in natural situations as well. Thus, it is said that ABC operator is capable enough to capture the most natural occurrences in the world.

The Fig. 4 is obtained with a slight variation in the $\xi _2$ parameter that appears in the hunting cooperation functional as described in the Table 1. By decreasing $\xi _2$ from 1.5 to 0.5 in the Fig. 4, it is observed that the peaks of the fluctuations within the susceptible prey and predator populations decrease including the peak in the infected prey. However, there are still limit cycles having varying structures are observed as can be seen in the Figs. 5 (2D phase-plane diagrams) and 6 (3 dimensional dynamics). While keeping the ICs same and varying some values of the parameters, we observe drastic change in the dynamics of the eco-epidemiological system as can be seen in the time series plots in the Fig. 7 wherein one can note that the not only peak of fluctuations decrease but the infected prey slightly increase also. One may also note that as value of fractional order $\sigma$ approaches 1, the fluctuations increase. Some interesting limit cycles in the form of phase-planes and 3 dimensional plots are also depicted in the Figs. 8 and 9; respectively.

Looking at the Fig. 10, one can observe that there comes huge change in the behavior of all three populations when parameters are varied particularly the parameters $\xi _3$ and $\xi _7$ with little bit high values while ICs and the fractional order $\sigma$ are still same as considered in previous figures. Limit cycles as shown in the Fig. 11 are reduced in size and this happens due to the fact that now there are not many fluctuations in the populations. Similarly, the Fig. 12 refers the chaotic behavior that lasts for smaller interval of time.

Likewise, upon carrying out numerous other simulations of the eco-epidemiological system as suggested in the present study under the novel fractional operator with the name of ABC, we have obtained interesting dynamics and patterns that were not not encountered with operators having no memory such as those classical ones also called integer-order derivatives. These other simulations based upon time series, phase-portraits and 3 dimensional structures can be visualized in the Figs. 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 and 27 wherein different parameters’ values are taken into consideration in order to obtain the various kinds of behavior for the system via ABC operator.

Conclusion

In this research study, numerical simulations of the Prey–Predator system is investigated using the ABC operator. We used the theorem of fixed-point to establish the occurrence and uniqueness of the results of the underlying system. Employing numerical approach, solutions of the system are produced that depict quite interesting dynamical features not possible to achieve under the classical approach of differential calculus. To understand the influence of fractional order $\sigma$, numerical investigations are illustrated under engaging various fractional orders of $\sigma$. To explain the chaotic behavior in deep, we have tried various values of the involved parameters in the model so that the state variables like susceptible prey, infected prey, and the predator populations could be visualized under ABC operator with different values of $\sigma$. It may be noted that such detailed analysis under the ABC operator has not been previously encountered in the existing literature for the eco-epidemiological system. Future studies would include the analysis of the discussed system with another operator called the Caputo-Fabrizio operator and some optimal control theory would also be discussed in the realm of fractional calculus.