Fractional-Order Dengue Disease Epidemic Model in Nepal

Abstract

The dengue disease epidemiological patterns of Nepal have become a geographical challenge. It is one of the emerging public health issues in the country. In Nepal, the disease has been reported since 2004 in both tropical and sub-tropical regions. In this work, the dengue disease epidemic model is formulated by using fractional-order derivatives. The least-squares method is used for estimation of the parameters with the help of the classical compartmental model of the dengue infections recorded in the year 2019, which is the largest-ever outbreak to occur in Nepal. The existence and uniqueness of a non-negative solution are discussed for the fractional-order model. An epidemiologically important dimensionless number, $R_0$ is obtained using the next-generation method. Two equilibriums disease free and endemic points are obtained and their stability is studied. The Euler’s method is implemented to solve the fractional-order model numerically. The numerical results suggest that the fractional model fits better with an appropriate choice of the memory level, $\alpha$ than the classical model based on the real data of Nepal.

Introduction

Dengue is highly infectious mosquito-borne viral disease. It has scattered throughout the tropics with local divergence due to the seasonal impact (rainfall, temperature) and unplanned rapid civic [37]. Dengue virus imparts to humans through the bite of infected Aedes mosquito, especially called Aedes Aegypti. The infected mosquito remains with one of the four dengue virus serotypes (DEN-1, DEN-2, DEN-3 and DEN-4) for life which transmits the virus to humans during feed [45]. Dengue can affect almost all age groups (infant to adult) of humans. The epidemic of dengue-like illnesses was reported in the French West Indies in 1635 and Panama in 1699. In 1780, doctors in Philadelphia, Pennsylvania recorded an epidemic of the disease later known as dengue [22]. About 390 million dengue virus infections occurs every year, of which 96 million manifest the disease apparently with any level of severity [8]. According to WHO [70], about 3.9 billion people are at risk with dengue virus including 129 countries, 70% are from Asia. Nowadays, dengue disease is affecting Asian and Latin American countries and has become a leading cause of hospitalization and death among children and adults [22]. According to WHO, mosquito transmit malaria, dengue, yellow fever, filariasis, and several other infectious diseases. This is due to the gradually increasing urbanization, uncontrolled population and civilization.

In the context of Nepal, Peters et al. [47] were first to study on mosquito and reported the existence of the species of Anopheles in the Terai region. Peters and Dewar [46] recorded culicine species of mosquito existing in Nepal. Darsie and Pradhan [13] focused their study on biological distribution and indentification of the mosquito in Nepal. Aedes Aegypti species was first reported in Nepal in 2009 [21] although the first dengue outbreak was reported in 2004 [30], and other outbreaks of dengue have been recorded from both tropical and subtropical regions of Nepal including the capital city Kathmandu [44, 54]. During 2004–2013 the major outbreaks of dengue epidemic was recorded in 2010 and 2013. In the years 2014–2019, a yearly outbreaks of the dengue have been more frequent than in the years 2004–2013. The number of confirmed annual dengue incidence varied from 336 to 17,992 in 2014–2019 [57]. The largest ever outbreak of dengue diseases in Nepal was reported in 2019. In this year the infectious cases was more than 15,000 people during mid-summer from a tropical region and then it spread to hilly subtropical locations (the Sunsari district, the eastern region of Nepal, the Makwanpur district and the southwest district of Kathmandu). A total nineteen deaths were reported from 2006 to 2019 from dengue infection [3, 40]. According to EDCD [40] of Nepal, there are around 564 dengue infection cases reported in 2002, most of the affected districts are Myagdi, Kaski, Sindhuli, Kailali, Sunsari, and Rupandehi. Dengue virus infection has now become an emerging disease in Nepal. Subedi and Robinson [64] revealed that the problem in finding timely medical treatment, poor facilities for disease diagnosis and a scarcity of mosquito control programs are major issues to cause increment in dengue cases in Nepal. Kawada et al. [30] observed the insecticides’ resistance status and its impact on the transmission and the prevention of dengue in Nepal (Fig. 1).

Fig. 1

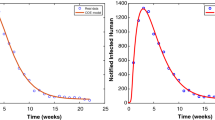
Dengue cases in Nepal from 2006 to 2020 (Data source: Epidemiology Disease Control Division, Nepal [40])

Mathematical modeling of dengue has become one of the effective strategies for the prevention and control of the disease [37]. Kermack and McKendrick contributed on upgrading the mathematical modeling of infectious diseases by SIR (Susceptible, Infected and Removed of individuals) compartmental model [31, 32]. Esteva and Vargas [18, 19] modified this model to study transmission dynamics of dengue disease. In the transmission of dengue virus, there are two periods of incubation, one is the time when the mosquito takes viremic bloodmeal and it becomes infectious (5–33 days), another is time from infection due to the bite of infected mosquito to the appearance of symptoms in human (2–10 days) [11]. Pongsumpun [52] studied the length of time during incubation of dengue virus in humans and mosquito, and analyzed how to reduce the outbreak of the dengue virus. The SEIR model [61] is proposed to study dengue disease transmission of dengue disease taking exposed classes of both vector and host population. Prevention of mosquito bites is one of the ways to prevent dengue disease. The developing countries may not be able to provide treatment to each infected individual. The transmission model with treatment by considering logistic growth of mosquito is formulated and analyzed by [62]. The effect of temperature and rainfall on mosquito to spread the dengue disease in a community is one of natural problems [2, 66]. In epidemic and endemic areas, awareness about dengue will lessen the contact rate between host and mosquito. Most of the epidemic model [9, 12, 60, 63] address the impact of media coverage to the spread and control of infectious diseases for social awareness and activity of social disturbances. Nicholson’s blowflies model [20] can be used for the study of dynamic of differential system. In Nepal, Phaijoo and Gurung [49, 50] studied a vector host epidemic model of dengue disease by considering control measures of the disease and also suggested that the proper management of human movement between patches helps to reduce the burden of dengue disease.

The fractional models are useful concord for the disease epidemics which frame the memory and nonlocal affects [1, 5]. Though fractional calculus was introduced more than 300 years ago and is applied into many fields of science and engineering, the development of applications is still an important task in the area of fractional calculus [51]. Fractional calculus has real world applications in science and engineering [65]. Authors in [29, 56] has studied the stability analysis, uniqueness and existence of dynamical system of fractional Duffing problem and applied fixed point theory for the stability of epidemic model by using fractional calculus. Hajiseyedazizi et al. [24] established the existence of a solution for a novel class of singular q-integro-differential equations on a time scale. Under certain boundary conditions on the time scale, Samei and Rezapour [58] evaluated the possibility of a solution for an m-dimensional system of fractional q-differential inclusions using the sum of two multi-term functions. Fractional-order differential equations are naturally related to systems with memory which exists in most biological systems. It is applicable with initial value differential equations [16]. Pooseh et al. [53] studied the fractional-order derivative in the dengue epidemic and showed a better realistic result than show by the classical model. Diethelm [15] formalized the fractional-order model for the simulation of an outbreak of dengue fever using the SIR compartment model. Authors in [26, 27] developed a fractional-order dengue epidemic models representing the human and mosquito dynamics. The effects of memory index, $\alpha$ is used in dengue disease transmission model [17, 59]. The fractional-order mathematical models in epidemic reflect the dynamical behaviors in real-world [65]. Transformation of a classical model into a fractional-order model with the order of memory level $\alpha$ gives more accurate result [15, 53, 59].

In the present work, the SEIR-SEI compartmental model is used to study transmission dynamics of dengue disease in Nepal. The model parameters like: birth rate, death rate, vector incubation rate are determined from the real data [40]. The deterministic model is used to estimate remaining model parameters applying the method of the least square, which is based on cumulative data of dengue patients of the year 2019. The reproduction number is obtained and used to study the stability of model. Furthermore, we formulate the model with fractional-order derivative and use the Euler’s method for the numerical simulation of the model.

Model Formulation

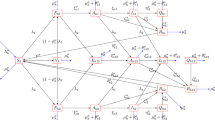
We represent the total mosquito population and the total human population by $N_m(t)$ and $H_h(t)$ respectively for $t>0$. The total population divided into different compartment as: susceptible $(M_s)$, exposed $(M_e)$ infected $(M_i)$ groups of the vector population and susceptible $(H_s)$, exposed $(H_e)$, infected $(H_i)$ and recovered $(H_r)$ groups of host population. The schematic diagram is presented in Fig. 2.

Fig. 2

Flow chart of the model

The differential equation of the model is as given;

$$\begin{aligned} {} \begin{aligned} \frac{dH_{s}}{dt}&= \mu _{h}H_{h} -\frac{b\beta _{h}}{H_{h}}H_{s}M_{i} - \mu _{h}H_{s}\\ \frac{dH_{e}}{dt}&= \frac{b\beta _{h}}{H_{h}}H_{s}M_{i} - (\mu _{h}+\alpha _{h})H_{e}\\ \frac{dH_{i}}{dt}&= \alpha _{h} H_{e} -(\gamma _h+\mu _h)H_{i}\\ \frac{dH_{r}}{dt}&= \gamma _{h} H_{i} - \mu _{h}H_{r}\\ \frac{dM_{s}}{dt}&= A -\frac{b\beta _{v}}{H_{h}}M_{s}H_{i}-\mu _{v}M_{s}\\ \frac{dM_{e}}{dt}&= \frac{b\beta _{v}}{H_{h}}M_{s}H_{i} -(k_v+ \mu _{v} )M_{e}\\ \frac{dM_{i}}{dt}&=k_v M_e- \mu _{v} M_{i} \end{aligned} \end{aligned}$$

(1)

with initial conditions $H_s(0)> 0$, $H_e(0) \ge 0$, $H_i(0)\ge 0$, $H_r(0)\ge 0$, $M_s(0)> 0$, $M_e(0)\ge 0$, $M_i(0)\ge 0$

The biological meaning of state variables and the parameters used in the model are presented in Table 1; where, $H_h = H_s+H_e+H_i+H_r$ and $N_v = M_s+M_e+M_i$ and $\displaystyle \frac{dN_v}{dt} = A-\mu _v N_v$.

Table 1 The parameters used in model

Again introducing the relations, $s_h=\displaystyle \frac{H_s}{H_h}$, $e_h=\displaystyle \frac{H_e}{H_h}$, $i_h=\displaystyle \frac{H_i}{H_h}$, $r_h=\displaystyle \frac{H_r}{H_h}$, $s_v=\displaystyle \frac{M_s}{\frac{A}{\mu _v}}$, $e_v=\displaystyle \frac{M_e}{\frac{A}{\mu _v}}$, $i_v=\displaystyle \frac{M_i}{\frac{A}{\mu _v}}$.

The Eq. (1) becomes

$$\begin{aligned} {} \begin{aligned} \frac{ds_h}{dt}&= \mu _h(1-s_h)- \frac{Ab \beta _h }{\mu _vH_h}s_hi_v\\ \frac{de_h}{dt}&= \frac{Ab \beta _h }{\mu _vH_h}s_hi_v-(\alpha _h+\mu _h)e_h\\ \frac{di_h}{dt}&=\alpha _h e_h-(\gamma _h+\mu _h)i_h\\ \frac{de_v}{dt}&= b \beta _vi_h(1-e_v-i_v)-(\mu _v+k_v)e_v\\ \frac{di_v}{dt}&=k_ve_v-\mu _v i_v \end{aligned} \end{aligned}$$

(2)

The system of Eq. (2) has the same qualitative behavior as the system of Eq. (1).

Parameter Estimations

The yearly dengue disease information is taken from Epidemiology and Diseases Control Division (EDCD) and Early Warning Reporting System (EWARS) which also includes death cases from the years 2006 to 2020 [40]. The study includes the new weekly dengue data available for Nepal in 2019. We used the disease cumulative weekly data for the model equations. For the prediction of new infected cases C(t) at time t is used for the solution of differential equation [55].

$$\begin{aligned} C(t) = \psi \alpha _h e_h N_h \end{aligned}$$

(3)

where, $\psi$ is the proportion of the reported cases of dengue. We apply the Fourth order Runge–Kutta method for the numerical solution of Eq. (2). Non-linear least square regression method is used for parameter estimation, which minimizes the sum of the square residuals

$$\begin{aligned} P(\theta ) = \sum _{i=1}^n \biggl [C(t_i)-{\overline{C}}(t_i)\biggr ]^2 \end{aligned}$$

(4)

where, $\theta = \{b, \beta _{h},\beta _{v}, \alpha _h,{\gamma _h}\}$ to be estimated and $C(t_i)$ and ${\overline{C}}(t_i)$ are given available data and new cases of weekly recorded infectious cases predicted by the model respectively. In this study, we use “ode45” (ODE Solver) and “fmincon”(Optimization) tools for simplification (Fig. 3).

Fig. 3

Cumulative weekly recorded dengue infection cases (circle) along with model curve (line)

The data available for weekly cumulative dengue infectious cases is fitted to the model for the estimation of the parameters. Estimated parameters are presented in Table 2.

Table 2 Estimated model parameters

Preliminaries on Fractional Derivative

Definition 4.1

[14, 39, 51] The Riemann–Liouville’s fractional integral of order $\alpha$ is defined by

$$\begin{aligned} I_{t}^{\alpha }f(t)= \frac{1}{\Gamma (\alpha )}\int _{0}^{t}\frac{f(s)ds}{(t-s)^{1-\alpha }} \end{aligned}$$

where $\alpha>0, \, t>0$, $\Gamma {(\alpha )}$ is gamma function of $\alpha$

Definition 4.2

[14, 39, 51] The Caputo fractional derivative of the function f(t) is defined by

$$\begin{aligned} D_{t}^{\alpha }f(t) =I_t^{n-\alpha }[f^n(t)]= \frac{1}{\Gamma (n-\alpha )} \int _{0}^{t}\frac{ D^{n} f(s)ds}{(t-s)^{\alpha -n+1}}, \quad {\textit{if}}\quad n-1 \le \alpha < n \end{aligned}$$

Definition 4.3

[14, 39, 51] The Laplace transform for the Caputo fractional derivative of the function f(t) is

$$\begin{aligned} {\mathscr {L}}[D_{t}^{\alpha }f(t) ]=s^{\alpha }F(s)- \sum _{k=0}^{n-1}s^{n-k-1}f^{(k)}(0),\quad n\in {\mathbb {N}},\quad n-1\le \alpha < n \end{aligned}$$

(5)

Definition 4.4

[14, 39, 51] The Mittag–Leffler function is defined by,

$$\begin{aligned} E_{\alpha ,\beta }(z)= \sum _{n=0}^{\infty } \frac{z^k}{\Gamma (\alpha k+\beta )},\quad \alpha ,\beta >0 \end{aligned}$$

(6)

and the Laplace transform formula for the Mittag–Leffler function is

$$\begin{aligned} \begin{aligned} {\mathscr {L}}[1-E_{\alpha }(\displaystyle \mp d t^{\alpha })]&= \frac{d}{s(s^{\alpha }\displaystyle \pm d)}\\ {\mathscr {L}}[E_{\alpha }(\displaystyle \mp d t^{\alpha })]&=\frac{s^{\alpha }}{s(s^{\alpha }\displaystyle \pm d)} \end{aligned} \end{aligned}$$

Theorem 4.1

[14, 16] Consider the two-parameter Mittag–Leffler function $E_{\alpha ,\beta }(z)$ for some $\alpha ,\beta >0$. The power series defining $E_{\alpha ,\beta }(z)$ is convergent for all $z\in {\mathbb {C}}$. In other words, $E_{\alpha ,\beta }(z)$ is an entire function.

Fractional Dengue Diseased Model

Pooseh et al. [53], Diethelm [15] and [17, 26, 27] introduced the fractional order derivative for different classical integer model. The memory effect plays a significant role in the transmission of the dengue disease from host to vector and vector to host which is taken as same in the model. Other parameters like birth, death, recovery rate do not have own memory. The Caputo fractional-order derivative model for the classical model Eq. (1) is,

$$\begin{aligned} {} \begin{aligned} D_{a}^{\alpha }H_{s}&= \mu _{h}H_{h} -\frac{b^{\alpha }\beta _{h}}{H_{h}}H_{s}M_{i} - \mu _{h}H_{s}\\ D_{a}^{\alpha }H_{e}&= \frac{b^{\alpha }\beta _{h}}{H_{h}}H_{s}M_{i} - (\mu _{h}+k_{h})H_{e}\\ D_{a}^{\alpha }H_{i}&= k_{h} H_{e} -(\gamma _h+\mu _h)H_{i}\\ D_{a}^{\alpha }H_{r}&= \gamma _{h} H_{i} - \mu _{h}H_{r}\\ D_{a}^{\alpha } M_{s}&= A -\frac{b^{\alpha }\beta _{v}}{H_{h}}M_{s}H_{i}-\mu _{v}M_{s}\\ D_{a}^{\alpha } M_{e}&= \frac{b^{\alpha }\beta _{v}}{H_{h}}M_{s}H_{i} -(k_v + \mu _{v} )M_{e}\\ D_{a}^{\alpha } M_{i}&=k_v M_e- \mu _{v} M_{i} \end{aligned} \end{aligned}$$

(7)

where, $0<\alpha \le 1$ and the initial conditions of the fractional model are $H_s(0) > 0$, $H_e(0) \ge 0$, $H_i(0) \ge 0$, $H_r(0) \ge 0$, $M_s(0) > 0$, $M_e(0) \ge 0$, $M_i(0) \ge 0$, for all $t\ge 0$. Here,

$$\begin{aligned} D_{a}^{\alpha } H_{h} = D_{a}^{\alpha }(H_s+H_e+ H_i+H_r) =0 \end{aligned}$$

and for the mosquito population

$$\begin{aligned} D_{a}^{\alpha } M= & {} D_{a}^{\alpha }(M_{s}+M_{e} + M_{i})\\= & {} D_{a}^{\alpha }(A-\mu _{v} M ) \end{aligned}$$

Positiveness and Boundedness

Consider the dynamic of Caputo fractional model Eq. (7) in the feasible region

$$\begin{aligned} {\mathcal {W}} = \{y:y(t)=(H_s,H_e,H_i,H_r,M_s,M_e,M_i) \in {\mathbb {R}}_{+}^7\cup \{0\}\} \end{aligned}$$

Theorem 6.1

(Generalized Mean Value Theorem) [42] Let $0<\alpha \le 1$, $f(t)\, \in \, C[a,b]$ and if $D_{t}^{\alpha }f(t) \in C[a,b]$, then

$$\begin{aligned} f(t)=f(a)+\frac{1}{\Gamma (\alpha )}(D_{t}^{\alpha }f)(s)(t-a)^{\alpha }\quad \hbox {with}\quad a<s<t \,\;\forall \,\; t \in (a,b] \end{aligned}$$

(8)

Remark 6.1

Let $f(t) \in C[a,b]$ and $D_{t}^{\alpha }f(t)\in C[a,b]$ for $0<\alpha \le 1$

• (i) If $D_{t}^{\alpha }f(t) \ge 0 ,\,\forall t\in (a,b)$, then f(t) is nondecreasing.

• (ii) If $D_{t}^{\alpha }f(t) \le 0 ,\,\forall t\in (a,b)$, then f(t) is nonincreasing.

Lemma 6.1

The set ${\mathcal {W}}$ attracts all positive solutions of the model Eq. (7) for given initial conditions with $t\ge 0$.

Proof

By applying theorem (6.1) and the Remark (6.1) for existence of the solution of the model Eq. (7) in $(0,\infty )$ with given initial conditions, we get the following relations,

$$\begin{aligned} D_{t}^{\alpha }H_{s}\bigg |_{H_s=0}= & {} \mu _h H_h>0\\ D_{t}^{\alpha }H_{e}\bigg |_{H_e=0}= & {} \frac{b^{\alpha }\beta _{h}}{H_{h}}H_{s}H_{i} \ge 0\\ D_{t}^{\alpha }H_{i}\bigg |_{H_i=0}= & {} k_h H_e \ge 0\\ D_{t}^{\alpha }H_{r}\bigg |_{H_r=0}= & {} \gamma _h H_i \ge 0\\ D_{t}^{\alpha }M_{s}\bigg |_{M_s=0}= & {} A >0 \\ D_{t}^{\alpha }M_{e}\bigg |_{M_e=0}= & {} \frac{b^{\alpha }\beta _{h}}{H_{h}}M_{s}H_{i} \ge 0 \\ D_{t}^{\alpha }M_{i}\bigg |_{M_i=0}= & {} k_v M_e \ge 0 \end{aligned}$$

Hence, the set ${\mathcal {W}}$ is non -negative orthant in ${\mathbb {R}}_{+}^7$ for all $t\ge 0$. $\square$

Theorem 6.2

The solution y(t) of the model Eq. (7) uniformly bounded.

Proof

From the model Eq. (7) we get,

$$\begin{aligned} {} D_{t}^{\alpha }H_h{(t)}= & {} 0 \end{aligned}$$

(9)

$$\begin{aligned} {} D_{t}^{\alpha }M(t)= & {} A-\mu _v M(t) \end{aligned}$$

(10)

For Eq. (9), we get $H_h(t) = k$ and $H_h(0) =k$, where k is arbitrary constant. That means, $H_h(t)$ is bounded.

From Eq. (10), we get

$$\begin{aligned} D_{t}^{\alpha }M(t)+\mu _v M(t)=A \end{aligned}$$

Taking Laplace Transform on both sides,

$$\begin{aligned} \begin{aligned}&s^{\alpha } {\mathscr {L}}[M(t)] -s^{\alpha -1}M(0)+\mu _v {\mathscr {L}}[M(t)] = \frac{A}{s}\\&{\mathscr {L}}[M(t)]\{ s^\alpha + \mu _v\} = \frac{A}{s}+s^{\alpha -1}M(0)\\&{\mathscr {L}}[M(t)] =\frac{A}{s(s^{\alpha }+\mu _v)} + M(0) \frac{s^{\alpha -1}}{s^{\alpha }+\mu _v} \end{aligned} \end{aligned}$$

Taking Laplace inverse on both sides

$$\begin{aligned} \begin{aligned} M(t)&= \frac{A}{\mu _v} {\mathscr {L}}^{-1} \biggl [\frac{\mu _v}{s(s^{\alpha }+\mu _v)} \biggr ] + M(0) {\mathscr {L}}^{-1} \biggl [ \frac{s^{\alpha -1}}{s^{\alpha }+\mu _v}\biggr ] \end{aligned} \end{aligned}$$

Using the definition (4.4), we get

$$\begin{aligned} \begin{aligned}&= \frac{A}{\mu _v} \biggl (1-E_{\alpha }(-\mu _vt^{\alpha })\biggr ) + M(0) E_{\alpha }(-\mu _vt^{\alpha })\\&= \frac{A}{\mu _v}- \biggl (\frac{A}{\mu _v}-M(0)\biggr )E_{\alpha }(-\mu _vt^{\alpha })\\ M(t)&= \frac{A}{\mu _v} -M_1 E_{\alpha }(-\mu _vt^{\alpha })\\ M(t)&\le \frac{A}{\mu _v} \end{aligned} \end{aligned}$$

Here, $M_1 = \biggl (\frac{A}{\mu _v}-M(0)\biggr )$. From theorem (4.1) $E_{\alpha ,1}(-\mu _vt^{\alpha })$ is bounded for all $t\ge 0$. Thus, the solution of model (7) is uniformly bounded and system will remain in ${\mathcal {W}}$ (from Lemma 6.1). $\square$

Uniqueness of Solution

Introducing the relations, $s_h=\displaystyle \frac{H_s}{H_h}$, $e_h=\displaystyle \frac{H_e}{H_h}$, $i_h=\displaystyle \frac{H_i}{H_h}$, $r_h=\displaystyle \frac{H_r}{H_h}$, $s_v=\displaystyle \frac{M_s}{\frac{A}{\mu _v}}$, $e_v=\displaystyle \frac{M_e}{\frac{A}{\mu _v}}$, $i_v=\displaystyle \frac{M_i}{\frac{A}{\mu _v}}$, $L = \displaystyle \frac{A}{\mu _vH_h}b^{\alpha } \beta _h$ and $W= b^{\alpha }\beta _v$. The Eq. (7) becomes

$$\begin{aligned} \begin{aligned} D_{t}^{\alpha }s_h&= \mu _h(1-s_h)-L s_hi_v\\ D_{t}^{\alpha }e_h&= L s_hi_v-(\alpha _h+\mu _h)e_h\\ D_{t}^{\alpha }i_h&=\alpha _h e_h-(\gamma _h+\mu _h)i_h\\ D_{t}^{\alpha }e_v&= Wi_h(1-e_v-i_v)-(\mu _v+k_v)e_v\\ D_{t}^{\alpha }i_v&=k_ve_v-\mu _v i_v \end{aligned} \end{aligned}$$

(11)

The system of Eq. (11) also satisfy non-negative with uniformly boundedness and has a biologically feasible region. Let us defined a region as

$$\begin{aligned} {\mathcal {W}}_1 = \{(s_h,e_h,i_h,e_m,i_m)\in {\mathbb {R}}_{+}^5 ; \hbox {max}(|s_h|,|e_h|,|i_h|,|e_v|,|i_v|\le B)\} \end{aligned}$$

where B is a finite positive value.

Lemma 7.1

[34] Consider the system

$$\begin{aligned} D_{t}^{\alpha }y(t) = f(t,x) ,\quad t_0>0 \end{aligned}$$

(12)

with initial condition $y(t_0) = y_{t_0}$, where $\alpha \in (0,1]$, $f:[t_0,\infty ) \times {\mathcal {W}} \rightarrow {\mathbb {R}}^n, C \subseteq {\mathbb {R}}^n$, if local Lipschitz condition is satisfied by f(t, x) with respect to x, then there exists a solution of (12) on $[t_0,\infty ) \times {\mathcal {W}}$ which is unique.

Theorem 7.1

For the initial value of each $D_0 = (s_h(0),e_h(0),i_h(0),e_v(0),i_v(0)) \in {\mathcal {W}}_1$ and there exists a unique solution of $D(t)\in {\mathcal {W}}_1$ of system of Eq. (11) for all $t \ge 0$.

Proof

Using the approaches [34, 35], let us define a relation $Z(D) =\{Z_1(D),Z_2(D),Z_3(D),Z_4(D),Z_5(D)\}$, where

$$\begin{aligned} {} \begin{aligned} Z_1(D)&= \mu _h(1-s_h)-L s_hi_v\\ Z_2(D)&= L s_hi_v-(\alpha _h+\mu _h)e_h\\ Z_3(D)&=\alpha _h e_h-(\gamma _h+\mu _h)i_h\\ Z_4(D)&= Wi_h(1-e_v-i_v)-(\mu _v+k_v)e_v\\ Z_5(D)&=k_ve_v-\mu _v i_v \end{aligned} \end{aligned}$$

(13)

For any $D,{\overline{D}} \in {\mathcal {W}}_1$,

$$\begin{aligned} \begin{aligned} ||Z(D)-Z({\overline{D}})||&= |Z_1(D)-Z_1({\overline{D}})|+ |Z_2(D)-Z_2({\overline{D}})| +|Z_3(D)-Z_3({\overline{D}})|\\&\quad +|Z_4(D)-Z_4({\overline{D}})|+|Z_5(D)-Z_5({\overline{D}})|\\&= |\mu _h(1-s_h)-L s_hi_v -\mu _h(1-\overline{s_h})+L\overline{s_h}\overline{i_v}|\\&\quad +|L s_hi_v-(\alpha _h+\mu _h) e_h-L \overline{s_h}\overline{i_v}+(\alpha _h+\mu _h) \overline{e_h}|\\&\quad +|\alpha _he_h-(\gamma _h+\mu _h)i_h -\alpha _h\overline{e_h}+(\gamma _h+\mu _h) \overline{i_h}|\\&\quad +|Wi_h(1-e_v-i_v)-(\mu _v+k_v)e_v-W\overline{i_h}(1-\overline{e_v}-\overline{i_v})+(\mu _v+k_v)\overline{e_v}|\\&\quad +|k_ve_v-\mu _v i_v - k_v \overline{e_v}+\mu _v \overline{i_v}| \\&\le |\mu _h(s_h -\overline{s_h})|+ |2L(s_hi_v-\overline{s_h}\overline{i_v})|+|(\alpha _h+\mu _h)(e_h-\overline{e_h})|\\&\quad +|\alpha _h(e_h-\overline{e_h})|+|(\gamma _h+\mu _h) (i_h-\overline{i_h})|+|W(i_h-\overline{i_h})|+|W(e_vi_h-\overline{e_v}\overline{i_h})|\\&\quad +|W(i_vi_h-\overline{i_v}\overline{i_h})| +|(\mu _v+k_v)(e_v-\overline{e_v})|+|k_v(e_v-\overline{e_v})|+|\mu _v(i_v-\overline{i_v})|\\&\le |\mu _h(s_h -\overline{s_h})|+ |2LB (s_h-\overline{s_h})|+|2LB (i_v-\overline{i_v})|+|WB(e_v-\overline{e_v})|\\&\quad +|2WB(i_h-\overline{i_h})|+|WB(i_v-\overline{i_v})|+|(\alpha _h+\mu _h)(e_h-\overline{e_h})|\\&\quad +|\alpha _h(e_h-\overline{e_h})|+|(\gamma _h+\mu _h) (i_h-\overline{i_h})|\\&\quad +|W(i_h-\overline{i_h})|+|(\mu _v+k_v)(e_v-\overline{e_v})|+|k_v(e_v-\overline{e_v})|+|\mu _v(i_v-\overline{i_v})|\\&\le (\mu _h +2LB)|(s_h -\overline{s_h})|+(2WB+W+\gamma _h+\mu _h)|(i_h-\overline{i_h})| \\&\quad +(2\alpha _h+\mu _h)|(e_h-\overline{e_h})|\\&\quad +(\mu _v+2k_v+WB)|(e_v-\overline{e_v})|+|(2LB+\mu _v+WB)(i_v-\overline{i_v})|\\&\le V||D - {\overline{D}}|| \end{aligned} \end{aligned}$$

Where, $V= \hbox {max} \{ \mu _h+2LB, 2WB+W+\gamma _h+\mu _h, 2\alpha _h+\mu _h, \mu _v+2k_v+WB, 2LB+\mu _v+WB \}$. Thus, Z(D) satisfies the Lipschitz condition with respect to D. Hence, from Lemma (7.1), D(t) has a unique solution of Eq. (11) with initial condition $D_0$. $\square$

Stability of Model

Basic Reproduction Number

Basic reproduction number [68] is the expected number of secondary infections caused by a single infectious individual during their entire infectious lifetime. Using next-generation operator method [67, 68], we find the expression for $R_0$. For this, we find the matrices F (infection new cases term) and V (transition terms) of Eq. (11). Here, $L = \frac{A}{\mu _vH_h}b^{\alpha } \beta _h$, $\beta = (\alpha _h+\mu _h)$, $k =\gamma _h+\mu _h$ and $W= b ^{\alpha }\beta _v$.

$$\begin{aligned} F= \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} L \\ 0 &{} 0 &{} W &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) \quad \text {and}\quad V= \left( \begin{array}{cccc} -\beta &{} 0 &{} 0 &{} L \\ 0 &{} -(k_v+\mu _v) &{} 0 &{} 0 \\ \alpha _h &{} 0 &{} -k &{} 0 \\ 0 &{} k_v&{} 0 &{} -\mu _{v} \\ \end{array} \right) \end{aligned}$$

Also,

$$\begin{aligned} V^{-1}= & {} \left( \begin{array}{cccc} -\frac{1}{\beta } &{} 0 &{} 0 &{} 0 \\ 0 &{} \displaystyle -\frac{1}{k_v+\mu _v} &{} 0 &{} 0 \\ \displaystyle -\frac{\alpha _h}{k \beta }&{} 0 &{} \displaystyle - \frac{1}{k} &{} 0 \\ 0 &{} \displaystyle -\frac{k_v}{k_v\mu _{v}+\mu _{v}^2} &{} 0 &{} \displaystyle -\frac{1}{\mu _{v}} \\ \end{array} \right) \\ F V^{-1}= & {} \left( \begin{array}{cccc} 0 &{}\displaystyle -\frac{k_v L}{k_v \mu _{v}+\mu _{v}^2} &{} 0&{}\displaystyle -\frac{L}{\mu _{v}} \\ \displaystyle -\frac{W\alpha }{k \beta } &{}0&{} \displaystyle - \frac{W}{k} &{} 0 \\ &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) \end{aligned}$$

The spectral radius of the next generation matrix is

$$\begin{aligned} R_0 = \sqrt{\displaystyle \frac{\alpha _hLWk_v}{k\beta \mu _{v}(k_v+\mu _{v})}} \end{aligned}$$

which is threshold condition equivalent to reproduction number of the model.

$$\begin{aligned} R_0(\alpha ) = \sqrt{\displaystyle \frac{b^{2\alpha }\alpha _hk_v\beta _{h}\beta _{v}A}{H_h \mu _v^2 (\gamma _h+\mu _h)(\alpha _h+\mu _h)(k_v+\mu _{v})}} \end{aligned}$$

(14)

The basic reproduction number in dimensionless form is

$$\begin{aligned} R_0 = \sqrt{\displaystyle \frac{b^2\alpha _hk_v\beta _{h}\beta _{v}A}{H_h \mu _v^2 (\gamma _h+\mu _h)(\alpha _h+\mu _h)(k_v+\mu _{v})}} \end{aligned}$$

(15)

Equilibrium Points

For the evaluation of equilibrium points, the system of Eq. (11) is formed as

$$\begin{aligned} D_{t}^{\alpha }s_h= D_{t}^{\alpha }e_h= D_{t}^{\alpha }i_h= D_{t}^{\alpha }e_v= D_{t}^{\alpha }i_v=0 \end{aligned}$$

So, using $L = \frac{A}{\mu _vH_h}b^{\alpha } \beta _h$, $\beta = (\alpha _h+\mu _h)$, $k =\gamma _h+\mu _h$ and $W= b ^{\alpha }\beta _v$

$$\begin{aligned} \begin{aligned} \mu _h(1-s_h)-L s_hi_v&=0\\ L s_hi_v-\beta e_h&=0\\ \alpha _h e_h-ki_h&=0\\ Wi_h(1-e_v-i_v)-(\mu _v+k_v)e_v&=0\\ k_ve_v-\mu _v i_v&=0 \end{aligned} \end{aligned}$$

(16)

After solving, we get a diseases free equilibrium (DFE) point $E_0 = (1,0,0,0,0)$ and the endemic equilibrium (EE) point $E^*=(s_h^{*}, e_h^{*}, i_h^{*}, e_v^{*}, i_v^{*} )$ where,

$$\begin{aligned} \begin{aligned} s_h^{*}&= \displaystyle \frac{(k_v +\mu _{v})(W\alpha _{h} \mu _{h} +k \mu _{v} )}{W\alpha _{h}(k_v(L+\mu _{h})+\mu _{h}\mu _{v})}\\ e_h^{*}&= \displaystyle \frac{\mu _h\mu _v k\beta (k_v+\mu _v)[R_0^2-1]}{W \beta \alpha _h(k_v(L+\mu _{h})+\mu _{h}\mu _{v})}\\ i_h^{*}&= \displaystyle \frac{\mu _h^2\mu _v k\beta (k_v+\mu _v)[R_0^2-1]}{W \beta k(k_v(L+\mu _{h})+\mu _{h}\mu _{v})}\\ e_v^{*}&= \displaystyle \frac{\mu _h\mu _v^2 k\beta [R_0^2-1]}{L k_v(\alpha _h\mu _{h}W+k\mu _{v}\beta )}\\ i_v^{*}&= \displaystyle \frac{\mu _h\mu _v k\beta [R_0^2-1]}{L(\alpha _h\mu _{h}W+k\mu _{v}\beta )} \end{aligned} \end{aligned}$$

(17)

Asymptotic Behaviour

Lemma 8.1

[36, 38, 48] Consider the fractional-order system

$$\begin{aligned} D_{t}^{\alpha }y(t) = f(t,x),\quad t_0>0 \end{aligned}$$

(18)

with initial condition $y(t_0) = t_0$, where $\alpha \in (0,1]$, $f\in {\mathbb {R}}^n$. The system is said to be locally asymptotically stable iff $|arg(\lambda _i)|>\frac{\alpha \pi }{2}$ for all eigenvalues $\lambda _i$ where, $i= 1,2,3,\ldots$ which is obtained from given Jacobian matrix.

Theorem 8.1

The disease free equilibrium $E_0$ is locally asymptotically stable if $R_0 <1$ and unstable if $R_0 >1$.

Proof

The Jacobian matrix $J(E_0)$ of the Eq. (11) about the diseases free equlibrium point is

$$\begin{aligned} J(E_0)= \left[ \begin{array}{ccccc} -\mu _h &{} 0 &{} 0 &{} 0&{}-L \\ 0 &{} -\beta &{} 0 &{} 0&{}L \\ 0 &{} \alpha _h &{} -k &{} 0&{}0 \\ 0 &{} 0 &{} W &{} -k_v-\mu _v&{}0 \\ 0 &{}0 &{}0 &{}k_v &{} -\mu _v \end{array} \right] \end{aligned}$$

The characteristics equations is;

$$\begin{aligned} |J(E_0)-\lambda I| = 0 \end{aligned}$$

(19)

where the eigenvalue is $\lambda = - \mu _h$ and for remaining Jacobian matrix of order 4 is

$$\begin{aligned} J_1(E_0)= \left[ \begin{array}{cccc} -\lambda -\beta &{} 0 &{} 0&{}L \\ \alpha _h &{} -\lambda -k &{} 0&{}0 \\ 0 &{} W &{} -\lambda -k_v-\mu _v&{}0 \\ 0 &{}0 &{}k_v &{} -\lambda -\mu _v \end{array} \right] =0 \end{aligned}$$

The characteristic equation of $J_1(E_0)$ is as

$$\begin{aligned} \lambda ^4+\lambda ^3 p_1+\lambda ^2 p_2+\lambda p_3+p_4 = 0 \end{aligned}$$

(20)

where

$$\begin{aligned} p_1= & {} k+\beta +k_v+2\mu _v\\ p_2= & {} k(k_v+2\mu _v+\beta )+\beta (k_v+2\mu _v+k)\\ p_3= & {} (k_v+\mu _v)(k\beta +k\mu _v+\beta \mu _v)+k\beta \mu _v\\ p_4= & {} (k_v+\mu _v)k\beta \mu _v[1-R_0^2] \end{aligned}$$

Here, the parameters $p_1,p_2,p_3$ are non-negative and $p_4$ is positive when $R_0 < 1$.

The approaches followed by [6, 25, 36, 62] for the characteristic Eq. (19) and the eigenvalue is $\lambda = - \mu _h$ and remaining are determined by polynomial Eq. (20). So,

$$\begin{aligned} |arg(\lambda )| = \pi > \frac{\alpha \pi }{2} \end{aligned}$$

where, $\alpha \in (0,1]$. Similarly, the argument of roots of characteristic polynomial Eq. (20) are also greater than $\frac{\alpha \pi }{2}$ in similar processes. Form the Lemma 8.1, we conclude that DFE is locally asymptotically stable for $R_0 < 1$. $\square$

Theorem 8.2

The endemic equilibrium $E^*=(s_h^{*}, e_h^{*}, i_h^{*}, e_v^{*}, i_v^{*} )$ of the system of Eq. (11) is locally asymptotically stable if $R_0>1$ and unstable if $R_0<1$.

Proof

The Jacobian matrix evaluated at endemic equlibrium point $E^*$ in (17) of the system of Eq. (11) is

$$\begin{aligned} J(E^*)= \left[ \begin{array}{ccccc} -a_1 &{} 0 &{} 0 &{} 0&{}-a_3 \\ a_2 &{} -\beta &{} 0 &{} 0&{}a_3 \\ 0 &{} \alpha _h &{} -k &{} 0&{}0 \\ 0 &{} 0 &{} a_4&{} -a_5&{} -a_6\\ 0 &{}0 &{}0 &{}k_v &{} -\mu _v \end{array} \right] \end{aligned}$$

where

$$\begin{aligned} a_1= & {} \mu _h+L\displaystyle \frac{\mu _h\mu _v \beta [R_0^2-1]}{ b_3},\\ a_2= & {} L\displaystyle \frac{\mu _h\mu _v \beta [R_0^2-1]}{ b_3},\\ a_3= & {} b_1\displaystyle \frac{(W\alpha _h\mu _h+ k \mu _v)}{W\alpha _hb_2},\\ a_4= & {} W\biggl [ 1-\displaystyle \frac{\mu _h\mu _v^2 k \beta [R_0^2-1]}{Lk_vb_3}-\displaystyle \frac{\mu _h\mu _v \beta [R_0^2-1]}{b_3}\biggr ],\\ a_5= & {} \biggl [ k_v+\mu _v+\displaystyle \frac{\mu _h^2\mu _v b_1[R_0^2-1]}{b_2}\biggr ],\\ a_6= & {} \displaystyle \frac{\mu _h^2\mu _v b_1[R_0^2-1]}{ b_2},\\ b_1= & {} k_v+\mu _v,\\ b_2= & {} k_v(L+\mu _h)+\mu _h\mu _v,\\ b_3= & {} \alpha _h\mu _hW+k\mu _v\beta \end{aligned}$$

The characteristic equation of $J(E^*)$ is as

$$\begin{aligned} \lambda ^5+\lambda ^4 \alpha +\lambda ^3 n_2+\lambda ^2 n_3+ \lambda n_4+n_5 = 0 \end{aligned}$$

(21)

where,

$$\begin{aligned} \begin{aligned} n_1&= [a_1+a_5+k+\beta +\mu _v]\\ n_2&= [a_1a_5+a_1k+a_5k+a_6k_v+a_1\beta -a_5\beta +k\beta +a_1\mu _v\\&\quad +a_5\mu _v+k\mu _v+\beta \mu _v]\\ n_3&= [a_1a_5k+a_1a_6k_v+a_6kk_v+a_1a_5\beta +a_1k \beta +a_5k\beta \\&\quad +a_6k_\beta +a_1a_5\mu _v+a_1k\mu _v+a_5k\mu _v\\&\quad +a_1\beta \mu _v+a_5\beta \mu _v+k\beta \mu _v] \\ n_4&= [a_1a_6kk_v -a_3a_4k_v\alpha _h+a_1a_5k\beta +a_1a_6k_v\beta +a_6kk_v\beta \\&\quad +a_1a_5k\mu _v+a_1a_5\beta \mu _v+a_1k\beta \mu _v+a_5k\beta \mu _v]\\ n_5&= [a_1k\beta (a_6k_v+a_5\mu _v)-\alpha _hk_va_3a_4(a_1-a_2)] \end{aligned} \end{aligned}$$

According to Routh–Hurwitz criterion followed in [4, 37, 38], we have the following associated conditions,

$$\begin{aligned} D_1= & {} n_1>0, \quad D_2 = \left| \begin{array}{cc} n_1&{}n_3\\ 1&{}n_2 \end{array} \right|>0, \quad D_3= \left| \begin{array}{ccc} n_1&{}n_3&{}n_5\\ 1&{}n_2 &{}n_4\\ 0&{}n_1&{}n_3\\ \end{array}\right|>0\\ D_4= & {} \left| \begin{array}{cccc} n_1&{}n_3&{}n_5&{}0\\ 1&{}n_2 &{}n_4&{}0\\ 0&{}n_1&{}n_3&{}n_5\\ 0&{}1&{}n_2&{}n_4 \end{array} \right|>0 \quad D_5= \left| \begin{array}{ccccc} n_1&{}n_3&{}n_5&{}0&{}0\\ 1&{}n_2 &{}n_4&{}0&{}0\\ 0&{}n_1&{}n_3&{}n_5&{}0\\ 0&{}1&{}n_2&{}n_4 &{}0\\ 0&{}0&{}n_1&{}n_3&{}n_5 \end{array} \right| >0 \end{aligned}$$

As followed by $n_i >0$ for all $i =1,2,3,4,5$ and the relation $n_1>0,n_2>0,n_3>0,n_4>0,n_5>0$, $n_1n_2n_3>n_3^2+n_1^2n_4$, $(n_1n_4-n_5)(n_1n_2n_3-n_3^2-n_1^2n_4) > n_5(n_1n_2-n_3)^2+n_1n_5^2$ is satisfied when $R_0>1$. Hence, the equilibrium point $E^*$ is locally asymptotically stable. Which complete the proof. $\square$

Basic Reproduction Number $R_0$ With Model Parameters

Figures 4 and 5 are simulated to observe the impacts of model parameters on the basic reproduction number. Figure 4a describes the relation between $R_0$, $\alpha$, and $b^\alpha$, which suggests that when level of memory increases $(\alpha \rightarrow 0)$, $b^{\alpha }$ increases and $R_0 \propto b^{\alpha }$. When biting rate increases, basic reproduction number $R_0$ also increases while $R_0$ decreases with the decrease in $\alpha$ (Fig. 4b). The variation in the value of $R_0$ versus the transmission rate of host $\beta _h$ and recovery rate $\gamma _h$ is shown in Fig. 5a. $R_0$ increases with increase in $\beta _h$ and $R_0$ decreases with increase in $\gamma _h$. From Fig. 5b the relation of $R_0$, transmission rate of vector $\beta _v$ and host incubation rate $\alpha _h$ is observed. The figures show that $R_0$ can be effectively reduced or increased with respective change in parameters $\beta _v$ and $\alpha _h$.

Fig. 4

Relation between a $R_0, \alpha , b^{\alpha }$, b $R_0, b, \alpha$

Fig. 5

Relation between a $R_0, \gamma _h, \beta _h$ and b $R_0, \alpha _h, \beta _v$

Numerical Results and Discussion

There are different numerical methods discussed in [28, 33, 41, 69] for the solution of the fractional order system of equation. The simulation technique used for the model (11) is the Euler’s method, which can be expressed as;

Consider the initial value problem

$$\begin{aligned} D_{t}^{\alpha }\theta (t) = l(t,\theta (t)) ,\quad q\le t\le r, \qquad \theta (q)= \theta _0 \end{aligned}$$

(22)

where, $t_i = q+ih$, $i = 0,1,2,3,\ldots ,n$ and $h = \frac{r-q}{n}$. The Euler’s method for (22) is,

$$\begin{aligned} \theta (t_{i+1})= \theta (t_i)+\frac{h^{\alpha }}{\Gamma (\alpha +1)}l(t_i,\theta (t_i)) \end{aligned}$$

(23)

Applying (23) to the model Eq. (11) we can write the equations for all $i = 1,2,\ldots ,n-1$, $t>0$ as;

$$\begin{aligned} {} \begin{aligned} s_h(t_{i+1})&=s_h(t_i)+ \frac{h^{\alpha }}{\Gamma (\alpha +1)}\biggl ( \mu _h(1-s_h(t_i))-Ls_h(t_i)i_v(t_i)\biggr )\\ e_h(t_{i+1})&=e_h(t_i)+ \frac{h^{\alpha }}{\Gamma (\alpha +1)}\biggl ( L s_h(t_i)i_v(t_i)-(\alpha _h+\mu _h) e_h(t_i)\biggr )\\ i_h(t_{i+1})&=i_h(t_i)+ \frac{h^{\alpha }}{\Gamma (\alpha +1)}\biggl ( \alpha _he_h(t_i)-(\gamma _h+\mu _h)i_h(t_i)\biggr )\\ e_v(t_{i+1})&=e_v(t_i)+ \frac{h^{\alpha }}{\Gamma (\alpha +1)}\biggl ( Wi_h(t_i)(1-e_v(t_i)-i_v(t_i))-(\mu _v+k_v)e_v(t_i)\biggr )\\ i_v(t_{i+1})&=i_v(t_i)+ \frac{h^{\alpha }}{\Gamma (\alpha +1)}\biggl ( k_ve_v(t_i)-\mu _v i_v(t_i)\biggr )\\ \hbox {with}&s_h(t_0) = sh0, \quad e_h(t_0) =e_h0, \quad i_h(t_0)=i_h0, \quad e_v(t_0)=e_v0,\quad i_v(t_0)= i_v0 \end{aligned} \end{aligned}$$

(24)

Fig. 6

a Fractional-order model validation, b simulation of $s_h,e_h, i_h, e_v,i_v$ at $\alpha =0.92$

For the numerical simulation, We have taken a 32 week’s data of nepal from July 2019 to December 2019. In this year, monsoon started from March, so the dengue cases were reported to appear from May affecting over 68 districts out of 77 districts of Nepal [43]. Around 97% dengue cases in Nepal are from Terai and mid-mountain region [23, 57]. According to Central Bureau of Statistics 2011 [10], the population size of Nepal is 26.5 million and around 51% population are living in Terai region. So, 20 million peoples are considered as a susceptible population for dengue cases. $\frac{1}{\mu _h}$ and $\frac{1}{\mu _v}$ are respectively the maximum life span of host and vector population taken as $\frac{1}{365 \times 70}$ and $\frac{1}{ 50}$ per day respectively [7, 50]. The vector incubation rate $k_v = \frac{1}{15}$ per day is taken for simulations [7, 55]. The parameters value taken from Table 2 and the initial values are taken according to available data of Nepal [40].

Fig. 7

Numerical simulation for the model (11) by using the Caputo derivative for $(\alpha =1,0.98,0.95,0.92,0.9)$

Figure 6a, presents the solution of classical model and the fractional-order model taking real infectious disease cases data of Nepal. This shows that the fractional order system fit better than the classical model system when the memory level $\alpha = 0.92$. The numerical simulations of $s_h,e_h, i_h, e_v,i_v$ are displayed in Fig. 6b for $\alpha =0.92$. When the suspectible humans come in contact with the infectious mosquito, they become infected. Then the suspectible population size decreases and the infected (exposed) population size starts to increase. This infected population size decreases after attaining its peak as the infected (exposed) people become infectious showing the symptoms of diseases and some infected people may die due to the natural cause. The infectious population size initially increases and the population size decreases later, due to recovery and natural death. The similar dynamics can be observed in the mosquito population (Fig. 6b).

Figure 7a–e are simulated with different values of $\alpha$ taking time in weeks and keeping other parameters constant. With the change in $\alpha$ there is a significant change in the disease dynamics. Interestingly, it is observed that $s_h$ drops rapidly in short period of time with the decrease in the values of $\alpha$ (Fig. 7a). There is noticeable variation in disease transmission with the change in the different values of $\alpha$. $e_h$ and $i_h$ also complete the chain of infection with increase value of the memory. Similar, dynamics of the populations can be observed with small change of memory $\alpha$. It is observed that the variation of fractional order $\alpha$ has a great influence on the infection level of dengue in both vector and host populations.

Conclusion

Fractional-order calculus has wide applications in real life problems. Nowadays, this calculus is being used in epidemic diseases modeling to obtain better results. Fractional-order derivative is used in the classical integer model (SEIR-SEI). The theoretical and epidemiological aspects of the dynamical behaviour of the diseases are studied in detail using the fractional-order system. The disease-free equilibrium is seen locally asymptotically stable whenever the associated basic reproduction number $R_0<1$, and the endemic equilibrium is observed to be locally asymptotically stable whenever $R_0>1$. We obtained feasible results for the dynamics of dengue infection with the variation in the memory index $\alpha$. Present study suggests that index of the memory has a logical effects for the system. The fractional-order model can explore the dengue epidemic disease transmission more accurately rather than the integer-order model under an appropriate choice of memory level. The transformation in fractional-order model with a small change in $\alpha$ produces a large change in the transmission dynamics. From the study of data structure of infectious cases, overall model dynamics shows that $R_0 =3.26$, and we observed that before July $R_0$ is less than unity, August–September $R_0$ is greater than unity where infections cases is in peak and after October $R_0$ is less than unity. This is due to the lack of preventive measures in society and a seasonal behaviours (temperature, rainfall). So, these behaviours can be introduced in the future work for an appropriate study of dengue disease spread in Nepal.